Što znači sustav linearnih jednadžbi? Definicije, pojmovi, oznake
Linearna jednadžba se zove homogena ako je njegov presjek nula, a nehomogen u suprotnom. Sustav koji se sastoji od homogene jednadžbe, naziva se homogenim i ima opći oblik:
Očito je da je svaki homogeni sustav konzistentan i ima nulto (trivijalno) rješenje. Prema tome, za homogene sustave linearne jednadžbečesto se mora tražiti odgovor na pitanje o postojanju rješenja različitih od nule. Odgovor na ovo pitanje može se formulirati kao sljedeći teorem.
Teorema . Homogen sustav linearnih jednadžbi ima rješenje različito od nule ako i samo ako mu je rang manje od broja nepoznato .
Dokaz: Pretpostavimo da sustav čiji je rang jednak ima rješenje različito od nule. Očito, ne prelazi . U slučaju da sustav ima jedinstveno rješenje. Budući da sustav homogenih linearnih jednadžbi uvijek ima nulto rješenje, upravo će nulto rješenje biti to jedinstveno rješenje. Dakle, rješenja različita od nule moguća su samo za .
Korolar 1 : Homogen sustav jednadžbi, u kojem je broj jednadžbi manji od broja nepoznanica, uvijek ima rješenje različito od nule.
Dokaz: Ako sustav jednadžbi ima, tada rang sustava ne prelazi broj jednadžbi, tj. . Dakle, uvjet je zadovoljen i stoga sustav ima rješenje različito od nule.
Posljedica 2 : Homogen sustav jednadžbi s nepoznanicama ima rješenje različito od nule ako i samo ako je njegova determinanta nula.
Dokaz: Pretpostavimo sustav linearnih homogenih jednadžbi čija matrica s determinantom ima rješenje različito od nule. Tada, prema dokazanom teoremu, , što znači da je matrica degenerirana, tj. .
Kronecker-Capellijev teorem: SLE je konzistentan ako i samo ako je rang matrice sustava jednako rangu proširena matrica ovog sustava. Sustav ur-th naziva se kompatibilnim ako ima barem jedno rješenje.Homogeni sustav linearnih algebarske jednadžbe .
Sustav od m linearnih jednadžbi s n varijabli naziva se sustavom linearnih homogenih jednadžbi ako su svi slobodni članovi jednaki 0. Sustav linearnih homogenih jednadžbi uvijek je kompatibilan, jer uvijek ima barem nulto rješenje. Sustav linearnih homogenih jednadžbi ima rješenje različito od nule ako i samo ako je rang njegove matrice koeficijenata kod varijabli manji od broja varijabli, tj. za rang A (n. Bilo koja linearna kombinacija
rješenja sustava linija. homogena ur-ii je također rješenje za ovaj sustav.
Sustav linearno neovisnih rješenja e1, e2,…,ek naziva se fundamentalnim ako je svako rješenje sustava linearna kombinacija rješenja. Teorem: ako je rang r matrice koeficijenata pri varijable sustava linearne homogene jednadžbe manji od broja varijabli n, tada se svaki temeljni sustav rješenja sustava sastoji od n-r rješenja. Zato zajednička odluka lin sustavi. singl ur-th ima oblik: c1e1+c2e2+…+ckek, gdje je e1, e2,…, ek bilo koji temeljni sustav rješenja, c1, c2,…,ck proizvoljni brojevi i k=n-r. Opće rješenje sustava od m linearnih jednadžbi s n varijabli jednako je zbroju
opće rješenje sustava koje mu odgovara je homogeno. linearne jednadžbe i proizvoljno partikularno rješenje ovog sustava.
7. Linearni prostori. Potprostori. Osnova, dimenzija. Linearna ljuska. Linearni prostor naziva se n-dimenzionalni, ako sadrži sustav linearnih nezavisni vektori, i bilo koji sustav iz više vektora je linearno ovisan. Broj je pozvan dimenzija (broj dimenzija) linearni prostor i označava se sa . Drugim riječima, dimenzija prostora je najveći broj linearno neovisnih vektora u tom prostoru. Ako takav broj postoji, onda se kaže da je prostor konačnodimenzionalan. Ako za bilo koji prirodni broj n u prostoru postoji sustav koji se sastoji od linearno neovisnih vektora, tada se takav prostor naziva beskonačnodimenzionalnim (pisati: ). U nastavku će se, osim ako nije drugačije navedeno, razmatrati konačnodimenzionalni prostori.
Osnova n-dimenzionalnog linearnog prostora je uređen skup linearno neovisnih vektora ( bazni vektori).
Teorem 8.1 o ekspanziji vektora po bazi. Ako je baza n-dimenzionalnog linearnog prostora, tada se svaki vektor može prikazati kao linearna kombinacija baznih vektora:
V=v1*e1+v2*e2+…+vn+en
i, štoviše, na jedinstven način, tj. koeficijenti su jednoznačno određeni. Drugim riječima, bilo koji prostorni vektor može se proširiti u bazi i, štoviše, na jedinstven način.
Doista, dimenzija prostora je . Sustav vektora je linearno neovisan (ovo je baza). Nakon spajanja na bazu bilo kojeg vektora , dobivamo linearno ovisan sustav(budući da se ovaj sustav sastoji od vektora n-dimenzionalni prostor). Po svojstvu 7 linearno zavisnih i linearno neovisnih vektora, dobivamo zaključak teorema.
Gaussova metoda ima brojne nedostatke: nemoguće je znati je li sustav konzistentan ili nije dok se ne izvrše sve transformacije potrebne u Gaussovoj metodi; Gaussova metoda nije prikladna za sustave sa slovnim koeficijentima.
Razmotrite druge metode za rješavanje sustava linearnih jednadžbi. Ove metode koriste koncept ranga matrice i smanjuju rješenje bilo kojeg zglobni sustav na rješenje sustava na koji vrijedi Cramerovo pravilo.
Primjer 1 Pronađite opće rješenje sljedeći sustav linearne jednadžbe korištenjem temeljnog sustava rješenja reduciranog homogenog sustava i partikularnog rješenja nehomogenog sustava.
1. Izrađujemo matricu A i proširena matrica sustava (1)


2. Istražite sustav (1) za kompatibilnost. Da bismo to učinili, pronalazimo rangove matrica A i https://pandia.ru/text/78/176/images/image006_90.gif" width="17" height="26 src=">). Ako se pokaže da , tada sustav (1) nekompatibilan. Ako to dobijemo , onda je ovaj sustav dosljedan i mi ćemo to riješiti. (Studija dosljednosti temelji se na Kronecker-Capellijevom teoremu).
a. Pronašli smo rA.
Pronaći rA, razmotrit ćemo sukcesivno različite minore prvog, drugog itd. reda matrice A i maloljetnici koji ih okružuju.
M1=1≠0 (uzimamo 1 slijeva gornji kut matrice A).
Obrubljivanje M1 drugi red i drugi stupac ove matrice.  . Nastavljamo do granice M1 drugi redak i treći stupac..gif" width="37" height="20 src=">. Sada obrubljujemo minor koji nije nula M2′ druga narudžba.
. Nastavljamo do granice M1 drugi redak i treći stupac..gif" width="37" height="20 src=">. Sada obrubljujemo minor koji nije nula M2′ druga narudžba.
Imamo:  (jer su prva dva stupca ista)
(jer su prva dva stupca ista)
 (jer su drugi i treći red proporcionalni).
(jer su drugi i treći red proporcionalni).
Vidimo to rA=2, A - osnovni mol matrice A.
b. Pronašli smo .
Dovoljno osnovni minor M2′ matrice A rub sa stupcem slobodnih članova i svim redovima (imamo samo zadnji red).
 . Iz ovoga proizlazi da M3′′ ostaje bazni minor matrice https://pandia.ru/text/78/176/images/image019_33.gif" width="168 height=75" height="75"> (2)
. Iz ovoga proizlazi da M3′′ ostaje bazni minor matrice https://pandia.ru/text/78/176/images/image019_33.gif" width="168 height=75" height="75"> (2)
Jer M2′- baza minor matrice A sustava (2) , onda je ovaj sustav ekvivalentan sustavu (3) , koji se sastoji od prve dvije jednadžbe sustava (2) (za M2′ nalazi se u prva dva reda matrice A).
 (3)
(3)
Budući da je osnovni minor https://pandia.ru/text/78/176/images/image021_29.gif" width="153" height="51"> (4)
U ovom sustavu dvije slobodne nepoznanice ( x2 I x4 ). Zato FSR sustava (4) sastoji se od dva rješenja. Da bismo ih pronašli, dodjeljujemo slobodne nepoznanice (4) vrijednosti prije svega x2=1 , x4=0 , i onda - x2=0 , x4=1 .
Na x2=1 , x4=0 dobivamo:
 .
.
Ovaj sustav već ima jedina stvar rješenje (može se pronaći Cramerovim pravilom ili bilo kojom drugom metodom). Oduzimanjem prve jednadžbe od druge jednadžbe dobivamo:
Njezina će odluka biti x1= -1 , x3=0 . S obzirom na vrijednosti x2 I x4 , koje smo dali, dobivamo prve temeljna odluka sustava (2) : .
Sada stavljamo (4) x2=0 , x4=1 . Dobivamo:
 .
.
Ovaj sustav rješavamo koristeći Cramerov teorem:

 .
.
Dobivamo drugo temeljno rješenje sustava (2) : .
Rješenja β1 , β2 i našminkati se FSR sustava (2) . Tada će njegovo opće rješenje biti
γ= C1 β1+S2β2=S1(-1, 1, 0, 0)+S2(5, 0, 4, 1)=(-S1+5S2, S1, 4S2, S2)
Ovdje C1 , C2 su proizvoljne konstante.
4. Pronađite jedan privatna riješenje heterogeni sustav(1) . Kao u paragrafu 3 , umjesto sustava (1) razmotrite ekvivalentni sustav (5) , koji se sastoji od prve dvije jednadžbe sustava (1) .
 (5)
(5)
Slobodne nepoznanice prenosimo na desne strane x2 I x4.
 (6)
(6)
Dajmo besplatne nepoznanice x2 I x4 proizvoljne vrijednosti, npr. x2=2 , x4=1 i uključite ih u (6) . Uhvatimo sustav

Ovaj sustav ima jedinstveno rješenje (jer njegova determinanta M2′0). Rješavajući ga (koristeći Cramerov teorem ili Gaussovu metodu), dobivamo x1=3 , x3=3 . S obzirom na vrijednosti slobodnih nepoznanica x2 I x4 , dobivamo partikularno rješenje nehomogenog sustava(1)α1=(3,2,3,1).
5. Sada ostaje napisati opće rješenje α nehomogenog sustava(1) : jednako je zbroju privatna odluka ovaj sustav i opće rješenje njegovog svedenog homogenog sustava (2) :
α=α1+γ=(3, 2, 3, 1)+(‑S1+5S2, S1, 4S2, S2).
To znači:  (7)
(7)
6. Ispitivanje. Da provjerite jeste li ispravno riješili sustav (1) , trebamo opće rješenje (7) zamijeniti u (1) . Ako svaka jednadžba postane identitet ( C1 I C2 treba uništiti), tada je rješenje pronađeno ispravno.
Mi ćemo zamijeniti (7) npr. samo u posljednjoj jednadžbi sustava (1) (x1 + x2 + x3 ‑9 x4 =‑1) .
Dobivamo: (3–S1+5S2)+(2+S1)+(3+4S2)–9(1+S2)=–1
(S1–S1)+(5S2+4S2–9S2)+(3+2+3–9)=–1
Gdje je -1=-1. Imamo identitet. To radimo sa svim ostalim jednadžbama sustava (1) .
Komentar. Provjera je obično prilično glomazna. Možemo preporučiti sljedeću "djelomičnu provjeru": u cjelokupnom rješenju sustava (1) dodijeliti neke vrijednosti proizvoljnim konstantama i zamijeniti rezultirajuće određeno rješenje samo u odbačene jednadžbe (tj. u one jednadžbe iz (1) koji nisu uključeni u (5) ). Ako dobijete identitete, onda vjerojatnije, rješenje sustava (1) pronađeno ispravno (ali takva provjera ne daje potpuno jamstvo ispravnosti!). Na primjer, ako je u (7) staviti C2=- 1 , C1=1, tada dobivamo: x1=-3, x2=3, x3=-1, x4=0. Zamjenom u posljednju jednadžbu sustava (1) imamo: - 3+3 - 1 - 9∙0= - 1 , tj. –1=–1. Imamo identitet.
Primjer 2 Pronađite opće rješenje sustava linearnih jednadžbi (1) , izražavajući glavne nepoznanice u terminima slobodnih.
Riješenje. Kao u primjer 1, sastaviti matrice A i https://pandia.ru/text/78/176/images/image010_57.gif" width="156" height="50"> ovih matrica. Sada ostavljamo samo one jednadžbe sustava (1) , čiji su koeficijenti uključeni u ovaj osnovni minor (tj. imamo prve dvije jednadžbe) i razmatramo sustav koji se od njih sastoji, što je ekvivalentno sustavu (1).
Prenesimo slobodne nepoznanice na desne strane ovih jednadžbi.
sustav (9) rješavamo Gaussovom metodom, smatrajući desne dijelove slobodnim članovima.
https://pandia.ru/text/78/176/images/image035_21.gif" width="202 height=106" height="106">

opcija 2.

https://pandia.ru/text/78/176/images/image039_16.gif" width="192" height="106 src=">

Opcija 4.
https://pandia.ru/text/78/176/images/image042_14.gif" width="172" height="80">
Opcija 5.
https://pandia.ru/text/78/176/images/image044_12.gif" width="179 height=106" height="106">
Opcija 6.
https://pandia.ru/text/78/176/images/image046_11.gif" width="195" height="106">
Sustav linearnih jednadžbi u kojem su svi slobodni članovi jednaki nuli naziva se homogena :
Svaki homogeni sustav uvijek je konzistentan, budući da uvijek jest nula (trivijalno ) riješenje. Postavlja se pitanje pod kojim uvjetima će homogeni sustav imati netrivijalno rješenje.
Teorem 5.2.Homogeni sustav ima netrivijalno rješenje ako i samo ako je rang temeljne matrice manji od broja njegovih nepoznanica.
Posljedica. Kvadratni homogeni sustav ima netrivijalno rješenje ako i samo ako determinanta glavne matrice sustava nije jednaka nuli.
Primjer 5.6. Odredite vrijednosti parametra l za koje sustav ima netrivijalna rješenja i pronađite ta rješenja:

Riješenje. Ovaj sustav će imati netrivijalno rješenje kada je determinanta glavne matrice jednaka nuli:
Dakle, sustav je netrivijalan kada je l=3 ili l=2. Za l=3, rang glavne matrice sustava je 1. Zatim, ostavljajući samo jednu jednadžbu i pretpostavljajući da g=a I z=b, dobivamo x=b-a, tj.
Za l=2, rang glavne matrice sustava je 2. Zatim, birajući kao osnovni minor:
![]()
dobivamo pojednostavljeni sustav
Odavde to nalazimo x=z/4, y=z/2. Pretpostavljajući z=4a, dobivamo
Skup svih rješenja homogenog sustava ima vrlo važan linearno svojstvo : ako je X stupaca 1 i X 2 - rješenja homogenog sustava AX = 0, zatim svaka njihova linearna kombinacija a x 1+b x 2 također će biti rješenje ovog sustava. Doista, jer SJEKIRA 1 = 0 I SJEKIRA 2 = 0 , To A(a x 1+b x 2) = a SJEKIRA 1+b SJEKIRA 2 = a · 0 + b · 0 = 0. Zbog ovog svojstva, ako linearni sustav ima više od jednog rješenja, tada će tih rješenja biti beskonačno mnogo.
Linearno nezavisni stupci E 1 , E 2 , E k, koja su rješenja homogenog sustava, naziva se temeljni sustav odluke homogeni sustav linearnih jednadžbi ako se opće rješenje tog sustava može napisati kao linearna kombinacija ovih stupaca:
Ako homogeni sustav ima n varijable, a rang glavne matrice sustava je jednak r, To k = n-r.
Primjer 5.7. Nađite temeljni sustav rješenja sljedećeg sustava linearnih jednadžbi:

Riješenje. Nađite rang glavne matrice sustava:

Dakle, skup rješenja ovog sustava jednadžbi tvori linearni podprostor dimenzije n - r= 5 - 2 = 3. Kao osnovni minor biramo
![]() .
.
Zatim, ostavljajući samo osnovne jednadžbe (ostatak će biti linearna kombinacija tih jednadžbi) i osnovne varijable (ostale, tzv. slobodne varijable, prenosimo udesno), dobivamo pojednostavljeni sustav jednadžbi:

Pretpostavljajući x 3 = a, x 4 = b, x 5 = c, pronašli smo
![]() ,
, ![]() .
.
Pretpostavljajući a= 1, b=c= 0, dobivamo prvo osnovno rješenje; pretpostavljajući b= 1, a = c= 0, dobivamo drugo osnovno rješenje; pretpostavljajući c= 1, a = b= 0, dobivamo treće osnovno rješenje. Kao rezultat, normalan temeljni sustav rješenja poprima oblik
Koristeći temeljni sustav, opće rješenje homogenog sustava može se napisati kao
x = aE 1 + biti 2 + cE 3 . a
Napomenimo neka svojstva rješenja nehomogenog sustava linearnih jednadžbi AX=B i njihov odnos s pripadajućim homogenim sustavom jednadžbi AX = 0.
Opće rješenje nehomogenog sustavajednak je zbroju općeg rješenja odgovarajućeg homogenog sustava AX = 0 i proizvoljnog partikularnog rješenja nehomogenog sustava. Doista, neka Y 0 je proizvoljno partikularno rješenje nehomogenog sustava, tj. AY 0 = B, I Y je opće rješenje nehomogenog sustava, tj. AY=B. Oduzimajući jednu jednakost od druge, dobivamo
A(Y-Y 0) = 0, tj. Y-Y 0 je opće rješenje odgovarajućeg homogenog sustava SJEKIRA=0. Stoga, Y-Y 0 = x, ili Y=Y 0 + x. Q.E.D.
Neka heterogeni sustav ima oblik AX = B 1 + B 2 . Tada se opće rješenje takvog sustava može napisati kao X = X 1 + x 2 , gdje je AX 1 = B 1 i AX 2 = B 2. Ovo svojstvo izražava univerzalno svojstvo bilo kojeg linearnog sustava općenito (algebarskog, diferencijalnog, funkcionalnog itd.). U fizici se to svojstvo naziva princip superpozicije, u elektrotehnici i radiotehnici - princip prekrivanja. Na primjer, u teoriji linearnog električni krugovi struja u bilo kojem krugu može se dobiti kao algebarski zbroj struje uzrokovane svakim izvorom energije zasebno.
Matrični podaci
Nađi: 1) aA - bB,
Riješenje: 1) Nalazimo sekvencijalno, koristeći pravila za množenje matrice brojem i zbrajanje matrica ..

2. Nađi A*B ako

Riješenje: Koristite pravilo množenja matrice

Odgovor: 
3. Za zadana matrica nađi minor M 31 i izračunaj determinantu.

Riješenje: Minor M 31 je determinanta matrice koja se dobiva iz A
nakon brisanja retka 3 i stupca 1. Pronađite

1*10*3+4*4*4+1*1*2-2*4*10-1*1*4-1*4*3 = 0.
Transformirajmo matricu A bez promjene njene determinante (napravimo nule u retku 1)
| -3*, -, -4* | |||
| -10 | -15 | ||
| -20 | -25 | ||
| -4 | -5 |
Sada izračunavamo determinantu matrice A širenjem duž retka 1

Odgovor: M 31 = 0, detA = 0
Rješavanje pomoću Gaussove i Cramerove metode.
2x 1 + x 2 + x 3 = 2
x 1 + x 2 + 3x 3 = 6
2x1 + x2 + 2x3 = 5
Riješenje: Provjerimo

Možete koristiti Cramerovu metodu

Rješenje sustava: x 1 = D 1 / D = 2, x 2 = D 2 / D = -5, x 3 = D 3 / D = 3
Primjenjujemo Gaussovu metodu.
Proširenu matricu sustava reduciramo na trokutasti oblik.
Radi praktičnosti izračuna, mijenjamo retke:
Pomnožite 2. red s (k = -1 / 2 = -1 / 2 ) i dodajte trećem:
| 1 / 2 | 7 / 2 |
Pomnožite prvi red s (k = -2 / 2 = -1 ) i dodajte 2.:
Sada se izvorni sustav može napisati kao:
x 1 = 1 - (1/2 x 2 + 1/2 x 3)
x 2 = 13 - (6x 3)
Iz 2. retka izražavamo
Iz 1. retka izražavamo
Rješenje je isto.
Odgovor: (2; -5; 3)
Pronađite opće rješenje sustava i FSR
13x 1 - 4x 2 - x 3 - 4x 4 - 6x 5 = 0
11x 1 - 2x 2 + x 3 - 2x 4 - 3x 5 = 0
5x 1 + 4x 2 + 7x 3 + 4x 4 + 6x 5 = 0
7x 1 + 2x 2 + 5x 3 + 2x 4 + 3x 5 = 0
Riješenje: Primijenite Gaussovu metodu. Proširenu matricu sustava reduciramo na trokutasti oblik.
| -4 | -1 | -4 | -6 | |
| -2 | -2 | -3 | ||
| x 1 | x2 | x 3 | x4 | x5 |
Pomnožite 1. red s (-11). Pomnožite 2. red s (13). Dodajmo 2. redak 1.:
| -2 | -2 | -3 | ||
Pomnožite 2. red s (-5). Pomnožite 3. red s (11). Dodajmo 3. redak 2.:
Pomnožite 3. red s (-7). Pomnožite 4. red s (5). Dodajmo 4. redak 3.:
Druga jednadžba je linearna kombinacija ostatka
Odredite rang matrice.
| -18 | -24 | -18 | -27 | |
| x 1 | x2 | x 3 | x4 | x5 |
Istaknuti maloljetnik ima najviši red(od mogućih minora) i razlikuje se od nule (it jednak je proizvodu elementi na obrnutoj dijagonali), pa je rang(A) = 2.
Ovaj minor je osnovni. Sadrži koeficijente za nepoznate x 1, x 2, što znači da su nepoznate x 1, x 2 ovisne (osnovne), a x 3, x 4, x 5 slobodne.
Sustav s koeficijentima ove matrice je ekvivalentan izvornom sustavu i ima oblik:
18x2 = 24x3 + 18x4 + 27x5
7x1 + 2x2 = - 5x3 - 2x4 - 3x5
Metodom eliminacije nepoznanica nalazimo zajednička odluka:
x 2 = - 4 / 3 x 3 - x 4 - 3 / 2 x 5
x 1 = - 1 / 3 x 3
Nalazimo temeljni sustav rješenja (FSR), koji se sastoji od (n-r) rješenja. U našem slučaju n=5, r=2, dakle, temeljni sustav rješenja sastoji se od 3 rješenja, a ta rješenja moraju biti linearno neovisna.
Da bi redovi bili linearno neovisni, potrebno je i dovoljno da rang matrice sastavljene od elemenata redaka bude jednak broju redaka, tj. 3.
Dovoljno je slobodnim nepoznanicama x 3 ,x 4 ,x 5 zadati vrijednosti iz redaka determinante 3. reda različite od nule i izračunati x 1 ,x 2 .
Najjednostavnija determinanta različita od nule je matrica identiteta.
Ali ovdje je prikladnije uzeti
Pomoću općeg rješenja nalazimo:
a) x 3 = 6, x 4 = 0, x 5 = 0 Þ x 1 = - 1/3 x 3 = -2, x 2 = - 4/3 x 3 - x 4 - 3/2 x 5 = - 4 Þ
I FSR odluka: (-2; -4; 6; 0; 0)
b) x 3 = 0, x 4 = 6, x 5 = 0 Þ x 1 = - 1/3 x 3 = 0, x 2 = - 4/3 x 3 - x 4 - 3/2 x 5 = - 6 Þ
Odluka II FSR: (0; -6; 0; 6; 0)
c) x 3 = 0, x 4 = 0, x 5 = 6 Þ x 1 = - 1/3 x 3 = 0, x 2 = - 4/3 x 3 - x 4 - 3/2 x 5 = -9 Þ
III FSR odluka: (0; - 9; 0; 0; 6)
Þ FSR: (-2; -4; 6; 0; 0), (0; -6; 0; 6; 0), (0; - 9; 0; 0; 6)
6. Zadano je: z 1 \u003d -4 + 5i, z 2 \u003d 2 - 4i. Nađi: a) z 1 - 2z 2 b) z 1 z 2 c) z 1 / z 2
Riješenje: a) z 1 – 2z 2 = -4+5i+2(2-4i) = -4+5i+4-8i = -3i
b) z 1 z 2 = (-4+5i)(2-4i) = -8+10i+16i-20i 2 = (i 2 = -1) = 12 + 26i

Odgovor: a) -3i b) 12+26i c) -1,4 - 0,3i
Homogeni sustav linearnih jednadžbi nad poljem
DEFINICIJA. Temeljni sustav rješenja sustava jednadžbi (1) je neprazan linear neovisni sustav njegovih rješenja, čiji se linearni raspon podudara sa skupom svih rješenja sustava (1).
Imajte na umu da homogeni sustav linearnih jednadžbi koji ima samo nulto rješenje nema temeljni sustav rješenja.
PROPOZICIJA 3.11. Bilo koja dva temeljna sustava rješenja homogenog sustava linearnih jednadžbi sastoje se od isti broj rješenja.
Dokaz. Doista, svaka dva temeljna sustava rješenja homogenog sustava jednadžbi (1) su ekvivalentna i linearno neovisna. Stoga su prema propoziciji 1.12 njihovi rangovi jednaki. Stoga je broj rješenja uključenih u jedan temeljni sustav jednak broju rješenja uključenih u bilo koji drugi temeljni sustav rješenja.
Ako je glavna matrica A homogenog sustava jednadžbi (1) nula, tada je bilo koji vektor iz rješenje sustava (1); u ovom slučaju, svaka zbirka linearno nezavisnih vektora iz je temeljni sustav rješenja. Ako je rang stupca matrice A , tada sustav (1) ima samo jedno rješenje - nulu; stoga u ovom slučaju sustav jednadžbi (1) nema temeljni sustav rješenja.
TEOREM 3.12. Ako je rang glavne matrice homogenog sustava linearnih jednadžbi (1) manji od broja varijabli , tada sustav (1) ima temeljni sustav rješenja koji se sastoji od rješenja.
Dokaz. Ako je rang glavne matrice A homogenog sustava (1) jednak nuli ili , tada je gore pokazano da je teorem točan. Stoga se u nastavku pretpostavlja da Uz pretpostavku , pretpostavit ćemo da su prvi stupci matrice A linearno neovisni. U ovom slučaju, matrica A je redom ekvivalentna reduciranoj stepenasta matrica, a sustav (1) je ekvivalentan sljedećem smanjenom stupnjevitom sustavu jednadžbi:

Lako je provjeriti da svakom sustavu vrijednosti slobodnih varijabli sustava (2) odgovara jedno i samo jedno rješenje sustava (2), a time i sustava (1). Konkretno, samo nulto rješenje sustava (2) i sustava (1) odgovara sustavu nultih vrijednosti.
U sustavu (2) dodijelit ćemo jedan od slobodnih varijabilna vrijednost, jednako 1, a ostatak varijabli - nulte vrijednosti. Kao rezultat toga dobivamo rješenja sustava jednadžbi (2) koje pišemo kao retke sljedeće matrice C:

Sustav redova ove matrice je linearno neovisan. Doista, za sve skalare iz jednakosti
slijedi jednakost
a time i jednakost
Dokažimo da se linearni raspon sustava redaka matrice C podudara sa skupom svih rješenja sustava (1).
Proizvoljno rješenje sustava (1). Zatim vektor
također je rješenje sustava (1), i
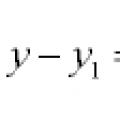 Jednadžbe pravaca i krivulja u ravnini
Jednadžbe pravaca i krivulja u ravnini Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda
Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda Zahvaljujući zarezu Zbog činjenice da u njihovim
Zahvaljujući zarezu Zbog činjenice da u njihovim