Nađite matrice inverzne zadanoj matrici a. Pronalaženje inverzne matrice online

Nalaženje inverzne matrice- problem koji se najčešće rješava na dva načina:

metoda algebarskih sabiranja, u kojoj se traži pronalaženje determinanti i transponiranje matrica;
Gaussova metoda eliminacije, koja zahtijeva elementarne transformacije matrica (zbrajanje redaka, množenje redaka s istim brojem itd.).

Za one posebno znatiželjne, postoje i druge metode, na primjer, metoda linearnih transformacija. U ovoj lekciji ćemo analizirati tri spomenute metode i algoritme za pronalaženje inverzne matrice tim metodama.

inverzna matrica ALI, takva se matrica naziva

ALI
. (1)

inverzna matrica , koji je potrebno pronaći za zadanu kvadratnu matricu ALI, takva se matrica naziva

proizvod kojim se matrice ALI s desne strane je matrica identiteta, tj.
. (1)

Matrica identiteta je dijagonalna matrica u kojoj su svi dijagonalni unosi jednaki jedinici.

Teorema.Za svaku nesingularnu (nesingularnu, nesingularnu) kvadratnu matricu može se naći inverzna matrica, štoviše, samo jedna. Za posebnu (degeneriranu, singularnu) kvadratnu matricu inverzna matrica ne postoji.

Kvadratna matrica se zove neposeban(ili nedegeneriran, nejedninski) ako njegova determinanta nije jednaka nuli, i poseban(ili degenerirati, jednina) ako je njegova determinanta nula.

Inverzna matrica se može pronaći samo za kvadratnu matricu. Naravno, inverzna matrica će također biti kvadratna i istog reda kao i dana matrica. Matrica za koju se može pronaći inverzna matrica naziva se invertibilna matrica.

Za inverzna matrica postoji prikladna analogija s recipročnom vrijednošću broja. Za svaki broj a, koji nije jednak nuli, postoji broj b da je djelo a i b jednako jedan: ab= 1. Broj b naziva se recipročna vrijednost broja b. Na primjer, za broj 7, inverz je broj 1/7, budući da je 7*1/7=1.

Nalaženje inverzne matrice metodom algebarskih sabiranja (union matrica)

Za nesingularnu kvadratnu matricu ALI inverz je matrica

gdje je determinanta matrice ALI, a je matrica pridružena matrici ALI.

Udruženi s kvadratnom matricom A je matrica istog reda čiji su elementi algebarski komplementi odgovarajućih elemenata determinante matrice transponirane u odnosu na matricu A. Dakle, ako

zatim

Algoritam za pronalaženje inverzne matrice metodom algebarskih sabiranja

1. Odredite determinantu ove matrice A. Ako je determinanta jednaka nuli, nalaženje inverzne matrice prestaje, jer je matrica degenerirana i za nju ne postoji inverz.

2. Pronađite matricu transponiranu u odnosu na A.

3. Izračunajte elemente unijske matrice kao algebarske komplemente marite pronađene u koraku 2.

4. Primijenite formulu (2): pomnožite recipročnu vrijednost determinante matrice A, na matricu unije koja se nalazi u koraku 4.

5. Provjerite rezultat dobiven u koraku 4 množenjem ove matrice A na inverznu matricu. Ako je umnožak ovih matrica jednak matrici identiteta, tada je inverzna matrica točno pronađena. U suprotnom ponovno pokrenite postupak rješenja.

Primjer 1 Za matricu

pronađite inverznu matricu.

Riješenje. Za pronalaženje inverzne matrice potrebno je pronaći determinantu matrice ALI. Pravilom trokuta nalazimo:

Prema tome, matrica ALI je nesingularan (nedegeneriran, nesingularan) i za njega postoji inverz.

Pronađimo matricu pridruženu zadanoj matrici ALI.

Nađimo matricu transponiranu u odnosu na matricu A:

Elemente unijske matrice izračunavamo kao algebarske komplemente matrice transponirane u odnosu na matricu A:

Prema tome, matrica konjugirana s matricom A, ima oblik

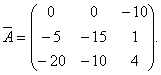
Komentar. Redoslijed izračunavanja elemenata i transpozicije matrice može biti različit. Najprije se mogu izračunati algebarski komplementi matrice A, a zatim transponirati matricu algebarskih komplemenata. Rezultat bi trebali biti isti elementi matrice unije.

Primjenom formule (2) nalazimo matricu inverznu matrici ALI:

Pronalaženje inverzne matrice Gaussovom eliminacijom nepoznanica

Prvi korak za pronalaženje inverzne matrice Gaussovom eliminacijom je dodjeljivanje matrici A matricu identiteta istog reda, odvajajući ih okomitom crtom. Dobivamo dvojnu matricu. Pomnožimo oba dijela ove matrice s , tada dobivamo

Algoritam za pronalaženje inverzne matrice Gaussovom eliminacijom nepoznanica

1. U matricu A dodijeliti matricu identiteta istog reda.

2. Transformirajte dobivenu dualnu matricu tako da se u njenom lijevom dijelu dobije matrica identiteta, tada će se automatski dobiti inverzna matrica u desnom dijelu umjesto matrice identiteta. Matrica A na lijevoj strani pretvara se u matricu identiteta elementarnim transformacijama matrice.

2. Ako se u procesu transformacije matrice A u matricu identiteta u bilo kojem retku ili u bilo kojem stupcu bit će samo nule, tada je determinanta matrice jednaka nuli, pa je stoga matrica A bit će degenerirana i nema inverznu matricu. U tom slučaju prestaje daljnje pronalaženje inverzne matrice.

Primjer 2 Za matricu

pronađite inverznu matricu.

a mi ćemo ga transformirati tako da se matrica identiteta dobije na lijevoj strani. Započnimo transformaciju.

Pomnožimo prvi redak lijeve i desne matrice s (-3) i dodamo ga u drugi red, a zatim pomnožimo prvi red s (-4) i dodamo ga u treći red, tada dobivamo

Kako, ako je moguće, ne bi bilo frakcijskih brojeva tijekom sljedećih transformacija, prvo ćemo stvoriti jedinicu u drugom redu na lijevoj strani dualne matrice. Da biste to učinili, pomnožite drugi redak s 2 i oduzmite treći red od njega, a zatim dobivamo

Dodajmo prvi red drugom, a zatim pomnožimo drugi red s (-9) i dodamo ga trećem redu. Onda dobivamo

Zatim treći red podijelite s 8

Pomnožite treći red s 2 i dodajte ga drugom redu. Ispada:

Zamjenom mjesta drugog i trećeg retka konačno dobivamo:

Vidimo da je matrica identiteta dobivena na lijevoj strani, dakle, inverzna matrica je dobivena na desnoj strani. Na ovaj način:

Točnost izračuna možete provjeriti množenjem izvorne matrice s pronađenom inverznom matricom:

Rezultat bi trebala biti inverzna matrica.

Primjer 3 Za matricu

pronađite inverznu matricu.

Riješenje. Sastavljanje dualne matrice

i mi ćemo ga transformirati.

Prvi red pomnožimo s 3, a drugi s 2 i oduzmemo od drugog, zatim prvi red pomnožimo s 5, a treći s 2 i oduzmemo od trećeg retka, tada dobijemo

Prvi red pomnožimo sa 2 i dodamo drugom, a zatim od trećeg reda oduzmemo drugi i dobijemo

Vidimo da su se u trećem retku s lijeve strane svi elementi pokazali jednakima nuli. Dakle, matrica je degenerirana i nema inverznu matricu. Zaustavljamo daljnje pronalaženje reversne marije.

Metode za pronalaženje inverzne matrice, . Razmotrimo kvadratnu matricu

Označimo Δ = det A.

Kvadratna matrica A naziva se nedegeneriran, ili neposeban ako je njegova determinanta različita od nule, i degenerirati, ili poseban, akoΔ = 0.

Kvadratna matrica B postoji za kvadratnu matricu A istog reda ako je njihov umnožak A B = B A = E, gdje je E matrica identiteta istog reda kao matrice A i B.

Teorema . Da bi matrica A imala inverznu matricu, potrebno je i dovoljno da njezina determinanta bude različita od nule.

Inverzna matrica matrici A, označena s A- 1 pa je B = A - 1 a izračunava se po formuli

, (1)

gdje su A i j - algebarski komplementi elemenata a i j matrice A..

Izračunavanje A -1 formulom (1) za matrice visokog reda vrlo je naporno, pa je u praksi zgodno pronaći A -1 pomoću metode elementarnih transformacija (EP). Bilo koja nesingularna matrica A može se reducirati EP-om samo stupaca (ili samo redaka) na matricu identiteta E. Ako se EP-ovi izvedeni na matrici A primjenjuju istim redoslijedom na matricu identiteta E, tada je rezultat inverzna matrica. Pogodno je izvesti EP na matricama A i E istovremeno, upisujući obje matrice jednu do druge kroz liniju. Još jednom napominjemo da kada se traži kanonski oblik matrice, da bi se on pronašao, mogu se koristiti transformacije redaka i stupaca. Ako trebate pronaći inverznu matricu, trebali biste koristiti samo retke ili samo stupce u procesu transformacije.

Primjer 2.10. Za matricu nađi A -1 .

Riješenje.Prvo nalazimo determinantu matrice A
pa inverzna matrica postoji i možemo je pronaći po formuli: , gdje su A i j (i,j=1,2,3) - algebarski komplementi elemenata a i j izvorne matrice.

Gdje .

Primjer 2.11. Metodom elementarnih transformacija pronađite A -1 za matricu: A=.

Riješenje.Izvornoj matrici s desne strane pridružujemo matricu identiteta istog reda: . Uz pomoć elementarnih transformacija stupca, lijevu “polovicu” reduciramo na onu identiteta, istovremeno izvodeći upravo takve transformacije na desnoj matrici.
Da biste to učinili, zamijenite prvi i drugi stupac: ~ . Trećem stupcu dodajemo prvi, a drugom prvi pomnožen s -2: . Od prvog stupca oduzimamo udvostručenu drugu, a od treće - drugu pomnoženu sa 6; . Dodajmo treći stupac prvom i drugom: . Pomnožite zadnji stupac s -1: . Kvadratna matrica dobivena desno od okomite trake je inverzna matrica danoj matrici A. Dakle,
.

U prvom dijelu razmatrana je metoda za pronalaženje inverzne matrice pomoću algebarskih adicija. Ovdje opisujemo drugu metodu za pronalaženje inverznih matrica: korištenje Gaussove i Gauss-Jordanove transformacije. Često se ova metoda pronalaženja inverzne matrice naziva metodom elementarnih transformacija.

Metoda elementarnih transformacija

Za primjenu ove metode zadana matrica $A$ i matrica identiteta $E$ zapisuju se u jednu matricu, tj. tvore matricu oblika $(A|E)$ (ova matrica se također naziva proširena matrica). Nakon toga, uz pomoć elementarnih transformacija izvedenih s redovima proširene matrice, matrica lijevo od retka postaje jedinica, a proširena matrica poprima oblik $\left(E| A^(-1) \right )$. Elementarne transformacije u ovoj situaciji uključuju sljedeće radnje:

Zamjena dva retka.
Množenje svih elemenata niza nekim brojem koji nije nula.
Dodavanje elementima jednog retka odgovarajućih elemenata drugog retka, pomnoženih bilo kojim faktorom.

Ove elementarne transformacije mogu se primijeniti na različite načine. Obično se bira Gaussova metoda ili Gauss-Jordanova metoda. Općenito, Gaussova i Gauss-Jordanova metoda namijenjene su rješavanju sustava linearnih algebarskih jednadžbi, a ne pronalaženju inverznih matrica. Frazu "primjena Gaussove metode za pronalaženje inverzne matrice" ovdje treba shvatiti kao "primjenu operacija svojstvenih Gaussovoj metodi za pronalaženje inverzne matrice."

Numeriranje primjera nastavlja se od prvog dijela. U primjerima se razmatra i uporaba Gaussove metode za pronalaženje inverzne matrice, a u primjerima se analizira uporaba Gauss-Jordanove metode. Treba napomenuti da ako se tijekom rješavanja svi elementi nekog retka ili stupca matrice koji se nalaze prije crte postave na nulu, tada inverzna matrica ne postoji.

Primjer #5

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( array )\desno)$.

U ovom primjeru, inverzna matrica će se pronaći pomoću Gaussove metode. Proširena matrica, koja je općenito $(A|E)$, u ovom primjeru ima sljedeći oblik: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

Svrha: pomoću elementarnih transformacija dovedite proširenu matricu u oblik $\left(E|A^(-1) \right)$. Primjenjuju se iste operacije koje se koriste u rješavanju sustava linearnih jednadžbi Gaussovom metodom. Za primjenu Gaussove metode prikladno je kada je prvi element prvog retka proširene matrice jedan. Da bismo to postigli, mijenjamo prvi i treći redak proširene matrice, što postaje: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(niz) \desno)$.

Sada prijeđimo na rješenje. Gaussova metoda podijeljena je u dvije faze: naprijed i natrag (detaljan opis ove metode za rješavanje sustava jednadžbi dan je u primjerima odgovarajuće teme). Ista dva koraka primijenit će se u procesu pronalaženja inverzne matrice.

udarac naprijed

Prvi korak

Uz pomoć prvog retka resetiramo elemente prvog stupca koji se nalaze ispod prvog retka:

Da malo komentiram što sam napravio. Oznaka $II-2\cdot I$ znači da su odgovarajući elementi prvog retka, prethodno pomnoženi s dva, oduzeti od elemenata drugog retka. Ova se radnja može zasebno napisati na sljedeći način:

Radnja $III-7\cdot I$ izvodi se na potpuno isti način. Ako postoje poteškoće s izvođenjem ovih operacija, one se mogu izvesti zasebno (slično akciji $II-2\cdot I$ prikazanoj gore), a rezultat se zatim unosi u proširenu matricu.

Drugi korak

Uz pomoć drugog retka resetiramo element drugog stupca koji se nalazi ispod drugog retka:

Treću liniju podijelite s 5:

Ravna vožnja je gotova. Svi elementi smješteni ispod glavne dijagonale matrice do crte vraćeni su na nulu.

Obrnuto

Prvi korak

Uz pomoć trećeg retka resetiramo elemente trećeg stupca koji se nalaze iznad trećeg retka:

Prije nego prijeđete na sljedeći korak, podijelite drugi red sa $7$:

Drugi korak

Uz pomoć drugog retka resetujemo elemente drugog stupca koji se nalaze iznad drugog retka:

Transformacije su dovršene, inverzna matrica je pronađena Gaussovom metodom: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \ 7/5 & -11/5 & -27/5 \end(niz) \desno)$. Provjeru, ako je potrebno, možete izvršiti na isti način kao u prethodnim primjerima. Ako preskočite sva objašnjenja, tada će rješenje imati oblik:

Odgovor: $A^(-1)=\lijevo(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & -27/5 \end(array) \right)$.

Primjer #6

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & - 4 & -3 \\ 1 & 4 & 0 & 6 \end(array) \right)$.

Da bismo pronašli inverznu matricu u ovom primjeru, koristit ćemo iste operacije koje se koriste u rješavanju sustava linearnih jednadžbi Gaussovom metodom. U nastavku su navedena detaljna objašnjenja, ali ovdje se ograničavamo na kratke komentare. Napišimo proširenu matricu: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(array) \right)$. Zamijenite prvi i četvrti redak ove matrice: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(array) \right)$.

udarac naprijed

Transformacije naprijed su dovršene. Svi elementi smješteni ispod glavne dijagonale matrice lijevo od crte postavljeni su na nulu.

Obrnuto

Pronađen Gaussov inverz, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & - 117/ 16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \ kraj( niz)\desno)$. Provjera, ako je potrebna, provodi se na isti način kao u primjerima br. 2 i br. 3.

Odgovor: $A^(-1)=\lijevo(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(niz) \ desno)$.

Primjer #7

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( array )\desno)$.

Za pronalaženje inverzne matrice primjenjujemo operacije karakteristične za Gauss-Jordanovu metodu. Razlika od Gaussove metode, razmatrane u prethodnim primjerima i , je u tome što se rješenje provodi u jednoj fazi. Dopustite mi da vas podsjetim da je Gaussova metoda podijeljena u 2 faze: pomak naprijed ("pravimo" nule ispod glavne dijagonale matrice na traku) i obrnuti pomak (resetiramo elemente iznad glavne dijagonale matrice do šanka). Za izračunavanje inverzne matrice Gauss-Jordanovom metodom nisu potrebna dva stupnja rješenja. Prvo, napravimo proširenu matricu: $(A|E)$:

$$ (A|E)=\lijevo(\početak(niz) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & -2 &0 & 0 & 1 \end(array) \right) $$

Prvi korak

Postavite sve elemente prvog stupca na nulu osim jednog. U prvom stupcu svi elementi su različiti od nule, tako da možemo odabrati bilo koji element. Uzmimo, na primjer, $(-4)$:

Odabrani element $(-4)$ nalazi se u trećem retku, tako da koristimo treći red da poništimo odabrane elemente prvog stupca:

Neka prvi element trećeg reda bude jednak jedan. Da bismo to učinili, dijelimo elemente trećeg retka proširene matrice s $(-4)$:

Sada počnimo nulirati odgovarajuće elemente prvog stupca:

U daljnjim koracima više neće biti moguće koristiti treći red, jer smo ga već primijenili u prvom koraku.

Drugi korak

Izaberimo neki ne-nulti element drugog stupca i postavimo sve ostale elemente drugog stupca na nulu. Možemo odabrati jedan od dva elementa: $\frac(11)(2)$ ili $\frac(39)(4)$. Element $\left(-\frac(5)(4) \right)$ nije moguće odabrati jer se nalazi u trećem retku, koji smo koristili u prethodnom koraku. Odaberimo element $\frac(11)(2)$ koji se nalazi u prvom redu. Promijenimo $\frac(11)(2)$ u jedan u prvom redu:

Sada postavimo odgovarajuće elemente drugog stupca na nulu:

U daljnjem obrazloženju ne može se koristiti prvi redak.

Treći korak

Potrebno je resetirati sve elemente treće kolone osim jednog. Moramo izabrati neki ne-nulti element treće kolone. Međutim, ne možemo uzeti $\frac(6)(11)$ ili $\frac(13)(11)$ jer se ti elementi nalaze u prvom i trećem retku koje smo ranije koristili. Izbor je mali: ostaje samo element $\frac(2)(11)$ koji se nalazi u drugom retku. Podijelite sve elemente drugog retka s $\frac(2)(11)$:

Sada postavimo odgovarajuće elemente treće kolone na nulu:

Transformacije Gauss-Jordanovom metodom su završene. Ostaje samo da matrica do crte postane jedinica. Da biste to učinili, morate promijeniti redoslijed redaka. Prvo zamijenite prvi i treći red:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(niz) \desno) $$

Sada zamijenimo drugi i treći redak:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(niz) \desno) $$

Dakle $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39 /4 & 11/2 & 19/4 \end(array) \right)$. Naravno, rješenje se može izvesti na drugačiji način, odabirom elemenata na glavnoj dijagonali. Obično je to upravo ono što rade, jer u ovom slučaju, na kraju rješenja, linije se neće morati mijenjati. Prethodno sam rješenje dao samo s jednom svrhom: da pokažem da izbor reda u svakom koraku nije temeljan. Odaberemo li dijagonalne elemente u svakom koraku, tada će rješenje biti sljedeće.

Neka je dana kvadratna matrica. Potrebno je pronaći inverznu matricu.

Prvi način. U teoremu 4.1 o postojanju i jedinstvenosti inverzne matrice naznačen je jedan od načina njezina pronalaženja.

1. Izračunajte determinantu zadane matrice. Ako, tada inverzna matrica ne postoji (matrica je degenerirana).

2. Sastavite matricu od algebarskih komplemenata elemenata matrice.

3. Transponiranjem matrice dobiva se pridružena matrica .

4. Nađite inverznu matricu (4.1) dijeljenjem svih elemenata pridružene matrice s determinantom

Drugi način. Za pronalaženje inverzne matrice mogu se koristiti elementarne transformacije.

1. Sastavite blok matricu dodjeljivanjem zadanoj matrici matrice identiteta istog reda.

2. Uz pomoć elementarnih transformacija izvedenih na redovima matrice, dovedite njen lijevi blok u najjednostavniji oblik. U ovom slučaju, blok matrica se reducira na oblik, gdje je kvadratna matrica dobivena kao rezultat transformacija iz matrice identiteta.

3. Ako je , tada je blok jednak inverznoj matrici, tj. Ako, tada matrica nema inverza.

Doista, uz pomoć elementarnih transformacija redaka matrice, njen lijevi blok može se svesti na pojednostavljeni oblik (vidi sliku 1.5). U ovom slučaju, blok matrica se transformira u oblik, gdje je elementarna matrica koja zadovoljava jednakost. Ako je matrica nesingularna, tada se, prema točki 2. napomene 3.3, njezin pojednostavljeni oblik podudara s matricom identiteta. Tada iz jednakosti slijedi da. Ako je matrica degenerirana, tada se njezin pojednostavljeni oblik razlikuje od matrice identiteta, a matrica nema inverz.

11. Matrične jednadžbe i njihovo rješenje. Matrična notacija SLAE. Matrična metoda (metoda inverzne matrice) za rješavanje SLAE i uvjeti njene primjenjivosti.

Matrične jednadžbe su jednadžbe oblika: A*X=C; X*A=C; A*X*B=C gdje su matrice A, B, C poznate, matrica X nije poznata, ako matrice A i B nisu degenerirane tada će rješenja izvornih matrica biti zapisana u odgovarajućem obliku: X=A -1 *C; X=C*A -1; X \u003d A -1 * C * B -1 Matrični oblik zapisa sustava linearnih algebarskih jednadžbi. Nekoliko matrica može biti pridruženo svakom SLAE; štoviše, sam SLAE može se napisati kao matrična jednadžba. Za SLAE (1), razmotrite sljedeće matrice:

Matrica A se zove matrica sustava. Elementi ove matrice su koeficijenti zadanog SLAE.

Matrica A˜ naziva se sustav proširene matrice. Dobiva se tako da se matrici sustava doda stupac koji sadrži slobodne članove b1,b2,...,bm. Obično je ovaj stupac odvojen okomitom linijom radi jasnoće.

Stupac matrice B naziva se matrica slobodnih članova, a matrica stupca X je matrica nepoznanica.

Koristeći gore uvedenu notaciju, SLAE (1) se može napisati u obliku matrične jednadžbe: A⋅X=B.

Bilješka

Matrice povezane sa sustavom mogu se napisati na različite načine: sve ovisi o redoslijedu varijabli i jednadžbi razmatranog SLAE. Ali u svakom slučaju, redoslijed nepoznanica u svakoj jednadžbi danog SLAE mora biti isti.

Matrična metoda je prikladna za rješavanje SLAE u kojima se broj jednadžbi podudara s brojem nepoznatih varijabli, a determinanta glavne matrice sustava je različita od nule. Ako sustav sadrži više od tri jednadžbe, pronalaženje inverzne matrice zahtijeva značajan računalni napor, stoga je u ovom slučaju preporučljivo koristiti za rješavanje Gaussova metoda.

12. Homogene SLAE, uvjeti postojanja njihovih rješenja različitih od nule. Svojstva parcijalnih rješenja homogenih SLAE.

Linearna jednadžba se naziva homogenom ako je njen slobodni član jednak nuli, a nehomogenom u suprotnom. Sustav koji se sastoji od homogenih jednadžbi naziva se homogenim i ima opći oblik:

13 .Pojam linearne neovisnosti i ovisnosti parcijalnih rješenja homogene SLAE. Temeljni sustav odlučivanja (FSR) i njegov nalaz. Prikaz općeg rješenja homogenog SLAE u smislu FSR-a.

Sustav funkcija g 1 (x ), g 2 (x ), …, g n (x ) Zove se linearno ovisna na intervalu ( a , b ) ako postoji skup konstantnih koeficijenata koji nisu jednaki nuli istovremeno, tako da je linearna kombinacija ovih funkcija identično jednaka nuli na ( a , b ): za . Ako je jednakost za moguća samo za , sustav funkcija g 1 (x ), g 2 (x ), …, g n (x ) Zove se linearno neovisni na intervalu ( a , b ). Drugim riječima, funkcije g 1 (x ), g 2 (x ), …, g n (x ) linearno ovisna na intervalu ( a , b ) ako postoji nula na ( a , b ) njihova netrivijalna linearna kombinacija. Funkcije g 1 (x ),g 2 (x ), …, g n (x ) linearno neovisni na intervalu ( a , b ) ako je samo njihova trivijalna linearna kombinacija identično jednaka nuli na ( a , b ).

Temeljni sustav odlučivanja (FSR) homogena SLAE osnova je ovog sustava stupova.

Broj elemenata u FSR jednak je broju nepoznanica u sustavu umanjenom za rang matrice sustava. Svako rješenje izvornog sustava je linearna kombinacija rješenja FSR-a.

Teorema

Opće rješenje nehomogenog SLAE jednako je zbroju partikularnog rješenja nehomogenog SLAE i općeg rješenja odgovarajućeg homogenog SLAE.

1 . Ako su stupci rješenja homogenog sustava jednadžbi, tada je svaka njihova linearna kombinacija također rješenje homogenog sustava.

Doista, iz jednakosti slijedi da

oni. linearna kombinacija rješenja je rješenje homogenog sustava.

2. Ako je rang matrice homogenog sustava , tada sustav ima linearno neovisna rješenja.

Doista, pomoću formula (5.13) općeg rješenja homogenog sustava možemo pronaći posebna rješenja pridjeljujući sljedeće slobodnim varijablama setovi zadanih vrijednosti (svaki put uz pretpostavku da je jedna od slobodnih varijabli jednaka jedinici, a ostale su jednake nuli):

koji su linearno neovisni. Doista, ako je matrica formirana iz ovih stupaca, tada njeni posljednji redovi tvore matricu identiteta. Dakle, minor koji se nalazi u posljednjim redovima nije jednak nuli (jednak je jedinici), tj. je osnovni. Stoga će rang matrice biti jednak. Stoga su svi stupci ove matrice linearno neovisni (vidi teorem 3.4).

Svaka zbirka linearno neovisnih rješenja homogenog sustava naziva se temeljni sustav (skup) rješenja .

14 Minor th reda, osnovni mol, rang matrice. Izračun ranga matrice.

Red k minor matrice A je determinanta neke od njezinih kvadratnih submatrica reda k.

U m x n matrici A, minor reda r naziva se bazičnim ako je različit od nule, a svi minori većeg reda, ako postoje, jednaki su nuli.

Stupci i redovi matrice A, u čijem sjecištu se nalazi baza minor, nazivaju se baznim stupcima i redovima matrice A.

Teorem 1. (O rangu matrice). Za svaku matricu, sporedni rang jednak je rangu retka i jednak rangu stupca.

Teorem 2. (O osnovnom minoru). Svaki stupac matrice rastavljen je u linearnu kombinaciju svojih osnovnih stupaca.

Rang matrice (ili manji rang) je red baznog minora ili, drugim riječima, najveći red za koji postoje minori različiti od nule. Rang nulte matrice se, po definiciji, smatra 0.

Primjećujemo dva očita svojstva manjeg ranga.

1) Rang matrice se ne mijenja prilikom transponiranja, jer kada se matrica transponira, sve njene submatrice se transponiraju, a minori se ne mijenjaju.

2) Ako je A' podmatrica matrice A, tada rang A' ne prelazi rang A, budući da je minor različit od nule uključen u A' također uključen u A.

15. Pojam -dimenzionalnog aritmetičkog vektora. Vektorska jednakost. Radnje na vektorima (zbrajanje, oduzimanje, množenje brojem, množenje matricom). Linearna kombinacija vektora.

Naručeno preuzimanje n realni ili kompleksni brojevi se zove n-dimenzionalni vektor. Brojevi se nazivaju vektorske koordinate.

Dva vektora (različita od nule). a i b jednaki ako su jednakosmjerni i imaju isti modul. Svi nulti vektori se smatraju jednakima. U svim ostalim slučajevima vektori nisu jednaki.

Zbrajanje vektora. Postoje dva načina zbrajanja vektora.1. pravilo paralelograma. Da bismo dodali vektore i, postavljamo ishodišta oba u istu točku. Dovršavamo paralelogram i iz iste točke povlačimo dijagonalu paralelograma. Ovo će biti zbroj vektora.

2. Drugi način zbrajanja vektora je pravilo trokuta. Uzmimo iste vektore i . Na kraj prvog vektora dodajemo početak drugog. Sada spojimo početak prve i kraj druge. Ovo je zbroj vektora i . Prema istom pravilu, možete dodati nekoliko vektora. Pričvršćujemo ih jedan po jedan, a zatim povezujemo početak prvog s krajem posljednjeg.

Oduzimanje vektora. Vektor je usmjeren suprotno od vektora. Duljine vektora su jednake. Sada je jasno što je oduzimanje vektora. Razlika vektora i je zbroj vektora i vektora .

Pomnožite vektor s brojem

Množenje vektora s brojem k rezultira vektorom čija je duljina k puta različita od duljine. Istosmjeran je s vektorom ako je k veći od nule, a suprotno usmjeren ako je k manji od nule.

Skalarni umnožak vektora umnožak je duljina vektora i kosinusa kuta između njih. Ako su vektori okomiti, njihov točkasti produkt je nula. I ovako se skalarni umnožak izražava preko koordinata vektora i .

Linearna kombinacija vektora

Linearna kombinacija vektora vektor poziva

gdje - koeficijenti linearne kombinacije. Ako a kombinacija se naziva trivijalnom ako je netrivijalna.

16 .Skalarni produkt aritmetičkih vektora. Duljina vektora i kut između vektora. Pojam ortogonalnosti vektora.

Skalarni produkt vektora a i b je broj

Skalarni produkt služi za izračunavanje: 1) pronalaženje kuta između njih; 2) pronalaženje projekcije vektora; 3) izračunavanje duljine vektora; 4) uvjet okomitosti vektora.

Duljina dužine AB je udaljenost između točaka A i B. Kut između vektora A i B naziva se kut α = (a, c), 0≤ α ≤P. Pri čemu je potrebno rotirati 1 vektor tako da se njegov smjer poklapa s drugim vektorom. Pod uvjetom da im se počeci podudaraju.

Orth a je vektor a koji ima jediničnu duljinu i smjer a.

17. Sustav vektora i njegova linearna kombinacija. Pojam linearne ovisnosti i neovisnosti sustava vektora. Teorem o potrebnim i dovoljnim uvjetima linearne ovisnosti sustava vektora.

Sustav vektora a1,a2,...,an naziva se linearno ovisnim ako postoje brojevi λ1,λ2,...,λn takvi da je barem jedan od njih različit od nule i λ1a1+λ2a2+...+λnan=0 . Inače se sustav naziva linearno neovisnim.

Dva vektora a1 i a2 nazivamo kolinearnima ako su im smjerovi jednaki ili suprotni.

Tri vektora a1,a2 i a3 nazivamo komplanarnima ako su paralelna s nekom ravninom.

Geometrijski kriteriji za linearnu ovisnost:

a) sustav (a1,a2) je linearno ovisan ako i samo ako su vektori a1 i a2 kolinearni.

b) sustav (a1,a2,a3) je linearno ovisan ako i samo ako su vektori a1,a2 i a3 koplanarni.

teorema. (Potreban i dovoljan uvjet za linearnu ovisnost sustava vektori.)

Vektorski sustav vektor prostor je linearno ovisan ako i samo ako je jedan od vektora sustava linearno izražen kroz ostale vektor ovaj sustav.

Posljedica.1. Sustav vektora u vektorskom prostoru je linearno neovisan ako i samo ako nijedan od vektora sustava nije linearno izražen preko drugih vektora ovog sustava.2. Vektorski sustav koji sadrži nulti vektor ili dva jednaka vektora je linearno ovisan.

Za bilo koju nesingularnu matricu A, postoji jedinstvena matrica A -1 takva da je

A*A -1 =A -1 *A = E,

gdje je E matrica identiteta istog reda kao A. Matrica A -1 se naziva inverzna matrica A.

Ako je netko zaboravio, u matrici identiteta, osim dijagonale popunjene jedinicama, sva ostala mjesta su popunjena nulama, primjer matrice identiteta:

Nalaženje inverzne matrice metodom adjungirane matrice

Inverzna matrica je definirana formulom:

gdje je A ij - elementi a ij .

Oni. Da biste izračunali inverziju matrice, morate izračunati determinantu ove matrice. Zatim pronađite algebarske dodatke za sve njegove elemente i napravite od njih novu matricu. Zatim morate transportirati ovu matricu. I podijelite svaki element nove matrice s determinantom izvorne matrice.

Pogledajmo nekoliko primjera.

Pronađite A -1 za matricu

Rješenje.Nađite A -1 metodom adjungirane matrice. Imamo det A = 2. Nađimo algebarske komplemente elemenata matrice A. U ovom slučaju, algebarski komplementi elemenata matrice bit će odgovarajući elementi same matrice, uzeti s predznakom u skladu s formula

Imamo A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Formiramo adjungiranu matricu

Transportiramo matricu A*:

Inverznu matricu nalazimo po formuli:

Dobivamo:

Upotrijebite metodu adjungirane matrice da pronađete A -1 if

Rješenje: Prije svega, izračunavamo zadanu matricu kako bismo bili sigurni da inverzna matrica postoji. Imamo

Ovdje smo elementima drugog reda dodali elemente trećeg reda, prethodno pomnožene s (-1), a zatim proširili determinantu drugim redom. Budući da je definicija ove matrice različita od nule, tada postoji matrica inverzna njoj. Da bismo konstruirali adjungiranu matricu, nalazimo algebarske komplemente elemenata te matrice. Imamo

Prema formuli

prenosimo matricu A*:

Zatim prema formuli

Nalaženje inverzne matrice metodom elementarnih transformacija

Osim metode pronalaženja inverzne matrice, koja slijedi iz formule (metoda pridružene matrice), postoji metoda za pronalaženje inverzne matrice, koja se naziva metoda elementarnih transformacija.

Elementarne matrične transformacije

Sljedeće transformacije nazivaju se transformacijama elementarne matrice:

1) permutacija redaka (stupaca);

2) množenje retka (stupca) brojem koji nije nula;

3) dodavanje elementima retka (stupca) odgovarajućih elemenata drugog retka (stupca), prethodno pomnoženih s određenim brojem.

Da bismo pronašli matricu A -1, konstruiramo pravokutnu matricu B \u003d (A | E) redova (n; 2n), dodjeljujući matrici A s desne strane matricu identiteta E kroz razdjelnu liniju:

Razmotrite primjer.

Metodom elementarnih transformacija pronađite A -1 if

Rješenje Formiramo matricu B:

Označimo redove matrice B kroz α 1 , α 2 , α 3 . Provedimo sljedeće transformacije na redovima matrice B.