Εύκολες τετραγωνικές εξισώσεις. Διακριτική εξίσωση στα μαθηματικά
Συνεχίζουμε να μελετάμε το θέμα " επίλυση εξισώσεων" Έχουμε ήδη εξοικειωθεί με τις γραμμικές εξισώσεις και προχωράμε στην εξοικείωση τετραγωνικές εξισώσεις.
Αρχικά θα δούμε τι είναι η τετραγωνική εξίσωση και πώς γράφεται γενική εικόνακαι δώστε σχετικούς ορισμούς. Μετά από αυτό, θα χρησιμοποιήσουμε παραδείγματα για να εξετάσουμε λεπτομερώς πώς επιλύονται τα ημιτελή προβλήματα. τετραγωνικές εξισώσεις. Στη συνέχεια, θα προχωρήσουμε στην επίλυση πλήρων εξισώσεων, θα λάβουμε τον τύπο της ρίζας, θα εξοικειωθούμε με τη διάκριση μιας τετραγωνικής εξίσωσης και θα εξετάσουμε λύσεις σε τυπικά παραδείγματα. Τέλος, ας εντοπίσουμε τις συνδέσεις μεταξύ των ριζών και των συντελεστών.
Πλοήγηση στη σελίδα.
Τι είναι μια τετραγωνική εξίσωση; Τα είδη τους
Πρώτα πρέπει να κατανοήσετε ξεκάθαρα τι είναι η τετραγωνική εξίσωση. Επομένως, είναι λογικό να ξεκινήσουμε μια συζήτηση για τις δευτεροβάθμιες εξισώσεις με τον ορισμό μιας τετραγωνικής εξίσωσης, καθώς και σχετικούς ορισμούς. Μετά από αυτό, μπορείτε να εξετάσετε τους κύριους τύπους τετραγωνικών εξισώσεων: μειωμένες και μη αναγωγικές, καθώς και πλήρεις και ημιτελείς εξισώσεις.
Ορισμός και παραδείγματα τετραγωνικών εξισώσεων
Ορισμός.
Τετραγωνική εξίσωσηείναι μια εξίσωση της μορφής a x 2 +b x+c=0, όπου x είναι μια μεταβλητή, a, b και c είναι κάποιοι αριθμοί και το a είναι μη μηδενικό.
Ας πούμε αμέσως ότι οι δευτεροβάθμιες εξισώσεις ονομάζονται συχνά εξισώσεις δεύτερου βαθμού. Αυτό οφείλεται στο γεγονός ότι η τετραγωνική εξίσωση είναι αλγεβρική εξίσωση δευτέρου βαθμού.
Ο αναφερόμενος ορισμός μας επιτρέπει να δώσουμε παραδείγματα τετραγωνικών εξισώσεων. Άρα 2 x 2 +6 x+1=0, 0,2 x 2 +2,5 x+0,03=0, κ.λπ. Αυτές είναι τετραγωνικές εξισώσεις.
Ορισμός.
Αριθμοί Τα α, β και γ λέγονται συντελεστές της δευτεροβάθμιας εξίσωσης a·x 2 +b·x+c=0, και ο συντελεστής a λέγεται ο πρώτος, ή ο υψηλότερος, ή ο συντελεστής x 2, b είναι ο δεύτερος συντελεστής, ή ο συντελεστής x, και c είναι ο ελεύθερος όρος .
Για παράδειγμα, ας πάρουμε μια τετραγωνική εξίσωση της μορφής 5 x 2 −2 x −3=0, εδώ ο κύριος συντελεστής είναι 5, ο δεύτερος συντελεστής είναι ίσος με −2 και ο ελεύθερος όρος είναι ίσος με −3. Σημειώστε ότι όταν οι συντελεστές b και/ή c είναι αρνητικοί, όπως στο παράδειγμα που μόλις δόθηκε, τότε σύντομη μορφήγράφοντας μια τετραγωνική εξίσωση της μορφής 5 x 2 −2 x−3=0, και όχι 5 x 2 +(−2) x+(−3)=0.
Αξίζει να σημειωθεί ότι όταν οι συντελεστές a και/ή b είναι ίσοι με 1 ή −1, συνήθως δεν υπάρχουν ρητά στην τετραγωνική εξίσωση, κάτι που οφείλεται στις ιδιαιτερότητες της γραφής τέτοιων . Για παράδειγμα, στην τετραγωνική εξίσωση y 2 −y+3=0 ο κύριος συντελεστής είναι ένας και ο συντελεστής του y είναι ίσος με −1.
Ανηγμένες και μη αναγωγικές τετραγωνικές εξισώσεις
Ανάλογα με την τιμή του προπορευόμενου συντελεστή, διακρίνονται μειωμένες και μη ανηγμένες τετραγωνικές εξισώσεις. Ας δώσουμε τους αντίστοιχους ορισμούς.
Ορισμός.
Καλείται μια τετραγωνική εξίσωση στην οποία ο κύριος συντελεστής είναι 1 δεδομένη τετραγωνική εξίσωση. Διαφορετικά η τετραγωνική εξίσωση είναι άθικτος.
Σύμφωνα με αυτόν τον ορισμό, τετραγωνικές εξισώσεις x 2 −3·x+1=0, x 2 −x−2/3=0 κ.λπ. – δίνεται, σε καθένα από αυτά ο πρώτος συντελεστής ίσο με ένα. A 5 x 2 −x−1=0, κ.λπ. - Οι μη αναγωγικές τετραγωνικές εξισώσεις, οι συντελεστές τους είναι διαφορετικοί από το 1.
Από οποιαδήποτε μη ανηγμένη τετραγωνική εξίσωση, διαιρώντας και τις δύο πλευρές με τον προπορευόμενο συντελεστή, μπορείτε να πάτε στη μειωμένη. Αυτή η ενέργεια είναι ένας ισοδύναμος μετασχηματισμός, δηλαδή, η μειωμένη τετραγωνική εξίσωση που λαμβάνεται με αυτόν τον τρόπο έχει τις ίδιες ρίζες με την αρχική μη ανηγμένη τετραγωνική εξίσωση ή, όπως αυτή, δεν έχει ρίζες.
Ας δούμε ένα παράδειγμα του τρόπου με τον οποίο εκτελείται η μετάβαση από μια μη ανηγμένη τετραγωνική εξίσωση σε μια ανηγμένη.
Παράδειγμα.
Από την εξίσωση 3 x 2 +12 x−7=0, πηγαίνετε στην αντίστοιχη ανηγμένη τετραγωνική εξίσωση.
Λύση.
Απλώς πρέπει να διαιρέσουμε και τις δύο πλευρές της αρχικής εξίσωσης με τον κύριο συντελεστή 3, είναι μη μηδενικός, ώστε να μπορούμε να εκτελέσουμε αυτήν την ενέργεια. Έχουμε (3 x 2 +12 x−7):3=0:3, που είναι το ίδιο, (3 x 2):3+(12 x):3−7:3=0, και μετά (3: 3) x 2 +(12:3) x−7:3=0, από όπου . Έτσι αποκτήσαμε τη μειωμένη τετραγωνική εξίσωση, η οποία είναι ισοδύναμη με την αρχική.
Απάντηση:
Πλήρεις και ημιτελείς τετραγωνικές εξισώσεις
Ο ορισμός μιας τετραγωνικής εξίσωσης περιέχει τη συνθήκη a≠0. Αυτή η συνθήκη είναι απαραίτητη ώστε η εξίσωση a x 2 + b x + c = 0 να είναι τετραγωνική, αφού όταν a = 0 γίνεται στην πραγματικότητα μια γραμμική εξίσωση της μορφής b x + c = 0.
Όσον αφορά τους συντελεστές b και c, μπορούν να είναι ίσοι με μηδέν, τόσο μεμονωμένα όσο και μαζί. Σε αυτές τις περιπτώσεις, η τετραγωνική εξίσωση ονομάζεται ελλιπής.
Ορισμός.
Λέγεται η τετραγωνική εξίσωση a x 2 +b x+c=0 ατελής, αν τουλάχιστον ένας από τους συντελεστές b, c είναι ίσος με μηδέν.
Με τη σειρά του
Ορισμός.
Πλήρης τετραγωνική εξίσωσηείναι μια εξίσωση στην οποία όλοι οι συντελεστές είναι διαφορετικοί από το μηδέν.
Τέτοια ονόματα δεν δόθηκαν τυχαία. Αυτό θα φανεί από τις επόμενες συζητήσεις.
Αν ο συντελεστής b είναι μηδέν, τότε η δευτεροβάθμια εξίσωση παίρνει τη μορφή a·x 2 +0·x+c=0, και είναι ισοδύναμη με την εξίσωση a·x 2 +c=0. Αν c=0, δηλαδή, η δευτεροβάθμια εξίσωση έχει τη μορφή a·x 2 +b·x+0=0, τότε μπορεί να ξαναγραφτεί ως a·x 2 +b·x=0. Και με b=0 και c=0 παίρνουμε την τετραγωνική εξίσωση a·x 2 =0. Οι εξισώσεις που προκύπτουν διαφέρουν από την πλήρη τετραγωνική εξίσωση στο ότι οι αριστερές πλευρές τους δεν περιέχουν ούτε όρο με τη μεταβλητή x ούτε έναν ελεύθερο όρο ή και τα δύο. Εξ ου και το όνομά τους - ημιτελείς τετραγωνικές εξισώσεις.
Άρα οι εξισώσεις x 2 +x+1=0 και −2 x 2 −5 x+0,2=0 είναι παραδείγματα πλήρων τετραγωνικών εξισώσεων, και x 2 =0, −2 x 2 =0, 5 x 2 +3=0 , −x 2 −5 x=0 είναι ημιτελείς τετραγωνικές εξισώσεις.
Επίλυση ημιτελών τετραγωνικών εξισώσεων
Από τις πληροφορίες της προηγούμενης παραγράφου προκύπτει ότι υπάρχει τρεις τύποι ημιτελών τετραγωνικών εξισώσεων:
- a·x 2 =0, σε αυτό αντιστοιχούν οι συντελεστές b=0 και c=0.
- a x 2 +c=0 όταν b=0 ;
- και a·x 2 +b·x=0 όταν c=0.
Ας εξετάσουμε με τη σειρά πώς λύνονται ημιτελείς τετραγωνικές εξισώσεις καθενός από αυτούς τους τύπους.
a x 2 =0
Ας ξεκινήσουμε με την επίλυση ημιτελών τετραγωνικών εξισώσεων στις οποίες οι συντελεστές b και c είναι ίσοι με μηδέν, δηλαδή με εξισώσεις της μορφής a x 2 =0. Η εξίσωση a·x 2 =0 είναι ισοδύναμη με την εξίσωση x 2 =0, η οποία προκύπτει από το πρωτότυπο διαιρώντας και τα δύο μέρη με έναν μη μηδενικό αριθμό α. Προφανώς, η ρίζα της εξίσωσης x 2 =0 είναι μηδέν, αφού 0 2 =0. Αυτή η εξίσωση δεν έχει άλλες ρίζες, κάτι που εξηγείται από το γεγονός ότι για οποιονδήποτε μη μηδενικό αριθμό p ισχύει η ανισότητα p 2 >0, που σημαίνει ότι για p≠0 η ισότητα p 2 =0 δεν επιτυγχάνεται ποτέ.
Άρα, η ημιτελής τετραγωνική εξίσωση a·x 2 =0 έχει μία μόνο ρίζα x=0.
Ως παράδειγμα, δίνουμε τη λύση στην ημιτελή τετραγωνική εξίσωση −4 x 2 =0. Είναι ισοδύναμη με την εξίσωση x 2 =0, η μόνη της ρίζα είναι x=0, επομένως, η αρχική εξίσωση έχει μια μοναδική ρίζα μηδέν.
Μια σύντομη λύση σε αυτήν την περίπτωση μπορεί να γραφτεί ως εξής:
−4 x 2 =0,
x 2 =0,
x=0.
a x 2 +c=0
Ας δούμε τώρα πώς λύνονται ημιτελείς δευτεροβάθμιες εξισώσεις στις οποίες ο συντελεστής b είναι μηδέν και c≠0, δηλαδή εξισώσεις της μορφής a x 2 +c=0. Γνωρίζουμε ότι η μετακίνηση ενός όρου από τη μια πλευρά της εξίσωσης στην άλλη με το αντίθετο πρόσημο, καθώς και η διαίρεση και των δύο πλευρών της εξίσωσης με έναν μη μηδενικό αριθμό, δίνει μια ισοδύναμη εξίσωση. Επομένως, μπορούμε να πραγματοποιήσουμε τα εξής ισοδύναμους μετασχηματισμούςημιτελής τετραγωνική εξίσωση a x 2 +c=0 :
- μετακίνηση από σε σωστη πλευρα, που δίνει την εξίσωση a x 2 =−c,
- και διαιρούμε και τις δύο πλευρές με ένα, παίρνουμε .
Η εξίσωση που προκύπτει μας επιτρέπει να βγάλουμε συμπεράσματα για τις ρίζες της. Ανάλογα με τις τιμές των a και c, η τιμή της παράστασης μπορεί να είναι αρνητική (για παράδειγμα, αν a=1 και c=2, τότε ) ή θετική (για παράδειγμα, εάν a=−2 και c=6, τότε ), δεν είναι μηδέν , αφού με συνθήκη c≠0. Ας δούμε τις περιπτώσεις ξεχωριστά.
Αν , τότε η εξίσωση δεν έχει ρίζες. Αυτή η δήλωση προκύπτει από το γεγονός ότι το τετράγωνο οποιουδήποτε αριθμού είναι ένας μη αρνητικός αριθμός. Από αυτό προκύπτει ότι όταν , τότε για οποιονδήποτε αριθμό p η ισότητα δεν μπορεί να είναι αληθής.
Αν , τότε η κατάσταση με τις ρίζες της εξίσωσης είναι διαφορετική. Σε αυτήν την περίπτωση, αν θυμηθούμε περίπου , τότε η ρίζα της εξίσωσης γίνεται αμέσως προφανής· είναι ο αριθμός, αφού . Είναι εύκολο να μαντέψει κανείς ότι ο αριθμός είναι επίσης η ρίζα της εξίσωσης, πράγματι, . Αυτή η εξίσωση δεν έχει άλλες ρίζες, οι οποίες μπορούν να φανούν, για παράδειγμα, με αντίφαση. Ας το κάνουμε.
Ας υποδηλώσουμε τις ρίζες της εξίσωσης που μόλις ανακοινώθηκε ως x 1 και −x 1 . Ας υποθέσουμε ότι η εξίσωση έχει μια ακόμη ρίζα x 2, διαφορετική από τις υποδεικνυόμενες ρίζες x 1 και −x 1. Είναι γνωστό ότι η αντικατάσταση των ριζών της σε εξίσωση αντί για x μετατρέπει την εξίσωση σε σωστή αριθμητική ισότητα. Για x 1 και −x 1 έχουμε , και για x 2 έχουμε . Οι ιδιότητες των αριθμητικών ισοτήτων μας επιτρέπουν να πραγματοποιούμε αφαίρεση κατά όρο των σωστών αριθμητικών ισοτήτων, οπότε αφαιρώντας τα αντίστοιχα μέρη των ισοτήτων δίνουμε x 1 2 −x 2 2 =0. Οι ιδιότητες των πράξεων με αριθμούς μας επιτρέπουν να ξαναγράψουμε την ισότητα που προκύπτει ως (x 1 −x 2)·(x 1 +x 2)=0. Γνωρίζουμε ότι το γινόμενο δύο αριθμών είναι ίσο με μηδέν αν και μόνο αν τουλάχιστον ένας από αυτούς είναι ίσος με μηδέν. Επομένως, από την προκύπτουσα ισότητα προκύπτει ότι x 1 −x 2 =0 και/ή x 1 +x 2 =0, που είναι το ίδιο, x 2 =x 1 και/ή x 2 =−x 1. Καταλήξαμε λοιπόν σε μια αντίφαση, αφού στην αρχή είπαμε ότι η ρίζα της εξίσωσης x 2 είναι διαφορετική από τα x 1 και −x 1. Αυτό αποδεικνύει ότι η εξίσωση δεν έχει άλλες ρίζες εκτός από και .
Ας συνοψίσουμε τις πληροφορίες σε αυτήν την παράγραφο. Η ημιτελής τετραγωνική εξίσωση a x 2 +c=0 είναι ισοδύναμη με την εξίσωση που
- δεν έχει ρίζες αν,
- έχει δύο ρίζες και , αν .
Ας δούμε παραδείγματα επίλυσης ημιτελών τετραγωνικών εξισώσεων της μορφής a·x 2 +c=0.
Ας ξεκινήσουμε με την τετραγωνική εξίσωση 9 x 2 +7=0. Αφού μετακινήσετε τον ελεύθερο όρο στη δεξιά πλευρά της εξίσωσης, θα πάρει τη μορφή 9 x 2 =−7. Διαιρώντας και τις δύο πλευρές της εξίσωσης που προκύπτει με το 9, καταλήγουμε στο . Εφόσον η δεξιά πλευρά έχει αρνητικό αριθμό, αυτή η εξίσωση δεν έχει ρίζες, επομένως, η αρχική ημιτελής τετραγωνική εξίσωση 9 x 2 +7 = 0 δεν έχει ρίζες.
Ας λύσουμε μια άλλη ημιτελή τετραγωνική εξίσωση −x 2 +9=0. Μετακινούμε το εννέα στη δεξιά πλευρά: −x 2 =−9. Τώρα διαιρούμε και τις δύο πλευρές με −1, παίρνουμε x 2 =9. Στη δεξιά πλευρά είναι θετικός αριθμός, από το οποίο συμπεραίνουμε ότι ή . Στη συνέχεια σημειώνουμε την τελική απάντηση: η ημιτελής τετραγωνική εξίσωση −x 2 +9=0 έχει δύο ρίζες x=3 ή x=−3.
a x 2 +b x=0
Μένει να βρούμε τη λύση τελευταίος τύποςημιτελείς τετραγωνικές εξισώσεις για c=0. Οι ημιτελείς τετραγωνικές εξισώσεις της μορφής a x 2 + b x = 0 σας επιτρέπουν να λύσετε μέθοδος παραγοντοποίησης. Προφανώς, μπορούμε, που βρίσκεται στην αριστερή πλευρά της εξίσωσης, για την οποία αρκεί να βγάλουμε τον κοινό παράγοντα x από αγκύλες. Αυτό μας επιτρέπει να μεταβούμε από την αρχική ημιτελή τετραγωνική εξίσωση στο ισοδύναμη εξίσωσητης μορφής x·(a·x+b)=0 . Και αυτή η εξίσωση είναι ισοδύναμη με ένα σύνολο δύο εξισώσεων x=0 και a·x+b=0, η τελευταία από τις οποίες είναι γραμμική και έχει ρίζα x=−b/a.
Άρα, η ημιτελής τετραγωνική εξίσωση a·x 2 +b·x=0 έχει δύο ρίζες x=0 και x=−b/a.
Για να εμπεδώσουμε το υλικό, θα αναλύσουμε τη λύση σε ένα συγκεκριμένο παράδειγμα.
Παράδειγμα.
Λύστε την εξίσωση.
Λύση.
Βγάζοντας x από αγκύλες δίνεται η εξίσωση . Ισοδυναμεί με δύο εξισώσεις x=0 και . Λύνουμε τη γραμμική εξίσωση που προκύπτει: , και εκτελούμε τη διαίρεση μικτός αριθμόςεπί κοινό κλάσμα, βρίσκουμε . Επομένως, οι ρίζες της αρχικής εξίσωσης είναι x=0 και .
Αφού αποκτήσετε την απαραίτητη πρακτική, οι λύσεις σε τέτοιες εξισώσεις μπορούν να γραφτούν εν συντομία:
Απάντηση:
x=0, .
Διάκριση, τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης
Για την επίλυση τετραγωνικών εξισώσεων, υπάρχει ένας τύπος ρίζας. Ας το γράψουμε τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης: , Οπου D=b 2 −4 a γ- τα λεγόμενα διάκριση μιας δευτεροβάθμιας εξίσωσης. Το λήμμα ουσιαστικά σημαίνει ότι .
Είναι χρήσιμο να γνωρίζουμε πώς προέκυψε ο τύπος ρίζας και πώς χρησιμοποιείται για την εύρεση των ριζών των τετραγωνικών εξισώσεων. Ας το καταλάβουμε αυτό.
Παραγωγή του τύπου για τις ρίζες μιας τετραγωνικής εξίσωσης
Ας χρειαστεί να λύσουμε την δευτεροβάθμια εξίσωση a·x 2 +b·x+c=0. Ας κάνουμε μερικούς ισοδύναμους μετασχηματισμούς:
- Μπορούμε να διαιρέσουμε και τις δύο πλευρές αυτής της εξίσωσης με έναν μη μηδενικό αριθμό α, με αποτέλεσμα την ακόλουθη τετραγωνική εξίσωση.
- Τώρα επιλέξτε ένα πλήρες τετράγωνοστην αριστερή του πλευρά: . Μετά από αυτό, η εξίσωση θα πάρει τη μορφή .
- Σε αυτό το στάδιο, είναι δυνατό να μεταφέρουμε τους δύο τελευταίους όρους στη δεξιά πλευρά με το αντίθετο πρόσημο, έχουμε .
- Και ας μεταμορφώσουμε επίσης την έκφραση στη δεξιά πλευρά: .
Ως αποτέλεσμα, καταλήγουμε σε μια εξίσωση που είναι ισοδύναμη με την αρχική τετραγωνική εξίσωση a·x 2 +b·x+c=0.
Έχουμε ήδη λύσει εξισώσεις παρόμοιες σε μορφή στις προηγούμενες παραγράφους, όταν εξετάσαμε. Αυτό μας επιτρέπει να βγάλουμε τα ακόλουθα συμπεράσματα σχετικά με τις ρίζες της εξίσωσης:
- αν , τότε η εξίσωση δεν έχει πραγματικές λύσεις.
- αν , τότε η εξίσωση έχει τη μορφή, άρα, , από την οποία φαίνεται η μόνη της ρίζα.
- αν , τότε ή , που είναι ίδιο με το ή , δηλαδή, η εξίσωση έχει δύο ρίζες.
Έτσι, η παρουσία ή η απουσία ριζών της εξίσωσης, και επομένως της αρχικής τετραγωνικής εξίσωσης, εξαρτάται από το πρόσημο της έκφρασης στη δεξιά πλευρά. Με τη σειρά του, το πρόσημο αυτής της παράστασης καθορίζεται από το πρόσημο του αριθμητή, αφού ο παρονομαστής 4·a 2 είναι πάντα θετικός, δηλαδή από το πρόσημο της παράστασης b 2 −4·a·c. Αυτή η έκφραση b 2 −4 a c ονομάστηκε διάκριση μιας δευτεροβάθμιας εξίσωσηςκαι ορίζεται από την επιστολή ρε. Από εδώ η ουσία της διάκρισης είναι ξεκάθαρη - με βάση την αξία και το πρόσημο της, συμπεραίνουν αν η τετραγωνική εξίσωση έχει πραγματικές ρίζες και αν ναι, ποιος είναι ο αριθμός τους - ένα ή δύο.
Ας επιστρέψουμε στην εξίσωση και ας την ξαναγράψουμε χρησιμοποιώντας τον διακριτικό συμβολισμό: . Και βγάζουμε συμπεράσματα:
- αν Δ<0 , то это уравнение не имеет действительных корней;
- αν D=0, τότε αυτή η εξίσωση έχει μία μόνο ρίζα.
- τέλος, αν D>0, τότε η εξίσωση έχει δύο ρίζες ή, οι οποίες μπορούν να ξαναγραφτούν με τη μορφή ή, και αφού επεκταθούν και μειωθούν τα κλάσματα σε κοινό παρονομαστήλαμβάνουμε .
Έτσι, εξάγαμε τους τύπους για τις ρίζες της δευτεροβάθμιας εξίσωσης, μοιάζουν με , όπου η διάκριση D υπολογίζεται με τον τύπο D=b 2 −4·a·c.
Με τη βοήθειά τους, με μια θετική διάκριση, μπορείτε να υπολογίσετε και τις δύο πραγματικές ρίζες μιας τετραγωνικής εξίσωσης. Όταν η διάκριση είναι ίση με μηδέν, και οι δύο τύποι δίνουν την ίδια τιμή της ρίζας, που αντιστοιχεί σε μια μοναδική λύση της τετραγωνικής εξίσωσης. Και με μια αρνητική διάκριση, όταν προσπαθούμε να χρησιμοποιήσουμε τον τύπο για τις ρίζες μιας δευτεροβάθμιας εξίσωσης, βρισκόμαστε αντιμέτωποι με την εξαγωγή της τετραγωνικής ρίζας ενός αρνητικού αριθμού, που μας βγάζει πέρα από τα όρια και σχολικό πρόγραμμα σπουδών. Με αρνητική διάκριση, η τετραγωνική εξίσωση δεν έχει πραγματικές ρίζες, αλλά έχει ένα ζεύγος σύνθετο συζυγέςρίζες, οι οποίες μπορούν να βρεθούν χρησιμοποιώντας τους ίδιους τύπους ρίζας που αποκτήσαμε.
Αλγόριθμος επίλυσης τετραγωνικών εξισώσεων με χρήση ριζικών τύπων
Στην πράξη, κατά την επίλυση τετραγωνικών εξισώσεων, μπορείτε να χρησιμοποιήσετε αμέσως τον τύπο ρίζας για να υπολογίσετε τις τιμές τους. Αλλά αυτό σχετίζεται περισσότερο με την εύρεση πολύπλοκων ριζών.
Ωστόσο, σε σχολικό μάθημαάλγεβρα συνήθως μιλάμε γιαόχι για μιγαδικές, αλλά για πραγματικές ρίζες μιας τετραγωνικής εξίσωσης. Σε αυτήν την περίπτωση, καλό είναι, πριν χρησιμοποιήσετε τους τύπους για τις ρίζες μιας τετραγωνικής εξίσωσης, να βρείτε πρώτα το διαχωριστικό, βεβαιωθείτε ότι είναι μη αρνητικό (διαφορετικά, μπορούμε να συμπεράνουμε ότι η εξίσωση δεν έχει πραγματικές ρίζες). και μόνο τότε υπολογίστε τις τιμές των ριζών.
Ο παραπάνω συλλογισμός μας επιτρέπει να γράψουμε αλγόριθμος για την επίλυση τετραγωνικής εξίσωσης. Για να λύσετε την τετραγωνική εξίσωση a x 2 +b x+c=0, χρειάζεται:
- Χρησιμοποιώντας τον τύπο διάκρισης D=b 2 −4·a·c, υπολογίστε την τιμή του.
- Καταλήξτε στο συμπέρασμα ότι μια τετραγωνική εξίσωση δεν έχει πραγματικές ρίζες εάν η διάκριση είναι αρνητική.
- Υπολογίστε τη μοναδική ρίζα της εξίσωσης χρησιμοποιώντας τον τύπο εάν D=0;
- Βρείτε δύο πραγματικές ρίζες μιας δευτεροβάθμιας εξίσωσης χρησιμοποιώντας τον τύπο της ρίζας εάν η διάκριση είναι θετική.
Εδώ απλώς σημειώνουμε ότι εάν η διάκριση είναι ίση με μηδέν, μπορείτε επίσης να χρησιμοποιήσετε τον τύπο· θα δώσει την ίδια τιμή με το .
Μπορείτε να προχωρήσετε σε παραδείγματα χρήσης του αλγορίθμου για την επίλυση τετραγωνικών εξισώσεων.
Παραδείγματα επίλυσης τετραγωνικών εξισώσεων
Ας εξετάσουμε λύσεις σε τρεις δευτεροβάθμιες εξισώσεις με θετική, αρνητική και μηδενική διάκριση. Έχοντας ασχοληθεί με τη λύση τους, κατ' αναλογία θα είναι δυνατή η επίλυση οποιασδήποτε άλλης τετραγωνικής εξίσωσης. Ας ξεκινήσουμε.
Παράδειγμα.
Να βρείτε τις ρίζες της εξίσωσης x 2 +2·x−6=0.
Λύση.
Στην περίπτωση αυτή, έχουμε τους παρακάτω συντελεστές της δευτεροβάθμιας εξίσωσης: a=1, b=2 και c=−6. Σύμφωνα με τον αλγόριθμο, πρέπει πρώτα να υπολογίσετε τη διάκριση· για να γίνει αυτό, αντικαθιστούμε τα υποδεικνυόμενα a, b και c στον τύπο διάκρισης, έχουμε D=b 2 −4·a·c=2 2 −4·1·(−6)=4+24=28. Αφού 28>0, δηλαδή η διακρίνουσα Πάνω απο το μηδέν, τότε η τετραγωνική εξίσωση έχει δύο πραγματικές ρίζες. Ας τις βρούμε χρησιμοποιώντας τον τύπο ρίζας, παίρνουμε , εδώ μπορείτε να απλοποιήσετε τις παραστάσεις που προκύπτουν κάνοντας μετακινώντας τον πολλαπλασιαστή πέρα από το σύμβολο της ρίζαςακολουθούμενη από μείωση του κλάσματος:
Απάντηση:
Ας περάσουμε στο επόμενο χαρακτηριστικό παράδειγμα.
Παράδειγμα.
Να λυθεί η δευτεροβάθμια εξίσωση −4 x 2 +28 x−49=0 .
Λύση.
Ξεκινάμε βρίσκοντας τη διάκριση: D=28 2 −4·(−4)·(−49)=784−784=0. Επομένως, αυτή η τετραγωνική εξίσωση έχει μια μοναδική ρίζα, την οποία βρίσκουμε ως , δηλαδή,
Απάντηση:
x=3,5.
Απομένει να εξετάσουμε το ενδεχόμενο επίλυσης δευτεροβάθμιων εξισώσεων με αρνητική διάκριση.
Παράδειγμα.
Λύστε την εξίσωση 5·y 2 +6·y+2=0.
Λύση.
Εδώ είναι οι συντελεστές της δευτεροβάθμιας εξίσωσης: a=5, b=6 και c=2. Αντικαθιστούμε αυτές τις τιμές στον τύπο διάκρισης, έχουμε D=b 2 −4·a·c=6 2 −4·5·2=36−40=−4. Η διάκριση είναι αρνητική, επομένως, αυτή η τετραγωνική εξίσωση δεν έχει πραγματικές ρίζες.
Εάν πρέπει να καθορίσετε σύνθετες ρίζες, χρησιμοποιήστε γνωστή φόρμουλαρίζες μιας τετραγωνικής εξίσωσης και εκτελέστε δράσεις με μιγαδικοί αριθμοί
:
Απάντηση:
δεν υπάρχουν πραγματικές ρίζες, οι σύνθετες ρίζες είναι: .
Ας σημειώσουμε για άλλη μια φορά ότι εάν η διάκριση μιας δευτεροβάθμιας εξίσωσης είναι αρνητική, τότε στο σχολείο συνήθως γράφουν αμέσως μια απάντηση στην οποία υποδεικνύουν ότι δεν υπάρχουν πραγματικές ρίζες και δεν βρίσκονται σύνθετες ρίζες.
Τύπος ρίζας για ακόμη και δεύτερους συντελεστές
Ο τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης, όπου D=b 2 −4·a·c σας επιτρέπει να αποκτήσετε έναν τύπο πιο συμπαγούς μορφής, που σας επιτρέπει να λύσετε τετραγωνικές εξισώσεις με άρτιο συντελεστή για x (ή απλά με συντελεστής που έχει τη μορφή 2·n, για παράδειγμα, ή 14· ln5=2·7·ln5 ). Ας τη βγάλουμε.
Ας υποθέσουμε ότι πρέπει να λύσουμε μια τετραγωνική εξίσωση της μορφής a x 2 +2 n x+c=0. Ας βρούμε τις ρίζες του χρησιμοποιώντας τον τύπο που γνωρίζουμε. Για να γίνει αυτό, υπολογίζουμε τη διάκριση D=(2 n) 2 −4 a c=4 n 2 −4 a c=4 (n 2 −a c), και στη συνέχεια χρησιμοποιούμε τον τύπο ρίζας:
Ας υποδηλώσουμε την παράσταση n 2 −a c ως D 1 (μερικές φορές συμβολίζεται με D ").Τότε ο τύπος για τις ρίζες της δευτεροβάθμιας εξίσωσης που εξετάζουμε με τον δεύτερο συντελεστή 2 n θα πάρει τη μορφή  , όπου D 1 =n 2 −a·c.
, όπου D 1 =n 2 −a·c.
Είναι εύκολο να δούμε ότι D=4·D 1, ή D 1 =D/4. Με άλλα λόγια, το D 1 είναι το τέταρτο μέρος της διάκρισης. Είναι σαφές ότι το πρόσημο του D 1 είναι το ίδιο με το πρόσημο του D . Δηλαδή, το πρόσημο D 1 είναι επίσης δείκτης παρουσίας ή απουσίας ριζών μιας τετραγωνικής εξίσωσης.
Άρα, για να λύσετε μια τετραγωνική εξίσωση με δεύτερο συντελεστή 2·n, χρειάζεστε
- Υπολογίστε D 1 =n 2 −a·c ;
- Αν Δ 1<0 , то сделать вывод, что действительных корней нет;
- Εάν D 1 =0, τότε υπολογίστε τη μοναδική ρίζα της εξίσωσης χρησιμοποιώντας τον τύπο.
- Αν D 1 >0, τότε βρείτε δύο πραγματικές ρίζες χρησιμοποιώντας τον τύπο.
Ας εξετάσουμε το ενδεχόμενο επίλυσης του παραδείγματος χρησιμοποιώντας τον τύπο ρίζας που λαμβάνεται σε αυτήν την παράγραφο.
Παράδειγμα.
Λύστε την δευτεροβάθμια εξίσωση 5 x 2 −6 x −32=0 .
Λύση.
Ο δεύτερος συντελεστής αυτής της εξίσωσης μπορεί να αναπαρασταθεί ως 2·(−3) . Δηλαδή, μπορείτε να ξαναγράψετε την αρχική τετραγωνική εξίσωση με τη μορφή 5 x 2 +2 (−3) x−32=0, εδώ a=5, n=−3 και c=−32, και να υπολογίσετε το τέταρτο μέρος του διακριτικός: D 1 =n 2 −a·c=(−3) 2 −5·(−32)=9+160=169. Εφόσον η τιμή της είναι θετική, η εξίσωση έχει δύο πραγματικές ρίζες. Ας τα βρούμε χρησιμοποιώντας τον κατάλληλο τύπο ρίζας:
Σημειώστε ότι ήταν δυνατό να χρησιμοποιηθεί ο συνήθης τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης, αλλά στην περίπτωση αυτή θα έπρεπε να εκτελεστεί περισσότερη υπολογιστική εργασία.
Απάντηση:
Απλοποίηση της μορφής των τετραγωνικών εξισώσεων
Μερικές φορές, πριν αρχίσετε να υπολογίζετε τις ρίζες μιας τετραγωνικής εξίσωσης χρησιμοποιώντας τύπους, δεν βλάπτει να κάνετε την ερώτηση: "Είναι δυνατόν να απλοποιήσετε τη μορφή αυτής της εξίσωσης;" Συμφωνήστε ότι από πλευράς υπολογισμών θα είναι ευκολότερο να λύσετε την εξίσωση του δευτεροβάθμιου 11 x 2 −4 x−6=0 παρά 1100 x 2 −400 x−600=0.
Συνήθως, η απλοποίηση της μορφής μιας τετραγωνικής εξίσωσης επιτυγχάνεται πολλαπλασιάζοντας ή διαιρώντας και τις δύο πλευρές με έναν ορισμένο αριθμό. Για παράδειγμα, στην προηγούμενη παράγραφο ήταν δυνατό να απλοποιηθεί η εξίσωση 1100 x 2 −400 x −600=0 διαιρώντας και τις δύο πλευρές με το 100.
Παρόμοιος μετασχηματισμός πραγματοποιείται με τετραγωνικές εξισώσεις, οι συντελεστές των οποίων δεν είναι . Σε αυτή την περίπτωση, συνήθως διαιρούμε και τις δύο πλευρές της εξίσωσης με απόλυτες τιμέςτους συντελεστές του. Για παράδειγμα, ας πάρουμε την τετραγωνική εξίσωση 12 x 2 −42 x+48=0. απόλυτες τιμές των συντελεστών του: GCD(12, 42, 48)= GCD(GCD(12, 42), 48)= GCD(6, 48)=6. Διαιρώντας και τις δύο πλευρές της αρχικής τετραγωνικής εξίσωσης με 6, καταλήγουμε στην ισοδύναμη τετραγωνική εξίσωση 2 x 2 −7 x+8=0.
Και ο πολλαπλασιασμός και των δύο πλευρών μιας τετραγωνικής εξίσωσης συνήθως γίνεται για να απαλλαγούμε από αυτήν κλασματικές πιθανότητες. Στην περίπτωση αυτή, ο πολλαπλασιασμός πραγματοποιείται με τους παρονομαστές των συντελεστών του. Για παράδειγμα, αν και οι δύο πλευρές της τετραγωνικής εξίσωσης πολλαπλασιαστούν με LCM(6, 3, 1)=6, τότε θα πάρει την απλούστερη μορφή x 2 +4·x−18=0.
Ολοκληρώνοντας αυτό το σημείο, σημειώνουμε ότι σχεδόν πάντα ξεφορτώνονται το μείον στον υψηλότερο συντελεστή μιας τετραγωνικής εξίσωσης αλλάζοντας τα πρόσημα όλων των όρων, που αντιστοιχεί στον πολλαπλασιασμό (ή στη διαίρεση) και των δύο πλευρών με −1. Για παράδειγμα, συνήθως κινείται κανείς από την δευτεροβάθμια εξίσωση −2 x 2 −3 x+7=0 στη λύση 2 x 2 +3 x−7=0 .
Σχέση μεταξύ ριζών και συντελεστών μιας τετραγωνικής εξίσωσης
Ο τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης εκφράζει τις ρίζες της εξίσωσης μέσω των συντελεστών της. Με βάση τον τύπο ρίζας, μπορείτε να αποκτήσετε άλλες σχέσεις μεταξύ ριζών και συντελεστών.
Οι πιο γνωστοί και εφαρμόσιμοι τύποι από το θεώρημα του Vieta είναι της μορφής και . Ειδικότερα, για τη δεδομένη τετραγωνική εξίσωση, το άθροισμα των ριζών είναι ίσο με τον δεύτερο συντελεστή με το αντίθετο πρόσημο και το γινόμενο των ριζών είναι ίσο με τον ελεύθερο όρο. Για παράδειγμα, βλέποντας τη μορφή της δευτεροβάθμιας εξίσωσης 3 x 2 −7 x + 22 = 0, μπορούμε αμέσως να πούμε ότι το άθροισμα των ριζών της είναι ίσο με 7/3 και το γινόμενο των ριζών είναι ίσο με 22 /3.
Χρησιμοποιώντας τους ήδη γραμμένους τύπους, μπορείτε να αποκτήσετε έναν αριθμό άλλων συνδέσεων μεταξύ των ριζών και των συντελεστών της τετραγωνικής εξίσωσης. Για παράδειγμα, μπορείτε να εκφράσετε το άθροισμα των τετραγώνων των ριζών μιας τετραγωνικής εξίσωσης μέσω των συντελεστών της: .
Βιβλιογραφία.
- Αλγεβρα:εγχειρίδιο για την 8η τάξη. γενική εκπαίδευση ιδρύματα / [Γιού. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; επεξεργάστηκε από S. A. Telyakovsky. - 16η έκδ. - Μ.: Εκπαίδευση, 2008. - 271 σελ. : Εγώ θα. - ISBN 978-5-09-019243-9.
- Mordkovich A. G.Αλγεβρα. 8η τάξη. Στις 2 μ.μ. Μέρος 1. Εγχειρίδιο για μαθητές Εκπαιδευτικά ιδρύματα/ A. G. Mordkovich. - 11η έκδ., σβησμένο. - Μ.: Μνημοσύνη, 2009. - 215 σελ.: εικ. ISBN 978-5-346-01155-2.
5x (x - 4) = 0
5 x = 0 ή x - 4 = 0
x = ± √ 25/4
Έχοντας μάθει να λύνεις εξισώσεις πρώτου βαθμού, φυσικά, θέλεις να συνεργαστείς με άλλους, ειδικότερα, με εξισώσεις δεύτερου βαθμού, που αλλιώς ονομάζονται τετραγωνικές.
Οι τετραγωνικές εξισώσεις είναι εξισώσεις όπως ax² + bx + c = 0, όπου η μεταβλητή είναι x, οι αριθμοί είναι a, b, c, όπου το a δεν είναι ίσο με μηδέν.
Εάν σε μια τετραγωνική εξίσωση ο ένας ή ο άλλος συντελεστής (c ή b) είναι ίσος με μηδέν, τότε αυτή η εξίσωση θα ταξινομηθεί ως ημιτελής τετραγωνική εξίσωση.
Πώς να λύσετε μια ημιτελή δευτεροβάθμια εξίσωση αν οι μαθητές μπορούσαν μέχρι τώρα να λύσουν μόνο εξισώσεις πρώτου βαθμού; Θεωρήστε ημιτελείς τετραγωνικές εξισώσεις ΔΙΑΦΟΡΕΤΙΚΟΙ ΤΥΠΟΙκαι απλούς τρόπους επίλυσής τους.
α) Εάν ο συντελεστής c είναι ίσος με 0 και ο συντελεστής b δεν είναι ίσος με μηδέν, τότε το ax ² + bx + 0 = 0 ανάγεται σε μια εξίσωση της μορφής ax ² + bx = 0.
Για να λύσετε μια τέτοια εξίσωση, πρέπει να γνωρίζετε τον τύπο για την επίλυση μιας ημιτελούς τετραγωνικής εξίσωσης, η οποία συνίσταται στην παραγοντοποίηση της αριστερής πλευράς της και αργότερα στη χρήση της συνθήκης ότι το γινόμενο είναι ίσο με μηδέν.
Για παράδειγμα, 5x² - 20x = 0. Συνυπολογίζουμε την αριστερή πλευρά της εξίσωσης, ενώ κάνουμε το συνηθισμένο μαθηματική πράξη: μετακίνηση του συνολικού συντελεστή εκτός παρενθέσεων
5x (x - 4) = 0
Χρησιμοποιούμε την προϋπόθεση ότι τα γινόμενα είναι ίσα με μηδέν.
5 x = 0 ή x - 4 = 0
Η απάντηση θα είναι: η πρώτη ρίζα είναι 0. η δεύτερη ρίζα είναι 4.
β) Αν b = 0, και ο ελεύθερος όρος δεν είναι ίσος με μηδέν, τότε η εξίσωση ax ² + 0x + c = 0 ανάγεται σε μια εξίσωση της μορφής ax ² + c = 0. Οι εξισώσεις λύνονται με δύο τρόπους : α) με παραγοντοποίηση του πολυωνύμου της εξίσωσης στην αριστερή πλευρά ; β) χρησιμοποιώντας τις ιδιότητες της αριθμητικής τετραγωνικής ρίζας. Μια τέτοια εξίσωση μπορεί να λυθεί χρησιμοποιώντας μία από τις μεθόδους, για παράδειγμα:
x = ± √ 25/4
x = ± 5/2. Η απάντηση θα είναι: η πρώτη ρίζα είναι 5/2. η δεύτερη ρίζα είναι ίση με - 5/2.
γ) Εάν το b είναι ίσο με 0 και το c είναι ίσο με 0, τότε το ax ² + 0 + 0 = 0 ανάγεται σε μια εξίσωση της μορφής ax ² = 0. Σε μια τέτοια εξίσωση το x θα είναι ίσο με 0.
Όπως μπορείτε να δείτε, οι ημιτελείς τετραγωνικές εξισώσεις δεν μπορούν να έχουν περισσότερες από δύο ρίζες.
Αυτό το θέμα μπορεί να φαίνεται δύσκολο στην αρχή λόγω πολλών όχι και τόσο απλοί τύποι. Όχι μόνο οι ίδιες οι τετραγωνικές εξισώσεις έχουν μακριές σημειώσεις, αλλά οι ρίζες βρίσκονται επίσης μέσω της διάκρισης. Συνολικά, λαμβάνονται τρεις νέοι τύποι. Δεν είναι πολύ εύκολο να θυμάστε. Αυτό είναι δυνατό μόνο μετά την επίλυση τέτοιων εξισώσεων συχνά. Τότε όλοι οι τύποι θα θυμούνται από μόνες τους.
Γενική άποψη τετραγωνικής εξίσωσης
Εδώ προτείνουμε τη ρητή καταγραφή τους, όταν τα περισσότερα υψηλός βαθμόςγραμμένο πρώτα και μετά με φθίνουσα σειρά. Υπάρχουν συχνά περιπτώσεις όπου οι όροι είναι ασυνεπείς. Τότε είναι καλύτερο να ξαναγράψουμε την εξίσωση με φθίνουσα σειρά του βαθμού της μεταβλητής.
Ας εισάγουμε κάποια σημειογραφία. Παρουσιάζονται στον παρακάτω πίνακα.
Εάν δεχθούμε αυτούς τους συμβολισμούς, όλες οι δευτεροβάθμιες εξισώσεις ανάγονται στον ακόλουθο συμβολισμό.

Επιπλέον, ο συντελεστής a ≠ 0. Ας οριστεί αυτός ο τύπος ως νούμερο ένα.
Όταν δίνεται μια εξίσωση, δεν είναι ξεκάθαρο πόσες ρίζες θα υπάρχουν στην απάντηση. Επειδή μία από τις τρεις επιλογές είναι πάντα δυνατή:
- η λύση θα έχει δύο ρίζες.
- η απάντηση θα είναι ένας αριθμός.
- η εξίσωση δεν θα έχει καθόλου ρίζες.
Και μέχρι να οριστικοποιηθεί η απόφαση, είναι δύσκολο να καταλάβουμε ποια επιλογή θα εμφανιστεί σε μια συγκεκριμένη περίπτωση.
Είδη καταγραφών τετραγωνικών εξισώσεων
Μπορεί να υπάρχουν διαφορετικές καταχωρήσεις στις εργασίες. Δεν θα μοιάζουν πάντα με τον γενικό τύπο της τετραγωνικής εξίσωσης. Μερικές φορές θα λείπουν κάποιοι όροι. Αυτό που γράφτηκε παραπάνω είναι η πλήρης εξίσωση. Εάν αφαιρέσετε τον δεύτερο ή τον τρίτο όρο σε αυτό, θα λάβετε κάτι άλλο. Αυτές οι εγγραφές ονομάζονται επίσης τετραγωνικές εξισώσεις, μόνο ελλιπείς.
Επιπλέον, μόνο όροι με συντελεστές "b" και "c" μπορούν να εξαφανιστούν. Ο αριθμός «α» δεν μπορεί σε καμία περίπτωση να είναι ίσος με μηδέν. Γιατί σε αυτή την περίπτωση ο τύπος μετατρέπεται σε γραμμική εξίσωση. Οι τύποι για την ημιτελή μορφή εξισώσεων θα είναι οι εξής:
Άρα, υπάρχουν μόνο δύο τύποι· εκτός από τους πλήρεις, υπάρχουν και ημιτελείς τετραγωνικές εξισώσεις. Αφήστε τον πρώτο τύπο να είναι ο αριθμός δύο και ο δεύτερος - τρία.
Διάκριση και εξάρτηση του αριθμού των ριζών από την αξία του
Πρέπει να γνωρίζετε αυτόν τον αριθμό για να υπολογίσετε τις ρίζες της εξίσωσης. Μπορεί πάντα να υπολογιστεί, ανεξάρτητα από το ποιος είναι ο τύπος της τετραγωνικής εξίσωσης. Για να υπολογίσετε τη διάκριση, πρέπει να χρησιμοποιήσετε την ισότητα που γράφεται παρακάτω, η οποία θα έχει τον αριθμό τέσσερα.
Αφού αντικαταστήσετε τις τιμές των συντελεστών σε αυτόν τον τύπο, μπορείτε να λάβετε αριθμούς με διαφορετικά σημάδια. Εάν η απάντηση είναι ναι, τότε η απάντηση στην εξίσωση είναι δύο διάφορες ρίζες. Στο αρνητικός αριθμόςθα λείπουν οι ρίζες της τετραγωνικής εξίσωσης. Αν είναι ίσο με μηδέν, θα υπάρχει μόνο μία απάντηση.
Πώς να λύσετε μια πλήρη τετραγωνική εξίσωση;
Μάλιστα, η εξέταση αυτού του θέματος έχει ήδη ξεκινήσει. Γιατί πρώτα πρέπει να βρεις έναν διακριτικό. Αφού διαπιστωθεί ότι υπάρχουν ρίζες της τετραγωνικής εξίσωσης και είναι γνωστός ο αριθμός τους, πρέπει να χρησιμοποιήσετε τύπους για τις μεταβλητές. Εάν υπάρχουν δύο ρίζες, τότε πρέπει να εφαρμόσετε τον ακόλουθο τύπο.

Δεδομένου ότι περιέχει ένα σύμβολο "±", θα υπάρχουν δύο τιμές. Η έκφραση κάτω από το σύμβολο της τετραγωνικής ρίζας είναι η διάκριση. Επομένως, ο τύπος μπορεί να ξαναγραφτεί διαφορετικά.
Φόρμουλα νούμερο πέντε. Από την ίδια εγγραφή είναι ξεκάθαρο ότι εάν η διάκριση είναι ίση με μηδέν, τότε και οι δύο ρίζες θα λάβουν τις ίδιες τιμές.
Εάν η επίλυση τετραγωνικών εξισώσεων δεν έχει ακόμη επεξεργαστεί, τότε είναι καλύτερο να γράψετε τις τιμές όλων των συντελεστών πριν εφαρμόσετε τους τύπους διάκρισης και μεταβλητής. Αργότερα αυτή η στιγμή δεν θα προκαλέσει δυσκολίες. Αλλά στην αρχή υπάρχει σύγχυση.

Πώς να λύσετε μια ημιτελή τετραγωνική εξίσωση;
Όλα είναι πολύ πιο απλά εδώ. Δεν υπάρχει καν ανάγκη για πρόσθετους τύπους. Και αυτά που έχουν ήδη γραφτεί για τον διακρίνοντα και τον άγνωστο δεν θα χρειαστούν.
Αρχικά, ας δούμε την ημιτελή εξίσωση νούμερο δύο. Σε αυτή την ισότητα, είναι απαραίτητο να βγάλουμε την άγνωστη ποσότητα από αγκύλες και να λύσουμε τη γραμμική εξίσωση, η οποία θα παραμείνει σε αγκύλες. Η απάντηση θα έχει δύο ρίζες. Το πρώτο είναι απαραίτητα ίσο με μηδέν, γιατί υπάρχει ένας πολλαπλασιαστής που αποτελείται από την ίδια τη μεταβλητή. Το δεύτερο θα ληφθεί λύνοντας μια γραμμική εξίσωση.
Η ημιτελής εξίσωση αριθμός τρία λύνεται μετακινώντας τον αριθμό από την αριστερή πλευρά της ισότητας προς τα δεξιά. Στη συνέχεια, πρέπει να διαιρέσετε με τον συντελεστή που βλέπει το άγνωστο. Το μόνο που μένει είναι να εξαγάγετε την τετραγωνική ρίζα και να θυμάστε να τη γράψετε δύο φορές με αντίθετα σημάδια.

Παρακάτω είναι μερικά βήματα που θα σας βοηθήσουν να μάθετε πώς να λύνετε κάθε είδους ισότητες που μετατρέπονται σε εξισώσεις δευτεροβάθμιας. Θα βοηθήσουν τον μαθητή να αποφύγει λάθη που οφείλονται σε απροσεξία. Αυτές οι ελλείψεις μπορούν να προκαλέσουν χαμηλούς βαθμούς κατά τη μελέτη του εκτενούς θέματος «Τετραγωνικές Εξισώσεις (8η Δημοτικού).» Στη συνέχεια, αυτές οι ενέργειες δεν θα χρειάζεται να εκτελούνται συνεχώς. Γιατί θα εμφανιστεί μια σταθερή ικανότητα.
- Πρώτα πρέπει να γράψετε την εξίσωση σε τυπική μορφή. Δηλαδή, πρώτα ο όρος με τον μεγαλύτερο βαθμό της μεταβλητής και μετά - χωρίς βαθμό, και τελευταίος - μόνο ένας αριθμός.
- Εάν εμφανιστεί ένα μείον πριν από τον συντελεστή "a", μπορεί να περιπλέξει τη δουλειά για έναν αρχάριο που μελετά τις δευτεροβάθμιες εξισώσεις. Είναι καλύτερα να το ξεφορτωθείς. Για το σκοπό αυτό, όλη η ισότητα πρέπει να πολλαπλασιαστεί με "-1". Αυτό σημαίνει ότι όλοι οι όροι θα αλλάξουν πρόσημο στο αντίθετο.
- Συνιστάται να απαλλαγείτε από τα κλάσματα με τον ίδιο τρόπο. Απλώς πολλαπλασιάστε την εξίσωση με τον κατάλληλο παράγοντα έτσι ώστε οι παρονομαστές να ακυρωθούν.

Παραδείγματα
Απαιτείται η επίλυση των ακόλουθων τετραγωνικών εξισώσεων:
x 2 − 7x = 0;
15 − 2x − x 2 = 0;
x 2 + 8 + 3x = 0;
12x + x 2 + 36 = 0;
(x+1) 2 + x + 1 = (x+1) (x+2).
Η πρώτη εξίσωση: x 2 − 7x = 0. Είναι ελλιπής, επομένως λύνεται όπως περιγράφεται για τον τύπο δύο.
Αφού το βγάλετε από αγκύλες, προκύπτει: x (x - 7) = 0.
Η πρώτη ρίζα παίρνει την τιμή: x 1 = 0. Η δεύτερη θα βρεθεί από γραμμική εξίσωση: x - 7 = 0. Είναι εύκολο να δούμε ότι x 2 = 7.
Δεύτερη εξίσωση: 5x 2 + 30 = 0. Και πάλι ημιτελής. Μόνο που λύνεται όπως περιγράφεται για τον τρίτο τύπο.
Αφού μετακινήσετε το 30 στη δεξιά πλευρά της εξίσωσης: 5x 2 = 30. Τώρα πρέπει να διαιρέσετε με το 5. Αποδεικνύεται: x 2 = 6. Οι απαντήσεις θα είναι οι αριθμοί: x 1 = √6, x 2 = - √6.
Η τρίτη εξίσωση: 15 − 2х − x 2 = 0. Εδώ και περαιτέρω, η επίλυση των δευτεροβάθμιων εξισώσεων θα ξεκινήσει με την επανεγγραφή τους σε τυπική όψη: − x 2 − 2x + 15 = 0. Τώρα ήρθε η ώρα να χρησιμοποιήσετε το δεύτερο χρήσιμες συμβουλέςκαι πολλαπλασιάζουμε τα πάντα με μείον ένα. Αποδεικνύεται x 2 + 2x - 15 = 0. Χρησιμοποιώντας τον τέταρτο τύπο, πρέπει να υπολογίσετε τη διάκριση: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. Είναι θετικός αριθμός. Από όσα ειπώθηκαν παραπάνω, προκύπτει ότι η εξίσωση έχει δύο ρίζες. Πρέπει να υπολογιστούν χρησιμοποιώντας τον πέμπτο τύπο. Αποδεικνύεται ότι x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Τότε x 1 = 3, x 2 = - 5.
Η τέταρτη εξίσωση x 2 + 8 + 3x = 0 μετατρέπεται σε αυτή: x 2 + 3x + 8 = 0. Η διάκρισή της είναι ίση με αυτήν την τιμή: -23. Δεδομένου ότι αυτός ο αριθμός είναι αρνητικός, η απάντηση σε αυτήν την εργασία θα είναι η ακόλουθη καταχώριση: "Δεν υπάρχουν ρίζες".
Η πέμπτη εξίσωση 12x + x 2 + 36 = 0 θα πρέπει να ξαναγραφτεί ως εξής: x 2 + 12x + 36 = 0. Μετά την εφαρμογή του τύπου για τη διάκριση, προκύπτει ο αριθμός μηδέν. Αυτό σημαίνει ότι θα έχει μία ρίζα, δηλαδή: x = -12/ (2 * 1) = -6.
Η έκτη εξίσωση (x+1) 2 + x + 1 = (x+1)(x+2) απαιτεί μετασχηματισμούς, οι οποίοι συνίστανται στην παρόμοιους όρους, πριν ανοίξετε τα στηρίγματα. Στη θέση της πρώτης θα υπάρχει η ακόλουθη έκφραση: x 2 + 2x + 1. Μετά την ισότητα, θα εμφανιστεί αυτή η καταχώρηση: x 2 + 3x + 2. Αφού μετρηθούν παρόμοιοι όροι, η εξίσωση θα πάρει τη μορφή: x 2 - x = 0. Έχει γίνει ημιτελής . Κάτι παρόμοιο έχει ήδη συζητηθεί λίγο πιο πάνω. Οι ρίζες αυτού θα είναι οι αριθμοί 0 και 1.
Είναι γνωστό ότι είναι μια συγκεκριμένη εκδοχή της ισότητας ax 2 + bx + c = o, όπου τα a, b και c είναι πραγματικοί συντελεστές για άγνωστο x, και όπου a ≠ o, και b και c θα είναι μηδενικά - ταυτόχρονα ή χωριστά. Για παράδειγμα, c = o, b ≠ o ή αντίστροφα. Σχεδόν θυμηθήκαμε τον ορισμό της τετραγωνικής εξίσωσης.
Το τριώνυμο δεύτερου βαθμού είναι μηδέν. Ο πρώτος του συντελεστής a ≠ o, b και c μπορεί να πάρει οποιεσδήποτε τιμές. Η τιμή της μεταβλητής x θα είναι τότε όταν η αντικατάσταση τη μετατρέψει σε σωστή αριθμητική ισότητα. Ας εστιάσουμε στις πραγματικές ρίζες, αν και οι εξισώσεις μπορεί να είναι και λύσεις.Συνηθίζεται να ονομάζουμε μια εξίσωση ολοκληρωμένη στην οποία κανένας από τους συντελεστές δεν είναι ίσος με o, a ≠ o, b ≠ o, c ≠ o.
Ας λύσουμε ένα παράδειγμα. 2x 2 -9x-5 = ω, βρίσκουμε
D = 81+40 = 121,
Το D είναι θετικό, που σημαίνει ότι υπάρχουν ρίζες, x 1 = (9+√121):4 = 5, και το δεύτερο x 2 = (9-√121):4 = -o.5. Ο έλεγχος θα σας βοηθήσει να βεβαιωθείτε ότι είναι σωστές.
Ακολουθεί μια βήμα προς βήμα λύση της τετραγωνικής εξίσωσης
Χρησιμοποιώντας το διαχωριστικό, μπορείτε να λύσετε οποιαδήποτε εξίσωση στην αριστερή πλευρά της οποίας υπάρχει μια γνωστή τετραγωνικό τριώνυμογια ένα ≠ ο. Στο παράδειγμά μας. 2x 2 -9x-5 = 0 (ax 2 +in+s = o)

Ας εξετάσουμε ποιες είναι οι ημιτελείς εξισώσεις δεύτερου βαθμού
- τσεκούρι 2 +σε = ο. Ο ελεύθερος όρος, ο συντελεστής c στο x 0, είναι ίσος με μηδέν εδώ, σε ≠ o.
Πώς να λύσετε μια ημιτελή τετραγωνική εξίσωση αυτού του τύπου; Ας βγάλουμε το x από αγκύλες. Ας θυμηθούμε όταν το γινόμενο δύο παραγόντων είναι ίσο με μηδέν.
x(ax+b) = o, αυτό μπορεί να είναι όταν x = o ή όταν ax+b = o.
Έχοντας λύσει το 2ο έχουμε x = -в/а.
Ως αποτέλεσμα, έχουμε ρίζες x 1 = 0, σύμφωνα με τους υπολογισμούς x 2 = -b/a. - Τώρα ο συντελεστής x είναι ίσος με o, και c δεν είναι ίσος με (≠) o.
x 2 +c = o. Ας μετακινήσουμε το c στη δεξιά πλευρά της ισότητας, παίρνουμε x 2 = -с. Αυτή η εξίσωση έχει πραγματικές ρίζες μόνο όταν -c είναι θετικός αριθμός (c ‹ o),
Το x 1 είναι τότε ίσο με √(-c), αντίστοιχα, το x 2 είναι -√(-c). Διαφορετικά, η εξίσωση δεν έχει καθόλου ρίζες. - Η τελευταία επιλογή: b = c = o, δηλαδή, ax 2 = o. Φυσικά, μια τόσο απλή εξίσωση έχει μία ρίζα, x = o.

Ειδικές περιπτώσεις
Εξετάσαμε πώς να λύσουμε μια ημιτελή τετραγωνική εξίσωση και τώρα ας πάρουμε οποιουσδήποτε τύπους.
- Σε μια πλήρη τετραγωνική εξίσωση, ο δεύτερος συντελεστής του x είναι ένας ζυγός αριθμός.
Έστω k = ο.5β. Έχουμε τύπους για τον υπολογισμό της διάκρισης και των ριζών.
D/4 = k 2 - ac, οι ρίζες υπολογίζονται ως x 1,2 = (-k±√(D/4))/a για D › o.
x = -k/a στο D = o.
Δεν υπάρχουν ρίζες για το D ‹ o. - Δίνονται τετραγωνικές εξισώσεις, όταν ο συντελεστής του x στο τετράγωνο είναι ίσος με 1, συνήθως γράφονται x 2 + рх + q = o. Όλοι οι παραπάνω τύποι ισχύουν για αυτούς, αλλά οι υπολογισμοί είναι κάπως απλούστεροι.
Παράδειγμα, x 2 -4x-9 = 0. Υπολογίστε το D: 2 2 +9, D = 13.
x 1 = 2+√13, x 2 = 2-√13. - Επιπλέον, είναι εύκολο να εφαρμοστεί σε αυτά που δίνονται. Λέει ότι το άθροισμα των ριζών της εξίσωσης είναι ίσο με -p, ο δεύτερος συντελεστής με μείον (εννοείται αντίθετο σημάδι), και το γινόμενο αυτών των ίδιων ριζών θα είναι ίσο με q, τον ελεύθερο όρο. Δείτε πόσο εύκολο θα ήταν να προσδιορίσετε προφορικά τις ρίζες αυτής της εξίσωσης. Για μη ανηγμένους συντελεστές (για όλους τους συντελεστές που δεν είναι ίσοι με μηδέν), αυτό το θεώρημα ισχύει ως εξής: το άθροισμα x 1 + x 2 είναι ίσο με -b/a, το γινόμενο x 1 · x 2 είναι ίσο με c/a.
Το άθροισμα του ελεύθερου όρου c και του πρώτου συντελεστή α είναι ίσο με τον συντελεστή β. Σε αυτήν την περίπτωση, η εξίσωση έχει τουλάχιστον μία ρίζα (εύκολη στην απόδειξη), η πρώτη είναι απαραίτητα ίση με -1 και η δεύτερη -c/a, αν υπάρχει. Μπορείτε να ελέγξετε πώς να λύσετε μόνοι σας μια ημιτελή τετραγωνική εξίσωση. Πανεύκολος. Οι συντελεστές μπορεί να βρίσκονται σε ορισμένες σχέσεις μεταξύ τους
- x 2 +x = o, 7x 2 -7 = o.
- Το άθροισμα όλων των συντελεστών είναι ίσο με o.
Οι ρίζες μιας τέτοιας εξίσωσης είναι 1 και c/a. Παράδειγμα, 2x 2 -15x+13 = o.
x 1 = 1, x 2 = 13/2.
Υπάρχουν πολλοί άλλοι τρόποι επίλυσης διαφόρων εξισώσεων δεύτερου βαθμού. Εδώ, για παράδειγμα, είναι μια μέθοδος εξαγωγής από ένα δεδομένο πολυώνυμο πλήρες τετράγωνο. Γραφικές μέθοδοιμερικοί. Όταν ασχολείσαι συχνά με τέτοια παραδείγματα, θα μάθεις να τα «κλικ»ς σαν σπόροι, γιατί όλες οι μέθοδοι σου έρχονται αυτόματα στο μυαλό.
Η χρήση των εξισώσεων είναι ευρέως διαδεδομένη στη ζωή μας. Χρησιμοποιούνται σε πολλούς υπολογισμούς, κατασκευές κατασκευών ακόμα και σε αθλήματα. Ο άνθρωπος χρησιμοποιούσε εξισώσεις στην αρχαιότητα, και από τότε η χρήση τους έχει αυξηθεί. Ο διαχωριστής σάς επιτρέπει να λύσετε οποιαδήποτε δευτεροβάθμια εξίσωση χρησιμοποιώντας γενικός τύπος, που μοιάζει με αυτό:
Ο τύπος διάκρισης εξαρτάται από το βαθμό του πολυωνύμου. Ο παραπάνω τύπος είναι κατάλληλος για την επίλυση τετραγωνικών εξισώσεων τον παρακάτω τύπο:
Η διάκριση έχει παρακάτω ιδιότητεςπράγματα που πρέπει να γνωρίζετε:
* Το "D" είναι 0 όταν το πολυώνυμο έχει πολλαπλές ρίζες ( ίσες ρίζες);
* Το "D" είναι ένα συμμετρικό πολυώνυμο σε σχέση με τις ρίζες του πολυωνύμου και επομένως είναι πολυώνυμο στους συντελεστές του. Επιπλέον, οι συντελεστές αυτού του πολυωνύμου είναι ακέραιοι ανεξάρτητα από την προέκταση στην οποία λαμβάνονται οι ρίζες.
Ας υποθέσουμε ότι μας δίνεται μια τετραγωνική εξίσωση της ακόλουθης μορφής:
1 εξίσωση
Σύμφωνα με τον τύπο έχουμε:
Αφού \, η εξίσωση έχει 2 ρίζες. Ας τις ορίσουμε:
Πού μπορώ να λύσω μια εξίσωση χρησιμοποιώντας έναν διαδικτυακό επιλύτη διάκρισης;
Μπορείτε να λύσετε την εξίσωση στην ιστοσελίδα μας https://site. Ο δωρεάν διαδικτυακός λύτης θα σας επιτρέψει να λύσετε διαδικτυακές εξισώσεις οποιασδήποτε πολυπλοκότητας μέσα σε λίγα δευτερόλεπτα. Το μόνο που χρειάζεται να κάνετε είναι απλώς να εισαγάγετε τα δεδομένα σας στο πρόγραμμα επίλυσης. Μπορείτε επίσης να παρακολουθήσετε τις οδηγίες βίντεο και να μάθετε πώς να λύσετε την εξίσωση στον ιστότοπό μας. Και εάν έχετε ερωτήσεις, μπορείτε να τις ρωτήσετε στην ομάδα VKontakte http://vk.com/pocketteacher. Γίνετε μέλος της ομάδας μας, είμαστε πάντα στην ευχάριστη θέση να σας βοηθήσουμε.
 Θωρηκτό «Victory» – Θρυλικά ιστιοφόρα
Θωρηκτό «Victory» – Θρυλικά ιστιοφόρα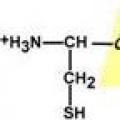 Σχηματισμός πεπτιδικού δεσμού Δύο ισοδύναμες μορφές
Σχηματισμός πεπτιδικού δεσμού Δύο ισοδύναμες μορφές Kasatkin Mikhail Alexandrovich (1902–1974) M Kasatkin
Kasatkin Mikhail Alexandrovich (1902–1974) M Kasatkin