Шматково лінійна функція задана формулою знайти в. Х = 1-точка зміни формул

7
Урок з алгебри у 9А класі вчителя Микитчук Ж.М. МОУ «ЗОШ №23»19.03.07гТема урока: «Шматково-задані функції» Цілі:

мовну культуру

В результаті узагальнення теми учні мають знати:

заданої функції

вміти:

будувати графік шматково-заданої функції; читати графік; задавати функцію аналітично за графіком.

Хід уроку

I. Організаційно-психологічний момент. Почнемо наш урок словами Д.К.Фадєєва «Яке б завдання ви не вирішували, в кінцевому підсумку чекає щаслива хвилина - радісне почуття успіху, зміцнення віри в свої сили. Нехай ці слова на нашому уроці знайдуть реальне підтвердження. ІІ. Перевірка домашнього завдання. Почнемо урок як завжди з перевірки д/з. Повторіть визначення шматкової функції та план дослідження функций.1). На дошцізобразити вигадані вами графіки шматочкових функцій (рис.1,2,3)2). Картки. №1. Розставте порядок дослідження властивостей функцій:

найменше значення

№2. Зобразіть схематично графіки функцій:

А) у = kx + b, k0; Б) y = kx, k0;

У) у = , k0.

3).Усна робота . - 2 хв

Яка функція називається шматковою?Шматковою називається функція, задана різними формуламина різних проміжках.

З яких функцій складаються шматкові функції, зображені на рис.1, 2, 3? Які ще назви функцій ви знаєте? Як називаються графіки відповідних функцій? Чи є графіком будь-якої функції, фігура, зображена на рис.4? Чому?Відповідь:ні, т.к. за визначенням функції, кожному значенню незалежної змінної х ставиться у відповідність єдине значення залежної змінної у. 4) Самоконтроль - 3 хв.Із запропонованих графіків та відповідних формул, що задають функції, виберіть правильні. З отриманих букв відповідей складіть знайоме слово. Відповідь: ГРАФІК Де в житті, в науці, у побуті ми ще зустрічаємося зі словом ГРАФІК?-Графік залежності маси від об'єму,-об'єму від тиску;- графік чергування;- графік руху поїздів; Об `єм промислового виробництвав Саратовській області в період з 1980 по 2002 рік. За цим графіком можна простежити за зниженням і зростанням виробництва в окремі роки. - Скажіть, графіком якої функції представлена дана інформація. Відповідь: шматкова функція.ІІІ. Повідомлення теми, цілі уроку. Тема урока:«Шматково-задані функції» Ціль:- на прикладі шматково-заданої функції згадати план дослідження функцій;

повторити кроки побудови шматково-заданої функції; застосовувати узагальнені знання під час вирішення нестандартних завдань.IV. Актуалізація раніше засвоєних знань. Поняття функції вперше зустрілося нам у 7 класі щодо вивчення лінійної залежності. З погляду моделювання реальних процесів, ця залежність відповідає рівномірним процесам. Приклад: Рух пішохода з постійною швидкістюза час t. Формула: s = vt, графік - відрізки прямої, розташований в I чверті.
Основна тема 8-го класу – квадратична функція, що моделює рівноприскорені процеси. Приклад: вивчена вами в 9-му класі формула визначення опору нагрітої лампи (R) при постійній потужності (Р) і змінній напрузі (U). Формула R =

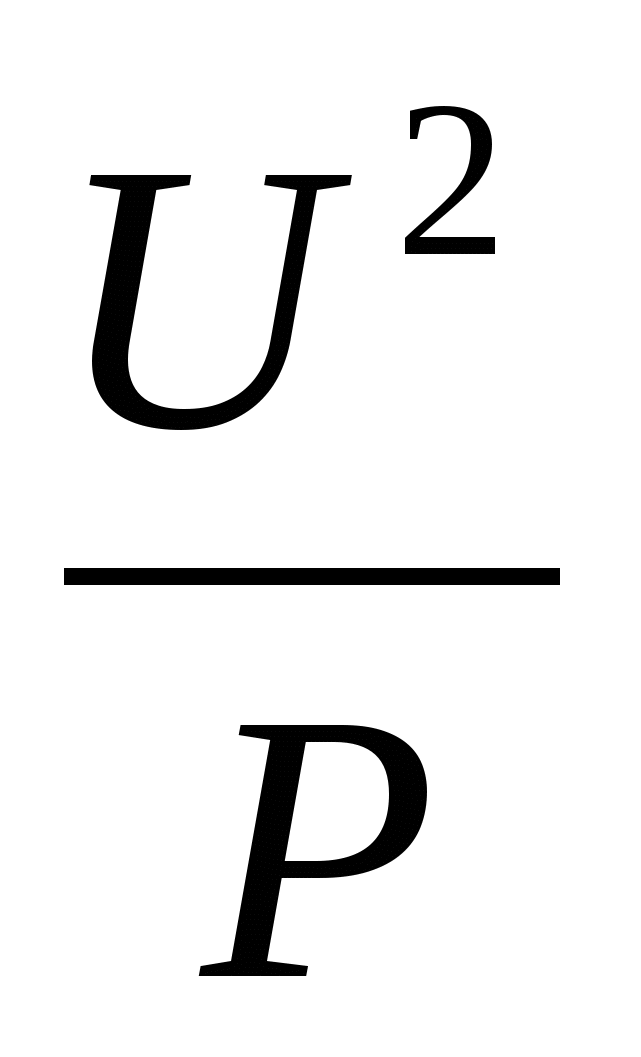, Графік - гілка параболи, розташована в I чверті.
Протягом трьох роківнаші знання про функції збагачувалися, кількість вивчених функцій зростала, поповнювався і набір завдань для вирішення яких доводиться вдаватися до графіків. Назвіть ці типи завдань… розв'язання рівнянь;- Вирішення систем рівнянь;- Розв'язання нерівностей;- Вивчення властивостей функцій.V.Підготовка уч-ся до узагальнюючої діяльності. Згадаймо один із типів завдань, а саме – дослідження властивостей функцій або читання графіка. Звернемося до підручника. Сторінка 65 рис.20а №250. Завдання:прочитати графік функції. Порядок дослідження функції маємо. 1. область визначення – (-∞; +∞)2. парність, непарність – ні парна, ні непарна3. монотонність-зростає [-3; +∞), зменшується[-5;-3], постійна (-∞; -5];4. обмеженість – обмежена знизу5. максимальне і менше значення функції – у найм = 0, у найб – немає;6. безперервність- безперервна по всій області визначення;7. область значень – , опукла і вниз і вгору (-∞; -5] і [-2; +∞).VI. Відтворення знань на новому рівні. Ви знаєте, що побудова та дослідження графіків шматково-заданих функцій, розглядаються у другій частині іспиту з алгебри у розділі функції та оцінюються 4-ма та 6-ма балами. Звернімося до збірки завдань.Сторінка 119 - №4.19-1).Рішення: 1).у = - x, - квадратична функція, графік - парабола, гілки вниз (а = -1, а 0). х -2 -1 0 1 2 у -4 -1 0 1 4 2) у = 3х - 10, - лінійна функція, графік – прямаСкладемо таблицю деяких значеньх 3

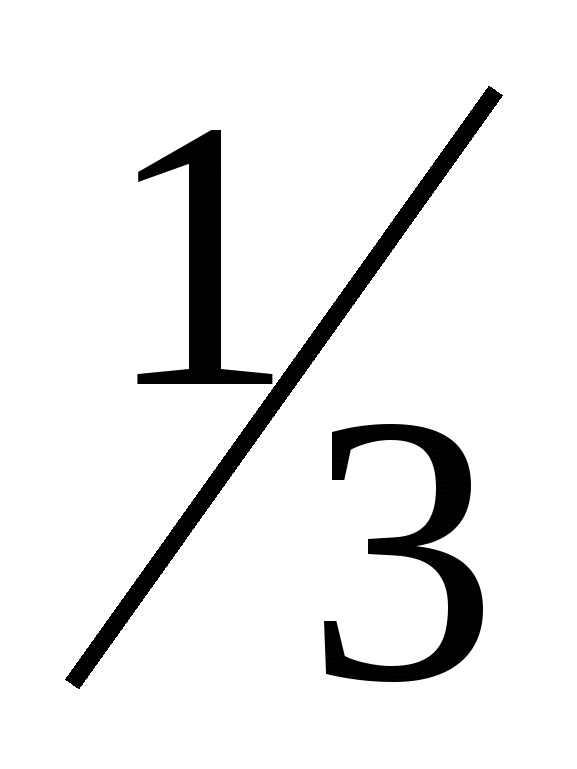3 у 0 -1 3) у = -3х -10, - лінійна функція, графік - прямаСкладемо таблицю деяких значеньх -3 -3 у 0 -1 4)Побудуємо графіки функцій у системі координат і виділимо частини графіків на заданих проміжках.
Знайдемо за графіком, за яких значеннях значення функції невід'ємні.Відповідь: f(x)  0 при х = 0 та при

 3 VII.Робота над нестандартними завданнями. №4.29-1), стор 121.Рішення: 1) Пряма (ліворуч) у = kx + b проходить через точки (-4; 0) і (-2; 2). Значить -4 k + b = 0, -2 k + b = 2;

k = 1, b = 4, у = х +4. Відповідь: х +4, якщо х -2у = якщо -2  х £ 3 3, якщо х  3
VIII.Контроль знань. Отже, підіб'ємо невеликий підсумок. Що ми повторили на уроці? План дослідження функцій, кроки побудови графіка шматкової функції, завдання аналітично. Перевіримо як ви засвоїли цей матеріал. Тестування на 4-5, 3 I варіант № У

2 1 -1 -1 1 Х

D(f) = , опукла і вгору і вниз на , опукла вгору і вниз на , зменшується на ________ Обмежена ____________ у наим немає, у наиб =_____ Безперервна по всій області визначення Е(f) = ____________ Випукла і вниз і вгору на всієї області визначення

Назад вперед

Увага! Попередній перегляд слайдів використовується виключно для ознайомлення та може не давати уявлення про всі можливості презентації. Якщо вас зацікавила дана робота, будь ласка, завантажте повну версію.

Підручник:Алгебра 8 клас за редакцією А. Г. Мордковича.

Тип уроку:Відкриття нового знання.

Цілі:

для вчителя цілі зафіксовані у кожному етапі уроку;

для учня:

Особистісні цілі:

Навчитися ясно, точно, грамотно викладати свої думки в усній та письмової мовирозуміти сенс поставленої задачі;
Навчитися застосовувати навчені знання та навички до вирішення нових проблем;
Навчитися контролювати процес та результат своєї діяльності;

Метапредметні цілі:

У пізнавальній діяльності:

Розвиток логічного мисленняі мови, вміння логічно доводити свої судження, проводити нескладні систематизації;
Навчитися висувати гіпотези при вирішенні завдань, розуміти необхідність їхньої перевірки;
Застосовувати знання в стандартної ситуації, навчитися самостійно виконувати завдання;
Здійснювати перенесення знань у змінену ситуацію, бачити завдання у контексті проблемної ситуації;

В інформаційно-комунікативній діяльності:

Навчитися вести діалог, визнавати декларація про іншу думку;

У рефлексивній діяльності:

Навчитися передбачати можливі наслідкисвоїх дій;
Навчитися усувати причини виникнення труднощів.

Предметні цілі:

Дізнатися, що таке кусково-задана функція;
Навчитися задавати шматково-задану функцію аналітично за її графіком;

Хід уроку

1. Самовизначення до навчальної діяльності

Мета етапу:

включити учнів до навчальної діяльності;
визначити змістовні рамки уроку: продовжуємо повторювати тему числові функції.

Організація навчального процесуна етапі 1:

Чим ми займалися на попередніх уроках?

Д: Повторювали тему числові функції.

У: Сьогодні ми продовжимо повторювати тему попередніх уроків, а також ми маємо сьогодні з'ясувати, що нового у цій темі ми можемо дізнатися.

2. Актуалізація знань та фіксація труднощів у діяльності

Мета етапу:

актуалізувати навчальний зміст, необхідне та достатнє для сприйняття нового матеріалу: згадати формули числових функцій, їх властивості та способи побудови;
актуалізувати розумові операції, необхідні та достатні для сприйняття нового матеріалу: порівняння, аналіз, узагальнення;
зафіксувати індивідуальну скруту в діяльності, що демонструє особистісно значному рівнінедостатність наявних знань: завдання шматково-заданої функції аналітично, а також побудови її графіка.

Організація навчального процесу на етапі 2:

Відповідь: На слайді зображено п'ять числових функцій. Визначте їхній вигляд.

1) дробово-раціональна;

2) квадратична;

3) ірраціональна;

4) функція з модулем;

5) статечна.

У: Назвіть формули, що відповідають їм.

3) ;

4) ;

У: Давайте обговоримо, яку роль виконує кожен коефіцієнт у формулах?

Д: Змінні "l" і "m" відповідають за зрушення графіків даних функцій вліво - вправо і вгору - вниз відповідно, коефіцієнт "к" у першій функції визначає положення гілок гіперболи: к>0 - гілки знаходяться в I та III чвертях, до< 0 - во II и IV четвертях, а коэффициент “а” определяет направление ветвей параболы: а>0 - гілки спрямовані вгору, а< 0 - вниз).

2. Слайд 2

У: Задайте аналітично функції, графіки яких зображені на малюнках. (з огляду на те, що рухають y=х 2). Вчитель виписує відповіді на дошці.

Д 1) );

2);

3. Слайд 3

У: Задайте аналітично функції, графіки яких зображені на малюнках. (враховуючи, що рухають). Вчитель виписує відповіді на дошці.

4. Слайд 4

У: Використовуючи попередні результати, задайте аналітично функції, графіки яких зображені на малюнках.

3. Виявлення причин труднощів та постановка мети діяльності

Мета етапу:

організувати комунікативна взаємодія, в ході якого виявляється і фіксується відмінна властивість завдання, що спричинило складне становище у навчальній діяльності;
узгодити мету та тему уроку.

Організація навчального процесу на етапі 3:

У: Що викликає у вас труднощі?

Д: На екрані представлені шматочки графіків.

Яка ж мета нашого уроку?

Д: Навчитися задавати аналітично шматочки функцій.

Сформулюйте тему уроку. (Діти намагаються самостійно сформулювати тему. Вчитель її уточнює. Тема: Шматково-задана функція.)

4. Побудова проекту виходу із скрути

Мета етапу:

організувати комунікативну взаємодію для побудови нового способу дії, що усуває причину виявленої скрути;
зафіксувати новий спосібдії.

Організація навчального процесу на етапі 4:

У: Давайте ще раз уважно прочитаємо завдання. Які результати як допомогу просять використати?

Д: Попередні, тобто. ті, що записані на дошці.

У: Чи можуть ці формули вже є відповіддю на дане завдання?

Д: Ні, т.к. цими формулами задається квадратична та раціональна функції, а на слайді зображені їхні шматочки.

У: Давайте обговоримо, яким проміжкам осі абсцис відповідають шматочки першої функції?

У: Тоді аналітичний спосіб завдання першої функції виглядає як: якщо

У: Що потрібно зробити, щоб виконати аналогічне завдання?

Д: Записати формулу та визначити, яким проміжкам осі абсцис відповідають шматочки даної функції.

5. Первинне закріплення у зовнішній мові

Мета етапу:

зафіксувати вивчений навчальний зміст у зовнішній промові.

Організація навчального процесу на етапі 5:

7. Включення в систему знань та повторення

Мета етапу:

тренувати навички використання нового змісту разом із раніше вивченим.

Організація навчального процесу на етапі 7:

У: Задайте аналітично функцію, графік якої зображено малюнку.

8. Рефлексія діяльності на уроці

Мета етапу:

зафіксувати новий зміст, вивчений на уроці;
оцінити свою діяльність на уроці;
подякувати однокласникам, які допомогли отримати результат уроку;
зафіксувати невирішені труднощі як напрями майбутньої навчальної діяльності;
обговорити та записати домашнє завдання.

Організація навчального процесу на етапі 8:

З чим ми сьогодні познайомилися на уроці?

Д: З шматково-заданою функцією.

Яку роботу ми вчилися сьогодні виконувати?

Д: Задавати даний видфункції аналітично.

У: Підніміть руку, хто зрозумів тему сьогоднішнього уроку? (З рештою дітей обговорити проблеми, що виникли).

Домашнє завдання

№21.12(а, в);
№21.13(a, в);
№22.41;
№22.44.

Реальні процеси, які у природі, можна описати з допомогою функцій. Так, можна виділити два основні типи перебігу процесів, протилежних один одному – це поступовеабо безперервнеі стрибкоподібне(прикладом може бути падіння м'яча та його отскок). Але якщо є розривні процеси, то існують і спеціальні засоби для їхнього опису. З цією метою вводяться в обіг функції, що мають розриви, стрибки, тобто на різних ділянках числової прямої функція поводиться за різними законами і, відповідно, задається різними формулами. Вводяться поняття точок розриву, усунення розриву.

Напевно, вам вже зустрічалися функції, задані декількома формулами, залежно від значень аргументу, наприклад:

y = (x - 3, при x> -3;
(-(x - 3), при x< -3.

Такі функції називаються шматочнимиабо шматково-заданими. Ділянки числової прямої з різними формулами завдання, назвемо складовимиобласть визначення. Об'єднання всіх складових є областю визначення шматкової функції. Ті точки, які ділять область визначення функції складові, називаються граничними точками. Формули, що визначають кусочну функцію на кожній складовій області визначення, називаються вхідними функціями. Графіки кусково-заданих функцій виходять у результаті об'єднання частин графіків, побудованих кожному з проміжків розбиття.

Вправи.

Побудувати графіки шматочкових функцій:

1) (-3, при -4 ≤ x< 0,
f(x) = (0, при x = 0,
(1, при 0< x ≤ 5.

Графік першої функції - пряма, що проходить через точку y = -3. Вона бере свій початок у точці з координатами (-4; -3), йде паралельно осі абсцис до точки з координатами (0; -3). Графік другої функції - точка з координатами (0; 0). Третій графік аналогічний першому - це пряма, що проходить через точку y = 1, але вже на ділянці від 0 до 5 по осі Ох.

Відповідь: рисунок 1.

2) (3, якщо x ≤ -4,
f(x) = (|x 2 – 4|x| + 3|, якщо -4< x ≤ 4,
(3 – (x – 4) 2 , якщо x > 4).

Розглянемо окремо кожну функцію та побудуємо її графік.

Так, f(x) = 3 – пряма, паралельна осі Ох, але зображати її треба лише дільниці, де x ≤ -4.

Графік функції f(x) = | x 2 - 4 | x | + 3 | може бути отриманий з параболи y = x 2 – 4x + 3. Побудувавши її графік, частину малюнка, що лежить над віссю Ox, необхідно залишити без змін, а частину, що лежить під віссю абсцис, симетрично відобразити щодо осі Ox. Потім симетрично відобразити частину графіка, де
x ≥ 0 щодо осі Oy для негативних x. Отриманий у результаті всіх перетворень графік залишаємо тільки дільниці від -4 до 4 по осі абсцис.

Графік третьої функції – парабола, гілки якої спрямовані вниз, а вершина перебуває у точці з координатами (4; 3). Креслення зображаємо лише ділянці, де x > 4.

Відповідь: рисунок 2.

3) (8 – (x + 6) 2 якщо x ≤ -6,
f(x) = (|x 2 – 6|x| + 8|, якщо -6 ≤ x< 5,
(3, якщо x ≥ 5).

Побудова пропонованої шматково-заданої функції аналогічна попередньому пункту. Тут графіки у перших двох функцій виходять із перетворень параболи, а графік третьої – пряма, паралельна Ох.

Відповідь: рисунок 3.

4) Побудувати графік функції y = x - | x | + (x - 1 - | x | / x) 2 .

Рішення.Область визначення цієї функції – все дійсні числакрім нуля. Розкриємо модуль. Для цього розглянемо два випадки:

1) За x > 0 отримаємо y = x – x + (x – 1 – 1) 2 = (x – 2) 2 .

2) При x< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

Таким чином, перед нами шматково-задана функція:

y = ((x – 2) 2 при x > 0;
( x 2 + 2x, при x< 0.

Графіки обох функцій – параболи, гілки яких спрямовані нагору.

Відповідь: рисунок 4.

5) Побудувати графік функції y = (x + | x | / x - 1) 2 .

Рішення.

Легко бачити, що область визначення функції є всі дійсні числа, крім нуля. Після розкриття модуля отримаємо шматково-задану функцію:

1) За x > 0 отримаємо y = (x + 1 – 1) 2 = x 2 .

2) При x< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

Перепишемо.

y = (x 2 при x > 0;
((x – 2) 2 , при x< 0.

Графіки цих функцій – параболи.

Відповідь: рисунок 5.

6) Чи існує функція, графік якої на координатної площинимає загальну точкуз будь-якої прямої?

Рішення.

Так, існує.

Прикладом може бути функція f(x) = x3. Справді, з вертикальною прямою х = а графік кубічної параболи перетинається у точці (а; а 3). Нехай тепер пряма задана рівнянням y = kx + b. Тоді рівняння
x 3 – kx – b = 0 має дійсний корінь х 0 (оскільки багаточлен непарного ступеня завжди має хоча б один дійсний корінь). Отже, графік функції перетинається із прямою y = kx + b, наприклад, у точці (х 0 ; х 0 3).

сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

Аналітичне завдання функції

Функція %%y = f(x), x \in X%% задана явним аналітичним способомякщо дана формула, що вказує послідовність математичних дій, які треба виконати з аргументом %%x%%, щоб отримати значення %%f(x)%% цієї функції.

приклад

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = sqrt(x), x \geq 0%%.

Так, наприклад, у фізиці при рівноприскореному прямолінійному русішвидкість тіла визначається формулою %%v = v_0 + a t%%, а формула для переміщення %%s%% тіла при рівномірно прискореному русіна проміжку часу від %%0%% до %%t%% записується у вигляді: %% s = s_0 + v_0 t + frac(a t^2)(2) %%.

Шматково-задані функції

Іноді функція, що розглядається, може бути задана декількома формулами, що діють на різних ділянках області її визначення, в якій змінюється аргумент функції. Наприклад: $$ y = \begin(cases) x ^ 2,~ якщо~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

Функції такого виду іноді називають складовимиабо шматково-заданими. Прикладом такої функції є %%y = |x|%%

Область визначення функції

Якщо функція задана явним аналітичним способом за допомогою формули, але область визначення функції у вигляді множини %%D%% не вказана, то під %%D%% завжди матимемо на увазі безліч значень аргументу %%x%%, при яких дана формуламає сенс. Так для функції %%y = x^2%% областю визначення служить безліч %%D = \mathbb(R) = (-\infty, +\infty)%%, оскільки аргумент %%x%% може приймати будь-які значення на числовий прямий. А для функції %%y = \frac(1)(\sqrt(1 - x^2))%% областю визначення буде безліч значень %%x%%, що задовольняють нерівності %%1 - x^2 > 0%%, т .е. %%D = (-1, 1)%%.

Переваги явного аналітичного завдання функції

Зазначимо, що явний аналітичний спосіб завдання функції досить компактний (формула, як правило, займає трохи місця), легко відтворюємо (формулу неважко записати) і найбільш пристосований до виконання над функціями математичних дій та перетворень.

Деякі з цих дій - алгебраїчні (додавання, множення та ін) - добре відомі з шкільного курсуматематики, інші (диференціювання, інтегрування) вивчатимемо надалі. Однак цей спосіб не завжди наочний, тому що не завжди чіткий характер залежності функції від аргументу, а для знаходження значень функції (якщо вони необхідні) потрібні іноді громіздкі обчислення.

Неявне завдання функції

Функція %%y = f(x)%% задана неявним аналітичним способом, якщо дано співвідношення $$F(x,y) = 0, ~~~~~~~~~~(1)$$ зв'язуюче значення функції %%y%% та аргументу %%x%%. Якщо задавати значення аргументу, то для знаходження значення %%y%%, що відповідає конкретному значенню %%x%%, необхідно вирішити рівняння %%(1)%% щодо %%y%% при цьому конкретному значенні %%x%%.

При за даному значенні%%x%% рівняння %%(1)%% може не мати рішення або мати більше одного рішення. В першому випадку задане значення%%x%% не належить області визначення неявно заданої функції, а в другому випадку задає багатозначну функцію, що має при даному значенні аргументу більше одного значення.

Зазначимо, що якщо рівняння %%(1)%% вдається явно дозволити щодо %%y = f(x)%%, то отримуємо ту саму функцію, але вже задану явним аналітичним способом. Так, рівняння %%x + y^5 - 1 = 0%%

і рівність %%y = \sqrt(1 - x)%% визначають одну й ту саму функцію.

Параметричне завдання функції

Коли залежність %%y%% від %%x%% не задана безпосередньо, а натомість дані залежності обох змінних %%x%% і %%y%% від деякої третьої допоміжної змінної %%t%% у вигляді

$$ \begin(cases) x = \varphi(t),\\ y = \psi(t), \end(cases) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$то говорять про параметричномуспосіб завдання функції;

тоді допоміжну змінну %%t%% називають параметром.

Якщо з рівнянь %%(2)%% вдається виключити параметр %%t%%, то приходять до функції, заданої явною або неявною аналітичною залежністю %%y%% від %%x%%. Наприклад, із співвідношень $$ \begin(cases) x = 2 t + 5, \\ y = 4 t + 12, \end(cases), ~~~t \in \mathbb(R), $$ винятком параметра % %t%% отримаємо залежність %%y = 2 x + 2%%, яка задає в площині %%xOy%% пряму.

Графічний спосіб

Приклад графічного завдання функції

Наведені вище приклади показують, що аналітичному способу завдання функції відповідає графічне зображення , яке можна розглядати як зручну та наочну форму опису функції. Іноді використовують графічний спосіб завдання функції, коли залежність %%y%% від %%x%% задають лінією на площині %%xOy%%. Однак при всій наочності він програє точно, оскільки значення аргументу і відповідні їм значення функції можна отримати з графіка лише приблизно. Похибка, що виникає при цьому, залежить від масштабу і точності вимірювання абсциси і ординати окремих точок графіка. Надалі графіку функції відведемо роль лише ілюстрації поведінки функції і тому обмежуватимемося побудовою «ескізів» графіків, що відбивають основні особливості функцій.

Табличний спосіб

Зазначимо табличний спосібзавдання функції, коли деякі значення аргументу та відповідні їм значення функції у певному порядку розміщуються у таблиці. Так побудовано відомі таблиці тригонометричних функцій, таблиці логарифмів і т.п. У вигляді таблиці зазвичай становлять залежність між величинами, що вимірюються при експериментальних дослідженнях, спостереження, випробування.

Недолік цього способу полягає у неможливості безпосереднього визначення значень функції для значень аргументу, що не входять до таблиці. Якщо є впевненість, що непредставлені в таблиці значення аргументу належать області визначення цієї функції, відповідні їм значення функції можуть бути обчислені приблизно за допомогою інтерполяції та екстраполяції.

приклад

x	3	5.1	10	12.5
y	9	23	80	110

Алгоритмічний та словесний способи завдання функцій

Функцію можна задати алгоритмічним(або програмним) способом, який широко використовують при обчисленнях на ЕОМ.

Зрештою, можна відзначити описовий(або словесний) спосіб завдання функції, коли правило відповідності значень функції значенням аргументу виражено словами.

Наприклад, функцію %%[x] = m~\forall (x \in )