Знайти матриці обернені заданої матриці а. Знаходження зворотної матриці онлайн

Знаходження зворотної матриці- завдання, яке найчастіше вирішується двома методами:

• методом додатків алгебри, при якому потрібно знаходити визначники і транспонувати матриці;
• методом виключення невідомих Гаусса, у якому потрібно проводити елементарні перетворення матриць (складати рядки, множити рядки одне й те число і т. буд.).

Для особливо допитливих існують інші методи, наприклад, метод лінійних перетворень. На цьому уроці розберемо три згадані методи та алгоритми знаходження зворотної матриці цими методами.

Зворотною матрицею А, називається така матриця

А
. (1)

Зворотною матрицею , яку потрібно знайти для цієї квадратної матриці А, називається така матриця

твір на яку матриці Аправоруч є одиничною матрицею, тобто,
. (1)

Одиничною матрицею називається діагональна матриця, яка має всі діагональні елементи рівні одиниці.

Теорема.Для кожної неособливої ​​(невиродженої, несингулярної) квадратної матриці можна знайти зворотну матрицю, і до того ж лише одну. Для особливої ​​(виродженої, сингулярної) квадратної матриці зворотна матриця немає.

Квадратна матриця називається неособливою(або невиродженою, несингулярною), якщо її визначник не дорівнює нулю, та особливою(або виродженою, сингулярною), якщо її визначник дорівнює нулю.

Зворотну матрицю можна знайти тільки для квадратної матриці. Звичайно, зворотна матриця також буде квадратною і того ж порядку, що і ця матриця. Матриця, на яку може бути знайдена зворотна матриця, називається оборотною матрицею.

Для зворотної матриці існує доречна аналогія зі зворотним числом. Для кожного числа a, не рівного нулю, існує таке число b, що твір aі bодно одиниці: ab= 1. Число bназивається зворотним для числа b. Наприклад, число 7 зворотним є число 1/7, оскільки 7*1/7=1.

Знаходження зворотної матриці методом додатків алгебри (союзної матриці)

Для неособливої ​​квадратної матриці Азворотною є матриця

де - визначник матриці А, а - матриця, союзна з матрицею А.

Союзної з квадратною матрицею Aназивається матриця того ж порядку, елементами якої є доповнення алгебри відповідних елементів визначника матриці , транспонованої щодо матриці A. Таким чином, якщо

то

і

Алгоритм знаходження зворотної матриці методом додатків алгебри

1. Знайти визначник цієї матриці A. Якщо визначник дорівнює нулю, знаходження зворотної матриці припиняється, оскільки матриця вироджена і обернена не існує.

2. Знайти матрицю, транспоновану щодо A.

3. Обчислити елементи союзної матриці як доповнення алгебри мариці, знайденої на кроці 2.

4. Застосувати формулу (2): помножити число, обернене до визначника матриці Aна союзну матрицю, знайдену на кроці 4.

5. Перевірити отриманий на кроці 4 результат, помноживши цю матрицю Aна зворотну матрицю. Якщо добуток цих матриць дорівнює одиничній матриці, отже зворотна матриця була знайдена правильно. Інакше розпочати процес вирішення знову.

приклад 1.Для матриці

знайти зворотну матрицю.

Рішення. Для знаходження зворотної матриці необхідно знайти визначник матриці А. Знаходимо за правилом трикутників:

Отже, матриця А- Неособлива (невироджена, несингулярна) і для неї існує зворотна.

Знайдемо матрицю, союзну з цією матрицею А.

Знайдемо матрицю, транспоновану щодо матриці A:

Обчислюємо елементи союзної матриці як додатки алгебри матриці, транспонованої щодо матриці A:

Отже, матриця , союзна з матрицею A, має вигляд

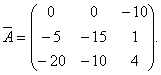
Зауваження.Порядок обчислення елементів та транспонування матриці може бути іншим. Можна спочатку обчислити додатки алгебри матриці A, а потім транспонувати матрицю додатків алгебри. В результаті повинні вийти самі елементи союзної матриці.

Застосовуючи формулу (2), знаходимо матрицю, зворотну матриці А:

Знаходження зворотної матриці методом виключення невідомих Гаусса

Перший крок для знаходження зворотної матриці методом виключення невідомих Гаус - приписати до матриці Aодиничну матрицю того ж порядку, відокремивши їх вертикальною межею. Ми отримаємо здвоєну матрицю. Помножимо обидві частини цієї матриці на , тоді отримаємо

,

Алгоритм знаходження зворотної матриці методом виключення невідомих Гаусса

1. До матриці Aприписати одиничну матрицю того самого порядку.

2. Отриману здвоєну матрицю перетворити так, щоб у лівій її частині вийшла одинична матриця, тоді у правій частині на місці одиничної матриці автоматично вийде зворотна матриця. Матриця Aу лівій частині перетворюється на одиничну матрицю шляхом елементарних перетворень матриці.

2. Якщо у процесі перетворення матриці Aв одиничну матрицю в якомусь рядку або в якомусь стовпці виявляться тільки нулі, то визначник матриці дорівнює нулю, і, отже, матриця Aбуде виродженою, і вона не має зворотної матриці. І тут подальше перебування зворотної матриці припиняється.

приклад 2.Для матриці

знайти зворотну матрицю.

і будемо її перетворювати, так щоб у лівій частині вийшла поодинока матриця. Починаємо перетворення.

Помножимо перший рядок лівої та правої матриці на (-3) і складемо її з другим рядком, а потім помножимо перший рядок на (-4) і складемо її з третім рядком, тоді отримаємо

.

Щоб по можливості не було дробових чисел при наступних перетвореннях, заздалегідь створимо одиницю в другому рядку в лівій частині здвоєної матриці. Для цього помножимо другий рядок на 2 і віднімемо з нього третій рядок, тоді отримаємо

.

Складемо перший рядок з другим, а потім помножимо другий рядок на (-9) і складемо його з третім рядком. Тоді отримаємо

.

Розділимо третій рядок на 8, тоді

.

Помножимо третій рядок на 2 і складемо його з другим рядком. Виходить:

.

Переставимо місцями другий та третій рядок, тоді остаточно отримаємо:

.

Бачимо, що у лівій частині вийшла одинична матриця, отже, у правій частині вийшла зворотна матриця . Таким чином:

.

Можна перевірити правильність обчислень, помножимо вихідну матрицю на знайдену матрицю зворотну:

В результаті повинна вийти зворотна матриця.

приклад 3.Для матриці

знайти зворотну матрицю.

Рішення. Складаємо здвоєну матрицю

і будемо її перетворювати.

Перший рядок множимо на 3, а другий на 2, і віднімаємо з другого, а потім перший рядок множимо на 5, а третій на 2 і віднімаємо з третього рядка, тоді отримаємо

.

Перший рядок множимо на 2 і складаємо його з другого, а потім з третього рядка віднімаємо другий, тоді отримаємо

.

В третьому рядку в лівій частині всі елементи вийшли рівними нулю. Отже, матриця вироджена та зворотної матриці не має. Подальше перебування зворотної мариці припиняємо.

Способи знаходження зворотної матриці, . Розглянемо квадратну матрицю

Позначимо Δ =det A.

Квадратна матриця А називається невиродженою,або неособливою, якщо її визначник відмінний від нуля, та виродженою,або особливою, якщоΔ = 0.

Квадратна матриця є для квадратної матриці А того ж порядку, якщо їх добуток А В = В А = Е, де Е - одинична матриця того ж порядку, що і матриці А і В.

Теорема . Для того щоб матриця А мала зворотну матрицю, необхідно і достатньо, щоб її визначник був відмінний від нуля.

Зворотна матриця матриці А позначається через А- 1 так що В = А - 1 та обчислюється за формулою

, (1)

де А i j - додатки алгебри елементів a i j матриці A..

Обчислення A -1 за формулою (1) для матриць високого порядку дуже трудомістке, тому практично зручно знаходити A -1 з допомогою методу елементарних перетворень (ЭП). Будь-яку неособливу матрицю А шляхом ЕП тільки стовпців (або лише рядків) можна привести до одиничної матриці Е. Якщо скоєні над матрицею А ЕП у тому ж порядку застосувати до одиничної матриці Е, то в результаті вийде зворотна матриця. Зручно здійснювати ЕП над матрицями А та Е одночасно, записуючи обидві матриці поряд через межу. Зазначимо вкотре, що з відшуканні канонічного виду матриці з метою знаходження можна скористатися перетвореннями рядків і стовпців. Якщо потрібно знайти зворотну матрицю, в процесі перетворення слід використовувати тільки рядки або тільки стовпці.

Приклад 2.10. Для матриці знайти A-1.

Рішення.Знаходимо спочатку детермінант матриці А
значить, зворотна матриця існує і ми її можемо знайти за такою формулою: , де А i j (i,j = 1,2,3) - додатки алгебри елементів а i j вихідної матриці.

Звідки .

Приклад 2.11. p align="justify"> Методом елементарних перетворень знайти A -1 для матриці: А = .

Рішення.Приписуємо до вихідної матриці праворуч одиничну матрицю того ж порядку: . За допомогою елементарних перетворень стовпців наведемо ліву "половину" до одиничної, здійснюючи одночасно такі перетворення над правою матрицею.
Для цього поміняємо місцями перший та другий стовпці: ~ . До третього стовпця додамо перший, а до другого - перший, помножений на -2: . З першого стовпця віднімемо подвоєний другий, та якщо з третього - помножений на 6 другий; . Додамо третій стовпець до першого та другого: . Помножимо останній стовпець на -1: . Отримана праворуч від вертикальної межі квадратна матриця є зворотною матрицею до даної матриці А. Отже,
.

У першій частині було розглянуто спосіб знаходження зворотної матриці за допомогою додатків алгебри. Тут ми опишемо інший метод знаходження зворотних матриць: з використанням перетворень методу Гауса та Гауса-Жордана. Найчастіше цей спосіб перебування зворотної матриці називають шляхом елементарних перетворень.

Метод елементарних перетворень

Для застосування цього методу одну матрицю записують задану матрицю $A$ і поодиноку матрицю $E$, тобто. становлять матрицю виду $(A|E)$ (цю матрицю називають також розширеною). Після цього за допомогою елементарних перетворень, що виконуються з рядками розширеної матриці, домагаються того, що матриця зліва від риси стане одиничною, причому розширена матриця набуде вигляду $\left(E|A^(-1) \right)$. До елементарних перетворень у цій ситуації відносять такі дії:

1. Зміна місць двох рядків.
2. Розмноження всіх елементів рядка на деяке число, що не дорівнює нулю.
3. Додавання до елементів одного рядка відповідних елементів іншого рядка, помножених на будь-який множник.

Застосовувати зазначені елементарні перетворення можна різними шляхами. Зазвичай вибирають метод Гауса або метод Гауса-Жордана. Взагалі, методи Гауса та Гауса-Жордана призначені для вирішення систем лінійних рівнянь алгебри, а не для знаходження зворотних матриць. p align="justify"> Фразу "застосування методу Гаусса для знаходження зворотної матриці" тут потрібно розуміти як "застосування операцій, властивих методу Гаусса, для знаходження зворотної матриці".

Нумерація прикладів продовжена з першої частини. У прикладах розглянуто застосування методу Гауса для знаходження зворотної матриці, а в прикладах і розібрано використання методу Гауса-Жордана. Слід зазначити, що якщо в ході рішення всі елементи деякого рядка або стовпця матриці, розташованої до межі, обнулилися, зворотної матриці не існує.

Приклад №5

Знайти матрицю $A^(-1)$, якщо $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( array) \right)$.

У цьому прикладі буде знайдено зворотну матрицю методом Гауса. Розширена матриця, що має в загальному випадку вигляд $(A|E)$, в даному прикладі набуде такої форми: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

Мета: за допомогою елементарних перетворень привести розширену матрицю до виду $ \ left (E | A ^ (-1) \ right) $. Застосуємо самі операції, що застосовуються під час вирішення систем лінійних рівнянь методом Гаусса. Для застосування методу Гауса зручно, коли першим елементом першого рядка розширеної матриці є одиниця. Щоб досягти цього, поміняємо місцями перший і третій рядки розширеної матриці, яка стане такою: $ \left(\begin(array) (ccc|ccc) 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(array) \right)$.

Тепер почнемо рішення. Метод Гауса ділиться на два етапи: прямий хід та зворотний (докладний опис цього методу для вирішення систем рівнянь дано у прикладах відповідної теми). Ті ж два етапи будуть використані і в процесі пошуку зворотної матриці.

Прямий хід

Перший крок

За допомогою першого рядка обнулюємо елементи першого стовпця, розташовані під першим рядком:

Трохи прокоментую виконану дію. Запис $II-2\cdot I$ означає, що від елементів другого рядка відняли відповідні елементи першого рядка, попередньо помножені на два. Цю дію можна записати окремо так:

Так само виконується і дія $III-7\dot I$. Якщо виникають складнощі з виконанням цих операцій, їх можна виконати окремо (аналогічно показаній вище дії $II-2\cdot I$), а результат потім внести до розширеної матриці.

Другий крок

За допомогою другого рядка обнуляємо елемент другого стовпця, розташований під другим рядком:

Розділимо третій рядок на 5:

Прямий хід закінчено. Всі елементи, розташовані під головною діагоналлю матриці до межі, обнулилися.

Зворотній хід

Перший крок

За допомогою третього рядка обнулюємо елементи третього стовпця, розташовані над третім рядком:

Перед переходом до наступного кроку розділимо другий рядок на $7$:

Другий крок

За допомогою другого рядка обнулюємо елементи другого стовпця, розташовані над другим рядком:

Перетворення закінчені, зворотна матриця методом Гауса знайдена: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \ 7/5 & -11/5 & -27/5 \end(array) \right)$. Перевірку, за потреби, можна зробити так само, як і в попередніх прикладах. Якщо пропустити всі пояснення, то рішення набуде вигляду:

Відповідь: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & ​​-27/5 \end(array) \right)$.

Приклад №6

Знайти матрицю $A^(-1)$, якщо $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & -4 & -3 \\ 1 & 4 & 0 & 6 \end(array) \right)$.

Для знаходження зворотної матриці в цьому прикладі використовуватимемо ті ж операції, що застосовуються при вирішенні систем лінійних рівнянь методом Гаусса. Детальні пояснення дано в , тут же обмежимося короткими коментарями. Запишемо розширену матрицю: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \\ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(array) \right)$. Поміняємо місцями перший і четвертий рядки даної матриці: $\left(\begin(array) (cccc|cccc) 1&4&0&6&0&0&0&1\\2&3&-2&1&0&1&0&0 \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(array) \right)$.

Прямий хід

Перетворення прямого ходу завершено. Всі елементи, розташовані під головною діагоналлю матриці зліва від межі, обнулилися.

Зворотній хід

Зворотну матрицю методом Гауса знайдено, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \ -19/8 & - 117/16 & 49/16 & 11/4 \ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \ end(array) \right)$. Перевірку, за потреби, проводимо так само, як і в прикладах №2 та №3.

Відповідь: $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(array) \ right) $.

Приклад №7

Знайти матрицю $A^(-1)$, якщо $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( array) \right)$.

Для знаходження зворотної матриці застосуємо операції, характерні методу Гаусса-Жордана. Відмінність від методу Гауса, розглянутого в попередніх прикладах і полягає в тому, що рішення здійснюється в один етап. Нагадаю, що метод Гауса ділиться на 2 етапи: прямий хід («робимо» нулі під головною діагоналлю матриці до межі) та зворотний хід (обнулюємо елементи над головною діагоналлю матриці до межі). Для обчислення зворотної матриці методом Гаус-Жордана двох стадій рішення не потрібно. Для початку складемо розширену матрицю: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & ​​-2 &0 & 0 & 1 \end(array) \right) $$

Перший крок

Облинули всі елементи першого стовпця крім одного. У першому стовпці всі елементи відмінні від нуля, тому можемо вибрати будь-який елемент. Візьмемо, наприклад, $(-4)$:

Вибраний елемент $(-4)$ знаходиться в третьому рядку, тому саме третій рядок ми використовуємо для обнулення виділених елементів першого стовпця:

Зробимо так, щоб перший елемент третього рядка дорівнював одиниці. Для цього розділимо елементи третього рядка розширеної матриці на $(-4)$:

Тепер приступимо до обнулення відповідних елементів першого стовпця:

У подальших кроках використовувати третій рядок вже буде не можна, бо ми його вже застосували на першому кроці.

Другий крок

Виберемо якийсь не рівний нулю елемент другого стовпця і обнулимо всі інші елементи другого стовпця. Ми можемо вибрати будь-який з двох елементів: $\frac(11)(2)$ або $\frac(39)(4)$. Елемент $\left(-\frac(5)(4) \right)$ вибрати не можна, бо він розташований у третьому рядку, який ми використовували на попередньому кроці. Виберемо елемент $\frac(11)(2)$, що у першому рядку. Зробимо так, щоб замість $\frac(11)(2)$ у першому рядку стала одиниця:

Тепер обнулимо відповідні елементи другого стовпця:

У подальших міркуваннях перший рядок використовувати не можна.

Третій крок

Потрібно обнулити всі елементи третього стовпця, крім одного. Нам треба вибрати якийсь відмінний від нуля елемент третього стовпця. Однак ми не можемо взяти $\frac(6)(11)$ або $\frac(13)(11)$, бо ці елементи розташовані в першому та третьому рядках, які ми використовували раніше. Вибір невеликий: залишається лише елемент $\frac(2)(11)$, що у другому рядку. Розділимо всі елементи другого рядка на $\frac(2)(11)$:

Тепер обнулимо відповідні елементи третього стовпця:

Перетворення методом Гаусса-Жордана завершено. Залишилося зробити так, щоб матриця до риси стала одиничною. Для цього доведеться змінювати порядок рядків. Для початку поміняємо місцями перший і третій рядки:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(array) \right) $$

Тепер поміняємо місцями другий і третій рядки:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(array) \right) $$

Отже, $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39/4 & 11/2 & 19/4 \end(array) \right)$. Звичайно, рішення можна провести і по-іншому, вибираючи елементи, що стоять на головній діагоналі. Зазвичай саме так і роблять, бо в такому разі наприкінці рішення не доведеться міняти місцями рядки. Я навів попереднє рішення лише з однією метою: показати, що вибір рядка на кожному кроці не є принциповим. Якщо вибирати на кожному кроці діагональні елементи, рішення стане таким.

Нехай дана квадратна матриця. Потрібно знайти зворотну матрицю.

Перший метод. У теоремі 4.1 існування та єдиності зворотної матриці вказано один із способів її знаходження.

1. Обчислити визначник цієї матриці. Якщо, то зворотної матриці немає (матриці народжена).

2. Скласти матрицю з додатків алгебри елементів матриці.

3. Транспонуючи матрицю, отримати приєднану матрицю .

4. Знайти зворотну матрицю (4.1), розділивши всі елементи приєднаної матриці на визначник

Другий спосіб. Для знаходження зворотної матриці можна використовувати елементарні перетворення.

1. Скласти блокову матрицю , приписавши до цієї матриці одиничну матрицю того ж порядку.

2. За допомогою елементарних перетворень, що виконуються над рядками матриці, привести її лівий блок до найпростішого вигляду. При цьому блокова матриця приводиться до виду, де квадратна матриця, отримана в результаті перетворень з одиничної матриці.

3. Якщо , то блокрівний зворотній матриці, тобто. Якщо, то матриця має зворотної.

Насправді, за допомогою елементарних перетворень рядків матриці можна навести її лівий блок спрощеного вигляду (див. рис. 1.5). При цьому блочна матриця перетворюється на вигляд, де - елементарна матриця, що задовольняє рівності. Якщо матриця невироджена, то згідно з п.2 зауважень 3.3 її спрощений вигляд збігається з одиничною матрицею. Тоді з рівності слід, що. Якщо ж матриці народжена, то її спрощений відрізняється від одиничної матриці, а матриця не має зворотної.

11. Матричні рівняння та їх вирішення. Матрична форма запису СЛАУ. Матричний спосіб (метод зворотної матриці) рішення СЛАУ та умови його застосування.

Матричними рівняннями називаються рівняння виду: A * X = C; X * A = C; A*X*B=C де матриця А,В,З відомі,матриця Х не відома, якщо матриці А і не вироджені, то рішення вихідних матриць запишеться у відповідному вигляді: Х=А -1 *С; Х = С * А -1; Х = А -1 * С * В -1 Матрична форма запису систем лінійних рівнянь алгебри.З кожною СЛАУ можна зв'язати декілька матриць; більше – саму СЛАУ можна записати як матричного рівняння. Для СЛАУ (1) розглянемо такі матриці:

Матриця A називається матрицею системи. Елементи даної матриці є коефіцієнтами заданої СЛАУ.

Матриця A˜ називається розширеною матрицею системи. Її одержують додаванням до матриці системи стовпця, що містить вільні члени b1, b2, ..., bm. Зазвичай цей стовпець відокремлюють вертикальною рисою для наочності.

Матриця-стовпець B називається матрицею вільних членів, а матриця-стовпець X - матрицею невідомих.

Використовуючи введені вище позначення, СЛАУ (1) можна записати у вигляді матричного рівняння: A⋅X=B.

Примітка

Матриці, пов'язані з системою, можна записати різними способами: все залежить від порядку проходження змінних і рівнянь аналізованої СЛАУ. Але в будь-якому випадку порядок слідування невідомих у кожному рівнянні заданої СЛАУ має бути однаковим.

Матричний метод підходить для розв'язання СЛАУ, у яких кількість рівнянь збігається з числом невідомих змінних та визначник основної матриці системи відмінний від нуля. Якщо система містить більше трьох рівнянь, то знаходження зворотної матриці вимагає значних обчислювальних зусиль, тому в цьому випадку доцільно використовувати для вирішення метод Гауса.

12. Однорідні СЛАУ, умови існування їх ненульових рішень. Властивості окремих рішень однорідних СЛАУ.

Лінійне рівняння називається однорідним, якщо його вільний член дорівнює нулю, і неоднорідним інакше. Система, що складається з однорідних рівнянь, називається однорідною і має загальний вигляд:

13 .Поняття лінійної незалежності та залежності приватних рішень однорідної СЛАУ. Фундаментальна система рішень (ФСР) та її знаходження. Подання загального рішення однорідної СЛАУ через ФСР.

Система функцій y 1 (x ), y 2 (x ), …, y n (x ) називається лінійно залежноюна інтервалі ( a , b ), якщо існує набір постійних коефіцієнтів , не рівних нулю одночасно, таких, що лінійна комбінація цих функцій тотожно дорівнює нулю на ( a , b ): для . Якщо рівність можлива тільки при , система функцій y 1 (x ), y 2 (x ), …, y n (x ) називається лінійно незалежноюна інтервалі ( a , b ). Іншими словами, функції y 1 (x ), y 2 (x ), …, y n (x ) лінійно залежніна інтервалі ( a , b ), якщо існує рівна нулю на ( a , b ) їхня нетривіальна лінійна комбінація. Функції y 1 (x ),y 2 (x ), …, y n (x ) лінійно незалежніна інтервалі ( a , b ), якщо тільки тривіальна їхня лінійна комбінація тотожно дорівнює нулю на ( a , b ).

Фундаментальною системою рішень (ФСР)Однорідною СЛАУ називається базис цієї системи стовпців.

Кількість елементів у ФСР дорівнює кількості невідомих системи мінус ранг матриці системи. Будь-яке рішення вихідної системи є лінійною комбінацією рішень ФСР.

Теорема

Загальне рішення неоднорідної СЛАУ дорівнює сумі приватного рішення неоднорідної СЛАУ та загального рішення відповідної однорідної СЛАУ.

1 . Якщо стовпці - рішення однорідної системи рівнянь, то будь-яка їхня лінійна комбінація також є рішенням однорідної системи.

Насправді, з рівностей випливає, що

тобто. Лінійна комбінація рішень є рішенням однорідної системи.

2. Якщо ранг матриці однорідної системи дорівнює , то система має лінійно незалежні рішення.

Справді, за формулами (5.13) загального рішення однорідної системи знайдемо приватні рішення, надаючи вільним змінним наступні стандартні набори значень (Кожного разу вважаючи, що з вільних змінних дорівнює одиниці, інші - рівні нулю):

які лінійно незалежні. Справді, якщо з цих стовпців скласти матрицю, останні її рядків утворюють одиничну матрицю. Отже, мінор, розташований останніх рядках не дорівнює нулю (він дорівнює одиниці), тобто. є базисним. Тому ранг матриці дорівнюватиме. Отже, усі стовпці цієї матриці лінійно незалежні (див. теорему 3.4).

Будь-яка сукупність лінійно незалежних рішень однорідної системи називається фундаментальною системою (сукупністю) рішень .

14 Мінор -ого порядку, базовий мінор, ранг матриці. Обчислення рангу матриці.

Мінором порядку k матриці називається детермінант деякої її квадратної підматриці порядку k.

У матриці розмірів m x n мінор порядку r називається базисним, якщо він відмінний від нуля, а всі мінори більшого порядку, якщо вони існують, рівні нулю.

Стовпці та рядки матриці А, на перетині яких стоїть базисний мінор, називаються базисними стовпцями та рядками А.

Теорема 1. (Про ранг матриці). У будь-якої матриці мінорний ранг дорівнює рядковому рангу і дорівнює стовпцевому рангу.

Теорема 2. (Про базисний мінор). Кожен стовпець матриці розкладається в лінійну комбінацію її базових стовпців.

Рангом матриці (або мінорним рангом) називається порядок базисного мінору або, інакше, найбільший порядок, для якого існують відмінні від нуля мінори. Ранг нульової матриці визначення вважають 0.

Зазначимо дві очевидні властивості мінорного рангу.

1) Ранг матриці не змінюється при транспонуванні, тому що при транспонуванні матриці всі її підматриці транспонуються та мінори не змінюються.

2) Якщо А'-підматриця матриці А, то ранг А' не перевищує рангу А, так як ненульовий мінор, що входить в А', входить і в А.

15. Концепція -мірного арифметичного вектора. Рівність векторів. Дії над векторами (додавання, віднімання, множення на число, множення на матрицю). Лінійна комбінація векторів.

Упорядкована сукупність nдійсних чи комплексних чисел називається n-вимірним вектором. Числа називаються координатами вектора.

Два (ненульові) вектори aі bрівні, якщо вони рівноспрямовані і мають один і той самий модуль. Усі нульові вектори вважаються рівними. У решті випадків вектори не рівні.

Складання векторів. Для складання векторів є два способи.1. Правило паралелограма. Щоб скласти вектори і поміщаємо початку обох в одну точку. Добудовуємо до паралелограма та з тієї ж точки проводимо діагональ паралелограма. Це і буде сума векторів.

2. Другий спосіб складання векторів – правило трикутника. Візьмемо ті ж вектори та . До кінця першого вектора влаштуємо початок другого. Тепер з'єднаємо початок першого та кінець другого. Це і є сума векторів та . За тим самим правилом можна скласти кілька векторів. Прилаштовуємо їх один за одним, а потім з'єднуємо початок першого з кінцем останнього.

Віднімання векторів. Вектор спрямований протилежно до вектора. Довжини векторіврівні. Тепер зрозуміло, що таке віднімання векторів. Різниця векторів і - це сума вектора та вектора.

Розмноження вектора на число

При множенні вектора число k виходить вектор, довжина якого в раз відрізняється від довжини. Він сонаправлен з вектором, якщо k більше нуля, і спрямований протилежно, якщо k менше нуля.

Скалярним твором векторів називається добуток довжин векторів на косинус кута між ними.Якщо вектори перпендикулярні, їх скалярний добуток дорівнює нулю. А ось так скалярний твір виражається через координати векторів та .

Лінійна комбінація векторів

Лінійна комбінація векторів називають вектор

де - Коефіцієнти лінійної комбінації. Якщо комбінація називається тривіальною, якщо – нетривіальною.

16 . Скалярне твір арифметичних векторів. Довжина вектор і кут між векторами. Концепція ортогональності векторів.

Скалярним твором векторів а і називається число,

Скалярний добуток використовується для обчислення:1)знаходження кута між ними;2)знаходження проекції векторів;3)обчислення довжини вектора;4)умови перпендикулярності векторів.

Довжиною відрізка АВ називають відстанню між точками А іВ. Кут між векторами А та В називають кут α=(а,в) ,0≤ α ≤П. На який необхідно повернути 1 вектор, щоб його напрямки збіглося з іншим вектором. За умови, що їх початку співпадуть.

Ортом а називається вектор а має одиничну довжину та напрямки а.

17. Система векторів та її лінійна комбінація. Концепція лінійної залежності та незалежності системи векторів. Теорема про необхідну та достатню умову лінійної залежності системи векторів.

Система векторів a1,a2,...,an називається лінійно залежною, якщо існують числа λ1,λ2,...,λnтакі, що хоча б одне з них відмінно від нуля і λ1a1+λ2a2+...+λnan=0. Інакше система називається лінійно незалежною.

Два вектори a1 і a2 називаються колінеарними, якщо їх напрями збігаються або протилежні.

Три вектори a1, a2 і a3 називаються компланарними, якщо вони паралельні деякій площині.

Геометричні критерії лінійної залежності:

а) система (a1,a2) лінійно залежна у тому й лише тому випадку, коли вектори a1 і a2 колінеарні.

б) система (a1,a2,a3) лінійно залежна у тому й лише тому випадку, коли вектори a1,a2 та a3компланарні.

теорема. (Необхідна та достатня умова лінійної залежності системивекторів.)

Система векторів векторного просторує лінійнозалежною тоді і лише тоді, коли один із векторів системи лінійно виражається через інші векторацієї системи.

Слідство.1. Система векторів векторного простору є лінійно незалежною тоді і лише тоді, коли жоден із векторів системи лінійно не виражається через інші вектори цієї системи. Система векторів, що містить нульовий вектор або два рівні вектори, є лінійно залежною.

Для будь-якої невиродженої матриці А існує і єдина матриця A -1 така, що

A*A -1 =A -1 *A = E,

де E — одинична матриця тих самих порядків, як і А. Матриця A -1 називається зворотної до матриці A.

Якщо хтось забув, в одиничній матриці, крім діагоналі, заповненої одиницями, всі інші позиції заповнені нулями, приклад одиничної матриці:

Знаходження зворотної матриці методом приєднаної матриці

Зворотна матриця визначається формулою:

де A ij - елементів a ij.

Тобто. для обчислення зворотної матриці потрібно обчислити визначник цієї матриці. Потім знайти додатки алгебри для всіх її елементів і скласти з них нову матрицю. Далі потрібно транспортувати цю матрицю. І кожен елемент нової матриці розділити на визначник вихідної матриці.

Розглянемо кілька прикладів.

Знайти A-1 для матриці

Розв'язання. Знайдемо A -1 методом приєднаної матриці. Маємо det A = 2. Знайдемо алгебраїчні доповнення елементів матриці A. У цьому випадку алгебраїчними доповненнями елементів матриці будуть відповідні елементи самої матриці, взяті зі знаком відповідно до формули

Маємо A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Утворимо приєднану матрицю

Транспортуємо матрицю A*:

Знаходимо зворотну матрицю за формулою:

Отримуємо:

Методом приєднаної матриці знайти A-1, якщо

Розв'язання. Перш за все обчислюємо визначтеся даної матриці, щоб переконатися в існуванні зворотної матриці. Маємо

Тут ми додали до елементів другого рядка елементи третього рядка, помножені попередньо (-1), а потім розкрили визначник по другому рядку. Оскільки визначитеся даної матриці відмінний від нуля, то зворотна до неї матриця існує. Для побудови приєднаної матриці знаходимо додатки алгебри елементів даної матриці. Маємо

Відповідно до формули

транспортуємо матрицю A*:

Тоді за формулою

Знаходження зворотної матриці методом елементарних перетворень

Крім методу знаходження зворотної матриці, що з формули (метод приєднаної матриці), існує метод знаходження зворотної матриці, званий методом елементарних перетворень.

Елементарні перетворення матриці

Елементарними перетвореннями матриці називаються такі перетворення:

1) перестановка рядків (стовпців);

2) множення рядка (стовпця) на число, відмінне від нуля;

3) додавання до елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця), попередньо помножених на деяке число.

Для знаходження матриці A -1 побудуємо прямокутну матрицю В = (А|Е) порядків (n; 2n), приписуючи до матриці А справа одиничну матрицю Е через роздільну межу:

Розглянемо приклад.

Методом елементарних перетворень знайти A -1 якщо

Рішення. Утворимо матрицю B:

Позначимо рядки матриці B через 1 , 2 , 3 . Зробимо над рядками матриці B наступні перетворення.