Пряме перетворення фур'є дозволяє визначити. Перетворення фур'є

Перетворення Фур'є- Це сімейство математичних методів, заснованих на розкладанні вихідної безперервної функції від часу на сукупність базисних гармонійних функцій (як яких виступають синусоїдальні функції) різної частоти, амплітуди та фази. З визначення видно, що основна ідея перетворення полягає в тому, що будь-яку функцію можна представити у вигляді нескінченної суми синусоїд, кожна з яких характеризуватиметься своєю амплітудою, частотою та початковою фазою.

Перетворення Фур'є є основоположником спектрального аналізу. Спектральний аналіз – це спосіб обробки сигналів, який дозволяє охарактеризувати частотний склад сигналу, що вимірюється. Залежно від цього, яким чином представлений сигнал, використовують різні перетворення Фур'є. Розрізняють кілька видів перетворення Фур'є:

– Безперервне перетворення Фур'є (в англомовній літературі Continue Time Fourier Transform – CTFTабо, скорочено, FT);

– Дискретне перетворення Фур'є (в англомовній літературі Discrete Fourier Transform – DFT);

– Швидке перетворення Фур'є (в англомовній літературі Fast Fourier transform – FFT).

Безперервне перетворення Фур'є

Перетворення Фур'є є математичним інструментом, що застосовується у різних наукових галузях. У деяких випадках його можна використовувати як рішення складних рівнянь, що описують динамічні процеси, які виникають під впливом електричної, теплової або світлової енергії. В інших випадках воно дозволяє виділяти регулярні складові у складному коливальному сигналі, завдяки чому можна правильно інтерпретувати експериментальні спостереження в астрономії, медицині та хімії. Безперервне перетворення фактично є узагальненням рядів Фур'є за умови, що період функції, що розкладається, спрямувати до нескінченності. Таким чином, класичне перетворення Фур'є має справу із спектром сигналу, взятим у всьому діапазоні існування змінної.

Існує кілька видів запису безперервного перетворення Фур'є, що відрізняються один від одного значенням коефіцієнта перед інтегралом (дві форми запису):

або

де і - Фур'є-образ функції або частотний спектр функції;

- Кругова частота.

Слід зазначити, що різні види запису зустрічаються в різних галузях науки та техніки. Нормувальний коефіцієнт необхідний для коректного масштабування сигналу з частотної області в часову. Нормуючий коефіцієнт зменшує амплітуду сигналу на виході зворотного перетворення для того, щоб вона збігалася з амплітудою вихідного сигналу. У математичній літературі пряме і зворотне перетворення Фур'є множаться на множник, тоді як у фізиці найчастіше при прямому перетворенні множник не ставлять, а при зворотному ставлять множник. Якщо послідовно розрахувати пряме перетворення Фур'є деякого сигналу, а потім узяти зворотне перетворення Фур'є, результат зворотного перетворення повинен повністю збігатися з вихідним сигналом.

Якщо функція непарна на інтервалі (−∞, +∞), то перетворення Фур'є може бути представлене через синус-функцію:

Якщо функція парна на інтервалі (−∞, +∞), то перетворення Фур'є може бути представлене через косинус-функцію:

Таким чином, безперервне перетворення Фур'є дозволяє уявити неперіодичну функцію у вигляді інтеграла функції, що представляє в кожній своїй точці коефіцієнт ряду Фур'є для неперіодичної функції.

Перетворення Фур'є є оборотним, тобто якщо за функцією був розрахований її Фур'є-образ, то за Фур'є-образом можна однозначно відновити вихідну функцію. Під зворотним перетворенням Фур'є розуміють інтеграл виду (дві форми запису):

або

де - Фур'є-образ функції або частотний спектр функції;

- Кругова частота.

Якщо функція непарна на інтервалі (−∞, +∞), то зворотне перетворення Фур'є може бути представлене через синус-функцію:

Якщо функція парна на інтервалі (−∞, +∞), то зворотне перетворення Фур'є може бути представлене через косинус-функцію:

Як приклад, розглянемо таку функцію . Графік досліджуваної експоненційної функції наведено нижче.

Оскільки функція є парною функцією, то безперервне перетворення Фур'є визначатиметься так:

В результаті отримали залежність зміни експоненціальної досліджуваної функції на частотному інтервалі (див. нижче).

Безперервне перетворення Фур'є використовують, як правило, в теорії при розгляді сигналів, які змінюються відповідно до заданих функцій, але на практиці зазвичай мають справу з результатами вимірювань, які є дискретними даними. Результати вимірювання фіксуються через рівні проміжки часу з певною частотою дискретизації, наприклад, 16000 Гц або 22000 Гц. Однак у загальному випадку дискретні відліки можуть бути нерівномірно, але це ускладнює математичний апарат аналізу, тому практично зазвичай не застосовується.

Існує важлива теорема Котельникова (в іноземній літературі зустрічається назва «теорема Найквіста-Шеннона», «теорема відліків»), яка свідчить, що аналоговий періодичний сигнал, що має кінцевий (обмежений шириною) спектр (0…fmax), може бути однозначно відновлений без спотворень і втрат за своїми дискретними відрахунками, взятими з частотою, більшою або рівною подвоєної верхньої частоти спектра - частота дискретизації (f дискр = 2 * fmax). Іншими словами, за частоти дискретизації 1000 Гц з аналогового періодичного сигналу можна відновити сигнал із частотою до 500 Гц. Слід зазначити, що дискретизація функції часу призводить до періодизації її спектра, а дискретизація спектра за частотою призводить до періодизації функції.

Це одне з перетворень Фур'є, які широко застосовуються в алгоритмах цифрової обробки сигналів.

Пряме дискретне перетворення Фур'є ставить у відповідність часової функції , яка визначена N-точками вимірювань на заданому часовому інтервалі, іншу функцію , яка визначена частотному інтервалі. Слід зазначити, що функція на часовому інтервалі визначається за допомогою N-відліків, а функція на частотному інтервалі визначається за допомогою K-кратного спектра.

k ˗ індекс частоти.

Частота k-го сигналу визначається за виразом

де T - період часу, протягом якого бралися вхідні дані.

Пряме дискретне перетворення може бути переписано через речову та уявну складові. Речова складова являє собою масив, що містить значення косинусоїдальних складових, а уявна складова являє собою масив, що містить значення синусоїдальних складових.

З останніх виразів видно, що перетворення розкладає сигнал на синусоїдальні складові (називаються гармоніками) з частотами від одного коливання за період до N коливань за період.

Дискретне перетворення Фур'є має особливість, оскільки дискретна послідовність може бути отримана сумою функцій з різним складом гармонійного сигналу. Інакше кажучи, дискретна послідовність розкладається на гармонійні змінні – неоднозначно. Тому при розкладанні дискретної функції за допомогою дискретного перетворення Фур'є у другій половині спектра виникають високочастотні складові, яких не було в оригінальному сигналі. Даний високочастотний спектр є дзеркальним відображенням першої частини спектра (частини, фази і амплітуди). Зазвичай друга половина спектра не розглядається, а амплітуди сигналу першої частини спектра – подвоюються.

Слід зазначити, що розкладання безперервної функції не призводить до появи дзеркального ефекту, оскільки безперервна функція однозначно розкладається гармонійні змінні.

Амплітуда постійної складової є середнім значенням функції за вибраний проміжок часу та визначається наступним чином:

Амплітуди та фази частотних складових сигналу визначаються за такими співвідношеннями:

Отримані значення амплітуди та фази називають полярним уявленням (polar notation). Результуючий вектор сигналу визначатиметься таким чином:

Розглянемо алгоритм перетворення дискретно заданої функції на заданому інтервалі (на заданому періоді) з кількістю вихідних точок

Дискретне перетворення Фур'є

В результаті перетворення отримуємо речове та уявне значення функції , яка визначена на частотному діапазоні.

p align="justify"> Зворотне дискретне перетворення Фур'є ставить у відповідність частотної функції , яка визначена K-кратним спектром на частотному інтервалі, іншу функцію , яка визначена на часовому інтервалі.

N - кількість значень сигналу, виміряних за період, а також кратність частотного спектра;

k ˗ індекс частоти.

Як було зазначено, дискретне перетворення Фур'є N-точкам дискретного сигналу ставить у відповідність N-комплексних спектральних відліків сигналу . Для обчислення одного спектрального відліку потрібно N операцій комплексного множення та додавання. Таким чином, обчислювальна складність алгоритму дискретного перетворення Фур'є є квадратичною, тобто потрібно операцій комплексного множення та додавання.

Перетворення Фур'є - перетворення, що зіставляє функції певної матеріальної змінної. Ця операція виконується кожного разу, коли ми сприймаємо різні звуки. Вухо здійснює автоматичне «обчислення», виконати яке наша свідомість здатна лише після вивчення відповідного розділу вищої математики. Орган слуху в людини будує перетворення, в результаті якого звук (коливальний рух умовних частинок в пружному середовищі, які поширюються у хвильовому вигляді у твердому, рідкому або газоподібному середовищі) надається у вигляді спектра значень рівня гучності тонів різної висоти, що послідовно йдуть. Після цього мозок перетворює цю інформацію на звичний всім звук.

Математичне перетворення Фур'є

Перетворення звукових хвиль або інших коливальних процесів (від світлового випромінювання та океанського припливу до циклів зоряної або сонячної активності) можна проводити і за допомогою математичних методів. Так, користуючись даними прийомами, можна розкласти функції, представивши коливальні процеси набором синусоїдальних складових, тобто хвилеподібних кривих, які переходять від мінімуму до максимуму, потім знову до мінімуму, подібно до морської хвилі. Перетворення Фур'є - перетворення, функція якого описує фазу або амплітуду кожної синусоїди, що відповідає певній частоті. Фаза є початковою точкою кривої, а амплітуда - її висоту.

Перетворення Фур'є (приклади наведені на фото) є дуже потужним інструментарієм, який застосовується у різноманітних галузях науки. В окремих випадках він використовується як засіб вирішення досить складних рівнянь, які описують динамічні процеси, що виникають під впливом світлової, теплової або електричної енергії. В інших випадках він дозволяє визначати регулярні складові в складних коливальних сигналах, завдяки цьому можна чітко інтерпретувати різні експериментальні спостереження в хімії, медицині та астрономії.

Історична довідка

Першою людиною, яка застосувала цей метод, став французький математик Жан Батіст Фур'є. Перетворення, назване згодом його ім'ям, використовувалося спочатку для опису механізму теплопровідності. Фур'є все своє свідоме життя займався вивченням властивостей тепла. Він зробив величезний внесок у математичну теорію визначення коренів рівнянь алгебри. Фур'є був професором аналізу в Політехнічній школі, секретарем Інституту єгиптології, перебував на імператорській службі, де відзначився під час будівництва дороги на Турін (під його керівництвом було осушено понад 80 тисяч квадратних кілометрів малярійних боліт). Однак ця активна діяльність не завадила вченому займатися математичним аналізом. У 1802 році їм було виведено рівняння, яке описує поширення тепла у твердих тілах. У 1807 році вчений відкрив метод розв'язання даного рівняння, яке і отримало назву "перетворення Фур'є".

Аналіз теплопровідності

Вчений застосував математичний метод опису механізму теплопровідності. Зручним прикладом, в якому не виникає труднощів з обчисленням, є поширення теплової енергії залізним кільцем, зануреним однією частиною у вогонь. Для проведення дослідів Фур'є розпалював до червона частина цього кільця і ​​закопував його в дрібний пісок. Після цього проводив вимірювання температури на протилежній його частині. Спочатку розподіл тепла є нерегулярним: частина кільця – холодна, а інша – гаряча, між цими зонами можна спостерігати різкий градієнт температури. Однак у процесі поширення тепла по всій поверхні металу вона стає рівномірнішою. Так, незабаром цей процес набуває вигляду синусоїди. Спочатку графік плавно наростає і так само плавно зменшується, точно за законами зміни функції косинуса чи синуса. Хвиля поступово вирівнюється і в результаті температура стає однаковою на всій поверхні кільця.

Автор цього методу припустив, що початковий нерегулярний розподіл цілком можна розкласти на ряд елементарних синусоїд. Кожна з них матиме свою фазу (початкове положення) та свій температурний максимум. При цьому кожна така компонента змінюється від мінімуму до максимуму та назад на повному обороті навколо кільця ціле число разів. Складова, що має один період, була названа основною гармонікою, а значення з двома та більше періодами - другий і так далі. Так, математична функція, яка описує температурний максимум, фазу чи позицію називає перетворенням Фур'є від функції розподілу. Вчений звів єдину складову, яка важко піддається математичному опису, до зручного у використанні інструменту - рядам косинуса і синуса, що в сумі дає вихідний розподіл.

Суть аналізу

Застосовуючи даний аналіз до перетворення поширення тепла з твердого предмета, що має кільцеву форму, математик розсудив, що підвищення періодів синусоїдальної компоненти призведе до її швидкого згасання. Це добре простежується на основній та другій гармоніках. В останній температура двічі досягає максимального та мінімального значень на одному проході, а в першій – лише один раз. Виходить, що відстань, яка долається теплом у другій гармоніці, буде вдвічі меншою, ніж в основній. Крім того, градієнт у другій також буде вдвічі крутішим, ніж у першої. Отже, оскільки інтенсивніший тепловий потік проходить відстань вдові менше, то дана гармоніка загасатиме вчетверо швидше, ніж основна, як функція часу. У наступних цей процес проходитиме ще швидше. Математик вважав, що це метод дозволяє розрахувати процес початкового розподілу температури у часі.

Виклик сучасникам

Алгоритм перетворення Фур'є став викликом теоретичним основ математики на той час. На початку дев'ятнадцятого століття більшість видатних учених, у тому числі Лагранж, Лаплас, Пуассон, Лежандр і Біо, не прийняли його твердження про те, що початковий розподіл температури розкладається на складові у вигляді основної гармоніки і більш високочастотні. Однак академія наук не могла проігнорувати результати, отримані математиком, та удостоїла його премії за теорію законів теплопровідності, а також порівняння її з фізичними експериментами. У підході Фур'є головне заперечення викликав те що, що розривна функція представлена ​​сумою кількох синусоїдальних функцій, які є безперервними. Адже вони описують прямі і криві лінії, що розриваються. Сучасники вченого будь-коли стикалися з подібною ситуацією, коли розривні функції описувалися комбінацією безперервних, як-от квадратична, лінійна, синусоїда чи експонента. У тому випадку, якщо математик мав рацію у своїх твердженнях, то сума нескінченного ряду тригонометричної функції повинна зводитися до точної ступінчастої. Тоді подібне твердження здавалося абсурдним. Однак, незважаючи на сумніви, деякі дослідники (наприклад, Клод Нав'є, Софі Жермен) розширили сферу досліджень і вивели їх за межі аналізу розподілу теплової енергії. А математики тим часом продовжували мучитися питанням про те, чи може сума кількох синусоїдальних функцій зводитись до точного уявлення розривної.

200-річна історія

Ця теорія розвивалася протягом двох століть, на сьогоднішній день вона остаточно сформувалася. З її допомогою просторові або часові функції розбиваються на синусоїдальні складові, які мають свою частоту, фазу та амплітуду. Це перетворення виходить двома різними математичними методами. Перший їх застосовується у разі, коли вихідна функція є безперервною, а другий - у разі, коли вона представлена ​​безліччю дискретних окремих змін. Якщо вираз отримано зі значень, які визначені дискретними інтервалами, то його можна розбити на кілька синусоїдальних виразів з дискретними частотами - від найнижчої і далі вдвічі, втричі тощо вище основний. Таку суму прийнято називати поряд Фур'є. Якщо початковий вираз задано значенням для кожного дійсного числа, його можна розкласти на кілька синусоїдальних всіх можливих частот. Його прийнято називати інтегралом Фур'є, а рішення має на увазі інтегральні перетворення функції. Незалежно від способу отримання перетворення, для кожної частоти слід зазначати два числа: амплітуду та частоту. Дані значення виражаються як єдиного Теорія висловів комплексних змінних разом із перетворенням Фур'є дозволила проводити обчислення при конструюванні різних електричних ланцюгів, аналіз механічних коливань, вивчення механізму поширення хвиль та інше.

Перетворення Фур'є сьогодні

В наші дні вивчення цього процесу в основному зводиться до знаходження ефективних методів переходу від функції до її перетвореного вигляду та назад. Таке рішення називається пряме та зворотне перетворення Фур'є. Що це означає? Для того, щоб і зробити пряме перетворення Фур'є, можна скористатися математичними методами, а можна і аналітичними. Незважаючи на те, що при їх використанні на практиці виникають певні труднощі, більшість інтегралів вже знайдені та внесені до математичних довідників. За допомогою чисельних методів можна розраховувати вирази, форма яких ґрунтується на експериментальних даних, або функції, інтеграли яких у таблицях відсутні та їх складно уявити в аналітичній формі.

До появи обчислювальної техніки розрахунки таких перетворень були дуже стомлюючими, вони вимагали ручного виконання великої кількості арифметичних операцій, що залежали від кількості точок, що описують функцію хвилі. Для полегшення розрахунків сьогодні існують спеціальні програми, що дозволили реалізувати нові Так, у 1965 році Джеймс Кулі та Джон Тьюкі створили програмне забезпечення, яке здобуло популярність як «швидке перетворення Фур'є». Воно дозволяє заощаджувати час проведення розрахунків з допомогою зменшення кількості множень під час аналізу кривої. Метод «швидке перетворення Фур'є» заснований на розподілі кривої велике число рівномірних вибіркових значень. Відповідно кількість множень знижується вдвічі за такого ж зниження кількості точок.

Застосування перетворення Фур'є

Цей процес використовують у різних галузях науки: у фізиці, обробці сигналів, комбінаториці, теорії ймовірності, криптографії, статистиці, океанології, оптиці, акустиці, геометрії та інших. Багаті можливості його застосування ґрунтуються на ряді корисних особливостей, які отримали назву "властивості перетворення Фур'є". Розглянемо їх.

1. Перетворення функції є лінійним оператором та з відповідною нормалізацією є унітарним. Ця властивість відома як теорема Парсеваля, або в загальному випадку теорема Планшереля, або дуалізм Понтрягіна.

2. Перетворення є оборотним. Причому зворотний результат має практично аналогічну форму, як і за прямому рішенні.

3. Синусоїдальні базові вирази є власними диференційованими функціями. Це означає, що таке уявлення змінює з постійним коефіцієнтом у звичайні алгебраїчні.

4. Відповідно до теореми «згортки», цей процес перетворює складну операцію на елементарне множення.

5. Дискретне перетворення Фур'є може бути розраховане на комп'ютері з використанням «швидкого» методу.

Різновиди перетворення Фур'є

1. Найчастіше цей термін використовується для позначення безперервного перетворення, що надає будь-який квадратично інтегрований вираз у вигляді суми комплексних показових виразів з конкретними кутовими частотами та амплітудами. Цей вид має кілька різних форм, які можуть відрізнятися постійними коефіцієнтами. Безперервний метод включає таблицю перетворень, яку можна знайти в математичних довідниках. Узагальненим випадком є ​​дробове перетворення, з якого даний процес можна звести в необхідну речовинну ступінь.

2. Безперервний спосіб є узагальненням ранньої методики рядів Фур'є, визначених для різних періодичних функцій або виразів, які існують в обмеженій ділянці та представляють їх як ряди синусоїд.

3. Дискретне перетворення Фур'є. Цей метод використовується в комп'ютерній техніці для проведення наукових розрахунків та цифрової обробки сигналів. Для проведення цього виду розрахунків потрібно мати функції, що визначають на дискретній множині окремі точки, періодичні або обмежені області замість безперервних інтегралів Фур'є. Перетворення сигналу у разі представлено як сума синусоїд. У цьому використання «швидкого» методу дозволяє застосовувати дискретні рішення будь-яких практичних завдань.

4. Віконне перетворення Фур'є є узагальненим виглядом класичного методу. На відміну від стандартного рішення, коли використовується який взятий у повному діапазоні існування даної змінної, тут особливий інтерес представляє лише локальне розподіл частоти за умови збереження початкової змінної (час).

5. Двовимірне перетворення Фур'є. Цей метод використовується для роботи з двовимірними масивами даних. У такому разі спочатку перетворення проводиться в одному напрямку, а потім – в іншому.

Висновок

Сьогодні метод Фур'є міцно закріпився у різних галузях науки. Наприклад, в 1962 році була відкрита форма подвійної ДНК-спіралі з використанням аналізу Фур'є в поєднанні з останніми фокусувалися на кристалах волокон ДНК, в результаті зображення, яке виходило при дифракції випромінювання, фіксувалися на плівці. Ця картинка дала інформацію про значення амплітуди під час використання перетворення Фур'є до цієї кристалічної структурі. Дані про фазу отримали шляхом зіставлення дифракційної карти ДНК з картами, які отримані під час аналізу подібних хімічних структур. В результаті біологи відновили кристалічну структуру – вихідну функцію.

Перетворення Фур'є грають величезну роль у вивченні космічного простору, фізики напівпровідникових матеріалів та плазми, мікрохвильової акустики, океанографії, радіолокації, сейсмології та медичних обстежень.

Ці перетворення є функціональними, оскільки вони перетворюють деяку функцію змінного на зовсім іншу функцію змінного , і навпаки.

Перетворення Фур'є мають вигляд:

Інтегральне рівняння (4.34) називається прямим, а рівняння (4.35) – зворотним перетворенням Фур'є. Скорочена форма запису цих рівнянь

Інтеграл Фур'є (пряме перетворення Фур'є) дозволяє розкласти неперіодичну функцію, що має властивість абсолютної інтегрованості в заданих межах, в нескінченний ряд гармонік, що утворюють безперервний спектр частот в інтервалі від до з нескінченно малим інтервалом частот між суміжними гармоніками (т. е. в межі

Метод перетворення Фур'є непридатний за ненульових початкових (або граничних) умов. Цей метод може застосовуватися лише тоді, коли шукані функції мають зображення Фур'є, тобто для абсолютно інтегрованих функцій часу, що задовольняють нерівність

Найбільш часто зустрічаються в теорії регулювання функціями є одинична ступінчаста функція (1.44) і добуток синусоїдальної функції на одиничну функцію (1.51). Перетворення Фур'є не застосовується до жодної з цих функцій, оскільки не задовольняється умова (4.38).

Зазначені недоліки обмежують використання методу перетворення Фур'є.

Щоб застосувати інтеграл Фур'є, необхідно вибрати функцію, досить близьку до досліджуваної, наприклад, до ступінчастої функції при кінцевих значеннях, але водночас задовольняє умові (4.38). Таку функцію можна отримати, помноживши

ступінчасту функцію де з - досить мала позитивна величина. Знову отримана допоміжна функція

Крім того, якщо обмежитися функціями , тотожно рівними нулю при то для великого класу функцій буде справедлива умова (4.38) і можна знайти частотний спектр функції, використовуючи вираз (4.34) . Замість введемо нове позначення так як ця величина тепер залежить і від:

Поклавши з знаходимо

Ця формула збігається із прямим перетворенням Лапласа (4.9).

Звідси випливає, що перетворення Фур'є можна як окремий випадок перетворення Лапласа.

Викладені вище методи перетворень дозволяють зробити такі висновки:

1) інтегро-диференціальні рівняння замінюються рівняннями алгебри;

2) відпадає операція визначення постійних інтегрування, оскільки початкові умови враховуються від початку при знаходженні зображення шуканої величини;

3) операція визначення коренів характеристичного рівняння повністю зберігається.

Найзручнішим на вирішення практичних завдань метод перетворення Лапласа. У дещо зміненій формі може бути застосований до дослідження дискретних САУ (див. гл. 7).

Розглянемо використання методу перетворень Лапласа на вирішення диференціального рівняння виду

Перетворимо це диференціальне рівняння, використовуючи пряме перетворення Лапласа (4.9) і теореми 1 і 2. В результаті отримаємо рівняння алгебри, записане для зображень:

де - Сума всіх членів, що містять початкові умови.

Звідси знаходиться зображення шуканої функції

За нульових початкових умов вирази (4.41) та (4.42) спрощуються:

Знаючи зображення шуканої функції можна знайти оригінал, наприклад, за таблицями зображень.

Якщо зображення шуканої величини є раціональним алгебраїчним дробом, то її намагаються записати у вигляді суми простих дробів з постійними коефіцієнтами. Зворотне перетворення кожної з цих простих дробів може бути отримано з таблиць, а остаточне вираз оригіналу представлено як сума окремих знайдених значень. Для визначення оригіналу можна скористатися теоремою розкладання.

Якщо зображення Лапласа є раціональним алгебраїчним дробом виду

Розглянемо основні властивості перетворення Фур'є.

Лінійність. Розглянемо функції та
, що мають спектри
і
:

(12)

Тоді спектр їхньої лінійної комбінації буде:

Затримка у часі. Вважаємо, що відомий спектр
сигналу

(14)

Розрахуємо спектр сигналу, зрушеного у часі:
. Позначимо аргумент функції нової змінної
тоді
і

Отримали, що затримка сигналу на якийсь час призводить до множення спектру на
.

Зміна масштабу.Вважаємо, що відомий спектр
сигналу
, як через
виражається спектр сигналу
. Вводимо нову змінну
, робимо заміну змінної інтегрування
.

(16)

Множення на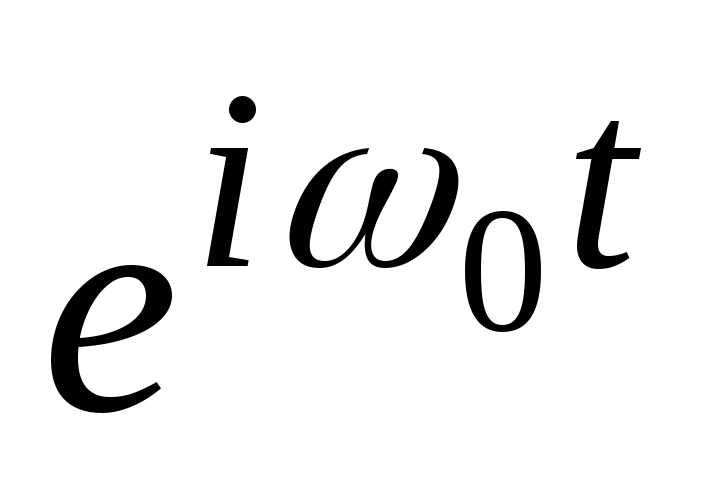
. Як і в попередньому випадку, вважаємо, що відомий спектр
сигналу
. Знайдемо спектр цього сигналу, помноженого на
.

Таким чином, множення сигналу на
призводить до зміщення спектру на .

Спектр похідної.У разі ключовим моментом є абсолютна інтегрованість функції. З того, що інтеграл від модуля функції має бути обмежений, випливає, що на нескінченності функція повинна прагнути нуля. Інтеграл від похідної функції береться вроздріб, вийшли внеинтегральные доданки рівні нулю, оскільки у нескінченності функція прагне нулю.

(18)

Спектр інтегралу.Знайдемо спектр сигналу
. Причому вважатимемо, що
тобто у сигналу відсутня постійна складова. Ця вимога необхідна, щоб позаінтегральні доданки дорівнювали нулю, коли інтеграл береться частинами.

(19)

Теорема про згортку.Відомо що
і
спектри функцій
і
відповідно. Потрібно виразити спектр згортки
через
і
. Для цього в інтегралі Фур'є від згортки в однієї з функцій виконаємо заміну зміною
тоді в показнику експоненти можна зробити заміну
. В результаті такої заміни дворазовий інтеграл дорівнюватиме твору двох інтегралів Фур'є.

(20)

Перетворення Фур'є згортки двох сигналів дає добуток спектрів цих сигналів.

Добуток сигналів.Відомо що
і
- Спектри функцій
і
відповідно. Потрібно висловити спектр твору
через спектри
і
. Підставимо в інтеграл Фур'є замість одного із сигналів, наприклад
, його вираз через зворотне перетворення Фур'є, та був змінимо порядок інтегрування.

(21)

Спектр добутку сигналів є згортка спектрів цих сигналів.

Спектр дискретного сигналу

p align="justify"> Особливу увагу варто приділити дискретним сигналам, так як саме такі сигнали використовуються в цифровій обробці. Дискретний сигнал на відміну безперервного є послідовністю чисел, що відповідають значенням безперервного сигналу в певні моменти часу. Умовно дискретний сигнал можна як безперервний сигнал, який у певні моменти часу приймає якісь значення, а решта дорівнює нулю. Таким чином, наприклад, дискретний
сигнал може бути заданий як добуток безперервного сигналу
на послідовність прямокутних імпульсів, що періодично повторюються.
- Тактуючих імпульсів (рис.1).

Рис. 1. Дискретизація сигналу.

(22)

Прямокутні імпульси мають тривалість , період повторення :

(23)

Амплітуда імпульсу обрана таким чином, щоб інтеграл імпульсу за періодом дорівнював . При цьому тактуючі імпульси безрозмірні. Розкладемо послідовність таких імпульсів у тригонометричний ряд:

(24)

Щоб отримати миттєві відліки сигналу
, треба спрямувати тривалість імпульсів до нуля:
. Такий тактуючий сигнал назвемо ідеальним. При цьому коефіцієнти розкладання
у ряд Фур'є всі дорівнюватимуть 1.

(25)

Такий самий вид має розкладання в ряд Фур'є функції:

(26)

Коефіцієнти розкладання тригонометричний ряд тактуючого сигналу
:

(27)

Тоді дискретний сигнал матиме вигляд:

При обчисленні перетворення Фур'є дискретного сигналу міняємо місцями операцію підсумовування та інтегрування, а потім використовуємо властивість δ -функції:

Спектр дискретного сигналу є періодичною функцією. Розглянемо експоненту в готельному доданку
як функцію частоти. Її період повторення дорівнює . Найбільший період повторення у доданків з номерами
, і це, відповідно, буде періодом повторення всього спектра. Тобто спектр дискретного сигналу має період повторення, що дорівнює частоті квантування.
.

Отримаємо ще одну виставу
. В силу того, що
є добутком функцій
і
, спектр дискретного сигналу
обчислюється як згортка спектрів безперервного сигналу
та спектру тактуючого сигналу
.

(30)

Обчислимо
, використовуючи (25). Так як
періодична функція, її діапазон дискретний.

Таким чином, згортка (30)

З виразу (32) випливає, що спектр дискретного сигналу являє собою функцію, що періодично повторюється
.

Сам факт того, що в результаті дискретизації в спектрі сигналу відбуваються якісні зміни, говорить про те, що вихідний сигнал може бути спотворений, оскільки він повністю визначається своїм спектром. Однак з іншого боку періодичне повторення одного й того самого спектру саме по собі не вносить нічого нового в спектр, тому за певних умов, знаючи значення сигналу в окремі моменти часу, можна знайти яке значення цей сигнал набував у будь-який інший момент часу, тобто отримати вихідний безперервний сигнал. У цьому полягає сенс теореми Котельникова, яка накладає умову вибір частоти квантування відповідно до максимальної частотою в спектрі сигналу.

Якщо ця умова порушена, то після оцифрування сигналу відбудеться накладення спектру, що періодично повторюється (рис. 2). Спектр, що вийшов в результаті накладання, буде відповідати іншому сигналу.

Рис. 2. Перекриття спектрів.

Цей ряд може бути записаний у вигляді:

(2),
де, k-я комплексна амплітуда.

Зв'язок між коефіцієнтами (1) та (3) виражається такими формулами:

Зазначимо, всі ці три уявлення низки Фур'є цілком рівнозначні. Іноді під час роботи з рядами Фур'є буває зручніше використовувати замість синусів і косінусів експоненти уявного аргументу, тобто використовувати перетворення Фур'є у комплексній формі. Але нам зручно використовувати формулу (1), де ряд Фур'є представлений у вигляді суми косінусоїд з відповідними амплітудами та фазами. У будь-якому разі неправильно говорити, що результатом перетворення Фур'є дійсного сигналу будуть комплексні амплітуди гармонік. Як правильно говориться в Вікі «Перетворення Фур'є (?) - операція, яка зіставляє однієї функції речової змінної іншу функцію, також речової змінної.»

Разом:
Математичною основою спектрального аналізу сигналів є перетворення Фур'є.

Перетворення Фур'є дозволяє представити безперервну функцію f(x) (сигнал), визначену на відрізку (0, T) у вигляді суми нескінченного числа (нескінченного ряду) тригонометричних функцій (синусоїд та косинусоід) ​​з певними амплітудами і фазами, також розглядаються на відрізку (0, T). Такий ряд називається поряд Фур'є.

Зазначимо ще деякі моменти, розуміння яких потрібно правильного застосування перетворення Фур'є до аналізу сигналів. Якщо розглянути ряд Фур'є (суму синусоїд) на всій осі Х, то можна побачити, що поза відрізком (0, T) функція представлена ​​поруч Фур'є буде періодично повторювати нашу функцію.

Наприклад, на графіці рис.7 вихідна функція визначена на відрізку (-T2, + T2), а ряд Фур'є представляє періодичну функцію, визначену на всій осі х.

Це тому, що синусоїди самі є періодичними функціями, відповідно і їх сума буде періодичною функцією.

рис.7 Подання неперіодичної вихідної функції поруч Фур'є

Таким чином:

Наша вихідна функція – безперервна, неперіодична, визначена на деякому відрізку довжиною T.
Спектр цієї функції – дискретний, тобто представлений у вигляді нескінченного ряду гармонійних складових – низки Фур'є.
За фактом, поряд Фур'є визначається деяка періодична функція, що збігається з нашою на відрізку (0, T), але для нас ця періодичність не суттєва.

Періоди гармонійних складових кратні величині відрізка (0, T), на якому визначено вихідну функцію f(x). Інакше кажучи, періоди гармонік кратні тривалості вимірювання сигналу. Наприклад, період першої гармоніки низки Фур'є дорівнює інтервалу Т, у якому визначено функцію f(x). Період другої гармоніки ряду Фур'є дорівнює інтервалу Т/2. І так далі (див. мал. 8).

рис.8 Періоди (частоти) гармонійних складових ряду Фур'є (тут Т=2?)

Відповідно, частоти гармонійних складових кратні величині 1/Т. Тобто частоти гармонійних складових Fk дорівнюють Fk= к\Т, де до пробігає значення від 0 до?, наприклад до=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к = 3 F3 = 3 \ T; ... Fk = к \ Т (при нульовій частоті - постійна складова).

Нехай наша вихідна функція є сигнал, записаний протягом Т=1 сек. Тоді період першої гармоніки дорівнюватиме тривалості нашого сигналу Т1=Т=1 сек і частота гармоніки дорівнює 1 Гц. Період другої гармоніки дорівнюватиме тривалості сигналу, поділеної на 2 (Т2=Т/2=0,5 сек) і частота дорівнює 2 Гц. Для третьої гармоніки Т3=Т/3 с і частота дорівнює 3 Гц. І так далі.

Крок між гармоніками у разі дорівнює 1 Гц.

Таким чином, сигнал тривалістю 1 сек можна розкласти на гармонійні складові (отримати спектр) з роздільною здатністю по частоті 1 Гц.
Щоб збільшити розподільну здатність в 2 рази до 0,5 Гц - треба збільшити тривалість вимірювання в 2 рази - до 2 сек. Сигнал тривалістю 10 с можна розкласти на гармонійні складові (отримати спектр) з роздільною здатністю по частоті 0,1 Гц. Інших способів збільшити роздільну здатність за частотою немає.

Існує спосіб штучного збільшення тривалості сигналу шляхом додавання нулів до масиву відліків. Але реальну роздільну здатність за частотою він не збільшує.

3. Дискретні сигнали та дискретне перетворення Фур'є

З розвитком цифрової техніки змінилися способи зберігання даних вимірювань (сигналів). Якщо раніше сигнал міг записуватися на магнітофон і зберігатися на стрічці у аналоговому вигляді, нині сигнали оцифровуються і зберігаються у файлах у пам'яті комп'ютера як набору чисел (отсчетов).

Звичайна схема вимірювання та оцифрування сигналу виглядає наступним чином.

рис.9 Схема вимірювального каналу

Сигнал із вимірювального перетворювача надходить на АЦП протягом періоду часу Т. Отримані за час Т відліки сигналу (вибірка) передаються в комп'ютер і зберігаються в пам'яті.

рис.10 Оцифрований сигнал - N відліків отриманих за час Т

Які вимоги висуваються до параметрів оцифрування? Пристрій, що перетворює вхідний аналоговий сигнал дискретний код (цифровий сигнал) називається аналого-цифровий перетворювач (АЦП, англ. Analog-to-digital converter, ADC) (Wiki).

Однією з основних параметрів АЦП є максимальна частота дискретизації (чи частота семплювання, англ. sample rate) - частота взяття відліків безперервного у часі сигналу за його дискретизації. Вимірюється у герцах. ((Wiki))

Згідно з теоремою Котельникова, якщо безперервний сигнал має спектр, обмежений частотою Fмакс, то він може бути повністю і однозначно відновлений за його дискретними відліками, взятими через інтервали часу , тобто. з частотою Fd? 2*Fмакс, де Fd – частота дискретизації; Fмакс – максимальна частота спектра сигналу. Іншими словами, частота оцифрування сигналу (частота дискретизації АЦП) повинна як мінімум у 2 рази перевищувати максимальну частоту сигналу, який ми хочемо виміряти.

А що буде, якщо ми братимемо відліки з меншою частотою, ніж потрібно за теоремою Котельникова?

У цьому випадку виникає ефект "аліасингу" (він же стробоскопічний ефект, муаровий ефект), при якому сигнал високої частоти після оцифрування перетворюється на сигнал низької частоти, якого насправді не існує. На рис. 5 червона синусоїда високої частоти – це реальний сигнал. Синя синусоїда нижчої частоти - фіктивний сигнал, що виникає внаслідок того, за час взяття відліку встигає пройти більше, ніж півперіоду високочастотного сигналу.

Рис. 11. Поява помилкового сигналу низької частоти за недостатньо високої частоти дискретизації

Щоб уникнути ефекту аліасингу перед АЦП ставлять спеціальний антиаліасинговий фільтр - ФНЧ (фільтр нижніх частот), який пропускає частоти нижче половини частоти дискретизації АЦП, а вищі частоти зарізає.

Для того щоб обчислити спектр сигналу за його дискретними відліками використовується дискретне перетворення Фур'є (ДПФ). Зазначимо ще раз, що спектр дискретного сигналу «за визначенням» обмежений частотою Fмакс меншою половиною частоти дискретизації Fd. Тому спектр дискретного сигналу може бути представлений сумою кінцевого числа гармонік, на відміну від нескінченної суми для ряду безперервного Фур'є сигналу, спектр якого може бути необмежений. Відповідно до теореми Котельникова максимальна частота гармоніки повинна бути такою, щоб на неї припадало щонайменше два відліки, тому число гармонік дорівнює половині числа відліків дискретного сигналу. Тобто якщо у вибірці є N відліків, то число гармонік у діапазоні дорівнюватиме N/2.

Розглянемо тепер дискретне перетворення Фур'є (ДПФ).

Порівнюючи з рядом Фур'є

Бачимо, що вони збігаються, за винятком того, що час у ДПФ має дискретний характер і кількість гармонік обмежена величиною N/2 – половиною числа відліків.

Формули ДПФ записуються у безрозмірних цілих змінних k, s, де k – номери відліків сигналу, s – номери спектральних складових.
Величина s показує кількість повних коливань гармоніки на періоді Т (тривалості вимірювання сигналу). Дискретне перетворення Фур'є використовується знаходження амплітуд і фаз гармонік чисельним методом, тобто. "на комп'ютері"

Повертаючись до результатів, отриманих на початку. Як було зазначено вище, при розкладанні у ряд Фур'є неперіодичної функції (нашого сигналу), отриманий ряд Фур'є фактично відповідає періодичної функції з періодом Т. (рис.12).

рис.12 Періодична функція f(x) з періодом Т0, з періодом вимірювання Т>T0

Як видно на рис.12 функція f(x) періодична з періодом Т0. Однак через те, що тривалість вимірювальної вибірки Т не збігається з періодом функції Т0, функція, що отримується як ряд Фур'є, має розрив у точці Т. В результаті спектр цієї функції міститиме велику кількість високочастотних гармонік. Якби тривалість вимірювальної вибірки Т збігалася з періодом функції Т0, то в отриманому після перетворення Фур'є спектрі була б присутня тільки перша гармоніка (синусоїда з періодом рівним тривалості вибірки), оскільки функція f(x) являє собою синусоїду.

Іншими словами, програма ДПФ «не знає», що наш сигнал є «шматком синусоїди», а намагається представити у вигляді ряду періодичну функцію, яка має розрив через нестикування окремих шматків синусоїди.

У результаті спектрі з'являються гармоніки, які мають у сумі зобразити форму функції, включаючи цей розрив.

Таким чином, щоб отримати «правильний» спектр сигналу, що є сумою кількох синусоїд з різними періодами, необхідно щоб на період вимірювання сигналу вкладалося ціле число періодів кожної синусоїди. На практиці цю умову можна виконати за досить великої тривалості вимірювання сигналу.

Рис.13 Приклад функції та спектра сигналу кінематичної похибки редуктора

За меншої тривалості картина виглядатиме «гірше»:

Рис.14 Приклад функції та спектру сигналу вібрації ротора

Насправді буває складно зрозуміти, де «реальні складові», а де «артефакти», викликані некратностью періодів складових і тривалості вибірки сигналу чи «стрибками і розривами» форми сигналу. Звичайно слова «реальні складові» та «артефакти» не дарма взяті у лапки. Наявність на графіку спектра безлічі гармонік не означає, що наш сигнал насправді з них «складається». Це все одно що вважати, що число 7 «складається» з чисел 3 і 4. Число 7 можна представити у вигляді суми чисел 3 і 4 - це правильно.

Так і наш сигнал… а точніше навіть не «наш сигнал», а періодичну функцію, складену шляхом повторення нашого сигналу (вибірки) можна у вигляді суми гармонік (синусоїд) з певними амплітудами та фазами. Але в багатьох важливих для практики випадках (див. малюнки вище) дійсно можна пов'язати отримані в спектрі гармоніки і з реальними процесами, що мають циклічний характер і значний внесок у форму сигналу.

Деякі підсумки

1. Реальний виміряний сигнал, тривалістю T сек, оцифрований АЦП, тобто представлений набором дискретних відліків (N штук), має неперіодичний дискретний спектр, представлений набором гармонік (N/2 штук).

2. Сигнал представлений набором дійсних значень та його спектр представлений набором дійсних значень. Частоти гармонік позитивні. Те, що математикам буває зручніше уявити спектр у комплексній формі з використанням негативних частот не означає, що так правильно і так завжди треба робити.

3. Сигнал, виміряний на відрізку часу Т визначено тільки на відрізку часу Т. Що було до того, як ми почали вимірювати сигнал, і що буде після того – науці це невідомо. І в нашому випадку – нецікаво. ДПФ обмеженого у часі сигналу дає його «справжній» спектр, у тому сенсі, що за певних умов дозволяє обчислити амплітуду та частоту його складових.

Використані матеріали та інші корисні матеріали.