Ранг матриці: визначення, методи знаходження, приклади, рішення. Знаходження рангу матриці Чому дорівнює ранг матриці 1123 5814

А також розглянемо важливий практичний додаток теми: дослідження системи лінійних рівнянь на сумісність.

Що таке ранг матриці?

У гумористичному епіграфі статті міститься велика частка істини. Саме слово «ранг» у нас зазвичай асоціюється з деякою ієрархією, найчастіше, зі службовими сходами. Чим більше людина знань, досвіду, здібностей, блату тощо. – тим вища його посада та спектр можливостей. Висловлюючись молодіжним, під рангом мають на увазі загальний ступінь «крутості».

І брати наші математичні живуть за тими самими принципами. Виведемо на прогулянку кілька довільних нульових матриць:

Замислимося, якщо у матриці одні нулі, то про який ранг може йтися? Усім знайомий неформальний вираз «повний нуль». У суспільстві матриць все так само:

Ранг нульової матрицібудь-яких розмірів дорівнює нулю.

Примітка : нульова матриця позначається грецькою літерою «тета»

З метою кращого розуміння рангу матриці тут і далі я залучатиму на допомогу матеріали аналітичної геометрії. Розглянемо нульовий векторнашого тривимірного простору, який не задає певного напряму і не є корисним для побудови афінного базису. З точки зору алгебри координати даного вектора записані в матрицю«один на три» та логічно (У зазначеному геометричному сенсі)вважати, що ранг цієї матриці дорівнює нулю.

Тепер розглянемо кілька ненульових векторів-стовпціві векторів-рядок:

У кожному екземплярі є хоча б один ненульовий елемент, і це вже дещо!

Ранг будь-якого ненульового вектора-рядки (вектора-стовпця) дорівнює одиниці

І взагалі - якщо у матриці довільних розмірівє хоча б один ненульовий елемент, то її ранг не меншеодиниці.

Алгебраїчні вектори-рядки та вектори-стовпці певною мірою абстрактні, тому знову звернемося до геометричної асоціації. Ненульовий векторзадає цілком певний напрямок у просторі та годиться для побудови базисутому ранг матриці будемо вважати рівним одиниці.

Теоретична довідка : у лінійній алгебрі вектор – це елемент векторного простору (визначається через 8 аксіом), який, зокрема, може являти собою впорядкований рядок (або стовпець) дійсних чисел з певними для них операціями складання та множення на дійсне число. З більш детальною інформацією про вектори можна ознайомитись у статті Лінійні перетворення.

лінійно залежні(Виражаються один через одного). З геометричної точки зору до другого рядка записані координати колінеарного вектора , який анітрохи не просунув справу у побудові тривимірного базису, будучи в цьому сенсі зайвим. Таким чином, ранг цієї матриці теж дорівнює одиниці.

Перепишемо координати векторів у стовпці ( транспонуємо матрицю):

Що змінилося з погляду рангу? Нічого. Стовпці пропорційні, отже, ранг дорівнює одиниці. До речі, зверніть увагу, що всі три рядки також пропорційні. Їх можна ототожнити з координатами трьохколінеарних векторів площини, з яких тільки одинкорисний для побудови «плоського» базису. І це повністю узгоджується з нашим геометричним змістом рангу.

З наведеного прикладу слід важливе твердження:

Ранг матриці по рядках дорівнює рангу матриці за стовпцями. Про це я вже трохи згадував на уроці про ефективні методи обчислення визначника.

Примітка : з лінійної залежності рядків випливає лінійна залежність стовпців (і навпаки). Але з метою економії часу, та й через звичку я майже завжди говоритиму про лінійну залежність рядків.

Продовжимо дресирувати нашого улюбленого вихованця. Додамо до матриці третій рядок координати ще одного колінеарного вектора :

Чи допоміг він нам у побудові тривимірного базису? Звичайно, ні. Всі три вектори гуляють туди-сюди однією доріжкою, і ранг матриці дорівнює одиниці. Можна взяти скільки завгодно колінеарних векторів, скажімо, 100, укласти їх координати в матрицю «сто на три» і ранг такого хмарочоса все одно залишиться поодиноким.

Познайомимося з матрицею, рядки якої лінійно незалежні. Пара неколлінеарних векторів придатна для побудови тривимірного базису. Ранг цієї матриці дорівнює двом.

А чому дорівнює ранг матриці? Рядки начебто не пропорційні ..., значить, за ідеєю трьом. Однак ранг цієї матриці теж дорівнює двом. Я склав перші два рядки і записав результат унизу, тобто лінійно висловивтретій рядок через перші два. Геометрично рядки матриці відповідають координатам трьох компланарних векторів, причому серед цієї трійки є пара неколлінеарних товаришів.

Як бачите, лінійна залежністьу розглянутій матриці не очевидна, і сьогодні ми навчимося виводити її «на чисту воду».

Думаю, багато хто здогадується, що таке ранг матриці!

Розглянемо матрицю, рядки якої лінійно незалежні. Вектори утворюють афінний базис, і ранг цієї матриці дорівнює трьом.

Як ви знаєте, будь-який четвертий, п'ятий, десятий вектор тривимірного простору лінійно виражатиметься через базисні вектори. Тому, якщо до матриці додати будь-яку кількість рядків, то її ранг все одно дорівнюватиме трьом.

Аналогічні міркування можна провести для матриць більших розмірів (зрозуміло, вже без геометричного змісту).

Визначення : ранг матриці – це максимальна кількість лінійно незалежних рядків. Або: ранг матриці – це максимальна кількість лінійно незалежних стовпців. Так, їхня кількість завжди збігається.

З вищесказаного також випливає важливий практичний орієнтир: ранг матриці не перевищує її мінімальної розмірності. Наприклад, у матриці чотири рядки та п'ять стовпців. Мінімальна розмірність - чотири, отже, ранг даної матриці явно не перевищить 4.

Позначення: у світовій теорії та практиці немає загальноприйнятого стандарту для позначення рангу матриці, найчастіше можна зустріти: – як кажуть, англієць пише одне, німець інше. Тому давайте за мотивами відомого анекдоту про американське та російське пекло позначати ранг матриці рідним словом. Наприклад: . А якщо матриця «безіменна», яких зустрічається дуже багато, можна просто записати .

Як знайти ранг матриці за допомогою мінорів?

Якби у бабусі нас у матриці був п'ятий стовпець, слід було б обчислити ще один мінор 4-го порядку («сині», «малиновий» + 5-й стовпець).

Висновок: максимальний порядок ненульового мінору дорівнює трьом, отже, .

Можливо, не всі остаточно осмислили цю фразу: мінор 4-го порядку дорівнює нулю, але серед мінорів 3-го порядку знайшовся ненульовий - тому максимальний порядок ненульовогомінору і дорівнює трьом.

Виникає питання, а чому б одразу не обчислити визначник? Ну, по-перше, у більшості завдань матриця не квадратна, а по-друге, навіть якщо у вас і вийде ненульове значення, то завдання з високою ймовірністю забракують, оскільки воно зазвичай має на увазі стандартне рішення «знизу нагору». А в розглянутому прикладі нульовий визначник 4-го порядку взагалі дозволяє стверджувати, що ранг матриці лише менше чотирьох.

Повинен зізнатися, розібране завдання я придумав сам, щоб якісніше пояснити метод мінорів. У реальній практиці все простіше:

Приклад 2

Знайти ранг матриці методом обрамляють мінорів

Рішення та відповідь наприкінці уроку.

Коли алгоритм працює найшвидше? Повернемося до тієї ж матриці «чотири на чотири» . Очевидно, рішення буде найкоротшим у разі «хороших» кутових мінорів: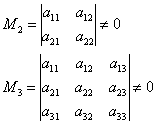

І, якщо , то , інакше – .

Роздуми зовсім не гіпотетичні – існує чимало прикладів, де вся справа і обмежується лише кутовими мінорами.

Однак у ряді випадків ефективніший і кращий інший спосіб:

Як знайти ранг матриці за допомогою методу Гауса?

Параграф розрахований на читачів, які вже знайомі з методом Гаусаі хоч трохи набили на ньому руку.

З технічної точки зору метод не відрізняється новизною:

1) за допомогою елементарних перетворень наводимо матрицю до ступінчастого вигляду;

2) ранг матриці дорівнює кількості рядків.

Цілком зрозуміло, що використання методу Гауса не змінює рангу матриці, І суть тут дуже проста: згідно з алгоритмом, в ході елементарних перетворень виявляються і видаляються всі зайві пропорційні (лінійно залежні) рядки, в результаті чого залишається «сухий залишок» – максимальна кількість лінійно незалежних рядків.

Перетворимо стару знайому матрицю з координатами трьох колінеарних векторів:

(1) До другого рядка додали перший рядок, помножений на -2. До третього рядка додали перший рядок.

(2) Нульові рядки видаляємо.

Таким чином, залишився один рядок, отже, . Що й казати, це набагато швидше, ніж розрахувати дев'ять нульових мінорів 2-го порядку і лише потім зробити висновок.

Нагадую, що у самій по собі алгебраїчної матрицінічого міняти не можна, і перетворення виконуються лише з метою з'ясування рангу! До речі, зупинімося ще раз на питанні, чому не можна? Вихідна матриця 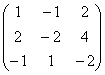несе інформацію, яка принципово відрізняється від інформації матриці та рядка . У деяких математичних моделях (без перебільшення) різниця в одному числі може бути питанням життя та смерті. …Згадалися шкільні вчителі математики початкових та середніх класів, які безжально зрізали оцінку на 1-2 бали за найменшу неточність чи відхилення від алгоритму. І було дуже прикро, коли замість, здавалося б, гарантованої «п'ятірки» виходило «добре» або ще гірше. Розуміння прийшло набагато пізніше – а як інакше довірити людині супутники, ядерні боєголовки та електростанції? Але ви не турбуйтеся, я не працюю у цих сферах =)

Перейдемо до змістовніших завдань, де також познайомимося з важливими обчислювальними прийомами методу Гауса:

Приклад 3

Знайти ранг матриці за допомогою елементарних перетворень

Рішення: дана матриця «чотири на п'ять», значить, її ранг свідомо не більше 4

У першому стовпці, відсутня 1 або –1, отже, необхідні додаткові дії, створені задля отримання хоча б однієї одиниці. За весь час існування сайту мені неодноразово ставили питання: «Чи можна під час елементарних перетворень переставляти стовпці?». Ось тут - переставили перший-другий стовпець, і все чудово! У більшості завдань, де використовується метод Гауса, стовпці справді переставляти можна. АЛЕ НЕ ПОТРІБНО. І справа навіть не в можливій плутанині зі змінними, справа в тому, що в класичному курсі навчання вищої математики дана дія традиційно не розглядається, тому на такий реверанс подивляться дуже криво (а то й змусять все переробляти).

Другий момент стосується чисел. У результаті рішення корисно керуватися наступним емпіричним правилом: елементарні перетворення наскільки можна зменшувати числа матриці. Адже з одиницею-двійкою-трійкою працювати значно легше, ніж, наприклад, з 23, 45 та 97. І перша дія спрямована не лише на отримання одиниці у першому стовпці, а й на ліквідацію чисел 7 та 11.

Спочатку повне рішення, потім коментарі:

(1) До другого рядка додали перший рядок, помножений на -2. До третього рядка додали перший рядок, помножений на -3. І до купи: до 4-го рядка додали 1-й рядок, помножений на -1.

(2) Останні три рядки пропорційні. Видалили 3-й і 4-й рядки, другий рядок перемістили на перше місце.

(3) До другого рядка додали перший рядок, помножений на –3.

У приведеній до ступінчастого виду матриці два рядки.

Відповідь:

Тепер ваша черга мучити матрицю «чотири на чотири»:

Приклад 4

Знайти ранг матриці методом Гауса

Нагадую, що метод Гаусане передбачає однозначної жорсткості, і ваше рішення, швидше за все, відрізнятиметься від мого рішення. Короткий зразок оформлення завдання наприкінці уроку.

Який метод використовуватиме знаходження рангу матриці?

Насправді часто взагалі сказано, який метод необхідно використовуватиме знаходження рангу. У такій ситуації слід аналізувати умову – для одних матриць раціональніше провести рішення через мінори, а для інших значно вигідніше застосувати елементарні перетворення:

Приклад 5

Знайти ранг матриці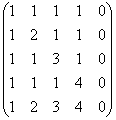

Рішення: перший спосіб якось відразу відпадає =)

Трохи вище я радив не чіпати стовпці матриці, але коли є нульовий стовпець, або пропорційні/збігаються стовпці, то все ж таки варто провести ампутацію:

(1) П'ятий стовпець нульовий, видалимо його з матриці. Таким чином, ранг матриці не більший за чотири. Перший рядок помножили на –1. Це ще одна фірмова фішка методу Гауса, що перетворює наступну дію на приємну прогулянку:

(2) До всіх рядків, починаючи з другого, додали перший рядок.

(3) Перший рядок помножили на –1, третій рядок розділили на 2, четвертий рядок розділили на 3. До п'ятого рядка додали другий рядок, помножений на –1.

(4) До п'ятого рядка додали третій рядок, помножений на -2.

(5) Останні два рядки пропорційні, видаляємо п'яту.

В результаті отримано 4 рядки.

Відповідь:

Стандартна п'ятиповерхівка для самостійного дослідження:

Приклад 6

Знайти ранг матриці

Коротке рішення та відповідь наприкінці уроку.

Слід зазначити, що словосполучення ранг матриці не так часто зустрінеш на практиці, і в більшості завдань можна взагалі обійтися без нього. Але існує одне завдання, де поняття, що розглядається, є головною дійовою особою, і на закінчення статті ми розглянемо цей практичний додаток:

Як дослідити систему лінійних рівнянь на сумісність?

Нерідко крім рішення системи лінійних рівняньза умовою попередньо потрібно досліджувати її на спільність, тобто довести, що будь-яке рішення взагалі існує. Ключову роль у такій перевірці грає теорема Кронекера-Капеллі, яку я сформулюю у необхідному вигляді:

Якщо ранг матриці системидорівнює рангу розширеної матриці системи, то система спільна, причому, якщо це число збігається з кількістю невідомих, то рішення єдине.

Таким чином, для дослідження системи на спільність потрібно перевірити рівність , де - матриця системи(Згадуємо термінологію з уроку Метод Гауса), а – розширена матриця системи(Тобто матриця з коефіцієнтами при змінних + стовпець вільних членів).

У цій статті йтиметься про таке поняття, як ранг матриці та необхідні додаткові поняття. Ми наведемо приклади та докази знаходження рангу матриці, а також розповімо, що таке мінор матриці, і чому він такий важливий.

Мінор матриці

Щоб зрозуміти, що таке ранг матриці необхідно розібратися з таким поняттям, як мінор матриці.

Визначення 1

Мінорk-ого порядку матриці - визначник квадратної матриці порядку k×k, яка складена з елементів матриці А, що знаходяться в заздалегідь обраних k-рядках і k-стовпцях, при цьому зберігається положення елементів матриці А.

Простіше кажучи, якщо в матриці А викреслити (p-k) рядків і (n-k) стовпців, а з тих елементів, які залишилися, скласти матрицю, зберігаючи розташування елементів матриці А, то визначник отриманої матриці є мінор порядку k матриці А.

З прикладу випливає, що мінори першого порядку матриці А є самі елементи матриці.

Можна навести кілька прикладів мінорів другого порядку. Виберемо два рядки та два стовпці. Наприклад, перший і другий рядок, третій і четвертий стовпець.

За такого вибору елементів мінором другого порядку буде - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

Іншим мінором 2-го порядку матриці є 0 0 1 1 = 0

Надамо ілюстрації побудови мінорів другого порядку матриці А:

Мінор 3-го порядку виходить, якщо викреслити третій стовпець матриці А:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

Ілюстрація, як виходить мінор 3-го порядку матриці А:

Для цієї матриці мінорів вище 3-го порядку немає, оскільки

k ≤ m i n (p , n) = m i n (3 , 4) = 3

Скільки існує мінорів k-ого порядку для матриці порядку p×n?

Число мінорів обчислюють за такою формулою:

C p k × C n k , де С p k = p ! k! (p - k)! і C n k = n! k! (n - k)! - Число поєднань з p по k, з n по k відповідно.

Після того, як ми визначилися, що таке мінори матриці А можна переходити до визначення рангу матриці А.

Ранг матриці: методи знаходження

Визначення 2

Ранг матриці - Найвищий порядок матриці, відмінний від нуля.

Позначення 1

Rank (A), Rg(A), Rang(A).

З визначення рангу матриці та мінору матриці ставати зрозуміло, що ранг нульової матриці дорівнює нулю, а ранг ненульової матриці відмінний від нуля.

Знаходження рангу матриці за визначенням

Визначення 3

Метод перебору мінорів - метод, що ґрунтується на визначенні рангу матриці.

Алгоритм дій способом перебору мінорів :

Необхідно знайти ранг матриці А порядку p× n. За наявності хоча б одного елемента, відмінного від нуля, то ранг матриці як мінімум дорівнює одиниці ( т.к. є мінор 1-го порядку, який не дорівнює нулю).

Далі слідує перебір мінорів 2-го порядку. Якщо всі мінори 2-го порядку дорівнюють нулю, то ранг дорівнює одиниці. При існуванні хоча б одного не рівного нулю мінору 2-го порядку, необхідно перейти до перебору мінорів 3-го порядку, а ранг матриці, в такому випадку, дорівнюватиме мінімум двом.

Аналогічно поступимо з рангом 3-го порядку: якщо всі мінори матриці дорівнюють нулю, то ранг дорівнюватиме двом. За наявності хоча б одного ненульового мінору 3-го порядку, ранг матриці дорівнює мінімум трьом. І так далі, за аналогією.

Приклад 2

Знайти ранг матриці:

А = - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

Оскільки матриця ненульова, її ранг мінімум дорівнює одиниці.

Мінор 2-го порядку - 1 1 2 2 = (-1) × 2 - 1 × 2 = 4 відмінний від нуля. Звідси випливає, що ранг матриці не менше двох.

Перебираємо мінори 3-го порядку: 3 3 × 5 3 = 1 5 ! 3! (5 - 3)! = 10 шт.

1 1 - 1 2 2 6 4 3 11 = (-1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (-1) × 6 × 1 + (-1) × 0 × 4 + (-2) × 2 × 11 - (-2) × 6 × 4 - (- 1) × 2 × 1 - (-1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (-1) × 2 × 1 + 1 × 0 × 4 + (-2) × 2 × 3 - (-2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (-7) + (-1) × (-4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (-7) + (-2) × (-4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (-1) × 0 × (-7) + (-2) × (-4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

Мінори 3-го порядку дорівнюють нулю, тому ранг матриці дорівнює двом.

Відповідь : Rank (A) = 2.

Знаходження рангу матриці методом облямівних мінорів

Визначення 3

Метод облямівних мінорів - метод, який дозволяє отримати результат за меншої обчислювальної роботи.

Облямовуючий мінор - мінор M o k (k + 1) -го порядку матриці А, який облямовує мінор M порядку k матриці А, якщо матриця, яка відповідає мінору M o k , «містить» матрицю, яка відповідає мінору М.

Простіше кажучи, матриця, яка відповідає мінеру М, що облямовується, виходить з матриці, що відповідає облямовує мінору M o k , викреслюванням елементів одного рядка і одного стовпця.

Приклад 3

Знайти ранг матриці:

А = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

Для знаходження рангу беремо мінор 2-го порядку М = 2 - 1 4 1

Записуємо всі мінори, що облямовують:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

Щоб обґрунтувати метод облямівних мінорів, наведемо теорему, формулювання якої не вимагає доказової бази.

Теорема 1

Якщо всі мінори, що оздоблюють мінор k-ого порядку матриці А порядку p на n, дорівнюють нулю, всі мінори порядку (k+1) матриці А дорівнює нулю.

Алгоритм дій :

Щоб знайти ранг матриці, необов'язково перебирати всі мінори, достатньо подивитися на облямовувачі.

Якщо мінори, що облямовують, дорівнюють нулю, то ранг матриці нульовий. Якщо існує хоча б один мінор, який не дорівнює нулю, то розглядаємо мінори, що облямовують.

Якщо вони рівні нулю, то Rank(A) дорівнює двом. За наявності хоча б одного ненульового мінера, що облямовує, то приступаємо до розгляду його облямовують мінорів. І так далі, аналогічно.

Приклад 4

Знайти ранг матриці методом обрамляють мінорів

А = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

Як вирішити?

Оскільки елемент а 11 матриці А не дорівнює нулю, візьмемо мінор 1-го порядку. Почнемо шукати мінер, що облямовує, відмінний від нуля:

2 1 4 2 = 2 × 2 - 1 × 4 = 0 2 0 4 1 = 2 × 1 - 0 × 4 = 2

Ми знайшли облямівний мінор 2-го порядку не рівний нулю 2 0 4 1 .

Здійснимо перебір обрамляючих мінорів - (їх (4 - 2) × (5 - 2) = 6 штук).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

Відповідь : Rank(A) = 2

Знаходження рангу матриці методом Гауса (за допомогою елементарних перетворень)

Пригадаємо, що є елементарні перетворення.

Елементарні перетворення:

шляхом перестановки рядків (стовпців) матриці;
шляхом множення всіх елементів будь-якого рядка (стовпця) матриці на довільне ненульове число k;

шляхом додавання до елементів будь-якого рядка (стовпця) елементів, які відповідають іншій стоки (стовпця) матриці, які помножені на довільне число k.

Визначення 5

Знаходження рангу матриці методом Гауса - метод, який ґрунтується на теорії еквівалентності матриць: якщо матриця отримана з матриці А за допомогою кінцевого числа елементарних перетворень, то Rank(A) = Rank(B).

Справедливість цього твердження випливає з визначення матриці:

у разі перестановки рядків чи стовпців матриці її визначник змінює знак. Якщо він дорівнює нулю, то при перестановці рядків або стовпців залишається рівним нулю;
у разі множення всіх елементів будь-якого рядка (стовпця) матриці на довільне число k, яке не дорівнює нулю, визначник отриманої матриці дорівнює визначнику вихідної матриці, яка помножена на k;

у разі додавання до елементів деякого рядка чи стовпця матриці відповідних елементів іншого рядка чи стовпця, які помножені на число k, не змінює її визначника.

Суть методу елементарних перетворень : привести матрицю, чий ранг необхідно знайти, до трапецієподібної за допомогою елементарних перетворень.

Для чого?

Ранг матриць такого виду досить легко знайти. Він дорівнює кількості рядків, у яких є хоча б один ненульовий елемент. А оскільки ранг під час проведення елементарних перетворень не змінюється, це і буде ранг матриці.

Проілюструємо цей процес:

для прямокутних матриць А порядку p на n, число рядків яких більше числа стовпців:

А ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 0 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n

А ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k(A) = k

для прямокутних матриць А порядку p на n, число рядків яких менше числа стовпців:

А ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 1 ⋯ b p n , R a n k (A) = p

А ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

для квадратних матриць порядку n на n:

А ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 0 , Rank (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k , k< n

Приклад 5

Знайти ранг матриці А за допомогою елементарних перетворень:

А = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

Як вирішити?

Оскільки елемент а 11 відмінний від нуля, необхідно помножити елементи першого рядка матриці А на 1 а 11 = 1 2:

А = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

Додаємо до елементів 2-го рядка відповідні елементи 1-го рядка, які помножені на (-3). До елементів 3-го рядка додаємо елементи 1-го рядка, які помножені на (-1):

~ А (1) = 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ А (2) = = 1 1 2 - 1 3 3 + 1 (-3) 0 + 1 2 (-3) 0 + (-1) (-3) - 1 + 3 (-3) 1 + 1 (-3) - 1 + 1 2 (-3) 2 + (- 1) (-1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) 7 + 1 (-7) 2 + 1 2 (-7) - 4 + (-1) (-7) 11 + 3 (-7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

Елемент а 22 (2) відмінний від нуля, тому ми множимо елементи 2-го рядка матриці А на А (2) на 1 а 22 (2) = - 2 3:

А (3) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ А (4) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (-2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (-2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

До елементів 3-го рядка отриманої матриці додаємо відповідні елементи 2-го рядка, які помножені на 3 2;
до елементів 4-го рядка - елементи 2-го рядка, які помножені на 9 2;
до елементів 5-го рядка - елементи 2-го рядка, які помножені на 3 2 .

Усі елементи рядків дорівнюють нулю. Таким чином, за допомогою елементарних перетворень ми привели матрицю до трапецеїдального вигляду, звідки видно, що R a n k (A (4)) = 2 . Звідси випливає, що ранг вихідної матриці також дорівнює двом.

Зауваження

Якщо проводити елементарні перетворення, не допускаються наближені значення!

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

У кожній матриці можна пов'язати два ранги: малий ранг (ранг системи рядків) та стовпцевий ранг (ранг системи стовпців).

Теорема

Рядковий ранг матриці дорівнює її стовпцевому рангу.

Ранг матриці

Визначення

Рангом матриці$A$ називається ранг її системи рядків чи стовпців.

Позначається $\operatorname(rang) A$

Насправді для знаходження рангу матриці використовують таке твердження: ранг матриці дорівнює кількості ненульових рядків після приведення матриці до ступінчастого виду.

Елементарні перетворення над рядками (стовпцями) матриці не змінюють її рангу.

Ранг ступінчастої матриці дорівнює кількості її ненульових рядків.

приклад

Завдання.Знайти ранг матриці $ A=\left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \ \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3)\end(array)\right) $

Рішення.За допомогою елементарних перетворень над її рядками наведемо матрицю $A$ до ступінчастого вигляду. Для цього спочатку від третього рядка заберемо дві другі:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3)\end(array)\right) $$

Від другого рядка віднімаємо четвертий рядок, помножений на 4; від третьої - дві четверті:

$$ A \sim \left(\begin(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3)\end(array)\right) $$

До другого рядка додамо п'ять перших, до третього - три треті:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(array)\right) $$

Змінюємо місцями перший і другий рядки:

$$ A \sim \left(\begin(array)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(array)\right) $$

$$ A \sim \left(\begin(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0)\end(array)\right) \Rightarrow \operatorname(rang) A=2 $$

Відповідь.$ \ operatorname (rang) A = 2 $

Метод облямування мінорів

На цій теоремі базується ще один метод знаходження рангу матриці. метод облямування мінорів. Суть цього методу полягає у знаходженні мінорів, починаючи з нижчих порядків і рухаючись до вищих. Якщо мінор $n$-го порядку не дорівнює нулю, а всі мінори $n+1$-го дорівнюють нулю, то ранг матриці дорівнюватиме $n$ .

приклад

Завдання.Знайти ранг матриці $ A=\left(\begin(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0 ) \\ (-1) & (-2) & (6) & (6) \ end (array) \ right) $ , використовуючи метод облямування мінорів.

Рішення.Мінорами мінімального порядку є мінори першого порядку, які дорівнюють елементам матриці $A$ . Розглянемо, наприклад, мінор $M_(1)=1 \neq 0$. розташований у першому рядку та першому стовпці. Обрамляємо його за допомогою другого рядка та другого стовпця, отримуємо мінор $ M_(2)^(1)=\left| \begin(array)(ll)(1) & (2) \\ (2) & (4)\end(array)\right|=0 $ ; розглянемо ще один мінор другого порядку, для цього мінор $M_1$ облямовуємо за допомогою другого рядка та третього стовпця, тоді маємо мінор $M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $ , тобто ранг матриці не менше двох. Далі розглядаємо мінори третього порядку, які облямовують мінор $ M_(2)^(2) $ . Таких мінорів два: комбінація третього рядка з другим стовпцем або четвертим стовпцем. Обчислюємо ці мінори.

§3. Ранг матриці

Визначення рангу матриці

Лінійно залежні рядки

Елементарні перетворення матриць

Еквівалентні матриці

Алгоритм знаходження рангу матриці за допомогою елементарних перетворень

§4. Визначники першого, другого та третього порядку

Визначник першого порядку

Визначник другого порядку

Визначник третього порядку

Правило Саррюса

§5. Обчислення визначників великих порядків

Алгебраїчне доповнення

Теорема Лапласа

Визначник трикутної матриці

Додаток. Поняття визначника п-го порядку у загальному вигляді.

§ 3. Ранг матриці

Кожну матрицю характеризує деяке число, що має важливе значення під час вирішення систем лінійних рівнянь. Це число називається рангом матриці.

Ранг матрицідорівнює числу її лінійно незалежних рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).

Рядки (стовпці) матриці називаються лінійно залежними, якщо відповідні елементи пропорційні.

Інакше кажучи, елементи одного з лінійно залежних рядків дорівнюють елементам іншого, помноженим на те саме число. Наприклад, рядки 1 та 2 матриці Алінійно залежні, якщо , Де (λ - деяке число).

приклад. Знайти ранг матриці

Рішення.

Другий рядок виходить із першого, якщо його елементи помножити на –3, третій виходить із першого, якщо його елементи помножити на 0, а четвертий рядок не може бути виражений через перший. Виходить, матриця має два лінійно-незалежні рядки, т.к. перший і четвертий рядки не пропорційні, отже, ранг матриці дорівнює 2.

Ранг матриці Апозначається rang Aабо r(A).

З визначення рангу матриці випливає:

1. Ранг матриці вбирається у найменшого її розмірів, тобто. для матриці А m × n .

2. Ранг матриці дорівнює нулю, якщо це нульова матриця.

У випадку визначення рангу матриці досить трудомістко. Для полегшення цього завдання використовують перетворення, що зберігають ранг матриці, які називаються елементарними перетвореннями:

1) відкидання нульового рядка (стовпця);

2) множення всіх елементів рядка (стовпця) на число, відмінне від нуля;

3) зміна порядку рядків (стовпців);

4) додавання до елементів одного рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на будь-яке число;

5) транспонування матриці.

Дві матриці називаються еквівалентнимиякщо одна виходить з іншої за допомогою кінцевого числа елементарних перетворень.

Еквівалентність матриць позначається знаком "~" (еквівалентно).

За допомогою елементарних перетворень будь-яку матрицю можна привести до трикутного вигляду, тоді обчислення її рангу не важко.

Процес обчислення рангу матриці за допомогою елементарних перетвореньрозглянемо з прикладу.

приклад. Знайти ранг матриці

А =

Рішення.

Наше завдання – привести матрицю до трикутного вигляду, тобто. за допомогою елементарних перетворень досягти того, щоб нижче головної діагоналі в матриці були тільки нулі.

1. Розглянемо перший рядок. Якщо елемент а 11 = 0, то при перестановці рядків або стовпців добиваємося того, щоб а 11 ¹ 0. У нашому прикладі поміняємо місцями, наприклад, перший і другий рядки матриці:

А =

Тепер елемент а 11 ¹ 0. Помножуючи перший рядок на відповідні числа і складаючи з іншими рядками, доб'ємося, щоб усі елементи першого стовпця (крім а 11) дорівнювали нулю.

2. Розглянемо тепер другий рядок. Якщо елемент а 22 = 0, то при перестановці рядків або стовпців добиваємося того, щоб а 22 ¹ 0. Якщо елемент а 22 ¹ 0 (а у нас а 22 = –1 ¹ 0), то, помножуючи другий рядок на відповідні числа і складаючи з іншими рядками, досягнемо того, щоб усі елементи другого стовпця (крім а 22) дорівнювали нулю.

3. Якщо в процесі перетворень виходять рядки (стовпці), що повністю складаються з нулів, то відкидаємо їх. У нашому прикладі відкинемо рядки 3-й і 4-й:

Остання матриця має ступінчастий вигляд і містить два рядки. Вони лінійно незалежні, отже, ранг матриці дорівнює 2.

§ 4. Визначники першого, другого та третього порядку

Серед усього різноманіття матриць окремо виділяють квадратні. Цей тип матриць хороший тим, що:

1. Поодинокі матриці – квадратні.

2. Можна множити та складати будь-які квадратні матриці одного порядку, при цьому виходить матриця того ж порядку.

3. Квадратні матриці можна зводити до ступеня.

Крім того, тільки для квадратних матриць може бути обчислений визначник.

Визначник матриці- Це особлива кількість, що обчислюється за деяким правилом. Визначник матриці Апозначається:

Або прямими дужками: ,

Або великою грецькою літерою «дельта»: Δ( A),

Або символом детермінант: det ( A).

Визначником матриці першого порядку А= (а 11) або визначником першого порядку, називається число, що дорівнює елементу матриці:

Δ 1 = =а 11

Визначником матриці другого порядку або визначником другого порядку

приклад:

Визначником матриці третього порядку або визначником третього порядку, називається число, яке обчислюється за формулою:

Визначник третього порядку можна вирахувати, користуючись правилом Саррюса .

Правило Саррюса. До визначника третього порядку праворуч підписують два перші стовпці і зі знаком плюс (+) беруть суму творів трьох елементів, розташованих на головній діагоналі визначника і на «прямих», паралельних головній діагоналі, зі знаком мінус (–) беруть суму творів елементів, розташованих на другий діагоналі і на «прямих», паралельних їй.

приклад:

Легко помітити, що кількість доданків у визначнику збільшується зі збільшенням його порядку. Взагалі у визначнику п-го порядку кількість доданків дорівнює 1 · 2 · 3 · ... · п = п!.

Перевіримо: для Δ 1 число доданків дорівнює 1! = 1,

для Δ 2 число доданків дорівнює 2! = 1 · 2 = 2,

для Δ 3 число доданків дорівнює 3! = 1 · 2 · 3 = 6.

Звідси випливає, що з визначника 4-го порядку число доданків дорівнює 4! = 1·2·3·4 = 24, отже обчислення такого визначника досить трудомістко, а про визначниках вищого порядку. З огляду на це обчислення визначників великих порядків намагаються звести до обчислення визначників другого або третього порядків.

§ 5. Обчислення визначників великих порядків

Введемо низку понять.

Нехай дана квадратна матриця А n-го порядку:

А =

Мінором M ij елементу a ij називається визначник ( п- 1)-го порядку, отриманої з матриці Авикреслюванням i-його рядка та j-го стовпця.

Наприклад, мінором елемента а 12 матриці третього порядку буде:

Алгебраїчним доповненням А ij елементу a ij називається його мінор, взятий зі знаком (−1) i + j:

А ij = (−1) i + j M ij

Інакше кажучи, А ij = M ij , якщо i+jпарне число,

А ij = − M ij , якщо i+jнепарне число.

приклад. Знайти додатки алгебри елементів другого рядка матриці

Рішення.

За допомогою додатків алгебри можна вираховувати визначники великих порядків, на підставі теореми Лапласа.

Теорема Лапласа. Визначник квадратної матриці дорівнює сумі творів елементів будь-якого його рядка (стовпця) на їх додатки алгебри:

– розкладання по i-му рядку;

( - Розкладання по j-му стовпцю).

приклад. Обчислити визначник матриці розкладанням по першому рядку.

Рішення.

Отже, визначник будь-якого порядку можна звести до обчислення кількох визначників меншого порядку. Очевидно, що для розкладання зручно вибирати рядок або стовпець, що містить якнайбільше нулів.

Розглянемо ще один приклад.

приклад. Обчислити визначник трикутної матриці

Рішення.

Отримали, що визначник трикутної матриці дорівнює добутку елементів її головної діагоналі .

Цей важливий висновок дозволяє легко визначити обчислювач будь-якої трикутної матриці. Це корисніше, що за необхідності будь-який визначник можна звести до трикутному виду. У цьому використовуються деякі властивості визначників.

додаток

Поняття визначника п-го порядку у загальному вигляді.

Взагалі можна дати строго визначення для визначника матриці п-го порядку, але цього необхідно запровадити ряд понять.

Перестановкоючисел 1, 2, ..., nназивається будь-яке розташування цих чисел у порядку. В елементарній алгебрі доводиться, що кількість всіх перестановок, які можна утворити з nчисел, що дорівнює 12...n = n!. Наприклад, із трьох чисел 1, 2, 3 можна утворити 3! = 6 перестановок: 123, 132, 312, 321, 231, 213.

Кажуть, що у цій перестановці числа iі jскладають інверсію(безлад), якщо i> j, але iстоїть у цій перестановці раніше j, тобто якщо більше число коштує ліворуч від меншого.

Перестановка називається парної(або непарною), якщо у ній відповідно парно (непарно) загальна кількість інверсій.

Операція, за допомогою якої від однієї перестановки переходять до іншої, складеної з тих самих nчисел, називається підстановкою n-ого ступеня.

Підстановка, що переводить одну перестановку в іншу, записується двома рядками в загальних дужках, причому числа, що займають однакові місця в перестановках, що розглядаються, називаються відповідними і пишуться одне під іншим. Наприклад, символ

позначає підстановку, в якій 3 переходить до 4, 1 – до 2, 2 – до 1, 4 – до 3. Підстановка називається парною (або непарною), якщо загальна кількість інверсій в обох рядках підстановки парна (непарно). Будь-яка підстановка n-ой ступеня може бути записана у вигляді

тобто. з натуральним розташуванням чисел у верхньому рядку.

Нехай нам дано квадратну матрицю порядку n

Розглянемо всі можливі твори з nелементів цієї матриці, взятих по одному і лише по одному з кожного рядка та кожного стовпця, тобто. творів виду:

де індекси q 1 , q 2 ,..., q nстановлять деяку перестановку з чисел
1, 2,..., n. Число таких творів дорівнює числу різних перестановок з nсимволів, тобто. одно n!. Знак твору , дорівнює (-1) q, де qчисло інверсій у перестановці других індексів елементів.

Визначником n-го порядкуназивається алгебраїчна сума всіх можливих творів за nелементів матриці, взятих по одному і лише по одному з кожного рядка та кожного стовпця, тобто. творів виду: . При цьому знак твору дорівнює (–1) q, де q- Число інверсій в перестановці других індексів елементів.

Лінійна алгебра

Розглянемо матрицю А розміру.

А =
Виділимо в ній рядок і стовпців (
).

Визначення 26:Мінором k-го порядку матриці А називається визначник квадратної матриці, що виходить з цієї виділенням у ній.

рядків і стовпців.

Визначення 27:Рангомматриці називається найбільший із порядків, відмінних від нуля, її мінорів, r(A).

Визначення 28:Мінор, порядок якого збігається з рангом називається базисним мінором.

Твердження:

1. Ранг виражається цілим числом.
)

2. r=0,
коли А – нульова.

Елементарні перетворення матриць.

До елементарних перетворень матриць належать такі:

1) множення всіх елементів будь-якого рядка (стовпця) матриці на те саме число.

2) додавання до елементів будь-якого рядка (стовпця) матриці відповідних елементів іншого рядка (стовпця) помножені на те саме число;

3) перестановка місцями рядків (стовпців) матриці;

4) відкидання нульового рядка (стовпця);

5) заміна рядків матриці відповідними стовпцями.

Визначення 29:Матриці, що виходять одна з іншої, при елементарних перетвореннях називається еквівалентними матрицями, позначаються “ ~“

Основна властивість еквівалентних матриць: Ранги еквівалентних матриць рівні.

Приклад 18:Обчислитиr(A),

Рішення:Перший рядок помножимо поетапно на (-4) (-2)

(-7) і потім додамо відповідно до другого, третього та четвертого рядків.

поміняємо місцями другий і четвертий рядки
другий рядок помножимо на (-2) і додамо до четвертого рядка; складемо другий і третій рядки.

складемо третій та четвертий рядки.

~
відкинемо нульовий рядок

~
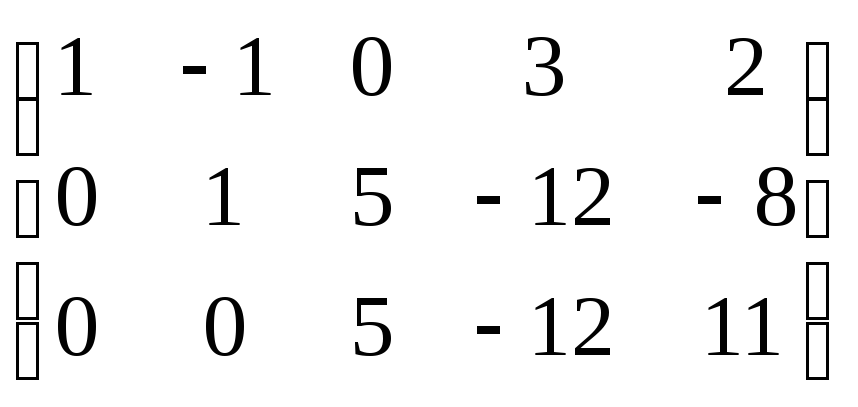r(A)=3
ранг вихідної матриці

дорівнює трьом.

Визначення 30:Назвемо матрицю А ступінчастою, якщо всі елементи головної діагоналі 0, а елементи під головною діагоналлю дорівнюють нулю.

Пропозиція:

1) ранг ступінчастої матриці дорівнює числу її рядків;

2) будь-яка матриця може бути приведена до ступінчастого виду за допомогою елементарних перетворень.

Приклад 19:При яких значеннях  матриця
має ранг, що дорівнює одиниці?

Рішення:Ранг дорівнює одиниці, якщо визначник другого порядку дорівнює нулю, тобто.

§6. Системи лінійних рівнянь загального вигляду.

Система виду
---(9) називається системою загального вигляду.

Визначення 31:Дві системи називаються рівносильними (еквівалентними), якщо кожне рішення першої системи є другою і навпаки.

У системі (1) матрицю А =
назвемо основною матрицею системи, а =
розширеною матрицею системи

Теорема.Кронекера-Капеллі

Для спільності системи (9) необхідний достатньо, щоб ранг основної матриці системи дорівнював рангу розширеної матриці, тобто r(A)=r( )

Теорема 1.Якщо ранг матриці спільної системи дорівнює числу невідомих, система має єдине рішення.

Теорема 2.Якщо ранг матриці спільної системи менше числа невідомих, то система має безліч рішень.

Правило розв'язання довільної системи лінійних рівнянь:

1)знайти ранги основної та розширеної матриць системи. Якщо
, то система не спільна.

2) Якщо
=r, то система спільна. Знайти який-небудь базисний мінор порядку. Базисним називатимемо мінор, на підставі якого визначався ранг матриці.

Невідомі, коефіцієнти яких входять у базисний мінор, називають головними (базисними) і залишають ліворуч, інші ж невідомі називають вільними і переносять праву частину рівняння.

3)Знайти висловлювання головних невідомих через вільні. Отримано загальне рішення системи.

Приклад 20:Дослідити систему та у разі її спільності знайти чи єдине чи загальне рішення