Розкладання чисел на прості множники, способи та приклади розкладання. Отримати канонічне розкладання числа на прості співмножники

Лекція 14 Випадкові процеси Канонічний розпад випадкових процесів. Спектральне розкладання стаціонарного довільного процесу. СлуЛекція 14
Випадкові процеси
Канонічне розкладання випадкових процесів.
Спектральне розкладання стаціонарного випадкового
процесу. Випадкові процеси з незалежними
перерізами. Марківські процеси та ланцюги Маркова.
Нормальні довільні процеси. Періодично
нестаціонарні випадкові процеси
(Ахметов С.К.)

Канонічне розкладання випадкових процесів

Будь-який СП X(t) м.б. представлений у
вигляді його розкладання, тобто. у вигляді суми
елементарних процесів:
Vk – випадкові величини
φk(t) – невипадкові функції (синусоїди, експоненти, статечні)
функції тощо)
Окремий випадок такого розкладання-Канонічне
розкладання
СП X(t), що має вигляд
mx(t) = M – математичне очікування СП X(t)
V1, V2…Vk – некорельовані та центровані СВ
D1, D2 …Dk-дисперсії СВ V1, V2…Vk
φk(t) – невипадкові функції аргументу t
Випадкові величини V1, V2…Vk називаються коефіцієнтами канонічного
розкладання,
а невипадкові функції φ1(t), φ2(t) φk(t) - координатними функціями
канонічного розкладання

Основні характеристики СП, заданого канонічним розкладанням

M – математичне очікування СП X(t)
Kx(t,t’) – кореляційна функція СП X(t)
Вираз
- канонічне розкладання кореляційної
функції
Якщо t=t', то відповідно до першого
властивістю кореляційної функції
Вираз
Dk(t) –
дисперсія
канонічне розкладання дисперсії СП X(t)

Спектральне розкладання стаціонарного СП

Стаціонарний СП м.б. представлений канонічним розкладанням
Vk та Uk – некорельовані та центровані СВ з дисперсіями
D = D = Dk
ω – невипадкова величина (частота)
У цьому випадку канонічне розкладання кореляційної функції
визначається виразом
Представлене
канонічне
розкладання
СП
X(t)
називається
спектральним розкладанням СП та
виражається у вигляді
Θk - фаза гармонійного коливання елементарного стаціонарного СП,
що є СВ рівномірно розподіленої в інтервалі (0, 2?);
Zk – СВ, що є амплітудою гармонійного коливання
елементарного стаціонарного СП

Спектральне розкладання стаціонарного СП (2)

Випадкові величини Θk та Zk залежні і для них справедливо:
Vk = Zk cos Θk
Uk = Zk sin Θk
Стаціонарний СП м.б. представлений у вигляді суми гармонійних
коливань з випадковими амплітудами Zk та випадковими фазами Θk на
різних невипадкових частотах ωk
Кореляційна функція стаціонарного СП X(t) є парною
функцією свого аргументу, тобто. kx(τ) = kx(-τ). Тому її на інтервалі (-Т,
Т) можна розкласти в ряд Фур'є за парними (косинусами) гармоніками:
Дисперсія стаціонарного СП X(t) дорівнює
сумі
дисперсій
всіх
гармонік
його
спектрального розкладання
Залежність Dk = f(wk) називається дискретним спектром дисперсій або
дискретний спектр стаціонарного СП.

Спектральне розкладання стаціонарного СП (3)

При ∆ω
→ 0 відбудеться перехід до безперервного спектру
Sx(ω) - спектральна щільність
Таким чином, кореляційна функція та спектральна щільність
пов'язані косинус - перетворенням Фур'є. Отже, спектральна
густина стаціонарного СП м.б. виражена через кореляційну
функцію формулою

Випадкові процеси із незалежними перерізами

У гідрології вважається, що ряд відповідає моделі випадкової
величини, якщо відсутня значуща кореляція між членами цього ряду
за будь-якого зрушення τ.
Випадковий процес із незалежними перерізами – це СП, для якого
при значеннях t та t’
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx при τ = 0 і 0 при τ ≠ 0)
Такий процес є стаціонарним і має ергодичний
властивістю
Для таких процесів характеристики одномірного закону розподілу
можна оцінити як за будь-яким перерізом, так і за будь-яким (досить
тривалої) реалізації
У таких процесів відсутня кореляція між членами всередині будь-якої
реалізації
Приймаючи таку модель, допускається, що ряд гідрологічних величин
є однією реалізацією СП
Випадковий процес із незалежними перерізами іноді називають
"білим шумом" за аналогією з білим світлом

Марківські процеси та ланцюги Маркова

Випадковий процес
називається марківським, якщо для будь-кого
моменту часу t ймовірність кожного зі станів системи у майбутньому
(При t > t0) залежить тільки від її стану в теперішньому (при t = t0) і не
залежить від її стану в минулому (при t< t0)
Марківським ланцюгом або простим марківським ланцюгом називається
марківський процес з дискретним станом та дискретним часом
Марковський СП повністю описується двовимірним законом
розподілу. Якщо Марківський процес є стаціонарним і
ергодичним, то його характеристики можна оцінити за однією
реалізації.
Ланцюг, в якому умовні ймовірності станів у майбутньому залежать
від її стану на кількох попередніх кроках, називається складною
ланцюгом Маркова.

Нормальні (гаусівські) випадкові процеси

Нормальним (гауссівським) випадковим процесом X(t) називається
СП, у якого у всіх перерізах СВ X(ti) має нормальне
розподіл
Періодично нестаціонарні СП
Під час вивчення річних, місячних, добових тощо. процесів, як правило,
спостерігаються внутрішньорічні та ін. коливання. У цьому випадку, як
математичної моделі можна використовувати модель періодично
нестаціонарного випадкового процесу (ПНСП)
Випадковий процес називають періодично нестаціонарним, якщо
його ймовірні характеристики інваріанти щодо зрушень на
позитивне число Т. Наприклад, при кроці дискретності один місяць
інваріантність повинна зберігатися при зсувах 12, 24, 36 і т.д.

Ця стаття дає відповіді питання про розкладанні числа на простирадлі множники. Розглянемо загальне уявлення про розкладання прикладами. Розберемо канонічну форму розкладання та її алгоритм. Буде розглянуто всі альтернативні способи за допомогою використання ознак ділимості та таблиці множення.

Yandex.RTB R-A-339285-1

Що означає розкласти число на звичайні множники?

Розберемо поняття прості множники. Відомо, кожен простий множник – це просте число. У творі виду 2 · 7 · 7 · 23 маємо, що у нас 4 простих множника у вигляді 2, 7, 7, 23.

Розкладання на множники передбачає його подання у вигляді творів простих. Якщо потрібно розкласти число 30 , тоді отримаємо 2 , 3 , 5 . Запис набуде вигляду 30 = 2 · 3 · 5 . Ймовірно, що множники можуть повторюватися. Таке число як 144 має 144 = 2 · 2 · 2 · 2 · 3 · 3 .

Не всі числа схильні до розкладання. Числа, які більше 1 і є цілими, можна розкласти на множники. Прості числа при розкладі діляться лише з 1 і самого себе, тому неможливо уявити ці числа як твори.

При z , що відноситься до цілих чисел, представляється у вигляді твору а та b , де z ділиться на а та на b . Складові числа розкладають на прості множники за допомогою основної теореми арифметики. Якщо число більше 1, його розкладання на множники p 1 , p 2 , … , p n набуває вигляду a = p 1 , p 2 , … , p n . Розкладання передбачається у єдиному варіанті.

Канонічне розкладання числа на прості множники

При розкладанні множники можуть повторюватися. Їх запис виконується компактно за допомогою ступеня. Якщо при розкладанні числа а маємо множник p 1 який зустрічається s 1 раз і так далі p n - S n разів. Таким чином розкладання набуде вигляду a = p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n. Цей запис має назву канонічного розкладання числа на прості множники.

При розкладанні числа 609 840 отримаємо, що 609 840 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 7 · 11 · 11, його канонічний вигляд буде 609 840 = 2 4 · 3 2 · 5 · 7 · 11 2 . За допомогою канонічного розкладання можна знайти всі дільники числа та їх кількість.

Щоб правильно розкласти на множники необхідно мати уявлення про прості та складові числа. Сенс полягає в тому, щоб отримати послідовну кількість дільників виду p 1 , p 2 , … , p n чисел a , a 1 , a 2 , … , a n - 1, це дає можливість отримати a = p 1 · a 1, де a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , де a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · a n, де a n = a n - 1: p n. При отриманні a n = 1, то рівність a = p 1 · p 2 · … · p nотримаємо розкладання числа, що шукається, а на прості множники. Зауважимо, що p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Для знаходження найменших спільних дільників потрібно використовувати таблицю простих чисел. Це виконується з прикладу знаходження найменшого простого дільника числа z . При взятті простих чисел 2, 3, 5, 11 і так далі, причому на них ділимо число z. Оскільки z не є простим числом, слід враховувати, що найменшим простим дільником більше z . Видно, що немає дільників z , тоді зрозуміло, що z є простим числом.

Приклад 1

Розглянемо з прикладу числа 87 . За його розподілі на 2 маємо, що 87: 2 = 43 із залишком рівним 1 . Звідси випливає, що 2 дільником не може бути, розподіл має проводитися націло. При розподілі на 3 отримаємо, що 87: 3 = 29 . Звідси висновок – 3 найменшим простим дільником числа 87 .

При розкладанні прості множники необхідно користуватися таблицею простих чисел, де a . При розкладанні 95 слід використовувати близько 10 простих чисел, а при 846 653 близько 1000 .

Розглянемо алгоритм розкладання на прості множники:

• знаходження найменшого множника при дільнику p 1 числа aза формулою a 1 = a: p 1 , коли a 1 = 1 , тоді а є простим числом і включено до розкладання на множники, коли не дорівнює 1 , тоді a = p 1 · a 1 і йдемо до пункту, що знаходиться нижче;
• знаходження простого дільника p 2 числа a 1 за допомогою послідовного перебору простих чисел, використовуючи a 2 = a 1: p 2 , коли a 2 = 1 , тоді розкладання набуде вигляду a = p 1 · p 2 , коли a 2 = 1 тоді а = p 1 · p 2 · a 2 , причому робимо перехід до наступного кроку;
• перебір простих чисел та знаходження простого дільника p 3числа a 2за формулою a 3 = a 2: p 3 коли a 3 = 1 , тоді отримаємо, що a = p 1 · p 2 · p 3 , коли не дорівнює 1, тоді a = p 1 · p 2 · p 3 · a 3 і робимо перехід до наступного кроку;
• проводиться перебування простого дільника p nчисла a n - 1за допомогою перебору простих чисел з p n - 1, а також a n = a n - 1: p n, де a n = 1 крок є завершальним, в результаті отримуємо, що a = p 1 · p 2 · … · p n .

Результат алгоритму записується як таблиці з розкладеними множниками з вертикальною рисою послідовно в стовпчик. Розглянемо малюнок, наведений нижче.

Отриманий алгоритм можна використовувати з розкладання чисел на прості множники.

Під час розкладання на прості множники слід дотримуватись основного алгоритму.

Приклад 2

Здійснити розкладання числа 78 на прості множники.

Рішення

Щоб знайти найменший простий дільник, необхідно перебрати всі прості числа, наявні в 78 . Тобто 78: 2 = 39. Поділ без залишку, це перший простий дільник, який позначимо як p 1 . Виходить, що a 1 = a: p 1 = 78: 2 = 39 . Прийшли до рівності виду a = p 1 · a 1 , де 78 = 2 · 39. Тоді a 1 = 39 тобто слід перейти до наступного кроку.

Зупинимося на знаходженні простого дільника p 2числа a 1 = 39. Слід перебрати прості числа, тобто 39: 2 = 19 (зуп. 1). Так як розподіл із залишком, що 2 не є дільником. При виборі числа 3 отримуємо, що 39: 3 = 13 . Отже, p 2 = 3 є найменшим простим дільником 39 за a 2 = a 1: p 2 = 39: 3 = 13 . Отримаємо рівність виду a = p 1 · p 2 · a 2у вигляді 78 = 2 · 3 · 13 . Маємо, що a 2 = 13 не дорівнює 1 тоді слід переходить далі.

Найменший простий дільник числа a 2 = 13 шукається з допомогою перебору чисел, починаючи з 3 . Отримаємо, що 13: 3 = 4 (зуп. 1). Звідси видно, що 13 не ділиться на 5, 7, 11, тому що 13: 5 = 2 (зуп. 3), 13: 7 = 1 (зуп. 6) і 13: 11 = 1 (зуп. 2). Видно, що 13 є простим числом. За формулою виглядає так: a 3 = a 2: p 3 = 13: 13 = 1 . Отримали, що a 3 = 1 що означає завершення алгоритму. Тепер множники записуються у вигляді 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Відповідь: 78 = 2 · 3 · 13 .

Приклад 3

Розкласти число 83006 на прості множники.

Рішення

Перший крок передбачає розкладання на прості множники p 1 = 2і a 1 = a: p 1 = 83006: 2 = 41503, де 83006 = 2 · 41503 .

Другий крок передбачає, що 2 , 3 і 5 не прості дільники для числа a 1 = 41503 , а 7 простий дільник, тому що 41503: 7 = 5929 . Отримуємо, що p 2 = 7 , a 2 = a 1: p 2 = 41503: 7 = 5929 . Очевидно, що 83006 = 2 · 7 · 5929 .

Знаходження найменшого простого дільника p 4 до a 3 = 847 дорівнює 7 . Видно, що a 4 = a 3: p 4 = 847: 7 = 121, тому 83006 = 2 · 7 · 7 · 7 · 121 .

Для знаходження простого дільника числа a 4 = 121 використовуємо число 11 тобто p 5 = 11 . Тоді отримаємо вираз виду a 5 = a 4: p 5 = 121: 11 = 11, і 83006 = 2 · 7 · 7 · 7 · 11 · 11 .

Для числа a 5 = 11число p 6 = 11є найменшим простим дільником. Звідси a 6 = a 5: p 6 = 11: 11 = 1 . Тоді a 6 = 1. Це свідчить про завершення алгоритму. Множники запишуться у вигляді 83006 = 2 · 7 · 7 · 7 · 11 · 11 .

Канонічний запис відповіді набуде вигляду 83 006 = 2 · 7 3 · 11 2 .

Відповідь: 83 006 = 2 · 7 · 7 · 7 · 11 · 11 = 2 · 7 3 · 11 2 .

Приклад 4

Провести розкладання числа 897924289 на множники.

Рішення

Для знаходження першого простого множника зробити перебір простих чисел, починаючи з 2 . Кінець перебору посідає число 937 . Тоді p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 та 897 924 289 = 937 · 958 297 .

Другий крок алгоритму полягає у переборі менших простих чисел. Тобто починаємо з числа 937 . Число 967 можна вважати простим, тому що воно є простим дільником числа a 1 = 958297 . Звідси отримуємо, що p 2 = 967 , то a 2 = a 1: p 1 = 958 297: 967 = 991 і 897924289 = 937 · 967 · 991 .

Третій крок свідчить, що 991 є простим числом, оскільки немає жодного простого дільника, який перевищує 991 . Приблизне значення підкореного виразу має вигляд 991< 40 2 . Иначе запишем как 991 < 40 2 . Звідси видно, що p 3 = 991 та a 3 = a 2: p 3 = 991: 991 = 1 . Отримаємо, що розкладання числа 897924289 на прості множники виходить як 897924289 = 937 · 967 · 991 .

Відповідь: 897924289 = 937 · 967 · 991 .

Використання ознак ділимості для розкладання на прості множники

Щоб розкласти число на прості множники, потрібно дотримуватись алгоритму. Коли є невеликі числа, допускається використання таблиці множення та ознак подільності. Це розглянемо на прикладах.

Приклад 5

Якщо необхідно розкласти на множники 10 , то таблиці видно: 2 · 5 = 10 . Числа 2 і 5 є простими, тому вони є простими множниками для числа 10 .

Приклад 6

Якщо необхідно розкласти число 48 , то таблиці видно: 48 = 6 · 8 . Але 6 і 8 – це прості множники, оскільки їх можна розкласти як 6 = 2 · 3 і 8 = 2 · 4 . Тоді повне розкладання звідси виходить як 48 = 6 · 8 = 2 · 3 · 2 · 4 . Канонічний запис набуде вигляду 48 = 2 4 · 3 .

Приклад 7

При розкладанні числа 3400 можна скористатися ознаками подільності. У разі актуальні ознаки подільності на 10 і 100 . Звідси отримуємо, що 3400 = 34 · 100, де 100 можна розділити на 10, тобто записати у вигляді 100 = 10 · 10, а значить, що 3400 = 34 · 10 · 10. Грунтуючись на ознакі подільності отримуємо, що 3400 = 34 · 10 · 10 = 2 · 17 · 2 · 5 · 2 · 5 . Усі множники прості. Канонічне розкладання набуває вигляду 3400 = 2 3 · 5 2 · 17.

Коли ми знаходимо прості множники, необхідно використовувати ознаки поділення та таблицю множення. Якщо уявити число 75 як твори множників, необхідно враховувати правило ділимості на 5 . Отримаємо, що 75 = 5 · 15, причому 15 = 3 · 5. Тобто розкладання приклад вид твору 75 = 5 · 3 · 5 .

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Випадкова величина Vназивається центрованої , якщо її математичне очікування дорівнює 0. Елементарним центрованим випадковим процесом називається добуток центрованої випадкової величини на невипадкову функцію φ(t):X(t)=Vφ(t). Елементарний центрований випадковий процес має такі характеристики:

Вираз виду
, де φ k ( t ), k = 1; 2; ... - Невипадкові функції; , k =1;2;…-некорельовані центровані випадкові величини, називається канонічним розкладанням випадкового процесуX ( t ), при цьому випадкові величини називаються коефіцієнтами канонічного розкладання; а невипадкові функції φ k ( t ) - координатними функціями канонічного розкладання.

Розглянемо характеристики випадкового процесу

Бо за умовою
то

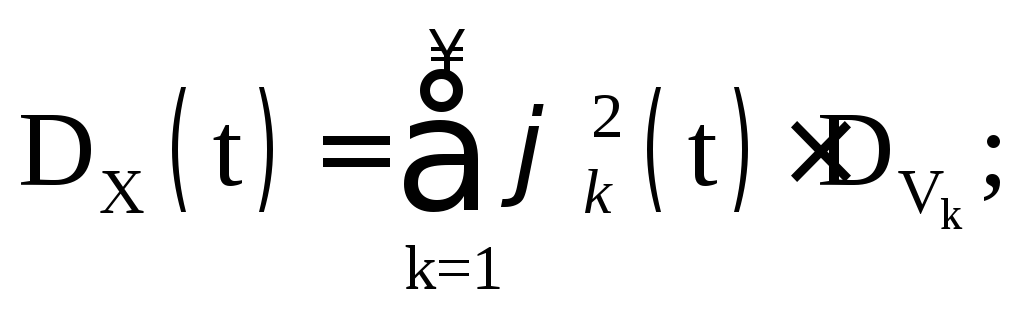
Очевидно, що той самий випадковий процес має різні види канонічного розкладання залежно від вибору координатних функцій. Більше того, навіть при виборі координатних функцій існує свавілля в розподілі випадкових величин V к. На практиці за підсумками експериментів отримують оцінки для математичного очікування та кореляційної функції:
. Після розкладання
у подвійний ряд Фур'є за координатними функціями φ до (t):

набувають значення дисперсій
випадкових величин Vk.

4.2. Концепція узагальненої функції. Дельта-функція Дірака. Інтегральне канонічне уявлення випадкових процесів.

Узагальненою функцією називається межа послідовності однопараметричного сімейства безперервних функцій.

Дельта-функція Дірака
- це узагальнена функція, що є результатом граничного переходу при
у сімействі функцій

Серед властивостей -функції відзначимо наступне:

2.

3. Якщо f(t) - безперервна функція, то

Випадковий процес Х( t ), кореляційна функція якого має вигляд називається нестаціонарним «білим шумом». Якщо W ( t 1 )= W - const , то Х ( t )-стаціонарний «білий шум».

Як випливає з визначення, ніякі два, навіть як завгодно близькі, перерізи «білого шуму» не корелювані. Вираз W(t) називається інтенсивністю "білого шуму".

Інтегральним канонічним уявленням випадкового процесу Х( t ) називається вираз виду
де
- Випадкова центрована функція;
- невипадкова функція безперервних аргументів

Кореляційна функція такого випадкового процесу має вигляд:

Можна показати, що існує невипадкова функція G(λ) така, що

де G(λ 1) - щільність дисперсії; δ(х) - дельта-функція Дірака. Отримуємо

Отже, дисперсія випадкового процесу Х(t):

.

4.3. Лінійні та нелінійні перетворення випадкових процесів

Розглядається таке завдання: на вхід системи (пристрою, перетворювача) Sподається «вхідний сигнал», що має характер випадкового процесу Х(t). Система перетворює його на «вихідний сигнал» Y(t):

.

Формально перетворення випадкового процесу Х(t) уY(t) може бути описано за допомогою так званого оператора системи А t:

Y(t)=A t (Х(t)).

Індекс tпоказує, що даний оператор здійснює перетворення за часом. Можливі такі постановки завдання перетворення випадкового процесу.

Відомі закони розподілу або загальні характеристики випадкового процесу Х(t) на вході в системуS, заданий оператор Аt системиS, потрібно визначити закон розподілу або загальні характеристики випадкового процесуY(t) на виході системиS.

Відомі закони розподілу (загальні характеристики) випадкового процесу Х(t) та вимоги до випадкового процесуY(t); треба визначити вид оператора А t системи S, що найкраще задовольняє заданим вимогам к Y (t).

Відомі закони розподілу (загальні характеристики) випадкового процесу Y(t) та заданий оператор Аt системи S; потрібно визначити закони розподілу чи загальні характеристики випадкового процесу Х(t).

П ринят наступна класифікація операторів А t системи S:

Оператори системи

Лінійні L Нелінійні N

Лінійні однорідні L 0 Лінійні неоднорідні L н

Розглянемо вплив лінійної неоднорідної системи

L н (...)=L 0 (…)+φ(t)

на випадковий процес Х(t), що має наступне канонічне розкладання:

.

Отримуємо:

введемо позначення

тоді канонічне розкладання Y(t) набуває вигляду:

.

Математичне очікування випадкового процесу Y(t):

кореляційна функція випадкового процесу Y(t):

отже,

З іншого боку

Дисперсія випадкового процесу Y(t):

На закінчення цього пункту зазначимо, що оператори диференціювання та інтегрування випадкових процесів є лінійними однорідними.

2. Розглядається квадратичне перетворення:

Y(t)=(X(t)) 2 ,

V k -центровані випадкові величини, що мають симетричний щодо нуля розподіл; будь-які чотири з них незалежні в сукупності. Тоді

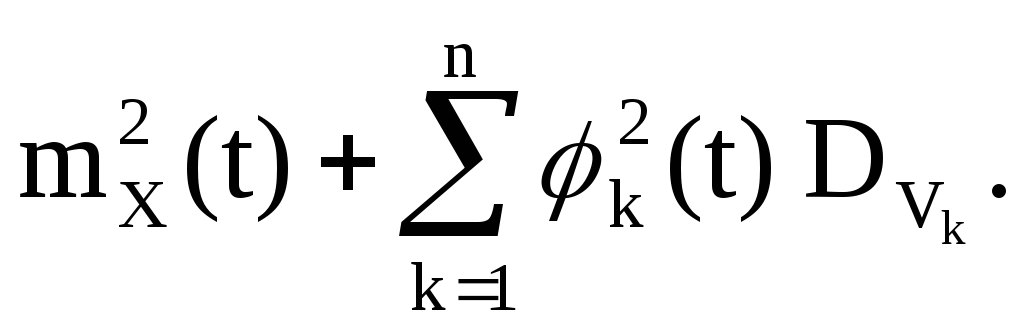
Введемо невипадкові функції

та випадкові величини

тоді випадковий процес Y(t) набуває вигляду

Отримано канонічне розкладання довільного процесу Y(t). Кореляційна функція Y(t):

Формулювання.Дано натуральне число n (n > 1). Отримати його канонічне розкладання на прості співмножники, тобто подати у вигляді добутку простих співмножників. При цьому в розкладанні допустимо вказувати множник 1. Наприклад, 264 = 2 * 2 * 2 * 3 * 11 (програмі допустимо видати відповідь 264 = 1 * 2 * 2 * 2 * 3 * 11).

Рішення.Це завдання має досить гарне рішення.

З основний теореми арифметикивідомо, що для будь-якого натурального числа більше 1 існує його канонічне розкладання на прості співмножники, причому це розкладання єдино з точністю до порядку проходження множників. Тобто, наприклад, 12 = 2 * 2 * 2 і 12 = 3 * 2 * 2 - це однакові розкладання.

Розглянемо канонічну форму будь-якого числа конкретному прикладі. Наприклад, 264 = 2*2*2*3*11. Яким чином можна виявити цю структуру? Щоб відповісти на це питання, згадаємо викладені в будь-якому шкільному курсі алгебри правила поділу одночленів, уявивши, що цифри в канонічному розкладі є змінними. Як відомо, якщо розділити вираз на змінну до певної міри, що міститься в цьому виразі в тій же мірі, воно викреслюється в її записі.

Тобто якщо ми розділимо 264 на 2, то в його канонічному розкладі піде одна двійка. Потім ми можемо перевірити, чи ділиться приватне, що знову вийшло, на 2. Відповідь буде позитивною, але втретє поділ дасть залишок. Тоді потрібно брати для розгляду наступне натуральне число 3 – на нього окремо розділиться один раз. У результаті, проходячи числову пряму в позитивному напрямку, ми дійдемо до числа 11, і після розподілу на 11 nбуде дорівнює 1, що говоритиме про необхідність закінчити процедуру.

Чому при такому «викреслюванні» знайдених співмножників ми не отримаємо подільності на складові числа? Насправді тут все просто – будь-яке складове число є твором простих співмножників, менших за нього. У результаті виходить, що ми викреслимо з nвсі співмножники будь-якого складового числа, поки дійдемо до нього самого в ланцюжку поділів. Наприклад, при такому переборі nніколи не розділиться на 4, тому що «по дорозі» до цього числа ми викреслимо з nвсі помножувачі-двійки.

Алгоритм природною мовою:

1) Введення n;

2) Присвоєння змінної pчисла 2;

3) Виведення числа n, знаку рівності та одиниці для оформлення розкладання;

4) Запуск циклу з передумовою n< > 1 . У циклі:

1. Якщо mmodp = 0, то вивести на екран знак множення та змінну p, потім розділити nна pінакше збільшити значення iна 1;

1. program PrimeFactors;
2. n, p: word;
3. begin
4. p:= 2;
5. readln(n);
6. write(n, '= 1');
7. while n<>1 do begin
8. if (n mod p) = 0 then begin
9. write(' * ', p);
10. n:= n div p
11. else begin
12. inc(p)