Tính liên tục của các hàm cơ bản

Các định lý về tính liên tục của các hàm theo trực tiếp từ các định lý về giới hạn tương ứng.

Định lý. Tổng, tích và thương của hai hàm liên tục là một hàm liên tục (đối với thương, ngoại trừ các giá trị của đối số trong đó số chia bằng 0).

Định lý. Hãy để các chức năng u= φ (x) liên tục tại điểm X 0 và hàm y = f(u) liên tục tại điểm u 0 = φ (X 0). Sau đó, hàm phức f(φ (x)) bao gồm các hàm liên tục là liên tục tại điểm x 0 .

Định lý. Nếu chức năng tại = f(X) là đơn âm liên tục và nghiêm ngặt trên [ một; b] trục Ồ, thì hàm ngược tại = φ (X) cũng liên tục và đơn điệu trên đoạn tương ứng [ c;d] trục Đơn vị tổ chức(không có bằng chứng).

Các hàm liên tục trên một khoảng có một số thuộc tính quan trọng. Chúng ta xây dựng chúng dưới dạng định lý mà không cần chứng minh.

Định lý (Weierstrass). Nếu một hàm liên tục trên một đoạn thì nó đạt giá trị lớn nhất và nhỏ nhất trên đoạn này.

Chức năng được hiển thị trong Hình 5 tại = f(x) liên tục trên khoảng [ một; b], nhận giá trị lớn nhất của nó M tại điểm x 1, và ít nhất m- tại điểm X 2. Cho bất cứ ai X [một; b] m ≤ f(x) ≤ M.

Hậu quả. Nếu một hàm liên tục trên một khoảng thì nó bị giới hạn trên khoảng này.

Định lý (Bolzano - Cauchy). Nếu chức năng tại= f(x) liên tục trên khoảng [ một; b] và nhận các giá trị không bằng nhau ở các đầu của nó f(một) = Một và f(b) = =TẠI, thì trên phân đoạn này, nó cũng nhận tất cả các giá trị trung gian giữa NHƯNG và TẠI.

Về mặt hình học, định lý là hiển nhiên (xem Hình 6).

Cho bất kỳ số nào Với kết luận giữa NHƯNG và TẠI, có một điểm với bên trong phân khúc này như vậy f(với) = Với. Thẳng tại = Với cắt đồ thị của hàm số ít nhất tại một điểm.

Hậu quả. Nếu chức năng tại = f(x) liên tục trên khoảng [ một; b] và nhận các giá trị của các dấu hiệu khác nhau ở đầu của nó, sau đó bên trong đoạn [ một; b] có ít nhất một điểm với, trong đó chức năng này f(x) biến mất: f(với) = 0.

Ý nghĩa hình học của định lý: nếu đồ thị của hàm số liên tục đi từ một phía của trục Ồđến cái khác, sau đó nó đi qua trục Con bò(Xem Hình 7).

Cơm. 7.

Định nghĩa 4. Một hàm được gọi là liên tục trên một đoạn nếu nó liên tục tại mọi điểm của đoạn này (tại điểm a nó liên tục ở bên phải, tức là, tại điểm b nó liên tục ở bên trái).

Tất cả các hàm cơ bản cơ bản là liên tục trong miền định nghĩa của chúng.

Các thuộc tính của hàm liên tục trên một đoạn:

• 1) Nếu một hàm liên tục trên một đoạn thì nó bị giới hạn trên đoạn này (định lý Weierstrass đầu tiên).
• 2) Nếu một hàm liên tục trên một đoạn thì trên đoạn này nó đạt giá trị nhỏ nhất và giá trị lớn nhất (định lý Weierstrass thứ hai) (xem Hình 2).
• 3) Nếu một hàm liên tục trên một đoạn và nhận các giá trị của các dấu khác nhau ở các đầu của nó, thì có ít nhất một điểm bên trong đoạn sao cho (định lý Bolzano-Cauchy).

Các điểm ngắt chức năng và phân loại của chúng

chức năng liên tục phân đoạn điểm

Các điểm không thỏa mãn điều kiện liên tục được gọi là điểm gián đoạn của hàm này. Nếu là điểm gián đoạn của một hàm, thì ít nhất một trong ba điều kiện cho tính liên tục của hàm được chỉ định trong Định nghĩa 1, 2 không được thỏa mãn trong đó, đó là:

1) Hàm được xác định trong vùng lân cận của điểm, nhưng không được xác định tại chính điểm. Vì vậy, hàm được xét trong ví dụ 2 a) có một điểm ngắt tại một điểm, vì nó không được xác định tại điểm này.

2) Hàm được xác định tại một điểm và lân cận của nó, có các giới hạn một phía và nhưng chúng không bằng nhau:. Ví dụ, hàm từ ví dụ 2 b) được xác định tại một điểm và vùng lân cận của nó, nhưng, vì, a.

3) Hàm số được xác định tại điểm và xung quanh của nó, có các giới hạn một phía và chúng bằng nhau, nhưng không bằng giá trị của hàm số tại điểm:. Ví dụ, chức năng. Đây là điểm phá vỡ: tại thời điểm này hàm được xác định, có các giới hạn một phía và bằng nhau, nhưng, tức là.

Các điểm ngắt chức năng được phân loại như sau.

Định nghĩa 5. Một điểm được gọi là điểm gián đoạn bậc nhất của một hàm số nếu có hữu hạn các giới hạn và tại điểm này, nhưng chúng không bằng nhau:. Khi đó đại lượng được gọi là bước nhảy của hàm tại điểm.

Định nghĩa 6. Một điểm được gọi là điểm thuộc tính gián đoạn di động của một hàm nếu tại điểm này có giới hạn hữu hạn và chúng bằng nhau :, nhưng bản thân hàm không được xác định tại điểm, hoặc được xác định, nhưng.

Định nghĩa 7. Một điểm được gọi là điểm gián đoạn bậc hai của hàm số nếu tại thời điểm này có ít nhất một trong các giới hạn một phía (hoặc) không tồn tại hoặc bằng vô cùng.

Ví dụ 3. Tìm điểm ngắt của các hàm sau và xác định kiểu của chúng: a) b)

Quyết định. a) Hàm được xác định và liên tục trên các khoảng u, vì trên mỗi khoảng này, nó được cho bởi các hàm cơ bản liên tục. Do đó, chỉ những điểm mà tại đó hàm thay đổi phép phân tích của nó mới có thể là những điểm gián đoạn của một hàm đã cho, tức là điểm i. Hãy tìm giới hạn một phía của hàm số tại điểm:

Vì giới hạn một phía tồn tại và hữu hạn, nhưng không bằng nhau, điểm là điểm gián đoạn của loại thứ nhất. Bước nhảy hàm:

Đối với một điểm chúng tôi tìm thấy.

CÁC TÍNH CHẤT CỦA CÁC CHỨC NĂNG LIÊN TỤC TRÊN MỘT PHỎNG VẤN

Chúng ta hãy xem xét một số tính chất của hàm số liên tục trên một khoảng. Chúng tôi trình bày những thuộc tính này mà không cần bằng chứng.

Hàm số y = f (x) triệu tập liên tục trên phân khúc [một, b], nếu nó liên tục ở tất cả các điểm bên trong của đoạn này và ở các điểm cuối của nó, tức là tại các điểm một và b, là liên tục ở bên phải và bên trái, tương ứng.

Định lý 1. Một hàm liên tục trên đoạn [ một, b], ít nhất một điểm của đoạn này nhận giá trị lớn nhất và ít nhất một điểm - nhỏ nhất.

Định lý phát biểu rằng nếu hàm y = f (x) liên tục trên đoạn [ một, b], thì có ít nhất một điểm x 1 Î [ một, b] sao cho giá trị của hàm f (x) tại thời điểm này sẽ là giá trị lớn nhất trong số tất cả các giá trị của nó trên phân khúc này: f (x1) ≥ f (x). Tương tự, có một điểm như vậy x2, trong đó giá trị của hàm sẽ nhỏ nhất trong tất cả các giá trị trên đoạn: f (x 1) ≤ f (x).

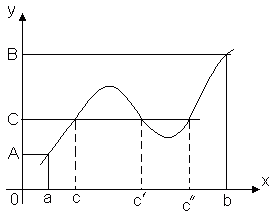
Rõ ràng là có thể có một số điểm như vậy, ví dụ, hình vẽ cho thấy hàm f (x) lấy giá trị nhỏ nhất tại hai điểm x2 và x 2 ".

Nhận xét. Phát biểu của định lý có thể trở thành sai nếu chúng ta coi giá trị của hàm số trên khoảng ( một, b). Thật vậy, nếu chúng ta xem xét hàm y = x trên (0, 2), sau đó nó liên tục trên khoảng này, nhưng không đạt đến các giá trị lớn nhất hoặc nhỏ nhất trong đó: nó đạt các giá trị này ở các đầu của khoảng, nhưng các đầu không thuộc về vùng đất.

Ngoài ra, định lý không còn đúng đối với các hàm không liên tục. Cho một ví dụ.

Hậu quả. Nếu chức năng f (x) liên tục trên [ một, b], thì nó được giới hạn trên phân đoạn này.

Định lý 2.Để chức năng y = f (x) liên tục trên đoạn [ một, b] và nhận các giá trị của các dấu hiệu khác nhau ở cuối đoạn này, khi đó có ít nhất một điểm bên trong đoạn x = C, nơi hàm biến mất: f (C)= 0, trong đó a< C< b

Định lý này có một ý nghĩa hình học đơn giản: nếu các điểm thuộc đồ thị của một hàm số liên tục y = f (x), tương ứng với các phần cuối của đoạn [ một, b] nằm trên các mặt đối diện của trục Con bò, thì biểu đồ này có ít nhất một điểm của đoạn giao với trục Con bò. Các chức năng liên tục có thể không có thuộc tính này.

Định lý này thừa nhận sự tổng quát hóa sau đây.

Định lý 3 (định lý về các giá trị trung gian).Để chức năng y = f (x) liên tục trên đoạn [ một, b] và f (a) = A, f (b) = B. Sau đó, cho bất kỳ số nào Cở giữa Một và B, có một điểm như vậy bên trong phân đoạn này CÎ [ một, b], Cái gì f (c) = C.

Định lý này là hiển nhiên về mặt hình học. Xét đồ thị của hàm y = f (x). Để cho được f (a) = A, f (b) = B. Sau đó, bất kỳ dòng nào y = C, ở đâu C- bất kỳ số nào giữa Một và B, cắt đồ thị của hàm số ít nhất tại một điểm. Abscissa của giao điểm sẽ là giá trị đó x = C, tại đó f (c) = C.

Do đó, một hàm liên tục, truyền từ một trong các giá trị của nó sang một giá trị khác, nhất thiết phải đi qua tất cả các giá trị trung gian. Đặc biệt:

Hậu quả. Nếu chức năng y = f (x) là liên tục trên một khoảng nào đó và nhận các giá trị lớn nhất và nhỏ nhất, sau đó trên khoảng này, nó nhận, ít nhất một lần, bất kỳ giá trị nào giữa các giá trị nhỏ nhất và lớn nhất của nó.

KHOẢNG CÁCH VÀ ỨNG DỤNG CỦA NÓ. ĐỊNH NGHĨA ĐA DẠNG

Hãy có một số chức năng y = f (x), xác định trên một số khoảng. Đối với mỗi giá trị đối số x từ khoảng thời gian này, hàm y = f (x) có ý nghĩa nhất định.

Hãy xem xét hai giá trị đối số: ban đầu x 0 và mới x.

Sự khác biệt x – x 0 được gọi là gia số của đối số x tại điểm x 0 và được ký hiệu Δx. Vì vậy, ∆x = x - x 0 (gia số đối số có thể là số dương hoặc số âm). Từ sự bình đẳng này, nó theo sau rằng x = x 0 + Δx, I E. giá trị ban đầu của biến đã nhận được một số gia tăng. Sau đó, nếu tại thời điểm x 0 giá trị hàm là f (x 0 ), sau đó ở điểm mới x hàm sẽ nhận giá trị f (x) = f (x 0 + ∆x).

Sự khác biệt y-y 0 = f (x) - f (x 0 ) triệu tập tăng hàm y = f (x) tại điểm x 0 và được biểu thị bằng ký hiệu Δy. Vì vậy,

Δy = f (x) - f (x 0 ) = f (x 0 + Δx) - f (x 0 ) .

(1)

Thông thường giá trị ban đầu của đối số x 0 được coi là cố định và giá trị mới x- Biến đổi. sau đó y 0 = f (x 0 ) hóa ra là không đổi và y = f (x)- Biến đổi. gia số Δy và Δx cũng sẽ là các biến và công thức (1) cho thấy rằng Dy là một hàm của biến Δx.

Soạn tỷ lệ số gia của hàm với số gia của đối số

Hãy để chúng tôi tìm giới hạn của mối quan hệ này tại Δx→ 0. Nếu tồn tại giới hạn này thì nó được gọi là đạo hàm của hàm này. f (x) tại điểm x 0 và biểu thị f "(x 0). Cho nên,

phát sinh Chức năng này y = f (x) tại điểm x 0 được gọi là giới hạn của tỉ số gia của hàm Δ yđến gia số của đối số Δ x khi cái sau tùy ý có xu hướng bằng không.

Lưu ý rằng đối với cùng một hàm thì đạo hàm tại các điểm khác nhau x có thể nhận các giá trị khác nhau, tức là đạo hàm có thể được coi là một hàm của đối số x. Chức năng này được ký hiệu là f "(x)

Đạo hàm được ký hiệu bằng các ký hiệu f "(x), y",. Giá trị cụ thể của đạo hàm tại x = a biểu thị f "(một) hoặc y "| x = a.

Các phép toán tìm đạo hàm của một hàm số f (x)được gọi là sự khác biệt của chức năng này.

Để tìm trực tiếp đạo hàm theo định nghĩa, bạn có thể áp dụng cách sau quy tắc ngón tay cái:

Các ví dụ.

Ý NGHĨA CƠ HỌC CỦA KHOẢNG CÁCH

Từ vật lý học người ta biết rằng định luật chuyển động đều có dạng s = v t, ở đâu S- đường đi đến thời điểm t, v là tốc độ của chuyển động thẳng đều.

Tuy nhiên, kể từ hầu hết các chuyển động xảy ra trong tự nhiên là không đồng đều, khi đó, trong trường hợp chung, tốc độ, và do đó, khoảng cách S sẽ phụ thuộc vào thời gian t, I E. sẽ là một hàm của thời gian.

Vậy để chất điểm chuyển động thẳng đều theo một chiều theo quy luật s = s (t).

Ghi chú một lúc kịp thời t 0. Đến thời điểm này, điểm đã vượt qua con đường s = s (t 0 ). Hãy xác định tốc độ v vật chất tại thời điểm t 0 .

Để làm điều này, hãy xem xét một số thời điểm khác kịp thời t 0 + Δ t. Nó tương ứng với quãng đường đã đi s = s (t 0 + Δ t). Sau đó trong khoảng thời gian Δ tđiểm đã đi được quãng đường Δs = s (t 0 + Δ t)–s (t).

Hãy xem xét mối quan hệ. Nó được gọi là tốc độ trung bình trong khoảng thời gian Δ t. Tốc độ trung bình không thể mô tả chính xác tốc độ chuyển động của một điểm tại thời điểm t 0 (vì chuyển động không đều). Để thể hiện chính xác hơn tốc độ thực này bằng tốc độ trung bình, bạn cần lấy một khoảng thời gian nhỏ hơn Δ t.

Vì vậy, tốc độ chuyển động tại một thời điểm nhất định t 0 (tốc độ tức thời) là giới hạn của tốc độ trung bình trong khoảng thời gian từ t 0 đến t 0 +Δ t khi Δ t→0:

,

những thứ kia. tốc độ chuyển động không đều là đạo hàm của quãng đường đi được đối với thời gian.

Ý NGHĨA HÌNH HỌC CỦA KHOẢNG CÁCH

Đầu tiên chúng ta hãy giới thiệu định nghĩa của một tiếp tuyến với một đường cong tại một điểm cho trước.

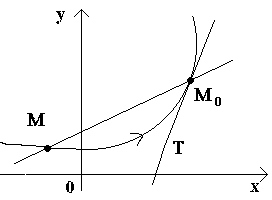
Để chúng ta có một đường cong và một điểm cố định trên đó M 0(xem hình). Hãy xem xét một điểm khác Mđường cong này và vẽ một mảnh M 0 M. Nếu điểm M bắt đầu di chuyển dọc theo đường cong và điểm M 0 vẫn đứng yên, người khai thác thay đổi vị trí của nó. Nếu, với điểm gần đúng không giới hạn Mđường cong đến điểm M 0ở bất kỳ mặt nào, người khai thác có xu hướng chiếm vị trí của một đường thẳng nhất định M 0 T, sau đó là đường thẳng M 0 Tđược gọi là tiếp tuyến của đường cong tại điểm đã cho M 0.

Điều đó., đường tiếp tuyếnđến đường cong tại một điểm nhất định M 0được gọi là vị trí giới hạn của secant M 0 M khi điểm M có xu hướng dọc theo đường cong đến một điểm M 0.

Bây giờ hãy xem xét hàm liên tục y = f (x) và đường cong tương ứng với chức năng này. Đối với một số giá trị X 0 hàm nhận một giá trị y0 = f (x0). Những giá trị x 0 và y 0 trên đường cong tương ứng với một điểm M 0 (x 0; y 0). Hãy đưa ra một lập luận x0 gia số Δ X. Giá trị mới của đối số tương ứng với giá trị tăng dần của hàm y 0 +Δ y = f (x 0 –Δ x). Chúng tôi nhận được một điểm M (x 0+Δ x; y 0+Δ y). Hãy vẽ một ly khai M 0 M và biểu thị bằng φ góc tạo bởi mặt cắt với chiều dương của trục Con bò. Hãy tạo một mối quan hệ và lưu ý rằng.

Nếu bây giờ Δ x→ 0, khi đó, do tính liên tục của hàm Δ tại→ 0, và do đó là điểm M, di chuyển dọc theo đường cong, tiếp cận điểm vô hạn M 0. Sau đó, người ly khai M 0 M sẽ có xu hướng lấy vị trí của một tiếp tuyến với đường cong tại điểm M 0, và góc φ → α tại Δ x→ 0, trong đó α biểu thị góc giữa tiếp tuyến và chiều dương của trục Con bò. Vì hàm tg φ liên tục phụ thuộc vào φ tại φ ≠ π / 2 nên tại φ → α tg φ → tg α và do đó, hệ số góc của tiếp tuyến sẽ là:

những thứ kia. f "(x)= tgα.

Do đó, về mặt hình học y "(x 0) biểu diễn hệ số góc của tiếp tuyến với đồ thị của hàm số này tại điểm x0, I E. cho một giá trị nhất định của đối số x, đạo hàm bằng tiếp tuyến của góc tạo bởi tiếp tuyến với đồ thị của hàm số f (x) tại điểm tương ứng M 0 (x; y) với hướng trục dương Con bò.

Ví dụ. Tìm hệ số góc của tiếp tuyến với đường cong y = x 2 tại điểm M(-1; 1).

Chúng tôi đã thấy rằng ( x 2)" = 2X. Nhưng hệ số góc của tiếp tuyến với đường cong là tg α = y"| x = -1 = - 2.

SỰ KHÁC BIỆT CỦA CÁC CHỨC NĂNG. SỰ LIÊN TỤC CỦA MỘT CHỨC NĂNG KHÁC NHAU

Hàm số y = f (x) triệu tập có thể phân biệtỞ một vài điểm x 0 nếu nó có một đạo hàm nào đó tại thời điểm này, tức là nếu giới hạn của quan hệ tồn tại và hữu hạn.

Nếu một chức năng có thể phân biệt được tại mọi điểm của một số đoạn [ một; b] hoặc khoảng ( một; b), sau đó họ nói rằng nó có thể phân biệt trên đoạn [ một; b] hoặc, tương ứng, trong khoảng ( một; b).

Định lý sau đây là hợp lệ, định lý này thiết lập mối liên hệ giữa các hàm phân biệt và liên tục.

Định lý. Nếu chức năng y = f (x) có thể phân biệt ở một số điểm x0, thì nó là liên tục tại thời điểm này.

Do đó, tính khác biệt của một chức năng bao hàm tính liên tục của nó.

Bằng chứng. Nếu một , sau đó

,

trong đó α là một giá trị thập phân, tức là số lượng có xu hướng về 0 tại Δ x→ 0. Nhưng sau đó

Δ y=f "(x0) Δ x+αΔ x=> Δ y→ 0 tại Δ x→ 0, tức là f (x) - f (x0)→ 0 lúc x→x 0, có nghĩa là hàm f (x) liên tục tại điểm x 0. Q.E.D.

Như vậy, tại các điểm gián đoạn, hàm số không thể có đạo hàm. Phát biểu ngược là không đúng: có những hàm liên tục không phân biệt ở một số điểm (nghĩa là chúng không có đạo hàm tại những điểm này).

Xem xét các điểm trong hình a, b, c.

Tại điểm một tại Δ x→ 0 quan hệ không có giới hạn (vì các giới hạn một phía là khác nhau đối với Δ x→ 0–0 và Δ x→ 0 + 0). Tại điểm Mộtđồ thị không có tiếp tuyến xác định, nhưng có hai tiếp tuyến một phía khác nhau có hệ số góc đến 1 và đến 2. Loại điểm này được gọi là điểm góc.

Tại điểm b tại Δ x→ 0 tỉ số có giá trị không đổi có giá trị lớn vô hạn. Hàm có vô số đạo hàm. Lúc này, đồ thị có một tiếp tuyến thẳng đứng. Loại điểm - "điểm uốn" với một tiếp tuyến thẳng đứng.

Tại điểm cđạo hàm một phía là số lượng lớn vô hạn của các dấu hiệu khác nhau. Tại thời điểm này, đồ thị có hai tiếp tuyến dọc hợp nhất. Loại - "đỉnh" với một tiếp tuyến thẳng đứng - một trường hợp đặc biệt của một điểm ở góc.

Theo quan điểm thực tế, thú vị nhất là việc sử dụng đạo hàm để tìm giá trị lớn nhất và nhỏ nhất của một hàm số. Nó được kết nối với cái gì? Tối đa hóa lợi nhuận, tối thiểu hóa chi phí, xác định tải trọng tối ưu của thiết bị… Nói cách khác, trong nhiều lĩnh vực của cuộc sống, người ta phải giải bài toán tối ưu hóa một số thông số. Và đây là bài toán tìm giá trị lớn nhất và nhỏ nhất của hàm số.

Cần lưu ý rằng giá trị lớn nhất và nhỏ nhất của một hàm thường được tìm kiếm trên khoảng X nào đó, là miền toàn bộ của hàm hoặc một phần của miền. Bản thân khoảng X có thể là một đoạn thẳng, một khoảng mở , một khoảng vô hạn.

Trong bài này, chúng ta sẽ nói về việc tìm giá trị lớn nhất và nhỏ nhất của một hàm số đã cho của một biến y = f (x).

Điều hướng trang.

Giá trị lớn nhất và nhỏ nhất của một hàm số - định nghĩa, hình ảnh minh họa.

Hãy để chúng tôi tìm hiểu ngắn gọn về các định nghĩa chính.

Giá trị lớn nhất của hàm , cho bất kỳ sự bất bình đẳng là đúng.

Giá trị nhỏ nhất của hàm y = f (x) trên khoảng X được gọi là giá trị nào , cho bất kỳ sự bất bình đẳng là đúng.

Các định nghĩa này rất trực quan: giá trị lớn nhất (nhỏ nhất) của một hàm là giá trị lớn nhất (nhỏ nhất) được chấp nhận trong khoảng thời gian được xem xét với abscissa.

Điểm tĩnh là các giá trị của đối số mà tại đó đạo hàm của hàm biến mất.

Tại sao khi tìm giá trị lớn nhất và nhỏ nhất ta cần điểm đứng yên? Câu trả lời cho câu hỏi này được đưa ra bởi định lý Fermat. Theo định lý này, nếu một hàm phân biệt có cực trị (cực tiểu cục bộ hoặc cực đại cục bộ) tại một thời điểm nào đó, thì điểm này là đứng yên. Như vậy, hàm số thường nhận giá trị lớn nhất (nhỏ nhất) trên khoảng X tại một trong những điểm đứng yên cách khoảng này.

Ngoài ra, một hàm thường có thể nhận các giá trị lớn nhất và nhỏ nhất tại các điểm mà tại đó đạo hàm cấp một của hàm này không tồn tại và bản thân hàm được xác định.

Hãy trả lời ngay một trong những câu hỏi phổ biến nhất về chủ đề này: "Có phải luôn luôn xác định được giá trị lớn nhất (nhỏ nhất) của một hàm số"? Không phải lúc nào cũng vậy. Đôi khi ranh giới của khoảng X trùng với ranh giới của miền hàm hoặc khoảng X là vô hạn. Và một số hàm ở vô cùng và trên các ranh giới của miền xác định có thể nhận cả giá trị lớn vô hạn và nhỏ vô hạn. Trong những trường hợp này, không thể nói gì về giá trị lớn nhất và nhỏ nhất của hàm số.

Để rõ ràng, chúng tôi đưa ra một minh họa đồ họa. Nhìn vào các bức tranh - và nhiều thứ sẽ trở nên rõ ràng.

Trên phân khúc

Trong hình đầu tiên, hàm nhận các giá trị lớn nhất (y max) và nhỏ nhất (y min) tại các điểm đứng yên bên trong đoạn [-6; 6].

Hãy xem xét trường hợp được hiển thị trong hình thứ hai. Thay đổi phân đoạn thành. Trong ví dụ này, giá trị nhỏ nhất của hàm đạt được tại một điểm đứng yên và lớn nhất - tại một điểm có hoành độ tương ứng với biên bên phải của khoảng.

Trong hình 3, các điểm biên của đoạn [-3; 2] là hoành độ của các điểm tương ứng với giá trị lớn nhất và nhỏ nhất của hàm số.

Trong phạm vi mở

Trong hình thứ tư, hàm nhận các giá trị lớn nhất (y max) và nhỏ nhất (y min) tại các điểm dừng trong khoảng mở (-6; 6).

Trên khoảng không rút ra được kết luận nào về giá trị lớn nhất.

Ở vô cùng

Trong ví dụ minh họa ở hình thứ bảy, hàm nhận giá trị lớn nhất (y max) tại một điểm đứng yên với hoành độ x = 1 và giá trị nhỏ nhất (min y) đạt được tại biên bên phải của khoảng. Tại trừ đi vô cùng, các giá trị của hàm tiệm cận đến y = 3.

Trên khoảng, hàm số không đạt giá trị nhỏ nhất hoặc lớn nhất. Khi x = 2 có xu hướng sang phải, các giá trị hàm có xu hướng trừ đi vô cùng (đường thẳng x = 2 là một tiệm cận đứng) và khi abscissa có xu hướng cộng với vô cùng, các giá trị hàm tiệm cận với y = 3 . Hình 8 minh họa bằng đồ họa cho ví dụ này.

Thuật toán tìm giá trị lớn nhất, nhỏ nhất của hàm số liên tục trên đoạn.

Chúng tôi viết một thuật toán cho phép chúng tôi tìm giá trị lớn nhất và nhỏ nhất của một hàm trên một đoạn.

1. Chúng tôi tìm miền của hàm và kiểm tra xem nó có chứa toàn bộ phân đoạn hay không.
2. Chúng tôi tìm thấy tất cả các điểm mà tại đó đạo hàm cấp một không tồn tại và được chứa trong phân đoạn (thường các điểm như vậy xảy ra trong các hàm có đối số dưới dấu mô-đun và trong các hàm lũy thừa với số mũ hữu tỉ phân số). Nếu không có điểm nào như vậy thì chuyển sang điểm tiếp theo.
3. Chúng tôi xác định tất cả các điểm đứng yên rơi vào phân đoạn. Để làm được điều này, chúng ta cân bằng nó với 0, giải phương trình kết quả và chọn các nghiệm nguyên thích hợp. Nếu không có điểm nào đứng yên hoặc không có điểm nào nằm trong đoạn thì hãy chuyển sang bước tiếp theo.
4. Ta tính các giá trị của hàm tại các điểm đứng yên đã chọn (nếu có), tại các điểm không tồn tại đạo hàm cấp một (nếu có), và cả tại x = a và x = b.
5. Từ các giá trị thu được của hàm, chúng ta chọn giá trị lớn nhất và nhỏ nhất - chúng sẽ lần lượt là giá trị lớn nhất và nhỏ nhất mong muốn của hàm.

Hãy phân tích thuật toán khi giải một ví dụ về tìm giá trị lớn nhất và nhỏ nhất của một hàm số trên một đoạn thẳng.

Ví dụ.

Tìm giá trị lớn nhất và nhỏ nhất của hàm số

• trên phân khúc;
• trên khoảng [-4; -1].

Quyết định.

Miền của hàm là toàn bộ tập hợp các số thực, ngoại trừ số 0, nghĩa là. Cả hai phân đoạn đều nằm trong miền định nghĩa.

Chúng tôi tìm đạo hàm của hàm liên quan đến:

Rõ ràng, đạo hàm của hàm số tồn tại tại mọi điểm thuộc đoạn và [-4; -1].

Điểm đứng yên được xác định từ phương trình. Căn thực duy nhất là x = 2. Điểm đứng yên này rơi vào đoạn đầu tiên.

Đối với trường hợp đầu tiên, chúng ta tính các giá trị của hàm tại hai đầu đoạn thẳng và tại một điểm đứng yên, nghĩa là đối với x = 1, x = 2 và x = 4:

Do đó, giá trị lớn nhất của hàm đạt được tại x = 1 và giá trị nhỏ nhất - tại x = 2.

Đối với trường hợp thứ hai, chúng tôi chỉ tính các giá trị của hàm tại các phần cuối của đoạn [-4; -1] (vì nó không chứa một điểm dừng duy nhất):

Quyết định.

Hãy bắt đầu với phạm vi của hàm. Tam thức bình phương ở mẫu số của một phân số không được biến mất:

Dễ dàng kiểm tra rằng tất cả các khoảng từ điều kiện của bài toán đều thuộc miền của hàm.

Hãy phân biệt chức năng:

Rõ ràng, đạo hàm tồn tại trên toàn bộ miền của hàm.

Hãy tìm điểm đứng yên. Đạo hàm biến mất lúc. Điểm đứng yên này nằm trong khoảng (-3; 1] và (-3; 2).

Và bây giờ bạn có thể so sánh kết quả thu được tại mỗi điểm với đồ thị của hàm số. Các đường chấm màu xanh lam cho biết không có triệu chứng.

Điều này có thể kết thúc bằng việc tìm giá trị lớn nhất và nhỏ nhất của hàm. Các thuật toán được thảo luận trong bài viết này cho phép bạn nhận được kết quả với một số hành động tối thiểu. Tuy nhiên, có thể hữu ích trước tiên là xác định các khoảng tăng và giảm của hàm số và chỉ sau đó mới rút ra kết luận về giá trị lớn nhất và nhỏ nhất của hàm số trên bất kỳ khoảng nào. Điều này mang lại một bức tranh rõ ràng hơn và một sự biện minh chặt chẽ về kết quả.

Tính liên tục của một hàm số trên một đoạn thẳng.

Cùng với tính liên tục của một hàm tại một điểm, người ta xem xét tính liên tục của nó trên các khoảng thời gian khác nhau.

Một hàm số f (x) được gọi là liên tục trên khoảng (a, b) nếu nó liên tục tại mọi điểm của khoảng này.

Một hàm số f (x) được gọi là liên tục trên khoảng [a, b] nếu nó liên tục trên khoảng (a, b), liên tục bên phải tại điểm a và liên tục bên trái tại điểm b.

Hàm được gọi là liên tục trên phân khúcnếu nó liên tục trong khoảng thời gian, liên tục ở bên phải tại điểm, I E và liên tục ở bên trái tại điểm, I E .

Nhận xét. Một hàm liên tục trên đoạn [a, b] có thể không liên tục tại các điểm a và b (Hình 1)

Tập hợp các hàm liên tục trên đoạn [a, b] được ký hiệu là C [a, b].

Các định lý cơ bản về hàm số liên tục trên một khoảng.

Định lý 1(về giới hạn của một hàm liên tục). Nếu hàm f (x) liên tục trên đoạn [a, b] thì nó bị giới hạn trên đoạn này, tức là tồn tại số C> 0 sao cho “x 0 [a, b] bất phương trình | f (x) | ≤ C.

Định lý 2(Weierstrass). Nếu hàm số f (x) liên tục trên đoạn [a, b] thì nó đạt giá trị lớn nhất M và giá trị nhỏ nhất m trên khoảng này, tức là. có các điểm α, β О [a, b] sao cho m = f (α) ≤ f (x) ≤ f (β) = M với mọi x О [a, b] (Hình 2).

Giá trị lớn nhất của M được kí hiệu là max x Về [a, b] f (x), và giá trị nhỏ nhất của m là ký hiệu min x Về [a, b] f (x).
Định lý 3(về sự tồn tại của số 0). Nếu hàm số f (x) liên tục trên đoạn [a, b] và nhận các giá trị khác không của các dấu khác nhau ở hai đầu đoạn thì trên khoảng (a, b) có ít nhất một điểm ξ mà f (ξ) = 0.
Ý nghĩa hình học của định lý là đồ thị của một hàm số thỏa mãn các điều kiện của định lý sẽ nhất thiết phải cắt trục CON BÒ(Hình 3).

Nhận xét.Định lý này là cơ sở cho phương pháp giải gần đúng của phương trình

f (x) = 0,

(1)

được gọi là phương pháp phân đôi (phân đôi), hay phương pháp phân giác.

Định lý 4(Bolzano-Cauchy). Nếu hàm số f (x) liên tục trên khoảng [a, b] thì nó đồng biến trên (a, b) tất cả các giá trị trung gian giữa f (a) và f (b).
Sự tồn tại của một hàm nghịch đảo liên tục
Cho hàm số y = f (x) xác định, đơn điệu và liên tục trên đoạn [a, b]. Khi đó trên đoạn [α, β] (α = f (a), β = f (b)) tồn tại một hàm ngược x = g (y), hàm này cũng đơn điệu và liên tục trên đoạn (α, β ).