Άλγεβρα - OGE. Εργασίες με λύση

Περιεχόμενο μαθήματος

Πρόσθεση κλασμάτων με ίδιους παρονομαστές

Η προσθήκη κλασμάτων είναι δύο τύπων:

1. Προσθήκη κλασμάτων με ίδιοι παρονομαστές
2. Προσθήκη κλασμάτων με διαφορετικούς παρονομαστές

Ας ξεκινήσουμε με την προσθήκη κλασμάτων με τους ίδιους παρονομαστές. Όλα είναι απλά εδώ. Για να προσθέσετε κλάσματα με τους ίδιους παρονομαστές, πρέπει να προσθέσετε τους αριθμητές τους και να αφήσετε τον παρονομαστή αμετάβλητο. Για παράδειγμα, ας προσθέσουμε τα κλάσματα και . Προσθέτουμε τους αριθμητές και αφήνουμε αμετάβλητο τον παρονομαστή:

Αυτό το παράδειγμα μπορεί να γίνει εύκολα κατανοητό αν σκεφτούμε μια πίτσα που χωρίζεται σε τέσσερα μέρη. Αν προσθέσετε πίτσα στην πίτσα, παίρνετε πίτσα:

Παράδειγμα 2Προσθέστε κλάσματα και .

Η απάντηση είναι ένα ακατάλληλο κλάσμα. Εάν έρθει το τέλος της εργασίας, τότε είναι συνηθισμένο να απαλλαγείτε από ακατάλληλα κλάσματα. Να ξεφορτωθώ ακατάλληλο κλάσμα, πρέπει να επιλέξετε ολόκληρο το μέρος σε αυτό. Στην περίπτωσή μας ολόκληρο μέροςξεχωρίζει εύκολα - δύο διαιρούμενα με δύο ισούται με ένα:

Αυτό το παράδειγμα μπορεί να γίνει εύκολα κατανοητό αν σκεφτούμε μια πίτσα που χωρίζεται σε δύο μέρη. Εάν προσθέσετε περισσότερες πίτσες στην πίτσα, θα έχετε μια ολόκληρη πίτσα:

Παράδειγμα 3. Προσθέστε κλάσματα και .

Και πάλι, προσθέστε τους αριθμητές και αφήστε τον παρονομαστή αμετάβλητο:

Αυτό το παράδειγμα μπορεί να γίνει εύκολα κατανοητό αν σκεφτούμε μια πίτσα που χωρίζεται σε τρία μέρη. Εάν προσθέσετε περισσότερες πίτσες στην πίτσα, θα λάβετε πίτσες:

Παράδειγμα 4Βρείτε την τιμή μιας έκφρασης

Αυτό το παράδειγμα επιλύεται ακριβώς με τον ίδιο τρόπο όπως τα προηγούμενα. Οι αριθμητές πρέπει να προστεθούν και ο παρονομαστής να παραμείνει αμετάβλητος:

Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας μια εικόνα. Εάν προσθέσετε πίτσες σε μια πίτσα και προσθέσετε περισσότερες πίτσες, θα λάβετε 1 ολόκληρη πίτσα και περισσότερες πίτσες.

Όπως μπορείτε να δείτε, η προσθήκη κλασμάτων με τους ίδιους παρονομαστές δεν είναι δύσκολη. Αρκεί να κατανοήσουμε τους ακόλουθους κανόνες:

1. Για να προσθέσετε κλάσματα με τον ίδιο παρονομαστή, πρέπει να προσθέσετε τους αριθμητές τους και να αφήσετε τον παρονομαστή αμετάβλητο.

Προσθήκη κλασμάτων με διαφορετικούς παρονομαστές

Τώρα θα μάθουμε πώς να προσθέτουμε κλάσματα με διαφορετικούς παρονομαστές. Όταν προσθέτουμε κλάσματα, οι παρονομαστές αυτών των κλασμάτων πρέπει να είναι οι ίδιοι. Δεν είναι όμως πάντα τα ίδια.

Για παράδειγμα, τα κλάσματα μπορούν να προστεθούν επειδή έχουν τους ίδιους παρονομαστές.

Αλλά τα κλάσματα δεν μπορούν να προστεθούν αμέσως, γιατί αυτά τα κλάσματα έχουν διαφορετικούς παρονομαστές. Σε τέτοιες περιπτώσεις, τα κλάσματα πρέπει να ανάγονται στον ίδιο (κοινό) παρονομαστή.

Υπάρχουν διάφοροι τρόποι αναγωγής κλασμάτων στον ίδιο παρονομαστή. Σήμερα θα εξετάσουμε μόνο ένα από αυτά, καθώς οι υπόλοιπες μέθοδοι μπορεί να φαίνονται περίπλοκες για έναν αρχάριο.

Η ουσία αυτής της μεθόδου έγκειται στο γεγονός ότι αναζητείται πρώτα (LCM) από τους παρονομαστές και των δύο κλασμάτων. Στη συνέχεια το LCM διαιρείται με τον παρονομαστή του πρώτου κλάσματος και προκύπτει ο πρώτος πρόσθετος παράγοντας. Κάνουν το ίδιο με το δεύτερο κλάσμα - το LCM διαιρείται με τον παρονομαστή του δεύτερου κλάσματος και προκύπτει ο δεύτερος πρόσθετος παράγοντας.

Τότε οι αριθμητές και οι παρονομαστές των κλασμάτων πολλαπλασιάζονται με τους πρόσθετους συντελεστές τους. Ως αποτέλεσμα αυτών των ενεργειών, τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατρέπονται σε κλάσματα που έχουν τους ίδιους παρονομαστές. Και ξέρουμε ήδη πώς να προσθέτουμε τέτοια κλάσματα.

Παράδειγμα 1. Προσθέστε κλάσματα και

Πρώτα απ 'όλα, βρίσκουμε το ελάχιστο κοινό πολλαπλάσιο των παρονομαστών και των δύο κλασμάτων. Ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 2. Το ελάχιστο κοινό πολλαπλάσιο αυτών των αριθμών είναι το 6

LCM (2 και 3) = 6

Τώρα πίσω στα κλάσματα και . Αρχικά, διαιρούμε το LCM με τον παρονομαστή του πρώτου κλάσματος και παίρνουμε τον πρώτο πρόσθετο παράγοντα. Το LCM είναι ο αριθμός 6 και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3. Διαιρέστε το 6 με το 3, παίρνουμε 2.

Ο αριθμός 2 που προκύπτει είναι ο πρώτος πρόσθετος παράγοντας. Το γράφουμε στο πρώτο κλάσμα. Για να γίνει αυτό, κάνουμε μια μικρή πλάγια γραμμή πάνω από το κλάσμα και σημειώνουμε τον πρόσθετο παράγοντα που βρέθηκε πάνω από αυτό:

Το ίδιο κάνουμε και με το δεύτερο κλάσμα. Διαιρούμε το LCM με τον παρονομαστή του δεύτερου κλάσματος και παίρνουμε τον δεύτερο πρόσθετο παράγοντα. Το LCM είναι ο αριθμός 6 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 2. Διαιρέστε το 6 με το 2, παίρνουμε 3.

Ο αριθμός 3 που προκύπτει είναι ο δεύτερος πρόσθετος παράγοντας. Το γράφουμε στο δεύτερο κλάσμα. Και πάλι, κάνουμε μια μικρή πλάγια γραμμή πάνω από το δεύτερο κλάσμα και γράφουμε τον πρόσθετο παράγοντα που βρέθηκε πάνω από αυτό:

Τώρα είμαστε έτοιμοι να προσθέσουμε. Απομένει να πολλαπλασιάσουμε τους αριθμητές και τους παρονομαστές των κλασμάτων με τους πρόσθετους συντελεστές τους:

Κοιτάξτε προσεκτικά σε τι έχουμε καταλήξει. Καταλήξαμε στο συμπέρασμα ότι τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατράπηκαν σε κλάσματα που είχαν τους ίδιους παρονομαστές. Και ξέρουμε ήδη πώς να προσθέτουμε τέτοια κλάσματα. Ας συμπληρώσουμε αυτό το παράδειγμα μέχρι το τέλος:

Έτσι τελειώνει το παράδειγμα. Για να προσθέσω αποδεικνύεται.

Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας μια εικόνα. Εάν προσθέσετε πίτσες σε μια πίτσα, θα έχετε μια ολόκληρη πίτσα και ένα άλλο έκτο της πίτσας:

Η αναγωγή των κλασμάτων στον ίδιο (κοινό) παρονομαστή μπορεί επίσης να απεικονιστεί χρησιμοποιώντας μια εικόνα. Φέρνοντας τα κλάσματα και σε έναν κοινό παρονομαστή, παίρνουμε τα κλάσματα και . Αυτά τα δύο κλάσματα θα αντιπροσωπεύονται από τις ίδιες φέτες πίτσας. Η μόνη διαφορά θα είναι ότι αυτή τη φορά θα διαιρεθούν σε ίσα μερίδια (μειωμένα στον ίδιο παρονομαστή).

Το πρώτο σχέδιο δείχνει ένα κλάσμα (τέσσερα κομμάτια από τα έξι) και η δεύτερη εικόνα δείχνει ένα κλάσμα (τρία κομμάτια από τα έξι). Συνδυάζοντας αυτά τα κομμάτια παίρνουμε (επτά κομμάτια στα έξι). Αυτό το κλάσμα είναι λανθασμένο, επομένως έχουμε επισημάνει το ακέραιο μέρος σε αυτό. Το αποτέλεσμα ήταν (μία ολόκληρη πίτσα και άλλη έκτη πίτσα).

Σημειώστε ότι έχουμε ζωγραφίσει αυτό το παράδειγμα με πάρα πολλές λεπτομέρειες. ΣΤΟ Εκπαιδευτικά ιδρύματαδεν συνηθίζεται να γράφουμε με τόσο λεπτομερή τρόπο. Πρέπει να είστε σε θέση να βρείτε γρήγορα το LCM τόσο των παρονομαστών όσο και των πρόσθετων παραγόντων σε αυτούς, καθώς και να πολλαπλασιάσετε γρήγορα τους πρόσθετους παράγοντες που βρέθηκαν από τους αριθμητές και τους παρονομαστές σας. Στο σχολείο, θα έπρεπε να γράψουμε αυτό το παράδειγμα ως εξής:

Αλλά υπάρχει επίσης πίσω πλευράμετάλλια. Εάν δεν γίνονται αναλυτικές σημειώσεις στα πρώτα στάδια της μελέτης των μαθηματικών, τότε ερωτήσεις του είδους «Από πού προέρχεται αυτός ο αριθμός;», «Γιατί τα κλάσματα μετατρέπονται ξαφνικά σε εντελώς διαφορετικά κλάσματα; «.

Για να διευκολύνετε την προσθήκη κλασμάτων με διαφορετικούς παρονομαστές, μπορείτε να χρησιμοποιήσετε τις παρακάτω οδηγίες βήμα προς βήμα:

1. Να βρείτε το LCM των παρονομαστών των κλασμάτων.
2. Διαιρέστε το LCM με τον παρονομαστή κάθε κλάσματος και λάβετε έναν επιπλέον πολλαπλασιαστή για κάθε κλάσμα.
3. Πολλαπλασιάστε τους αριθμητές και τους παρονομαστές των κλασμάτων με τους πρόσθετους συντελεστές τους.
4. Προσθέστε κλάσματα που έχουν τους ίδιους παρονομαστές.
5. Εάν η απάντηση αποδείχθηκε ότι είναι ακατάλληλο κλάσμα, επιλέξτε ολόκληρο το μέρος του.

Παράδειγμα 2Βρείτε την τιμή μιας έκφρασης .

Ας χρησιμοποιήσουμε τις παραπάνω οδηγίες.

Βήμα 1. Βρείτε το LCM των παρονομαστών των κλασμάτων

Βρείτε το LCM των παρονομαστών και των δύο κλασμάτων. Οι παρονομαστές των κλασμάτων είναι οι αριθμοί 2, 3 και 4

Βήμα 2. Διαιρέστε το LCM με τον παρονομαστή κάθε κλάσματος και λάβετε έναν επιπλέον πολλαπλασιαστή για κάθε κλάσμα

Διαιρέστε το LCM με τον παρονομαστή του πρώτου κλάσματος. LCM είναι ο αριθμός 12 και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 2. Διαιρούμε το 12 με το 2, παίρνουμε 6. Πήραμε τον πρώτο πρόσθετο παράγοντα 6. Τον γράφουμε πάνω στο πρώτο κλάσμα:

Τώρα διαιρούμε το LCM με τον παρονομαστή του δεύτερου κλάσματος. LCM είναι ο αριθμός 12 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 3. Διαιρούμε το 12 με το 3, παίρνουμε 4. Πήραμε τον δεύτερο πρόσθετο παράγοντα 4. Το γράφουμε πάνω στο δεύτερο κλάσμα:

Τώρα διαιρούμε το LCM με τον παρονομαστή του τρίτου κλάσματος. Το LCM είναι ο αριθμός 12 και ο παρονομαστής του τρίτου κλάσματος είναι ο αριθμός 4. Διαιρούμε το 12 με το 4, παίρνουμε 3. Πήραμε τον τρίτο πρόσθετο παράγοντα 3. Το γράφουμε πάνω στο τρίτο κλάσμα:

Βήμα 3. Πολλαπλασιάστε τους αριθμητές και τους παρονομαστές των κλασμάτων με τους πρόσθετους συντελεστές σας

Πολλαπλασιάζουμε τους αριθμητές και τους παρονομαστές με τους πρόσθετους συντελεστές μας:

Βήμα 4. Προσθέστε κλάσματα που έχουν τους ίδιους παρονομαστές

Καταλήξαμε στο συμπέρασμα ότι τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατράπηκαν σε κλάσματα που έχουν τους ίδιους (κοινούς) παρονομαστές. Απομένει να προσθέσουμε αυτά τα κλάσματα. Προσθέτω:

Η προσθήκη δεν χωρούσε σε μία γραμμή, οπότε μετακινήσαμε την υπόλοιπη έκφραση στην επόμενη γραμμή. Αυτό επιτρέπεται στα μαθηματικά. Όταν μια έκφραση δεν ταιριάζει σε μια γραμμή, μεταφέρεται στην επόμενη γραμμή και είναι απαραίτητο να βάλετε ένα σύμβολο ίσου (=) στο τέλος της πρώτης γραμμής και στην αρχή μιας νέας γραμμής. Το σύμβολο ίσου στη δεύτερη γραμμή υποδηλώνει ότι πρόκειται για συνέχεια της έκφρασης που υπήρχε στην πρώτη γραμμή.

Βήμα 5. Εάν η απάντηση αποδείχθηκε ότι είναι ακατάλληλο κλάσμα, επιλέξτε ολόκληρο το μέρος σε αυτό

Η απάντησή μας είναι ένα ακατάλληλο κλάσμα. Πρέπει να ξεχωρίσουμε ολόκληρο το κομμάτι του. Τονίζουμε:

Πήρε μια απάντηση

Αφαίρεση κλασμάτων με ίδιους παρονομαστές

Υπάρχουν δύο τύποι αφαίρεσης κλασμάτων:

1. Αφαίρεση κλασμάτων με ίδιους παρονομαστές
2. Αφαίρεση κλασμάτων με διαφορετικούς παρονομαστές

Αρχικά, ας μάθουμε πώς να αφαιρούμε κλάσματα με τους ίδιους παρονομαστές. Όλα είναι απλά εδώ. Για να αφαιρέσετε ένα άλλο από ένα κλάσμα, πρέπει να αφαιρέσετε τον αριθμητή του δεύτερου κλάσματος από τον αριθμητή του πρώτου κλάσματος και να αφήσετε τον παρονομαστή τον ίδιο.

Για παράδειγμα, ας βρούμε την τιμή της έκφρασης . Για να λύσετε αυτό το παράδειγμα, είναι απαραίτητο να αφαιρέσετε τον αριθμητή του δεύτερου κλάσματος από τον αριθμητή του πρώτου κλάσματος και να αφήσετε τον παρονομαστή αμετάβλητο. Ας το κάνουμε:

Αυτό το παράδειγμα μπορεί να γίνει εύκολα κατανοητό αν σκεφτούμε μια πίτσα που χωρίζεται σε τέσσερα μέρη. Εάν κόψετε πίτσες από μια πίτσα, θα πάρετε πίτσες:

Παράδειγμα 2Βρείτε την τιμή της έκφρασης.

Και πάλι, από τον αριθμητή του πρώτου κλάσματος, αφαιρέστε τον αριθμητή του δεύτερου κλάσματος και αφήστε τον παρονομαστή αμετάβλητο:

Αυτό το παράδειγμα μπορεί να γίνει εύκολα κατανοητό αν σκεφτούμε μια πίτσα που χωρίζεται σε τρία μέρη. Εάν κόψετε πίτσες από μια πίτσα, θα πάρετε πίτσες:

Παράδειγμα 3Βρείτε την τιμή μιας έκφρασης

Αυτό το παράδειγμα επιλύεται ακριβώς με τον ίδιο τρόπο όπως τα προηγούμενα. Από τον αριθμητή του πρώτου κλάσματος, πρέπει να αφαιρέσετε τους αριθμητές των υπόλοιπων κλασμάτων:

Όπως μπορείτε να δείτε, δεν υπάρχει τίποτα περίπλοκο στην αφαίρεση των κλασμάτων με τους ίδιους παρονομαστές. Αρκεί να κατανοήσουμε τους ακόλουθους κανόνες:

1. Για να αφαιρέσετε ένα άλλο από ένα κλάσμα, πρέπει να αφαιρέσετε τον αριθμητή του δεύτερου κλάσματος από τον αριθμητή του πρώτου κλάσματος και να αφήσετε τον παρονομαστή αμετάβλητο.
2. Εάν η απάντηση αποδείχθηκε ότι ήταν ακατάλληλο κλάσμα, τότε πρέπει να επιλέξετε ολόκληρο το μέρος σε αυτό.

Αφαίρεση κλασμάτων με διαφορετικούς παρονομαστές

Για παράδειγμα, ένα κλάσμα μπορεί να αφαιρεθεί από ένα κλάσμα, αφού αυτά τα κλάσματα έχουν τους ίδιους παρονομαστές. Αλλά ένα κλάσμα δεν μπορεί να αφαιρεθεί από ένα κλάσμα, γιατί αυτά τα κλάσματα έχουν διαφορετικούς παρονομαστές. Σε τέτοιες περιπτώσεις, τα κλάσματα πρέπει να ανάγονται στον ίδιο (κοινό) παρονομαστή.

Ο κοινός παρονομαστής βρίσκεται σύμφωνα με την ίδια αρχή που χρησιμοποιήσαμε όταν προσθέταμε κλάσματα με διαφορετικούς παρονομαστές. Πρώτα απ 'όλα, βρείτε το LCM των παρονομαστών και των δύο κλασμάτων. Στη συνέχεια το LCM διαιρείται με τον παρονομαστή του πρώτου κλάσματος και προκύπτει ο πρώτος πρόσθετος παράγοντας, ο οποίος γράφεται πάνω στο πρώτο κλάσμα. Ομοίως, το LCM διαιρείται με τον παρονομαστή του δεύτερου κλάσματος και προκύπτει ένας δεύτερος πρόσθετος παράγοντας, ο οποίος γράφεται πάνω στο δεύτερο κλάσμα.

Τα κλάσματα στη συνέχεια πολλαπλασιάζονται με τους πρόσθετους συντελεστές τους. Ως αποτέλεσμα αυτών των πράξεων, τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατρέπονται σε κλάσματα που έχουν τους ίδιους παρονομαστές. Και ξέρουμε ήδη πώς να αφαιρούμε τέτοια κλάσματα.

Παράδειγμα 1Βρείτε την τιμή μιας έκφρασης:

Αυτά τα κλάσματα έχουν διαφορετικούς παρονομαστές, επομένως πρέπει να τα φέρετε στον ίδιο (κοινό) παρονομαστή.

Αρχικά, βρίσκουμε το LCM των παρονομαστών και των δύο κλασμάτων. Ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 4. Το ελάχιστο κοινό πολλαπλάσιο αυτών των αριθμών είναι το 12

LCM (3 και 4) = 12

Τώρα πίσω στα κλάσματα και

Ας βρούμε έναν επιπλέον παράγοντα για το πρώτο κλάσμα. Για να γίνει αυτό, διαιρούμε το LCM με τον παρονομαστή του πρώτου κλάσματος. Το LCM είναι ο αριθμός 12 και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3. Διαιρούμε το 12 με το 3, παίρνουμε 4. Γράφουμε τα τέσσερα στο πρώτο κλάσμα:

Το ίδιο κάνουμε και με το δεύτερο κλάσμα. Διαιρούμε το LCM με τον παρονομαστή του δεύτερου κλάσματος. Το LCM είναι ο αριθμός 12 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 4. Διαιρέστε το 12 με το 4, παίρνουμε 3. Γράψτε ένα τριπλό στο δεύτερο κλάσμα:

Τώρα είμαστε όλοι έτοιμοι για αφαίρεση. Απομένει να πολλαπλασιάσουμε τα κλάσματα με τους πρόσθετους συντελεστές τους:

Καταλήξαμε στο συμπέρασμα ότι τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατράπηκαν σε κλάσματα που είχαν τους ίδιους παρονομαστές. Και ξέρουμε ήδη πώς να αφαιρούμε τέτοια κλάσματα. Ας συμπληρώσουμε αυτό το παράδειγμα μέχρι το τέλος:

Πήρε μια απάντηση

Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας μια εικόνα. Αν κόψεις πίτσες από πίτσα, παίρνεις πίτσες.

Αυτή είναι η λεπτομερής έκδοση της λύσης. Όντας στο σχολείο, θα έπρεπε να λύσουμε αυτό το παράδειγμα με πιο σύντομο τρόπο. Μια τέτοια λύση θα μοιάζει με αυτό:

Η αναγωγή των κλασμάτων και σε έναν κοινό παρονομαστή μπορεί επίσης να απεικονιστεί χρησιμοποιώντας μια εικόνα. Φέρνοντας αυτά τα κλάσματα σε έναν κοινό παρονομαστή, παίρνουμε τα κλάσματα και . Αυτά τα κλάσματα θα αντιπροσωπεύονται από τις ίδιες φέτες πίτσας, αλλά αυτή τη φορά θα χωριστούν στα ίδια κλάσματα (ανάγεται στον ίδιο παρονομαστή):

Το πρώτο σχέδιο δείχνει ένα κλάσμα (οκτώ κομμάτια από τα δώδεκα) και η δεύτερη εικόνα δείχνει ένα κλάσμα (τρία κομμάτια από τα δώδεκα). Κόβοντας τρία κομμάτια από οκτώ, παίρνουμε πέντε από τα δώδεκα. Το κλάσμα περιγράφει αυτά τα πέντε κομμάτια.

Παράδειγμα 2Βρείτε την τιμή μιας έκφρασης

Αυτά τα κλάσματα έχουν διαφορετικούς παρονομαστές, επομένως πρέπει πρώτα να τα φέρετε στον ίδιο (κοινό) παρονομαστή.

Βρείτε το LCM των παρονομαστών αυτών των κλασμάτων.

Οι παρονομαστές των κλασμάτων είναι οι αριθμοί 10, 3 και 5. Το ελάχιστο κοινό πολλαπλάσιο αυτών των αριθμών είναι το 30

LCM(10, 3, 5) = 30

Τώρα βρίσκουμε πρόσθετους παράγοντες για κάθε κλάσμα. Για να γίνει αυτό, διαιρούμε το LCM με τον παρονομαστή κάθε κλάσματος.

Ας βρούμε έναν επιπλέον παράγοντα για το πρώτο κλάσμα. Το LCM είναι ο αριθμός 30 και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 10. Διαιρούμε το 30 με το 10, παίρνουμε τον πρώτο πρόσθετο παράγοντα 3. Τον γράφουμε πάνω στο πρώτο κλάσμα:

Τώρα βρίσκουμε έναν πρόσθετο παράγοντα για το δεύτερο κλάσμα. Διαιρέστε το LCM με τον παρονομαστή του δεύτερου κλάσματος. Το LCM είναι ο αριθμός 30 και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 3. Διαιρούμε το 30 με το 3, παίρνουμε τον δεύτερο πρόσθετο παράγοντα 10. Το γράφουμε πάνω στο δεύτερο κλάσμα:

Τώρα βρίσκουμε έναν πρόσθετο παράγοντα για το τρίτο κλάσμα. Διαιρέστε το LCM με τον παρονομαστή του τρίτου κλάσματος. Το LCM είναι ο αριθμός 30 και ο παρονομαστής του τρίτου κλάσματος είναι ο αριθμός 5. Διαιρούμε το 30 με το 5, παίρνουμε τον τρίτο πρόσθετο παράγοντα 6. Το γράφουμε πάνω στο τρίτο κλάσμα:

Τώρα όλα είναι έτοιμα για αφαίρεση. Απομένει να πολλαπλασιάσουμε τα κλάσματα με τους πρόσθετους συντελεστές τους:

Καταλήξαμε στο συμπέρασμα ότι τα κλάσματα που είχαν διαφορετικούς παρονομαστές μετατράπηκαν σε κλάσματα που έχουν τους ίδιους (κοινούς) παρονομαστές. Και ξέρουμε ήδη πώς να αφαιρούμε τέτοια κλάσματα. Ας τελειώσουμε αυτό το παράδειγμα.

Η συνέχεια του παραδείγματος δεν χωράει σε μια γραμμή, οπότε μεταφέρουμε τη συνέχεια στην επόμενη γραμμή. Μην ξεχνάτε το σύμβολο ίσου (=) στη νέα γραμμή:

Η απάντηση αποδείχθηκε σωστό κλάσμα και όλα φαίνονται να μας ταιριάζουν, αλλά είναι πολύ δυσκίνητη και άσχημη. Θα πρέπει να το κάνουμε πιο εύκολο. Τί μπορεί να γίνει? Μπορείτε να μειώσετε αυτό το κλάσμα.

Για να μειώσετε ένα κλάσμα, πρέπει να διαιρέσετε τον αριθμητή και τον παρονομαστή του με (gcd) τους αριθμούς 20 και 30.

Έτσι, βρίσκουμε το GCD των αριθμών 20 και 30:

Τώρα επιστρέφουμε στο παράδειγμά μας και διαιρούμε τον αριθμητή και τον παρονομαστή του κλάσματος με το GCD που βρέθηκε, δηλαδή με το 10

Πήρε μια απάντηση

Πολλαπλασιάζοντας ένα κλάσμα με έναν αριθμό

Για να πολλαπλασιάσετε ένα κλάσμα με έναν αριθμό, πρέπει να πολλαπλασιάσετε τον αριθμητή του δεδομένου κλάσματος με αυτόν τον αριθμό και να αφήσετε τον παρονομαστή ίδιο.

Παράδειγμα 1. Πολλαπλασιάστε το κλάσμα με τον αριθμό 1.

Πολλαπλασιάστε τον αριθμητή του κλάσματος με τον αριθμό 1

Η είσοδος μπορεί να γίνει κατανοητή ως λήψη μισού 1 χρόνου. Για παράδειγμα, αν πάρετε πίτσα 1 φορά, θα πάρετε πίτσα

Από τους νόμους του πολλαπλασιασμού, γνωρίζουμε ότι εάν ο πολλαπλασιαστής και ο πολλαπλασιαστής ανταλλάσσονται, τότε το γινόμενο δεν θα αλλάξει. Εάν η έκφραση γραφτεί ως , τότε το γινόμενο θα εξακολουθεί να είναι ίσο με . Και πάλι, ο κανόνας για τον πολλαπλασιασμό ενός ακέραιου και ενός κλάσματος λειτουργεί:

Αυτή η καταχώρηση μπορεί να γίνει κατανοητή ως λήψη του μισού της μονάδας. Για παράδειγμα, αν υπάρχει 1 ολόκληρη πίτσα και πάρουμε τη μισή, τότε θα έχουμε πίτσα:

Παράδειγμα 2. Βρείτε την τιμή μιας έκφρασης

Πολλαπλασιάστε τον αριθμητή του κλάσματος με το 4

Η απάντηση είναι ένα ακατάλληλο κλάσμα. Ας πάρουμε ένα ολόκληρο μέρος του:

Η έκφραση μπορεί να γίνει κατανοητή ως λήψη δύο τετάρτων 4 φορές. Για παράδειγμα, αν πάρετε πίτσες 4 φορές, θα πάρετε δύο ολόκληρες πίτσες.

Και αν ανταλλάξουμε τον πολλαπλασιαστή και τον πολλαπλασιαστή σε θέσεις, παίρνουμε την έκφραση. Θα είναι επίσης ίσο με 2. Αυτή η έκφραση μπορεί να γίνει κατανοητή ως λήψη δύο πίτσες από τέσσερις ολόκληρες πίτσες:

Πολλαπλασιασμός κλασμάτων

Για να πολλαπλασιάσετε τα κλάσματα, πρέπει να πολλαπλασιάσετε τους αριθμητές και τους παρονομαστές τους. Εάν η απάντηση είναι ένα ακατάλληλο κλάσμα, πρέπει να επιλέξετε ολόκληρο το μέρος σε αυτό.

Παράδειγμα 1Βρείτε την τιμή της έκφρασης.

Πήρε μια απάντηση. Είναι επιθυμητό να μειωθεί δεδομένο κλάσμα. Το κλάσμα μπορεί να μειωθεί κατά 2. Τότε τελική απόφασηθα λάβει την εξής μορφή:

Η έκφραση μπορεί να γίνει κατανοητή σαν να παίρνεις μια πίτσα από μισή πίτσα. Ας πούμε ότι έχουμε μισή πίτσα:

Πώς να πάρετε τα δύο τρίτα από αυτό το μισό; Πρώτα πρέπει να χωρίσετε αυτό το μισό σε τρία ίσα μέρη:

Και πάρτε δύο από αυτά τα τρία κομμάτια:

Θα πάρουμε πίτσα. Θυμηθείτε πώς μοιάζει μια πίτσα χωρισμένη σε τρία μέρη:

Μια φέτα από αυτή την πίτσα και οι δύο φέτες που πήραμε θα έχουν τις ίδιες διαστάσεις:

Με άλλα λόγια, μιλαμεπερίπου στο ίδιο μέγεθος πίτσα. Επομένως, η αξία της έκφρασης είναι

Παράδειγμα 2. Βρείτε την τιμή μιας έκφρασης

Πολλαπλασιάστε τον αριθμητή του πρώτου κλάσματος με τον αριθμητή του δεύτερου κλάσματος και τον παρονομαστή του πρώτου κλάσματος με τον παρονομαστή του δεύτερου κλάσματος:

Η απάντηση είναι ένα ακατάλληλο κλάσμα. Ας πάρουμε ένα ολόκληρο μέρος του:

Παράδειγμα 3Βρείτε την τιμή μιας έκφρασης

Πολλαπλασιάστε τον αριθμητή του πρώτου κλάσματος με τον αριθμητή του δεύτερου κλάσματος και τον παρονομαστή του πρώτου κλάσματος με τον παρονομαστή του δεύτερου κλάσματος:

Η απάντηση αποδείχθηκε σωστό κλάσμα, αλλά θα είναι καλό αν μειωθεί. Για να μειώσετε αυτό το κλάσμα, πρέπει να διαιρέσετε τον αριθμητή και τον παρονομαστή αυτού του κλάσματος με τον μεγαλύτερο κοινό διαιρέτη (GCD) των αριθμών 105 και 450.

Ας βρούμε λοιπόν το GCD των αριθμών 105 και 450:

Τώρα διαιρούμε τον αριθμητή και τον παρονομαστή της απάντησής μας στο GCD που βρήκαμε τώρα, δηλαδή, με το 15

Αναπαράσταση ακέραιου ως κλάσματος

Οποιοσδήποτε ακέραιος αριθμός μπορεί να αναπαρασταθεί ως κλάσμα. Για παράδειγμα, ο αριθμός 5 μπορεί να αναπαρασταθεί ως . Από αυτό, το πέντε δεν θα αλλάξει το νόημά του, αφού η έκφραση σημαίνει "ο αριθμός πέντε διαιρούμενος με ένα", και αυτό, όπως γνωρίζετε, είναι ίσο με πέντε:

Αντίστροφοι αριθμοί

Τώρα θα εξοικειωθούμε με ενδιαφέρον θέμαστα μαθηματικά. Ονομάζεται «αντίστροφοι αριθμοί».

Ορισμός. Αντίστροφη στον αριθμόένα είναι ο αριθμός που, όταν πολλαπλασιαστεί μεένα δίνει μια μονάδα.

Ας αντικαταστήσουμε σε αυτόν τον ορισμό αντί για μια μεταβλητή ένανούμερο 5 και προσπαθήστε να διαβάσετε τον ορισμό:

Αντίστροφη στον αριθμό 5 είναι ο αριθμός που, όταν πολλαπλασιαστεί με 5 δίνει μια μονάδα.

Είναι δυνατόν να βρεθεί ένας αριθμός που πολλαπλασιαζόμενος με το 5 να δίνει ένα; Αποδεικνύεται ότι μπορείτε. Ας παραστήσουμε το πέντε ως κλάσμα:

Στη συνέχεια πολλαπλασιάστε αυτό το κλάσμα από μόνο του, απλώς αλλάξτε τον αριθμητή και τον παρονομαστή. Με άλλα λόγια, ας πολλαπλασιάσουμε το κλάσμα από μόνο του, μόνο ανεστραμμένο:

Ποιο θα είναι το αποτέλεσμα από αυτό; Αν συνεχίσουμε να λύνουμε αυτό το παράδειγμα, θα έχουμε ένα:

Αυτό σημαίνει ότι το αντίστροφο του αριθμού 5 είναι ο αριθμός, αφού όταν το 5 πολλαπλασιαστεί με ένα, προκύπτει ένα.

Το αντίστροφο μπορεί επίσης να βρεθεί για οποιονδήποτε άλλο ακέραιο.

Μπορείτε επίσης να βρείτε το αντίστροφο για οποιοδήποτε άλλο κλάσμα. Για να γίνει αυτό, αρκεί να το αναποδογυρίσετε.

Διαίρεση ενός κλάσματος με έναν αριθμό

Ας πούμε ότι έχουμε μισή πίτσα:

Ας το χωρίσουμε εξίσου στα δύο. Πόσες πίτσες θα πάρει ο καθένας;

Μπορεί να φανεί ότι μετά το χωρισμό της μισής πίτσας, προέκυψαν δύο ίσα κομμάτια, καθένα από τα οποία αποτελεί μια πίτσα. Έτσι όλοι παίρνουν μια πίτσα.

Η διαίρεση των κλασμάτων γίνεται με τη χρήση αντίστροφων. Τα αντίστροφα σάς επιτρέπουν να αντικαταστήσετε τη διαίρεση με πολλαπλασιασμό.

Για να διαιρέσετε ένα κλάσμα με έναν αριθμό, πρέπει να πολλαπλασιάσετε αυτό το κλάσμα με το αντίστροφο του διαιρέτη.

Χρησιμοποιώντας αυτόν τον κανόνα, θα γράψουμε τη διαίρεση της μισής μας πίτσας σε δύο μέρη.

Επομένως, πρέπει να διαιρέσετε το κλάσμα με τον αριθμό 2. Εδώ το μέρισμα είναι κλάσμα και ο διαιρέτης είναι 2.

Για να διαιρέσετε ένα κλάσμα με τον αριθμό 2, πρέπει να πολλαπλασιάσετε αυτό το κλάσμα με το αντίστροφο του διαιρέτη 2. Το αντίστροφο του διαιρέτη 2 είναι ένα κλάσμα. Πρέπει λοιπόν να πολλαπλασιάσετε με

1. Ο κανόνας για την πρόσθεση κλασμάτων με τους ίδιους παρονομαστές:

Παράδειγμα 1:

Παράδειγμα 2:

Κανόνας για την πρόσθεση κλασμάτων με διαφορετικούς παρονομαστές:

Παράδειγμα 1:

Παράδειγμα 2:

Εδώ οι παρονομαστές δεν πολλαπλασιάστηκαν, αλλά λήφθηκε ο λιγότερο κοινός παράγοντας a2.
(Ο παρονομαστής είναι η υψηλότερη δύναμη του 2.)
Πρόσθετος πολλαπλασιαστής για το πρώτο κλάσμα 1, για το δεύτερο α.

2. Ο κανόνας για την αφαίρεση κλασμάτων με ίδιους παρονομαστές:

Κανόνας αφαίρεσης κλασμάτων με διαφορετικούς παρονομαστές:

3. Ο κανόνας για τον πολλαπλασιασμό των συνηθισμένων κλασμάτων:

4. Ο κανόνας για τη διαίρεση των κλασμάτων:

Παράδειγμα:

Κανονικό (απλό) κλάσμα. Ο αριθμητής και ο παρονομαστής ενός κλάσματος.
Σωστό και ακατάλληλο κλάσμα. Μικτός αριθμός.
Ατελές πηλίκο. Ακέραιο και κλασματικό μέρος. Αντίστροφα κλάσματα.Ένα μέρος μιας μονάδας ή πολλά από τα μέρη της ονομάζεται συνηθισμένο ή απλό κλάσμα. Ποσότητα ίσα μέρη, στην οποία διαιρείται η μονάδα, ονομάζεται παρονομαστής και ο αριθμός των μερών που λαμβάνονται ονομάζεται αριθμητής. Το κλάσμα γράφεται ως:

Εδώ 3 είναι ο αριθμητής, 7 είναι ο παρονομαστής.

Αν ο αριθμητής μικρότερο από τον παρονομαστή, τότε καλείται το κλάσμα μικρότερο του 1 κατάλληλο κλάσμα . Αν ο αριθμητής είναι ίσος με τον παρονομαστή, τότε το κλάσμα είναι 1. Αν ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή, τότε το κλάσμα είναι μεγαλύτερο από 1. Και στα δύο πρόσφατες περιπτώσειςτο κλάσμα λέγεται ακατάλληλο. Εάν ο αριθμητής διαιρείται με τον παρονομαστή, τότε αυτό το κλάσμα είναι ίσο με το πηλίκο: 63 / 7 = 9. Εάν η διαίρεση εκτελείται με υπόλοιπο, τότε αυτό το ακατάλληλο κλάσμα μπορεί να αναπαρασταθεί μικτός αριθμός:

Εδώ 9 - ατελές πηλίκο(το ακέραιο μέρος του μικτού αριθμού), το 2 είναι το υπόλοιπο (ο αριθμητής του κλασματικού μέρους), το 7 είναι ο παρονομαστής.
Συχνά είναι απαραίτητο να αποφασίσετε αντίστροφο πρόβλημα – αντιστρέψτε έναν μικτό αριθμόσε κλάσμα. Για να το κάνετε αυτό, πολλαπλασιάστε το ακέραιο μέρος του μικτού αριθμού με τον παρονομαστή και προσθέστε τον αριθμητή του κλασματικού μέρους. Αυτός θα είναι ο αριθμητής ενός συνηθισμένου κλάσματος και ο παρονομαστής παραμένει ο ίδιος.

Τα αντίστροφα είναι δύο κλάσματα των οποίων το γινόμενο είναι 1. Για παράδειγμα, 3/7 και 7/3. 15/1 και 1/15 κ.λπ.

Διαστολή κλάσματος. Αναγωγή κλασμάτων. Σύγκριση κλασμάτων.
Αναγωγή σε κοινό παρονομαστή. Πρόσθεση και αφαίρεσηκλάσματα.
Πολλαπλασιασμός κλασμάτων. Διαίρεση κλασμάτων
Διαστολή κλάσματος.Η τιμή ενός κλάσματος δεν αλλάζει εάν ο αριθμητής και ο παρονομαστής του πολλαπλασιαστούν με τον ίδιο μη μηδενικό αριθμό με επέκταση του κλάσματος.

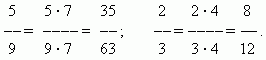
Αναγωγή κλασμάτων. Η τιμή ενός κλάσματος δεν αλλάζει αν ο αριθμητής και ο παρονομαστής του διαιρεθούν με τον ίδιο μη μηδενικό αριθμό.. Αυτός ο μετασχηματισμός ονομάζεταιμείωση του κλάσματος. Για παράδειγμα,

Σύγκριση κλασμάτων.Από δύο κλάσματα με τον ίδιο αριθμητή, το μεγαλύτερο είναι αυτό με τον μικρότερο παρονομαστή:

Από δύο κλάσματα με τους ίδιους παρονομαστές, αυτό με τον μεγαλύτερο αριθμητή είναι μεγαλύτερο:

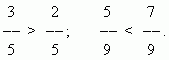
Για να συγκρίνετε κλάσματα που έχουν διαφορετικούς αριθμητές και παρονομαστές, πρέπει να τα επεκτείνετε για να τα φέρετε σε έναν κοινό παρονομαστή.
ΠΑΡΑΔΕΙΓΜΑ Συγκρίνετε δύο κλάσματα:

Ο μετασχηματισμός που χρησιμοποιείται εδώ ονομάζεται αναγωγή κλασμάτων σε κοινό παρονομαστή.
Πρόσθεση και αφαίρεση κλασμάτων.Εάν οι παρονομαστές των κλασμάτων είναι οι ίδιοι, τότε για να προσθέσετε κλάσματα, πρέπει να προσθέσετε τους αριθμητές τους και για να αφαιρέσετε τα κλάσματα, πρέπει να αφαιρέσετε τους αριθμητές τους (με την ίδια σειρά). Το άθροισμα ή η διαφορά που προκύπτει θα είναι ο αριθμητής του αποτελέσματος. ο παρονομαστής θα παραμείνει ο ίδιος. Εάν οι παρονομαστές των κλασμάτων είναι διαφορετικοί, θα πρέπει πρώτα να μειώσετε τα κλάσματα σε έναν κοινό παρονομαστή. Όταν προστεθεί μικτούς αριθμούςΤα ακέραια και τα κλασματικά τους μέρη προστίθενται χωριστά. Κατά την αφαίρεση μικτών αριθμών, σας συνιστούμε να τους μετατρέψετε πρώτα στη μορφή ακατάλληλων κλασμάτων, στη συνέχεια να αφαιρέσετε το ένα από το άλλο και στη συνέχεια να μειώσετε ξανά το αποτέλεσμα, εάν είναι απαραίτητο, στη μορφή μικτού αριθμού.
ΠΑΡΑΔΕΙΓΜΑ

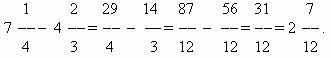
Πολλαπλασιασμός κλασμάτων.Για να πολλαπλασιάσουμε έναν αριθμό με ένα κλάσμα σημαίνει να τον πολλαπλασιάσουμε με τον αριθμητή και να διαιρέσουμε το γινόμενο με τον παρονομαστή. Ως εκ τούτου έχουμε γενικός κανόναςπολλαπλασιάζοντας κλάσματα:για να πολλαπλασιάσετε τα κλάσματα, πρέπει να πολλαπλασιάσετε χωριστά τους αριθμητές και τους παρονομαστές τους και να διαιρέσετε το πρώτο γινόμενο με το δεύτερο.
ΠΑΡΑΔΕΙΓΜΑ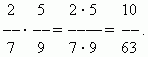
Διαίρεση κλασμάτων. Για να διαιρέσουμε έναν συγκεκριμένο αριθμό με ένα κλάσμα, είναι απαραίτητο να πολλαπλασιάσουμε αυτόν τον αριθμό με τον αντίστροφο. Αυτός ο κανόνας προκύπτει από τον ορισμό της διαίρεσης (βλ. ενότητα «Αριθμητικές πράξεις»).
ΠΑΡΑΔΕΙΓΜΑ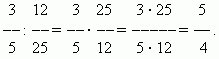

Δεκαδικός. Ολόκληρο μέρος. Δεκαδικό σημείο.
Δεκαδικά. Ιδιότητες δεκαδικών κλασμάτων.
Περιοδικό δεκαδικό. Περίοδος
Δεκαδικόςείναι το αποτέλεσμα της διαίρεσης ενός προς δέκα, εκατό, χίλια κ.λπ. εξαρτήματα. Αυτά τα κλάσματα είναι πολύ βολικά για υπολογισμούς, καθώς βασίζονται στο ίδιο σύστημα θέσης στο οποίο βασίζεται η μέτρηση και η σημειογραφία των ακεραίων. Εξαιτίας αυτού, η σημείωση και οι κανόνες για τους δεκαδικούς αριθμούς είναι στην πραγματικότητα οι ίδιοι με τους ακέραιους αριθμούς. Όταν γράφετε δεκαδικά κλάσματα, δεν χρειάζεται να σημειώσετε τον παρονομαστή, αυτό καθορίζεται από τη θέση που καταλαμβάνει το αντίστοιχο σχήμα. Πρώτη ορθογραφίαολόκληρο μέρος αριθμούς και μετά βάλε στα δεξιάδεκαδικό σημείο. Το πρώτο ψηφίο μετά την υποδιαστολή σημαίνει τον αριθμό των δέκατων, το δεύτερο - τον αριθμό των εκατοστών, το τρίτο - τον αριθμό των χιλιοστών κ.λπ. Καλούνται οι αριθμοί μετά την υποδιαστολήδεκαδικά ψηφία.
ΠΑΡΑΔΕΙΓΜΑ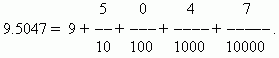
Ένα από τα πλεονεκτήματα των δεκαδικών κλασμάτων είναι ότι μετατρέπονται εύκολα σε συνηθισμένα κλάσματα: ο αριθμός μετά την υποδιαστολή (στην περίπτωσή μας 5047) είναι ο αριθμητής. ο παρονομαστής είναι ίσος n -ο βαθμός 10, όπου n - τον αριθμό των δεκαδικών ψηφίων (στην περίπτωσή μας n = 4):
Εάν το δεκαδικό κλάσμα δεν περιέχει ακέραιο μέρος, τότε ένα μηδέν τοποθετείται πριν από την υποδιαστολή:

Ιδιότητες δεκαδικών κλασμάτων.

1. Το δεκαδικό δεν αλλάζει αν προστεθούν μηδενικά στα δεξιά:

2. Το δεκαδικό κλάσμα δεν αλλάζει εάν αφαιρέσετε τα μηδενικά που βρίσκονται
στο τέλος δεκαδικό κλάσμα :

0.00123000 = 0.00123 .

Προσοχή! Δεν μπορείτε να διαγράψετε μηδενικά που δεν βρίσκονται στο τέλος δεκαδικό!br />

Αυτές οι ιδιότητες σάς επιτρέπουν να πολλαπλασιάσετε και να διαιρέσετε γρήγορα τα δεκαδικά με το 10, το 100, το 1000 και ούτω καθεξής.

Περιοδικό δεκαδικόπεριέχει μια άπειρα επαναλαμβανόμενη ομάδα ψηφίων που ονομάζεται τελεία. Η περίοδος γράφεται σε αγκύλες. Για παράδειγμα, 0.12345123451234512345… = 0.(12345).

ΠΑΡΑΔΕΙΓΜΑ Αν διαιρέσουμε το 47 με το 11, θα έχουμε 4,27272727… = 4.(27).

Πολλαπλασιασμός δεκαδικών αριθμών.
Διαίρεση δεκαδικών.

Πρόσθεση και αφαίρεση δεκαδικών κλασμάτων.Αυτές οι πράξεις εκτελούνται με τον ίδιο τρόπο όπως η πρόσθεση και η αφαίρεση ακεραίων. Είναι απαραίτητο μόνο να γράψετε τα αντίστοιχα δεκαδικά ψηφία το ένα κάτω από το άλλο.
ΠΑΡΑΔΕΙΓΜΑ

Πολλαπλασιασμός δεκαδικών αριθμών.Στο πρώτο βήμα, πολλαπλασιάζουμε τα δεκαδικά κλάσματα ως ακέραιους, χωρίς να λάβουμε υπόψη την υποδιαστολή. Στη συνέχεια εφαρμόζεται ο ακόλουθος κανόνας: ο αριθμός των δεκαδικών ψηφίων στο γινόμενο είναι ίσος με το άθροισμα των δεκαδικών ψηφίων σε όλους τους παράγοντες.
Παρατήρηση: πριν βάλετε την υποδιαστολήΔεν μπορείτε να ρίξετε μηδενικά στο τέλος του προϊόντος!
ΠΑΡΑΔΕΙΓΜΑ

Το άθροισμα των αριθμών των δεκαδικών ψηφίων στους συντελεστές είναι: 3 + 4 = 7. Το άθροισμα των ψηφίων στο γινόμενο είναι 6. Επομένως, πρέπει να προσθέσετε ένα μηδέν στα αριστερά: 0197056 και να βάλετε μια υποδιαστολή μπροστά από αυτό: 0,0197056.
Δεκαδική διαίρεση
Διαιρέστε ένα δεκαδικό με έναν ακέραιο
Αν μέρισμα λιγότερο διαιρέτης , γράφουμε μηδέν στο ακέραιο μέρος του πηλίκου και μετά βάζουμε υποδιαστολή. Στη συνέχεια, μη λαμβάνοντας υπόψη την υποδιαστολή του μερίσματος, προσθέτουμε το επόμενο ψηφίο του κλασματικού μέρους στο ακέραιο μέρος του και συγκρίνουμε πάλι το ακέραιο μέρος του μερίσματος που προκύπτει με τον διαιρέτη. Εάν ο νέος αριθμός είναι και πάλι μικρότερος από τον διαιρέτη, βάλτε ένα ακόμη μηδέν μετά την υποδιαστολή στο πηλίκο και προσθέστε το επόμενο ψηφίο του κλασματικού μέρους του στο ακέραιο μέρος του μερίσματος. Αυτή η διαδικασία επαναλαμβάνεται έως ότου το προκύπτον μέρισμα γίνει μεγαλύτερο από το διαιρέτη. Μετά από αυτό, η διαίρεση εκτελείται όπως για τους ακέραιους αριθμούς. Αν το μέρισμα είναι μεγαλύτερο ή ίσο του διαιρέτη, πρώτα διαιρούμε το ακέραιο μέρος του, γράφουμε το αποτέλεσμα της διαίρεσης ιδιωτικά και βάζουμε υποδιαστολή. Μετά από αυτό, η διαίρεση συνεχίζεται, όπως στην περίπτωση των ακεραίων.
ΠΑΡΑΔΕΙΓΜΑ Διαιρέστε το 1.328 με το 64.
Απόφαση: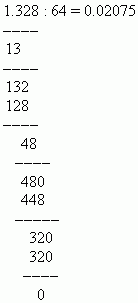
Διαίρεση ενός δεκαδικού κλάσματος με ένα άλλο.
Αρχικά μεταφέρουμε τα δεκαδικά ψηφία στο μέρισμα και τον διαιρέτη με τον αριθμό των δεκαδικών ψηφίων στον διαιρέτη, δηλαδή κάνουμε τον διαιρέτη ακέραιο. Τώρα εκτελούμε τη διαίρεση, όπως στην προηγούμενη περίπτωση.
ΠΑΡΑΔΕΙΓΜΑ Διαιρέστε το 0,04569 με το 0,0006.
Λύση: Μετακινήστε τα δεκαδικά ψηφία 4 θέσεις προς τα δεξιά και διαιρέστε το 456,9 με το 6:

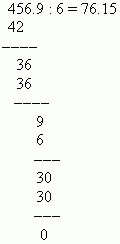
Για να μετατρέψετε ένα δεκαδικό σε κοινό κλάσμα, πρέπει να πάρετε τον αριθμό μετά την υποδιαστολή ως αριθμητή και να πάρετε την nη δύναμη του δέκα ως παρονομαστή (εδώ n είναι ο αριθμός των δεκαδικών ψηφίων). Το μη μηδενικό ακέραιο μέρος διατηρείται στο κοινό κλάσμα. το μηδενικό ακέραιο μέρος παραλείπεται. Για παράδειγμα:
Για να μετατρέψετε ένα κοινό κλάσμα σε δεκαδικό, διαιρέστε τον αριθμητή με τον παρονομαστή σύμφωνα με τους κανόνες διαίρεσης..
ΠΑΡΑΔΕΙΓΜΑ Μετατρέψτε το 5/8 σε δεκαδικό.
Λύση: Διαιρώντας το 5 με το 8 προκύπτει το 0,625. (Ελέγξτε παρακαλώ!).
Στις περισσότερες περιπτώσεις, αυτή η διαδικασία μπορεί να συνεχιστεί επ 'αόριστον. Τότε είναι αδύνατο να μετατραπεί με ακρίβεια ένα συνηθισμένο κλάσμα σε δεκαδικό. Αλλά στην πράξη αυτό δεν απαιτείται ποτέ. Η διαίρεση ματαιώνεται εάν έχουν ήδη ληφθεί τα δεκαδικά ψηφία ενδιαφέροντος.
ΠΑΡΑΔΕΙΓΜΑ Μετατρέψτε το 1/3 σε δεκαδικό.
Λύση: Η διαίρεση 1 με 3 θα είναι άπειρη: 1:3 = 0,3333… .
Ελέγξτε το παρακαλώ!

Πολλαπλασιασμός και διαίρεση κλασμάτων.

Προσοχή!
Υπάρχουν επιπλέον
υλικό στο Ειδικό Τμήμα 555.
Για όσους έντονα "όχι πολύ..."
Και για όσους "πολύ...")

Αυτή η πράξη είναι πολύ πιο ωραία από την πρόσθεση-αφαίρεση! Γιατί είναι πιο εύκολο. Σας υπενθυμίζω: για να πολλαπλασιάσετε ένα κλάσμα με ένα κλάσμα, πρέπει να πολλαπλασιάσετε τους αριθμητές (αυτός θα είναι ο αριθμητής του αποτελέσματος) και οι παρονομαστές (αυτός θα είναι ο παρονομαστής). Αυτό είναι:

Για παράδειγμα:

Όλα είναι εξαιρετικά απλά. Και σε παρακαλώ μην κοιτάς κοινό παρονομαστή! Δεν χρειάζεται εδώ...

Για να διαιρέσετε ένα κλάσμα με ένα κλάσμα, πρέπει να αναστρέψετε δεύτερος(αυτό είναι σημαντικό!) κλάσμα και πολλαπλασιάστε το, δηλ.:

Για παράδειγμα:

Εάν συλληφθεί ο πολλαπλασιασμός ή η διαίρεση με ακέραιους αριθμούς και κλάσματα, δεν πειράζει. Όπως και με την πρόσθεση, κάνουμε ένα κλάσμα από έναν ακέραιο αριθμό με μια μονάδα στον παρονομαστή - και πάμε! Για παράδειγμα:

Στο γυμνάσιο, συχνά πρέπει να ασχοληθείς με τριώροφα (ή και τετραώροφα!) κλάσματα. Για παράδειγμα:

Πώς να φέρετε αυτό το κλάσμα σε μια αξιοπρεπή μορφή; Ναι, πολύ εύκολο! Χρησιμοποιήστε τη διαίρεση σε δύο σημεία:

Αλλά μην ξεχνάτε τη σειρά διαίρεσης! Σε αντίθεση με τον πολλαπλασιασμό, αυτό είναι πολύ σημαντικό εδώ! Φυσικά, δεν θα μπερδεύουμε το 4:2 ή το 2:4. Αλλά σε ένα τριώροφο κλάσμα είναι εύκολο να κάνεις λάθος. Σημειώστε, για παράδειγμα:

Στην πρώτη περίπτωση (έκφραση στα αριστερά):

Στο δεύτερο (έκφραση στα δεξιά):

Νιώθεις τη διαφορά; 4 και 1/9!

Ποια είναι η σειρά διαίρεσης; Ή αγκύλες, ή (όπως εδώ) το μήκος των οριζόντιων παύλων. Αναπτύξτε ένα μάτι. Και αν δεν υπάρχουν αγκύλες ή παύλες, όπως:

μετά διαιρέστε-πολλαπλασιάστε με τη σειρά, από αριστερά προς τα δεξιά!

Και άλλο ένα πολύ απλό και σημαντικό κόλπο. Σε δράσεις με πτυχία θα σου φανεί χρήσιμο! Ας διαιρέσουμε τη μονάδα με οποιοδήποτε κλάσμα, για παράδειγμα, με το 13/15:

Ο πυροβολισμός ανατράπηκε! Και συμβαίνει πάντα. Όταν διαιρούμε το 1 με οποιοδήποτε κλάσμα, το αποτέλεσμα είναι το ίδιο κλάσμα, μόνο ανεστραμμένο.

Αυτές είναι όλες οι ενέργειες με τα κλάσματα. Το πράγμα είναι αρκετά απλό, αλλά δίνει περισσότερα από αρκετά λάθη. Σημείωση πρακτικές συμβουλές, και αυτά (λάθη) θα είναι λιγότερα!

Πρακτικές συμβουλές:

1. Το πιο σημαντικό πράγμα όταν εργάζεστε με κλασματικές εκφράσεις είναι η ακρίβεια και η προσοχή! Δεν είναι κοινές λέξεις, όχι καλές ευχές! Αυτή είναι μια σοβαρή ανάγκη! Κάντε όλους τους υπολογισμούς στις εξετάσεις ως μια ολοκληρωμένη εργασία, με συγκέντρωση και σαφήνεια. Είναι προτιμότερο να γράψετε δύο επιπλέον γραμμές σε ένα προσχέδιο παρά να μπερδεύετε κατά τον υπολογισμό στο κεφάλι σας.

2. Στα παραδείγματα με ΔΙΑΦΟΡΕΤΙΚΟΙ ΤΥΠΟΙκλάσματα - μεταβείτε σε συνηθισμένα κλάσματα.

3. Μειώνουμε όλα τα κλάσματα στο τέλος.

4. Πολυώροφο κλασματικές εκφράσειςανάγουμε σε συνηθισμένες χρησιμοποιώντας διαίρεση μέσω δύο σημείων (ακολουθούμε τη σειρά διαίρεσης!).

5. Χωρίζουμε τη μονάδα σε κλάσμα στο μυαλό μας, απλώς αναποδογυρίζοντας το κλάσμα.

Εδώ είναι οι εργασίες που πρέπει να ολοκληρώσετε. Οι απαντήσεις δίνονται μετά από όλες τις εργασίες. Χρησιμοποιήστε τα υλικά αυτού του θέματος και πρακτικές συμβουλές. Υπολογίστε πόσα παραδείγματα θα μπορούσατε να λύσετε σωστά. Η πρώτη φορά! Χωρίς αριθμομηχανή! Και βγάλτε τα σωστά συμπεράσματα...

Θυμηθείτε τη σωστή απάντηση που λαμβάνεται από τη δεύτερη (ειδικά την τρίτη) φορά - δεν μετράει!Τέτοια είναι η σκληρή ζωή.

Ετσι, επίλυση σε λειτουργία εξέτασης ! Παρεμπιπτόντως, πρόκειται για προετοιμασία για τις εξετάσεις. Λύνουμε ένα παράδειγμα, ελέγχουμε, λύνουμε τα παρακάτω. Αποφασίσαμε τα πάντα - ελέγξαμε ξανά από τον πρώτο έως τον τελευταίο. Μόνο μετάκοιτάξτε τις απαντήσεις.

Υπολογίζω:

Αποφασίσατε;

Ψάχνετε για απαντήσεις που ταιριάζουν με τις δικές σας. Τα έγραψα συγκεκριμένα σε χάλια, μακριά από τον πειρασμό, ας πούμε... Εδώ είναι οι απαντήσεις, γραμμένες με ερωτηματικό.

0; 17/22; 3/4; 2/5; 1; 25.

Και τώρα βγάζουμε συμπεράσματα. Αν όλα πήγαν καλά - χαρούμενος για εσάς! Οι στοιχειώδεις υπολογισμοί με κλάσματα δεν είναι δικό σου πρόβλημα! Μπορεί να κάνει περισσότερα σοβαρά πράγματα. Αν όχι...

Άρα έχετε ένα από τα δύο προβλήματα. Ή και τα δύο ταυτόχρονα.) Έλλειψη γνώσης και (ή) απροσεξία. Αλλά αυτό διαλυτός Προβλήματα.

Αν σας αρέσει αυτό το site...

Παρεμπιπτόντως, έχω μερικές ακόμη ενδιαφέρουσες τοποθεσίες για εσάς.)

Μπορείτε να εξασκηθείτε στην επίλυση παραδειγμάτων και να μάθετε το επίπεδό σας. Δοκιμή με άμεση επαλήθευση. Μάθηση - με ενδιαφέρον!)

μπορείτε να εξοικειωθείτε με συναρτήσεις και παραγώγους.

Ενέργειες με κλάσματα. Σε αυτό το άρθρο, θα αναλύσουμε παραδείγματα, όλα είναι λεπτομερή με επεξηγήσεις. Θα εξετάσουμε κοινά κλάσματα. Στο μέλλον, θα αναλύσουμε τα δεκαδικά. Προτείνω να παρακολουθήσετε ολόκληρο και να μελετήσετε διαδοχικά.

1. Άθροισμα κλασμάτων, διαφορά κλασμάτων.

Κανόνας: όταν προσθέτουμε κλάσματα με ίσους παρονομαστές, το αποτέλεσμα είναι ένα κλάσμα - ο παρονομαστής του οποίου παραμένει ο ίδιος και ο αριθμητής του θα είναι ισούται με το άθροισμααριθμητές κλασμάτων.

Κανόνας: κατά τον υπολογισμό της διαφοράς των κλασμάτων με τους ίδιους παρονομαστές, παίρνουμε ένα κλάσμα - ο παρονομαστής παραμένει ο ίδιος και ο αριθμητής του δεύτερου αφαιρείται από τον αριθμητή του πρώτου κλάσματος.

Τυπική σημειογραφία του αθροίσματος και της διαφοράς των κλασμάτων με ίσους παρονομαστές:

Παραδείγματα (1):

Είναι σαφές ότι όταν δίνονται συνηθισμένα κλάσματα, τότε όλα είναι απλά, αλλά αν αναμειγνύονται; Τίποτα περίπλοκο...

Επιλογή 1- μπορείτε να τα μετατρέψετε σε συνηθισμένα και μετά να τα υπολογίσετε.

Επιλογή 2- μπορείτε να "δουλέψετε" χωριστά με τα ακέραια και τα κλασματικά μέρη.

Παραδείγματα (2):

Περισσότερο:

Και αν η διαφορά των δύο μικτά κλάσματακαι ο αριθμητής του πρώτου κλάσματος θα είναι μικρότερος από τον αριθμητή του δεύτερου; Μπορεί επίσης να γίνει με δύο τρόπους.

Παραδείγματα (3):

* Μεταφράστηκε σε συνηθισμένα κλάσματα, υπολόγισε τη διαφορά, μετέτρεψε το ακατάλληλο κλάσμα που προέκυψε σε μικτό.

* Διαιρέθηκε σε ακέραια και κλασματικά μέρη, πήρε τρία, μετά παρουσιάστηκε το 3 ως το άθροισμα του 2 και του 1, με τη μονάδα να παρουσιάζεται ως 11/11, στη συνέχεια βρέθηκε η διαφορά μεταξύ 11/11 και 7/11 και υπολόγισε το αποτέλεσμα. Το νόημα των παραπάνω μετασχηματισμών είναι να πάρουμε (επιλέξουμε) τη μονάδα και να την παρουσιάσουμε ως κλάσμα με τον παρονομαστή που χρειαζόμαστε, τότε από αυτό το κλάσμα μπορούμε ήδη να αφαιρέσουμε ένα άλλο.

Ενα άλλο παράδειγμα:

Συμπέρασμα: υπάρχει μια καθολική προσέγγιση - για να υπολογίσετε το άθροισμα (διαφορά) μικτών κλασμάτων με ίσους παρονομαστές, μπορούν πάντα να μετατραπούν σε ακατάλληλα και στη συνέχεια να εκτελέσετε την απαραίτητη ενέργεια. Μετά από αυτό, εάν ως αποτέλεσμα πάρουμε ένα ακατάλληλο κλάσμα, το μεταφράζουμε σε μικτό.

Παραπάνω, εξετάσαμε παραδείγματα με κλάσματα που έχουν ίσους παρονομαστές. Τι γίνεται αν οι παρονομαστές διαφέρουν; Στην περίπτωση αυτή, τα κλάσματα μειώνονται στον ίδιο παρονομαστή και εκτελείται η καθορισμένη ενέργεια. Για την αλλαγή (μετατροπή) ενός κλάσματος, χρησιμοποιείται η κύρια ιδιότητα του κλάσματος.

Εξετάστε απλά παραδείγματα:

Σε αυτά τα παραδείγματα, βλέπουμε αμέσως πώς ένα από τα κλάσματα μπορεί να μετατραπεί για να πάρει ίσους παρονομαστές.

Εάν ορίσουμε τρόπους μείωσης των κλασμάτων σε έναν παρονομαστή, τότε αυτός θα ονομάζεται ΜΕΘΟΔΟΣ ΠΡΩΤΗ.

Δηλαδή, αμέσως όταν "αξιολογείτε" το κλάσμα, πρέπει να καταλάβετε εάν μια τέτοια προσέγγιση θα λειτουργήσει - ελέγχουμε αν ο μεγαλύτερος παρονομαστής διαιρείται με τον μικρότερο. Και αν διαιρεθεί, τότε εκτελούμε τον μετασχηματισμό - πολλαπλασιάζουμε τον αριθμητή και τον παρονομαστή έτσι ώστε οι παρονομαστές και των δύο κλασμάτων να γίνουν ίσοι.

Δείτε τώρα αυτά τα παραδείγματα:

Αυτή η προσέγγιση δεν ισχύει για αυτούς. Υπάρχουν άλλοι τρόποι για να μειώσετε τα κλάσματα σε έναν κοινό παρονομαστή, εξετάστε τους.

Μέθοδος ΔΕΥΤΕΡΗ.

Πολλαπλασιάστε τον αριθμητή και τον παρονομαστή του πρώτου κλάσματος με τον παρονομαστή του δεύτερου και τον αριθμητή και τον παρονομαστή του δεύτερου κλάσματος με τον παρονομαστή του πρώτου:

*Μάλιστα, φέρνουμε τα κλάσματα στη μορφή όταν οι παρονομαστές γίνονται ίσοι. Στη συνέχεια, χρησιμοποιούμε τον κανόνα της προσθήκης δειλά με ίσους παρονομαστές.

Παράδειγμα:

*Αυτή η μέθοδος μπορεί να ονομαστεί καθολική και λειτουργεί πάντα. Το μόνο αρνητικό είναι ότι μετά τους υπολογισμούς, μπορεί να προκύψει ένα κλάσμα που θα πρέπει να μειωθεί περαιτέρω.

Εξετάστε ένα παράδειγμα:

Φαίνεται ότι ο αριθμητής και ο παρονομαστής διαιρούνται με το 5:

Μέθοδος ΤΡΙΤΗ.

Βρείτε το ελάχιστο κοινό πολλαπλάσιο (LCM) των παρονομαστών. Αυτός θα είναι ο κοινός παρονομαστής. Ποιος είναι αυτός ο αριθμός; Αυτός είναι ο μικρότερος φυσικός αριθμός που διαιρείται με κάθε έναν από τους αριθμούς.

Κοιτάξτε, εδώ είναι δύο αριθμοί: 3 και 4, υπάρχουν πολλοί αριθμοί που διαιρούνται με αυτούς - αυτοί είναι 12, 24, 36, ... Ο μικρότερος από αυτούς είναι το 12. Ή το 6 και το 15, το 30, το 60, το 90 είναι διαιρείται με αυτά .... Τουλάχιστον 30. Ερώτηση - πώς να προσδιορίσετε αυτό το λιγότερο κοινό πολλαπλάσιο;

Υπάρχει ένας σαφής αλγόριθμος, αλλά συχνά αυτό μπορεί να γίνει αμέσως χωρίς υπολογισμούς. Για παράδειγμα, σύμφωνα με τα παραπάνω παραδείγματα (3 και 4, 6 και 15), δεν χρειάζεται αλγόριθμος, πήραμε μεγάλους αριθμούς (4 και 15), τους διπλασιάσαμε και είδαμε ότι διαιρούνται με τον δεύτερο αριθμό, αλλά ζεύγη αριθμών μπορεί να είναι άλλα, όπως 51 και 119.

Αλγόριθμος. Για να προσδιορίσετε το ελάχιστο κοινό πολλαπλάσιο πολλών αριθμών, πρέπει:

- επεκτείνετε κάθε έναν από τους αριθμούς σε ΑΠΛΟΙ πολλαπλασιαστές

- γράψτε την αποσύνθεση των ΜΕΓΑΛΥΤΕΡΩΝ από αυτά

- πολλαπλασιάστε το με τους συντελεστές που λείπουν άλλων αριθμών

Εξετάστε παραδείγματα:

50 και 60 50 = 2∙5∙5 60 = 2∙2∙3∙5

σε αποσύνθεση περισσότερολείπει ένα πέντε

=> LCM(50,60) = 2∙2∙3∙5∙5 = 300

48 και 72 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

στην επέκταση μεγαλύτερου αριθμού λείπουν δύο και τρία

=> LCM(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Ελάχιστο κοινό πολλαπλάσιο του δύο πρώτοι αριθμοίίσο με το γινόμενο τους

Ερώτηση! Και γιατί είναι χρήσιμο να βρείτε το λιγότερο κοινό πολλαπλάσιο, επειδή μπορείτε να χρησιμοποιήσετε τη δεύτερη μέθοδο και απλά να μειώσετε το κλάσμα που προκύπτει; Ναι, μπορείτε, αλλά δεν είναι πάντα βολικό. Δείτε ποιος θα είναι ο παρονομαστής για τους αριθμούς 48 και 72 αν απλώς τους πολλαπλασιάσετε 48∙72 = 3456. Συμφωνήστε ότι είναι πιο ευχάριστο να δουλεύετε με μικρότερους αριθμούς.

Εξετάστε παραδείγματα:

*51 = 3∙17 119 = 7∙17

στην επέκταση ενός μεγαλύτερου αριθμού λείπει ένα τριπλό

=> LCM(51.119) = 3∙7∙17

Και τώρα εφαρμόζουμε την πρώτη μέθοδο:

* Κοιτάξτε τη διαφορά στους υπολογισμούς, στην πρώτη περίπτωση υπάρχει ένα ελάχιστο από αυτά και στη δεύτερη πρέπει να εργαστείτε ξεχωριστά σε ένα κομμάτι χαρτί και ακόμη και το κλάσμα που πήρατε πρέπει να μειωθεί. Η εύρεση του LCM απλοποιεί σημαντικά την εργασία.

Περισσότερα παραδείγματα:

* Στο δεύτερο παράδειγμα είναι ξεκάθαρο ότι μικρότερος αριθμός, το οποίο διαιρείται με το 40 και το 60 είναι ίσο με 120.

ΣΥΝΟΛΟ! ΓΕΝΙΚΟΣ ΑΛΓΟΡΙΘΜΟΣ ΥΠΟΛΟΓΙΣΜΟΥ!

- φέρνουμε κλάσματα στα συνηθισμένα, αν υπάρχει ακέραιο μέρος.

- φέρνουμε τα κλάσματα σε έναν κοινό παρονομαστή (πρώτα κοιτάμε να δούμε αν ο ένας παρονομαστής διαιρείται με τον άλλον, αν διαιρείται, μετά πολλαπλασιάζουμε τον αριθμητή και τον παρονομαστή αυτού του άλλου κλάσματος, αν δεν διαιρείται ενεργούμε μέσω του άλλου μεθόδους που αναφέρονται παραπάνω).

- έχοντας λάβει κλάσματα με ίσους παρονομαστές, εκτελούμε ενέργειες (πρόσθεση, αφαίρεση).

- αν χρειαστεί, μειώνουμε το αποτέλεσμα.

- εάν είναι απαραίτητο, επιλέξτε ολόκληρο το τμήμα.

2. Γινόμενο κλασμάτων.

Ο κανόνας είναι απλός. Κατά τον πολλαπλασιασμό των κλασμάτων, οι αριθμητές και οι παρονομαστές τους πολλαπλασιάζονται:

Παραδείγματα:

Ανάλυση της εργασίας Νο. 1 με θέμα: "Ενέργειες με κλάσματα: πολλαπλασιασμός και αφαίρεση, επιλογή ακέραιου μέρους από ακατάλληλο κλάσμα, αντίστροφες πράξεις"

Πρόσθετα υλικά
Αγαπητοί χρήστες, μην ξεχάσετε να αφήσετε τα σχόλια, τα σχόλια, τις προτάσεις σας! Όλα τα υλικά ελέγχονται από ένα πρόγραμμα προστασίας από ιούς.

Διδακτικά βοηθήματα και προσομοιωτές στο ηλεκτρονικό κατάστημα "Integral" για την 9η τάξη
Συνδυαστική και θεωρία πιθανοτήτων Εξισώσεις και ανισώσεις

Παιδιά, η εργασία νούμερο 1 καλύπτει θέματα που καλύπτονται κυρίως στις τάξεις 5-6.

Για σωστή απόφαση δοθείσα εργασίααπαιτούμενη δεξιότητα:

• εργασία με απλά και δεκαδικά κλάσματα,
• ΜΕΤΑΦΟΡΑ απλά κλάσματασε δεκαδικά ψηφία και αντίστροφα
• αύξηση αριθμών σε ακέραια δύναμη
• καθώς και κατανόηση των εννοιών των ρητών και των πραγματικών αριθμών.

Μαθήματα που θα σας βοηθήσουν να προετοιμαστείτε για αυτήν την εργασία:

1. Πρόσθεση δεκαδικών κλασμάτων, παραδείγματα.
2. Πρόσθεση φυσικών αριθμών, παραδείγματα.
3. Ιδιότητες αφαίρεσης αριθμών, παραδείγματα.
4. Αφαίρεση δεκαδικών κλασμάτων: κανόνες και παραδείγματα.
5. Πρόσθεση και αφαίρεση αρνητικών αριθμών, κανόνων και παραδειγμάτων.
6. Αναλογίες και σχέσεις.
7. Πολλαπλασιασμός δεκαδικών κλασμάτων, παραδείγματα.
8. Πρόσθεση και αφαίρεση κλασμάτων, παραδείγματα.
9. Πολλαπλασιασμός και διαίρεση κλασμάτων, παραδείγματα.
10. Αύξηση σε ακέραιο αριθμό, παραδείγματα - σύντομα.

Ας ρίξουμε μια πιο προσεκτική ματιά σε παραδείγματα εργασιών που μπορεί να αντιμετωπίσετε.

Παράδειγμα 1
ΣΤΟ αυτό το παράδειγμαθα χρειαστείτε τη δυνατότητα να πολλαπλασιάσετε και να αφαιρέσετε κλάσματα, να επιλέξετε ολόκληρο το τμήμα από ένα ακατάλληλο κλάσμα και επίσης να εκτελέσετε την αντίστροφη πράξη.
Βρείτε αξία επόμενη έκφραση: $1\frac(2)(5)*2\frac(2)(3)-1\frac(2)(3)*3\frac(1)(2)$.

Απόφαση.
Παιδιά, ας χωρίσουμε τη λύση σε διάφορες ενέργειες. Το πρώτο πράγμα που γνωρίζουμε είναι ότι δεν μπορούμε να πολλαπλασιάσουμε κλάσματα με ένα ακέραιο μέρος. Άρα, πρέπει να μετατρέψουμε κάθε κλάσμα σε ακατάλληλο κλάσμα.
1. Θυμηθείτε τον κανόνα για τη μετατροπή σε ακατάλληλο κλάσμα: για να λάβετε τον αριθμητή, το ολόκληρο μέρος πρέπει να πολλαπλασιαστεί με τον παρονομαστή και ο αριθμητής του αρχικού κλάσματος πρέπει να προστεθεί στον αριθμό που προκύπτει. Ο παρονομαστής παραμένει ο ίδιος, ο αριθμητής είναι πάντα μεγαλύτερος από τον παρονομαστή:
$1\frac(2)(5)=\frac(1*5+2)(5)=\frac(7)(5)$.
Ας εκτελέσουμε παρόμοιες πράξεις για τα υπόλοιπα κλάσματα:
$\frac(7)(5)*\frac(2*3+2)(3)-\frac(1*3+2)(3)*\frac(3*2+1)(2)=\ frac(7)(5)*\frac(8)(3)-\frac(5)(3)*\frac(7)(2)$.

2. Όλοι θυμούνται πολύ καλά ότι ο πολλαπλασιασμός γίνεται πριν από την πρόσθεση και την αφαίρεση. Στη συνέχεια, πρέπει να θυμόμαστε τον κανόνα για τον πολλαπλασιασμό δύο κλασμάτων, πολλαπλασιάζουμε τον αριθμητή με τον αριθμητή, τον παρονομαστή με τον παρονομαστή:
$\frac(7)(5)*\frac(8)(3)-\frac(5)(3)*\frac(7)(2)=\frac(56)(15)-\frac(35 )(6)$.

3. Πρέπει να αφαιρέσουμε δύο κλάσματα. Θυμηθείτε ότι κατά την πρόσθεση και την αφαίρεση, πρέπει πρώτα να βρείτε τον κοινό παρονομαστή δύο κλασμάτων, δηλαδή το λιγότερο κοινό πολλαπλάσιο. Έχουμε δύο παρονομαστές - τους αριθμούς 15 και 6. Για αυτούς τους δύο αριθμούς, το λιγότερο κοινό πολλαπλάσιο θα είναι ο αριθμός 30.
Εάν πολλαπλασιάσετε τον αριθμητή και τον παρονομαστή με τον ίδιο αριθμό, τότε η τιμή του κλάσματος δεν θα αλλάξει.
$\frac(56)(15)-\frac(35)(6)=\frac(56*2)(15*2)-\frac(35*5)(6*5)=\frac(112) (30)-\frac(175)(30)=-\frac(63)(30)$.

4. Πρέπει να μεταφράσουμε κλάσμασε δεκαδικό, γιατί στο φύλλο απαντήσεων του OGE, μπορούμε να γράψουμε τους αριθμούς σε δεκαδική μορφή.
Επιλέγουμε το ακέραιο μέρος και μετά μειώνουμε το κλάσμα.
$-\frac(63)(30)=-2\frac(3)(30)=-2\frac(1)(10)=-2,1$.

Ας ξαναγράψουμε τη λύση:
$1\frac(2)(5)*2\frac(2)(3)-1\frac(2)(3)*3\frac(1)(2)=\frac(1*5+2)( 5)*\frac(2*3+2)(3)-\frac(1*3+2)(3)*\frac(3*2+1)(2)=\frac(7)(5) *\frac(8)(3)-\frac(5)(3)*\frac(7)(2)=$ $=\frac(56)(15)-\frac(35)(6)=\ frac(56*2)(15*2)-\frac(35*5)(6*5)=\frac(112)(30)-\frac(175)(30)=-\frac(63)( 30)=-2\frac(3)(30)=-2\frac(1)(10)=-2,1$.
Απάντηση: -2,1$.

Παράδειγμα 2
Υπολογίστε την τιμή της έκφρασης $0,007*0,00007*700$.

Απόφαση.
Σε αυτό το παράδειγμα, μπορούμε να ενεργήσουμε με δύο τρόπους: 1) να πολλαπλασιάσουμε όλους τους αριθμούς "άμεσα". 2) χρησιμοποιήστε τις γνώσεις του θέματος της αύξησης σε ακέραιο βαθμό.

1. Το πρώτο πράγμα που πρέπει να προσέξετε είναι ότι σε κάθε αριθμό εμφανίζεται ο αριθμός 7. Αυτό έγινε για κάποιο λόγο. Ας προσπαθήσουμε να απλοποιήσουμε τους παρουσιαζόμενους κλασματικούς αριθμούς. Πώς μπορείτε να αντιπροσωπεύσετε τον αριθμό 0,007 ως προϊόν; $0,007=0,001*$7.

Μην φοβάστε να απλοποιήσετε τους κλασματικούς αριθμούς. Αν στην αρχή κλασματικός αριθμόςυπάρχουν όλα τα μηδενικά και αυτό το κλάσμα τελειώνει με έναν ορισμένο αριθμό, τότε μπορεί πάντα να αναπαρασταθεί ως γινόμενο.
Για παράδειγμα: $0,0256=0,0001*256$; $0,00008=0,00001*8$; $0,3562=0,0001*3562$.
Το κύριο πράγμα είναι να διατηρήσετε τον αριθμό των ψηφίων στο προκύπτον κλάσμα.
$0,007*0,00007*700=0,001*7*0,00001*7*7*100$.

2. Στη συνέχεια, χρειαζόμαστε γνώση και ικανότητα να ανεβάζουμε αριθμούς σε ακέραια δύναμη.
Αν μας δοθεί ένα κλάσμα στο οποίο όλα τα μηδενικά και τελειώνει με ένα, τότε μπορεί πάντα να αναπαρασταθεί ως ο αριθμός 10 στο αρνητικό βαθμό. Επιπλέον, ο αριθμός των μηδενικών πριν από τη μονάδα θα είναι δύναμη του δέκα. Ας ρίξουμε μια πιο προσεκτική ματιά στους αριθμούς στο παράδειγμά μας. $0,001=10^(-3)$, υπάρχουν τρία μηδενικά πριν από τη μονάδα, οπότε τα τρία θα είναι η δύναμη του δέκα, απλά μην ξεχάσετε να βάλετε ένα μείον.
$0,00001=10^(-5)$, υπάρχουν πέντε μηδενικά πριν από το ένα, άρα πέντε θα είναι η δύναμη του δέκα.

Μετά από μετασχηματισμούς, παίρνουμε: $0,001*7*0,00001*7*7*100=10^(-3)*7*10^(-5)*7*7*100$.

3. Χρειάζεται μόνο να μετατρέψουμε τον αριθμό 100 ως αριθμό σε δύναμη. Εάν ένας αριθμός έχει μια μονάδα στην πρώτη θέση και όλα τα άλλα ψηφία είναι μηδέν, τότε οποιοσδήποτε τέτοιος αριθμός μπορεί να αναπαρασταθεί ως δύναμη του 10 και η ισχύς των δεκάδων θα συμπίπτει με τον αριθμό των μηδενικών.
Για παράδειγμα: $10000=10^4$; $1000000=10^6$.
Λαμβάνουμε: $10^(-3)*7*10^(-5)*7*7*10^2=7*7*7*10^(-3)*10^(-5)*10^2 $ .
Με ποια σειρά θα πολλαπλασιάσουμε τους αριθμούς που προκύπτουν δεν έχει σημασία. Όταν πολλαπλασιάζουμε αριθμούς με ακέραιο εκθέτη και την ίδια βάση- η βάση του βαθμού παραμένει η ίδια και οι εκθέτες προστίθενται.
$7*7*7*10^{-3}*10^{-5}*10^2=243*{10}^{-3-5+2}=243*10^{-6}$.

4. Απομένει να εκτελέσετε τη λειτουργία, το αντίστροφο του σημείου δύο. Στη δύναμη του δέκα, έχουμε -6, που σημαίνει ότι ο αριθμός θα είναι κλασματικός, αφού μείον - θα υπάρχουν έξι μηδενικά στον αριθμό μας.
$243*10^{-6}=243*0,000001=0,000243$.

Ας γράψουμε ξανά τη λύση: $0,007*0,00007*700=0,001*7*0,00001*7*7*100=10^(-3)*7*10^(-5)*7*7*10^2 =$ $ =7*7*7*10^(-3)*10^(-5)*10^2=243*10^(-3-5+2)=243*10^(-6)= 243*0,000001 = 0,000243 $.
Απάντηση: 0,000243 $.

Παράδειγμα 3
Βρείτε την τιμή της έκφρασης: $6,3*1,8-3,6*2,1$.

Απόφαση.
Αυτό το παράδειγμα μπορεί να λυθεί "στο μέτωπο" εάν είστε καλοί στον πολλαπλασιασμό κλασματικών αριθμών σε μια στήλη. Δεν θα θεωρήσουμε αυτό το παράδειγμα «στο μέτωπο», αλλά θα δώσουμε άλλες δύο λύσεις.

Μέθοδος 1. Εάν δεν είστε πολύ καλοί στον πολλαπλασιασμό των κλασματικών αριθμών σε μια στήλη, τότε μπορείτε να πολλαπλασιάσετε την αρχική έκφραση επί εκατό, αλλά το πιο σημαντικό, τότε μην ξεχάσετε να διαιρέσετε ξανά με το εκατό.
$\frac((6,3*1,8-3,6*2,1)*100)(100)=\frac(63*18-36*21)(100)=\frac(1134-756) (100)=\frac(378 ) (100) $.
Ας διαιρέσουμε τον αριθμό που προκύπτει με το 100, κάτι που είναι αρκετά εύκολο, αφού έχουμε δύο μηδενικά, τότε η υποδιαστολή του κλασματικού αριθμού θα μετατοπίσει 2 ψηφία από τα δεξιά προς τα αριστερά.
$\frac(378)(100)=3,78 $.

Μέθοδος 2. Μπορείτε να δείτε ότι οι αρχικοί αριθμοί έχουν τους ίδιους παράγοντες, δηλαδή, καθένας από τους παρουσιαζόμενους αριθμούς πρέπει να παριστάνεται ως γινόμενο ενός ακέραιου και ενός κλάσματος.
$6,3=7*0,9$.
$1,8=6*0,3$.
$3,6=6*0,6$.
$2,1=7*0,3$.
6,3$*1,8-3,6*2,1=7*0,9*6*0,3-6*0,6*7*0,3=42*0,27-42*0, 18=$=4*(0,27-0,18)=42*0,09=\ frac(42*9)(100)=\frac(378)(100)=3,78$.
Η επιλογή της λύσης εξαρτάται μόνο από τις προτιμήσεις σας.

Παράδειγμα 4
Γράψτε τους αριθμούς των αληθινών ισοτήτων:
1) $2*\frac(1)(3)-\frac(1)(4)=\frac(1)(6)$.
2) $\frac( \frac(11)(14))(3\frac(1)(7))=0,25$.
3) $1,75-2\frac(1)(3)=-\frac(7)(12)$.
4) $\frac(1,6)(\frac(\frac(2)(3))(\frac(5)(6)))=4$.

Απόφαση.
Δεν έχουμε άλλη επιλογή από το να ελέγξουμε κάθε έκφραση.

1) Σε αυτό το παράδειγμα, πρέπει να θυμόμαστε ότι ο πολλαπλασιασμός ενός ακέραιου με ένα κλάσμα δεν είναι το ίδιο πράγμα με ένα κλάσμα στο οποίο επισημαίνεται το ακέραιο μέρος. Ας λύσουμε αυτό το παράδειγμα.
$2*\frac(1)(3)-\frac(1)(4)=\frac(2)(1)*\frac(1)(3)-\frac(1)(4)=\frac( 2)(3)-\frac(1)(4)=\frac(2*4)(3*4)-\frac(1*3)(4*3)=\frac(8)(12)- \frac(3)(12)=\frac(5)(12)$.
Διαπιστώσαμε ότι η παρουσιαζόμενη ισότητα δεν είναι αληθινή.

2) Πρώτα απ 'όλα, πρέπει να απαλλαγείτε από το ακέραιο μέρος και στη συνέχεια να χρησιμοποιήσετε τον κανόνα για τη διαίρεση των κλασμάτων. $\frac(\frac(11)(14))(3\frac(1)(7))=\frac(\frac(11)(14))(\frac(3*7+1)(7) )=\frac(\frac(11)(14))(\frac(22)(7))=\frac(11)(14)*\frac(7)(22)$.
Τώρα μπορούμε να χρησιμοποιήσουμε τον κανόνα μείωσης κλασμάτων.
$\frac(11)(14)*\frac(7)(22)=\frac(1)(2)*\frac(1)(2)=\frac(1)(4)$.
Απομένει μόνο να μετατρέψουμε το κλάσμα που προκύπτει σε δεκαδικό.
$\frac(1)(4)=0,25$.
Έχουμε τη σωστή ισορροπία.

3) Σε αυτό το παράδειγμα, για αρχή, πρέπει να μετατρέψουμε το δεκαδικό κλάσμα σε κοινό. $1,75=1 \frac(75)(100)=1\frac(3)(4)$.
Τώρα ας απαλλαγούμε από το ακέραιο μέρος και ας πάρουμε ένα ακατάλληλο κλάσμα: $1\frac(3)(4)-2\frac(1)(3)=\frac(7)(4)-\frac(7)(3 )$.
Αφαιρέστε δύο κλάσματα: $\frac(7)(4)-\frac(7)(3)=\frac(21)(12)-\frac(28)(12)=-\frac(7)(12 ) $.
Έχουμε τη σωστή ισορροπία.

Ας ξαναγράψουμε τη λύση:
$1,75-2\frac(1)(3)=1\frac(3)(4)-2\frac(1)(3)=\frac(7)(4)-\frac(7)(3)= \frac(21)(12)-\frac(28)(12)=-\frac(7)(12)$.

4) Και πάλι, ας περάσουμε από το δεκαδικό στο συνηθισμένο.
$1,6=1\frac(6)(10)=\frac(16)(10)$.
Θυμόμαστε καλά ότι η πρώτη ενέργεια εκτελείται σε παρένθεση.
$\frac(\frac(2)(3))(\frac(5)(6))=\frac(2)(3)*\frac(6)(5)=\frac(2)(1) *\frac(2)(5)=\frac(4)(5)$.
Ας διαιρέσουμε έξω από τις αγκύλες: $\frac(\frac(16)(10))(\frac(4)(5))=\frac(16)(10)*\frac(5)(4)=\frac ( 4)(2)*\frac(1)(1)=2$.
Βρήκαμε ότι η αρχική ισότητα είναι λάθος.
Απάντηση: 23.

Παράδειγμα 5
Βρείτε το νόημα των εκφράσεων. Σε απάντηση, υποδείξτε τη μεγαλύτερη από τις τιμές που βρέθηκαν.
1) $1,8-\frac(3)(5)$.
2) $\frac(1\frac(1)(3))(\frac(1)(6))$.
3) $\frac(0,8+0,3)(1,2)$.
Απόφαση.

1) Ας περάσουμε στο δεκαδικό κλάσμα.
$1,8-\frac(3)(5)=1,8-0,6=1,2$.

2) Ας προχωρήσουμε στο ακατάλληλο κλάσμα και ας κάνουμε τη διαίρεση των κλασμάτων. $\frac(1\frac(1)(3))(\frac(1)(6))=\frac(\frac(4)(3))(\frac(1)(6))=\frac (4)(3)*\frac(6)(1)=\frac(4)(1)*2=8$.

3) Εκτελέστε πρόσθεση στους αριθμητές του κλάσματος. $\frac(0,8+0,3)(1,2)=\frac(1,1)(1,2)=\frac(1,1*10)(1,2*0)=\frac (11)(12)$.
Απομένει να επιλέξουμε τη μεγαλύτερη λύση, προφανώς, θα είναι 8.
Απάντηση: 8.

Αλεξάντερ Σαμπαλίν