Ο κανόνας λέει ότι αν οι συναρτήσεις φά(Χ) και σολ(Χ) έχουν το ακόλουθο σύνολο προϋποθέσεων:

τότε υπάρχει . Επιπλέον, το θεώρημα ισχύει και για άλλες βάσεις (η απόδειξη θα δοθεί για την υποδεικνυόμενη).

Ιστορία

Μια μέθοδος για την αποκάλυψη αυτού του είδους της αβεβαιότητας δημοσιεύτηκε από τον Lopital στο έργο του "Analysis of infinitesimals", που δημοσιεύτηκε το έτος. Στον πρόλογο αυτού του έργου, ο Lopital επισημαίνει ότι χρησιμοποίησε τις ανακαλύψεις του Leibniz και των αδελφών Bernoulli χωρίς κανένα δισταγμό και «δεν έχει τίποτα εναντίον τους να δείχνουν τα πνευματικά τους δικαιώματα σε ό,τι θέλουν». Ο Johann Bernoulli διεκδίκησε ολόκληρο το έργο του L'Hospital, και συγκεκριμένα, μετά το θάνατο του L'Hospital, δημοσίευσε ένα έργο με τον αξιοσημείωτο τίτλο "Βελτίωση της μεθόδου μου που δημοσιεύτηκε στο Infinitesimal Analysis για τον προσδιορισμό της τιμής ενός κλάσματος, του αριθμητή και του παρονομαστή εκ των οποίων μερικές φορές εξαφανίζονται», .

Απόδειξη

Η αναλογία των απειροελάχιστων

Ας αποδείξουμε το θεώρημα για την περίπτωση που τα όρια των συναρτήσεων είναι ίσα με μηδέν (η λεγόμενη αβεβαιότητα της μορφής ).

Αφού εξετάζουμε τις συναρτήσεις φάκαι σολμόνο στη δεξιά τρυπημένη ημιγειτονιά του σημείου ένα, μπορούμε συνεχώς να τα επαναπροσδιορίζουμε σε αυτό το σημείο: ας φά(ένα) = σολ(ένα) = 0 . Ας πάρουμε μερικά Χαπό την υπό εξέταση ημιγειτονιά και εφαρμόστε το θεώρημα Cauchy στο τμήμα. Με αυτό το θεώρημα παίρνουμε:

,

αλλά φά(ένα) = σολ(ένα) = 0 , να γιατί .

src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> για το όριο τέλους και src="/pictures/wiki/files/101/e8b2f2b8861947c8861947c8861947c8861947c8861947c8861947c8861947c8861947c. ,

που είναι ο ορισμός του ορίου του λόγου των συναρτήσεων.

Η αναλογία του απείρως μεγάλου

Ας αποδείξουμε το θεώρημα για τις αβεβαιότητες της μορφής .

Έστω, για αρχή, το όριο του λόγου των παραγώγων είναι πεπερασμένο και ίσο με ΕΝΑ. Στη συνέχεια, ενώ αγωνιζόταν Χπρος την έναστα δεξιά, αυτή η σχέση μπορεί να γραφτεί ως ΕΝΑ+ α , όπου α - (1). Ας γράψουμε αυτή τη συνθήκη:

.

Ας φτιάξουμε tαπό το τμήμα και εφαρμόστε το θεώρημα Cauchy σε όλα Χαπό το τμήμα:

, που μπορεί να οδηγήσει σε επόμενο είδος: .

Για Χ, αρκετά κοντά σε ένα, η έκφραση έχει νόημα. όριο του πρώτου παράγοντα της δεξιάς πλευράς ίσο με ένα(επειδή φά(t) και σολ(t) είναι σταθερές και φά(Χ) και σολ(Χ) τείνουν στο άπειρο). Επομένως, αυτός ο παράγοντας είναι ίσος με 1 + β, όπου το β είναι μια απειροελάχιστη συνάρτηση ως Χπρος την έναστα δεξιά. Γράφουμε τον ορισμό αυτού του γεγονότος, χρησιμοποιώντας την ίδια τιμή όπως στον ορισμό για το α:

.

Βρήκαμε ότι ο λόγος των συναρτήσεων μπορεί να αναπαρασταθεί με τη μορφή (1 + β)( ΕΝΑ+ α) , και . Για κάθε δεδομένο, μπορεί κανείς να βρει τέτοιο ώστε το μέτρο της διαφοράς μεταξύ των αναλογιών των συναρτήσεων και ΕΝΑήταν μικρότερο, πράγμα που σημαίνει ότι το όριο του λόγου των συναρτήσεων είναι πραγματικά ίσο με ΕΝΑ .

Αν το όριο ΕΝΑείναι άπειρο (ας πούμε ότι είναι ίσο με συν άπειρο), τότε

(x))(g"(x))>2M)" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">.

Στον ορισμό του β θα πάρουμε ; ο πρώτος παράγοντας της δεξιάς πλευράς θα είναι μεγαλύτερος από το 1/2 όταν Χ, αρκετά κοντά σε ένα, και μετά src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">.

Για άλλες βάσεις, οι αποδείξεις είναι παρόμοιες με αυτές που δίνονται.

Παραδείγματα

(Μόνο εάν ο αριθμητής και ο παρονομαστής ΚΑΙ ΟΙ ΔΥΟ τείνουν είτε στο 0, είτε στο ; είτε στο .)

Ίδρυμα Wikimedia. 2010 .

Δείτε τι είναι ο "κανόνας L'Hopital" σε άλλα λεξικά:

Ιστορικά λανθασμένη ονομασία για έναν από τους βασικούς κανόνες για την αποκάλυψη αβεβαιοτήτων. Το L. p. βρέθηκε από τον I. Bernoulli και αναφέρθηκε από αυτόν στον G. L'Hopital (Βλ. L'Hopital), ο οποίος δημοσίευσε αυτόν τον κανόνα το 1696. Δείτε Αόριστες εκφράσεις ... Μεγάλη Σοβιετική Εγκυκλοπαίδεια

Αποκάλυψη αβεβαιοτήτων της μορφής με μείωση του ορίου του λόγου των συναρτήσεων στο όριο του λόγου των παραγώγων των υπό εξέταση συναρτήσεων. Έτσι, για την περίπτωση που πραγματικές λειτουργίεςΤα f και g ορίζονται σε μια τρυπημένη δεξιά γειτονιά ενός αριθμητικού σημείου ... ... Μαθηματική Εγκυκλοπαίδεια

Ο κανόνας του Bernoulli L' Hospital είναι μια μέθοδος για την εύρεση των ορίων των συναρτήσεων, αποκαλύπτοντας αβεβαιότητες της μορφής u. Το θεώρημα που δικαιολογεί τη μέθοδο δηλώνει ότι υπό ορισμένες συνθήκες το όριο του λόγου των συναρτήσεων είναι ίσο με το όριο του λόγου των παραγώγων τους. ... ... Wikipedia

Στη μαθηματική ανάλυση, ο κανόνας του L'Hopital είναι μια μέθοδος για την εύρεση των ορίων των συναρτήσεων, αποκαλύπτοντας αβεβαιότητες της μορφής 0/0 και. Το θεώρημα που δικαιολογεί τη μέθοδο δηλώνει ότι υπό ορισμένες συνθήκες το όριο του λόγου των συναρτήσεων είναι ίσο με το όριο ... ... Wikipedia

Στη μαθηματική ανάλυση, ο κανόνας του L'Hopital είναι μια μέθοδος για την εύρεση των ορίων των συναρτήσεων, αποκαλύπτοντας αβεβαιότητες της μορφής 0/0 και. Το θεώρημα που δικαιολογεί τη μέθοδο δηλώνει ότι υπό ορισμένες συνθήκες το όριο του λόγου των συναρτήσεων είναι ίσο με το όριο ... ... Wikipedia

Εξαρτήσεις των συντεταγμένων από το χρόνο κατά την κίνηση υλικό σημείοστο αεροπλάνο

Προσδιορίστε την ταχύτητα της μονάδας (

Α. Το μέτρο της ταχύτητας ενός υλικού σημείου από το χρόνο εκφράζεται με τον τύπο:

Β. . Η μονάδα επιτάχυνσης ενός υλικού σημείου από το χρόνο εκφράζεται με τον τύπο:

Αυτές οι εξισώσεις περιγράφουν την κίνηση ενός υλικού σημείου με σταθερή επιτάχυνση

Ο δορυφόρος περιστρέφεται γύρω από τη γη σε μια κυκλική τροχιά σε ύψος

Ένας δορυφόρος που κινείται σε κυκλική τροχιά υπόκειται στη δύναμη της βαρύτητας

Αυτός ο τύπος μπορεί να απλοποιηθεί ως εξής. Σε βάρος σώματος

Με αυτόν τον τρόπο, ταχύτητα γραμμήςδορυφόρος είναι

και η γωνιακή ταχύτητα

Και οι δύο μπάλες που εξετάζονται στο πρόβλημα σχηματίζουν ένα κλειστό σύστημα και στη θήκη ελαστικό σοκτόσο η ορμή του συστήματος όσο και η μηχανική (κινητική) ενέργεια διατηρούνται. Ας γράψουμε και τους δύο νόμους διατήρησης (λαμβάνοντας υπόψη την ακινησία της δεύτερης μπάλας πριν από την πρόσκρουση):

Έτσι, η προσπίπτουσα (πρώτη) σφαίρα ως αποτέλεσμα της πρόσκρουσης μείωσε την ταχύτητά της από 1,05 m/s σε 0,45 m/s, αν και συνέχισε να κινείται προς την ίδια κατεύθυνση, και η προηγουμένως ακίνητη (δεύτερη) μπάλα απέκτησε ταχύτητα ίση στο 1, 5 m/s και τώρα και οι δύο μπάλες κινούνται στην ίδια ευθεία και στην ίδια κατεύθυνση.

Δεδομένου ότι η μάζα του αερίου στον κύλινδρο αλλάζει, η αρχική και η τελική κατάσταση του αερίου στον κύλινδρο δεν μπορούν να συσχετιστούν ούτε με τον νόμο Boyle-Mariotte ούτε με τον νόμο του Charles. Εάν το αέριο στον κύλινδρο αλλάξει με εξίσωση, τότε το Οι αρχικές και τελικές καταστάσεις του αερίου στον κύλινδρο δεν μπορούν να συσχετιστούν με το νόμο Boyle-Mariotte. Κάθε κατάσταση γράφει την εξίσωση Mendeleev-Clapeyron

Πώς να βρείτε το όριο μιας συνάρτησης χωρίς να χρησιμοποιήσετε τον κανόνα λοπιαίο

Έκδοση συστήματος:
7.47 (16.04.2018)

Γενικά νέα:
13.04.2018, 10:33

Τελευταία ερώτηση:
26.07.2018, 15:23

Τελευταία απάντηση:
27.07.2018, 13:48

ΕΝΟΤΗΤΑ Μαθηματικά

Διαβουλεύσεις και επίλυση προβλημάτων σε άλγεβρα, γεωμετρία, ανάλυση, διακριτά μαθηματικά.

Οι καλύτεροι ειδικοί σε αυτό το τμήμα

Γειά σου! Δυσκολεύομαι με αυτήν την ερώτηση:

Βρείτε το όριο μιας συνάρτησης χωρίς να χρησιμοποιήσετε τον κανόνα του L'Hopital

lim (2x+3) [ ln (x+2) - ln x ] (κάτω από το lim γράφεται "x τείνει στο άπειρο")

Υπήρχαν πολλά παραδείγματα ορίων στην εργασία, αλλά αυτό μπέρδεψε. Δεν ξέρω πώς να το λύσω. Ίσως χρησιμοποιήσει με κάποιο τρόπο το δεύτερο υπέροχο όριο, αλλά πώς (μόνο αυτή η σκέψη έρχεται στο μυαλό);

Επιτρέψτε μου απλώς να ρωτήσω στην ίδια ερώτηση εάν λαμβάνει χώρα μια τέτοια δήλωση του προβλήματος (αν συμβαίνει, θα τη δημοσιεύσω αργότερα ως πληρωμένη ερώτηση): Εφαρμόζοντας τον τύπο Taylor με έναν υπόλοιπο όρο στη μορφή Lagrange στη συνάρτηση, υπολογίστε την τιμή με ακρίβεια 0,001. a = 0,29.
Εδώ δεν καταλαβαίνω τι λειτουργία; Δεν έχει οριστεί (;), η εργασία ακούγεται ακριβώς όπως την έγραψα. Ίσως μπορείτε να αναλάβετε τη λειτουργία μόνοι σας, αλλά ποια;

Κατάσταση: Η διαβούλευση έκλεισε

Γεια σου Aleksandrkib!
Είναι το 2ο που πρέπει να χρησιμοποιήσετε! Για να ξεκινήσουμε, ας απλοποιήσουμε:
lim (2x+3) [ ln (x+2) - ln x ] = lim (2x+3) ln ((x+2)/x) = lim (2x+3) ln (1+2/x) = lim ln ((1+2/x)^(2x+3)) = lim ln ((1+2/x)^2x)+lim ln ((1+2/x)^3) [το δεύτερο όριο είναι μηδέν, αφού το 2/x τείνει στο μηδέν και το ln 1 = 0]
Ας κάνουμε την αλλαγή y = x/2, μετά lim ln ((1+2/x)^2x) = 4 lim ln ((1+1/y)^y) = 4 * ln e =4. Απάντηση: 4.

Πρέπει να υπάρχει κάποια λειτουργία.

Στείλε μηνύματα
οι συντονιστές μπορούν
μόνο μέλη της πύλης.
ΕΙΣΟΔΟΣ ΣΤΗΝ ΠΥΛΗ »
εγγραφή"

Κανόνας του L'Hopital: θεωρία και παραδείγματα λύσεων

Κανόνας της L'Hopital και αποκάλυψη αβεβαιοτήτων

Η αποκάλυψη αβεβαιοτήτων της μορφής 0/0 ή ∞/∞ και ορισμένων άλλων αβεβαιοτήτων που προκύπτουν κατά τον υπολογισμό του ορίου του λόγου δύο απειροελάχιστων ή απείρως μεγάλων συναρτήσεων απλοποιείται σημαντικά χρησιμοποιώντας τον κανόνα του L'Hopital (στην πραγματικότητα δύο κανόνες και σχόλια επ' αυτών ).

ουσία κανόνες του L'Hospital είναι ότι στην περίπτωση που ο υπολογισμός του ορίου του λόγου δύο απείρως μικρών ή απείρως μεγάλων συναρτήσεων δίνει αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων μπορεί να αντικατασταθεί από το όριο του την αναλογία των παραγώγων τους και, έτσι, μπορεί να ληφθεί ένα ορισμένο αποτέλεσμα.

Ας περάσουμε στη διατύπωση των κανόνων του L'Hopital.

Ο κανόνας του L'Hopital για την περίπτωση του ορίου δύο απείρως μικρών τιμών. Εάν λειτουργεί φά(Χ) και σολ(Χ ένα ένα, και σε αυτή τη γειτονιά σολ‘(Χ έναίσα μεταξύ τους και ίσα με μηδέν

(),

τότε το όριο του λόγου αυτών των συναρτήσεων είναι ίσο με το όριο του λόγου των παραγώγων τους

().

Ο κανόνας του L'Hôpital για την περίπτωση του ορίου δύο απείρως μεγάλων ποσοτήτων. Εάν λειτουργεί φά(Χ) και σολ(Χ) είναι διαφοροποιήσιμες σε κάποια γειτονιά του σημείου ένα, με πιθανή εξαίρεση το σημείο ένα, και σε αυτή τη γειτονιά σολ‘(Χ)≠0 και αν και αν τα όρια αυτών των συναρτήσεων ως x τείνει στην τιμή της συνάρτησης στο σημείο έναίσα μεταξύ τους και ίσα με το άπειρο

(),

Με άλλα λόγια, για αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων ισούται με το όριο του λόγου των παραγώγων τους, αν υπάρχει η τελευταία (πεπερασμένη ή άπειρη).

Παρατηρήσεις.

1. Οι κανόνες της L'Hopital ισχύουν επίσης κατά τις λειτουργίες φά(Χ) και σολ(Χ) δεν ορίζονται στο Χ = ένα.

2. Αν, κατά τον υπολογισμό του ορίου του λόγου των παραγώγων συναρτήσεων φά(Χ) και σολ(Χ) ερχόμαστε και πάλι σε μια αβεβαιότητα της μορφής 0/0 ή ∞/∞, τότε οι κανόνες του L'Hopital θα πρέπει να εφαρμόζονται επανειλημμένα (τουλάχιστον δύο φορές).

3. Οι κανόνες του L'Hopital ισχύουν επίσης όταν το όρισμα των συναρτήσεων (x) τείνει να μην τελικός αριθμός ένακαι στο άπειρο ( Χ → ∞).

Οι αβεβαιότητες άλλων τύπων μπορούν επίσης να μειωθούν σε αβεβαιότητες των τύπων 0/0 και ∞/∞.

Αποκάλυψη αβεβαιοτήτων των τύπων "μηδέν διαιρούμενο με μηδέν" και "άπειρο διαιρούμενο με άπειρο"

Παράδειγμα 1

ΧΤο =2 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, η παράγωγος κάθε συνάρτησης και παίρνουμε

Στον αριθμητή υπολογίστηκε η παράγωγος του πολυωνύμου και στον παρονομαστή η παράγωγος του μιγαδικού λογαριθμική συνάρτηση. Πριν από το τελευταίο πρόσημο ίσου, υπολογίστηκε το συνηθισμένο όριο, αντικαθιστώντας ένα δίδυμο αντί για ένα x.

Παράδειγμα 2Υπολογίστε το όριο του λόγου δύο συναρτήσεων χρησιμοποιώντας τον κανόνα του L'Hospital:

Παράδειγμα 3Υπολογίστε το όριο του λόγου δύο συναρτήσεων χρησιμοποιώντας τον κανόνα του L'Hospital:

Λύση. Αντικατάσταση σε δεδομένη λειτουργίααξίες ΧΤο =0 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, υπολογίζουμε τις παραγώγους των συναρτήσεων στον αριθμητή και στον παρονομαστή και παίρνουμε:

Παράδειγμα 4Υπολογίζω

Λύση. Η αντικατάσταση της τιμής του x ίση με συν άπειρο σε μια δεδομένη συνάρτηση οδηγεί σε απροσδιοριστία της μορφής ∞/∞. Επομένως, εφαρμόζουμε τον κανόνα του L'Hopital:

Σχόλιο. Ας προχωρήσουμε σε παραδείγματα στα οποία ο κανόνας L'Hopital πρέπει να εφαρμοστεί δύο φορές, δηλαδή να φτάσει στο όριο του λόγου των δεύτερων παραγώγων, αφού το όριο του λόγου των πρώτων παραγώγων είναι αβεβαιότητα της μορφής 0/0 ή ∞/∞.

Παράδειγμα 5Υπολογίστε το όριο του λόγου δύο συναρτήσεων χρησιμοποιώντας τον κανόνα του L'Hospital:

Εδώ ο κανόνας του L'Hospital εφαρμόζεται δύο φορές, αφού τόσο το όριο του λόγου των συναρτήσεων όσο και το όριο του λόγου των παραγώγων δίνουν μια αβεβαιότητα της μορφής ∞/∞.

Παράδειγμα 6Υπολογίζω

Εδώ ο κανόνας του L'Hospital εφαρμόζεται δύο φορές, αφού τόσο το όριο του λόγου των συναρτήσεων όσο και το όριο του λόγου των παραγώγων δίνουν μια αβεβαιότητα της μορφής 0/0.

Παράδειγμα 7Υπολογίζω

Εδώ ο κανόνας του L'Hopital εφαρμόζεται δύο φορές, αφού τόσο το όριο του λόγου των συναρτήσεων όσο και το όριο του λόγου των παραγώγων δίνουν πρώτα μια αβεβαιότητα της μορφής - ∞/∞ και μετά μια αβεβαιότητα της μορφής 0/0.

Παράδειγμα 8Υπολογίζω

Εδώ ο κανόνας του L'Hospital εφαρμόζεται δύο φορές, αφού τόσο το όριο του λόγου των συναρτήσεων όσο και το όριο του λόγου των παραγώγων δίνουν πρώτα μια αβεβαιότητα της μορφής ∞/∞ και μετά μια αβεβαιότητα της μορφής 0/0.

Εφαρμόστε μόνοι σας τον κανόνα του L'Hopital και μετά δείτε τη λύση

Παράδειγμα 9Υπολογίζω

Ενδειξη. Εδώ πρέπει να φυσήξετε λίγο περισσότερο από το συνηθισμένο στη μετατροπή των εκφράσεων κάτω από το οριακό πρόσημο.

Παράδειγμα 10Υπολογίζω

.

Ενδειξη. Εδώ ο κανόνας του L'Hopital θα πρέπει να εφαρμοστεί τρεις φορές.

Αποκάλυψη αβεβαιοτήτων της μορφής "μηδέν πολλαπλασιασμένο επί άπειρο"

Παράδειγμα 11.Υπολογίζω

(εδώ έχουμε μετατρέψει την αβεβαιότητα της μορφής 0∙∞ στη μορφή ∞/∞, αφού

και στη συνέχεια εφάρμοσε τους κανόνες της L'Hopital).

Παράδειγμα 12.Υπολογίζω

.

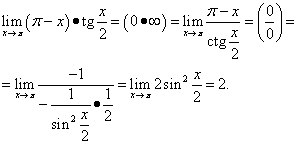
Αυτό το παράδειγμα χρησιμοποιεί την τριγωνομετρική ταυτότητα.

Αποκάλυψη αβεβαιοτήτων των τύπων «μηδέν στη δύναμη του μηδέν», «άπειρο στη δύναμη του μηδέν» και «ένα προς τη δύναμη του άπειρου»

Οι αβεβαιότητες της φόρμας ή συνήθως μειώνονται στη μορφή 0/0 ή ∞/∞ χρησιμοποιώντας τον λογάριθμο μιας συνάρτησης της φόρμας

Για να υπολογίσετε το όριο μιας έκφρασης, θα πρέπει να χρησιμοποιήσετε λογαριθμική ταυτότητα, ειδική περίπτωση του οποίου είναι και η ιδιότητα του λογαρίθμου .

Χρησιμοποιώντας τη λογαριθμική ταυτότητα και την ιδιότητα συνέχειας της συνάρτησης (να υπερβαίνει το πρόσημο του ορίου), το όριο θα πρέπει να υπολογιστεί ως εξής:

Ξεχωριστά, θα πρέπει να βρει κανείς το όριο της έκφρασης στον εκθέτη και να δημιουργήσει μιστον βαθμό που βρέθηκε.

Παράδειγμα 13

.

.

Παράδειγμα 14Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

.

.

Παράδειγμα 15Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

Υπολογίστε το όριο της έκφρασης στον εκθέτη

.

Αποκάλυψη αβεβαιοτήτων της μορφής "άπειρο μείον άπειρο"

Πρόκειται για περιπτώσεις όπου ο υπολογισμός του ορίου της διαφοράς των συναρτήσεων οδηγεί στην αβεβαιότητα «άπειρο μείον άπειρο»: .

Ο υπολογισμός ενός τέτοιου ορίου σύμφωνα με τον κανόνα του L'Hopital στο γενική εικόναως εξής:

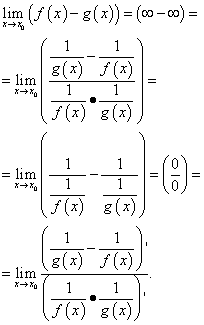
Αυτές οι μετατροπές συχνά καταλήγουν σε σύνθετες εκφράσεις, επομένως, είναι σκόπιμο να χρησιμοποιηθούν τέτοιοι μετασχηματισμοί της διαφοράς συναρτήσεων όπως η αναγωγή σε κοινό παρονομαστή, πολλαπλασιασμός και διαίρεση με τον ίδιο αριθμό, χρήση τριγωνομετρικές ταυτότητεςκαι τα λοιπά.

Παράδειγμα 16Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

.

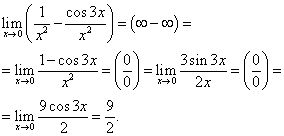
Παράδειγμα 17.Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

.

Υπολογίστε τα όρια χρησιμοποιώντας τον κανόνα lopital

Η αβεβαιότητα επίσης δεν αντιστέκεται στο να μετατραπεί σε ή:

Κανόνες του L'Hospital

Συνεχίζουμε να αναπτύσσουμε το θέμα, το οποίο μας έριξε το μέλος της Ακαδημίας Επιστημών του Παρισιού, Marquis Guillaume Francois de Lopital. Το άρθρο αποκτά έναν έντονο πρακτικό χρωματισμό και σε μια αρκετά κοινή εργασία απαιτείται:

Για να μην συρρικνωθεί, υπολογίζουμε το όριο του δείκτη ξεχωριστά:

Ένας άλλος Παπούας παραιτείται επίσης πριν από τη φόρμουλα. Σε αυτήν την περίπτωση:

Οι κανόνες του L'Hopital είναι μια πολύ ισχυρή μέθοδος που σας επιτρέπει να εξαλείψετε γρήγορα και αποτελεσματικά αυτές τις αβεβαιότητες, δεν είναι τυχαίο ότι σε συλλογές προβλημάτων, σε δοκιμές, δοκιμές, βρίσκεται συχνά μια σταθερή σφραγίδα: "υπολογίστε το όριο, χωρίς να χρησιμοποιήσει τον κανόνα του L'Hopital". Αφιερωμένο με έντονουςη απαίτηση είναι δυνατή με καθαρή συνείδησηανάθεση και σε οποιοδήποτε όριο μαθήματος Όρια. Παραδείγματα λύσεων, Αξιοσημείωτα όρια. Μέθοδοι επίλυσης ορίων, Αξιοσημείωτες Ισοδυναμίες, όπου εμφανίζεται η αβεβαιότητα "μηδέν στο μηδέν" ή "άπειρο στο άπειρο". Ακόμα κι αν η εργασία διατυπωθεί εν συντομία - "υπολογίστε τα όρια", τότε εννοείται σιωπηρά ότι θα χρησιμοποιήσετε ό,τι θέλετε, αλλά όχι τους κανόνες του L'Hospital.

Οι μεταμορφώσεις συνεχίζονται, τώρα έχει βγει η αβεβαιότητα «μηδέν στο μηδέν». Κατ 'αρχήν, μπορείτε να απαλλαγείτε από το συνημίτονο υποδεικνύοντας ότι τείνει προς την ενότητα. Αλλά μια σοφή στρατηγική είναι να διασφαλίσουμε ότι κανείς δεν θα φτάσει στο κάτω μέρος του τίποτα. Επομένως, εφαρμόζουμε αμέσως τον κανόνα L'Hopital, όπως απαιτείται από την κατάσταση του προβλήματος:

Μια παρόμοια εργασία για μια ανεξάρτητη λύση:

Όπως μπορείτε να δείτε, η διαφοροποίηση του αριθμητή και του παρονομαστή μας οδήγησε στην απάντηση με μισή στροφή: βρήκαμε δύο απλές παραγώγους, αντικαταστήσαμε το "δύο" σε αυτές και αποδείχθηκε ότι η αβεβαιότητα εξαφανίστηκε χωρίς ίχνος!

Υπολογίστε το όριο μιας συνάρτησης χρησιμοποιώντας τον κανόνα του L'Hopital

Με τη σειρά τους, οι σύντροφοι που πίνουν και οι πιο εξωτικοί σύντροφοι σύρονται στο φως. Η μέθοδος μετασχηματισμού είναι απλή και τυπική:

Το εξεταζόμενο παράδειγμα καταστρέφεται και διαμέσου υπέροχα όρια , μια παρόμοια περίπτωση συζητείται στο τέλος του άρθρου Σύνθετα όρια.

Θα κάνω μια κράτηση αμέσως ότι οι κανόνες θα δοθούν σε μια συνοπτική "πρακτική" μορφή και εάν πρέπει να περάσετε τη θεωρία, σας συνιστώ να απευθυνθείτε στο σχολικό βιβλίο για πιο αυστηρούς υπολογισμούς.

6) Ισχύει τελευταίος κανόναςπληροφορίες για το δεύτερο υπέροχο σύνορο

Η γνωστοποίηση των αβεβαιοτήτων μειώνεται στις προηγουμένως συζητηθείσες αβεβαιότητες. Εάν, και στο, τότε εφαρμόστε τον μετασχηματισμό

άπειρο ή μηδέν με μηδέν είναι η εφαρμογή του κανόνα του L'Hopital: το όριο της αναλογίας δύο

Στην περίπτωση των τριών τελευταίων αβεβαιοτήτων, πρέπει να εφαρμοστούν μετασχηματισμοί

5) Υπάρχει απροσδιοριστία της μορφής άπειρο έως άπειρο.

άπειρες μικρές ή δύο απείρως μεγάλες συναρτήσεις είναι ίσες με το όριο του λόγου των παραγώγων τους,

3) Δεδομένης της αβεβαιότητας, εφαρμόστε τον προηγούμενο κανόνα

Υπολογισμός ορίων σύμφωνα με τον κανόνα του L'Hopital

Ένας αποτελεσματικός τρόπος υπολογισμού των ορίων των συναρτήσεων που έχουν ιδιομορφίες τύπου άπειρο

Λύση. 1) Με αντικατάσταση, διαπιστώνουμε ότι έχουμε αβεβαιότητα της μορφής μηδέν προς μηδέν. Να ξεφορτωθώ

Και πάλι έχουμε την αβεβαιότητα της φόρμας και εφαρμόζουμε ξανά τον κανόνα του L'Hospital

2) Όπως και στο προηγούμενο παράδειγμα, έχουμε αβεβαιότητα. Σύμφωνα με τον κανόνα του L'Hopital, βρίσκουμε

Η εφαρμογή του κανόνα της L'Hopital έδειξε όλες τις δυνατότητες αποκάλυψης αβεβαιοτήτων.

Ο αριθμός επιλέγεται με τέτοιο τρόπο ώστε να ικανοποιείται η ισότητα (1) και, επομένως, . Έτσι, για μια συνάρτηση στο διάστημα

Στην περιοχή του σημείου x 0 , δηλ. στο (x 0 ,x), οι συνθήκες του θεωρήματος Cauchy ικανοποιούνται για τις συναρτήσεις f(x) και g(x). Επομένως, υπάρχει ένα σημείο σО(x 0 , x) τέτοιο ώστε

Ο κανόνας του L'Hopital

Ωστόσο, είναι δυνατή μια κατάσταση όταν η συνάρτηση θα έχει ένα άκρο στο σημείο x 0 στην περίπτωση που η παράγωγος δεν υπάρχει.

Έστω η συνάρτηση n φορές διαφορίσιμη σε μια γειτονιά του σημείου x 0. Ας βρούμε ένα πολυώνυμο βαθμού όχι μεγαλύτερο από n-1, έτσι ώστε

Έστω οι συναρτήσεις f(x) και g(x) συνεχείς και διαφοροποιήσιμες σε κάποια γειτονιά του σημείου x 0 , εκτός από το ίδιο το σημείο x 0, επιπλέον. Αφήστε, . Τότε αν υπάρχει ένα όριο του λόγου των παραγώγων των συναρτήσεων, τότε υπάρχει ένα όριο του λόγου των ίδιων των συναρτήσεων, και είναι ίσες μεταξύ τους, δηλ. .

Συμπέρασμα: εκθετικη συναρτηση(y=a n) αυξάνεται πάντα ταχύτερα από τον νόμο ισχύος (y=x n).

Ως παράδειγμα της εφαρμογής του τύπου Maclaurin, προσδιορίζουμε τον αριθμό των όρων στην επέκταση μιας συνάρτησης σε όρους τύποςνα υπολογίσετε την τιμή του με ακρίβεια 0,001 για οποιοδήποτε x από το διάστημα [-1,1].

Ορισμός:Η συνάρτηση καλείται μη φθίνουσα (μη αυξανόμενη)έως (α;β) εάν για οποιαδήποτε x 1 Δημοσιεύτηκε σε Χρήσιμα άρθρα

Εύρεση του ορίου μιας συνάρτησης σε ένα σημείο σύμφωνα με τον κανόνα του L'Hopital

Βρίσκοντας το όριο μιας συνάρτησης, σύμφωνα με τον κανόνα του L'Hopital, αποκαλύπτοντας αβεβαιότητες της μορφής 0/0 και ∞/∞.

Η αριθμομηχανή παρακάτω βρίσκει το όριο της συνάρτησης σύμφωνα με τον κανόνα L'Hospital (μέσω των παραγώγων του αριθμητή και του παρονομαστή). Δείτε την περιγραφή του κανόνα παρακάτω.

Όριο συνάρτησης σε σημείο - κανόνας L'Hopital

Έγκυρες λειτουργίες: + - / * ^ Σταθερές: pi Λειτουργίες: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Ο κανόνας του L'Hopital

Εάν πληρούνται οι ακόλουθες προϋποθέσεις:

• τα όρια των συναρτήσεων f(x) και g(x) είναι ίσα μεταξύ τους και ίσα με μηδέν ή άπειρο:
  ή;
• Οι συναρτήσεις g(x) και f(x) είναι διαφοροποιήσιμες στη διάτρητη γειτονιά a.
• η παράγωγος της συνάρτησης g(x) δεν είναι ίση με μηδέν στη διάτρητη γειτονιά a
• και υπάρχει ένα όριο στην αναλογία της παραγώγου f(x) προς την παράγωγο g(x):

Τότε υπάρχει ένα όριο του λόγου των συναρτήσεων f(x) και g(x):
,

Και είναι ίσο με το όριο του λόγου της παραγώγου της συνάρτησης f(x) προς την παράγωγο της συνάρτησης g(x):

Ο τύπος επιτρέπει τη χρήση του αριθμού pi (pi), του εκθέτη (e), των ακόλουθων μαθηματικών τελεστών:

+ - πρόσθεση
— - αφαίρεση
* - πολλαπλασιασμός
/ - διαίρεση
^ - εκθεσιμότητα

και τα ακόλουθα χαρακτηριστικά:

sqrt - τετραγωνική ρίζα

ρίζα Π- ρίζα βαθμού Π, για παράδειγμα root3(x) είναι η κυβική ρίζα

exp - e στην καθορισμένη ισχύ

lb - λογάριθμος βάσης 2

lg - βάση 10 λογάριθμος

ln- φυσικός λογάριθμος(με βάση το ε)

κούτσουρο Π- λογάριθμος βάσης Π, για παράδειγμα log7(x) - λογάριθμος βάσης 7

αμαρτία - ημίτονο

cos - συνημίτονο

tg - εφαπτομένη

ctg - συνεφαπτομένη

sec - secant

cosec - συνεκτικός

arcsin - arcsin

τόξο - τόξο συνημίτονο

arctg - εφαπτομένη τόξου

arcctg - εφαπτομένη τόξου

arcsec - arcsecant

arccosec - arccosecant

versin - versinus

vercos - coversine

harsin - χαίρσινος

exsec - exsecant

excsc - excosecant

sh - υπερβολικό ημίτονο

ch - υπερβολικό συνημίτονο

ου - υπερβολική εφαπτομένη

cth - υπερβολική συνεφαπτομένη

sech - υπερβολική διατομή

csch - υπερβολική συνέκταση

κοιλιακοί- απόλυτη τιμή(μονάδα μέτρησης)

sgn - signum (σημάδι)

• Ενοικίαση Gazelle ή Sable Van χωρίς οδηγό Gazelle-Business, 1 οδηγός + 2 επιβάτες. Σώμα: 3 μ. μήκος, 2 μ. ύψος, butka. Ο όγκος του κύβου 10.5. Κινητήρας: UMZ-4216 (βενζίνη), euro-4, 106,8 […]
• Στοιχεία πληρωμής φόρων και εισφορών το 2017-2018 Τα στοιχεία για την πληρωμή φόρων το 2017-2018 αποτελούν αναπόσπαστο μέρος κάθε πληρωμής. Συμπληρώστε σωστά την εντολή πληρωμής [...]
• Η διαδικασία προς εξέταση από το Συμβούλιο της Ομοσπονδίας του εγκρίθηκε Κρατική Δούμα Ομοσπονδιακός νόμος(Άρθρα 103–110) Άρθρο 103. Έγκριση ομοσπονδιακού νόμου προς εξέταση από την […]
• Ποινικό δίκαιο. Γενικό μέρος Κανόνας ποινικού δικαίου Ένας κανόνας ποινικού δικαίου είναι ένας κανόνας συμπεριφοράς που θεσπίζεται από το κράτος που παρέχει τους συμμετέχοντες δημόσιες σχέσεις […]
• Το μέγεθος της ποινής καθυστέρησης σε υποθήκη είναι περιορισμένο Στις 24 Ιουλίου θα τεθεί σε ισχύ νόμος που περιορίζει το ύψος της ποινής για μη εκπλήρωση ή ακατάλληλη εκπλήρωση […]
• Δολοφονία με επιβαρυντικές περιστάσεις τιμωρία Σύμφωνα με την ισχύουσα ποινική νομοθεσία, η απλή δολοφονία (μέρος 1 του άρθρου 105 του Ποινικού Κώδικα της Ρωσικής Ομοσπονδίας) «τιμωρείται με φυλάκιση για […]

Αποκάλυψη αβεβαιοτήτων της μορφής 0/0 ή ∞/∞ και κάποιων άλλων αβεβαιοτήτων που προκύπτουν στον υπολογισμό όριοη σχέση δύο απειροελάχιστων ή απείρως μεγάλων συναρτήσεων απλοποιείται πολύ με τη βοήθεια του κανόνα του L'Hospital (στην πραγματικότητα δύο κανόνες και παρατηρήσεις σε αυτές).

ουσία κανόνες του L'Hospital είναι ότι στην περίπτωση που ο υπολογισμός του ορίου των αναλογιών δύο απείρως μικρών ή απείρως μεγάλων συναρτήσεων δίνει αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων μπορεί να αντικατασταθεί από το όριο του η αναλογία τους παράγωγακαι έτσι έχετε ένα συγκεκριμένο αποτέλεσμα.

Ας περάσουμε στη διατύπωση των κανόνων του L'Hopital.

Ο κανόνας του L'Hopital για την περίπτωση του ορίου δύο απείρως μικρών τιμών. Εάν λειτουργεί φά(Χ) και σολ(Χ έναένα, και σε αυτή τη γειτονιά σολ"(Χ έναίσα μεταξύ τους και ίσα με μηδέν

().

Ο κανόνας του L'Hôpital για την περίπτωση του ορίου δύο απείρως μεγάλων ποσοτήτων. Εάν λειτουργεί φά(Χ) και σολ(Χ) είναι διαφοροποιήσιμες σε κάποια γειτονιά του σημείου ένα, με πιθανή εξαίρεση το σημείο ένα, και σε αυτή τη γειτονιά σολ"(Χ)≠0 και αν και αν τα όρια αυτών των συναρτήσεων ως x τείνει στην τιμή της συνάρτησης στο σημείο έναίσα μεταξύ τους και ίσα με το άπειρο

(),

τότε το όριο του λόγου αυτών των συναρτήσεων είναι ίσο με το όριο του λόγου των παραγώγων τους

().

Με άλλα λόγια, για αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων ισούται με το όριο του λόγου των παραγώγων τους, αν υπάρχει η τελευταία (πεπερασμένη ή άπειρη).

Παρατηρήσεις.

1. Οι κανόνες της L'Hopital ισχύουν επίσης κατά τις λειτουργίες φά(Χ) και σολ(Χ) δεν ορίζονται στο Χ = ένα.

2. Αν, κατά τον υπολογισμό του ορίου του λόγου των παραγώγων συναρτήσεων φά(Χ) και σολ(Χ) ερχόμαστε και πάλι σε μια αβεβαιότητα της μορφής 0/0 ή ∞/∞, τότε οι κανόνες του L'Hopital θα πρέπει να εφαρμόζονται επανειλημμένα (τουλάχιστον δύο φορές).

3. Οι κανόνες του L'Hopital ισχύουν επίσης όταν το όρισμα των συναρτήσεων (x) τείνει σε έναν μη πεπερασμένο αριθμό ένακαι στο άπειρο ( Χ → ∞).

Οι αβεβαιότητες άλλων τύπων μπορούν επίσης να μειωθούν σε αβεβαιότητες των τύπων 0/0 και ∞/∞.

Αποκάλυψη αβεβαιοτήτων των τύπων "μηδέν διαιρούμενο με μηδέν" και "άπειρο διαιρούμενο με άπειρο"

Παράδειγμα 1

ΧΤο =2 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, η παράγωγος κάθε συνάρτησης και παίρνουμε

Στον αριθμητή, υπολογίστηκε η παράγωγος του πολυωνύμου και στον παρονομαστή - παράγωγο μιγαδικής λογαριθμικής συνάρτησης. Πριν από το τελευταίο πρόσημο ίσου, το συνηθισμένο όριο, αντικαθιστώντας ένα δίδυμο αντί του x.

Παράδειγμα 2Υπολογίστε το όριο του λόγου δύο συναρτήσεων χρησιμοποιώντας τον κανόνα του L'Hospital:

Λύση. Αντικατάσταση σε μια δεδομένη συνάρτηση τιμής Χ

Παράδειγμα 3Υπολογίστε το όριο του λόγου δύο συναρτήσεων χρησιμοποιώντας τον κανόνα του L'Hospital:

Λύση. Αντικατάσταση σε μια δεδομένη συνάρτηση τιμής ΧΤο =0 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, υπολογίζουμε τις παραγώγους των συναρτήσεων στον αριθμητή και στον παρονομαστή και παίρνουμε:

Παράδειγμα 4Υπολογίζω

Λύση. Η αντικατάσταση της τιμής του x ίση με συν άπειρο σε μια δεδομένη συνάρτηση οδηγεί σε απροσδιοριστία της μορφής ∞/∞. Επομένως, εφαρμόζουμε τον κανόνα του L'Hopital:

Σχόλιο. Ας προχωρήσουμε σε παραδείγματα στα οποία ο κανόνας L'Hopital πρέπει να εφαρμοστεί δύο φορές, δηλαδή να φτάσει στο όριο του λόγου των δεύτερων παραγώγων, αφού το όριο του λόγου των πρώτων παραγώγων είναι αβεβαιότητα της μορφής 0/0 ή ∞/∞.

Εφαρμόστε μόνοι σας τον κανόνα του L'Hopital και μετά δείτε τη λύση

Αποκάλυψη αβεβαιοτήτων της μορφής "μηδέν πολλαπλασιασμένο επί άπειρο"

Παράδειγμα 12.Υπολογίζω

.

Λύση. Παίρνουμε

Αυτό το παράδειγμα χρησιμοποιεί την τριγωνομετρική ταυτότητα.

Αποκάλυψη αβεβαιοτήτων των τύπων «μηδέν στη δύναμη του μηδέν», «άπειρο στη δύναμη του μηδέν» και «ένα προς τη δύναμη του άπειρου»

Οι αβεβαιότητες της φόρμας ή συνήθως μειώνονται στη μορφή 0/0 ή ∞/∞ χρησιμοποιώντας τον λογάριθμο μιας συνάρτησης της φόρμας

Για τον υπολογισμό του ορίου της έκφρασης, θα πρέπει να χρησιμοποιηθεί η λογαριθμική ταυτότητα, μια ειδική περίπτωση της οποίας είναι η ιδιότητα του λογαρίθμου .

Χρησιμοποιώντας τη λογαριθμική ταυτότητα και την ιδιότητα συνέχειας της συνάρτησης (να υπερβαίνει το πρόσημο του ορίου), το όριο θα πρέπει να υπολογιστεί ως εξής:

Ξεχωριστά, θα πρέπει να βρει κανείς το όριο της έκφρασης στον εκθέτη και να δημιουργήσει μιστον βαθμό που βρέθηκε.

Παράδειγμα 13

Λύση. Παίρνουμε

.

.

Παράδειγμα 14Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

Λύση. Παίρνουμε

Υπολογίστε το όριο της έκφρασης στον εκθέτη

.

.

Παράδειγμα 15Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital

Αυτό μαθηματική αριθμομηχανή online θα σας βοηθήσει αν χρειαστεί υπολογίστε το όριο συνάρτησης. Πρόγραμμα λύσεις περιορισμούόχι μόνο δίνει την απάντηση στο πρόβλημα, αλλά οδηγεί λεπτομερής λύσημε εξηγήσεις, δηλ. εμφανίζει την πρόοδο του υπολογισμού του ορίου.

Αυτό το πρόγραμμα μπορεί να είναι χρήσιμο για μαθητές γυμνασίου σχολεία γενικής εκπαίδευσηςσε προετοιμασία για εργασίες ελέγχουκαι εξετάσεις, κατά τον έλεγχο γνώσεων πριν από τις εξετάσεις, οι γονείς να ελέγχουν την επίλυση πολλών προβλημάτων στα μαθηματικά και την άλγεβρα. Ή μήπως είναι πολύ ακριβό για εσάς να προσλάβετε δάσκαλο ή να αγοράσετε νέα σχολικά βιβλία; Ή απλά θέλετε να το κάνετε το συντομότερο δυνατό; εργασία για το σπίτιμαθηματικά ή άλγεβρα; Σε αυτήν την περίπτωση, μπορείτε επίσης να χρησιμοποιήσετε τα προγράμματά μας με μια λεπτομερή λύση.

Έτσι, μπορείτε να πραγματοποιήσετε τη δική σας δική σας εκπαίδευσηή/και την εκπαίδευσή τους μικρότερα αδέρφιαή αδελφές, ενώ αυξάνεται το επίπεδο εκπαίδευσης στον τομέα των εργασιών που επιλύονται.

Εισαγάγετε μια έκφραση συνάρτησης

Υπολογισμός ορίου

Διαπιστώθηκε ότι ορισμένα σενάρια που απαιτούνται για την επίλυση αυτής της εργασίας δεν φορτώθηκαν και το πρόγραμμα ενδέχεται να μην λειτουργεί.
Μπορεί να έχετε ενεργοποιημένο το AdBlock.
Σε αυτήν την περίπτωση, απενεργοποιήστε το και ανανεώστε τη σελίδα.

Έχετε απενεργοποιήσει τη JavaScript στο πρόγραμμα περιήγησής σας.
Η JavaScript πρέπει να είναι ενεργοποιημένη για να εμφανιστεί η λύση.
Ακολουθούν οδηγίες σχετικά με τον τρόπο ενεργοποίησης της JavaScript στο πρόγραμμα περιήγησής σας.

Επειδή Υπάρχουν πολλοί άνθρωποι που θέλουν να λύσουν το πρόβλημα, το αίτημά σας βρίσκεται στην ουρά.
Μετά από μερικά δευτερόλεπτα, η λύση θα εμφανιστεί παρακάτω.
Περίμενε Παρακαλώ δευτερόλεπτο...

Αν εσύ παρατήρησε ένα σφάλμα στη λύση, τότε μπορείτε να γράψετε σχετικά στη Φόρμα σχολίων.
Μην ξεχάσεις υποδεικνύουν ποια εργασίαεσύ αποφασίζεις τι εισάγετε στα πεδία.

Τα παιχνίδια, τα παζλ, οι εξομοιωτές μας:

Λίγη θεωρία.

Το όριο της συνάρτησης στο x-> x 0

Αφήστε τη συνάρτηση f(x) να οριστεί σε κάποιο σύνολο X και έστω το σημείο \(x_0 \σε X \) ή \(x_0 \όχι στο X \)

Πάρτε από το X μια ακολουθία σημείων εκτός από το x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
συγκλίνοντας στο x*. Οι τιμές συναρτήσεων στα σημεία αυτής της ακολουθίας σχηματίζουν επίσης μια αριθμητική ακολουθία
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
και μπορεί κανείς να θέσει το ζήτημα της ύπαρξης του ορίου του.

Ορισμός. Ο αριθμός A ονομάζεται όριο της συνάρτησης f (x) στο σημείο x \u003d x 0 (ή στο x -> x 0), εάν για οποιαδήποτε ακολουθία (1) τιμών του ορίσματος x που συγκλίνει στο x 0, διαφορετικό από το x 0, η αντίστοιχη ακολουθία (2) συνάρτησης τιμών συγκλίνει στον αριθμό A.

$$ \lim_(x\έως x_0)( f(x)) = A $$

Η συνάρτηση f(x) μπορεί να έχει μόνο ένα όριο στο σημείο x 0. Αυτό προκύπτει από το γεγονός ότι η ακολουθία
(f(x n)) έχει μόνο ένα όριο.

Υπάρχει ένας άλλος ορισμός του ορίου μιας συνάρτησης.

ΟρισμόςΟ αριθμός Α ονομάζεται όριο της συνάρτησης f(x) στο σημείο x = x 0 αν για οποιονδήποτε αριθμό \(\varepsilon > 0 \) υπάρχει ένας αριθμός \(\δέλτα > 0 \) τέτοιος ώστε για όλους \ (x \σε X, \; x \neq x_0 \) που ικανοποιεί την ανισότητα \(|x-x_0| Χρησιμοποιώντας λογικά σύμβολα, αυτός ο ορισμός μπορεί να γραφτεί ως
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Σημειώστε ότι οι ανισώσεις \(x \neq x_0 , \; |x-x_0| Ο πρώτος ορισμός βασίζεται στην έννοια του ορίου σειρά αριθμών, γι' αυτό και αναφέρεται συχνά ως ο ορισμός της "γλώσσας ακολουθίας". Ο δεύτερος ορισμός ονομάζεται ορισμός "γλώσσας \(\varepsilon - \delta \)".
Αυτοί οι δύο ορισμοί του ορίου μιας συνάρτησης είναι ισοδύναμοι και μπορείτε να χρησιμοποιήσετε έναν από αυτούς, όποιο είναι πιο βολικό για την επίλυση ενός συγκεκριμένου προβλήματος.

Σημειώστε ότι ο ορισμός του ορίου μιας συνάρτησης "στη γλώσσα των ακολουθιών" ονομάζεται επίσης ορισμός του ορίου μιας συνάρτησης σύμφωνα με τον Heine και ο ορισμός του ορίου μιας συνάρτησης "στη γλώσσα \(\varepsilon - \δέλτα \)" ονομάζεται επίσης ο ορισμός του ορίου μιας συνάρτησης σύμφωνα με τον Cauchy.

Όριο συνάρτησης στο x->x 0 - και στο x->x 0 +

Στη συνέχεια, θα χρησιμοποιήσουμε τις έννοιες των μονόπλευρων ορίων μιας συνάρτησης, οι οποίες ορίζονται ως εξής.

ΟρισμόςΟ αριθμός A ονομάζεται δεξιό (αριστερό) όριο της συνάρτησης f (x) στο σημείο x 0 εάν για οποιαδήποτε ακολουθία (1) που συγκλίνει στο x 0, της οποίας τα στοιχεία x n είναι μεγαλύτερα (λιγότερα) από x 0, η αντίστοιχη ακολουθία (2) συγκλίνει στο Α.

Συμβολικά γράφεται ως εξής:
$$ \lim_(x \έως x_0+) f(x) = A \; \left(\lim_(x \έως x_0-) f(x) = A \δεξιά) $$

Μπορεί κανείς να δώσει έναν ισοδύναμο ορισμό των μονόπλευρων ορίων μιας συνάρτησης "στη γλώσσα \(\varepsilon - \delta \)":

Ορισμόςο αριθμός A ονομάζεται δεξιό (αριστερό) όριο της συνάρτησης f(x) στο σημείο x 0 εάν για οποιοδήποτε \(\varepsilon > 0 \) υπάρχει \(\δέλτα > 0 \) τέτοιο ώστε για όλα τα x ικανοποιητικά οι ανισότητες \(x_0 Συμβολικές εγγραφές:

\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x, \; x_0

Έχουμε ήδη αρχίσει να ασχολούμαστε με τα όρια και τη λύση τους. Ας συνεχίσουμε στο hot pursuit και ας ασχοληθούμε με τη λύση των ορίων σύμφωνα με τον κανόνα του L'Hopital. Αυτό απλός κανόναςικανός να σας βοηθήσει να ξεφύγετε από τις ύπουλες και δύσκολες παγίδες που λατρεύουν οι δάσκαλοι να χρησιμοποιούν στα παραδείγματα του λογισμικού ελέγχου ανώτερα μαθηματικάκαι μαθηματική ανάλυση. Η λύση με τον κανόνα του L'Hopital είναι απλή και γρήγορη. Το κύριο πράγμα είναι να μπορείς να διαφοροποιήσεις.

Κανόνας του L'Hopital: Ιστορία και ορισμός

Στην πραγματικότητα, αυτός δεν είναι ακριβώς ο κανόνας της L'Hopital, αλλά ο κανόνας L' Hospital-Bernoulli. Διατυπώθηκε από έναν Ελβετό μαθηματικό Γιόχαν Μπερνούλι, και οι Γάλλοι Guillaume Lopitalπρωτοδημοσιεύτηκε στο σχολικό του βιβλίο απειροελάχιστα στο ένδοξο 1696 έτος. Μπορείτε να φανταστείτε πώς έπρεπε οι άνθρωποι να λύσουν τα όρια με την αποκάλυψη αβεβαιοτήτων πριν συμβεί αυτό; Δεν είμαστε.

Πριν προχωρήσετε στην ανάλυση του κανόνα L'Hopital, σας συνιστούμε να διαβάσετε το εισαγωγικό άρθρο σχετικά με και τις μεθόδους επίλυσής τους. Συχνά στις εργασίες υπάρχει μια διατύπωση: βρείτε το όριο χωρίς να χρησιμοποιήσετε τον κανόνα L'Hopital. Μπορείτε επίσης να διαβάσετε για τις τεχνικές που θα σας βοηθήσουν σε αυτό στο άρθρο μας.

Εάν έχετε να κάνετε με τα όρια ενός κλάσματος δύο συναρτήσεων, να είστε προετοιμασμένοι: σύντομα θα συναντήσετε μια αβεβαιότητα της μορφής 0/0 ή άπειρο/άπειρο. Τι σημαίνει? Στον αριθμητή και στον παρονομαστή, οι εκφράσεις τείνουν στο μηδέν ή στο άπειρο. Τι να κάνουμε με ένα τέτοιο όριο, με την πρώτη ματιά, είναι εντελώς ακατανόητο. Ωστόσο, αν εφαρμόσεις τον κανόνα της L'Hopital και σκεφτείς λίγο, όλα μπαίνουν στη θέση τους.

Ας διατυπώσουμε όμως τον κανόνα L'Hospital-Bernoulli. Για να είμαστε απόλυτα ακριβείς, εκφράζεται με ένα θεώρημα. Κανόνας του L'Hopital, ορισμός:

Αν δύο συναρτήσεις είναι διαφοροποιήσιμες σε μια γειτονιά ενός σημείου x=a εξαφανίζονται σε αυτό το σημείο, και υπάρχει ένα όριο στην αναλογία των παραγώγων αυτών των συναρτήσεων, τότε για Χ φιλοδοξώντας να ένα υπάρχει ένα όριο στον λόγο των ίδιων των συναρτήσεων, το οποίο είναι ίσο με το όριο του λόγου των παραγώγων.

Ας γράψουμε τον τύπο και όλα θα γίνουν αμέσως πιο εύκολα. Κανόνας του L'Hopital, τύπος:

Εφόσον μας ενδιαφέρει η πρακτική πλευρά του ζητήματος, δεν θα παρουσιάσουμε εδώ την απόδειξη αυτού του θεωρήματος. Είτε θα πρέπει να δεχτείτε τη λέξη μας, είτε να το βρείτε σε οποιοδήποτε εγχειρίδιο λογισμού και να βεβαιωθείτε ότι το θεώρημα είναι σωστό.

Παρεμπιπτόντως! Για τους αναγνώστες μας υπάρχει τώρα έκπτωση 10%.

Αποκάλυψη αβεβαιοτήτων σύμφωνα με τον κανόνα της L'Hopital

Ποιες αβεβαιότητες μπορεί να βοηθήσει να αποκαλυφθούν ο κανόνας του L'Hospital; Νωρίτερα μιλήσαμε κυρίως για αβεβαιότητα 0/0 . Ωστόσο, αυτό απέχει πολύ από τη μόνη αβεβαιότητα που μπορεί να συναντήσει κανείς. Ακολουθούν άλλοι τύποι αβεβαιοτήτων:

Ας εξετάσουμε τους μετασχηματισμούς που μπορούν να χρησιμοποιηθούν για να φέρουν αυτές τις αβεβαιότητες στη μορφή 0/0 ή άπειρο/άπειρο. Μετά τον μετασχηματισμό, θα μπορείτε να εφαρμόσετε τον κανόνα L'Hospital-Bernoulli και να κάνετε κλικ σε παραδείγματα όπως καρύδια.

Αβεβαιότητα ειδών άπειρο/άπειρο ανάγεται σε απροσδιοριστία της μορφής 0/0 απλός μετασχηματισμός:

Ας υπάρχει ένα γινόμενο δύο συναρτήσεων, εκ των οποίων η μία τείνει στο μηδέν και η δεύτερη στο άπειρο. Εφαρμόζουμε τον μετασχηματισμό και το γινόμενο του μηδενός και του απείρου μετατρέπεται σε απροσδιοριστία 0/0 :

Για να βρείτε όρια με αβεβαιότητες τύπου άπειρο μείον άπειρο χρησιμοποιούμε τον ακόλουθο μετασχηματισμό που οδηγεί σε αβεβαιότητα 0/0 :

Για να χρησιμοποιήσετε τον κανόνα του L'Hopital, πρέπει να είστε σε θέση να λαμβάνετε παράγωγα. Παρακάτω είναι ένας πίνακας παραγώγων στοιχειώδεις λειτουργίες, το οποίο μπορείτε να χρησιμοποιήσετε κατά την επίλυση παραδειγμάτων, καθώς και τους κανόνες για τον υπολογισμό των παραγώγων μιγαδικών συναρτήσεων:

Τώρα ας περάσουμε στα παραδείγματα.

Παράδειγμα 1

Βρείτε το όριο σύμφωνα με τον κανόνα του L'Hospital:

Παράδειγμα 2

Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital:

Σημαντικό σημείο! Αν το όριο της δεύτερης και των επόμενων παραγώγων συναρτήσεων υπάρχει για Χ φιλοδοξώντας να ένα , τότε ο κανόνας του L'Hopital μπορεί να εφαρμοστεί πολλές φορές.

Ας βρούμε το όριο ( n – φυσικός αριθμός). Για να το κάνετε αυτό, εφαρμόστε τον κανόνα του L'Hospital n μια φορά:

Σας ευχόμαστε καλή τύχη στη μάθηση μαθηματική ανάλυση. Και αν πρέπει να βρείτε το όριο χρησιμοποιώντας τον κανόνα L'Hopital, γράψτε μια περίληψη σύμφωνα με τον κανόνα L'Hopital, υπολογίστε τις ρίζες διαφορική εξίσωσηή ακόμα και να υπολογίσετε τον τανυστή αδράνειας ενός σώματος, επικοινωνήστε με τους συγγραφείς μας. Θα χαρούν να σας βοηθήσουν να καταλάβετε τις περιπλοκές της λύσης.