Jaotuse binoom. Diskreetsete juhuslike suuruste tõenäosusjaotused

Tõenäosusteooria on meie elus nähtamatult kohal. Me ei pööra sellele tähelepanu, kuid igal sündmusel meie elus on üks või teine ​​tõenäosus. Pööra tähelepanu suur summa sündmuste arendamise võimalusi, on meil vaja kindlaks teha neist kõige tõenäolisem ja kõige vähem tõenäoline. Selliseid tõenäosusandmeid on kõige mugavam analüüsida graafiliselt. Levitamine võib meid selles aidata. Binoom on üks lihtsamaid ja täpsemaid.

Enne otse matemaatika ja tõenäosusteooria juurde asumist mõelgem välja, kes oli esimene, kes seda tüüpi jaotuse välja mõtles ja milline on arengulugu matemaatiline aparaat selle kontseptsiooni jaoks.

Lugu

Tõenäosuse mõiste on tuntud juba iidsetest aegadest. Muistsed matemaatikud aga ei omistanud sellele erilist tähtsust ja suutsid panna aluse vaid teooriale, millest hiljem sai tõenäosusteooria. Nad lõid mõned kombinatoorsed meetodid, mis aitas suuresti neid, kes hiljem teooria enda loosid ja arendasid.

XVII sajandi teisel poolel algas tõenäosusteooria põhimõistete ja meetodite kujunemine. Juhuslike suuruste definitsioonid, liht- ja mõne kompleksse sõltumatu ja tõenäosuse arvutamise meetodid sõltuvad sündmused. Selle huvi juhuslike muutujate ja tõenäosuste vastu tingis hasartmängud: Iga inimene tahtis teada, millised on nende võimalused mängu võita.

Järgmine etapp oli matemaatilise analüüsi meetodite rakendamine tõenäosusteoorias. Selle ülesande võtsid endale silmapaistvad matemaatikud nagu Laplace, Gauss, Poisson ja Bernoulli. Just nemad viisid selle matemaatika valdkonna edasi uus tase. James Bernoulli avastas binoomjaotuse seaduse. Muide, nagu hiljem teada saame, tehti selle avastuse põhjal veel mitmeid, mis võimaldasid luua normaaljaotuse seaduse ja palju muud.

Nüüd, enne kui hakkame binoomjaotust kirjeldama, värskendame pisut oma mälu tõenäosusteooria mõistete osas, mis oleme ilmselt juba kooliajast unustanud.

Tõenäosusteooria alused

Vaatleme selliseid süsteeme, mille tulemusel on võimalikud ainult kaks tulemust: "edu" ja "ebaõnnestumine". Seda on lihtne mõista näitega: viskame mündi, lootes, et see tuleb pähe. Iga võimaliku sündmuse (peade kukkumine - "edu", langevad pead - "ebaõnnestumine") tõenäosus on 50 protsenti, kui münt on täiesti tasakaalus ja puuduvad muud tegurid, mis võivad katset mõjutada.

See oli kõige lihtsam üritus. Kuid on ka keerulised süsteemid, milles sooritatakse järjestikuseid toiminguid, ja nende toimingute tulemuste tõenäosus on erinev. Mõelgem näiteks järgmisele süsteemile: kastis, mille sisu me ei näe, on kuus täiesti identset palli, kolm paari sinist, punast ja valged lilled. Peame saama paar palli juhuslikult. Seega, tõmmates esimesena välja ühe valge palli, vähendame oluliselt tõenäosust, et järgmisena saame ka valge palli. See juhtub seetõttu, et objektide arv süsteemis muutub.

IN järgmine jaotis vaatame keerulisemaid matemaatilised mõisted, mis viib meid sõnade tähendusele lähemale " normaaljaotus", "binoomjaotus" jms.

Matemaatilise statistika elemendid

Statistikas, mis on tõenäosusteooria üks rakendusvaldkondi, on palju näiteid, kus analüüsimiseks vajalikke andmeid pole selgesõnaliselt antud. See tähendab, et mitte numbriliselt, vaid tunnuste järgi, näiteks soo järgi. Selleks, et rakendada sellistele andmetele matemaatilist aparatuuri ja teha saadud tulemustest mõningaid järeldusi, on vaja algandmed teisendada numbri vorming. Tavaliselt omistatakse selleks positiivsele tulemusele väärtus 1 ja negatiivsele tulemusele 0. Nii saame statistilisi andmeid, mida saab analüüsida matemaatilisi meetodeid kasutades.

Järgmine samm juhusliku suuruse binoomjaotuse mõistmiseks on määrata juhusliku suuruse dispersioon ja matemaatiline ootus. Sellest räägime järgmises jaotises.

Oodatud väärtus

Tegelikult pole matemaatilise ootuse mõistmine keeruline. Mõelge süsteemile, milles on palju erinevaid üritusi koos nende erinevad tõenäosused. Matemaatiline ootus on kogus võrdne summaga nende sündmuste väärtuste produktid (ja matemaatiline vorm, millest me rääkisime viimases jaotises) nende rakendamise tõenäosuse kohta.

Binoomjaotuse matemaatiline ootus arvutatakse sama skeemi järgi: võtame juhusliku suuruse väärtuse, korrutame selle positiivse tulemuse tõenäosusega ja seejärel liidame saadud andmed kõigi muutujate kohta. Neid andmeid on väga mugav esitada graafiliselt – nii on erinevate väärtuste matemaatiliste ootuste erinevus paremini tajutav.

Järgmises osas räägime teile veidi teisest mõistest - juhusliku muutuja dispersioon. Samuti on see tihedalt seotud binoomtõenäosuse jaotuse mõistega ja on sellele iseloomulik.

Binoomjaotuse dispersioon

See väärtus on tihedalt seotud eelmisega ja iseloomustab ka statistiliste andmete jaotust. Ta esindab keskmine ruut väärtuste kõrvalekalded nende matemaatilistest ootustest. See tähendab, et juhusliku suuruse dispersioon on juhusliku suuruse väärtuse ja selle matemaatilise ootuse vaheliste erinevuste ruudu summa, mis on korrutatud selle sündmuse tõenäosusega.

Üldiselt on see kõik, mida peame dispersiooni kohta teadma, et mõista, mis on binoomne tõenäosusjaotus. Liigume nüüd otse meie põhiteema juurde. Nimelt sellele, mis sellise pealtnäha üsna taga peitub keeruline fraas"Binoomjaotuse seadus".

Binoomjaotus

Mõelgem kõigepealt välja, miks see jaotus on binoomne. See pärineb sõnast "binom". Võib-olla olete kuulnud Newtoni binoomist – valemist, mida saab kasutada mis tahes kahe arvu a ja b summa laiendamiseks mis tahes mittenegatiivse astmeni n.

Nagu te ilmselt juba arvasite, on Newtoni binoomvalem ja binoomjaotuse valem peaaegu samad. Ainsa erandiga, mis teisel on rakendatud väärtus Sest konkreetsed kogused, ja esimene on vaid üldine matemaatiline tööriist, mille rakendused praktikas võivad olla erinevad.

Jaotusvalemid

Binoomjaotusfunktsiooni saab kirjutada järgmiste terminite summana:

(n!/(n-k)!k!)*p k *q n-k

Siin n on sõltumatute juhuslike katsete arv, p on edukate tulemuste arv, q on ebaõnnestunud tulemuste arv, k on katse arv (võib võtta väärtused 0 kuni n),! - faktoriaali tähistus, arvu funktsioon, mille väärtus on võrdne kõigi sellele eelnevate arvude korrutisega (näiteks arvule 4: 4!=1*2*3*4=24).

Lisaks saab binoomjaotusfunktsiooni kirjutada mittetäieliku beetafunktsioonina. See on aga keerulisem definitsioon, mida kasutatakse vaid keeruliste statistiliste probleemide lahendamisel.

Binoomjaotus, mille näited me eespool üle vaadasime, on üks populaarsemaid lihtsad tüübid jaotused tõenäosusteoorias. Samuti on olemas normaaljaotus, mis on teatud tüüpi binoom. Seda kasutatakse kõige sagedamini ja seda on kõige lihtsam arvutada. Samuti on olemas Bernoulli jaotused, Poissoni jaotused ja tingimuslikud jaotused. Kõik need iseloomustavad graafiliselt konkreetse protsessi tõenäosusvahemikke erinevates tingimustes.

Järgmises osas käsitleme selle matemaatilise aparaadi kasutamisega seotud aspekte päris elu. Esmapilgul tundub muidugi, et tegemist on lihtsalt järjekordse matemaatilise asjaga, mis nagu ikka, päriselus rakendust ei leia ja mida peale matemaatikute endi pole üldjuhul vaja. See aga nii ei ole. Lõppude lõpuks, igat tüüpi distributsioonid ja nende graafilised esitused on loodud eranditult praktilistel eesmärkidel, ja mitte teadlaste kapriisina.

Rakendus

Jaotuse kõige olulisem rakendus on muidugi statistikas, sest seal on vaja terviklik analüüs palju andmeid. Nagu praktika näitab, on paljudel andmekogumitel ligikaudu sama väärtuste jaotus: väga madalate ja väga kõrgete väärtustega kriitilised piirkonnad sisaldavad reeglina vähem elemente kui keskmised väärtused.

Suurte andmekogumite analüüs ei ole vajalik ainult statistikas. See on asendamatu näiteks sisse füüsikaline keemia. Selles teaduses kasutatakse seda paljude suuruste määramiseks, mis on seotud aatomite ja molekulide juhuslike vibratsioonide ja liikumisega.

Järgmises jaotises mõistame, kui oluline on seda kasutada statistilised mõisted, nagu binoom juhusliku suuruse jaotus sisse Igapäevane elu sinu ja minu jaoks.

Miks ma seda vajan?

Paljud inimesed küsivad endalt seda küsimust, kui tegemist on matemaatikaga. Muide, matemaatikat ei nimetata asjata teaduste kuningannaks. See on füüsika, keemia, bioloogia, majanduse alus ja kõigis neis teadustes kasutatakse ka mingit jaotust: kas see on diskreetne binoomjaotus või normaaljaotus, pole vahet. Ja kui me ümbritsevat maailma lähemalt vaatame, näeme, et matemaatikat kasutatakse kõikjal: igapäevaelus, tööl ja isegi inimsuhted saab esitada statistiliste andmete kujul ja analüüsida (seda, muide, need, kes töötavad eriorganisatsioonid seotud teabe kogumisega).

Räägime nüüd veidi sellest, mida teha, kui peate selle teema kohta palju rohkem teadma, kui selles artiklis kirjeldasime.

Selles artiklis esitatud teave pole kaugeltki täielik. Jaotamise vormis on palju nüansse. Binoomjaotus, nagu me juba teada saime, on üks peamisi tüüpe, millel tervik matemaatika statistika ja tõenäosusteooria.

Kui tunnete huvi või peate oma tööga seoses sellel teemal palju rohkem teadma, peate õppima erialakirjandust. Alustada tuleks ülikoolikursusest matemaatiline analüüs ja jõuda tõenäosusteooria osani. Kasuks tulevad ka teadmised seeriate kohta, sest binoomne tõenäosusjaotus pole midagi muud kui järjestikuste liikmete jada.

Järeldus

Enne artikli lõpetamist tahaksime teile öelda veel ühe huvitava asja. See puudutab otseselt meie artikli teemat ja kogu matemaatikat üldiselt.

Paljud inimesed ütlevad, et matemaatika on kasutu teadus ja miski, mida nad koolis õppisid, polnud neile kasulik. Kuid teadmised pole kunagi üleliigsed ja kui miski pole teile elus kasulik, tähendab see, et te lihtsalt ei mäleta seda. Kui teil on teadmisi, saavad nad teid aidata, aga kui teil pole, siis ei saa te neilt abi oodata.

Niisiis, vaatasime binoomjaotuse mõistet ja kõiki sellega seotud definitsioone ning rääkisime, kuidas seda meie elus rakendatakse.

Vaatleme binoomjaotust, arvutame selle matemaatilise ootuse, dispersiooni ja mooduse. Kasutades MS EXCEL funktsiooni BINOM.DIST() joonistame jaotusfunktsiooni ja tõenäosustiheduse graafikud. Hindame jaotuse parameetrit p, jaotuse matemaatilist ootust ja standardhälve. Vaatleme ka Bernoulli jaotust.

Definitsioon. Las need toimuvad n katsed, millest igaühes võib toimuda ainult 2 sündmust: sündmus "eduneb" tõenäosusega lk või tõenäosusega "tõrke" sündmus q =1-p (nn Bernoulli skeem,Bernoullikatsumused).

Täpselt kättesaamise tõenäosus x edu nendes n testid on võrdne:

Valimi õnnestumiste arv x on juhuslik muutuja, millel on Binoomjaotus(Inglise) Binoomlevitamine) lk Ja n– on selle jaotuse parameetrid.

Pidage seda kasutamiseks meeles Bernoulli skeemid ja vastavalt binoomjaotus, peavad olema täidetud järgmised tingimused:

• Igal testil peab olema täpselt kaks tulemust, mida tavaliselt nimetatakse eduks ja ebaõnnestumiseks.
• iga testi tulemus ei tohiks sõltuda eelmiste testide tulemustest (testi sõltumatus).
• õnnestumise tõenäosus lk peab olema kõigi testide jaoks konstantne.

Binoomjaotus MS EXCELIS

MS EXCELIS, alates versioonist 2010, jaoks Binoomjaotus on funktsioon BINOM.DIST(), Ingliskeelne nimi- BINOM.DIST(), mis võimaldab arvutada tõenäosuse, et valim täpselt sisaldab X"edu" (st. tõenäosustiheduse funktsioon p(x), vt ülaltoodud valemit) ja kumulatiivne jaotusfunktsioon(tõenäosus, et proovis on x või vähem õnnestumisi, sealhulgas 0).

Enne MS EXCEL 2010 oli EXCELIS funktsioon BINOMDIST(), mis võimaldab ka arvutada jaotusfunktsioon Ja tõenäosustihedus p(x). BINOMIST() on ühilduvuse tagamiseks jäetud MS EXCEL 2010-sse.

Näidisfail sisaldab graafikuid tõenäosustiheduse jaotus Ja .

Binoomjaotus omab tähistust B(n; lk) .

Märge: Ehitamiseks kumulatiivne jaotusfunktsioon täiuslik tüübidiagramm Ajakava, Sest jaotustihedus – Histogramm koos rühmitamisega. Diagrammide loomise kohta lisateabe saamiseks lugege artiklit Diagrammide põhitüübid.

Märge: Valemite kirjutamise mugavuse huvides on näidisfailis loodud parameetrite nimed Binoomjaotus: n ja p.

Näidisfail näitab erinevaid tõenäosusarvutusi, kasutades MS EXCELi funktsioone:

Nagu näete ülaltoodud pildil, eeldatakse, et:

• Lõpmatu populatsioon, millest valim võetakse, sisaldab 10% (või 0,1) kehtivaid elemente (parameeter lk, funktsiooni kolmas argument = BINOM.DIST() )
• Arvutada tõenäosus, et 10 elemendist koosnevas valimis (parameeter n, funktsiooni teine ​​argument) on täpselt 5 kehtivat elementi (esimene argument), peate kirjutama valemi: =BINOM.DIST(5, 10, 0,1, VÄÄR)
• Viimane, neljas element on seatud = FALSE, st. tagastab funktsiooni väärtuse jaotustihedus.

Kui neljanda argumendi väärtus on TRUE, tagastab funktsioon BINOM.DIST() väärtuse kumulatiivne jaotusfunktsioon või lihtsalt Jaotusfunktsioon. Sel juhul saate arvutada tõenäosuse, et sobivate elementide arv valimis pärineb teatud vahemik, näiteks 2 või vähem (sh 0).

Selleks peate kirjutama valemi:
= BINOM.DIST(2; 10; 0,1; TRUE)

Märge: x mittetäisarvulise väärtuse korral . Näiteks järgmised valemid tagastavad sama väärtuse:
=BINOM.DIST( 2 ; 10; 0,1; TÕSI)
=BINOM.DIST( 2,9 ; 10; 0,1; TÕSI)

Märge: Näidisfailis tõenäosustihedus Ja jaotusfunktsioon arvutatakse ka definitsiooni ja funktsiooni NUMBERCOMB() abil.

Jaotusnäitajad

IN näidisfail töölehel Näide Mõnede jaotusnäitajate arvutamiseks on olemas valemid:

• =n*p;
• (standardhälve ruudus) = n*p*(1-p);
• = (n+1)*p;
• =(1-2*p)*JUUR(n*p*(1-p)).

Tuletame valemi matemaatiline ootus Binoomjaotus kasutades Bernoulli ringrada.

A-prioor juhuslik väärtus X sisse Bernoulli skeem(Bernoulli juhuslik muutuja) on jaotusfunktsioon:

Seda jaotust nimetatakse Bernoulli jaotus.

Märge: Bernoulli jaotus – erijuhtum Binoomjaotus parameetriga n=1.

Loome 3 massiivi 100 numbrist, millest igaühel on erinev edu tõenäosus: 0,1; 0,5 ja 0,9. Selleks aknas Põlvkond juhuslikud arvud installida järgmised parameetrid iga tõenäosuse p kohta:

Märge: kui määrate valiku Juhuslik hajumine (Juhuslik seeme), siis saate valida konkreetse juhuslik komplekt genereeritud numbrid. Näiteks kui määrate selle valiku =25, saate genereerida erinevates arvutites samu juhuslike arvude komplekte (juhul, kui muud jaotuse parameetrid on muidugi samad). Optsiooni väärtus võib võtta täisarvud vahemikus 1 kuni 32 767 Juhuslik hajumine võib olla segane. Parem oleks see tõlkida kui Vali number juhuslike numbritega.

Selle tulemusena saame 3 veergu 100 numbriga, mille põhjal saame näiteks hinnata edu tõenäosust lk valemi järgi: Õnnestumiste arv/100(cm. Näidisfailileht GenerationBernoulli).

Märge: Sest Bernoulli distributsioonid p=0.5 korral saab kasutada valemit =RANDBETWEEN(0;1), mis vastab .

Juhuslike arvude genereerimine. Binoomjaotus

Oletame, et proovis on 7 defektset toodet. See tähendab, et on "väga tõenäoline", et defektsete toodete osakaal on muutunud lk, mis on meie tootmisprotsessile iseloomulik. Kuigi selline olukord on "väga tõenäoline", on olemas võimalus (alfa risk, 1. tüüpi viga, "valehäire"). lk jäi muutumatuks ning defektsete toodete arvu suurenemine oli tingitud juhuslikust proovivõtust.

Nagu on näha alloleval joonisel, on 7 defektsete toodete arv, mis on vastuvõetav protsessi jaoks, mille p=0,21 sama väärtuse juures Alfa. See näitab, et kui proovis olevate defektsete esemete läviväärtus on ületatud, lk"tõenäoliselt" on suurenenud. Väljend "kõige tõenäolisemalt" tähendab, et on vaid 10% tõenäosus (100%-90%), et defektsete toodete osakaalu hälve üle läve on tingitud ainult juhuslikest põhjustest.

Seega võib proovis olevate defektsete toodete piirarvu ületamine olla signaaliks, et protsess on häiritud ja on hakanud tootma kasutatud tooteid. O suurem defektsete toodete protsent.

Märge: Enne MS EXCEL 2010 oli EXCELil funktsioon CRITBINOM(), mis on samaväärne funktsiooniga BINOM.INV(). CRITBINOM() jäetakse ühilduvuse tagamiseks MS EXCEL 2010 ja uuemates versioonides.

Binoomjaotuse seos teiste jaotustega

Kui parameeter n Binoomjaotus kipub lõpmatuseni, ja lk kipub olema 0, siis antud juhul Binoomjaotus saab ligikaudselt hinnata.
Saame sõnastada tingimused, kui lähendus Poissoni jaotus töötab hästi:

• lk<0,1 (vähem lk ja veel n, seda täpsem on lähendus);
• lk>0,9 (võttes arvesse, et q=1- lk, tuleb sel juhul arvutused läbi teha q(A X tuleb asendada n- x). Seetõttu, mida vähem q ja veel n, seda täpsem on lähendus).

Kell 0,1<=p<=0,9 и n*p>10 Binoomjaotus saab ligikaudselt hinnata.

Omakorda Binoomjaotus võib olla hea ligikaudne väärtus, kui populatsiooni suurus on N Hüpergeomeetriline jaotus palju suurem kui valimi suurus n (st N>>n või n/N<<1).

Lisateavet ülaltoodud jaotuste vahelise seose kohta leiate artiklist. Seal on ka näiteid lähendusest ning selgitatakse tingimusi, millal ja millise täpsusega see on võimalik.

NÕUANNE: Teiste MS EXCELi distributsioonide kohta saate lugeda artiklist.

Binoomjaotus on diskreetselt muutuva juhusliku suuruse üks olulisemaid tõenäosusjaotusi. Binoomjaotus on arvu tõenäosusjaotus m sündmuse toimumine A V nüksteisest sõltumatud vaatlused. Sageli sündmus A Seda nimetatakse vaatluse "edukuks" ja vastupidist sündmust "ebaõnnestumiseks", kuid see määratlus on väga tingimuslik.

Binoomjaotuse tingimused:

• kokku läbi viidud n katsed, milles sündmus A võib tekkida või mitte;
• sündmus A igas testis võib esineda sama tõenäosusega lk;
• testid on üksteisest sõltumatud.

Tõenäosus, et sisse n testimisüritus A see tuleb täpselt m korda, saab arvutada Bernoulli valemi abil:

,

Kus lk- sündmuse toimumise tõenäosus A;

q = 1 - lk- vastupidise sündmuse toimumise tõenäosus.

Selgitame välja miks on binoomjaotus seotud Bernoulli valemiga ülalkirjeldatud viisil? . Sündmus – kordaminekute arv kell n testid on jagatud mitmeks valikuks, millest igaühes saavutatakse edu m testid ja ebaõnnestumine - sisse n - m testid. Mõelgem ühele neist võimalustest - B1 . Kasutades tõenäosuste liitmise reeglit, korrutame vastupidiste sündmuste tõenäosused:

,

ja kui me tähistame q = 1 - lk, See

.

Mis tahes muu variant, milles m edu ja n - m ebaõnnestumisi. Selliste valikute arv on võrdne võimaluste arvuga n proovi saada m edu.

Kõigi tõenäosuste summa m sündmuste esinemisnumbrid A(numbrid 0 kuni n) on võrdne ühega:

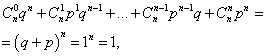
kus iga liige tähistab üht liiget Newtoni binoomis. Seetõttu nimetatakse vaadeldavat jaotust binoomjaotuseks.

Praktikas on sageli vaja arvutada tõenäosusi "mitte rohkem kui m edu sisse n testid" või "vähemalt m edu sisse n testid". Selleks kasutatakse järgmisi valemeid.

Integraalfunktsioon, see tähendab tõenäosus F(m) mis sees on n vaatlusüritus A rohkem ei tule müks kord, saab arvutada järgmise valemi abil:

Omakorda tõenäosus F(≥m) mis sees on n vaatlusüritus A ei tule vähem müks kord, arvutatakse järgmise valemiga:

Mõnikord on mugavam arvutada selle tõenäosus n vaatlusüritus A rohkem ei tule m korda, vastupidise sündmuse tõenäosuse kaudu:

.

Millist valemit kasutada, sõltub sellest, kummal neist on vähem termineid sisaldav summa.

Binoomjaotuse karakteristikud arvutatakse järgmiste valemite abil .

Oodatud väärtus: .

Dispersioon:.

Standardhälve: .

Binoomjaotus ja arvutused MS Excelis

Binoomtõenäosus P n ( m) ja integraalfunktsiooni väärtused F(m) saab arvutada MS Exceli funktsiooni BINOM.DIST abil. Vastava arvutuse aken on näidatud allpool (suurendamiseks klõpsake vasakut nuppu).

MS Excel nõuab järgmiste andmete sisestamist:

• õnnestumiste arv;
• testide arv;
• õnnestumise tõenäosus;
• integraal - loogiline väärtus: 0 - kui teil on vaja arvutada tõenäosus P n ( m) ja 1 – kui tõenäosus F(m).

Näide 1. Firmajuht võttis kokku info viimase 100 päeva müüdud kaamerate arvu kohta. Tabelis on kokku võetud teave ja arvutatud tõenäosus, et teatud arv kaameraid müüakse päevas.

Päev lõpeb kasumiga, kui müüakse 13 või enam kaamerat. Tõenäosus, et päev kulgeb kasumlikult:

Tõenäosus, et päev töötatakse tulutult:

Olgu tõenäosus, et päev töötatakse kasumiga, konstantne ja võrdne 0,61-ga ning päevas müüdavate kaamerate arv ei sõltu päevast. Siis saame kasutada binoomjaotust, kus sündmus A- päev töötatakse kasumiga, - tulutult.

Tõenäosus, et kõik 6 päeva töötatakse kasumiga:

.

Sama tulemuse saame MS Exceli funktsiooni BINOM.DIST abil (integraali väärtuseks on 0):

P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.

Tõenäosus, et 6 päevast töötatakse kasumiga 4 või enam päeva:

Kus ,

,

Kasutades MS Exceli funktsiooni BINOM.DIST, arvutame välja tõenäosuse, et 6 päevast ei saa kasumit rohkem kui 3 päeva (integraalväärtuse väärtus on 1):

P 6 (≤3 ) = BINOM.DIST(3; 6; 0,61; 1) = 0,435.

Tõenäosus, et kõik 6 päeva mööduvad kahjumiga:

,

Sama näitaja saame arvutada MS Exceli funktsiooni BINOM.DIST abil:

P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.

Lahendage probleem ise ja seejärel vaadake lahendust

Näide 2. Urnis on 2 valget ja 3 musta palli. Urnist võetakse pall välja, värvitakse ja pannakse tagasi. Katset korratakse 5 korda. Valgete pallide esinemiste arv on diskreetne juhuslik suurus X, jaotatud binoomseaduse järgi. Koostage juhusliku suuruse jaotusseadus. Määratlege režiim, matemaatiline ootus ja dispersioon.

Jätkame koos probleemide lahendamist

Näide 3. Kulleriteenistusest läksime objektidele n= 5 kullerit. Iga kuller on tõenäoline lk= 0,3, olenemata teistest, jääb objektile hiljaks. Diskreetne juhuslik suurus X- hilinenud kullerite arv. Koostage selle juhusliku muutuja jaotusseeria. Leidke selle matemaatiline ootus, dispersioon, standardhälve. Leidke tõenäosus, et vähemalt kaks kullerit jäävad objektidele hiljaks.

Binoomjaotus

mõne sündmuse esinemiste arvu tõenäosusjaotus korduvate sõltumatute katsete käigus. Kui iga katse ajal on sündmuse toimumise tõenäosus võrdne R, ja 0 ≤ lk≤ 1, siis selle sündmuse esinemiste arv μ juures n sõltumatud katsed on juhuslikud muutujad, mis võtavad väärtusi m = 1, 2,.., n tõenäosustega

Kus q= 1 - p, a - binoomkoefitsiendid (sellest ka nimi B. R.). Ülaltoodud valemit nimetatakse mõnikord Bernoulli valemiks. Matemaatiline ootus ja väärtuse μ dispersioon, millel on B. r., on võrdsed M(μ) = n.p. Ja D(μ) = npq, vastavalt. Üldiselt n, Laplace'i teoreemi alusel (vt Laplace'i teoreem), B. r. normaaljaotuse lähedal (vt Normaaljaotus), mida praktikas kasutatakse. Väikeste jaoks n peate kasutama B. r tabeleid.

Lit.: Bolšev L. N., Smirnov N. V., Matemaatilise statistika tabelid, M., 1965.

Suur Nõukogude entsüklopeedia. - M.: Nõukogude entsüklopeedia. 1969-1978 .

Vaadake, mis on "binoomiline jaotus" teistes sõnaraamatutes:

Tõenäosusfunktsioon ... Wikipedia

- (binoomjaotus) Jaotus, mis võimaldab arvutada mitmete sõltumatute sündmuste vaatluse tulemusel saadud mis tahes juhusliku sündmuse toimumise tõenäosust, kui selle elementaarkomponentide esinemise tõenäosus ... ... Majandussõnastik

- (Bernoulli jaotus) kindla sündmuse esinemiste arvu tõenäosusjaotus korduvate sõltumatute katsete käigus, kui selle sündmuse toimumise tõenäosus igas katses on võrdne p(0 p 1). Täpselt, number? selle sündmuse juhtumid on ...... Suur entsüklopeediline sõnaraamat

binoomjaotus- - Telekommunikatsiooni teemad, põhimõisted EN binoomjaotus ...

- (Bernoulli jaotus), teatud sündmuse esinemiste arvu tõenäosusjaotus korduvate sõltumatute katsete käigus, kui selle sündmuse toimumise tõenäosus igas katses on võrdne p (0≤p≤1). Nimelt selle sündmuse esinemiste arv μ... ... entsüklopeediline sõnaraamat

binoomjaotus- 1.49. binoomjaotus Diskreetse juhusliku suuruse X tõenäosusjaotus, võttes mis tahes täisarvu väärtused vahemikus 0 kuni n, nii et x = 0, 1, 2, ..., n ja parameetrite n = 1, 2, ... ja 0< p < 1, где Источник … Normatiivse ja tehnilise dokumentatsiooni terminite sõnastik-teatmik

Bernoulli jaotus, juhusliku suuruse X tõenäosusjaotus, võttes vastavalt täisarvude väärtusi tõenäosustega (binoomkoefitsient; B. r. parameeter p, mida nimetatakse positiivse tulemuse tõenäosuseks, võttes väärtusi ... Matemaatiline entsüklopeedia

- (Bernoulli jaotus), teatud sündmuse esinemiste arvu tõenäosusjaotus korduvate sõltumatute katsete ajal, kui selle sündmuse toimumise tõenäosus igas katses on võrdne p (0<или = p < или = 1). Именно, число м появлений … Loodusteadus. entsüklopeediline sõnaraamat

Binoomne tõenäosusjaotus- (binoomjaotus) Jaotus, mida täheldatakse juhtudel, kui iga sõltumatu katse (statistilise vaatluse) tulemuseks on üks kahest võimalikust väärtusest: võit või lüüasaamine, kaasamine või väljajätmine, pluss või ... Majandus- ja matemaatikasõnastik

binoomne tõenäosusjaotus- Jaotus, mida jälgitakse juhtudel, kui iga sõltumatu katse (statistilise vaatluse) tulemusel on üks kahest võimalikust väärtusest: võit või lüüasaamine, kaasamine või väljajätmine, pluss või miinus, 0 või 1. See tähendab... ... Tehniline tõlkija juhend

Raamatud

• Tõenäosusteooria ja matemaatiline statistika ülesannetes. Rohkem kui 360 probleemi ja harjutust, D. A. Borzykh. Kavandatav käsiraamat sisaldab erineva keerukusega ülesandeid. Põhirõhk on siiski keskmise keerukusega ülesannetel. Seda tehakse tahtlikult, et julgustada õpilasi...
• Tõenäosusteooria ja matemaatiline statistika ülesannetes: Rohkem kui 360 ülesannet ja harjutust, Borzykh D.. Kavandatav käsiraamat sisaldab erineva keerukusega probleeme. Põhirõhk on siiski keskmise keerukusega ülesannetel. Seda tehakse tahtlikult, et julgustada õpilasi...

7. peatükk.

Juhuslike suuruste jaotuse spetsiifilised seadused

Diskreetsete juhuslike suuruste jaotusseaduste tüübid

Olgu väärtused diskreetne juhuslik suurus X 1 , X 2 , …, x n,…. Nende väärtuste tõenäosusi saab arvutada erinevate valemite abil, kasutades näiteks tõenäosusteooria põhiteoreeme, Bernoulli valemit või mõnda muud valemit. Mõne sellise valemi puhul on jaotusseadusel oma nimi.

Diskreetse juhusliku suuruse levinumad jaotuse seadused on binoomne, geomeetriline, hüpergeomeetriline ja Poissoni jaotuse seadus.

Binoomjaotuse seadus

Las toodetakse n sõltumatud katsed, millest igaühes võib sündmus esineda või mitte A. Selle sündmuse toimumise tõenäosus igas üksikus katses on konstantne, ei sõltu katse numbrist ja on võrdne R=R(A). Sellest tuleneb ka tõenäosus, et sündmust ei toimu A igas testis on samuti konstantne ja võrdne q=1–R. Mõelge juhuslikule muutujale X võrdne sündmuse esinemiste arvuga A V n testid. Ilmselt on selle koguse väärtused võrdsed

X 1 =0 – sündmus A V n teste ei ilmunud;

X 2 =1 – sündmus A V n esines kord katsetel;

X 3 =2 – sündmus A V n testid ilmusid kaks korda;

…………………………………………………………..

x n +1 = n- sündmus A V n kõik ilmnes katsete käigus nüks kord.

Nende väärtuste tõenäosusi saab arvutada Bernoulli valemi (4.1) abil:

Kus To=0, 1, 2, …,n .

Binoomjaotuse seadus X, võrdub õnnestumiste arvuga aastal n Bernoulli testid, edu tõenäosusega R.

Seega on diskreetsel juhuslikul muutujal binoomjaotus (või jaotatakse vastavalt binoomseadusele), kui selle võimalikud väärtused on 0, 1, 2, ..., n, ja vastavad tõenäosused arvutatakse valemi (7.1) abil.

Binoomjaotus sõltub kahest parameetrid R Ja n.

Binoomseaduse järgi jaotatud juhusliku suuruse jaotusrida on järgmisel kujul:

X			…	k	…	n
R			…		…

Näide 7.1 . Sihtmärki tehakse kolm iseseisvat lasku. Iga lasu tabamise tõenäosus on 0,4. Juhuslik väärtus X– sihtmärgi tabamuste arv. Koostage selle jaotusseeria.

Lahendus. Juhusliku suuruse võimalikud väärtused X on X 1 =0; X 2 =1; X 3 =2; X 4 =3. Leiame Bernoulli valemi abil vastavad tõenäosused. Pole raske näidata, et selle valemi kasutamine siin on täiesti õigustatud. Pange tähele, et tõenäosus, et ühe lasuga sihtmärki ei taba, on 1-0,4=0,6. Saame

Jaotussarja vorm on järgmine:

X
R	0,216	0,432	0,288	0,064

Lihtne on kontrollida, kas kõigi tõenäosuste summa on võrdne 1-ga. Juhuslik suurus ise X jagatud binoomseaduse järgi. ■

Leiame binoomseaduse järgi jaotatud juhusliku suuruse matemaatilise ootuse ja dispersiooni.

Näite 6.5 lahendamisel näidati, et sündmuse esinemiste arvu matemaatiline ootus A V n sõltumatud katsed, kui esinemise tõenäosus A igas testis on konstantne ja võrdne R, võrdub n· R

Selles näites kasutati juhuslikku muutujat, mis on jaotatud binoomseaduse järgi. Seetõttu on näite 6.5 lahendus sisuliselt järgmise teoreemi tõestus.

Teoreem 7.1. Binoomseaduse järgi jaotatud diskreetse juhusliku suuruse matemaatiline ootus on võrdne katsete arvu ja “edukuse” tõenäosuse korrutisega, s.o. M(X)=n· R.

Teoreem 7.2. Binoomseaduse järgi jaotatud diskreetse juhusliku suuruse dispersioon on võrdne katsete arvu korrutisega “edu” tõenäosusega ja “ebaõnnestumise” tõenäosusega, s.o. D(X)=nрq.

Binoomseaduse järgi jaotatud juhusliku suuruse asümmeetria ja kurtoos määratakse valemitega

Neid valemeid saab saada alg- ja keskmomendi mõistet kasutades.

Binoomjaotuse seadus on paljude tegelike olukordade aluseks. Suurte väärtuste jaoks n Binoomjaotust saab ligikaudselt hinnata teiste jaotuste, eriti Poissoni jaotuse abil.

Poissoni jaotus

Las olla n Bernoulli testid koos testide arvuga n piisavalt suur. Varem näidati, et sel juhul (kui pealegi on tõenäosus R sündmused A väga väike), et leida tõenäosus, et sündmus A ilmuma T Testides saate kasutada Poissoni valemit (4.9). Kui juhuslik suurus X tähendab sündmuse esinemiste arvu A V n Bernoulli testid, siis tõenäosus, et X võtab väärtuse k saab arvutada valemi abil

, (7.2)

Kus λ = nr.

Poissoni jaotamise seadus nimetatakse diskreetse juhusliku suuruse jaotuseks X, mille võimalikud väärtused on mittenegatiivsed täisarvud ja tõenäosused r t need väärtused leitakse valemi (7.2) abil.

Suurusjärk λ = nr helistas parameeter Poissoni jaotused.

Poissoni seaduse järgi jaotatud juhuslik suurus võib omandada lõpmatu arvu väärtusi. Kuna selle jaotuse korral on tõenäosus R Sündmuse esinemine igas katses on väike, siis nimetatakse seda jaotust mõnikord haruldaste sündmuste seaduseks.

Poissoni seaduse järgi jaotatud juhusliku suuruse jaotusridadel on vorm

X					…	T	…
R					…		…

Lihtne on kontrollida, kas teise rea tõenäosuste summa on võrdne 1-ga. Selleks peate meeles pidama, et funktsiooni saab laiendada Maclaurini seeriaks, mis koondub mis tahes X. Sel juhul on meil

. (7.3)

Nagu märgitud, asendab Poissoni seadus teatud piiravatel juhtudel binoomseadust. Näiteks on juhuslik muutuja X, mille väärtused on võrdsed rikete arvuga teatud aja jooksul tehnilise seadme korduval kasutamisel. Eeldatakse, et tegemist on ülimalt töökindla seadmega, s.t. Ühe rakenduse ebaõnnestumise tõenäosus on väga väike.

Lisaks sellistele piiravatele juhtudele on praktikas Poissoni seaduse järgi jaotatud juhuslikud muutujad, mida binoomjaotusega ei seostata. Näiteks kasutatakse Poissoni jaotust sageli, kui käsitletakse teatud ajaperioodi sündmuste arvu (telefonikeskjaama saabunud kõnede arv tunni jooksul, autopesulasse saabunud autode arv päeva jooksul, masina peatumiste arv nädalas jne). Kõik need sündmused peaksid moodustama nn sündmuste voo, mis on järjekorrateooria üks põhimõisteid. Parameeter λ iseloomustab sündmuste voo keskmist intensiivsust.