Tükkide kaupa lineaarne funktsioon antakse valemiga find in. X=1 – valemi muutmise punkt

7
Algebratund 9A klassis õpetaja Mikitšuk Zh.N. Munitsipaalõppeasutus "Keskkool nr 23"19.03.2007Tunni teema: "Tükkide kaupa määratletud funktsioonid" Eesmärgid:

kõnekultuur

Teema üldistamise tulemusena peaksid õpilased tean:

antud funktsioon

suutma:

tükkhaaval antud funktsiooni graafiku koostamine; loe diagrammi; defineerida funktsiooni analüütiliselt graafiku abil.

Tundide ajal

I. Organisatsiooniline ja psühholoogiline moment. Alustame oma õppetundi D.K. Fadejevi sõnadega: "Ükskõik, mis probleemi te lahendate, ootab teid rõõmus hetk - rõõmus edutunne, mis tugevdab usku teie tugevusse. II. Kodutööde kontrollimine. Alustame õppetundi nagu tavaliselt d/z kontrollimisega - Korrake funktsioonide definitsiooni ja funktsioonide õppimise plaani 1). Töölaual joonesta enda leiutatud tükkhaaval funktsioonide graafikud (joon. 1, 2, 3)2). Kaardid.№1. Järjesta funktsioonide omaduste uurimise järjekord:

väikseim väärtus

Nr 2. Joonistage skemaatiliselt funktsioonide graafikud:

A) y = kx + b, k0; B) y = kx, k0;

B) y = , k0.

3).Suuline töö . - 2 minutit

Millist funktsiooni nimetatakse tükkhaaval?Nimetatakse osade kaupa funktsiooni erinevad valemid erinevate intervallidega.

Millistest funktsioonidest koosnevad joonistel 1, 2, 3 näidatud tükipõhised funktsioonid? Milliseid funktsioonide nimesid te veel teate? Kuidas nimetatakse vastavate funktsioonide graafikuid? Kas joonisel 4 kujutatud joonis on mõne funktsiooni graafik? Miks?Vastus: ei, sest Funktsiooni definitsiooni järgi on sõltumatu muutuja x iga väärtus seotud sõltuva muutuja y ühe väärtusega. 4) Enesekontroll - 3 min Pakutud graafikute ja vastavate funktsioone määratlevate valemite hulgast valige õiged. Koostage saadud vastuste tähtedest tuttav sõna. Vastus: GRAAFIK kus me elus, teaduses, igapäevaelus kohtame veel sõna GRAAFILINE - massi sõltuvuse graafik - graafik - töögraafik; esitada mitmesugust teavet, näiteks mahtu tööstuslik tootmine Saratovi piirkonnas ajavahemikul 1980 kuni 2002. Selle graafiku abil saate jälgida toodangu vähenemist ja suurenemist üksikutel aastatel – öelge, milline funktsioonigraafik seda teavet esindab. Vastus: tükkhaaval funktsioon.III. Teema sõnum, tunni eesmärk. Tunni teema:"Tükkide kaupa määratletud funktsioonid" Sihtmärk:- tükikaupa etteantud funktsiooni näitel tuletada meelde funktsioonide uurimise plaan;

korrake tükkhaaval etteantud funktsiooni konstrueerimise etappe; rakendada üldistatud teadmisi mittestandardsete ülesannete lahendamisel.IV. Varem omandatud teadmiste värskendamine. Esimest korda puutusime funktsiooni mõistega kokku 7. klassis õppimise ajal lineaarne sõltuvus. Reaalsete protsesside modelleerimise seisukohalt vastab see sõltuvus ühtsetele protsessidele Näide: Jalakäija liikumine koos püsikiirus ajaks t. Valem: s =vt, graafik – joonelõigud, paiknevad I kvartalis.
8. klassi põhiteema on ruutfunktsioon, simuleerides ühtlaselt kiirendatud protsesse Näide: 9. klassis õpitud valem kuumutatud lambi takistuse (R) määramiseks konstantse võimsuse (P) ja muutuva pinge (U) juures. ValemR =

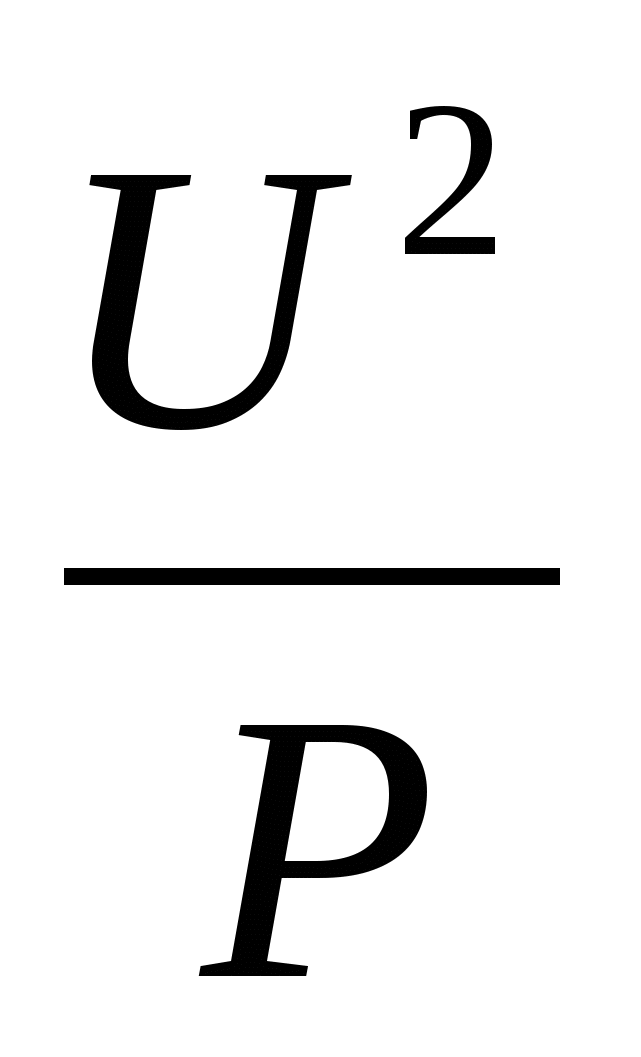, graafik on esimeses kvartalis paikneva parabooli haru.
Sest kolm aastat rikastusid meie teadmised funktsioonidest, kasvas uuritavate funktsioonide hulk ning laienes ülesannete komplekt, mille lahendamiseks tuli kasutada graafikuid Nimeta seda tüüpi ülesandeid... -. võrrandite lahendamine;- võrrandisüsteemide lahendamine;- ebavõrdsuse lahendamine;- funktsioonide omaduste uurimine.V. Õpilaste ettevalmistamine üldistustegevusteks. Meenutagem üht ülesannete liiki, nimelt funktsioonide omaduste uurimist või graafiku lugemist. Pöördume õpiku poole. Lk 65 Joon. 20a alates nr 250. Harjutus: loe funktsiooni graafikut. Funktsiooni uurimise protseduur on meie ees. 1. määratluspiirkond – (-∞; +∞)2. paaris, paaritu – ei paaris ega paaritu3. monotoonsus - suureneb [-3; +∞), väheneb[-5;-3], konstant (-∞; -5];4. piiritus – altpoolt piiratud5. funktsiooni suurim ja väikseim väärtus – y max = 0, y max – ei eksisteeri;6. järjepidevus – pidev kogu määratlusvaldkonnas;7. Väärtuste vahemik on kumer nii alla kui üles (-∞; -5] ja [-2; +∞).VI. Teadmiste taastootmine uuel tasemel. Teate seda graafikute koostamine ja uurimine tükkhaaval määratletud funktsioonid, on käsitletud algebra eksami teises osas funktsioonide osas ning on väärt 4 ja 6 punkti. Pöördume ülesannete kogumi poole lk 119 - nr 4.19-1 Lahendus: 1).y = - x, - ruutfunktsioon, graafik - parabool, hargneb alla (a = -1, a 0). x -2 -1 0 1 2 y -4 -1 0 1 4 2) y = 3x – 10, - lineaarne funktsioon, graafik – sirgeTeeme mõnede väärtuste tabelix 3

3 y 0 -1 3) y= -3x -10, - lineaarfunktsioon, graafik - sirgeTeeme mõnede väärtuste tabeli x -3 -3 y 0 -1 4) Koostame ühes koordinaatsüsteemis funktsioonide graafikud ja valime graafikute osad etteantud intervallidega.
Leiame graafikult, millistel x väärtustel on funktsiooni väärtused mittenegatiivsed. Vastus: f(x)  0 x = 0 ja at

 3 VII.Töö mittestandardsete ülesannetega. nr 4.29-1), lk 121. Lahendus: 1) Sirge (vasakul) y = kx + b läbib punkte (-4;0) ja (-2;2). See tähendab -4 k + b = 0, -2 k + b = 2;

k = 1, b = 4, y = x+4. Vastus: x +4, kui x -2 y = kui -2  x £ 3 3 kui x  3
VIII.Teadmiste kontroll. Niisiis, teeme lühidalt kokkuvõtte. Mida me tunnis kordasime funktsioonide uurimise plaani, tükipõhise funktsiooni graafiku koostamise samme, funktsiooni analüütiliselt täpsustades? Vaatame, kuidas olete seda materjali õppinud. "4" - "5", "3" testimine I variant nr U

2 1 -1 -1 1 X

D(f) = , kumer üles ja alla , kumer üles ja alla , väheneb ____________ Piiratud ____________ ei eksisteeri üldse, maksimaalselt =_____ Pidev kogu definitsioonipiirkonna ulatuses E(f) = ____________ Kumerad mõlemad alla ja üles kogu määratluspiirkonnas

Tagasi ette

Tähelepanu! Slaidide eelvaated on ainult informatiivsel eesmärgil ja ei pruugi esindada kõiki esitluse funktsioone. Kui olete huvitatud see töö, laadige alla täisversioon.

Õpik: Algebra 8. klass, toimetanud A. G. Mordkovich.

Tunni tüüp: Uute teadmiste avastamine.

Eesmärgid:

õpetaja jaoks eesmärgid fikseeritakse igas tunni etapis;

õpilase jaoks:

Isiklikud eesmärgid:

Õppige selgelt, täpselt, asjatundlikult väljendama oma mõtteid verbaalselt ja kirjutamine, mõista ülesande tähendust;
Õppida rakendama omandatud teadmisi ja oskusi uute probleemide lahendamisel;
Õppige kontrollima oma tegevuse protsessi ja tulemusi;

Meta-aine eesmärgid:

Kognitiivses tegevuses:

Areng loogiline mõtlemine ja kõne, oskus oma hinnanguid loogiliselt põhjendada ja teha lihtsaid süstematiseerimisi;
Õppige püstitama hüpoteese, millal probleemi lahendamine, mõistab nende kontrollimise vajadust;
Rakenda teadmisi sisse standardne olukord, õppida iseseisvalt ülesandeid täitma;
Kanna teadmisi muutunud olukorda, näe ülesannet probleemsituatsiooni kontekstis;

Teabe- ja kommunikatsioonitegevuses:

Õppida dialoogi pidama, tunnustama õigust teistsugusele arvamusele;

Peegeldustegevuses:

Õppige ette nägema võimalikud tagajärjed teie tegevus;
Õppige kõrvaldama raskuste põhjuseid.

Õppeaine eesmärgid:

Uurige, mis on tükipõhine funktsioon;
Õppige defineerima osade kaupa antud funktsiooni analüütiliselt selle graafikust;

Tundide ajal

1. Enesemääramine haridustegevus

Lava eesmärk:

kaasata õpilasi õppetegevustesse;
määrake tunni sisu: jätkame arvuliste funktsioonide teema kordamist.

Organisatsioon haridusprotsess etapis 1:

T: Mida me eelmistes tundides tegime?

D: Kordasime numbriliste funktsioonide teemat.

U: Täna jätkame eelmiste tundide teema kordamist ja täna peame välja selgitama, mida uut selles teemas õppida saame.

2. Teadmiste uuendamine ja tegevustes esinevate raskuste fikseerimine

Lava eesmärk:

värskendada hariv sisu, vajalik ja piisav uue materjali tajumiseks: jäta meelde valemid numbrilised funktsioonid, nende omadused ja ehitusviisid;
värskendada vaimsed operatsioonid, vajalik ja piisav uue materjali tajumiseks: võrdlus, analüüs, üldistus;
fikseerige individuaalne raskus tegevuses, mis seda isiklikult demonstreerib märkimisväärsel tasemel olemasolevate teadmiste puudulikkus: tükikaupa antud funktsiooni analüütiline täpsustamine, samuti selle graafiku koostamine.

Haridusprotsessi korraldamine etapis 2:

T: Slaid näitab viit numbrilist funktsiooni. Määrake nende tüüp.

1) murd-ratsionaalne;

2) ruutkeskmine;

3) irratsionaalne;

4) funktsioon koos mooduliga;

5) rahusti.

T: Nimetage neile vastavad valemid.

3) ;

4) ;

U: Arutame, millist rolli mängib iga koefitsient nendes valemites?

D: Muutujad "l" ja "m" vastutavad nende funktsioonide graafikute nihutamise eest vastavalt vasakule - paremale ja üles - alla, koefitsient "k" esimeses funktsioonis määrab hüperbooli harude asukoha: k> 0 - oksad on I ja III kvartalis, k< 0 - во II и IV четвертях, а коэффициент “а” определяет направление ветвей параболы: а>0 - oksad on suunatud ülespoole ja< 0 - вниз).

2. Slaid 2

U: Määratlege analüütiliselt funktsioonid, mille graafikud on näidatud joonistel. (arvestades, et nad liiguvad y=x2). Õpetaja kirjutab vastused tahvlile.

D: 1) );

2);

3. Slaid 3

U: Määratlege analüütiliselt funktsioonid, mille graafikud on näidatud joonistel. (arvestades, et nad liiguvad). Õpetaja kirjutab vastused tahvlile.

4. Slaid 4

U: Kasutades eelmisi tulemusi, defineerige analüütiliselt funktsioonid, mille graafikud on joonistel näidatud.

3. Raskuste põhjuste väljaselgitamine ja tegevusele eesmärkide seadmine

Lava eesmärk:

korraldada kommunikatiivne suhtlemine, mille käigus tehakse kindlaks ja fikseeritakse ülesande eristav omadus, mis põhjustas õppetegevuses raskusi;
leppida kokku tunni eesmärk ja teema.

Haridusprotsessi korraldamine etapis 3:

T: Mis sulle raskusi tekitab?

D: Ekraanil kuvatakse graafikutükid.

T: Mis on meie tunni eesmärk?

D: õppige funktsioonide osi analüütiliselt määratlema.

T: Sõnastage tunni teema. (Lapsed püüavad teemat iseseisvalt sõnastada. Õpetaja teeb selgeks. Teema: Tükkide kaupa antud funktsioon.)

4. Projekti koostamine raskusest väljumiseks

Lava eesmärk:

organiseerima kommunikatiivset suhtlust uue loomiseks toimeviis, kõrvaldades tuvastatud raskuse põhjuse;
parandada uus viis tegevused.

Haridusprotsessi korraldamine etapis 4:

T: Loeme ülesande uuesti hoolikalt läbi. Milliseid tulemusi palutakse abina kasutada?

D: Eelmised, st. need, mis on tahvlile kirjutatud.

U: Võib-olla on need valemid juba selle ülesande vastus?

D: Ei, sest need valemid defineerivad ruut- ja ratsionaalne funktsioon ja slaidil kuvatakse nende osad.

U: Arutame, millised x-telje intervallid vastavad esimese funktsiooni tükkidele?

U: Siis näeb esimese funktsiooni määramise analüütiline viis välja selline: kui

T: Mida on vaja teha sarnase ülesande täitmiseks?

D: Kirjutage valem üles ja määrake, millised abstsisstelje intervallid vastavad selle funktsiooni osadele.

5. Esmane konsolideerumine väliskõnes

Lava eesmärk:

fikseerima õpitud õppesisu väliskõnes.

Haridusprotsessi korraldamine etapis 5:

7. Teadmiste süsteemi kaasamine ja kordamine

Lava eesmärk:

koolitada oskusi uue sisu kasutamiseks koos varem õpitud sisuga.

Haridusprotsessi korraldamine etapis 7:

U: defineerige analüütiliselt funktsioon, mille graafik on näidatud joonisel.

8. Tegevuste refleksioon tunnis

Lava eesmärk:

jäädvustada tunnis õpitud uut sisu;
hinnata oma tegevust tunnis;
tänada klassikaaslasi, kes aitasid tunni tulemusi saada;
fikseerige lahendamata raskused tulevaste õppetegevuste suunistena;
arutage ja kirjutage kodutööd üles.

Haridusprotsessi korraldamine etapis 8:

T: Mida me täna tunnis õppisime?

D: Tükkide kaupa antud funktsiooniga.

T: Mis tööd me täna tegema õppisime?

D: Küsi seda tüüpi toimib analüütiliselt.

T: Tõstke käsi, kes sai tänase tunni teemast aru? (Arutage tekkinud probleeme teiste lastega).

Kodutöö

nr 21.12(a, c);
nr 21.13(a, c);
№22.41;
№22.44.

Looduses toimuvaid reaalseid protsesse saab kirjeldada funktsioonide abil. Seega võime eristada kahte peamist protsesside tüüpi, mis on üksteisele vastandlikud - need on järkjärguline või pidev Ja spasmiline(näiteks pall, mis langeb ja põrkab). Aga kui on katkendlikke protsesse, siis on nende kirjeldamiseks spetsiaalsed vahendid. Selleks tutvustatakse funktsioone, millel on katkestusi ja hüppeid, st arvurea erinevates osades käitub funktsioon erinevate seaduste järgi ja vastavalt sellele on määratud erinevate valemitega. Tutvustatakse katkestuspunktide ja eemaldatava katkestuse mõisteid.

Kindlasti olete juba kohanud funktsioone, mis on määratletud mitme valemiga, sõltuvalt argumendi väärtustest, näiteks:

y = (x – 3, kui x > -3;
(-(x – 3), punktis x< -3.

Selliseid funktsioone nimetatakse tükkhaaval või tükkhaaval täpsustatud. Nimetagem numbrirea lõigud täpsustamiseks erinevate valemitega komponendid domeeni. Kõikide komponentide liit on tükipõhise funktsiooni määratluspiirkond. Nimetatakse neid punkte, mis jagavad funktsiooni määratluspiirkonna komponentideks piiripunktid. Nimetatakse valemeid, mis defineerivad definitsioonipiirkonna iga komponendi osade kaupa funktsiooni sissetulevad funktsioonid. Tükkide kaupa antud funktsioonide graafikud saadakse, kombineerides graafikuid, mis on koostatud iga partitsiooniintervalli kohta.

Harjutused.

Koostage tükkhaaval funktsioonide graafikud:

1) (-3, -4 ≤ x< 0,
f(x) = (0, kui x = 0,
(1, kell 0< x ≤ 5.

Esimese funktsiooni graafik on punkti y = -3 läbiv sirge. See pärineb punktist koordinaatidega (-4; -3), kulgeb paralleelselt x-teljega punktini, mille koordinaadid (0; -3). Teise funktsiooni graafik on punkt koordinaatidega (0; 0). Kolmas graafik on sarnane esimesega - see on sirgjoon, mis läbib punkti y = 1, kuid juba piirkonnas 0 kuni 5 piki Ox telge.

Vastus: Joonis 1.

2) (3 kui x ≤ -4,
f(x) = (|x 2 – 4|x| + 3|, kui -4< x ≤ 4,
(3 – (x – 4) 2, kui x > 4.

Vaatleme iga funktsiooni eraldi ja koostame selle graafiku.

Seega on f(x) = 3 sirge, mis on paralleelne Ox-teljega, kuid seda tuleb kujutada ainult piirkonnas, kus x ≤ -4.

Funktsiooni f(x) = |x 2 – 4|x| graafik + 3| võib saada paraboolist y = x 2 – 4x + 3. Pärast selle graafiku koostamist tuleb jätta muutmata joonise see osa, mis asub Ox-teljest kõrgemal, ning abstsisstelje all olev osa tuleb kuvada sümmeetriliselt suhteliselt härja teljele. Seejärel kuvage sümmeetriliselt graafiku osa, kus
x ≥ 0 Oy telje suhtes negatiivse x korral. Jätame kõigi teisenduste tulemusel saadud graafiku ainult abstsisstellje vahemikku -4 kuni 4.

Kolmanda funktsiooni graafik on parabool, mille harud on suunatud allapoole ja tipp on koordinaatidega (4; 3) punktis. Joonist kujutame ainult piirkonnas, kus x > 4.

Vastus: Joonis 2.

3) (8 – (x + 6) 2, kui x ≤ -6,
f(x) = (|x 2 – 6|x| + 8|, kui -6 ≤ x< 5,
(3, kui x ≥ 5.

Pakutud tükkhaaval antud funktsiooni konstruktsioon on sarnane eelmise lõiguga. Siin saadakse parabooli teisendustest kahe esimese funktsiooni graafikud ja kolmanda graafik on Ox-iga paralleelne sirge.

Vastus: Joonis 3.

4) Joonistage funktsioon y = x – |x| + (x – 1 – |x|/x) 2 .

Lahendus. Selle funktsiooni ulatus on kõik reaalarvud, välja arvatud null. Laiendame moodulit. Selleks kaaluge kahte juhtumit:

1) Kui x > 0, saame y = x – x + (x – 1 – 1) 2 = (x – 2) 2.

2) x juures< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

Seega on meil tükkhaaval määratletud funktsioon:

y = ((x – 2) 2, kui x > 0;
( x 2 + 2x, x< 0.

Mõlema funktsiooni graafikud on paraboolid, mille harud on suunatud ülespoole.

Vastus: Joonis 4.

5) Joonistage funktsiooni y = (x + |x|/x – 1) graafik 2.

Lahendus.

On lihtne näha, et funktsiooni domeeniks on kõik reaalarvud peale nulli. Pärast mooduli laiendamist saame osade kaupa antud funktsiooni:

1) Kui x > 0 saame y = (x + 1 – 1) 2 = x 2 .

2) x juures< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

Kirjutame ümber.

y = (x 2, kui x > 0;
((x – 2) 2, punktis x< 0.

Nende funktsioonide graafikud on paraboolid.

Vastus: Joonis 5.

6) Kas on funktsioon, mille graafik on koordinaattasand Sellel on ühine punkt mingist sirgjoonest?

Lahendus.

Jah, see on olemas.

Näiteks võib tuua funktsiooni f(x) = x 3 . Tõepoolest, kuupparabooli graafik lõikub vertikaaljoonega x = a punktis (a; a 3). Olgu nüüd sirge antud võrrandiga y = kx + b. Siis võrrand
x 3 – kx – b = 0 reaaljuur x 0 (kuna paaritu astmega polünoomil on alati vähemalt üks reaaljuur). Järelikult lõikub funktsiooni graafik sirgega y = kx + b näiteks punktis (x 0; x 0 3).

veebisaidil, materjali täielikul või osalisel kopeerimisel on vajalik link allikale.

Analüütilise funktsiooni määramine

Funktsioon %%y = f(x), x \in X%% on antud selgesõnalisel analüütilisel viisil, kui antakse valem, mis näitab matemaatiliste toimingute jada, mis tuleb sooritada argumendiga %%x%%, et saada selle funktsiooni väärtuse %%f(x)%%.

Näide

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = \sqrt(x), x \geq 0%%.

Nii näiteks füüsikas ühtlase kiirendusega sirge liikumine keha kiirus määratakse valemiga %%v = v_0 + a t%% ja keha nihke %%s%% valem ühtlasel kiirendatud liikumine ajavahemikus %%0%% kuni %%t%% kirjutatakse järgmiselt: %% s = s_0 + v_0 t + \frac(a t^2)(2) %%.

Tükkide kaupa määratletud funktsioonid

Mõnikord saab kõnealust funktsiooni täpsustada mitme valemiga, mis toimivad selle definitsioonipiirkonna erinevates osades ja milles funktsiooni argument muutub. Näiteks: $$ y = \begin(cases) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

Seda tüüpi funktsioone nimetatakse mõnikord komposiit või tükkhaaval täpsustatud. Sellise funktsiooni näide on %%y = |x|%%

Funktsiooni domeen

Kui funktsioon on määratud eksplitsiitselt analüütiliselt valemi abil, kuid funktsiooni määratluspiirkond hulga %%D%% kujul pole määratud, siis %%D%% all peame alati silmas hulka mille jaoks argumendi %%x%% väärtustest see valem omab tähendust. Seega on funktsiooni %%y = x^2%% määratlusdomeen komplekt %%D = \mathbb(R) = (-\infty, +\infty)%%, kuna argument %%x%% võib võtta mis tahes väärtusi numbririda. Ja funktsiooni %%y = \frac(1)(\sqrt(1 - x^2))%% jaoks on definitsiooni domeen väärtuste komplekt %%x%%, mis rahuldab ebavõrdsust %%1 - x^2 > 0%, t .e. %%D = (-1, 1)%%.

Funktsiooni selgesõnalise analüütilise määramise eelised

Pange tähele, et funktsiooni määramise eksplitsiitne analüütiline meetod on üsna kompaktne (valem võtab reeglina vähe ruumi), seda on lihtne reprodutseerida (valemit pole keeruline kirjutada) ja see sobib kõige paremini matemaatiliste toimingute ja teisenduste tegemiseks funktsioonide kohta.

Mõned neist operatsioonidest - algebralised (liitmine, korrutamine jne) - on hästi tuntud koolikursus matemaatikat, edaspidi õpitakse teisi (diferentseerimine, lõiming). Kuid see meetod ei ole alati selge, kuna funktsiooni argumendist sõltuvuse olemus ei ole alati selge ja mõnikord on funktsiooni väärtuste leidmiseks vaja tülikaid arvutusi (kui need on vajalikud).

Kaudne funktsiooni määramine

Funktsioon %%y = f(x)%% määratletud kaudsel analüütilisel viisil, kui on antud seos $$F(x,y) = 0, siis ~~~~~~~~~~~(1)$$ ühendab funktsiooni %%y%% ja argumendi %% väärtused x%%. Kui määrate argumendi väärtused, siis selleks, et leida %%y%% väärtus, mis vastab konkreetsele väärtusele %%x%%, peate lahendama võrrandi %%(1)%% jaoks %% y%% sellel konkreetsel väärtusel %%x%%.

Sest antud väärtus%%x%% võrrandil %%(1)%% ei pruugi olla lahendust või võib olla rohkem kui üks lahendus. Esimesel juhul seatud väärtus%%x%% ei kuulu kaudselt määratud funktsiooni ulatusse, kuid teisel juhul määrab see mitme väärtusega funktsioon, millel on antud argumendi väärtuse jaoks rohkem kui üks tähendus.

Pange tähele, et kui võrrandit %%(1)%% saab selgesõnaliselt lahendada suhtega %%y = f(x)%%, siis saame sama funktsiooni, kuid juba selgesõnaliselt analüütiliselt määratletud. Seega võrrand %%x + y^5 - 1 = 0%%

ja võrdus %%y = \sqrt(1 - x)%% määratlevad sama funktsiooni.

Parameetriliste funktsioonide spetsifikatsioon

Kui %%y%% sõltuvust %%x%%-st ei anta otse, vaid on antud mõlema muutuja %%x%% ja %%y%% sõltuvused mõnest kolmandast abimuutujast %%t%% vormis

$$ \begin(cases) x = \varphi(t),\\ y = \psi(t), \end(cases) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$ millest nad räägivad parameetriline funktsiooni määramise meetod;

siis abimuutujat %%t%% nimetatakse parameetriks.

Kui võrranditest %%(2)%%, on võimalik parameeter %%t%% elimineerida, siis jõuame funktsioonini, mis on defineeritud %%y%% eksplitsiitse või kaudse analüütilise sõltuvusega %%x%%st. . Näiteks seostest $$ \begin(cases) x = 2 t + 5, \\ y = 4 t + 12, \end(cases), ~~~t \in \mathbb(R), $$ v.a. % parameetri %t%% jaoks saame sõltuvuse %%y = 2 x + 2%%, mis defineerib sirge tasandis %%xOy%%.

Graafiline meetod

Graafilise funktsiooni definitsiooni näide

Ülaltoodud näited näitavad, et funktsiooni määramise analüütiline meetod vastab selle funktsioonile graafiline pilt , mida võib pidada funktsiooni kirjeldamise mugavaks ja visuaalseks vormiks. Vahel kasutatud graafiline meetod funktsiooni määramine, kui %%y%% sõltuvus %%x%%-st on määratud joonega tasapinnal %%xOy%%. Kuid vaatamata kogu selgusele kaotab see täpsuse, kuna argumendi väärtused ja vastavad funktsiooni väärtused saab graafikult saada ainult ligikaudselt. Saadud viga sõltub graafiku üksikute punktide abstsissi ja ordinaadi mõõtmise skaalast ja täpsusest. Tulevikus omistame funktsiooni graafikule vaid funktsiooni käitumist illustreeriva rolli ning seetõttu piirdume funktsioonide põhitunnuseid kajastavate graafikute “visandite” konstrueerimisega.

Tabelimeetod

Märge tabeli meetod funktsioonide määramine, kui mõned argumendi väärtused ja vastavad funktsiooni väärtused paigutatakse tabelisse kindlas järjekorras. Nii ehitatakse kuulsad lauad trigonomeetrilised funktsioonid, logaritmi tabelid jne. Mõõdetud suuruste suhe eksperimentaalsed uuringud, vaatlused, testid.

Selle meetodi puuduseks on see, et tabelisse mittekuuluvate argumentide väärtuste funktsiooniväärtusi pole võimalik otseselt määrata. Kui on kindel, et tabelis esitamata argumentide väärtused kuuluvad kõnealuse funktsiooni määratluspiirkonda, saab vastavad funktsiooni väärtused ligikaudselt arvutada interpolatsiooni ja ekstrapolatsiooni abil.

Näide

x	3	5.1	10	12.5
y	9	23	80	110

Funktsioonide täpsustamise algoritmilised ja verbaalsed meetodid

Funktsiooni saab seadistada algoritmiline(või tarkvara) viisil, mida kasutatakse laialdaselt arvutiarvutustes.

Lõpuks võib märkida kirjeldav(või verbaalne) funktsiooni määramise viis, kui funktsiooni väärtuste argumendi väärtustega sobitamise reegel on väljendatud sõnadega.

Näiteks funktsioon %%[x] = m~\forall (x \in )