Kahe vektori lineaarne sõltuvus. Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid

Et kontrollida, kas vektorite süsteem on lineaarselt sõltuv, on vaja koostada nendest vektoritest lineaarne kombinatsioon ja kontrollida, kas see võib olla null, kui vähemalt üks koefitsient on null.

Juhtum 1. Vektorite süsteem on antud vektoritega

Teeme lineaarse kombinatsiooni

Oleme saanud homogeense võrrandisüsteemi. Kui sellel on nullist erinev lahendus, peab determinant olema võrdne nulliga. Teeme determinandi ja leiame selle väärtuse.

Determinant on null, seetõttu on vektorid lineaarselt sõltuvad.

Juhtum 2. Vektorite süsteem on antud analüütiliste funktsioonidega:

a)
, kui identiteet on tõene, on süsteem lineaarselt sõltuv.

Teeme lineaarse kombinatsiooni.

Tuleb kontrollida, kas leidub selliseid a, b, c (millest vähemalt üks ei võrdu nulliga), mille puhul antud avaldis on võrdne nulliga.

Kirjutame hüperboolsed funktsioonid

,
, siis

siis on vektorite lineaarne kombinatsioon järgmine:

Kus
, võtame näiteks, siis lineaarne kombinatsioon on võrdne nulliga, seega on süsteem lineaarselt sõltuv.

Vastus: Süsteem on lineaarselt sõltuv.

b)
, koostame lineaarse kombinatsiooni

Lineaarne vektorite kombinatsioon peab x mis tahes väärtuse korral olema null.

Kontrollime erijuhtumeid.

Lineaarne vektorite kombinatsioon on null ainult siis, kui kõik koefitsiendid on nullid.

Seetõttu on süsteem lineaarselt sõltumatu.

Vastus: Süsteem on lineaarselt sõltumatu.

5.3. Leidke mingi alus ja määrake lahenduste lineaarruumi mõõde.

Moodustame laiendatud maatriksi ja toome selle Gaussi meetodil trapetsi kujule.

Aluse saamiseks asendame suvalised väärtused:

Hankige ülejäänud koordinaadid

Vastus:

5.4. Leia vektori X koordinaadid baasis, kui see on baasis antud.

Vektori koordinaatide leidmine uues baasis taandub võrrandisüsteemi lahendamisele

1. meetod. Otsimine üleminekumaatriksi abil

Koostage üleminekumaatriks

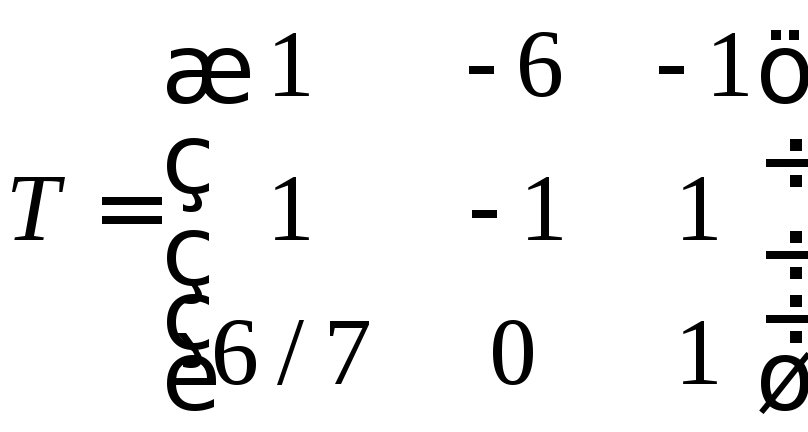
Leiame uues baasis vektori valemi järgi

Leia pöördmaatriks ja korruta

,

2. meetod. Leidmine võrrandisüsteemi koostamise teel.

Koosta baasi koefitsientidest baasvektorid

,
,

Vektori leidmisel uues aluses on vorm

, kus d see on antud vektor x.

Saadud võrrandi saab lahendada mis tahes viisil, vastus on sama.

Vastus: vektor uuel alusel
.

5.5. Olgu x = (x 1 , x 2 , x 3 ) . Kas järgmised teisendused on lineaarsed.

Koostame antud vektorite kordajatest lineaaroperaatorite maatriksid.

Kontrollime lineaartehte omadust iga lineaaroperaatori maatriksi puhul.

Vasak pool leitakse maatrikskorrutamise teel AGA vektori kohta

Õige külje leiame, korrutades antud vektori skalaariga
.

Me näeme seda
seega ei ole teisendus lineaarne.

Kontrollime teisi vektoreid.

, teisendus ei ole lineaarne.

, teisendus on lineaarne.

Vastus: Oh- mitte lineaarne teisendus, Vx- mitte lineaarne Cx- lineaarne.

Märge. Antud vektoreid hoolikalt vaadates saate seda ülesannet palju lihtsamalt täita. AT Oh näeme, et on termineid, mis ei sisalda elemente X, mida ei saanud lineaarse operatsiooni tulemusena saada. AT Vx element on olemas X kolmandale astmele, mida samuti ei saanud vektoriga korrutades saada X.

5.6. Antud x = { x 1 , x 2 , x 3 } , Ax = { x 2 – x 3 , x 1 , x 1 + x 3 } , bx = { x 2 , 2 x 3 , x 1 } . Tehke etteantud toiming: ( A ( B – A )) x .

Kirjutame välja lineaaroperaatorite maatriksid.

Teeme maatriksitega tehte

Korrutades saadud maatriksi X-ga, saame

Vastus:

Ülesanne 1. Uurige, kas vektorite süsteem on lineaarselt sõltumatu. Vektorite süsteem defineeritakse süsteemi maatriksiga, mille veerud koosnevad vektorite koordinaatidest.

.

Lahendus. Laske lineaarne kombinatsioon võrdub nulliga. Pärast selle võrrandi kirjutamist koordinaatidesse saame järgmise võrrandisüsteemi:

.

Sellist võrrandisüsteemi nimetatakse kolmnurkseks. Tal on ainus lahendus. . Siit ka vektorid on lineaarselt sõltumatud.

2. ülesanne. Uurige, kas vektorite süsteem on lineaarselt sõltumatu.

.

Lahendus. Vektorid on lineaarselt sõltumatud (vt ülesanne 1). Tõestame, et vektor on vektorite lineaarne kombinatsioon . Vektori laienduskoefitsiendid määratakse võrrandisüsteemist

.

Sellel süsteemil, nagu ka kolmnurksel, on ainulaadne lahendus.

Seetõttu vektorite süsteem lineaarselt sõltuv.

Kommenteeri. Nimetatakse selliseid maatrikse nagu ülesandes 1 kolmnurkne ja ülesandes 2 – astmeline kolmnurkne . Vektorite süsteemi lineaarse sõltuvuse küsimus on kergesti lahendatav, kui nende vektorite koordinaatidest koosnev maatriks on astmeliselt kolmnurkne. Kui maatriks seda ei tee eriline liik, seejärel kasutades elementaarstringi teisendused , säilitades veergudevahelised lineaarsed suhted, saab selle taandada astmeliseks kolmnurkseks.

Elementaarsed teisendused read maatriksiteks (EPS) nimetatakse maatriksi järgmisi tehteid:

1) joonte permutatsioon;

2) stringi korrutamine nullist erineva arvuga;

3) stringile teise stringi lisamine, mis on korrutatud suvalise arvuga.

3. ülesanne. Leidke maksimaalne lineaarselt sõltumatu alamsüsteem ja arvutage vektorite süsteemi järk

.

Lahendus. Taandagem süsteemi maatriks EPS-i abil astmeliseks-kolmnurkseks. Protseduuri selgitamiseks tähistatakse teisendatava maatriksi numbriga rida sümboliga . Noole järel olev veerg näitab toiminguid, mis tuleb teisendatud maatriksi ridadel teha uue maatriksi ridade saamiseks.

.

Ilmselt on saadud maatriksi kaks esimest veergu lineaarselt sõltumatud, kolmas veerg on nende lineaarne kombinatsioon ja neljas ei sõltu kahest esimesest. Vektorid nimetatakse põhilisteks. Need moodustavad süsteemi maksimaalse lineaarselt sõltumatu alamsüsteemi , ja süsteemi auaste on kolm.

Alus, koordinaadid

4. ülesanne. Leia hulgal vektorite alus ja koordinaadid selles baasis geomeetrilised vektorid, mille koordinaadid vastavad tingimusele .

Lahendus. Hulk on alguspunkti läbiv tasapind. Tasapinnal olev suvaline alus koosneb kahest mittekollineaarsest vektorist. Vektorite koordinaadid valitud baasis määratakse vastava lineaarvõrrandisüsteemi lahendamise teel.

Selle probleemi lahendamiseks on veel üks viis, kui leiate aluse koordinaatide järgi.

Koordinaadid ruumid ei ole tasapinna koordinaadid, kuna need on seotud seosega st nad ei ole iseseisvad. Sõltumatud muutujad ja (neid nimetatakse vabadeks) määravad üheselt tasapinnal oleva vektori ja seetõttu saab neid valida koordinaatideks . Siis alus koosneb vektoritest, mis asuvad vabade muutujate hulgal ja vastavad neile ja , see on .

5. ülesanne. Leidke selle aluse vektorite alus ja koordinaadid ruumi kõigi vektorite hulgast, mille paaritud koordinaadid on üksteisega võrdsed.

Lahendus. Valime, nagu eelmises ülesandes, koordinaadid ruumis.

Sest , siis vabad muutujad defineerivad üheselt vektori alates ja on seetõttu koordinaadid. Vastav alus koosneb vektoritest .

6. ülesanne. Leidke sellel alusel vektorite alus ja koordinaadid vormi kõigi maatriksite hulgast , kus on suvalised arvud.

Lahendus. Iga maatriksit saab unikaalselt esitada järgmiselt:

See seos on vektori laienemine aluse mõttes
koordinaatidega .

Ülesanne 7. Leidke vektorite süsteemi lineaarse ulatuse mõõde ja alus

.

Lahendus. EPS-i abil teisendame maatriksi süsteemivektorite koordinaatidest astmeliseks kolmnurkseks vormiks.

.

veerud viimasest maatriksist on lineaarselt sõltumatud ja veerud väljendatakse nende kaudu lineaarselt. Siit ka vektorid moodustavad aluse ja .

Kommenteeri. Alus sisse mitmetähenduslikult valitud. Näiteks vektorid moodustavad ka aluse .

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Lahendus. Otsivad ühine otsus võrrandisüsteemid

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

Gaussi meetod. Selleks kirjutame selle homogeense süsteemi koordinaatidesse:

Süsteemi maatriks

Lubatud süsteem näeb välja selline: (r A = 2, n= 3). Süsteem on järjepidev ja määratlemata. Selle üldine lahendus ( x 2 – vaba muutuja): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . Nullist erineva privaatlahenduse olemasolu, näiteks , näitab, et vektorid a 1 , a 2 , a 3 lineaarselt sõltuv.

Näide 2

Uurige, kas see on nii see süsteem lineaarselt sõltuvad või lineaarselt sõltumatud vektorid:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Lahendus. Vaatleme homogeenset võrrandisüsteemi a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

või laiendatud (koordinaatide järgi)

Süsteem on homogeenne. Kui see pole degenereerunud, on sellel ainulaadne lahendus. Millal homogeenne süsteem on null (triviaalne) lahendus. Seega on vektorite süsteem antud juhul sõltumatu. Kui süsteem on degenereerunud, siis on sellel nullist erinevad lahendused ja seetõttu on see sõltuv.

Süsteemi degeneratsiooni kontrollimine:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Süsteem on mittedegenereerunud ja seega ka vektorid a 1 , a 2 , a 3 on lineaarselt sõltumatud.

Ülesanded. Uurige, kas antud vektorite süsteem on lineaarselt sõltuv või lineaarselt sõltumatu:

1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.

2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.

3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.

6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.

7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.

8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.

9. Tõesta, et vektorite süsteem on lineaarselt sõltuv, kui see sisaldab:

a) kaks võrdset vektorit;

b) kaks võrdelist vektorit.

Vektorid, nende omadused ja tegevused nendega

Vektorid, toimingud vektoritega, lineaarne vektorruum.

Vektorid on piiratud arvu reaalarvude järjestatud kogum.

Tegevused: 1. Vektori korrutamine arvuga: lambda * vektor x \u003d (lamda * x 1, lambda * x 2 ... lambda * x n). (3,4, 0,7) * 3 \u003d (9, 12,0,21) )

2. Vektorite liitmine (need kuuluvad samasse vektorruumi) vektor x + vektor y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vektor 0=(0,0…0)---n E n – n-mõõtmeline (lineaarruum) vektor x + vektor 0 = vektor x

Teoreem. Selleks, et n-st vektoritest koosnev süsteem n-mõõtmelises lineaarruumis oleks lineaarselt sõltuv, on vajalik ja piisav, et üks vektoritest oleks teiste lineaarne kombinatsioon.

Teoreem. Suvaline hulk n-mõõtmelise lineaarruumi yavl n+ 1. vektorit. lineaarselt sõltuv.

Vektorite liitmine, vektorite korrutamine arvudega. Vektorite lahutamine.

Kahe vektori summa on vektor, mis on suunatud vektori algusest vektori lõppu, eeldusel, et algus langeb kokku vektori lõpuga. Kui vektorid on antud nende laiendustega alusvektoritena, siis vektorite liitmisel saadakse nende vastavad koordinaadid.

Vaatleme seda Descartes'i koordinaatsüsteemi näitel. Lase

Näitame seda

Joonis 3 näitab seda

Summa mis tahes lõplik arv vektoreid saab leida hulknurga reegli abil (joonis 4): lõpliku arvu vektorite summa koostamiseks piisab, kui ühendada iga järgneva vektori algus eelmise lõpuga ja konstrueerida algust ühendav vektor esimesest vektorist koos viimase lõpuga.

Vektorite liitmise operatsiooni omadused:

Nendes avaldistes on m, n arvud.

Vektorite erinevust nimetatakse vektoriks.Teine liige on vektorile vastandsuunaline, kuid pikkuselt võrdne vektor.

Seega asendatakse vektori lahutamise tehe liitmistehtega

Vektorit, mille algus on koordinaatide alguspunktis ja lõpp punktis A (x1, y1, z1), nimetatakse punkti A raadiusvektoriks ja tähistatakse või lihtsalt. Kuna selle koordinaadid ühtivad punkti A koordinaatidega, on selle vektorites laienemine kujul

Vektori, mis algab punktis A(x1, y1, z1) ja lõpeb punktis B(x2, y2, z2), saab kirjutada järgmiselt

kus r 2 on punkti B raadiuse vektor; r 1 - punkti A raadiuse vektor.

Seetõttu on vektori paisumisel ortide kujul vorm

Selle pikkus võrdub punktide A ja B vahelise kaugusega

KORRUTAMINE

Nii et juhul lennuki probleem vektori a = (ax; ay) ja arvu b korrutis leitakse valemiga

a b = (ax b; ay b)

Näide 1. Leia vektori a = (1; 2) korrutis 3-ga.

3 a = (3 1; 3 2) = (3; 6)

Nii et juhul ruumiline probleem vektori a = (ax; ay; az) ja arvu b korrutis leitakse valemiga

a b = (ax b; ay b; az b)

Näide 1. Leia vektori a = (1; 2; -5) korrutis 2-ga.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Vektorite punktkorrutis ja kus on nurk vektorite ja ; kui kumbki, siis

Skalaarkorrutise definitsioonist järeldub, et

kus näiteks on vektori projektsiooni väärtus vektori suunale .

Vektori skalaarruut:

Punkti toote omadused:

Punktkorrutis koordinaatides

Kui a siis

Nurk vektorite vahel

Nurk vektorite vahel – nurk nende vektorite suundade vahel (väikseim nurk).

Vektorkorrutis (kahe vektori vektorkorrutis.)- see on pseudovektor, tasapinnaga risti, mis on üles ehitatud kahe teguri abil, mis on kolmemõõtmelise eukleidilise ruumi vektorite üle kahendtehte "vektori korrutamine" tulemus. Korrutis ei ole kommutatiivne ega assotsiatiivne (see on antikommutatiivne) ja erineb vektorite punktkorrutisest. Paljude inseneri- ja füüsikaülesannete puhul on vaja osata ehitada vektorit, mis on risti kahe olemasolevaga – vektorkorrutis annab selle võimaluse. Ristkorrutis on kasulik vektorite perpendikulaarsuse "mõõtmiseks" - kahe vektori ristkorrutise pikkus võrdub nende pikkuste korrutisega, kui need on risti, ja väheneb nullini, kui vektorid on paralleelsed või antiparalleelsed.

Vektorprodukt on määratletud ainult kolme- ja seitsmemõõtmelistes ruumides. Vektorkorrutise tulemus, nagu ka skalaarkorrutis, sõltub eukleidilise ruumi meetrikast.

Erinevalt punktkorrutise arvutamise valemist vektorite koordinaatide põhjal kolmemõõtmelises ristkülikukujulises koordinaatsüsteemis sõltub ristkorrutise valem orientatsioonist ristkülikukujuline süsteem koordinaadid või teisisõnu selle "kiraalsus"

Vektorite kollineaarsus.

Kahte nullist erinevat (mitte 0-ga) vektorit nimetatakse kollineaarseks, kui need asuvad paralleelsel sirgel või samal sirgel. Lubame, kuid ei soovita, sünonüümi - "paralleelsed" vektorid. Kollineaarsed vektorid võib olla suunatud samas suunas ("kaassuunatud") või vastupidiselt (sisse viimane juhtum neid nimetatakse mõnikord "antikollineaarseteks" või "antiparalleelseteks").

vektorite segakorrutis( a,b,c)- vektori a skalaarkorrutis ning vektorite b ja c vektorkorrutis:

(a,b,c)=a ⋅(b×c)

mõnikord nimetatakse kolmekordseks skalaarkorrutis vektorid, ilmselt tänu sellele, et tulemuseks on skalaar (täpsemalt pseudoskalaar).

geomeetriline tunne: segakorrutise moodul on arvuliselt võrdne vektorite moodustatud rööptahuka ruumalaga (a,b,c) .

Omadused

Segatoode on kõigi oma argumentide suhtes kaldsümmeetriline: see tähendab, e) mis tahes kahe teguri permutatsioon muudab toote märki. Sellest järeldub, et segatoode paremal Descartes'i süsteem koordinaadid (ortonormaalsel alusel) on võrdne maatriksi determinandiga, mis koosneb vektoritest ja:

Segakorrutis vasakpoolses Descartes'i koordinaatsüsteemis (ortonormaalses aluses) on võrdne vektoritest koosneva maatriksi determinandiga, mis on võetud miinusmärgiga:

Eriti,

Kui mis tahes kaks vektorit on paralleelsed, moodustavad nad mis tahes kolmanda vektoriga segatud korrutise, mis on võrdne nulliga.

Kui kolm vektorit on lineaarselt sõltuvad (st. tasapinnalised, asuvad samal tasapinnal), siis on nende segakorrutis null.

Geomeetriline tunnetus – segatoode poolt absoluutväärtus on võrdne vektoritega ja moodustatud rööptahuka ruumalaga (vt joonist); märk sõltub sellest, kas see vektorite kolmik on parem- või vasakpoolne.

Vektorite komplanaarsus.

Kolm vektorit (või rohkem) nimetatakse koplanaarseteks, kui neid taandatakse ühine algus, lamavad samas tasapinnas

Sarnasusomadused

Kui vähemalt üks kolm vektorit- null, siis loetakse kolm vektorit ka tasapinnalisteks.

Kollineaarsete vektorite paari sisaldav vektorite kolmik on koplanaarne.

Koplanaarsete vektorite segakorrutis. See on kolme vektori samatasandilisuse kriteerium.

Koplanaarsed vektorid on lineaarselt sõltuvad. See on ka koplanaarsuse kriteerium.

3-mõõtmelises ruumis moodustavad 3 mittetasapinnalist vektorit

Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid.

Lineaarselt sõltuvad ja sõltumatud vektorite süsteemid.Definitsioon. Vektorite süsteemi nimetatakse lineaarselt sõltuv, kui nende vektorite mittetriviaalne lineaarne kombinatsioon on võrdne nullvektoriga. Vastasel juhul, st. kui ainult antud vektorite triviaalne lineaarne kombinatsioon on võrdne nullvektoriga, nimetatakse vektoreid lineaarselt sõltumatu.

Teoreem (lineaarse sõltuvuse kriteerium). Et lineaarses ruumis paiknev vektorite süsteem oleks lineaarselt sõltuv, on vajalik ja piisav, et vähemalt üks neist vektoritest oleks teiste lineaarne kombinatsioon.

1) Kui vektorite hulgas on vähemalt üks nullvektor, siis on kogu vektorite süsteem lineaarselt sõltuv.

Tõepoolest, kui näiteks , siis, eeldades , on meil mittetriviaalne lineaarne kombinatsioon .▲

2) Kui mõned vektoritest moodustavad lineaarselt sõltuva süsteemi, siis on kogu süsteem lineaarselt sõltuv.

Tõepoolest, olgu vektorid , , lineaarselt sõltuvad. Seega on olemas mittetriviaalne lineaarne kombinatsioon, mis on võrdne nullvektoriga. Aga siis, eeldades , saame ka mittetriviaalse lineaarse kombinatsiooni, mis on võrdne nullvektoriga.

2. Alus ja mõõde. Definitsioon. Lineaarselt sõltumatute vektorite süsteem vektorruum helistas alus seda ruumi, kui suvalist vektorit saab esitada selle süsteemi vektorite lineaarse kombinatsioonina, st. iga vektori jaoks on olemas reaalarvud selline, et võrdsus kehtib. Seda võrdsust nimetatakse vektori lagunemine aluse ja numbrite järgi helistas vektori koordinaadid baasi suhtes(või alusel) .

Teoreem (laienduse ainulaadsuse kohta aluse osas). Iga ruumivektorit saab aluse osas laiendada ainulaadsel viisil, s.o. iga baasi vektori koordinaadid on määratletud üheselt.

Vektorite süsteemi nimetatakse lineaarselt sõltuv, kui on selliseid numbreid , millest vähemalt üks erineb nullist, et võrdus https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src =" >.

Kui see võrdsus kehtib ainult siis, kui kõik , siis kutsutakse vektorite süsteemi lineaarselt sõltumatu.

Teoreem. Vektorite süsteem tahe lineaarselt sõltuv siis ja ainult siis, kui vähemalt üks selle vektor on teiste lineaarne kombinatsioon.

Näide 1 Polünoom on polünoomide lineaarne kombinatsioon https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Polünoomid moodustavad lineaarselt sõltumatu süsteemi, kuna https polünoom: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Näide 2 Maatrikssüsteem , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> on lineaarselt sõltumatu, kuna lineaarne kombinatsioon on võrdne nullmaatriks ainult siis, kui https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text/78/ 624 /images/image022_26.gif" width="40" height="21"> lineaarselt sõltuv.

Lahendus.

Koostage nendest vektoritest lineaarne kombinatsioon https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" height =" 22">.

Samanimeliste koordinaatide võrdsustamine võrdsed vektorid, saame https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Lõpuks saame

ja

Süsteemil on ainult üks triviaalne lahendus, seega on nende vektorite lineaarne kombinatsioon võrdne nulliga ainult juhul, kui kõik koefitsiendid on võrdsed nulliga. Seetõttu on see vektorite süsteem lineaarselt sõltumatu.

Näide 4 Vektorid on lineaarselt sõltumatud. Millised on vektorite süsteemid

a).;

b).?

Lahendus.

a). Koostage lineaarne kombinatsioon ja võrdsustage see nulliga

Kasutades lineaarruumis vektoritega tehte omadusi, kirjutame viimase võrrandi ümber kujul

Kuna vektorid on lineaarselt sõltumatud, peavad koefitsiendid for olema võrdsed nulliga, st.gif" width="12" height="23 src=">

Saadud võrrandisüsteemil on ainulaadne triviaalne lahendus .

Alates võrdsusest (*) täidetakse ainult aadressil https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – lineaarselt sõltumatu;

b). Koostage võrdsus https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Sarnast arutluskäiku rakendades saame

Lahendades võrrandisüsteemi Gaussi meetodil, saame

või

Viimasel süsteemil on lõpmatu hulk lahendusi https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Seega on olemas nullist erinev koefitsientide komplekt, mille võrdsus (**) . Seetõttu vektorite süsteem on lineaarselt sõltuv.

Näide 5 Vektorsüsteem on lineaarselt sõltumatu ja vektorsüsteem on lineaarselt sõltuv..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

Võrdsuses (***) . Tõepoolest, puhul oleks süsteem lineaarselt sõltuv.

Suhtest (***) saame või Tähistage .

Hangi

Ülesanded jaoks sõltumatu otsus(publiku hulgas)

1. Nullvektorit sisaldav süsteem on lineaarselt sõltuv.

2. Ühe vektori süsteem a, on lineaarselt sõltuv siis ja ainult siis, a=0.

3. Kahest vektorist koosnev süsteem on lineaarselt sõltuv siis ja ainult siis, kui vektorid on võrdelised (st üks neist saadakse teisest arvuga korrutades).

4. Kui k on lineaarne sõltuv süsteem kui lisate vektori, saate lineaarselt sõltuva süsteemi.

5. Kui lineaarsest sõltumatu süsteem vektor kustutada, siis on saadud vektorite süsteem lineaarselt sõltumatu.

6. Kui süsteem S lineaarselt sõltumatu, kuid muutub lineaarselt sõltuvaks vektori lisamisel b, siis vektor b lineaarselt väljendatud süsteemi vektoritega S.

c). Maatriksite süsteem , , teist järku maatriksite ruumis.

10. Olgu vektorite süsteem a,b,c vektorruum on lineaarselt sõltumatu. Tõesta lineaarne iseseisvus järgmised süsteemid vektorid:

a).a+b, b, c.

b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– suvaline arv

c).a+b, a+c, b+c.

11. Lase a,b,c on kolm tasandi vektorit, mida saab kasutada kolmnurga moodustamiseks. Kas need vektorid on lineaarselt sõltuvad?

12. Antud kaks vektorit a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Võtke üles veel kaks 4D-vektorit a3 jaa4 nii et süsteem a1,a2,a3,a4 oli lineaarselt sõltumatu .