Veebikalkulaator vektori laiendamine aluse järgi. Vektori lagunemine aluse järgi
(MATEMAATIKA MAJANDUSES)
Vektori lagunemine
Vektori lagunemine A komponentideks - vektori asendamise toiming A mitmed teised vektorid ab, a2, a3 jne, mis kokku liitmisel moodustavad algvektori A; sel juhul nimetatakse vektoreid db a2, a3 jne vektori komponentideks A. Teisisõnu, mis tahes ...(FÜÜSIKA)
Vektorite süsteemi alus ja järk
Vaatleme vektorite süsteemi (1.18) Vektorite süsteemi maksimaalne sõltumatu alamsüsteem(1.I8) on selle süsteemi vektorite osaline hulk, mis vastab kahele tingimusele: 1) selle hulga vektorid on lineaarselt sõltumatud; 2) süsteemi (1.18) mis tahes vektor on lineaarselt väljendatud selle hulga vektoritega....(MATEMAATIKA MAJANDUSES)
Vektoresitus sisse erinevad süsteemid koordinaadid.
Vaatleme kahte ortogonaalset sirgjoonelist koordinaatsüsteemi koos ortide (i, j, k) ja (i j, k") komplektidega ning esitage neis vektor a. Oletame tinglikult, et praimitud vektorid vastavad uued süsteemid e koordinaadid ja ilma löökideta - vana. Kujutagem vektorit laiendusena piki nii vana kui ka uue süsteemi telge...Vektori dekomponeerimine ortogonaalsel alusel
Kaaluge ruumi alust Rn, milles iga vektor on ortogonaalne ülejäänud alusvektoritega: Ortogonaalsed alused on teada ja hästi esindatud tasapinnal ja ruumis (joonis 1.6). Seda tüüpi alused on mugavad esiteks seetõttu, et suvalise vektori lagunemise koordinaadid määratakse ...(MATEMAATIKA MAJANDUSES)
Vektorid ja nende esitused koordinaatsüsteemides
Vektori mõiste on seotud teatud füüsikalised kogused, mida iseloomustab nende intensiivsus (suurus) ja suund ruumis. Sellised suurused on näiteks materiaalsele kehale mõjuv jõud, kiirus teatud punkt selle keha, materiaalse osakese kiirendus...(PIDEV MEEDIA MEHAANIKA: SRESSITEOORIA JA PÕHIMUDELID)
Algloomad analüütilised esitused suvaline elliptiline funktsioon
Elliptilise funktsiooni esitamine elementaarelementide summana. Lase / (z) on järjekorra s elliptiline funktsioon lihtsate poolustega jjt, $s, lamades perioodide rööpkülikul. Märgistades läbi bk funktsiooni jääk pooluse suhtes, meil on, et 2 ?l = 0 (§ 1» lk 3, teoreem ...(SISSEJUHATUS KOMPLEKSMUUUTUJA FUNKTSIOONIDE TEOORIASSE)
Ruumi alus nimetada sellist vektorite süsteemi, milles kõiki teisi ruumi vektoreid saab esitada baasis sisalduvate vektorite lineaarse kombinatsioonina.
Praktikas on see kõik üsna lihtne. Alust kontrollitakse reeglina tasapinnal või ruumis ja selleks peate leidma vektorite koordinaatidest koosneva teist, kolmandat järku maatriksi determinandi. Skemaatiliselt kirjutatud allpool tingimused, mille korral vektorid moodustavad aluse

To laiendada vektorit b baasvektorite järgi
e,e...,e[n] on vaja leida koefitsiendid x, ..., x[n], mille puhul vektorite e,e...,e[n] lineaarne kombinatsioon on võrdne vektor b:
x1*e+ ... + x[n]*e[n] = b.
Selleks tuleks vektorvõrrand teisendada lineaarvõrrandisüsteemiks ja leida lahendused. Seda on ka üsna lihtne rakendada.
Nimetatakse leitud koefitsiendid x, ..., x[n] vektori b koordinaadid baasis e,e...,e[n].
Liigume edasi teema praktilise poole juurde.
Vektori lagunemine alusvektorites
Ülesanne 1. Kontrolli, kas vektorid a1, a2 moodustavad tasapinnal aluse
1) a1 (3; 5), a2 (4; 2)
Lahendus: koostage vektorite koordinaatidest determinant ja arvutage see
![]()
Determinant ei ole võrdne nulliga, järelikult vektorid on lineaarselt sõltumatud, mis tähendab, et nad moodustavad aluse.
2) a1 (2; -3), a2 (5; -1)
Lahendus: Arvutame vektoritest koosneva determinandi ![]()
Determinant on võrdne 13-ga (ei võrdu nulliga) - sellest järeldub, et vektorid a1, a2 on tasandi aluseks.
---=================---
Kaaluge tüüpilised näited IAPM programmist erialal "Kõrgmatemaatika".
2. ülesanne. Näidake, et vektorid a1, a2, a3 moodustavad kolmemõõtmelise vektorruumi aluse ja laiendage vektorit b selles baasis (lineaarse süsteemi lahendamisel algebralised võrrandid kasutada Crameri meetodit).
1) a1 (3; 1; 5), a2 (3; 2; 8), a3 (0; 1; 2), b (−3; 1; 2).
Lahendus: kõigepealt vaatleme vektorite süsteemi a1, a2, a3 ja kontrollige maatriksi A determinanti
ehitatud muudele vektoritele kui null. Maatriksis on üks nullelement, mistõttu on otstarbekam arvutada determinant esimese veeru või kolmanda rea graafikuna. 
Arvutuste tulemusena leidsime, et determinant erineb seega nullist vektorid a1, a2, a3 on lineaarselt sõltumatud.
Definitsiooni järgi moodustavad vektorid R3 aluse. Kirjutame üles vektori b ajakava aluse mõttes 
Vektorid on võrdsed, kui nende vastavad koordinaadid on võrdsed.
Seetõttu saame vektorvõrrandist lineaarsete võrrandite süsteemi 
Lahendage SLAE Crameri meetod. Selleks kirjutame võrrandisüsteemi vormile
SLAE põhideterminant on alati võrdne baasvektoritest koosneva determinandiga
Seetõttu praktikas seda kaks korda ei arvutata. Abideterminantide leidmiseks paneme peadeterminandi iga veeru asemele vabade terminite veeru. Determinandid arvutatakse kolmnurkade reegli järgi 


Asenda leitud determinandid Crameri valemis ![]()
![]()
![]()
Seega on vektori b laiendus aluse suhtes kujul b=-4a1+3a2-a3 . Vektori b koordinaadid baasis a1, a2, a3 on (-4,3, 1).
2)a1 (1; -5; 2), a2 (2; 3; 0), a3 (1; -1; 1), b (3; 5; 1).
Lahendus: kontrollime vektoreid aluse jaoks - koostame vektorite koordinaatidest determinandi ja arvutame selle 
Seetõttu ei ole determinant võrdne nulliga vektorid moodustavad ruumis aluse. Jääb üle leida vektori b ajakava antud baasi järgi. Selleks kirjutame vektori võrrandi 
ja teisendada lineaarvõrrandisüsteemiks 
Kirjutame üles maatriksvõrrand
Järgmisena leiame Crameri valemite jaoks abideterminandid 


Crameri valemite rakendamine ![]()
![]()
Niisiis antud vektor b-l on ajakava läbi kahe baasvektori b=-2a1+5a3 ja selle koordinaadid baasis on b(-2,0, 5).
Alus(vanakreeka βασις, alus) - selliste vektorite kogum vektorruumis, et selle ruumi mis tahes vektorit saab üheselt esitada selle hulga vektorite lineaarse kombinatsioonina - baasvektorid
Alus ruumis R n on mis tahes süsteem, millest pärit n-lineaarselt sõltumatud vektorid. Iga vektorit R n-st, mis ei sisaldu baasis, võib esitada baasvektorite lineaarse kombinatsioonina, st. laiendada üle aluse.
Laskma olema ruumi R n ja . Siis on arvud λ 1 , λ 2 , …, λ n nii, et ![]() .
.
Laienduskoefitsiente λ 1 , λ 2 , ..., λ n nimetatakse baasis B oleva vektori koordinaatideks. Kui alus on antud, siis määratakse vektori koefitsiendid üheselt.
Kommenteeri. Igas n-mõõtmeline vektorruum, saab valida lugematu arv erinevad alused. Erinevates alustes on sama vektor erinevaid koordinaate, kuid valitud alusel ainulaadne. Näide. Laiendage vektorit .
Lahendus. ![]() . Asendage kõigi vektorite koordinaadid ja tehke nendega toiminguid:
. Asendage kõigi vektorite koordinaadid ja tehke nendega toiminguid: ![]()
Võrdstades koordinaadid, saame võrrandisüsteemi:
Lahendame selle: ![]() .
.
Seega saame laienduse: ![]() .
.
Aluses on vektoril koordinaadid .
Töö lõpp -
See teema kuulub:
Vektori mõiste. Lineaartehted vektoritega
Vektor on suunatud segment, millel on teatud pikkus, st segment teatud pikkus millel on üks piiripunkt.. vektori pikkust nimetatakse selle mooduliks ja tähistatakse vektori sümbolmooduliga.. vektorit nimetatakse nulliks tähistatakse kui selle algus ja lõpp langevad kokku.nullvektoril pole kindlat ..
Kui vajate lisamaterjal sellel teemal või te ei leidnud seda, mida otsisite, soovitame kasutada otsingut meie tööde andmebaasis:
Mida teeme saadud materjaliga:
Kui see materjal osutus teile kasulikuks, saate selle sotsiaalvõrgustikes oma lehele salvestada:
L. 2-1 Vektoralgebra põhimõisted. Lineaartehted vektoritega.
Vektori lagunemine aluse järgi.
Vektoralgebra põhimõisted
Vektor on kõigi suunatud segmentide hulk, millel on sama pikkusega ja suund  .
.





Omadused:

Lineaarsed operatsioonidüle vektorite
1.

Parallelogrammi reegel:
KOOS  ummah kaks vektorit
ummah kaks vektorit  Ja
Ja  nimetatakse vektoriks
nimetatakse vektoriks  , mis väljuvad nende ühisest algpunktist ja on vektoritele ehitatud rööpküliku diagonaal
, mis väljuvad nende ühisest algpunktist ja on vektoritele ehitatud rööpküliku diagonaal  Ja
Ja  nagu külgedel.
nagu külgedel.
Hulknurga reegel:
Suvalise arvu vektorite summa koostamiseks peate asetama 2. vektori alguse 1. liikme lõppu, 3. vektori alguse teise liikme lõppu ja nii edasi. Vektor, mis sulgeb tulemuse katkendlik joon, on summa. Selle algus langeb kokku esimese algusega ja lõpp viimase lõpuga.
Omadused:

2.

Vektortoode  numbri kohta
numbri kohta  , nimetatakse vektoriks, mis vastab järgmistele tingimustele:
, nimetatakse vektoriks, mis vastab järgmistele tingimustele:  .
.
Omadused:

3.

erinevus vektorid  Ja
Ja  kõne vektor
kõne vektor  võrdne vektori summaga
võrdne vektori summaga  ja vektorile vastandlik vektor
ja vektorile vastandlik vektor  , st.
, st.  .
.
 - vastupidise elemendi (vektori) seadus.
- vastupidise elemendi (vektori) seadus.
Vektori lagunemine aluse järgi
Vektorite summa määratakse ainulaadsel viisil  (aga ainult
(aga ainult  ). Pöördoperatsioon, vektori lagunemine mitmeks komponendiks, on mitmetähenduslik: Selle ühemõtteliseks muutmiseks on vaja näidata suunad, milles vaadeldava vektori laienemine toimub, või, nagu öeldakse, on vaja näidata alus.
). Pöördoperatsioon, vektori lagunemine mitmeks komponendiks, on mitmetähenduslik: Selle ühemõtteliseks muutmiseks on vaja näidata suunad, milles vaadeldava vektori laienemine toimub, või, nagu öeldakse, on vaja näidata alus.

Aluse määramisel on oluline vektorite mittetasapinnalisuse ja mittekollineaarsuse nõue. Selle nõude tähenduse mõistmiseks on vaja arvestada vektorite lineaarse sõltuvuse ja lineaarse sõltumatuse mõistega.
Vormi meelevaldne väljendus: , nn lineaarne kombinatsioon vektorid  .
.
Nimetatakse mitme vektori lineaarset kombinatsiooni triviaalne kui kõik selle koefitsiendid on võrdsed nulliga.
Vektorid  helistas lineaarselt sõltuv, kui nende vektorite mittetriviaalne lineaarne kombinatsioon on võrdne nulliga:
helistas lineaarselt sõltuv, kui nende vektorite mittetriviaalne lineaarne kombinatsioon on võrdne nulliga:  (1), tingimusel
(1), tingimusel  . Kui võrdsus (1) kehtib ainult kõigi kohta
. Kui võrdsus (1) kehtib ainult kõigi kohta  samaaegselt võrdne nulliga, siis nullist erineva vektoriga
samaaegselt võrdne nulliga, siis nullist erineva vektoriga  tahe lineaarselt sõltumatu.
tahe lineaarselt sõltumatu.
Seda on lihtne tõestada: kõik kaks kollineaarset vektorit on lineaarselt sõltuvad ja kaks mittekollineaarset vektorit on lineaarselt sõltumatud.
Tõestust alustame esimese väitega.
Las vektorid  Ja
Ja  kollineaarne. Näitame, et need on lineaarselt sõltuvad. Tõepoolest, kui need on kollineaarsed, siis erinevad nad üksteisest ainult arvulise teguri poolest, s.t.
kollineaarne. Näitame, et need on lineaarselt sõltuvad. Tõepoolest, kui need on kollineaarsed, siis erinevad nad üksteisest ainult arvulise teguri poolest, s.t.  , järelikult
, järelikult  . Kuna saadud lineaarne kombinatsioon on selgelt mittetriviaalne ja võrdub "0-ga", siis vektorid
. Kuna saadud lineaarne kombinatsioon on selgelt mittetriviaalne ja võrdub "0-ga", siis vektorid  Ja
Ja  lineaarselt sõltuv.
lineaarselt sõltuv.
Vaatleme nüüd kahte mittekollineaarset vektorit  Ja
Ja  . Tõestame, et nad on lineaarselt sõltumatud. Me konstrueerime tõestuse vastuolu abil.
. Tõestame, et nad on lineaarselt sõltumatud. Me konstrueerime tõestuse vastuolu abil.
Eeldame, et need on lineaarselt sõltuvad. Siis peab eksisteerima mittetriviaalne lineaarne kombinatsioon  . Teeskleme seda
. Teeskleme seda  , Siis
, Siis  . Saadud võrdus tähendab, et vektorid
. Saadud võrdus tähendab, et vektorid  Ja
Ja  on vastupidiselt meie esialgsele eeldusele kollineaarsed.
on vastupidiselt meie esialgsele eeldusele kollineaarsed.
Samamoodi saab tõestada: mis tahes kolm samatasandilist vektorit on lineaarselt sõltuvad ja kaks mittetasatasandilist vektorit on lineaarselt sõltumatud.
Tulles tagasi aluse mõiste ja vektori teatud baasis laiendamise probleemi juurde, võime öelda, et alus tasapinnal ja ruumis moodustatakse lineaarselt sõltumatute vektorite hulgast. Selline aluse mõiste on üldine, kuna see on rakendatav mis tahes mõõtmetega ruumi jaoks.
Väljend nagu:  , nimetatakse vektori lagunemiseks
, nimetatakse vektori lagunemiseks  vektorite järgi
vektorite järgi  ,…,
,…, .
.
Kui vaadelda kolmemõõtmelise ruumi baasi, siis vektori lagunemist  alus
alus  tahe
tahe  , Kus
, Kus  -vektori koordinaadid
-vektori koordinaadid .
.
Suvalise vektori mingil alusel laiendamise probleemi puhul on väga oluline järgmine väide: mis tahes vektor saab antud alusel ainulaadsel viisil lagundada
saab antud alusel ainulaadsel viisil lagundada  .
Teisisõnu koordinaadid
.
Teisisõnu koordinaadid  mis tahes vektori jaoks
mis tahes vektori jaoks  aluse suhtes
aluse suhtes
 on määratletud üheselt.
on määratletud üheselt.
Aluse sisseviimine ruumis ja tasapinnal võimaldab omistada igale vektorile  järjestatud numbrite kolmik (paar) - selle koordinaadid. See väga oluline tulemus, mis võimaldab luua seose geomeetriliste objektide ja numbrite vahel, võimaldab analüütiliselt kirjeldada ja uurida füüsiliste objektide asukohta ja liikumist.
järjestatud numbrite kolmik (paar) - selle koordinaadid. See väga oluline tulemus, mis võimaldab luua seose geomeetriliste objektide ja numbrite vahel, võimaldab analüütiliselt kirjeldada ja uurida füüsiliste objektide asukohta ja liikumist.
Punkti ja aluse kombinatsiooni nimetatakse koordinaatsüsteem.
Kui aluse moodustavad vektorid on ühikulised ja paarikaupa risti, siis kutsutakse koordinaatsüsteemi ristkülikukujuline, ja alus ortonormaalne.
L. 2-2 Vektorite korrutis
Vektori lagunemine aluse järgi 
Mõelge vektorile  , antud selle koordinaatidega:
, antud selle koordinaatidega:  .
.



 - vektorkomponendid
- vektorkomponendid  baasvektorite suundades
baasvektorite suundades 
 .
.
Vormi väljendamine  nimetatakse vektori lagunemiseks
nimetatakse vektori lagunemiseks  alus
alus
 .
.
Samamoodi võib laguneda alus  vektor
vektor  :
:
 .
.
Vaadeldava vektori moodustatud nurkade koosinused  baasvektoritega
baasvektoritega  helistas suunakoosinused
helistas suunakoosinused
 ;
;
 ;
; .
.
Vektorite skalaarkorrutis.
Kahe vektori skalaarkorrutis  Ja
Ja  nimetatakse arvuks, mis võrdub nende vektorite moodulite korrutisega nendevahelise nurga koosinusega
nimetatakse arvuks, mis võrdub nende vektorite moodulite korrutisega nendevahelise nurga koosinusega

Kahe vektori skalaarkorrutist võib pidada ühe neist vektoritest mooduli ja teise vektori ortogonaalprojektsiooni korrutiseks esimese vektori suunas.  .
.
Omadused:

Kui vektorite koordinaadid on teada  Ja
Ja  , siis, olles vektoreid aluse osas laiendanud
, siis, olles vektoreid aluse osas laiendanud
 :
:
 Ja
Ja  , leia
, leia 
 , sest
, sest  ,
, , See
, See
 .
.
 .
.
Vektorite perpendikulaarsuse tingimus:  .
.
Kollineaarsuse tingimus rektoritele:  .
.
Vektorite ristkorrutis
 või
või 
vektorkunst  vektori kohta
vektori kohta  sellist vektorit nimetatakse
sellist vektorit nimetatakse  , mis vastab järgmistele tingimustele:
, mis vastab järgmistele tingimustele:

Omadused:

Vaadeldavad algebralised omadused võimaldavad leida ristkorrutisele analüütilise avaldise koostisosavektorite koordinaatidena ortonormaalsel alusel.
Arvestades:  Ja
Ja  .
.
sest ,  ,
, ,
, ,
, ,
, ,
, , See
, See 


 . Selle valemi saab kirjutada lühemalt, kolmandat järku determinandi kujul:
. Selle valemi saab kirjutada lühemalt, kolmandat järku determinandi kujul:
 .
.
Vektorite segakorrutis
Kolme vektori segakorrutis  ,
, Ja
Ja  nimetatakse arvuks, mis on võrdne vektorkorrutisega
nimetatakse arvuks, mis on võrdne vektorkorrutisega  , korrutatuna skalaarselt vektoriga
, korrutatuna skalaarselt vektoriga  .
.
Järgmine võrdsus on tõsi:  , seega kirjutatakse segaprodukt
, seega kirjutatakse segaprodukt  .
.
Nagu definitsioonist tuleneb, on segatoote tulemus kolm vektorit on arv. Sellel numbril on selge geomeetriline tähendus:
Segatoodete moodul  on võrdne taandatule ehitatud rööptahuka ruumalaga ühine algus vektorid
on võrdne taandatule ehitatud rööptahuka ruumalaga ühine algus vektorid  ,
, Ja
Ja  .
.
Segatud toote omadused:
Kui vektorid  ,
, ,
, on antud ortonormaalsel alusel
on antud ortonormaalsel alusel  nende koordinaadid, segatoote arvutamine toimub valemi järgi
nende koordinaadid, segatoote arvutamine toimub valemi järgi
 .
.
Tõepoolest, kui  , See
, See
 ;
; ;
; , Siis
, Siis  .
.
Kui vektorid  ,
, ,
, on koplanaarsed, siis vektorkorrutis
on koplanaarsed, siis vektorkorrutis  vektoriga risti
vektoriga risti  . Ja vastupidi, kui
. Ja vastupidi, kui  , siis on rööptahuka ruumala null ja see on võimalik ainult siis, kui vektorid on koplanaarsed (lineaarselt sõltuvad).
, siis on rööptahuka ruumala null ja see on võimalik ainult siis, kui vektorid on koplanaarsed (lineaarselt sõltuvad).
Seega on kolm vektorit tasapinnalised siis ja ainult siis, kui nende segakorrutis on null.
Lineaarne sõltuvus Ja lineaarne iseseisvus vektorid.
Vektorite alused. Afiinne koordinaatsüsteem
Publiku hulgas on käru šokolaadiga ja täna saab iga külastaja endale maguspaari - analüütilise geomeetria koos lineaaralgebraga. See artikkel hõlmab kahte osa korraga. kõrgem matemaatika, ja vaatame, kuidas nad ühes ümbrises läbi saavad. Tehke paus, sööge Twixi! ... kurat, noh, vaidlemine jama. Kuigi okei, ma ei löö, peaks lõpuks olema õppimisse positiivne suhtumine.
Vektorite lineaarne sõltuvus, vektorite lineaarne sõltumatus, vektori alus ja teistel terminitel pole mitte ainult geomeetriline tõlgendus, vaid eelkõige algebraline tähendus. "Vektori" mõiste lineaaralgebra seisukohast pole kaugeltki alati "tavaline" vektor, mida saame kujutada tasapinnal või ruumis. Tõestust pole vaja kaugelt otsida, proovige joonistada viiemõõtmelise ruumi vektor ![]() . Või ilmavektor, mille pärast just Gismeteos käisin: - temperatuur ja Atmosfääri rõhk vastavalt. Näide on muidugi vektoriruumi omaduste seisukohalt vale, kuid sellegipoolest ei keela keegi neid parameetreid vektorina vormistada. Sügise hingeõhk...
. Või ilmavektor, mille pärast just Gismeteos käisin: - temperatuur ja Atmosfääri rõhk vastavalt. Näide on muidugi vektoriruumi omaduste seisukohalt vale, kuid sellegipoolest ei keela keegi neid parameetreid vektorina vormistada. Sügise hingeõhk...
Ei, ma ei hakka sulle laadima teooriat, lineaarne vektorruumid, ülesanne on aru saada definitsioonid ja teoreemid. Uued terminid (lineaarsõltuvus, sõltumatus, lineaarne kombinatsioon, baas jne) on algebralisest vaatenurgast rakendatavad kõikidele vektoritele, kuid näited tuuakse geomeetriliselt. Seega on kõik lihtne, ligipääsetav ja visuaalne. Lisaks analüütilise geomeetria probleemidele käsitleme ka mõnda tüüpilised ülesanded algebra. Materjali omandamiseks on soovitatav tutvuda õppetundidega Mannekeenide vektorid Ja Kuidas determinanti arvutada?
Tasapinnavektorite lineaarne sõltuvus ja sõltumatus.
Tasapinnaline alus ja afiinne koordinaatsüsteem
Mõelge oma arvutilaua tasapinnale (ainult laud, öökapp, põrand, lagi, mis iganes teile meeldib). Ülesanne koosneb järgmistest toimingutest:
1) Valige tasapinna alus. Jämedalt öeldes on lauaplaadil pikkus ja laius, seega on intuitiivselt selge, et aluse ehitamiseks on vaja kahte vektorit. Ühest vektorist selgelt ei piisa, kolm vektorit on liiga palju.
2) Valitud alusel määrata koordinaatsüsteem(koordinaatide ruudustik), et määrata koordinaadid kõigile tabeli üksustele.
Ärge imestage, esialgu jäävad selgitused näppudele. Pealegi sinu omal. Palun asetage vasaku käe nimetissõrm lauaplaadi servale, nii et ta vaatab monitori. Sellest saab vektor. Nüüd koht väike sõrm parem käsi
laua servale samamoodi - nii, et see on suunatud monitori ekraanile. Sellest saab vektor. Naerata, sa näed hea välja! Mida saab öelda vektorite kohta? Andmevektorid kollineaarne, mis tähendab lineaarselt väljendatakse üksteise kaudu:
, hästi või vastupidi: , kus on nullist erinev arv.
Pilti sellest tegevusest näete õppetükis. Mannekeenide vektorid, kus selgitasin vektori arvuga korrutamise reeglit.
Kas teie sõrmed panevad aluse arvutilaua tasapinnale? Ilmselgelt mitte. Kollineaarsed vektorid liiguvad edasi-tagasi üksi suunas, samas kui tasapinnal on pikkus ja laius.
Selliseid vektoreid nimetatakse lineaarselt sõltuv.
Viide: Sõnad "lineaarne", "lineaarne" viitavad asjaolule, et in matemaatilised võrrandid, avaldistes pole ruute, kuupe, muid astmeid, logaritme, siinusi jne. On ainult lineaarsed (1. astme) avaldised ja sõltuvused.
Kaks tasapinnalist vektorit lineaarselt sõltuv siis ja ainult siis, kui need on kollineaarsed.
Ristke oma sõrmed lauale nii, et nende vahel oleks mis tahes nurk, välja arvatud 0 või 180 kraadi. Kaks tasapinnalist vektoritlineaarselt Mitte on sõltuvad siis ja ainult siis, kui nad ei ole kollineaarsed. Niisiis, alus on kätte saadud. Pole vaja häbeneda, et alus osutus erineva pikkusega mitteperpendikulaarsete vektoritega "viltuks". Varsti näeme, et selle ehitamiseks ei sobi mitte ainult 90-kraadine nurk, vaid mitte ainult võrdse pikkusega ühikvektorid
Ükskõik milline tasapinnaline vektor ainus viis laiendatud aluse poolest: ![]() , kus on reaalarvud. Numbrid kutsutakse vektori koordinaadid sellel alusel.
, kus on reaalarvud. Numbrid kutsutakse vektori koordinaadid sellel alusel.
Nad ütlevad ka seda vektorkujul lineaarne kombinatsioon baasvektorid. See tähendab, et väljendit nimetatakse vektori laguneminealus või lineaarne kombinatsioon baasvektorid.
Näiteks võib öelda, et vektorit laiendatakse tasandi ortonormaalses aluses, või võib öelda, et see on kujutatud vektorite lineaarse kombinatsioonina.
Sõnastame aluse määratlus ametlikult: lennuki alusel on lineaarselt sõltumatute (mittekollineaarsete) vektorite paar, , kus ükskõik milline tasapindvektor on baasvektorite lineaarne kombinatsioon.
Definitsiooni põhipunkt on asjaolu, et vektorid on võetud kindlas järjekorras. alused ![]() Need on kaks täiesti erinevat alust! Nagu öeldakse, vasaku käe väikest sõrme ei saa liigutada parema käe väikese sõrme kohale.
Need on kaks täiesti erinevat alust! Nagu öeldakse, vasaku käe väikest sõrme ei saa liigutada parema käe väikese sõrme kohale.
Arvutasime aluse välja, kuid sellest ei piisa, kui määrata koordinaatide ruudustiku ja määrata igale arvutilaua elemendile koordinaadid. Miks mitte piisavalt? Vektorid on vabad ja rändavad üle kogu tasapinna. Niisiis, kuidas määrata koordinaadid neile väikestele määrdunud lauatäppidele, mis on jäänud metsikust nädalavahetusest järele? Lähtepunkti on vaja. Ja selline võrdluspunkt on kõigile tuttav punkt – koordinaatide alguspunkt. Koordinaatsüsteemi mõistmine:
Alustan "kooli" süsteemist. Juba sissejuhatavas tunnis Mannekeenide vektorid Tõin esile mõned erinevused ristkülikukujulise koordinaatsüsteemi ja ortonormaalse aluse vahel. Siin on standardpilt:

Kui räägitakse ristkülikukujuline koordinaatsüsteem, siis enamasti tähendavad need koordinaatide päritolu, koordinaatteljed ja mõõtkava piki telge. Proovige otsingumootorisse kirjutada “ristkülikukujuline koordinaatsüsteem” ja näete, et paljud allikad räägivad teile 5.-6. klassist tuttavatest koordinaattelgedest ja punktide joonistamisest tasapinnal.
Teisest küljest tundub, et ristkülikukujuline süsteem koordinaate saab määrata ortonormaalsel alusel . Ja peaaegu on. Sõnastus on järgmine:
päritolu, Ja ortonormaalne baaskomplekt Tasapinna ristkoordinaatide süsteem . See tähendab, et ristkülikukujuline koordinaatsüsteem kindlasti on defineeritud ühe punkti ja kahe ühikulise ortogonaalvektoriga. Sellepärast näete joonist, mille ma ülal andsin - sisse geomeetrilised probleemid sageli (aga mitte mingil juhul alati) joonestada nii vektoreid kui ka koordinaatide telgi.
Ma arvan, et kõik saavad sellest aru punkti (päritolu) ja ortonormaalse aluse abil Lennuki MIS TAHES PUNKT ja lennuki MIS TAHES VEKTOR koordinaate saab määrata. Piltlikult öeldes "lennukis saab kõike nummerdada".
Kas koordinaatvektorid peavad olema ühikulised? Ei, neil võib olla suvaline nullist erinev pikkus. Vaatleme punkti ja kahte suvalise nullist erineva pikkusega ortogonaalvektorit:

Sellist alust nimetatakse ortogonaalne. Koordinaatide alguspunkt vektoritega määrab koordinaatide ruudustiku ja igal tasandi punktil, igal vektoril on antud baasil oma koordinaadid. Näiteks või. Ilmselge ebamugavus seisneb selles, et koordinaatvektorid V üldine juhtum
on erineva pikkusega peale ühtsuse. Kui pikkused on võrdsed ühega, saadakse tavaline ortonormaalne alus.
! Märge : ortogonaalsel alusel ja ka allpool sisse afiinsed alused vaadeldakse tasapinna ja ruumi ühikuid piki telge TINGIMUSLIK. Näiteks üks ühik abstsissil sisaldab 4 cm, üks ühik ordinaadil 2 cm. Sellest teabest piisab, et vajaduse korral "mittestandardsed" koordinaadid "meie tavalisteks sentimeetriteks" teisendada.
Ja teine küsimus, millele on tegelikult juba vastatud – kas baasvektorite vaheline nurk on tingimata 90 kraadi? Ei! Nagu definitsioon ütleb, peavad baasvektorid olema ainult mittekollineaarne. Vastavalt sellele võib nurk olla mis tahes peale 0 ja 180 kraadi.
Punkt lennukis kutsus päritolu, Ja mittekollineaarne vektorid, , komplekt tasapinna afiinne koordinaatsüsteem :

Mõnikord nimetatakse seda koordinaatsüsteemi kaldus süsteem. Punktid ja vektorid on näidatud joonisel näidetena: 
Nagu teate, on afiinne koordinaatsüsteem veelgi vähem mugav, vektorite ja segmentide pikkuste valemid, mida me õppetunni teises osas käsitlesime, selles ei tööta. Mannekeenide vektorid, palju maitsvaid valemeid, mis on seotud vektorite skalaarkorrutis. Kuid kehtivad vektorite lisamise ja vektori arvuga korrutamise reeglid, segmendi jagamise valemid selles osas, aga ka mõned muud tüüpi probleemid, mida peagi käsitleme.
Ja järeldus on, et kõige mugavam erijuhtum afiinne süsteem koordinaadid on Descartes'i ristkülikukujuline süsteem. Seetõttu tuleb teda, tema oma, kõige sagedamini näha. ... Samas on siin elus kõik suhteline – on palju olukordi, kus sobib kaldus (või mõni muu nt. polaarne) koordinaatsüsteem. Jah, ja humanoididele võivad sellised süsteemid maitsele tulla =)
Liigume edasi praktilise osa juurde. Kõik ülesanded see õppetund kehtivad nii ristkülikukujulise koordinaatsüsteemi kui ka üldise afiinse käände korral. Siin pole midagi keerulist, kogu materjal on isegi koolipoisile kättesaadav.
Kuidas määrata tasapinnaliste vektorite kollineaarsust?
Tüüpiline asi. Selleks, et kaks tasapinnalist vektorit ![]() on kollineaarsed, on vajalik ja piisav, et nende vastavad koordinaadid oleksid proportsionaalsed.Sisuliselt on see ilmse seose koordinaatide-koordinaatide haaval täpsustamine.
on kollineaarsed, on vajalik ja piisav, et nende vastavad koordinaadid oleksid proportsionaalsed.Sisuliselt on see ilmse seose koordinaatide-koordinaatide haaval täpsustamine.
Näide 1
a) Kontrollige, kas vektorid on kollineaarsed ![]() .
.
b) Kas vektorid moodustavad aluse? ![]() ?
?
Lahendus:
a) Uurige, kas vektorid on olemas ![]() proportsionaalsuskoefitsient, nii et võrdsused on täidetud:
proportsionaalsuskoefitsient, nii et võrdsused on täidetud: ![]()
Kindlasti räägin teile selle reegli rakendamise "foppish" versioonist, mis praktikas töötab üsna hästi. Idee on kohe koostada proportsioon ja vaadata, kas see on õige:
Teeme vektorite vastavate koordinaatide suhetest proportsiooni:
Lühendame:
, seega on vastavad koordinaadid võrdelised, seega
Seost saab luua ja vastupidi, see on samaväärne variant:
Enesetestimiseks võib kasutada tõsiasja, et kollineaarsed vektorid väljendatakse üksteise kaudu lineaarselt. IN sel juhul on võrdsused ![]() . Nende kehtivust saab hõlpsasti kontrollida vektoritega tehtavate elementaarsete toimingute abil:
. Nende kehtivust saab hõlpsasti kontrollida vektoritega tehtavate elementaarsete toimingute abil: 
b) Kaks tasapinnalist vektorit moodustavad aluse, kui nad ei ole kollineaarsed (lineaarselt sõltumatud). Uurime vektorite kollineaarsust ![]() . Loome süsteemi:
. Loome süsteemi: 
Esimesest võrrandist järeldub, et , teisest võrrandist järeldub, et , mis tähendab, süsteem on ebaühtlane(lahendused puuduvad). Seega ei ole vektorite vastavad koordinaadid võrdelised.
Järeldus: vektorid on lineaarselt sõltumatud ja moodustavad aluse.
Lahenduse lihtsustatud versioon näeb välja selline:
Koostage vektorite vastavatest koordinaatidest proportsioon ![]() :
:
, seega on need vektorid lineaarselt sõltumatud ja moodustavad aluse.
Tavaliselt arvustajad seda võimalust ei lükka, kuid probleem tekib juhtudel, kui mõned koordinaadid on nulliga võrdsed. Nagu nii: ![]() . Või niimoodi:
. Või niimoodi: ![]() . Või niimoodi:
. Või niimoodi: ![]() . Kuidas siin proportsiooni läbi töötada? (Tõesti, nulliga jagada ei saa). Just sel põhjusel nimetasin lihtsustatud lahendust "foppiks".
. Kuidas siin proportsiooni läbi töötada? (Tõesti, nulliga jagada ei saa). Just sel põhjusel nimetasin lihtsustatud lahendust "foppiks".
Vastus: a) , b) vorm.
Väike loominguline eeskuju Sest sõltumatu otsus:
Näide 2
Millise parameetrivektorite väärtuse juures ![]() on kollineaarne?
on kollineaarne?
Näidislahenduses leitakse parameeter proportsiooni kaudu.
Vektorite kollineaarsuse kontrollimiseks on olemas elegantne algebraline viis. Süstematiseerime oma teadmised ja lisame need lihtsalt viienda punktina:
Kahe tasapinnalise vektori puhul on järgmised väited samaväärsed:
2) vektorid moodustavad aluse;
3) vektorid ei ole kollineaarsed;
+ 5) nende vektorite koordinaatidest koosnev determinant on nullist erinev.
vastavalt järgmised vastupidised väited on samaväärsed:
1) vektorid on lineaarselt sõltuvad;
2) vektorid ei moodusta alust;
3) vektorid on kollineaarsed;
4) vektoreid saab üksteise kaudu lineaarselt väljendada;
+ 5) nende vektorite koordinaatidest koosnev determinant on võrdne nulliga.
Ma väga-väga loodan, et hetkel te juba mõistate kõiki termineid ja väiteid, mis ette on tulnud.
Vaatame lähemalt uut, viiendat punkti: kaks tasapinnalist vektorit ![]() on kollineaarsed siis ja ainult siis, kui antud vektorite koordinaatidest koosnev determinant on võrdne nulliga:. Selle funktsiooni kasutamiseks peate loomulikult suutma seda teha determinante leidma.
on kollineaarsed siis ja ainult siis, kui antud vektorite koordinaatidest koosnev determinant on võrdne nulliga:. Selle funktsiooni kasutamiseks peate loomulikult suutma seda teha determinante leidma.
Meie otsustame Näide 1 teisel viisil:
a) Arvutage vektorite koordinaatidest koosnev determinant ![]() :
:![]() , seega on need vektorid kollineaarsed.
, seega on need vektorid kollineaarsed.
b) Kaks tasapinnalist vektorit moodustavad aluse, kui nad ei ole kollineaarsed (lineaarselt sõltumatud). Arvutame vektorite koordinaatidest koosneva determinandi ![]() :
:![]() , seega on vektorid lineaarselt sõltumatud ja moodustavad aluse.
, seega on vektorid lineaarselt sõltumatud ja moodustavad aluse.
Vastus: a) , b) vorm.
See näeb välja palju kompaktsem ja ilusam kui proportsioonidega lahendus.
Vaadeldava materjali abil on võimalik tuvastada mitte ainult vektorite kollineaarsust, vaid ka tõestada lõikude, sirgete paralleelsust. Mõelge paarile probleemile konkreetsete geomeetriliste kujunditega.
Näide 3
Antud on nelinurga tipud. Tõesta, et nelinurk on rööpkülik.
Tõestus: Ülesandes pole vaja joonist koostada, kuna lahendus on puhtalt analüütiline. Pidage meeles rööpküliku määratlust:
Parallelogramm
Nimetatakse nelinurka, mille vastasküljed on paarikaupa paralleelsed.
Seega on vaja tõestada:
1) vastaskülgede paralleelsus ja;
2) vastaskülgede paralleelsus ja .
Tõestame:
1) Leidke vektorid: 
![]()
2) Leidke vektorid: 
Tulemuseks oli sama vektor ("kooli järgi" - võrdsed vektorid). Kollineaarsus on üsna ilmne, kuid parem on teha otsus õigesti, korraldusega. Arvutage vektorite koordinaatidest koosnev determinant: ![]() , Nii et need vektorid on kollineaarsed ja .
, Nii et need vektorid on kollineaarsed ja .
Järeldus: vastasküljed nelinurgad on paarikaupa paralleelsed, seega on definitsiooni järgi rööpkülik. Q.E.D.
Veel häid ja erinevaid figuure:
Näide 4
Antud on nelinurga tipud. Tõesta, et nelinurk on trapets.
Tõestuse rangemaks sõnastamiseks on muidugi parem hankida trapetsi definitsioon, kuid piisab, kui meenutada, kuidas see välja näeb.
See on iseseisva otsuse ülesanne. Täielik lahendus tunni lõpus.
Ja nüüd on aeg aeglaselt lennukist kosmosesse liikuda:
Kuidas määrata ruumivektorite kollineaarsust?
Reegel on väga sarnane. Selleks, et kaks ruumivektorit oleksid kollineaarsed, on vajalik ja piisav, et nende vastavad koordinaadid on võrdelised.
Näide 5
Uurige, kas järgmised ruumivektorid on kollineaarsed:
A) ;
b)
V) ![]()
Lahendus:
a) Kontrollige, kas vektorite vastavate koordinaatide jaoks on olemas proportsionaalsuskordaja:
Süsteemil pole lahendust, mis tähendab, et vektorid ei ole kollineaarsed.
"Lihtsustatud" saadakse proportsiooni kontrollimise teel. Sel juhul:
– vastavad koordinaadid ei ole proportsionaalsed, mis tähendab, et vektorid ei ole kollineaarsed.
Vastus: vektorid ei ole kollineaarsed.
b-c) Need on punktid iseseisvaks otsustamiseks. Proovige seda kahel viisil.
On olemas meetod ruumivektorite kollineaarsuse kontrollimiseks ja kolmandat järku determinandi abil, nii artiklis käsitletud Vektorite ristkorrutis.
Sarnaselt tasapinnalise juhtumiga saab vaadeldavaid tööriistu kasutada ruumilõikude ja sirgete paralleelsuse uurimiseks.
Tere tulemast teise sektsiooni:
Kolmemõõtmeliste ruumivektorite lineaarne sõltuvus ja sõltumatus.
Ruumiline alus ja afiinne koordinaatsüsteem
Paljud seaduspärasused, millega oleme lennukis arvestanud, kehtivad ka kosmose kohta. Üritasin teooria kokkuvõtet minimeerida, kuna lõviosa infost on juba näritud. Sellegipoolest soovitan sissejuhatav osa hoolikalt läbi lugeda, kuna ilmuvad uued terminid ja mõisted.
Nüüd uurime arvutilaua tasapinna asemel kolmemõõtmelist ruumi. Esiteks loome selle aluse. Keegi on praegu toas, keegi on väljas, kuid igal juhul ei saa me eemale kolmest mõõtmest: laius, pikkus ja kõrgus. Seetõttu on aluse konstrueerimiseks vaja kolme ruumivektorit. Ühest või kahest vektorist ei piisa, neljas on üleliigne.
Ja jälle soojendame sõrmedel. Palun tõstke käsi üles ja sirutage laiali erinevad küljed pöial, nimetissõrm ja keskmine sõrm. Need on vektorid, nad näevad eri suundades, on erineva pikkusega ja neil on erinevad nurgad. Õnnitleme, kolmemõõtmelise ruumi alus on valmis! Muide, te ei pea seda õpetajatele demonstreerima, ükskõik kuidas sõrmi keerate, kuid definitsioonidest te ei pääse =)
Järgmiseks küsime oluline küsimus, kas kolm vektorit moodustavad aluse kolmemõõtmeline ruum ? Palun vajutage kolme sõrmega tugevalt arvuti lauaplaadile. Mis juhtus? Kolm vektorit asuvad samal tasapinnal ja jämedalt öeldes oleme kaotanud ühe mõõtmise - kõrguse. Sellised vektorid on koplanaarne ja täiesti ilmselgelt, et kolmemõõtmelise ruumi alust ei looda.
Tuleb märkida, et samatasandilised vektorid ei pea asuma samal tasapinnal, nad võivad olla sees paralleelsed tasapinnad(ära tee seda sõrmedega, ainult Salvador Dali tuli niimoodi ära =)).
Definitsioon: kutsutakse vektoreid koplanaarne kui on olemas tasapind, millega nad on paralleelsed. Siin on loogiline lisada, et kui sellist tasandit ei eksisteeri, siis vektorid ei ole ka tasapinnalised.
Kolm samatasandilist vektorit on alati lineaarselt sõltuvad, see tähendab, et neid väljendatakse lineaarselt üksteise kaudu. Lihtsuse huvides kujutage jälle ette, et need asuvad samal tasapinnal. Esiteks, vektorid pole mitte ainult koplanaarsed, vaid võivad olla ka kollineaarsed, siis saab mis tahes vektorit väljendada mis tahes vektori kaudu. Teisel juhul, kui näiteks vektorid ei ole kollineaarsed, siis kolmandat vektorit väljendatakse nende kaudu ainulaadsel viisil: ![]() (ja miks, seda on lihtne arvata eelmise osa materjalidest).
(ja miks, seda on lihtne arvata eelmise osa materjalidest).
Tõsi on ka vastupidine: kolm mittetasatasandilist vektorit on alati lineaarselt sõltumatud st need ei väljendu kuidagi üksteise kaudu. Ja ilmselgelt saavad ainult sellised vektorid moodustada kolmemõõtmelise ruumi aluse.
Definitsioon: Kolmemõõtmelise ruumi alus nimetatakse lineaarselt sõltumatute (mittetasandiliste) vektorite kolmikuks, võetud kindlas järjekorras, samas kui mis tahes ruumi vektor ainus viis laieneb antud baasis , kus on antud baasi vektori koordinaadid
Meeldetuletuseks võite ka öelda, et vektorit kujutatakse kui lineaarne kombinatsioon baasvektorid.
Koordinaatsüsteemi mõiste tutvustatakse täpselt samamoodi nagu jaoks lame korpus, piisab ühest punktist ja mis tahes kolmest lineaarselt sõltumatust vektorist:
päritolu, Ja mitte-tasapinnaline vektorid, võetud kindlas järjekorras, komplekt kolmemõõtmelise ruumi afiinne koordinaatsüsteem
:
Muidugi on koordinaatide ruudustik "kaldus" ja ebamugav, kuid sellegipoolest võimaldab konstrueeritud koordinaatsüsteem meil kindlasti määrata mis tahes vektori koordinaadid ja mis tahes ruumipunkti koordinaadid. Sarnaselt tasapinnaga ei tööta ka ruumi afiinses koordinaatsüsteemis mõned valemid, mida ma juba mainisin.
Afiinse koordinaatsüsteemi kõige tuttavam ja mugavam erijuhtum, nagu igaüks võib arvata, on ristkülikukujuline ruumi koordinaatsüsteem:
ruumipunkt, mida nimetatakse päritolu, Ja ortonormaalne baaskomplekt Ruumi ristkoordinaatide süsteem
. tuttav pilt: 
Enne praktiliste ülesannete juurde asumist süstematiseerime teabe uuesti:
Kolme ruumivektori puhul on järgmised väited samaväärsed:
1) vektorid on lineaarselt sõltumatud;
2) vektorid moodustavad aluse;
3) vektorid ei ole tasapinnalised;
4) vektoreid ei saa üksteise kaudu lineaarselt väljendada;
5) nende vektorite koordinaatidest koosnev determinant erineb nullist.
Vastupidised väited on minu arvates arusaadavad.
Ruumivektorite lineaarset sõltuvust / sõltumatust kontrollitakse traditsiooniliselt determinandi abil (punkt 5). Ülejäänud praktilisi ülesandeid on väljendunud algebralise iseloomuga. On aeg riputada geomeetriline kepp küünele ja vehkida lineaarse algebra pesapallikurikaga:
Kolm ruumivektorit on tasapinnalised siis ja ainult siis, kui antud vektorite koordinaatidest koosnev determinant on võrdne nulliga:  .
.
Juhin teie tähelepanu väikesele tehnilisele nüansile: vektorite koordinaate saab kirjutada mitte ainult veergudesse, vaid ka ridadesse (determinandi väärtus sellest ei muutu - vt determinantide omadusi). Kuid veergudes on see palju parem, kuna see on kasulikum mõne praktilise probleemi lahendamisel.
Neile lugejatele, kes on determinantide arvutamise meetodid pisut unustanud või on nad üldse halvasti orienteeritud, soovitan ühte oma vanimaid õppetükke: Kuidas determinanti arvutada?
Näide 6
Kontrollige, kas järgmised vektorid moodustavad kolmemõõtmelise ruumi aluse:
Lahendus: Tegelikult taandub kogu lahendus determinandi arvutamisele.
a) Arvutage vektorite koordinaatidest koosnev determinant (determinant laiendatakse esimesel real): 
, mis tähendab, et vektorid on lineaarselt sõltumatud (mitte tasapinnalised) ja moodustavad kolmemõõtmelise ruumi aluse.
Vastus: need vektorid moodustavad aluse
b) See on sõltumatu otsuse punkt. Täislahendus ja vastus tunni lõpus.
kohtuda ja loomingulised ülesanded:
Näide 7
Millise parameetri väärtuse korral on vektorid tasapinnalised?
Lahendus: vektorid on tasapinnalised siis ja ainult siis, kui antud vektorite koordinaatidest koosnev determinant on võrdne nulliga: 
Põhimõtteliselt on vaja võrrandit lahendada determinandiga. Lendame nullidesse nagu tuulelohed jerboadesse - kõige tulusam on avada determinant teises reas ja kohe miinustest lahti saada: 
Teostame täiendavaid lihtsustusi ja taandame asja kõige lihtsamale lineaarvõrrand:![]()
Vastus: kell
Siin on lihtne kontrollida, selleks peate asendama saadud väärtuse algse determinandiga ja veenduma, et  selle uuesti avamisega.
selle uuesti avamisega.
Lõpuks kaaluge veel üht tüüpiline ülesanne, mis on olemuselt algebralisem ja kuulub traditsiooniliselt lineaaralgebra käigus. See on nii tavaline, et väärib eraldi teemat:
Tõesta, et 3 vektorit moodustavad kolmemõõtmelise ruumi aluse
ja leida antud baasis 4. vektori koordinaadid
Näide 8
Vektorid on antud. Näidake, et vektorid moodustavad kolmemõõtmelise ruumi aluse ja leidke sellel alusel vektori koordinaadid.
Lahendus: Tegeleme kõigepealt tingimusega. Tingimuse järgi on antud neli vektorit ja nagu näha, on neil juba mingis aluses koordinaadid. Mis on alus - meid ei huvita. Ja järgmine asi pakub huvi: kolm vektorit võivad moodustada uue aluse. Ja esimene samm on täiesti sama, mis näite 6 lahendus, on vaja kontrollida, kas vektorid on tõesti lineaarselt sõltumatud:
Arvutage vektorite koordinaatidest koosnev determinant: 
, seega on vektorid lineaarselt sõltumatud ja moodustavad kolmemõõtmelise ruumi aluse.
! Tähtis : vektori koordinaadid Tingimata Kirjuta üles veergudesse determinant, mitte stringid. Vastasel juhul tekib edasises lahendusalgoritmis segadus.
 Kümnendmurru teisendamine tavaliseks murruks ja vastupidi: reegel, näited
Kümnendmurru teisendamine tavaliseks murruks ja vastupidi: reegel, näited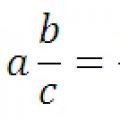 Kümnendarvude teisendamine harilikeks murdudeks
Kümnendarvude teisendamine harilikeks murdudeks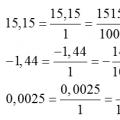 Hariliku murru teisendamine kümnendmurruks ja vastupidi, reeglid, näited
Hariliku murru teisendamine kümnendmurruks ja vastupidi, reeglid, näited