Pronađite vrijednost vjerojatnosti. Dolje s neizvjesnošću, ili kako pronaći vjerojatnost
kao ontološka kategorija odražava mjeru mogućnosti nastanka bilo kojeg entiteta u bilo kojim uvjetima. Za razliku od matematičkih i logičkih tumačenja ovog pojma, ontološki V. ne povezuje se s nužnošću kvantitativnog izraza. Vrijednost V. otkriva se u kontekstu razumijevanja determinizma i prirode razvoja uopće.
Sjajna definicija
Nepotpuna definicija ↓
VJEROJATNOST
pojam koji karakterizira količine. mjera mogućnosti pojave određenog događaja na određenom. Uvjeti. U znanstvenom znanja postoje tri tumačenja V. Klasični koncept V., koji je proizašao iz matemat. analiza kockanja koju su najpotpunije razvili B. Pascal, J. Bernoulli i P. Laplace, smatra V. kao omjer broja povoljnih slučajeva prema ukupnom broju svih jednako mogućih. Na primjer, kada bacate kocku koja ima 6 strana, može se očekivati da svaka od njih dobije V jednak 1/6, budući da nijedna strana nema prednosti nad drugom. Takva simetrija ishoda iskustva posebno se uzima u obzir pri organiziranju igara, ali je relativno rijetka u proučavanju objektivnih događaja u znanosti i praksi. klasična V. je tumačenje ustupilo mjesto statističkom. V.-ove koncepcije, u središtu kojih vrijede. promatranje pojave određenog događaja tijekom trajanja. iskustvo pod točno određenim uvjetima. Praksa potvrđuje da što se neki događaj češće događa to je veći stupanj objektivne mogućnosti njegovog nastanka odnosno V. Stoga statistič. V.-ova interpretacija temelji se na konceptu odnosi. frekvencije, rez se može odrediti empirijski. V. kao teorijski. koncept se nikada ne podudara s empirijski određenom učestalošću, međutim, na mnogo načina. slučajeva, praktički se malo razlikuje od relativnog. učestalost utvrđena kao rezultat trajanja. zapažanja. Mnogi statističari V. smatraju "dvostrukim" referencijama. frekvencija, rub je određen statističkim. proučavanje rezultata promatranja
ili eksperimenti. Manje je realistična bila definicija V. što se tiče granice. frekvencije masovnih događaja, odnosno kolektiva, koje je predložio R. Mises. Kao daljnji razvoj frekvencijskog pristupa V., postavlja se dispozicijsko, ili sklonost, tumačenje V. (K. Popper, J. Hecking, M. Bunge, T. Setl). Prema ovom tumačenju, V. karakterizira svojstvo generiranja uvjeta, na primjer. eksperiment. instalacija, kako bi se dobio niz masivnih slučajnih događaja. Upravo taj stav rađa tjelesno dispozicije, ili predispozicije, V. to-rykh može se provjeriti pomoću relativ. frekvencije.
Statistički V. tumačenje dominira znanstvenim. znanja, jer ono odražava specifič. priroda obrazaca svojstvenih masovnim pojavama slučajne prirode. U mnogim fizičkim, biološkim, ekonomskim, demografskim i tako dalje. društvenih procesa potrebno je uzeti u obzir djelovanje mnogih slučajnih čimbenika, to-rye karakterizira stabilna učestalost. Identifikacija ove stabilne frekvencije i količina. njegova procjena uz pomoć V. omogućuje otkrivanje nužnosti, koja se probija kroz kumulativno djelovanje mnogih nezgoda. Tu se očituje dijalektika transformacije slučajnosti u nužnost (vidi F. Engels, u knjizi: K. Marx i F. Engels, Soch., sv. 20, str. 535-36).
Logičko ili induktivno zaključivanje karakterizira odnos između premisa i zaključka nedemonstrativnog i, posebice, induktivnog zaključivanja. Za razliku od dedukcije, premise indukcije ne jamče istinitost zaključka, već ga samo čine više ili manje vjerojatnim. Ta se vjerodostojnost, s precizno formuliranim premisama, ponekad može procijeniti pomoću V. Vrijednost ovog V. najčešće se utvrđuje usporedbom. pojmova (veće od, manje od ili jednako), a ponekad i na numerički način. Logika interpretacija se često koristi za analizu induktivnog zaključivanja i izgradnju različitih sustava probabilističke logike (R. Carnap, R. Jeffrey). U semantičkom logički pojmovi. V. se često definira kao stupanj potvrde jedne tvrdnje od strane drugih (na primjer, hipoteza njezinih empirijskih podataka).
U vezi s razvojem teorija odlučivanja i igara, tzv. personalistička interpretacija V. Iako V. istovremeno izražava stupanj uvjerenja subjekta i pojavu određenog događaja, sami V. moraju biti odabrani tako da su zadovoljeni aksiomi izračuna V.. Stoga V. ovakvim tumačenjem izražava ne toliko stupanj subjektivne koliko razumske vjere . Posljedično, odluke donesene na temelju takvog V. bit će racionalne, jer ne uzimaju u obzir psihološki. osobine i sklonosti subjekta.
Iz epistemoloških t. sp. razlika između statistič., logično. i personalističkih tumačenja V. leži u činjenici da ako prvi karakterizira objektivna svojstva i odnose masovnih pojava slučajne prirode, onda posljednja dva analiziraju značajke subjektivnog, spoznatnog. ljudske aktivnosti u uvjetima neizvjesnosti.
VJEROJATNOST
jedan od najvažnijih pojmova znanosti, koji karakterizira posebnu sustavnu viziju svijeta, njegovu strukturu, evoluciju i spoznaju. Specifičnost probabilističkog pogleda na svijet otkriva se kroz uključivanje u broj Osnovni koncepti postojanje pojmova slučajnosti, neovisnosti i hijerarhije (ideje o razinama u strukturi i determiniranosti sustava).
Ideje o vjerojatnosti nastale su u antici i vezane uz karakteristike našeg znanja, pri čemu se priznaje postojanje probabilističkog znanja koje se razlikuje od pouzdano znanje a od lažnog. Utjecaj ideje vjerojatnosti na znanstveno mišljenje, na razvoj znanja izravno je povezan s razvojem teorije vjerojatnosti kao matematičke discipline. Podrijetlo matematičke doktrine vjerojatnosti seže u 17. stoljeće, kada se razvija jezgra koncepata koji dopuštaju. kvantitativne (numeričke) karakteristike i izražavanje vjerojatnosne ideje.
Intenzivne primjene vjerojatnosti na razvoj znanja spadaju u 2. kat. 19- 1. kat. 20. stoljeće Vjerojatnost je ušla u strukture takvih fundamentalne znanosti o prirodi, poput klasične statističke fizike, genetike, kvantne teorije, kibernetike (teorije informacija). Prema tome, vjerojatnost personificira onu fazu u razvoju znanosti, koja se danas definira kao neklasična znanost. Da bismo otkrili novost, značajke probabilističkog načina razmišljanja, potrebno je krenuti od analize predmeta teorije vjerojatnosti i temelja njezinih brojnih primjena. Teorija vjerojatnosti obično se definira kao matematička disciplina koja proučava zakone masovnih slučajnih pojava pod određenim uvjetima. Slučajnost znači da u okviru masovnosti postojanje svake elementarne pojave ne ovisi i nije određeno postojanjem drugih pojava. Istovremeno, sama masovnost pojava ima stabilna struktura, sadrži određene pravilnosti. Masovna pojava prilično je strogo podijeljena na podsustave, a relativni broj elementarnih pojava u svakom od podsustava (relativna učestalost) vrlo je stabilan. Ta se stabilnost uspoređuje s vjerojatnošću. Masovni fenomen u cjelini karakterizira raspodjela vjerojatnosti, tj. dodjela podsustava i njihovih odgovarajućih vjerojatnosti. Jezik teorije vjerojatnosti je jezik distribucije vjerojatnosti. U skladu s tim, teorija vjerojatnosti definirana je kao apstraktna znanost o radu s distribucijama.
Vjerojatnost je u znanosti potaknula ideje o statističkim pravilnostima i statističkim sustavima. Potonji su sustavi formirani od nezavisnih ili kvazineovisnih entiteta, njihovu strukturu karakteriziraju distribucije vjerojatnosti. Ali kako je moguće formirati sustave od neovisnih entiteta? Obično se pretpostavlja da je za nastanak sustava s integralnim karakteristikama potrebno da između njihovih elemenata postoje dovoljno stabilne veze koje cementiraju sustave. Stabilnost statističkih sustava daje prisutnost vanjskih uvjeta, vanjsko okruženje, vanjski, ne unutarnje sile. Sama definicija vjerojatnosti uvijek se temelji na postavljanju uvjeta za nastanak početne masovne pojave. Druga važna ideja koja karakterizira probabilističku paradigmu je ideja hijerarhije (subordinacije). Ova ideja izražava odnos između karakteristika pojedinačnih elemenata i integralnih karakteristika sustava: potonje su, takoreći, izgrađene na prvima.
Značenje probabilističkih metoda u spoznaji je u tome što nam omogućuju istraživanje i teorijski izraz obrazaca strukture i ponašanja objekata i sustava koji imaju hijerarhijsku, "dvorazinsku" strukturu.
Analiza prirode vjerojatnosti temelji se na njenoj učestalosti, statističkoj interpretaciji. Međutim, vrlo Dugo vrijeme u znanosti je dominiralo takvo shvaćanje vjerojatnosti koje se nazivalo logička, odnosno induktivna vjerojatnost. Logičku vjerojatnost zanimaju pitanja valjanosti zasebnog, pojedinačnog suda pod određenim uvjetima. Je li moguće kvantitativno ocijeniti stupanj potvrde (pouzdanosti, istinitosti) induktivnog zaključka (hipotetskog zaključka)? Tijekom formiranja teorije vjerojatnosti, takva su se pitanja više puta raspravljala, a počelo se govoriti o stupnjevima potvrde hipotetskih zaključaka. Ovu mjeru vjerojatnosti određuju informacije kojima određena osoba raspolaže, njezino iskustvo, pogledi na svijet i psihološki način razmišljanja. U svim takvim slučajevima, veličina vjerojatnosti nije podložna strogim mjerenjima i praktički je izvan nadležnosti teorije vjerojatnosti kao konzistentne matematičke discipline.
Objektivno, učestalo tumačenje vjerojatnosti uspostavljeno je u znanosti uz znatne poteškoće. U početku je shvaćanje prirode vjerojatnosti bilo snažan utjecaj ona filozofska i metodološka stajališta koja su bila svojstvena klasičnoj znanosti. Povijesno gledano, formiranje probabilističkih metoda u fizici dogodilo se pod odlučujućim utjecajem ideja mehanike: statistički sustavi tretirani su jednostavno kao mehanički. Budući da odgovarajući problemi nisu riješeni strogim metodama mehanike, pojavile su se tvrdnje da je pozivanje na probabilističke metode i statističke zakonitosti rezultat nepotpunosti našeg znanja. U povijesti razvoja klasičnog statistička fizika učinjeni su brojni pokušaji da se to potkrijepi na temelju klasične mehanike, ali svi su propali. Osnova vjerojatnosti je da izražava značajke strukture određene klase sustava, osim sustava mehanike: stanje elemenata tih sustava karakterizira nestabilnost i posebna (koja se ne može svesti na mehaniku) priroda interakcija .
Ulazak vjerojatnosti u spoznaju dovodi do negiranja koncepta krutog determinizma, do negiranja temeljnog modela bića i spoznaje razvijenog u procesu formiranja klasične znanosti. Osnovni modeli koje predstavljaju statističke teorije drugačije su, općenitije prirode: oni uključuju ideje slučajnosti i neovisnosti. Ideja vjerojatnosti povezana je s otkrivanjem unutarnje dinamike objekata i sustava, koja se ne može u potpunosti odrediti vanjskim uvjetima i okolnostima.
Koncept probabilističke vizije svijeta, utemeljen na apsolutizaciji ideja o neovisnosti (kao i prije, paradigma krute determiniranosti), sada je otkrio svoja ograničenja, što najjače utječe na tranziciju moderna znanost Do analitičke metode proučavanje složenih sustava i fizikalnih i matematičkih temelja fenomena samoorganizacije.
Sjajna definicija
Nepotpuna definicija ↓
Nemojmo dugo razmišljati o uzvišenom – krenimo odmah s definicijom.
Bernoullijeva shema je kada se izvodi n neovisnih eksperimenata iste vrste, u svakom od kojih se može pojaviti događaj koji nas zanima A, a vjerojatnost tog događaja je poznata P (A) \u003d p. Potrebno je odrediti vjerojatnost da će se događaj A dogoditi točno k puta tijekom n pokušaja.
Zadaci koji se rješavaju prema Bernoullijevoj shemi iznimno su raznoliki: od jednostavnih (kao što je “pronaći vjerojatnost da strijelac pogodi 1 put od 10”) do vrlo teških (na primjer, zadaci za postotke ili kartanje). U stvarnosti se ova shema često koristi za rješavanje problema vezanih uz kontrolu kvalitete proizvoda i pouzdanost različitih mehanizama, čije sve karakteristike moraju biti poznate prije početka rada.
Vratimo se na definiciju. Budući da je riječ o neovisnim pokusima, au svakom pokusu je vjerojatnost događaja A ista, moguća su samo dva ishoda:
- A je pojava događaja A s vjerojatnošću p;
- "nije A" - događaj A se nije pojavio, što se događa s vjerojatnošću q = 1 − p.
Najvažniji uvjet bez kojeg Bernoullijeva shema gubi smisao je konstantnost. Bez obzira koliko pokusa proveli, zainteresirani smo za isti događaj A koji se dogodi s istom vjerojatnošću p.
Usput, ne mogu se svi problemi u teoriji vjerojatnosti svesti na konstantne uvjete. O tome će vam reći svaki kompetentan učitelj više matematike. Čak i nešto tako jednostavno kao što je vađenje obojenih kuglica iz kutije nije eksperiment s konstantnim uvjetima. Izvadili su još jednu loptu - promijenio se omjer boja u kutiji. Stoga su se i vjerojatnosti promijenile.
Ako su uvjeti konstantni, može se točno odrediti vjerojatnost da će se događaj A dogoditi točno k puta od n mogućih. Ovu činjenicu formuliramo u obliku teorema:
Bernoullijev teorem. Neka je vjerojatnost pojavljivanja događaja A u svakom eksperimentu konstantna i jednaka p. Tada se vjerojatnost da će se u n neovisnih pokusa događaj A pojaviti točno k puta izračunava se formulom:
gdje je C n k broj kombinacija, q = 1 − p.
Ova se formula naziva Bernoullijeva formula. Zanimljivo je primijetiti da su problemi ispod potpuno riješeni bez korištenja ove formule. Na primjer, možete primijeniti formule zbrajanja vjerojatnosti. Međutim, količina izračuna bit će jednostavno nerealna.
Zadatak. Vjerojatnost proizvodnje neispravnog proizvoda na stroju je 0,2. Odredite vjerojatnost da će u seriji od deset dijelova proizvedenih na određenom stroju točno k biti bez nedostataka. Riješite zadatak za k = 0, 1, 10.
Pod uvjetom nas zanima događaj A puštanja proizvoda bez nedostataka koji se događa svaki put s vjerojatnošću p = 1 − 0,2 = 0,8. Moramo odrediti vjerojatnost da će se ovaj događaj dogoditi k puta. Događaj A je suprotstavljen događaju “ne A”, tj. proizvodnja proizvoda s nedostatkom.
Dakle, imamo: n = 10; p=0,8; q = 0,2.
Dakle, nalazimo vjerojatnost da su svi dijelovi u seriji neispravni (k = 0), da je samo jedan dio neispravan (k = 1) i da uopće nema neispravnih dijelova (k = 10):

Zadatak. Novčić se baca 6 puta. Gubitak grba i repa jednako je vjerojatan. Nađite vjerojatnost da:
- grb će pasti tri puta;
- grb će jednom pasti;
- grb će se pojaviti najmanje dva puta.
Dakle, zanima nas događaj A kada padne grb. Vjerojatnost ovog događaja je p = 0,5. Događaju A suprotstavlja se događaj “ne A”, kada dođe do repova, što se događa s vjerojatnošću q = 1 − 0,5 = 0,5. Potrebno je odrediti vjerojatnost da će grb ispasti k puta.
Dakle, imamo: n = 6; p = 0,5; q = 0,5.
Odredimo vjerojatnost da je grb ispao tri puta, t.j. k = 3:
Sada odredimo vjerojatnost da je grb ispao samo jednom, tj. k = 1:
Ostaje utvrditi s kojom vjerojatnošću će grb ispasti barem dva puta. Glavna začkoljica je u izrazu "ništa manje". Ispada da će nam odgovarati bilo koji k, osim 0 i 1, tj. trebate pronaći vrijednost zbroja X \u003d P 6 (2) + P 6 (3) + ... + P 6 (6).
Primijetimo da je i ovaj zbroj jednak (1 − P 6 (0) − P 6 (1)), tj. od svih mogućih opcija dovoljno je “izrezati” one kada je grb ispao 1 put (k = 1) ili uopće nije ispao (k = 0). Budući da P 6 (1) već znamo, ostaje pronaći P 6 (0):

Zadatak. Vjerojatnost da TV ima skrivene nedostatke je 0,2. U skladište je stiglo 20 televizora. Koji je događaj vjerojatniji: da u ovoj seriji postoje dva televizora sa skrivenim nedostacima ili tri?
Događaj od interesa A je prisutnost latentnog defekta. Ukupno televizora n = 20, vjerojatnost skrivenog kvara p = 0,2. Sukladno tome, vjerojatnost da dobijete televizor bez skrivenog kvara je q = 1 − 0,2 = 0,8.
Dobivamo polazne uvjete za Bernoullijevu shemu: n = 20; p = 0,2; q = 0,8.
Nađimo vjerojatnost da dobijemo dva "neispravna" televizora (k = 2) i tri (k = 3):
\[\begin(array)(l)(P_(20))\left(2 \right) = C_(20)^2(p^2)(q^(18)) = \frac((20}{{2!18!}} \cdot {0,2^2} \cdot {0,8^{18}} \approx 0,137\\{P_{20}}\left(3 \right) = C_{20}^3{p^3}{q^{17}} = \frac{{20!}}{{3!17!}} \cdot {0,2^3} \cdot {0,8^{17}} \approx 0,41\end{array}\]!}
Očito je P 20 (3) > P 20 (2), tj. vjerojatnost da ćete dobiti tri televizora sa skrivenim nedostacima je veća da ćete dobiti samo dva takva televizora. Štoviše, razlika nije slaba.
Mala napomena o faktorijelima. Mnogi ljudi dožive nejasan osjećaj nelagode kada vide unos "0!" (čitaj "nula faktorijel"). Dakle, 0! = 1 po definiciji.
P. S. A najveća vjerojatnost u zadnjem zadatku je dobiti četiri televizora sa skrivenim nedostacima. Izračunajte i uvjerite se sami.
Želite li znati kolike su matematičke šanse da vaša oklada bude uspješna? Onda su tu dva za vas. dobre vijesti. Prvo: da biste izračunali sposobnost cross-country, ne morate provoditi složene izračune i trošiti veliki broj vrijeme. Dovoljno je koristiti jednostavne formule, s kojima će vam trebati nekoliko minuta. Drugo, nakon čitanja ovog članka, lako ćete moći izračunati vjerojatnost prolaska bilo koje od vaših trgovina.
Da biste ispravno odredili prohodnost, morate poduzeti tri koraka:
- Izračunati postotak vjerojatnosti ishoda događaja prema kladionici;
- Sami izračunajte vjerojatnost iz statističkih podataka;
- Saznajte vrijednost oklade s obzirom na obje vjerojatnosti.
Razmotrimo detaljno svaki od koraka, koristeći ne samo formule, već i primjere.
Brzi prolaz
Izračun vjerojatnosti ugrađen u koeficijente klađenja
Prvi korak je saznati s kojom vjerojatnošću kladionica procjenjuje šanse za određeni ishod. Uostalom, jasno je da kladionice ne klade koeficijente tek tako. Za to koristimo sljedeću formulu:
PB=(1/K)*100%,
gdje je P B vjerojatnost ishoda prema kladionici;
K - tečaj kladionice za ishod.

Recimo da je na pobjedu londonskog Arsenala u dvoboju protiv Bayerna koeficijent 4. To znači da se vjerojatnost njegove pobjede od strane BC-a smatra (1/4) * 100% = 25%. Ili Đoković igra protiv Juga. Množitelj za Novakovu pobjedu je 1,2, njegove šanse su jednake (1/1,2)*100%=83%.
Ovako sama kladionica procjenjuje šanse za uspjeh svakog igrača i tima. Nakon što smo završili prvi korak, prelazimo na drugi.
Izračun vjerojatnosti događaja od strane igrača
Druga točka našeg plana je naša vlastita procjena vjerojatnosti događaja. Budući da matematički ne možemo uzeti u obzir parametre kao što su motivacija, ton igre, koristit ćemo se pojednostavljenim modelom i koristiti samo statistiku prethodnih susreta. Za izračunavanje statističke vjerojatnosti ishoda koristimo se formulom:
PI\u003d (UM / M) * 100%,
GdjePI- vjerojatnost događaja prema igraču;
UM - broj uspješnih utakmica u kojima se dogodio takav događaj;
M - ukupnošibice.

Da bi bilo jasnije, navedimo primjere. Andy Murray i Rafael Nadal odigrali su 14 mečeva. U njih 6 zabilježeno je ukupno manje od 21 utakmice, u 8 ukupno više. Potrebno je saznati vjerojatnost da će se sljedeća utakmica odigrati za ukupni over: (8/14)*100=57%. Valencia je na Mestalli protiv Atlética odigrala 74 utakmice u kojima je ostvarila 29 pobjeda. Vjerojatnost pobjede Valencije: (29/74)*100%=39%.
A to svi znamo samo zahvaljujući statistici prethodnih utakmica! Naravno, takva se vjerojatnost ne može izračunati za neku novu momčad ili igrača, tako da je ova strategija klađenja prikladna samo za utakmice u kojima se protivnici ne susreću prvi put. Sada znamo kako odrediti klađenje i vlastite vjerojatnosti ishoda, te imamo svo znanje da idemo do posljednjeg koraka.
Određivanje vrijednosti oklade
Vrijednost (procjena) oklade i prolaznost su izravno povezani: što je veća procjena, veća je šansa za prolaz. Vrijednost se izračunava na sljedeći način:
V=PI*K-100%,
gdje je V vrijednost;
P I - vjerojatnost ishoda prema boljem;
K - tečaj kladionice za ishod.
Recimo, želimo se kladiti na pobjedu Milana u utakmici protiv Rome i izračunali smo da je vjerojatnost pobjede Crveno-crnih 45%. Kladionica nam nudi koeficijent 2,5 za ovaj ishod. Bi li takva oklada bila vrijedna? Izvodimo izračune: V \u003d 45% * 2,5-100% \u003d 12,5%. Odlično, imamo vrijednu okladu s dobrim izgledima za prolaz.
Uzmimo drugi slučaj. Marija Šarapova igra protiv Petre Kvitove. Želimo se dogovoriti da Marija pobijedi, što je, prema našim izračunima, s vjerojatnošću od 60 posto. Kladionice nude množitelj od 1,5 za ovaj ishod. Odredite vrijednost: V=60%*1,5-100=-10%. Kao što vidite, ova oklada nema nikakvu vrijednost i treba je se suzdržati.

U početku, budući da je bila samo zbirka informacija i empirijskih opažanja igre kocke, teorija vjerojatnosti postala je čvrsta znanost. Fermat i Pascal su prvi dali matematički okvir.
Od razmišljanja o vječnom do teorije vjerojatnosti
Dva pojedinca kojima teorija vjerojatnosti duguje mnoge temeljne formule, Blaise Pascal i Thomas Bayes, poznati su kao duboko religiozni ljudi, potonji je bio prezbiterijanski svećenik. Očigledno je želja ove dvojice znanstvenika da dokažu pogrešnost mišljenja o određenoj Fortune, darujući sreću njezinim miljenicima, dala poticaj istraživanjima na ovom području. Uostalom, zapravo je svaka igra na sreću, sa svojim dobicima i gubicima, samo simfonija matematičkih principa.
Zahvaljujući uzbuđenju Chevaliera de Merea, koji je u jednako bio kockar i osoba koja nije bila ravnodušna prema znanosti, Pascal je bio prisiljen pronaći način za izračunavanje vjerojatnosti. De Merea je zanimalo ovo pitanje: "Koliko puta trebate baciti dvije kocke u paru da vjerojatnost dobivanja 12 bodova bude veća od 50%?". Drugo pitanje koje je iznimno zanimalo gospodina: "Kako podijeliti ulog između sudionika u nedovršenoj igri?" Naravno, Pascal je uspješno odgovorio na oba pitanja de Merea, koji je postao nesvjesni inicijator razvoja teorije vjerojatnosti. Zanimljivo je da je osoba de Mere ostala poznata na ovim prostorima, a ne u književnosti.
Prije toga nijedan matematičar još nije pokušao izračunati vjerojatnosti događaja, jer se vjerovalo da je to samo nagađanje. Blaise Pascal je dao prvu definiciju vjerojatnosti događaja i pokazao da je to specifična brojka koja se može opravdati matematički. Teorija vjerojatnosti postala je temelj statistike i naširoko se koristi u modernoj znanosti.
Što je slučajnost
Ako uzmemo u obzir test koji se može ponoviti beskonačan broj puta, tada možemo definirati slučajni događaj. Ovo je jedan od mogućih ishoda iskustva.
Iskustvo je provedba specifičnih radnji u stalnim uvjetima.

Kako bi se moglo raditi s rezultatima iskustva, događaji se obično označavaju slovima A, B, C, D, E...
Vjerojatnost slučajnog događaja
Da bismo mogli prijeći na matematički dio vjerojatnosti, potrebno je definirati sve njezine komponente.
Vjerojatnost događaja je numerička mjera mogućnosti pojave nekog događaja (A ili B) kao rezultat iskustva. Vjerojatnost se označava kao P(A) ili P(B).
Teorija vjerojatnosti je:
- pouzdan događaj će se zajamčeno dogoditi kao rezultat eksperimenta R(Ω) = 1;
- nemoguće događaj se nikada ne može dogoditi R(Ø) = 0;
- slučajan događaj se nalazi između sigurnog i nemogućeg, odnosno vjerojatnost njegovog događanja je moguća, ali nije zajamčena (vjerojatnost slučajni događaj uvijek unutar 0≤P(A)≤1).
Odnosi među događajima
I jedan i zbroj događaja A + B uzimaju se u obzir kada se događaj računa u implementaciji barem jedne od komponenti, A ili B, ili obje - A i B.
U međusobnom odnosu, događaji mogu biti:
- Jednako moguće.
- kompatibilan.
- Nespojivo.
- Suprotno (međusobno se isključuje).
- Ovisna.
Ako se dva događaja mogu dogoditi s jednakom vjerojatnošću, onda oni jednako moguće.
Ako pojava događaja A ne poništava vjerojatnost pojave događaja B, tada oni kompatibilan.
Ako se događaji A i B nikada ne dogode u isto vrijeme u istom eksperimentu, tada se oni nazivaju nekompatibilan. Bacanje novčića dobar je primjer: dobivanje repova automatski ne znači i dobivanje glava.

Vjerojatnost za zbroj takvih nespojivi događaji sastoji se od zbroja vjerojatnosti svakog od događaja:
P(A+B)=P(A)+P(B)
Ako pojava jednog događaja onemogućuje pojavu drugog, onda se oni nazivaju suprotnim. Zatim je jedan od njih označen kao A, a drugi - Ā (čitaj kao "ne A"). Događaj A znači da se Ā nije dogodio. Ova dva događaja čine potpunu grupu sa zbrojem vjerojatnosti jednakim 1.

Ovisni događaji imaju međusobni utjecaj, međusobno smanjujući ili povećavajući vjerojatnost.
Odnosi među događajima. Primjeri
Puno je lakše razumjeti principe teorije vjerojatnosti i kombinacije događaja koristeći primjere.
Eksperiment koji će se provesti je izvlačenje kuglica iz kutije, a rezultat svakog eksperimenta je elementarni ishod.
Događaj je jedan od mogućih ishoda iskustva - crvena lopta, plava lopta, lopta s brojem šest itd.
Test broj 1. Ima 6 kuglica od kojih su tri plave s neparnim brojevima, a ostale tri crvene s parnim brojevima.

Test broj 2. Sudjeluje 6 lopti plave boje brojevima od jedan do šest.

Na temelju ovog primjera možemo imenovati kombinacije:
- Pouzdan događaj. Na španjolskom br. 2, događaj "uzmi plavu loptu" je pouzdan, jer je vjerojatnost njegovog pojavljivanja 1, jer su sve kuglice plave i ne može biti promašaja. Dok je događaj "uzmi loptu s brojem 1" slučajan.
- Nemoguć događaj. Na španjolskom br. 1 s plavim i crvenim kuglicama, događaj "dobiti ljubičastu loptu" je nemoguć, jer je vjerojatnost njegove pojave 0.
- Ekvivalentni događaji. Na španjolskom br. 1, jednako su vjerojatni događaji „dobiti loptu brojem 2” i „dobiti loptu brojem 3”, a događaji „dobiti loptu parnim brojem” i „dobiti loptu brojem 2” ” imaju različite vjerojatnosti.
- Kompatibilni događaji. Dobivanje šestice u procesu bacanja kocke dvaput zaredom su kompatibilni događaji.
- Nespojivi događaji. Na istom španjolskom Događaji br. 1 "dobiti crvenu loptu" i "dobiti loptu s neparnim brojem" ne mogu se kombinirati u istom iskustvu.
- suprotnih događaja. Najupečatljiviji primjer za to je bacanje novčića, gdje je izvlačenje glave isto što i ne izvlačenje repa, a zbroj njihovih vjerojatnosti je uvijek 1 (puna grupa).
- Ovisni događaji. Dakle, na španjolskom Broj 1, možete si postaviti cilj da dva puta zaredom izvučete crvenu loptu. Izdvajanje ili ne izdvajanje prvi put utječe na vjerojatnost izdvajanja drugi put.

Vidljivo je da prvi događaj značajno utječe na vjerojatnost drugog (40% i 60%).
Formula vjerojatnosti događaja
Prijelaz s proricanja sudbine na točne podatke događa se prijenosom teme na matematičku razinu. To jest, prosudbe o slučajnom događaju poput "visoke vjerojatnosti" ili "minimalne vjerojatnosti" mogu se prevesti u specifične numeričke podatke. Već je dopušteno ocjenjivati, uspoređivati i uvoditi takav materijal u složenije izračune.
Sa stajališta izračuna, definicija vjerojatnosti događaja je omjer broja elementarnih pozitivnih ishoda prema broju svih mogućih ishoda iskustva s obzirom na određeni događaj. Vjerojatnost je označena s P (A), gdje P znači riječ "vjerojatnost", koja se s francuskog prevodi kao "vjerojatnost".
Dakle, formula za vjerojatnost događaja je:
Gdje je m broj povoljnih ishoda za događaj A, n je zbroj svih mogućih ishoda za ovo iskustvo. Vjerojatnost događaja uvijek je između 0 i 1:
0 ≤ P(A) ≤ 1.
Proračun vjerojatnosti događaja. Primjer
Uzmimo španjolski. 1 s kuglicama, koje su ranije opisane: 3 plave kuglice s brojevima 1/3/5 i 3 crvene kuglice s brojevima 2/4/6.

Na temelju ovog testa može se razmotriti nekoliko različitih zadataka:
- A - ispuštanje crvene lopte. Postoje 3 crvene kuglice, a ukupno 6 opcija. Ovo je najjednostavniji primjer, u kojem je vjerojatnost događaja P(A)=3/6=0,5.
- B - ispuštanje parnog broja. Ukupno ima 3 (2,4,6) parna broja, a ukupan broj mogućih numeričkih opcija je 6. Vjerojatnost ovog događaja je P(B)=3/6=0,5.
- C - gubitak broja većeg od 2. Postoje 4 takve opcije (3,4,5,6) od ukupnog broja mogućih ishoda 6. Vjerojatnost događaja C je P(C)=4/6= 0,67.
Kao što se može vidjeti iz izračuna, događaj C ima veću vjerojatnost, jer je broj mogućih pozitivnih ishoda veći nego u A i B.
Nespojivi događaji
Takvi se događaji ne mogu pojaviti istovremeno u istom iskustvu. Kao na španjolskom Broj 1, nemoguće je dobiti plavu i crvenu loptu u isto vrijeme. Odnosno, možete dobiti ili plavu ili crvenu loptu. Na isti način, paran i neparan broj ne mogu se pojaviti u kockici u isto vrijeme.
Vjerojatnost dva događaja smatra se vjerojatnošću njihovog zbroja ili umnoška. Zbroj takvih događaja A + B smatra se događajem koji se sastoji u pojavi događaja A ili B, a umnožak njihovih AB - u pojavi oba. Na primjer, pojavljivanje dvije šestice odjednom na stranama dviju kockica u jednom bacanju.

Zbroj više događaja je događaj koji podrazumijeva pojavu barem jednog od njih. Proizvod nekoliko događaja je zajednička pojava svih njih.
U teoriji vjerojatnosti, u pravilu, uporaba unije "i" označava zbroj, unije "ili" - množenje. Formule s primjerima pomoći će vam razumjeti logiku zbrajanja i množenja u teoriji vjerojatnosti.
Vjerojatnost zbroja nekompatibilnih događaja
Ako se uzme u obzir vjerojatnost zajednički događaji, tada je vjerojatnost zbroja događaja jednaka zbroju njihovih vjerojatnosti:
P(A+B)=P(A)+P(B)
Na primjer: izračunavamo vjerojatnost da u španjolskom. Broj 1 s plavim i crvenim kuglicama ispustit će broj između 1 i 4. Računat ćemo ne jednom akcijom, već zbrojem vjerojatnosti elementarnih komponenti. Dakle, u takvom eksperimentu postoji samo 6 lopti ili 6 od svih mogućih ishoda. Brojevi koji zadovoljavaju uvjet su 2 i 3. Vjerojatnost da dobijete broj 2 je 1/6, vjerojatnost broja 3 je također 1/6. Vjerojatnost da dobijete broj između 1 i 4 je:
Vjerojatnost zbroja nekompatibilnih događaja kompletne grupe je 1.
Dakle, ako u eksperimentu s kockom zbrojimo vjerojatnosti dobivanja svih brojeva, tada kao rezultat dobivamo jedan.
To vrijedi i za suprotne događaje, npr. u pokusu s novčićem, gdje je jedna njegova strana događaj A, a druga suprotni događaj Ā, kao što je poznato,
R(A) + R(Ā) = 1
Vjerojatnost stvaranja nekompatibilnih događaja
Množenje vjerojatnosti koristi se kada se razmatra pojava dva ili više nekompatibilnih događaja u jednom opažanju. Vjerojatnost da će se događaji A i B u njemu pojaviti u isto vrijeme jednaka je umnošku njihovih vjerojatnosti, odnosno:
P(A*B)=P(A)*P(B)
Na primjer, vjerojatnost da u Broj 1 kao rezultat dva pokušaja, plava kuglica će se pojaviti dva puta, jednako
Odnosno, vjerojatnost da će se dogoditi događaj kada će se, kao rezultat dva pokušaja izvlačenja kuglica, izvući samo plave kuglice, iznosi 25%. Vrlo je jednostavno izvesti praktične pokuse na ovom problemu i vidjeti je li to doista tako.
Zajednički događaji
Događaji se smatraju zajedničkim kada se pojavljivanje jednog od njih može podudarati s pojavljivanjem drugog. Unatoč činjenici da su zajednički, razmatra se vjerojatnost neovisnih događaja. Primjerice, bacanje dviju kockica može dati rezultat kada na objema padne broj 6. Iako su se događaji poklopili i pojavili u isto vrijeme, oni su neovisni jedan o drugome – mogla je ispasti samo jedna šestica, druga kocka nema utjecaj na to.

Vjerojatnost zajedničkih događaja smatra se vjerojatnošću njihovog zbroja.
Vjerojatnost zbroja zajedničkih događaja. Primjer
Vjerojatnost zbroja događaja A i B, koji su zajednički jedan prema drugome, jednaka je zbroju vjerojatnosti događaja umanjenom za vjerojatnost njihovog umnoška (odnosno njihove zajedničke provedbe):
R zglob. (A + B) \u003d P (A) + P (B) - P (AB)
Pretpostavimo da je vjerojatnost pogotka mete jednim hicem 0,4. Zatim događaj A - pogađanje mete u prvom pokušaju, B - u drugom. Ovi događaji su zajednički, jer je moguće da je moguće pogoditi metu i iz prvog i iz drugog hica. Ali događaji nisu ovisni. Kolika je vjerojatnost događaja pogotka mete s dva hica (barem jednim)? Prema formuli:
0,4+0,4-0,4*0,4=0,64
Odgovor na pitanje je: "Vjerojatnost pogotka cilja s dva hica je 64%."
Ova formula za vjerojatnost događaja može se primijeniti i na nekompatibilne događaje, gdje je vjerojatnost zajedničkog pojavljivanja događaja P(AB) = 0. To znači da se vjerojatnost zbroja nekompatibilnih događaja može smatrati posebnim slučajem predložene formule.
Geometrija vjerojatnosti za jasnoću
Zanimljivo je da se vjerojatnost zbroja zajedničkih događaja može prikazati kao dva područja A i B koja se međusobno sijeku. Kao što možete vidjeti na slici, površina njihovog spoja jednaka je ukupnoj površini minus površina njihovog sjecišta. Ovo geometrijsko objašnjenje čini naizgled nelogičnu formulu razumljivijom. Imajte na umu da geometrijska rješenja nisu neuobičajena u teoriji vjerojatnosti.

Definicija vjerojatnosti zbroja skupa (više od dva) zajedničkih događaja prilično je glomazna. Da biste ga izračunali, morate koristiti formule koje su predviđene za ove slučajeve.
Ovisni događaji
Ovisni događaji nazivaju se ako pojava jednog (A) od njih utječe na vjerojatnost pojavljivanja drugog (B). Štoviše, uzima se u obzir utjecaj i pojave događaja A i njegovog nepojavljivanja. Iako se događaji po definiciji nazivaju ovisnima, samo je jedan od njih zavisan (B). Uobičajena vjerojatnost označavana je kao P(B) ili vjerojatnost neovisnih događaja. Kod zavisnih se uvodi novi koncept - uvjetna vjerojatnost P A (B), koja je vjerojatnost ovisnog događaja B pod uvjetom da se dogodio događaj A (hipoteza) o kojem on ovisi.
Ali događaj A je također slučajan, pa također ima vjerojatnost koja se mora i može uzeti u obzir u izračunima. Sljedeći primjer pokazat će kako raditi s ovisnim događajima i hipotezom.
Primjer izračuna vjerojatnosti zavisnih događaja
Dobar primjer za izračunavanje zavisnih događaja je standardni špil karata.

Na primjeru špila od 36 karata, razmotrite ovisne događaje. Potrebno je odrediti vjerojatnost da će druga izvučena karta iz špila biti karo, ako je prva izvučena karta:
- Tamburin.
- Drugo odijelo.
Očito, vjerojatnost drugog događaja B ovisi o prvom događaju A. Dakle, ako je prva opcija točna, što je 1 karta (35) i 1 karo (8) manje u špilu, vjerojatnost događaja B:
P A (B) \u003d 8 / 35 \u003d 0,23
Ako je druga opcija točna, tada je u špilu 35 karata, a ukupni broj tambura (9), tada je vjerojatnost sljedećeg događaja B:
P A (B) \u003d 9/35 \u003d 0,26.
Može se vidjeti da ako je događaj A uvjetovan činjenicom da je prva karta karo, tada se vjerojatnost događaja B smanjuje, i obrnuto.
Množenje zavisnih događaja
Na temelju prethodnog poglavlja prvi događaj (A) prihvaćamo kao činjenicu, ali on u biti ima slučajan karakter. Vjerojatnost ovog događaja, odnosno vađenja tamburice iz špila karata, jednaka je:
P(A) = 9/36=1/4
Budući da teorija ne postoji sama za sebe, već je pozvana da služi praktične svrhe, pošteno je primijetiti da je najčešće potrebna vjerojatnost umnoška zavisnih događaja.
Prema teoremu o umnošku vjerojatnosti ovisnih događaja, vjerojatnost pojavljivanja zajednički ovisnih događaja A i B jednaka je vjerojatnosti jednog događaja A, pomnoženoj s uvjetnom vjerojatnošću događaja B (ovisno o A):
P (AB) \u003d P (A) * PA (B)
Zatim u primjeru sa špilom, vjerojatnost izvlačenja dviju karata s karo je:
9/36*8/35=0,0571 ili 5,7%
A vjerojatnost da prvo ne izvadite dijamante, a zatim dijamante, jednaka je:
27/36*9/35=0,19 ili 19%
Vidi se da je vjerojatnost događanja događaja B veća, pod uvjetom da se prva izvuče karta boje koja nije karo. Ovaj rezultat je sasvim logičan i razumljiv.
Ukupna vjerojatnost događaja
Kada problem s uvjetnim vjerojatnostima postane višestruk, ne može se izračunati konvencionalnim metodama. Kada postoji više od dvije hipoteze, naime A1, A2, ..., A n , .. čini potpunu grupu događaja pod uvjetom:
- P(A i)>0, i=1,2,…
- A i ∩ A j =Ø,i≠j.
- Σ k A k =Ω.
Dakle, formula puna vjerojatnost za događaj B s potpunom grupom slučajnih događaja A1, A2, ..., A n je:

Pogled u budućnost
Vjerojatnost slučajnog događaja bitna je u mnogim područjima znanosti: ekonometriji, statistici, fizici itd. Kako se neki procesi ne mogu deterministički opisati, jer su sami po sebi probabilistički, potrebne su posebne metode rada. Teorija vjerojatnosti događaja može se koristiti u bilo kojem tehnološkom području kao način utvrđivanja mogućnosti pogreške ili kvara.
Može se reći da prepoznavanjem vjerojatnosti na neki način činimo teorijski korak u budućnost, gledajući je kroz prizmu formula.
U svom blogu, prijevod sljedećeg predavanja kolegija "Principles of Game Balance" dizajnera igara Jana Schreibera, koji je radio na projektima kao što su Marvel Trading Card Game i Playboy: the Mansion.
Prije danas gotovo sve o čemu smo razgovarali bilo je determinističko, a prošlog smo tjedna pomno pogledali tranzitivnu mehaniku, razlažući je na onoliko detalja koliko mogu objasniti. Ali do sada nismo obraćali pozornost na druge aspekte mnogih igara, naime, nedeterminističke momente - drugim riječima, slučajnost.
Razumijevanje prirode nasumičnosti vrlo je važno za dizajnere igara. Stvaramo sustave koji utječu na korisničko iskustvo u određenoj igri, stoga moramo znati kako ti sustavi funkcioniraju. Ako u sustavu postoji slučajnost, moramo razumjeti prirodu te slučajnosti i znati kako je promijeniti da bismo dobili rezultate koji su nam potrebni.
Kocke
Počnimo s nečim jednostavnim - bacanjem kockica. Kada većina ljudi pomisli na kocku, pomisli na šestostranu kocku poznatu kao d6. Ali većina igrača je vidjela mnoge druge kockice: četverostrane (d4), osmostrane (d8), dvanaestostrane (d12), dvadesetostrane (d20). Ako ste pravi geek, možda negdje imate kockice od 30 ili 100 zrna.
Ako niste upoznati s ovom terminologijom, d označava kockicu, a broj iza nje je broj njezinih lica. Ako je broj ispred d, tada označava broj kockica prilikom bacanja. Na primjer, u igri Monopoly bacate 2d6.
Dakle u ovaj slučaj izraz "kocka" - simbol. Postoji ogroman broj drugih generatora slučajnih brojeva koji ne izgledaju kao plastične figure, ali imaju istu funkciju - generiraju slučajni broj od 1 do n. Obični novčić također se može prikazati kao diedralna d2 matrica.
Vidio sam dva dizajna sedmostrane matrice: jedna je izgledala kao kocka, a druga je više ličila na sedmostranu drvenu olovku. Tetraedarski dreidel, također poznat kao titotum, analog je tetraedralne kosti. Ploča za igru sa strelicom koja se okreće u Chutes & Ladders, gdje rezultat može biti od 1 do 6, odgovara kockici sa šest strana.
Generator slučajnih brojeva u računalu može generirati bilo koji broj od 1 do 19 ako dizajner da takvu naredbu, iako računalo nema 19-stranu kocku (općenito, više ću govoriti o vjerojatnosti dobivanja brojeva na računalo sljedeći tjedan). Sve te stavke izgledaju drugačije, ali zapravo su jednake: imate jednaku šansu za svaki od nekoliko mogućih ishoda.
Kockice imaju neka zanimljiva svojstva koja moramo znati. Prvo, vjerojatnost da će se bilo koje lice pojaviti je ista (pretpostavljam da bacate kockice s točnim geometrijski oblik). Ako želite znati prosječnu vrijednost bacanja (poznatu kao matematičko očekivanje onima koji vole teoriju vjerojatnosti), zbrojite vrijednosti na svim rubovima i podijelite ovaj broj s brojem rubova.
Zbroj vrijednosti svih lica za standardnu kockicu sa šest strana je 1 + 2 + 3 + 4 + 5 + 6 = 21. Podijelite 21 s brojem lica i dobijete prosječnu vrijednost bacanja: 21 / 6 = 3,5. Ovaj poseban slučaj, jer pretpostavljamo da su svi ishodi jednako vjerojatni.
Što ako imate posebne kockice? Na primjer, vidio sam igru hexa kocke s posebnim naljepnicama na stranama: 1, 1, 1, 2, 2, 3, pa se ponaša poput čudne trostrane kocke, koja će vjerojatnije baciti 1 nego 2, a vjerojatnije je baciti 2 nego a 3. Koja je prosječna vrijednost bacanja za ovu kockicu? Dakle, 1 + 1 + 1 + 2 + 2 + 3 = 10, podijelite sa 6 - dobit ćete 5/3 ili otprilike 1,66. Dakle, ako imate posebne kockice i igrači bacaju tri kockice i zatim zbrajaju rezultate, znate da će njihov ukupni broj biti oko 5, i možete uravnotežiti igru na temelju te pretpostavke.
Kocka i neovisnost
Kao što sam već rekao, polazimo od pretpostavke da je ispadanje svakog lica jednako vjerojatno. Ovdje nije važno koliko kockica bacite. Svako bacanje kockice je neovisno, što znači da prethodna bacanja ne utječu na rezultate sljedećih bacanja. Uz dovoljno pokušaja, sigurno ćete primijetiti niz brojeva - na primjer, bacanje većinom viših ili nižih vrijednosti - ili druge značajke, ali to ne znači da su kockice "vruće" ili "hladne". Razgovarat ćemo o ovome kasnije.
Ako bacite standardnu šesterostranu kockicu i broj 6 se pojavi dvaput zaredom, vjerojatnost da će rezultat sljedećeg bacanja biti 6 također je 1/6. Vjerojatnost se ne povećava jer se kockica "zagrijala" ". Pritom se vjerojatnost ne smanjuje: netočno je tvrditi da je broj 6 već ispao dva puta zaredom, što znači da sada mora ispasti još jedno lice.
Naravno, ako bacite kockicu dvadeset puta i svaki put se pojavi broj 6, vjerojatnost da će 6 ispasti dvadeset i prvi put prilično je velika: možda imate krivi kockicu. Ali ako je kockica ispravna, vjerojatnost dobivanja svakog od lica je ista, bez obzira na rezultate drugih bacanja. Također možete zamisliti da svaki put mijenjamo kockicu: ako se broj 6 bacio dva puta zaredom, uklonite "vruću" kockicu iz igre i zamijenite je novom. Žao mi je ako je netko od vas već znao za ovo, ali morao sam ovo razjasniti prije nego što nastavim.
Kako postići da kockice budu više-manje nasumične
Razgovarajmo o tome kako dobiti različite rezultate na različitim kockicama. Ako kockicu bacite samo jednom ili nekoliko puta, igra će se činiti nasumičnijom kada kockica ima više rubova. Što češće bacate kockice i što više kockica bacate, rezultati se više približavaju prosjeku.
Na primjer, u slučaju 1d6 + 4 (to jest, ako jednom bacite standardnu šesterostranu kockicu i rezultatu dodate 4), prosjek će biti broj između 5 i 10. Ako bacite 5d2, prosjek također će biti broj između 5 i 10. Rezultat bacanja 5d2 bit će uglavnom brojevi 7 i 8, rjeđe druge vrijednosti. Ista serija, čak ista prosječna vrijednost (7,5 u oba slučaja), ali priroda slučajnosti je drugačija.
Pričekaj minutu. Nisam li upravo rekao da se kockice ne "grijaju" niti "hlade"? I sada kažem: ako bacate puno kockica, rezultati bacanja su bliži prosječnoj vrijednosti. Zašto?
Dopustite da objasnim. Ako bacite jednu kockicu, vjerojatnost da će se svako lice pojaviti je ista. To znači da ako bacite mnogo kockica tijekom vremena, svako lice će se pojaviti otprilike isti broj puta. Što više kockica bacite, to će se ukupni rezultat više približavati prosjeku.
To nije zato što bačeni broj "uzrokuje" bacanje drugog broja koji još nije bačen. Jer mali niz bacanja broja 6 (ili 20, ili što već) na kraju neće napraviti veliku razliku ako kockicu bacite još deset tisuća puta i to uglavnom prosjek. Sada ćete ih imati nekoliko velike brojke, a kasnije i nekoliko malih - i s vremenom će se približiti prosječnoj vrijednosti.
To nije zato što prethodna bacanja utječu na kockice (ozbiljno, kockica je napravljena od plastike, nema dovoljno mozga da pomisli: "Oh, prošlo je mnogo vremena otkako se pojavila dvojka"), već zato što se to obično događa s puno bacanja.igranje kockica.
Dakle, prilično je lako izračunati za jedno nasumično bacanje kocke - izračunajte barem prosječnu vrijednost bacanja. Također postoje načini da se izračuna "koliko je nasumično" nešto i kaže da će rezultati bacanja 1d6 + 4 biti "nasumičniji" od 5d2. Za 5d2, valjani rezultati će biti ravnomjernije raspoređeni. Da biste to učinili, morate izračunati standardnu devijaciju: što je veća vrijednost, to će rezultati biti slučajniji. Ne bih danas davao toliko kalkulacija, kasnije ću objasniti ovu temu.
Jedina stvar koju ću vas zamoliti da zapamtite je da, kao opće pravilo, što manje kockica bacite, to je nasumičnije. A što više strana ima kockica, to je veća slučajnost, budući da postoji više mogućih opcija za vrijednost.
Kako izračunati vjerojatnost pomoću brojanja
Možda imate pitanje: kako možemo izračunati točnu vjerojatnost bacanja određeni rezultat? Zapravo, ovo je vrlo važno za mnoge igre: ako u početku bacite kockicu, vjerojatno će postojati neki optimalan ishod. Odgovor je: trebamo izračunati dvije vrijednosti. Prvo, ukupni broj ishode pri bacanju kocke, a drugo, broj povoljnih ishoda. Dijeljenjem druge vrijednosti s prvom dobivate željenu vjerojatnost. Dobiti postotak, pomnožite rezultat sa 100.
Primjeri
Evo vrlo jednostavnog primjera. Želite baciti 4 ili više i jednom baciti kocku sa šest strana. Maksimalan broj ishoda je 6 (1, 2, 3, 4, 5, 6). Od toga su 3 ishoda (4, 5, 6) povoljna. Dakle, da bismo izračunali vjerojatnost, podijelimo 3 sa 6 i dobijemo 0,5 ili 50%.
Evo primjera koji je malo kompliciraniji. Želite da bacanje 2d6 dobije paran broj. Maksimalan broj ishoda je 36 (6 opcija za svaku kockicu, jedna kockica ne utječe na drugu, tako da množimo 6 sa 6 i dobivamo 36). Složenost pitanja ove vrste je da je lako brojati dvaput. Na primjer, pri bacanju 2d6, dva su moguća ishoda 3: 1+2 i 2+1. Izgledaju isto, ali razlika je u tome koji je broj prikazan na prvoj, a koji na drugoj kockici.
Možete zamisliti i da kockice različite boje: tako, na primjer, u ovom slučaju, jedna kockica je crvena, druga je plava. Zatim izbrojite broj mogućih pojavljivanja parnog broja:
- 2 (1+1);
- 4 (1+3);
- 4 (2+2);
- 4 (3+1);
- 6 (1+5);
- 6 (2+4);
- 6 (3+3);
- 6 (4+2);
- 6 (5+1);
- 8 (2+6);
- 8 (3+5);
- 8 (4+4);
- 8 (5+3);
- 8 (6+2);
- 10 (4+6);
- 10 (5+5);
- 10 (6+4);
- 12 (6+6).
Ispada da postoji 18 opcija za povoljan ishod od 36 - kao iu prethodnom slučaju, vjerojatnost je 0,5 ili 50%. Možda neočekivano, ali sasvim točno.
Monte Carlo simulacija
Što ako imate previše kockica za ovaj izračun? Na primjer, želite znati koja je vjerojatnost da će ukupno 15 ili više ispasti pri bacanju 8d6. Za osam kockica ima veliko mnoštvo različite rezultate, a njihovo ručno brojanje trajalo bi jako dugo - čak i kad bismo mogli pronaći neko dobro rješenje za grupiranje različitih serija bacanja kockica.
U ovom slučaju, najlakši način je ne brojati ručno, već koristiti računalo. Postoje dva načina izračuna vjerojatnosti na računalu. Prvi način može dobiti točan odgovor, ali uključuje malo programiranja ili skriptiranja. Računalo će pogledati svaku mogućnost, procijeniti i prebrojati ukupan broj ponavljanja i broj ponavljanja koji odgovaraju željenom rezultatu, a zatim dati odgovore. Vaš kod može izgledati otprilike ovako:
Ako niste programer i želite približan odgovor umjesto točnog, možete simulirati ovu situaciju u Excelu, gdje prebacite 8d6 nekoliko tisuća puta i dobijete odgovor. Za okretanje 1d6 u Excelu koristite formulu =FLOOR(RAND()*6)+1.
Postoji naziv za situaciju kada ne znate odgovor i samo pokušavate mnogo puta - Monte Carlo simulacija. Ovo je sjajno rješenje na koje se možete osloniti kada je preteško izračunati vjerojatnost. Sjajno je to što u ovom slučaju ne moramo razumjeti kako matematika funkcionira i znamo da će odgovor biti "prilično dobar" jer, kao što već znamo, što više bacanja, to se rezultat više približava Prosječna vrijednost.
Kako kombinirati neovisna ispitivanja
Ako pitate o više ponovljenih, ali neovisnih pokušaja, tada ishod jednog bacanja ne utječe na ishod drugih bacanja. Postoji još jedno jednostavnije objašnjenje za ovu situaciju.
Kako razlikovati nešto ovisno od neovisnog? U načelu, ako možete izolirati svako bacanje (ili seriju bacanja) kockice kao zaseban događaj, onda je neovisan. Na primjer, bacili smo 8d6 i želimo baciti ukupno 15. Ovaj događaj ne može se podijeliti u nekoliko neovisnih bacanja kockica. Da biste dobili rezultat, izračunavate zbroj svih vrijednosti, tako da rezultat bačen na jednoj kockici utječe na rezultate koji bi trebali pasti na ostalima.
Evo primjera neovisnih bacanja: igrate igru kockica i nekoliko puta bacate šesterostrane kockice. Prvo bacanje mora pasti 2 ili više da biste ostali u igri. Za drugo bacanje - 3 ili više. Za treće je potrebno 4 ili više, za četvrto 5 ili više, a za peto 6. Ako je svih pet bacanja uspješno, pobjeđujete. U ovom slučaju sva su bacanja neovisna. Da, ako jedno bacanje ne uspije, to će utjecati na ishod cijele igre, ali jedno bacanje ne utječe na drugo. Na primjer, ako je vaše drugo bacanje kocke vrlo dobro, to ne znači da će i sljedeća bacanja biti jednako dobra. Stoga možemo zasebno razmatrati vjerojatnost svakog bacanja kocke.
Ako imate neovisne vjerojatnosti i želite znati koja je vjerojatnost da će se svi događaji dogoditi, odredite svaku pojedinačnu vjerojatnost i pomnožite ih. Drugi način: ako koristite veznik “i” za opis nekoliko uvjeta (na primjer, koja je vjerojatnost da se dogodi neki slučajni događaj i neki drugi neovisni slučajni događaj?) - izračunajte pojedinačne vjerojatnosti i pomnožite ih.
Nije važno što mislite - nikad ne zbrajajte neovisne vjerojatnosti. Ovo je uobičajena pogreška. Da biste razumjeli zašto je to pogrešno, zamislite situaciju u kojoj bacate novčić i želite znati kolika je vjerojatnost da dobijete glavu dvaput zaredom. Vjerojatnost ispadanja sa svake strane je 50%. Ako zbrojite ove dvije vjerojatnosti, imate 100% šanse da dobijete heads, ali znamo da to nije točno, jer bi se mogla pojaviti dva uzastopna repa. Ako umjesto toga pomnožite dvije vjerojatnosti, dobit ćete 50% * 50% = 25% - što je točan odgovor za izračun vjerojatnosti dobivanja glava dvaput zaredom.
Primjer
Vratimo se igri šesterostranih kockica, gdje prvo treba baciti broj veći od 2, zatim veći od 3 – i tako sve do 6. Kolike su šanse da u zadanom nizu od pet bacanja svi hoće li rezultati biti povoljni?
Kao što je gore spomenuto, ovo su neovisna ispitivanja, tako da izračunavamo vjerojatnost za svaki pojedinačni bacanje, a zatim ih množimo. Vjerojatnost da će ishod prvog bacanja biti povoljan je 5/6. Drugi - 4/6. Treći - 3/6. Četvrti - 2/6, peti - 1/6. Sve rezultate pomnožimo jedan s drugim i dobijemo oko 1,5%. Dobici u ovoj igri su prilično rijetki, pa ako dodate ovaj element u svoju igru, trebat će vam prilično veliki jackpot.
Negacija
Evo još jednog koristan savjet: ponekad je teško izračunati vjerojatnost da će se događaj dogoditi, ali je lakše odrediti šanse da se događaj neće dogoditi. Na primjer, pretpostavimo da imamo još jednu igru: bacite 6d6 i pobijedite ako barem jednom bacite 6. Kolika je vjerojatnost pobjede?
U ovom slučaju postoji mnogo opcija koje treba razmotriti. Moguće je da će ispasti jedan broj 6, odnosno na jednoj od kockica će pasti broj 6, a na ostalima brojevi od 1 do 5, tada postoji 6 opcija koja će od kockica imati a 6. Možete dobiti broj 6 na dvije kockice, ili tri, ili čak više, i svaki put ćete morati napraviti poseban izračun, tako da se ovdje lako zbuniti.
Ali pogledajmo problem s druge strane. Gubite ako niti jedna kocka ne baci 6. U ovom slučaju imamo 6 neovisnih pokušaja. Vjerojatnost da će svaka kocka baciti broj različit od 6 je 5/6. Pomnožite ih - i dobiti oko 33%. Dakle, vjerojatnost gubitka je jedan prema tri. Dakle, vjerojatnost dobitka je 67% (ili dva do tri).
Iz ovog primjera je očito da ako izračunavate vjerojatnost da se događaj neće dogoditi, trebate oduzeti rezultat od 100%. Ako je vjerojatnost dobitka 67%, tada je vjerojatnost gubitka 100% minus 67%, odnosno 33%, i obrnuto. Ako je teško izračunati jednu vjerojatnost, ali je lako izračunati suprotnu, izračunajte suprotnu, a zatim oduzmite ovaj broj od 100%.
Uvjeti povezivanja za jedan nezavisni test
Rekao sam malo ranije da nikada ne biste trebali zbrajati vjerojatnosti u neovisnim ispitivanjima. Postoje li slučajevi u kojima je moguće zbrojiti vjerojatnosti? Da, u jednoj konkretnoj situaciji.
Ako želite izračunati vjerojatnost više nepovezanih povoljnih ishoda u istom pokusu, zbrojite vjerojatnosti svakog povoljnog ishoda. Na primjer, vjerojatnost bacanja 4, 5 ili 6 na 1d6 jednaka je zbroju vjerojatnosti bacanja 4, vjerojatnosti bacanja 5 i vjerojatnosti bacanja 6. Ova situacija može se predstaviti na sljedeći način: ako koristite uniju "ili" u pitanju vjerojatnosti (na primjer, koja je vjerojatnost jednog ili drugog ishoda jednog slučajnog događaja?) - izračunajte pojedinačne vjerojatnosti i zbrojite ih.
Imajte na umu: kada izračunavate sve moguće ishode igre, zbroj vjerojatnosti njihovog pojavljivanja mora biti jednak 100%, inače je vaš izračun napravljen netočno. Ovo je dobar način da provjerite svoje izračune. Na primjer, analizirali ste vjerojatnost dobivanja svih kombinacija u pokeru. Ako zbrojite sve rezultate koje dobijete, trebali biste dobiti točno 100% (ili barem vrijednost prilično blizu 100%: ako koristite kalkulator, može doći do male pogreške zaokruživanja, ali ako zbrajate točne brojke rukom, sve bi se trebalo zbrojiti. ). Ako se zbroj ne zbraja, najvjerojatnije niste uzeli u obzir neke kombinacije ili ste krivo izračunali vjerojatnosti nekih kombinacija te je izračune potrebno ponovno provjeriti.
Nejednake vjerojatnosti
Do sada smo pretpostavljali da svaka strana kockice ispada istom frekvencijom, jer kockica tako radi. Ali ponekad se možete susresti sa situacijom u kojoj su mogući različiti ishodi i imaju različite šanse da ispadnu.
Na primjer, u jednom od dodataka kartaškoj igri Nuclear War postoji igralište sa strelicom koja određuje rezultat lansiranja rakete. Najčešće nanosi uobičajenu štetu, veću ili manju, ali ponekad se šteta udvostruči ili utrostruči, ili raketa eksplodira na lansirnoj rampi i naškodi vam, ili se dogodi neki drugi događaj. Za razliku od ploče sa strelicama u Chutes & Ladders ili A Game of Life, rezultati ploče u Nuclear Waru nisu jednako vjerojatni. Neki dijelovi igrališta su veći i na njima se strelica zaustavlja puno češće, dok su drugi dijelovi vrlo mali i na njima se strelica zaustavlja rijetko.
Dakle, na prvi pogled kost izgleda otprilike ovako: 1, 1, 1, 2, 2, 3 - već smo pričali o tome, to je nešto poput ponderiranog 1d3. Dakle, sve te odjeljke trebamo podijeliti na jednake dijelove, pronaći najmanju mjernu jedinicu, djelitelj, kojemu je sve višekratnik, a zatim prikazati situaciju u obliku d522 (ili nekom drugom), gdje je skup kockica lica će predstavljati istu situaciju, nos veliki iznos ishodi. Ovo je jedan od načina rješavanja problema, tehnički je izvediv, ali postoji lakša opcija.
Vratimo se našim standardnim šesterostranim kockama. Rekli smo da za izračunavanje prosječne vrijednosti bacanja normalne kocke morate zbrojiti vrijednosti svih lica i podijeliti ih s brojem lica, ali kako se točno izračunava? Možete to izraziti drugačije. Za kocku sa šest strana, vjerojatnost da se svako lice pojavi je točno 1/6. Sada množimo ishod svakog aspekta s vjerojatnošću tog ishoda (u ovom slučaju 1/6 za svaki aspekt), a zatim zbrajamo dobivene vrijednosti. Dakle, zbrajanje (1 * 1/6) + (2 * 1/6) + (3 * 1/6) + (4 * 1/6) + (5 * 1/6) + (6 * 1/6), dobivamo isti rezultat (3.5) kao u gornjem izračunu. Zapravo, to izračunavamo svaki put: svaki ishod množimo s vjerojatnošću tog ishoda.
Možemo li napraviti isti izračun za strelicu na ploči za igru u Nuklearnom ratu? Naravno da možemo. A ako zbrojimo sve pronađene rezultate, dobivamo prosječnu vrijednost. Sve što trebamo učiniti je izračunati vjerojatnost svakog ishoda za strelicu na polju za igru i pomnožiti s vrijednošću ishoda.
Još jedan primjer
Spomenuta metoda izračuna prosjeka također je prikladna ako su rezultati jednako vjerojatni, ali imaju različite prednosti - na primjer, ako bacite kockicu i dobijete više na nekim licima nego na drugima. Na primjer, uzmimo igru koja se odvija u kasinu: stavite okladu i bacite 2d6. Ako se dođu tri broja najmanja vrijednost(2, 3, 4) ili četiri broja velike vrijednosti (9, 10, 11, 12) - osvojit ćete iznos jednak vašem ulogu. Brojevi s najnižom i najvećom vrijednošću su posebni: ako se pojavi 2 ili 12, dobit ćete dvostruko više od vaše oklade. Ako se pojavi bilo koji drugi broj (5, 6, 7, 8), izgubit ćete svoju okladu. Ovo je prilično jednostavna igra. Ali kolika je vjerojatnost dobitka?
Počnimo s brojanjem koliko puta možete pobijediti. Maksimalni broj ishoda pri bacanju 2d6 je 36. Koliki je broj povoljnih ishoda?
- Postoji 1 opcija koja će baciti 2 i 1 opcija koja će baciti 12.
- Postoje 2 opcije za 3 i 2 opcije za 11.
- Postoje 3 opcije za 4 i 3 opcije za 10.
- Postoje 4 opcije koje će baciti 9.
Zbrajajući sve opcije, dobivamo 16 povoljnih ishoda od 36. Dakle, sa normalnim uvjetima dobit ćete 16 puta od 36 mogućih - vjerojatnost dobitka je nešto manja od 50%.
Ali dva puta od tih šesnaest dobit ćete duplo više – to je kao da ste dva puta pobijedili. Ako ovu igru igrate 36 puta, svaki put ulažući 1 $, a svaki od svih mogućih ishoda pojavi se jednom, osvojit ćete ukupno 18 $ (zapravo ste pobijedili 16 puta, ali dva se računaju kao dva dobitka). Ako igrate 36 puta i osvojite 18 dolara, ne znači li to da su vjerojatnosti jednake?
Uzmite si vremena. Ako računate koliko puta možete izgubiti, dobit ćete 20, a ne 18. Ako igrate 36 puta, ulažući svaki put 1 $, osvojit ćete ukupno 18 $ kada se pokažu svi izgledi. Ali izgubit ćete ukupno 20 USD na svih 20 loših ishoda. Kao rezultat toga, malo ćete zaostajati: gubite u prosjeku 2 $ neto za svakih 36 igara (možete također reći da gubite u prosjeku 1/18 $ dnevno). Sada vidite kako je lako pogriješiti u ovom slučaju i krivo izračunati vjerojatnost.
permutacija
Do sada smo pretpostavljali da redoslijed kojim se brojevi bacaju nije bitan prilikom bacanja kockica. Bacanje 2 + 4 isto je što i bacanje 4 + 2. U većini slučajeva ručno brojimo povoljne ishode, ali ponekad je ova metoda nepraktična i bolje je koristiti matematičku formulu.
Primjer ove situacije je iz igre s kockicama Farkle. Za svaku novu rundu bacate 6d6. Ako imate sreće i svi mogući ishodi 1-2-3-4-5-6 (Straight) se pojave, dobit ćete veliki bonus. Koja je vjerojatnost da se to dogodi? U ovom slučaju postoji mnogo opcija za gubitak ove kombinacije.
Rješenje je sljedeće: na jednoj od kockica (i samo na jednoj) treba ispasti broj 1. Koliko je opcija da na jednoj kockici ispadne broj 1? Postoji 6 opcija, budući da postoji 6 kockica, a na bilo koju od njih može pasti broj 1. Prema tome, uzmite jednu kockicu i stavite je sa strane. Sada bi na jednoj od preostalih kockica trebao pasti broj 2. Za to postoji 5 opcija. Uzmite drugu kocku i stavite je sa strane. Tada 4 od preostalih kockica mogu pasti na 3, 3 preostale kockice mogu pasti na 4, a 2 preostale kockice mogu pasti na 5. Kao rezultat toga, ostaje vam jedna kockica na kojoj je broj Trebalo bi pasti 6 (u potonjem slučaju, kocka ima samo jednu kost i nema izbora).
Kako bismo izbrojali broj povoljnih ishoda za ispravnu kombinaciju, množimo sve različite neovisne opcije: 6 x 5 x 4 x 3 x 2 x 1 = 720 - čini se da postoji prilično velik broj opcija za ova kombinacija da dođe.
Da bismo izračunali vjerojatnost dobivanja ravne kombinacije, moramo podijeliti 720 s brojem svih mogućih ishoda za bacanje 6d6. Koliki je broj svih mogućih ishoda? Svaka kocka može baciti 6 lica, tako da množimo 6 x 6 x 6 x 6 x 6 x 6 = 46656 (mnogo veći broj od prethodnog). Podijelimo 720 sa 46656 i dobijemo vjerojatnost jednaku oko 1,5%. Ako ste dizajnirali ovu igru, bilo bi korisno da to znate kako biste mogli stvoriti odgovarajući sustav bodovanja. Sada razumijemo zašto u Farkleu dobivate tako veliki bonus ako pogodite pravu kombinaciju: ova situacija je prilično rijetka.
Rezultat je zanimljiv i iz još jednog razloga. Primjer pokazuje kako rijetko u kratkom razdoblju ispadne rezultat koji odgovara vjerojatnosti. Naravno, kad bismo bacili nekoliko tisuća kockica, različita lica dosta bi često ispadale kockice. Ali kada bacimo samo šest kockica, gotovo nikada se ne dogodi da svaka kockica ispadne. Postaje jasno da je glupo očekivati da će sada ispasti faca koje još nije bilo, jer "brojku 6 odavno nismo ispustili". Gle, tvoj generator slučajnih brojeva je pokvaren.
To nas dovodi do uobičajene zablude da se svi ishodi pojavljuju istom brzinom u kratkom vremenskom razdoblju. Ako kockicu bacimo nekoliko puta, frekvencija svakog od lica neće biti ista.
Ako ste ikada prije radili na online igri s nekom vrstom generatora slučajnih brojeva, onda ste najvjerojatnije naišli na situaciju u kojoj igrač piše tehničkoj podršci s pritužbom da generator slučajnih brojeva ne prikazuje slučajne brojeve. Do ovog je zaključka došao jer je ubio 4 čudovišta za redom i dobio 4 potpuno iste nagrade, a te bi nagrade trebale pasti samo 10% vremena, tako da se to očito gotovo nikada ne bi trebalo dogoditi.
Radiš matematiku. Vjerojatnost je 1/10 * 1/10 * 1/10 * 1/10, odnosno 1 ishod od 10 tisuća prilično je rijedak slučaj. To vam igrač pokušava reći. Postoji li problem u ovom slučaju?
Sve ovisi o okolnostima. Koliko je igrača sada na vašem poslužitelju? Pretpostavimo da imate prilično popularnu igru i svaki dan je igra 100 000 ljudi. Koliko će igrača ubiti četiri čudovišta zaredom? Možda sve, nekoliko puta dnevno, ali uzmimo da se polovica samo mijenja različite predmete na aukcijama, prepisuje na RP poslužiteljima ili izvodi druge radnje u igri - dakle, samo polovica njih lovi čudovišta. Koja je vjerojatnost da će netko dobiti istu nagradu? U ovoj situaciji možete očekivati da će se to dogoditi barem nekoliko puta dnevno.
Usput, zato se čini da svakih nekoliko tjedana netko dobije na lutriji, čak i ako taj netko nikada niste bili vi ili netko koga poznajete. Ako dovoljno ljudi redovito igra, velike su šanse da će se negdje naći barem jedan sretnik. Ali ako sami igrate na lutriji, malo je vjerojatno da ćete dobiti, vjerojatnije je da ćete biti pozvani da radite u Infinity Wardu.
Karte i ovisnost
Razgovarali smo o neovisnim događajima, kao što je bacanje kocke, a sada znamo mnogo moćnih alata za analizu slučajnosti u mnogim igrama. Izračun vjerojatnosti malo je kompliciraniji kada je riječ o izvlačenju karata iz špila, jer svaka karta koju izvadimo utječe na one koje ostaju u špilu.
Ako imate standardni špil od 52 karte, iz njega izvučete 10 srca i želite znati kolika je vjerojatnost da će sljedeća karta biti iste boje - vjerojatnost se promijenila u odnosu na izvornu jer ste već uklonili jednu karticu srca iz karte špil. Svaka karta koju uklonite mijenja vjerojatnost pojavljivanja sljedeće karte u špilu. U ovom slučaju prethodni događaj utječe na sljedeći, pa ovu vjerojatnost nazivamo ovisnom o vjerojatnosti.
Imajte na umu da kad kažem "karte", mislim na bilo koju mehaniku igre koja ima skup objekata i vi uklonite jedan od objekata bez da ga vratite na mjesto. “Špil karata” je u ovom slučaju analogan vrećici žetona iz koje izvadite jedan žeton, ili urni iz koje se vade šarene kuglice (nikada nisam vidio igre s urnom iz koje bi se uzimale šarene kuglice van, ali nastavnici teorije vjerojatnosti na što je iz nekog razloga ovaj primjer preferiran).
Svojstva ovisnosti
Želio bih pojasniti da što se tiče karata, pretpostavljam da izvlačite karte, gledate ih i uklanjate iz špila. Svaka od ovih radnji je važno svojstvo. Kad bih imao špil od, recimo, šest karata označenih brojevima od 1 do 6, promiješao bih ih i izvukao jednu kartu, zatim ponovno promiješao svih šest karata - to bi bilo slično bacanju šesterostrane kocke, jer jedan rezultat ne utjecati ovdje za sljedeće. A ako izvučem karte i ne zamijenim ih, tada izvlačenjem 1 karte povećavam vjerojatnost da sljedeći put izvučem kartu s brojem 6. Vjerojatnost će se povećavati dok na kraju ne izvučem ovu kartu ili promiješam špil.
Važna je i činjenica da gledamo u karte. Ako izvadim kartu iz špila i ne pogledam je, neću ni imati dodatne informacije a zapravo se vjerojatnost neće promijeniti. Ovo može zvučati nelogično. Kako jednostavno okretanje karte može magično promijeniti izglede? Ali to je moguće jer vjerojatnost za nepoznate stavke možete izračunati samo na temelju onoga što znate.
Na primjer, ako promiješate standardni špil karata, otkrijete 51 kartu i nijedna od njih nije dama od trefa, tada možete biti 100% sigurni da je preostala karta dama od trefa. Ako promiješate standardni špil karata i izvučete 51 kartu bez gledanja u njih, tada je vjerojatnost da je preostala karta dama od trefa još uvijek 1/52. Kako otvarate svaku karticu, dobivate više informacija.
Izračun vjerojatnosti za ovisne događaje slijedi iste principe kao i za neovisne događaje, osim što je malo kompliciraniji, jer se vjerojatnosti mijenjaju kada otvorite karte. Dakle, morate puno množiti različite vrijednosti, umjesto množenja iste vrijednosti. Zapravo, to znači da trebamo kombinirati sve izračune koje smo napravili u jednu kombinaciju.
Primjer
Promiješate standardni špil od 52 karte i izvučete dvije karte. Koja je vjerojatnost da ćete izvaditi par? Postoji nekoliko načina za izračunavanje te vjerojatnosti, no možda je najjednostavniji sljedeći: kolika je vjerojatnost da nakon izvlačenja jedne karte nećete moći izvući par? Ova je vjerojatnost jednaka nuli, tako da nije bitno koju ćete prvu kartu izvući, sve dok odgovara drugoj. Nije važno koju ćemo kartu prvu izvući, još uvijek imamo priliku izvući par. Stoga je vjerojatnost uzimanja para nakon vađenja prve karte 100%.
Kolika je vjerojatnost da će druga karta odgovarati prvoj? Ostala je 51 karta u špilu, a 3 od njih odgovaraju prvoj karti (zapravo bi bilo 4 od 52, ali ste već uklonili jednu od odgovarajućih karata kada ste izvukli prvu kartu), tako da je vjerojatnost 1/ 17. Dakle, sljedeći put kada tip preko puta vas za stolom igra Texas Hold'em, on kaže: “Cool, još jedan par? Danas imam sreće”, znat ćete da s velikom vjerojatnošću blefira.
Što ako dodamo dva jokera, pa imamo 54 karte u špilu, a želimo znati kolika je vjerojatnost izvlačenja para? Prva karta može biti joker, a tada će u špilu biti samo jedna karta koja odgovara, a ne tri. Kako pronaći vjerojatnost u ovom slučaju? Podijelimo vjerojatnosti i pomnožimo svaku mogućnost.
Naša prva karta može biti joker ili neka druga karta. Vjerojatnost izvlačenja jokera je 2/54, vjerojatnost izvlačenja neke druge karte je 52/54. Ako je prva karta joker (2/54), tada je vjerojatnost da će druga karta odgovarati prvoj 1/53. Množimo vrijednosti (možemo ih množiti jer su to odvojeni događaji i želimo da se dogode oba događaja) i dobivamo 1/1431 - manje od jedne desetine postotka.
Ako prvo izvučete neku drugu kartu (52/54), vjerojatnost podudaranja druge karte je 3/53. Pomnožimo vrijednosti i dobijemo 78/1431 (malo više od 5,5%). Što ćemo s ova dva rezultata? Oni se ne sijeku, a mi želimo znati vjerojatnost svakog od njih, pa zbrajamo vrijednosti. Dobivamo konačni rezultat 79/1431 (još uvijek oko 5,5%).
Kad bismo htjeli biti sigurni u točnost odgovora, mogli bismo izračunati vjerojatnost svih ostalih mogućih ishoda: izvlačenje džokera i nespajanje druge karte ili izvlačenje neke druge karte i nespajanje druge karte. Zbrajajući te vjerojatnosti i vjerojatnost dobitka, dobili bismo točno 100%. Ovdje neću iznositi matematiku, ali možete pokušati s matematikom da još jednom provjerite.
Paradoks Montyja Halla
To nas dovodi do prilično poznatog paradoksa koji mnoge često zbunjuje, Monty Hall paradoksa. Paradoks je dobio ime po voditelju TV emisije Hajde da se dogovorimo.Za one koji nikada nisu gledali ovu TV emisiju reći ću da je bila suprotnost od The Price Is Right.
U The Price Is Right, domaćin (koji je prije bio Bob Barker, sada Drew Carey? Nema veze) je vaš prijatelj. Želi da osvojiš novac ili super nagrade. Pokušava vam pružiti svaku priliku za pobjedu, sve dok možete pogoditi koliko sponzorirani predmeti zapravo vrijede.
Monty Hall se ponašao drugačije. Bio je poput zlog blizanca Boba Barkera. Cilj mu je bio učiniti da ispadneš idiot na nacionalnoj televiziji. Ako ste bili u emisiji, on je bio vaš protivnik, igrali ste protiv njega i izgledi su bili u njegovu korist. Možda sam prestrog, ali gledajući predstavu u koju ćete vjerojatnije ući ako nosite smiješan kostim, to je upravo ono na što dolazim.
Jedan od najpoznatijih memeova u emisiji bio je sljedeći: ispred vas su troja vrata, vrata broj 1, vrata broj 2 i vrata broj 3. Jedna vrata možete odabrati besplatno. Iza jednog od njih stoji veličanstvena nagrada - na primjer, novi automobil. Iza druga dvoja vrata nema nagrada, obje nemaju nikakvu vrijednost. Oni bi vas trebali poniziti, pa iza njih ne stoji ništa, nego nešto glupo, na primjer, koza ili ogromna tuba paste za zube - sve samo ne novi auto.
Odabereš jedna od vrata, Monty će ih otvoriti da ti javi jesi li pobijedio ili ne... ali čekaj. Prije nego što saznamo, pogledajmo jedna od onih vrata koja nisi odabrao. Monty zna iza kojih je vrata nagrada i uvijek može otvoriti vrata iza kojih nema nagrade. “Birate li vrata broj 3? Onda otvorimo vrata broj 1 da pokažemo da iza njih nije stajala nagrada." A sada, iz velikodušnosti, nudi vam mogućnost da odabrana vrata broj 3 zamijenite za ono što se nalazi iza vrata broj 2.
U ovom trenutku postavlja se pitanje vjerojatnosti: povećava li ova prilika vašu vjerojatnost dobitka ili je smanjuje ili ostaje nepromijenjena? Kako misliš?
Točan odgovor: mogućnost odabira drugih vrata povećava šanse za dobitak s 1/3 na 2/3. Ovo je nelogično. Ako se dosad niste susreli s ovim paradoksom, onda najvjerojatnije razmišljate: čekaj, kako to: otvaranjem jednih vrata magično smo promijenili vjerojatnost? Kao što smo vidjeli na primjeru s kartama, upravo se to događa kada dobijemo više informacija. Očito, kada odaberete prvi put, vjerojatnost dobitka je 1/3. Kada se jedna vrata otvore, to uopće ne mijenja vjerojatnost dobitka za prvi izbor: vjerojatnost je i dalje 1/3. Ali vjerojatnost da su druga vrata ispravna sada je 2/3.
Pogledajmo ovaj primjer s druge strane. Vi birate vrata. Vjerojatnost dobitka je 1/3. Predlažem da promijenite druga dvoja vrata, što radi Monty Hall. Naravno, otvori jedna od vrata kako bi pokazao da iza njih nema nagrade, ali to uvijek može učiniti, tako da to zapravo ništa ne mijenja. Naravno, poželjet ćete odabrati druga vrata.
Ako ne razumijete sasvim pitanje i trebate uvjerljivije objašnjenje, kliknite na ovu poveznicu da biste otišli na sjajnu malu Flash aplikaciju koja će vam omogućiti da detaljnije istražite ovaj paradoks. Možete početi s otprilike 10 vrata, a zatim postupno prijeći na igru s troja vrata. Tu je i simulator gdje možete igrati s bilo kojim brojem vrata od 3 do 50 ili pokrenuti nekoliko tisuća simulacija i vidjeti koliko biste puta pobijedili da ste igrali.
Odaberite jedna od tri vrata - vjerojatnost dobitka je 1/3. Sada imate dvije strategije: promijeniti izbor nakon otvaranja pogrešnih vrata ili ne. Ako ne promijenite svoj izbor, tada će vjerojatnost ostati 1/3, jer je izbor samo u prvoj fazi i morate odmah pogoditi. Ako promijeniš, onda možeš pobijediti ako prvo izabereš kriva vrata (onda otvore druga pogrešna, prava ostaju - promijeniš odluku, samo je prihvatiš). Vjerojatnost da odaberete kriva vrata na početku je 2/3 – pa ispada da promjenom odluke udvostručujete vjerojatnost dobitka.
Primjedba učiteljice viša matematika i specijalist za ravnoteža igre Maxim Soldatov - naravno, Schreiber je nije imao, ali bez nje je prilično teško razumjeti ovu čarobnu transformaciju
Ponovni pregled Monty Hall paradoksa
Što se tiče samog showa, iako Monty Hallovi suparnici nisu bili dobri u matematici, on je bio dobar u njoj. Evo što je učinio da malo promijeni igru. Ako ste birali vrata iza kojih je dobitak, uz vjerojatnost 1/3, uvijek vam je nudio opciju da odaberete druga vrata. Odabereš auto i onda ga zamijeniš za kozu i izgledaš prilično glupo - što je upravo ono što ti treba, jer je Hall na neki način zao tip.
Ali ako odaberete vrata koja nemaju nagradu, on će vam ponuditi druga vrata samo pola vremena ili će vam samo pokazati vašu novu kozu i vi ćete napustiti pozornicu. Analizirajmo ovu novu igru u kojoj Monty Hall može odlučiti hoće li vam ponuditi priliku da odaberete druga vrata ili ne.
Pretpostavimo da slijedi ovaj algoritam: ako odaberete vrata s nagradom, on vam uvijek nudi mogućnost da odaberete druga vrata, u suprotnom je jednako vjerojatno da će vam ponuditi da odaberete druga vrata ili će vam dati kozu. Koja je vjerojatnost vašeg dobitka?
U jednoj od tri opcije odmah birate vrata iza kojih se nalazi nagrada, a domaćin vas poziva da odaberete druga.
Od preostale dvije opcije od tri (inicijalno birate vrata bez nagrade), u polovici slučajeva domaćin će vam ponuditi da promijenite odluku, a u drugoj polovici slučajeva neće.
Pola od 2/3 je 1/3, odnosno u jednom slučaju od tri dobit ćete kozu, u jednom slučaju od tri ćete odabrati pogrešna vrata i domaćin će vam ponuditi da odaberete druga, a u jednom slučaju od tri ćete odabrati ispravna vrata, ali on opet ponuditi druga.
Ako voditelj ponudi da odaberemo druga vrata, već znamo da se nije dogodio jedan od tri slučaja kada nam da kozu i mi odemo. Ovaj korisne informacije: znači da su se naše šanse za pobjedu promijenile. Dva od tri slučaja u kojima imamo izbor: u jednom slučaju to znači da smo pogodili točno, a u drugom slučaju da smo pogodili netočno, pa ako nam je uopće ponuđen izbor, tada je vjerojatnost našeg dobitka 1 /2 , a matematički je svejedno hoćete li ostati pri svom izboru ili ćete izabrati druga vrata.
Kao i poker, to je psihološka igra, a ne matematička. Zašto ti je Monty ponudio izbor? Misli li da ste vi glupan koji ne zna da je odabir drugih vrata “ispravna” odluka i tvrdoglavo će se držati svog izbora (uostalom, situacija je psihički kompliciranija kada odaberete auto pa ga izgubite) ?
Ili vam on, odlučivši da ste pametni i odaberete druga vrata, ponudi tu priliku, jer zna da ste u početku dobro pogodili i napali na kuku? Ili je možda neobično ljubazan i tjera vas da učinite nešto dobro za vas, jer već dugo nije davao automobile, a producenti kažu da je publici dosadno i da bi bilo bolje da uskoro daju veliku nagradu pa jel pala gledanost?
Tako Monty ponekad uspijeva ponuditi izbor, dok ukupna vjerojatnost dobitka ostaje jednaka 1/3. Zapamtite da je vjerojatnost da ćete odmah izgubiti 1/3. Postoji 1/3 šanse da ćete odmah pogoditi, a 50% tih puta ćete pobijediti (1/3 x 1/2 = 1/6).
Vjerojatnost da isprva pogrešno pogodite, ali zatim imate priliku odabrati druga vrata je 1/3, au polovici ovih slučajeva ćete pobijediti (također 1/6). Zbrojite dvije nezavisne mogućnosti dobitka i dobit ćete vjerojatnost od 1/3, tako da nije bitno hoćete li ostati pri svom izboru ili odabrati druga vrata - ukupna vjerojatnost vašeg dobitka tijekom cijele igre je 1/3.
Vjerojatnost ne postaje veća nego u situaciji kada ste pogodili vrata, a domaćin vam jednostavno pokaže što je iza njih, bez ponude da odaberete druga. Poanta prijedloga nije promijeniti vjerojatnost, već učiniti proces donošenja odluka zabavnijim za gledanje televizije.
Usput, ovo je jedan od razloga zašto poker može biti tako zanimljiv: u većini formata između rundi, kada se prave oklade (na primjer, flop, turn i river u Texas Hold'emu), karte se postupno otkrivaju, i ako na početku igre imate jednu priliku za dobitak, tada se nakon svake runde klađenja, kada je otvoreno više karata, ta vjerojatnost mijenja.
Paradoks dječaka i djevojčice
Ovo nas dovodi do još jednog dobro poznatog paradoksa koji svakoga zbunjuje, paradoksa dječak-djevojčica. Jedina stvar o kojoj danas pišem nije izravno povezana s igrama (iako pretpostavljam da vas samo moram potaknuti da stvorite odgovarajuću mehaniku igre). Ovo je više zagonetka, ali zanimljiva, a da biste je riješili, morate razumjeti uvjetnu vjerojatnost o kojoj smo govorili gore.
Zadatak: Imam prijatelja s dvoje djece, barem jedno od njih je djevojčica. Kolika je vjerojatnost da i drugo dijete bude djevojčica? Pretpostavimo da su u bilo kojoj obitelji šanse za djevojčicu i dječaka 50/50, a to vrijedi za svako dijete.
Zapravo, neki muškarci imaju više spermija s kromosomom X ili kromosomom Y u svojoj spermi, tako da izgledi malo variraju. Ako znate da je jedno dijete djevojčica, šansa da dobijete drugu djevojčicu je malo veća, a postoje i druga stanja, poput hermafroditizma. Ali da bismo riješili ovaj problem, nećemo to uzeti u obzir i pretpostaviti da je rođenje djeteta samostalan događaj a rođenje dječaka i djevojčice jednako je vjerojatno.
Budući da govorimo o šansi 1/2, intuitivno očekujemo da će odgovor biti 1/2 ili 1/4, ili neki drugi višekratnik dva u nazivniku. Ali odgovor je 1/3. Zašto?
Poteškoća u ovom slučaju je u tome što informacije koje imamo smanjuju broj mogućnosti. Pretpostavimo da su roditelji obožavatelji Ulice Sesame i bez obzira na spol djece nazvali su ih A i B. Pod normalnim uvjetima, postoje četiri jednako vjerojatne mogućnosti: A i B su dva dječaka, A i B su dvije djevojčice, A je dječak i B je djevojčica, A je djevojčica i B je dječak. Budući da znamo da je barem jedno dijete djevojčica, možemo isključiti mogućnost da su A i B dva dječaka. Dakle, ostaju nam tri mogućnosti - još uvijek jednako vjerojatne. Ako su sve mogućnosti jednako vjerojatne i postoje ih tri, tada je vjerojatnost svake od njih 1/3. Samo u jednoj od ove tri opcije su oboje djece djevojčice, pa je odgovor 1/3.
I opet o paradoksu dječaka i djevojčice
Rješenje problema postaje još nelogičnije. Zamislite da moj prijatelj ima dvoje djece i jedno od njih je djevojčica koja je rođena u utorak. Pretpostavimo da je pod normalnim uvjetima jednako vjerojatno da će se dijete roditi svakog od sedam dana u tjednu. Kolika je vjerojatnost da i drugo dijete bude djevojčica?
Možda mislite da bi odgovor ipak bio 1/3: što znači utorak? Ali u ovom slučaju, intuicija nas iznevjerava. Odgovor je 13/27, što ne samo da nije intuitivno, već je vrlo čudno. Što je u ovom slučaju?
Zapravo, utorak mijenja vjerojatnost jer ne znamo koja je beba rođena u utorak ili su možda obje rođene u utorak. U ovom slučaju koristimo se istom logikom: računamo sve moguće kombinacije kada je barem jedno dijete djevojčica rođena u utorak. Kao u prethodnom primjeru, pretpostavimo da su djeca nazvana A i B. Kombinacije izgledaju ovako:
- A je djevojčica rođena u utorak, B je dječak (u ovoj situaciji postoji 7 mogućnosti, po jedna za svaki dan u tjednu kada je dječak mogao biti rođen).
- B - djevojčica rođena u utorak, A - dječak (također 7 mogućnosti).
- A je djevojčica rođena u utorak, B je djevojčica rođena drugog dana u tjednu (6 mogućnosti).
- B - djevojčica rođena u utorak, A - djevojčica koja nije rođena u utorak (također 6 vjerojatnosti).
- A i B su dvije djevojčice koje su rođene u utorak (1 mogućnost, morate obratiti pažnju na to da ne brojite dva puta).
Zbrojimo i dobijemo 27 različitih jednako mogućih kombinacija rođenja djece i dana s barem jednom mogućnošću da se djevojčica rodi u utorak. Od toga je 13 mogućnosti kada se rode dvije djevojčice. Također izgleda potpuno nelogično – izgleda zadani zadatak je izmišljen samo da izazove glavobolju. Ako ste još uvijek zbunjeni, web stranica teoretičara igara Jespera Juhla ima dobro objašnjenje ovoga.
Ako trenutno radite na igrici
Ako u igri koju dizajnirate postoji slučajnost, ovo je izvrsna prilika da je analizirate. Odaberite bilo koji element koji želite analizirati. Prvo se zapitajte kolika bi bila vjerojatnost danog elementa u kontekstu igre.
Na primjer, ako izrađujete RPG i razmišljate o tome kolika je vjerojatnost da će igrač pobijediti čudovište u borbi, zapitajte se što postotak pobjede ti se čini ispravnim. Obično, u slučaju RPG-ova za konzole, igrači se jako uzrujaju kad izgube, pa je bolje da gube rijetko - 10% vremena ili manje. Ako ste RPG dizajner, vjerojatno znate bolje od mene, ali morate imati osnovnu ideju o tome kolika bi trebala biti vjerojatnost.
Zatim se zapitajte jesu li vaše vjerojatnosti ovisne (kao s kartama) ili neovisne (kao s kockicama). Razgovarajte o svim mogućim ishodima i njihovim vjerojatnostima. Provjerite je li zbroj svih vjerojatnosti 100%. I, naravno, usporedite svoje rezultate sa svojim očekivanjima. Je li moguće bacati kockice ili izvlačiti karte kako ste namjeravali ili je jasno da se vrijednosti moraju prilagoditi. I, naravno, ako pronađete nedostatke, možete koristiti iste izračune da odredite koliko trebate promijeniti vrijednosti.
Domaća zadaća
Vaša ovotjedna "domaća zadaća" pomoći će vam da usavršite svoje vještine vjerojatnosti. Ovdje su dvije igre s kockicama i kartaška igra koju morate analizirati pomoću vjerojatnosti, kao i čudna mehanika igre koju sam jednom razvio, a na kojoj ćete testirati Monte Carlo metodu.
Igra #1 - Zmajeve kosti
Ovo je igra s kockicama koju smo jednom osmislili moji kolege i ja (zahvaljujući Jebu Havensu i Jesseju Kingu) - namjerno oduševljava ljude svojom vjerojatnošću. Ovo je jednostavna casino igra pod nazivom "Dragon Dice" i to je natjecanje u kockanju između igrača i ustanove.
Dobivate regularnu kockicu 1d6. Cilj igre je baciti broj veći od broja kuće. Tom je dobio nestandardni 1d6 - isti kao i vaš, ali na jednom od njegovih lica umjesto na jednom - slika zmaja (dakle, kockarnica ima kockicu zmaj-2-3-4-5-6). Ako institucija dobije zmaja, ona automatski pobjeđuje, a vi gubite. Ako oboje dobiju isti broj, to je izvlačenje i ponovno bacate kocku. Pobjeđuje onaj koji baci najveći broj.
Naravno, nije sve u potpunosti u korist igrača, jer kasino ima prednost u vidu lica zmaja. No, je li stvarno tako? To je ono što morate izračunati. Ali prvo provjerite svoju intuiciju.
Recimo da je dobitak 2 prema 1. Dakle, ako pobijedite, zadržavate svoju okladu i dobivate dvostruki iznos. Na primjer, ako uložite 1 $ i pobijedite, zadržavate taj dolar i dobivate još 2 $ na vrhu, za ukupno 3 $. Ako izgubite, gubite samo svoju okladu. Biste li igrali? Osjećate li intuitivno da je vjerojatnost veća od 2 prema 1 ili ipak mislite da je manja? Drugim riječima, u prosjeku tijekom 3 utakmice, očekujete li pobjedu više od jednom, ili manje, ili jednom?
Nakon što maknete svoju intuiciju s puta, primijenite matematiku. Postoji samo 36 mogućih pozicija za obje kockice, tako da ih lako možete sve prebrojati. Ako niste sigurni u ovu ponudu 2-na-1, razmislite o ovome: Recimo da ste igrali igru 36 puta (kladeći se svaki put 1 $). Za svaku pobjedu dobivate 2 $, za svaki gubitak gubite 1 $, a remi ne mijenja ništa. Prebrojite sve svoje vjerojatne dobitke i gubitke i odlučite hoćete li izgubiti nešto dolara ili dobiti. Zatim se zapitajte koliko se vaša intuicija pokazala ispravnom. I onda shvati kakav sam negativac.
I, da, ako ste već razmišljali o ovom pitanju - namjerno vas zbunjujem iskrivljujući stvarnu mehaniku igara s kockicama, ali siguran sam da ovu prepreku možete premostiti samo dobrom mišlju. Pokušajte sami riješiti ovaj problem.
Igra #2 - Roll of Luck
Ovo je igra s kockicama koja se zove Roll of Luck (također i Birdcage jer se ponekad kockice ne bacaju već se stavljaju u veliki žičani kavez, koji podsjeća na Bingo kavez). Igra je jednostavna, u osnovi se svodi na ovo: Uložite, recimo, $1 na broj između 1 i 6. Zatim bacite 3d6. Za svaku kockicu koja pogodi vaš broj, dobivate $1 (i zadržavate svoju izvornu okladu). Ako vaš broj ne padne ni na jednu kocku, kasino će dobiti vaš dolar, a vi ništa. Dakle, ako se kladite na 1 i dobijete 1 na lice tri puta, dobit ćete 3 dolara.
Intuitivno se čini da su u ovoj igri šanse izjednačene. Svaka kocka je individualna šansa za dobitak 1 od 6, tako da je vaša šansa za dobitak 3 do 6 pri tri bacanja. Međutim, zapamtite, naravno, da slažete tri odvojene kockice i dopušteno vam je dodavati samo ako smo govoreći o zasebnim dobitnim kombinacijama istih kockica. Nešto što ćete morati umnožiti.
Nakon što ste izračunali sve moguće ishode (vjerojatno lakše u Excelu nego ručno, ima ih 216), igra na prvi pogled i dalje izgleda par-nepar. Zapravo, još uvijek postoji veća vjerojatnost da će kasino dobiti - koliko više? Konkretno, koliko novca očekujete da ćete izgubiti u prosjeku po rundi igre?
Sve što trebate učiniti je zbrojiti pobjede i poraze svih 216 rezultata i zatim podijeliti s 216, što bi trebalo biti prilično jednostavno. Ali kao što vidite, postoji nekoliko zamki u koje možete upasti, zbog čega kažem da ako mislite da postoji jednaka šansa za pobjedu u ovoj igri, pogrešno ste razumjeli.
Igra #3 - 5 Card Stud
Ako ste se već zagrijali na prethodnim igrama, provjerimo što znamo o uvjetnoj vjerojatnosti na primjeru ove kartaške igre. Zamislimo poker sa špilom od 52 karte. Zamislimo i 5 card stud gdje svaki igrač dobiva samo 5 karata. Ne možete odbaciti kartu, ne možete izvući novu, nema zajedničkog špila - dobivate samo 5 karata.
Royal flush je 10-J-Q-K-A u jednoj kombinaciji, ukupno ih je četiri, dakle četiri su moguće načine primite ROYAL FLUSH. Izračunajte vjerojatnost da ćete dobiti jednu od ovih kombinacija.
Moram vas upozoriti na jednu stvar: zapamtite da ovih pet karata možete izvući bilo kojim redoslijedom. Odnosno, u početku možete izvući asa ili desetku, nije važno. Dakle, kada radite svoje izračune, imajte na umu da zapravo postoji više od četiri načina da dobijete royal flush, pod pretpostavkom da su karte podijeljene redom.
Igra #4 - MMF lutrija
Četvrti zadatak neće biti tako lako riješiti pomoću metoda o kojima smo danas govorili, ali možete jednostavno simulirati situaciju koristeći programiranje ili Excel. Na primjeru ovog problema možete razraditi Monte Carlo metodu.
Ranije sam spomenuo igru Chron X na kojoj sam jednom radio, a bila je jedna vrlo zanimljiva karta- IMF lutrija. Evo kako je funkcioniralo: upotrijebili ste ga u igri. Nakon što je runda završila, karte su ponovno raspodijeljene i postojala je šansa od 10% da će karta biti izvan igre i da će nasumični igrač dobiti 5 od svake vrste resursa koji je imao žeton na toj karti. Karta je stavljena u igru bez ijednog žetona, ali svaki put kada je ostala u igri na početku sljedeće runde, dobila je jedan žeton.
Dakle, postojalo je 10% šanse da je stavite u igru, runda bi završila, karta bi izašla iz igre i nitko ne bi dobio ništa. Ako se ne dogodi (uz 90% šanse), postoji 10% šanse (zapravo 9%, budući da je to 10% od 90%) da će ona napustiti igru u sljedećem krugu i netko će dobiti 5 resursa. Ako karta napusti igru nakon jedne runde (10% od 81% dostupnih, dakle vjerojatnost je 8,1%), netko će dobiti 10 jedinica, druga runda - 15, još jedna 20, i tako dalje. Pitanje: koja je očekivana vrijednost broja resursa koje ćete dobiti od ove kartice kada konačno napusti igru?
Obično bismo pokušali riješiti ovaj problem izračunavanjem vjerojatnosti svakog ishoda i množenjem s brojem svih ishoda. Postoji 10% šanse da ćete dobiti 0 (0,1 * 0 = 0). 9% da ćete dobiti 5 jedinica resursa (9% * 5 = 0,45 resursa). 8,1% onoga što dobijete je 10 (8,1% * 10 = 0,81 resursa - općenito, očekivana vrijednost). I tako dalje. A onda bismo sve zbrojili.
I sada vam je problem očit: uvijek postoji šansa da karta neće izaći iz igre, može ostati u igri zauvijek, beskonačno mnogo rundi, tako da nema načina da se izračuna bilo kakva vjerojatnost. Metode koje smo danas naučili ne dopuštaju nam izračunavanje beskonačne rekurzije, pa ćemo je morati stvoriti umjetno.
Ako ste dovoljno dobri u programiranju, napišite program koji će simulirati ovu karticu. Trebali biste imati vremensku petlju koja dovodi varijablu na početnu poziciju nule, prikazuje nasumični broj i s 10% šanse da varijabla izlazi iz petlje. Inače, dodaje 5 varijabli i petlja se ponavlja. Kada konačno izađe iz petlje, povećajte ukupni broj probnih pokretanja za 1 i ukupni broj resursa (za koliko ovisi o tome gdje se varijabla zaustavila). Zatim resetirajte varijablu i počnite ispočetka.
Pokrenite program nekoliko tisuća puta. Na kraju podijelite ukupne resurse s ukupnim brojem trčanja – to će biti vaša očekivana vrijednost Monte Carlo metode. Pokrenite program nekoliko puta kako biste bili sigurni da su brojevi koje dobijete otprilike isti. Ako je raspon još uvijek velik, povećajte broj ponavljanja u vanjskoj petlji dok ne počnete dobivati podudaranja. Možete biti sigurni da će sve brojke koje dobijete biti približno točne.
Ako ste novi u programiranju (čak i ako jeste), evo male vježbe za testiranje vaših Excel vještina. Ako ste dizajner igrica, ove vam vještine nikada neće biti suvišne.
Sada će vam funkcije if i rand biti vrlo korisne. Rand ne zahtijeva vrijednosti, samo vraća nasumično decimalni broj od 0 do 1. Obično ga kombiniramo s podom te plusevima i minusima kako bismo simulirali bacanje kockice, što sam ranije spomenuo. Međutim, u ovom slučaju samo ostavljamo 10% šanse da će karta napustiti igru, tako da možemo samo provjeriti je li rand manji od 0,1 i više ne brinuti o tome.
Ako ima tri vrijednosti. Redom, uvjet koji je istinit ili nije, zatim vrijednost koja se vraća ako je uvjet istinit i vrijednost koja se vraća ako je uvjet lažan. Tako sljedeća funkcija vratit će 5% vremena, a 0 ostalih 90% vremena: =IF(RAND()<0.1,5,0) .
Postoji mnogo načina za postavljanje ove naredbe, ali ja bih upotrijebio ovu formulu za ćeliju koja predstavlja prvi krug, recimo da je to ćelija A1: =IF(RAND()<0.1,0,-1) .
Ovdje koristim negativnu varijablu koja znači "ova karta nije napustila igru i još nije dala nikakve resurse". Dakle, ako je prva runda završila i karta je izvan igre, A1 je 0; inače je -1.
Za sljedeću ćeliju koja predstavlja drugi krug: =IF(A1>-1, A1, IF(RAND()<0.1,5,-1)) . Dakle, ako prva runda završi i karta odmah napusti igru, A1 je 0 (broj resursa) i ova ćelija će jednostavno kopirati tu vrijednost. U suprotnom, A1 je -1 (karta još nije izašla iz igre), a ova ćelija se nastavlja nasumično kretati: 10% vremena vratit će 5 jedinica resursa, ostatak vremena će njezina vrijednost i dalje biti - 1. Ako ovu formulu primijenimo na dodatne ćelije, dobit ćemo dodatne runde, a s kojom god ćelijom završite, dobit ćete konačni rezultat (ili -1 ako karta nije napustila igru nakon svih odigranih rundi).
Uzmite ovaj red ćelija, koji je jedini krug s ovom karticom, i kopirajte i zalijepite nekoliko stotina (ili tisuća) redaka. Možda nećemo moći napraviti beskonačni test za Excel (postoji ograničen broj ćelija u tablici), ali barem možemo pokriti većinu slučajeva. Zatim odaberite jednu ćeliju u koju ćete staviti prosjek rezultata svih rundi - Excel ljubazno nudi funkciju prosječno() za to.
U sustavu Windows barem možete pritisnuti F9 da ponovno izračunate sve nasumične brojeve. Kao i prije, učinite ovo nekoliko puta i vidite hoćete li dobiti iste vrijednosti. Ako je raspon prevelik, udvostručite broj pokretanja i pokušajte ponovno.
Neriješeni problemi
Ako ste slučajno diplomirali teoriju vjerojatnosti i gornji zadaci vam se čine prelaki - evo dva zadatka o kojima se godinama češkam po glavi, ali, nažalost, nisam toliko dobar u matematici da bih ih riješio.
Neriješen problem #1: MMF lutrija
Prvi neriješeni problem je prethodna domaća zadaća. Lako mogu koristiti Monte Carlo metodu (koristeći C++ ili Excel) i biti siguran u odgovor na pitanje "koliko će resursa igrač dobiti", ali ne znam točno kako matematički dati točan dokaziv odgovor (ovo je beskonačan niz).
Neriješeni problem #2: nizovi oblika
Ovaj zadatak (također nadilazi zadatke koji se rješavaju na ovom blogu) mi je dobacio poznati igrač prije više od deset godina. Dok je igrao blackjack u Vegasu, primijetio je jednu zanimljivost: izvlačeći karte iz cipele s 8 špilova, vidio je deset figura u nizu (figura ili karta s licem je 10, Joker, King ili Queen, tako da ih je ukupno 16 u standardni špil od 52 karte ili 128 u papučici od 416 karata).
Koja je vjerojatnost da ova cipela sadrži barem jedan niz od deset ili više komada? Pretpostavimo da su pošteno promiješani, nasumičnim redoslijedom. Ili, ako vam je draže, koja je vjerojatnost da nigdje ne postoji niz od deset ili više oblika?
Možemo pojednostaviti zadatak. Ovdje je niz od 416 dijelova. Svaki dio je 0 ili 1. Postoji 128 jedinica i 288 nula nasumično razbacanih kroz niz. Na koliko načina postoji da se nasumično ispreplete 128 jedinica s 288 nula i koliko će puta postojati barem jedna grupa od deset ili više jedinica na te načine?
Svaki put kad sam krenuo u rješavanje tog problema, činilo mi se lako i očiglednim, ali čim sam ušao u detalje, odjednom je pao u vodu i činilo se jednostavno nemogućim.
Zato nemojte žuriti da izbrbljate odgovor: sjednite, dobro razmislite, proučite uvjete, pokušajte uključiti stvarne brojke, jer svi ljudi s kojima sam razgovarao o ovom problemu (uključujući i nekoliko diplomiranih studenata koji rade u ovom području) reagirali su jako na isti način: "Potpuno je očito... o ne, čekaj, uopće nije očito." To je slučaj kada nemam metodu za izračunavanje svih opcija. Naravno, mogao bih grubo forsirati problem kroz računalni algoritam, ali bilo bi mnogo zanimljivije otkriti matematički način da ga riješim.
 Pretvaranje decimalnog razlomka u obični razlomak i obrnuto: pravilo, primjeri
Pretvaranje decimalnog razlomka u obični razlomak i obrnuto: pravilo, primjeri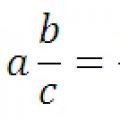 Pretvaranje decimalnih brojeva u obične razlomke
Pretvaranje decimalnih brojeva u obične razlomke Pretvaranje običnog razlomka u decimalni razlomak i obrnuto, pravila, primjeri
Pretvaranje običnog razlomka u decimalni razlomak i obrnuto, pravila, primjeri