Osnovni teoremi dinamike. Opći teoremi dinamike

Predavanje 3 Opći teoremi dinamike

Dinamika sustava materijalnih točaka je važna grana teorijske mehanike. Ovdje uglavnom razmatramo probleme gibanja mehaničkih sustava (sustava materijalnih točaka) s konačan broj stupnjevi slobode - maksimalni broj neovisnih parametara koji određuju položaj sustava. glavni zadatak dinamika sustava - proučavanje zakona gibanja krutog tijela i mehaničkih sustava.

Najjednostavniji pristup proučavanju gibanja sustava koji se sastoji od N materijalnih točaka, svodi se na razmatranje kretanja svake pojedine točke sustava. U tom slučaju moraju se odrediti sve sile koje djeluju na svaku točku sustava, uključujući sile interakcije između točaka.

Određujući akceleraciju svake točke u skladu s drugim Newtonovim zakonom (1.2), dobivamo za svaku točku tri skalarna diferencijalna zakona gibanja drugog reda, t.j. 3 N diferencijalni zakon gibanja za cijeli sustav.

Za pronalaženje jednadžbi gibanja mehanički sustav dobivene zadane sile i početni uvjeti za svaku točku sustava diferencijalni zakoni treba integrirati. Ovaj je problem težak čak iu slučaju dviju materijalnih točaka koje se kreću samo pod djelovanjem sila međudjelovanja prema zakonu univerzalnog privlačenja (problem dvaju tijela), a iznimno je težak u slučaju tri međusobno povezane točke (problem dvaju tijela). problem tri tijela).

Stoga je potrebno pronaći takve metode za rješavanje problema koje bi dovele do rješivih jednadžbi i dale predodžbu o kretanju mehaničkog sustava. Opći teoremi dinamike, kao posljedica diferencijalnih zakona gibanja, omogućuju izbjegavanje složenosti koja nastaje tijekom integracije i dobivanje potrebnih rezultata.

3.1 Opće napomene

Točke mehaničkog sustava bit će numerirane indeksima i, j, k itd. koji se provlače kroz sve vrijednosti 1, 2, 3… N, gdje N je broj bodova sustava. Fizičke veličine koje se odnose na k th točka su označene istim indeksom kao i točka. Na primjer, izražavaju vektor radijusa i brzinu k-ta točka.

Na svaku točku sustava djeluju sile dva porijekla: prvo, sile čiji izvori leže izvan sustava, tzv. vanjski sile i označava se sa ; drugo, sile iz drugih točaka ovog sustava, tzv unutarnje sile i označava se sa . Unutarnje sile zadovoljavaju treći Newtonov zakon. Razmotrimo najjednostavnija svojstva unutarnjih sila koje djeluju na cijeli mehanički sustav u bilo kojem od njegovih stanja.

Prva nekretnina. Geometrijski zbroj svih unutarnjih sila sustava (glavni vektor unutarnjih sila) jednak je nuli.

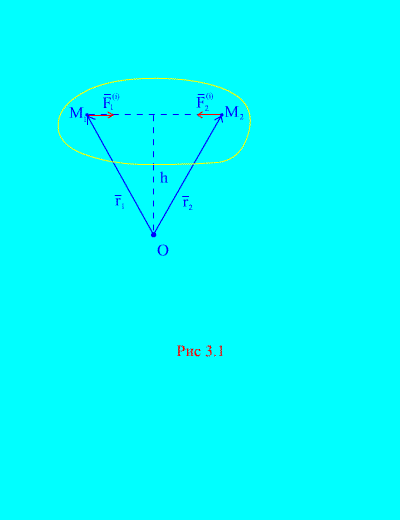
Doista, ako uzmemo u obzir bilo koje dvije proizvoljne točke sustava, na primjer, i (slika 3.1), zatim za njih , jer sile djelovanja i reakcije uvijek su jednake po apsolutnoj vrijednosti, djeluju duž jedne linije djelovanja u suprotnom smjeru, koji povezuje točke međusobnog djelovanja. Dakle, glavni vektor unutarnjih sila sastoji se od parova sila međudjelujućih točaka

(3.1)

Drugo vlasništvo. Geometrijski zbroj momenata svih unutarnjih sila u odnosu na proizvoljnu točku u prostoru je nula.

Razmotrimo sustav momenata sila i s obzirom na točku O(slika 3.1). Iz (slika 3.1). jasno je da

,

jer obje sile imaju iste krakove i suprotne smjerove vektorskih momenata. Glavni moment unutarnjih sila oko točke O sastoji se od vektorskog zbroja takvih izraza i jednak je nuli. Stoga,

Neka vanjski i unutarnje sile djelujući na mehanički sustav koji se sastoji od N bodova (slika 3.2). Ako se rezultanta vanjskih sila i rezultanta svih unutarnjih sila primjenjuju na svaku točku sustava, tada za bilo koju k U točki sustava, moguće je sastaviti diferencijalne jednadžbe gibanja. Ukupno će takve jednadžbe biti N:

te u projekcijama na fiksne koordinatne osi 3 N:

(3.4)

Vektorske jednadžbe (3.3) ili ekvivalentne skalarne jednadžbe (3.4) predstavljaju diferencijalne zakone gibanja materijalnih točaka cijelog sustava. Ako se sve točke kreću paralelno s jednom ravninom ili jednom ravnom linijom, tada će broj jednadžbi (3.4) u prvom slučaju biti 2 N, u drugom N.

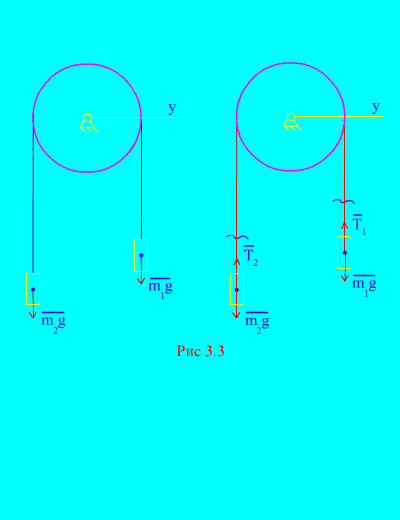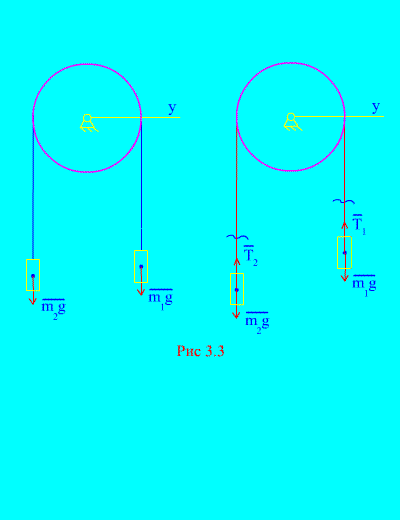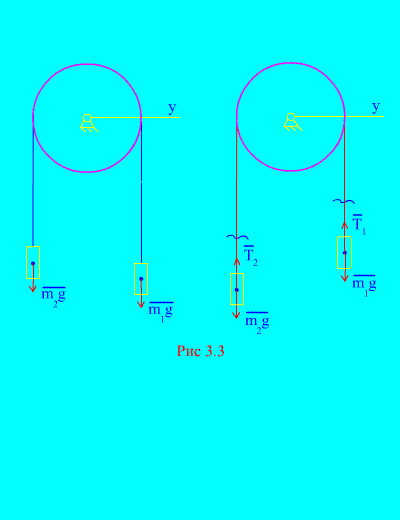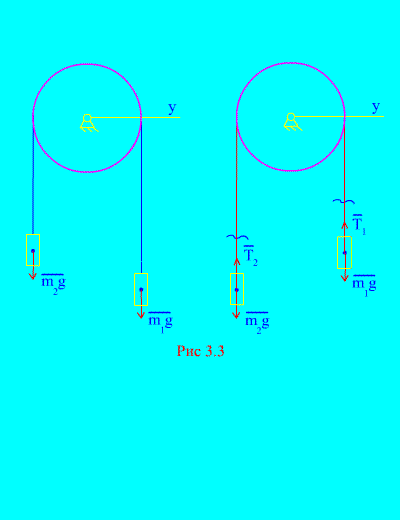
Primjer 1 Dva tereta mase i međusobno su povezani nerastezljivim kabelom prebačenim preko bloka (slika 3.3). Zanemarujući sile trenja, kao i masu bloka i sajle, određuju se zakon kretanja tereta i napetost sajle.

Odluka. Sustav se sastoji od dva materijalna tijela (povezana nerastezljivim kabelom) koja se kreću paralelno s jednom osi X. Zapišimo diferencijalne zakone gibanja u projekcijama na os x za sve.

Neka se desni uteg spušta s ubrzanjem, a zatim će lijevi uteg rasti s ubrzanjem. Mentalno se oslobađamo veze (kabla) i zamjenjujemo reakcijama i (slika 3.3). Uz pretpostavku da su tijela slobodna, sastavit ćemo diferencijalne zakone gibanja u projekciji na os x(što znači da su napetosti niti unutarnje sile, a težina tereta vanjske):

Budući da i (tijela su povezana nerastezljivim kabelom), dobivamo

Rješavanje ovih jednadžbi za ubrzanje i napetost kabela T, dobivamo

.

Imajte na umu da napetost kabela na nije jednaka težini odgovarajućeg opterećenja.

3. 2. Teorem o gibanju središta mase

Poznato je da se kruto tijelo i mehanički sustav u ravnini mogu prilično teško kretati. Do prvog teorema o gibanju tijela i mehaničkog sustava može se doći na sljedeći način: ispusti c.-l. predmet koji se sastoji od mnogo čvrstih tijela spojenih zajedno. Jasno je da će letjeti u paraboli. To se pokazalo proučavanjem gibanja točke. Međutim, sada objekt nije točka. Okreće se, njiše u procesu leta oko nekog učinkovitog središta, koje se kreće po paraboli. Prvi teorem gibanja teške predmete kaže da je određeno efektivno središte centar mase pokretnog objekta. Središte mase nije nužno smješteno u samom tijelu, može ležati negdje izvan njega.

Teorema. Središte mase mehaničkog sustava giba se kao materijalna točka s masom jednaka masi cijeli sustav na koji se primjenjuju sve vanjske sile koje djeluju na sustav.

Da bismo dokazali teorem, prepisujemo diferencijalne zakone gibanja (3.3) u sljedeći obrazac:

(3.5)

gdje N je broj bodova sustava.

Zbrojimo jednadžbe pojam po član:

(a)

Položaj središta mase mehaničkog sustava u odnosu na odabrani koordinatni sustav određen je formulom (2.1): gdje M je masa sustava. Tada je zapisana lijeva strana jednakosti (a).

Prvi zbroj, koji stoji na desnoj strani jednakosti (a), jednak je glavnom vektoru vanjskih sila, a posljednji, po svojstvu unutarnjih sila, jednak je nuli. Tada će se jednakost (a), uzimajući u obzir (b), prepisati

, (3.6)

oni. umnožak mase sustava i akceleracije njegova središta mase jednak je geometrijski zbroj sve vanjske sile koje djeluju na sustav.

Iz jednadžbe (3.6) proizlazi da unutarnje sile ne utječu izravno na gibanje središta mase. Međutim, u nekim slučajevima oni su uzrok pojave vanjskih sila koje djeluju na sustav. Dakle, unutarnje sile koje rotiraju pogonske kotače automobila uzrokuju djelovanje vanjske sile prianjanja na naplatku kotača na njega.

Primjer 2 Mehanizam, smješten u okomitoj ravnini, postavljen je na vodoravnu glatku ravninu i pričvršćen na nju šipkama čvrsto pričvršćenim na površinu. Do i L (slika 3.4).

Radijus diska 1 R nepomično. Disk 2 masa m i radijus r pričvršćena polugom, dužina R+ r u točki Od 2. Ručica se vrti konstantno

kutna brzina. NA početni trenutak radilica je zauzela desni horizontalni položaj. Zanemarujući masu radilice, odredite najveće horizontalne i vertikalne sile koje djeluju na šipke, ako Totalna tezina ležaj i kotač 1 jednak je M. Također razmotrite ponašanje mehanizma u nedostatku šipki.

Odluka. Sustav se sastoji od dvije mase ( N=2 ): fiksni disk 1 s okvirom i pomični disk 2. Usmjerimo os na kroz težište fiksnog diska okomito prema gore, os x- zajedno horizontalna ravnina.

Teorem o gibanju središta mase (3.6) zapisujemo u koordinatnom obliku

Vanjske sile ovog sustava su: težina okvira i fiksnog diska - mg, težina pokretnog diska mg, - ukupna horizontalna reakcija vijaka, - normalna ukupna reakcija ravnine. Stoga,

Zatim se prepisuju zakoni gibanja (b).

Izračunajmo koordinate središta mase mehaničkog sustava:

; (G)

kao što se vidi iz (slika 3.4), , , (kut rotacije poluge), . Zamjena ovih izraza u (r) i izračunavanje drugih derivacija s obzirom na vrijeme t iz , , dobivamo to

(e)

Zamjenom (c) i (e) u (b), nalazimo

Horizontalni pritisak koji djeluje na šipke ima najveći i najmanju vrijednost, kada cos = 1 odnosno, tj.

Pritisak mehanizma na horizontalnu ravninu ima najveću i najnižu vrijednost kada grijeh odnosno, tj.

Zapravo, riješen je prvi problem dinamike: prema poznatim jednadžbama gibanja središta mase sustava (e) obnavljaju se sile uključene u gibanje.

U nedostatku rešetki K i L (slika 3.4), mehanizam može početi poskakivati ​​iznad horizontalne ravnine. To će se dogoditi kada, t.j. kada , slijedi da kutna brzina rotacije radilice, pri kojoj mehanizam odbija, mora zadovoljiti jednakost

.

3. 3. Zakon održanja gibanja središta mase

Ako je glavni vektor vanjskih sila koje djeluju na sustav jednak nuli, t.j. , zatim iz(3.6)slijedi da je akceleracija središta mase nula, dakle, brzina centra mase je konstantna po veličini i smjeru. Ako, posebno, u početnom trenutku središte mase miruje, onda miruje cijelo vrijeme dok glavni vektor vanjskih sila ne bude jednak nuli.

Iz ovog teorema slijedi nekoliko posljedica.

· Same unutarnje sile ne mogu promijeniti prirodu kretanja središta mase sustava.

· Ako je glavni vektor vanjskih sila koje djeluju na sustav jednak nuli, tada središte mase miruje ili se giba jednoliko i pravocrtno.

· Ako je projekcija glavnog vektora vanjskih sila sustava na neku fiksnu os jednaka nuli, tada se projekcija brzine središta mase sustava na tu os ne mijenja.

· Nekoliko sila koje se primjenjuju na kruto tijelo ne mogu promijeniti gibanje njegova središta mase (može uzrokovati samo rotaciju tijela oko središta mase).

Razmotrimo primjer koji ilustrira zakon održanja gibanja središta mase.

Primjer 3 Dva utega s masama i povezani su nerastezljivom niti prebačenom preko bloka (slika 3.5), fiksiran na klin s masom M. Klin se oslanja na glatku horizontalnu ravninu. U početku je sustav mirovao. Pronađite pomak klina duž ravnine kada se prvi teret spusti na visinu N. Zanemarite masu bloka i niti.

Odluka. Vanjske sile koje djeluju na klin zajedno s utezima su sile gravitacije , i mg, kao i normalna reakcija glatka horizontalna površina N. Dakle,

Budući da je sustav u početnom trenutku mirovao, imamo .

Izračunajmo koordinatu središta mase sustava u iu trenutku t 1 kada je težina tereta g spustiti se u visinu H.

Na trenutak:

,

gdje , , X- koordinate središta mase tereta težine g, g i klina vaganja Mg.

Pretpostavimo da se klin u trenutku pomiče u pozitivnom smjeru osi Vol po iznosu L ako težina tereta padne na visinu N. Zatim, na trenutak

jer tereti zajedno s klinom će se pomaknuti u L s desne strane, a uteg će se pomaknuti na razdaljinu prema klinu. Budući da , nakon izračuna dobivamo

.

3.4. Količina sustava kretanja

3.4.1. Izračunavanje količine gibanja sustava

Zamah materijalne točke je vektorska veličina, jednak proizvodu masa točke na njenom vektoru brzine

Mjerna jedinica količine kretanja -

Moć gibanja mehaničkog sustava naziva se vektorski zbroj količine gibanja pojedinih točaka sustava, t.j.

gdje N je broj bodova sustava.

Zamah mehaničkog sustava može se izraziti u smislu mase sustava M i brzina centra mase. Stvarno,

oni. impuls sustava jednak je umnošku mase cijelog sustava i brzine njegova središta mase. Smjer je isti kao i smjer (slika 3.6)

U projekcijama na pravokutne osi imamo

gdje je , , - projekcije brzine središta mase sustava.

Ovdje M je masa mehaničkog sustava; ne mijenja kako se sustav kreće.

Posebno je prikladno koristiti ove rezultate pri izračunavanju impulsa krutih tijela.

Iz formule (3.7) se može vidjeti da ako se mehanički sustav giba tako da njegovo središte mase ostaje nepomično, tada impuls sustava ostaje jednak nuli.

3.4.2. Elementarni i impuls pune snage

Djelovanje sile na materijalnu točku tijekom vremena dt može se okarakterizirati elementarnim impulsom. Ukupni impuls sile u vremenu t, ili impuls sile , određuje se formulom

ili u projekcijama na koordinate osi

(3.8a)

Jedinica impulsa sile je .

3.4.3. Teorem o promjeni količine gibanja sustava

Neka se na točke sustava primjenjuju vanjske i unutarnje sile. Tada za svaku točku sustava možemo primijeniti diferencijalne zakone gibanja (3.3), imajući na umu da :

.

Zbrajanjem svih točaka sustava dobivamo

Svojstvom unutarnjih sila i po definiciji imamo

(3.9)

Množenjem obje strane ove jednadžbe sa dt, dobivamo teorem o promjeni količine gibanja u diferencijalni oblik:

, (3.10)

oni. diferencijal impulsa mehaničkog sustava jednak je vektorskom zbroju elementarnih impulsa svih vanjskih sila koje djeluju na točke mehaničkog sustava.

Izračunavanje integrala oba dijela (3.10) tijekom vremena od 0 do t, dobivamo teorem u konačnom ili integralnom obliku

(3.11)

U projekcijama na koordinatne osi imat ćemo

Promjena količine gibanja mehaničkog sustava tijekom vremenat, jednak je vektorskom zbroju svih impulsa vanjskih sila koje djeluju na točke mehaničkog sustava u isto vrijeme.

Primjer 4 Opterećenje mase m silazeći niz nagnuta ravnina iz mirovanja pod djelovanjem sile F, proporcionalno vremenu: , gdje (slika 3.7). Kolika je brzina tijela nakon t sekundi nakon početka kretanja, ako je koeficijent trenja klizanja tereta na nagnutoj ravnini jednak f.

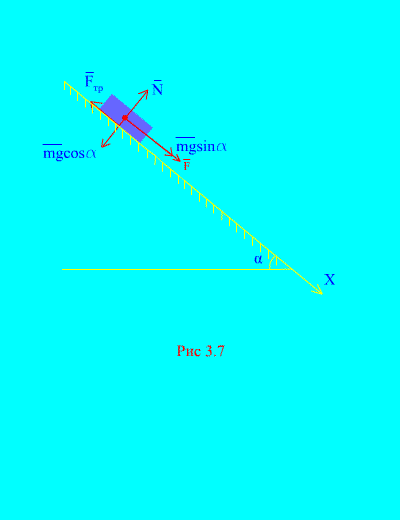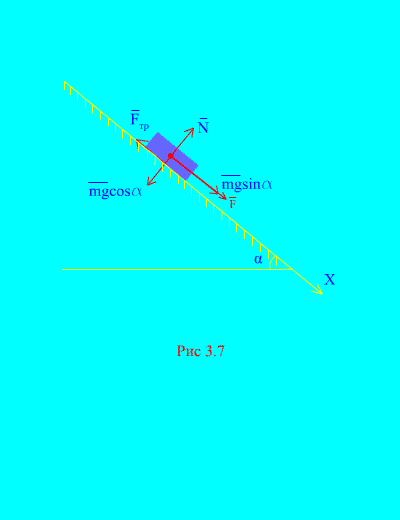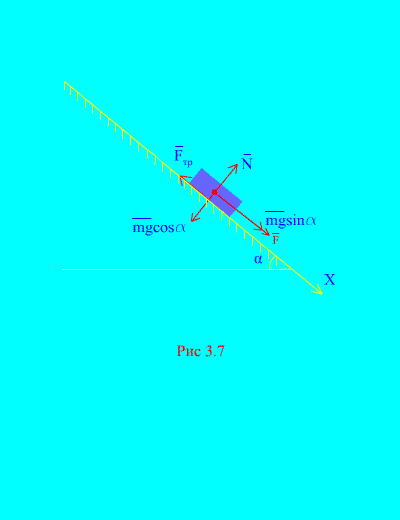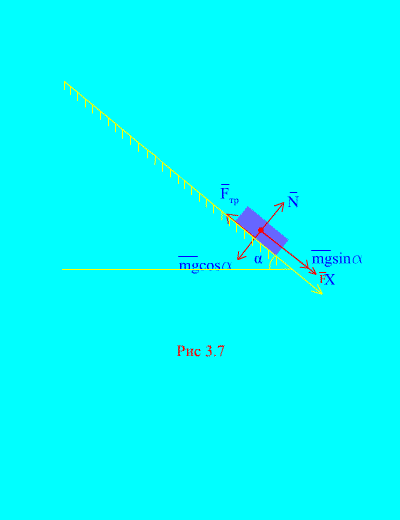
Odluka. Opišimo sile koje djeluju na opterećenje: mg - gravitacija tereta, N je normalna reakcija ravnine, je sila trenja klizanja tereta na ravnini, i . Prikazan je smjer svih sila (slika 3.7).

Usmjerimo os x niz nagnutu ravninu. Napišimo teorem o promjeni količine gibanja (3.11) u projekciji na os x:

(a)

Po uvjetu, jer u početnom trenutku vremena teret je mirovao. Zbroj projekcija impulsa svih sila na os x je

Stoga,

,

.

3.4.4. Zakoni održanja količine gibanja

Zakoni održanja dobiveni su kao posebni slučajevi teorema promjene količine gibanja. Moguća su dva posebna slučaja.

· Ako je vektorski zbroj svih vanjskih sila primijenjenih na sustav jednak nuli, t.j. , onda to slijedi iz teorema (3.9) , što ,

oni. ako je glavni vektor vanjskih sila sustava jednak nuli, tada je zamah sustava konstantan po veličini i smjeru.

· Ako je projekcija glavnog vektora vanjskih sila na bilo koju koordinatna os jednaka je nuli, na primjer Oh, t.j. , tada je projekcija količine gibanja na ovu os konstantna.

Razmotrimo primjer primjene zakona održanja količine gibanja.

Primjer 5 Balističko njihalo je tijelo mase, obješeno na dugu strunu (slika 3.8).

Metak mase koji se kreće brzinom V i padajući u nepomično tijelo, zaglavi se u njemu, a tijelo se odbija. Kolika je bila brzina metka ako se tijelo podiglo u visinu h ?

Odluka. Neka tijelo sa zaglavljenim metkom dobije brzinu. Zatim, koristeći zakon održanja količine gibanja u interakciji dvaju tijela, možemo napisati .

Brzina se može izračunati korištenjem zakona održanja mehanička energija . Zatim . Kao rezultat, nalazimo

.

Primjer 6. Voda ulazi u fiksni kanal (slika 3.9) promjenjiv presjek s brzinom pod kutom prema horizontu; kvadrat presjek kanal na ulazu; brzina vode na izlazu iz kanala i čini kut s horizontom.

Odrediti horizontalnu komponentu reakcije koju voda vrši na stijenke kanala. Gustoća vode .

Odluka. Odredit ćemo horizontalnu komponentu reakcije koju vrše stijenke kanala na vodu. Ta je sila jednaka po apsolutnoj vrijednosti i suprotna po predznaku od željene sile. Imamo, prema (3.11a),

. (a)

Izračunavamo masu volumena tekućine koja ulazi u kanal za vrijeme t:

Naziva se vrijednost rAV 0 druga masa - masa tekućine koja teče kroz bilo koji dio cijevi u jedinici vremena.

Ista količina vode napušta kanal u isto vrijeme. Početna i konačna brzina dane su u uvjetu.

Izračunaj desna strana jednakost (a) koja određuje zbroj projekcija na horizontalnu os vanjskih sila koje djeluju na sustav (vodu). Jedina horizontalna sila je horizontalna komponenta rezultirajuće reakcije zidova Rx. Ova sila je konstantna tijekom ravnomjernog kretanja vode. Tako

. (u)

Zamjenom (b) i (c) u (a), dobivamo

3.5. Kinetički moment sustava

3.5.1. Glavni moment količine gibanja sustava

Neka je radijus vektor točke s masom sustava u odnosu na neku točku A, koja se zove središte (slika 3.10).

Moment zamaha (kinetički moment) točke u odnosu na centar A zove vektor , određena formulom

. (3.12)

U ovom slučaju, vektor usmjeren okomito na ravninu koja prolazi kroz središte ALI i vektor .

Moment momenta (kinetički moment) točke oko osi naziva se projekcija na ovu os kutnog momenta točke u odnosu na bilo koje središte odabrano na ovoj osi.

Glavni moment količine gibanja (kinetički moment) sustava u odnosu na središte A naziva se količina

(3.13)

Glavni moment količine gibanja (kinetički moment) sustava oko osi naziva se projekcija na ovu os glavnog momenta količine gibanja sustava u odnosu na bilo koji odabran na zadanoj središnja os.

3.5.2. Moment rotacije krutog tijela oko osi rotacije

Kompatibilna fiksna točka O tijelo koje leži na osi rotacije Oz, s ishodištem koordinatnog sustava Ohuz, čije će se osi rotirati s tijelom (slika 3.11). Dopustiti biti radijus-vektor točke tijela u odnosu na ishodište koordinata, njegove projekcije na osi će biti označene s , , . Vektorske projekcije kutna brzina tijela na istim osi bit će označena s 0, 0, ().

Vrlo često je moguće razlikovati važne značajke gibanje mehaničkog sustava bez pribjegavanja integraciji sustava diferencijalnih jednadžbi gibanja. To se postiže primjenom općih teorema dinamike.

5.1. Osnovni pojmovi i definicije

Vanjske i unutarnje sile. Svaka sila koja djeluje na točku u mehaničkom sustavu nužno je ili aktivna snaga, ili reakcija veze. Cijeli skup sila koje djeluju na točke sustava može se različito podijeliti u dvije klase: na vanjske sile i unutarnje sile (subkripte e i i - od latinske riječi externus – vanjski i internus – unutarnji). Vanjske sile nazivaju se sile koje djeluju na točke sustava iz točaka i tijela koja nisu dio razmatranog sustava. Sile interakcije između točaka i tijela razmatranog sustava nazivaju se unutarnjim.

Ova podjela ovisi o tome koje materijalne točke i tijela istraživač uključuje u razmatrani mehanički sustav. Ako se sastav sustava proširi na dodatne točke i tijela, tada neke sile koje su bile vanjske za prethodni sustav mogu postati unutarnje za prošireni sustav.

Svojstva unutarnjih sila. Budući da su te sile sile interakcije između dijelova sustava, one su uključene u cjeloviti sustav unutarnjih sila u "dvojke" organizirane u skladu s aksiomom djelovanje-reakcija. Svaka takva "dvojka" sila

glavni vektor i glavna točka u odnosu na proizvoljno središte jednaki su nuli. Budući da se kompletan sustav unutarnjih sila sastoji samo od "dvojke", onda

1) glavni vektor sustava unutarnjih sila jednak je nuli,

2) glavni moment sustava unutarnjih sila u odnosu na proizvoljnu točku jednak je nuli.

Masa sustava je aritmetički zbroj masa mk svih točaka i tijela koja tvore sustav:

centar gravitacije(centar inercije) mehaničkog sustava naziva se geometrijska točka C, čiji su polumjerni vektor i koordinate određeni formulama

gdje su radijus vektori i koordinate točaka koje tvore sustav.

Za kruto tijelo u jednoličnom gravitacijskom polju, položaji središta mase i težišta se poklapaju; u drugim slučajevima to su različite geometrijske točke.

Zajedno s inercijskim referentnim okvirom, često se istovremeno razmatra neinercijski referentni okvir koji se kreće naprijed. Njegove koordinatne osi (Koenigove osi) biraju se tako da se referentna točka C uvijek poklapa sa središtem mase mehaničkog sustava. U skladu s definicijom, središte mase je fiksirano u Koenigovim osi i nalazi se na ishodištu koordinata.

Trenutak tromosti sustava o osi se zove skalarni jednak zbroju umnožak masa mk svih točaka sustava kvadratima njihovih udaljenosti do osi:

Ako je mehanički sustav kruto tijelo, da biste pronašli 12, možete koristiti formulu

gdje je gustoća, volumen koji zauzima tijelo.

Razmotrimo gibanje određenog sustava materijalnih volumena u odnosu na fiksni koordinatni sustav.Kada sustav nije slobodan, onda se može smatrati slobodnim, ako odbacimo ograničenja koja su nametnuta sustavu i zamijenimo njihovo djelovanje odgovarajućim reakcijama.

Podijelimo sve sile koje se primjenjuju na sustav na vanjske i unutarnje; oba mogu uključivati ​​reakcije odbačenih

veze. Označimo sa i glavni vektor i glavni moment vanjskih sila u odnosu na točku A.

1. Teorem o promjeni količine gibanja. Ako je zamah sustava, tada (vidi )

tj. vrijedi teorem: vremenska derivacija zamaha sustava jednaka je glavnom vektoru svih vanjskih sila.

Zamjenom vektora kroz njegov izraz gdje je masa sustava, je brzina centra mase, jednadžbi (4.1) može se dati drugačiji oblik:

Ova jednakost znači da se središte mase sustava giba kao materijalna točka čija je masa jednaka masi sustava i na koju se primjenjuje sila koja je geometrijski jednaka glavnom vektoru svih vanjskih sila sustava. Posljednja tvrdnja naziva se teorem o gibanju središta mase (centra tromosti) sustava.

Ako onda iz (4.1) slijedi da je vektor zamaha konstantan po veličini i smjeru. Projicirajući ga na koordinatnu os, dobivamo tri skalarna prva integrala diferencijalnih jednadžbi dvostrukog lanca sustava:

Ti se integrali nazivaju integrali momenta. Kada je brzina centra mase konstantna, tj. giba se jednoliko i pravocrtno.

Ako je projekcija glavnog vektora vanjskih sila na bilo koju os, na primjer, na os, jednaka nuli, tada imamo jedan prvi integral, ili ako su dvije projekcije glavnog vektora jednake nuli, tada postoje dva integrala količine gibanja.

2. Teorem o promjeni kinetičkog momenta. Neka je A neka proizvoljna točka u prostoru (pokretna ili stacionarna), koja se ne podudara nužno s nekom određenom materijalnom točkom sustava tijekom cijelog vremena kretanja. Njegova brzina u fiksnom sustavu koordinata bit će označena Teoremom o promjeni kutnog momenta materijalni sustav s obzirom na točku A ima oblik

Ako je točka A fiksna, tada jednakost (4.3) poprima jednostavniji oblik:

Ova jednakost izražava teorem o promjeni kutne količine gibanja sustava s obzirom na fiksna točka: vremenska derivacija kutnog momenta sustava, izračunata s obzirom na neku fiksnu točku, jednaka je glavnom momentu svih vanjskih sila u odnosu na tu točku.

Ako je tada, prema (4.4), vektor kutnog momenta konstantan po veličini i smjeru. Projicirajući ga na koordinatnu os, dobivamo skalarne prve integrale diferencijalnih jednadžbi gibanja sustava:

Ti se integrali nazivaju integrali kutnog momenta ili integrali površina.

Ako se točka A podudara sa središtem mase sustava, tada prvi član s desne strane jednakosti (4.3) nestaje i teorem o promjeni kutnog momenta ima isti oblik (4.4) kao u slučaju fiksne točka A. Imajte na umu (vidi 4. § 3.) da se u razmatranom slučaju apsolutni kutni moment sustava na lijevoj strani jednakosti (4.4) može zamijeniti jednakim kutnim momentom sustava u njegovom gibanju u odnosu na središte mase.

Neka je neka konstantna os ili os stalnog smjera koja prolazi kroz središte mase sustava, i neka je kutni moment sustava u odnosu na ovu os. Iz (4.4) slijedi da

gdje je moment vanjskih sila oko osi. Ako tijekom cijelog vremena gibanja tada imamo prvi integral

U djelima S. A. Chaplygina dobiveno je nekoliko generalizacija teorema o promjeni kutnog momenta, koje su potom primijenjene u rješavanju niza zadataka o kotrljanju kuglica. U radovima su sadržane daljnje generalizacije teorema o promjeni kpnetološkog momenta i njihove primjene u problemima dinamike krutog tijela. Glavni rezultati ovih radova odnose se na teorem o promjeni kutnog momenta u odnosu na pokretni, koji neprestano prolazi kroz neku pokretnu točku A. Neka - jedinični vektor usmjerena duž ove osi. Množenjem skalarno s obje strane jednakosti (4.3) i dodavanjem člana na oba njegova dijela, dobivamo

Kada je kinematički uvjet ispunjen

jednadžba (4.5) slijedi iz (4.7). A ako je uvjet (4.8) zadovoljen tijekom cijelog vremena gibanja, tada postoji prvi integral (4.6).

Ako su veze sustava idealne i omogućuju rotaciju sustava kao krutog tijela oko osi i u broju virtualnih pomaka, tada je glavni moment reakcija oko osi i jednak nuli, a zatim vrijednost na desna strana jednadžbe (4.5) glavni je moment svih vanjskih aktivnih sila oko osi i . Jednakost s nulom ovog trenutka i zadovoljivost relacije (4.8) bit će u razmatranom slučaju dovoljne uvjete za postojanje integrala (4.6).

Ako je smjer osi i nepromijenjen, tada se uvjet (4.8) može zapisati kao

Ova jednakost znači da su projekcije brzine središta mase i brzine točke A na os i na ravninu okomitu na nju paralelne. U djelu S. A. Chaplygina, umjesto (4.9), traži se da je manje od opće stanje gdje je X proizvoljna konstanta.

Imajte na umu da uvjet (4.8) ne ovisi o izboru točke na . Doista, neka je P proizvoljna točka na osi. Zatim

i zbog toga

Zaključno, napominjemo Resalovu geometrijsku interpretaciju jednadžbi (4.1) i (4.4): vektori apsolutne brzine krajevi vektora i jednaki su glavnom vektoru i glavnom momentu svih vanjskih sila u odnosu na točku A.

MINISTARSTVO POLJOPRIVREDE I PREHRANE REPUBLIKE BELORUSIJE

Odgojno-obrazovna ustanova „BELORUSKI DRŽAVNI AGRAR

TEHNIČKO SVEUČILIŠTE"

Zavod za teorijsku mehaniku i teoriju mehanizama i strojeva

TEORIJSKA MEHANIKA

metodički kompleks za studente grupe specijalnosti

74 06 Poljoprivredna tehnika

U 2 dijela 1. dio

UDK 531.3(07) LBC 22.213ya7 T 33

Sastavio:

Kandidat fizikalno-matematičkih znanosti, izvanredni profesor Yu. S. Biza, kandidat tehničke znanosti, izvanredni profesor N. L. Rakova, viši predavačI. A. Tarasevich

Recenzenti:

Zavod za teorijsku mehaniku obrazovne ustanove „Bjeloruski nacionalni Tehničko sveučilište» (glava

Zavod za teorijsku mehaniku BNTU Doktor fizikalno-matematičkih znanosti, profesor A. V. Chigarev);

Vodeći istraživač Laboratorija "Vibrozaštita strojarskih sustava" Državne znanstvene ustanove "Zajednički institut za strojarstvo

Nacionalna akademija znanosti Bjelorusije”, kandidat tehničkih znanosti, izvanredni profesor A. M. Goman

Teorijska mehanika. Rubrika "Dinamika": edukativna

Metoda T33. kompleks. U 2 dijela, 1. dio / komp.: Yu. S. Biza, N. L. Rakova, I. A. Tarasevich. - Minsk: BGATU, 2013. - 120 str.

ISBN 978-985-519-616-8.

NA obrazovni i metodički kompleks predstavlja materijale o proučavanju sekcije "Dinamika", 1. dio, koji je dio discipline "Teorijska mehanika". Uključuje tečaj predavanja, osnovne materijale za implementaciju praktične vježbe, zadaci i uzorci zadataka za samostalan rad i kontrolu aktivnosti učenja puno radno vrijeme i dopisni obrasci učenje.

UDK 531.3(07) LBC 22.213ya7

UVOD ................................................. ........................................................
1. ZNANSTVENI I TEORIJSKI SADRŽAJ OBRAZOVNOG
METODOLOŠKOG KOMPLESA ................................................ ..
1.1. Glosar................................................. ................................
1.2. Teme predavanja i njihov sadržaj .................................................. ...
Poglavlje 1. Uvod u dinamiku. Osnovni koncepti
klasična mehanika ................................................................ ...................................................
Tema 1. Dinamika materijalne točke........................................ ....
1.1. Zakoni dinamike materijalne točke
(zakoni Galilea - Newtona) .............................................. ...........
1.2. Diferencijalne jednadžbe pokreti
1.3. Dva glavna zadatka dinamike ................................................. ............
Tema 2. Dinamika relativnog gibanja
materijalna točka ................................................................ ........................................
Pitanja za pregled ................................................................ ............................................
Tema 3. Dinamika mehaničkog sustava ........................................ ....
3.1. Geometrija mase. Središte mase mehaničkog sustava.....
3.2. Unutarnje snage ................................................ ................................................
Pitanja za pregled ................................................................ ............................................
Tema 4. Momenti tromosti krutog tijela ........................................
4.1. Momenti tromosti krutog tijela
u odnosu na os i pol ........................................................ ...................... .....
4.2. Teorem o momentima tromosti krutog tijela
o paralelnim osovinama
(Huygens-Steinerov teorem) ........................................ ... ...
4.3. Centrifugalni momenti inercije ................................................... .
Pitanja za pregled ................................................................ ........................................
2. Poglavlje

Tema 5. Teorem o gibanju središta mase sustava ...................................
Pitanja za pregled ................................................................ ............................................
Zadaci za samostalno učenje ................................................. .......
Tema 6. Količina kretanja materijalne točke
i mehanički sustav ................................................. ................ ...................
6.1. Količina kretanja materijalne točke 43
6.2. Impuls sile ................................................. ...................................
6.3. Teorem o promjeni količine gibanja
materijalna točka ................................................................ ................ ...................
6.4. Teorem o promjeni glavnog vektora
impuls mehaničkog sustava ................................................
Pitanja za pregled ................................................................ ............................................
Zadaci za samostalno učenje ................................................. .......
Tema 7. Moment količine gibanja materijalne točke
i mehanički sustav u odnosu na središte i os ...................................
7.1. Moment količine gibanja materijalne točke
u odnosu na centar i os ................................................ ........................................
7.2. Teorem o promjeni kutnog momenta
materijalna točka u odnosu na središte i os ......................
7.3. Teorem o promjeni kinetičkog momenta
mehanički sustav u odnosu na središte i os ...................................
Pitanja za pregled ................................................................ ............................................
Zadaci za samostalno učenje ................................................. .......
Tema 8. Rad i snaga sila ................................................... .........
Pitanja za pregled ................................................................ ............................................
Zadaci za samostalno učenje ................................................. .......
Tema 9. Kinetička energija materijalne točke
i mehanički sustav ................................................. ................ ...................
9.1. Kinetička energija materijalne točke
i mehanički sustav. Koenigov teorem .................................
9.2. Kinetička energija krutog tijela
s različitim pokretima ................................................................. ...................................................
9.3. Promjena teorema kinetička energija
materijalna točka ................................................................ ................ ...................

9.4. Teorem promjene kinetičke energije
mehanički sustav ................................................................ ................................................
Pitanja za pregled ................................................................ ............................................
Zadaci za samostalno učenje ................................................. .......
Tema 10. Polje potencijalnih sila
i potencijalna energija ................................................. ................ .................
Pitanja za pregled ................................................................ ............................................
Tema 11. Dinamika krutog tijela........................................ .........................
Pitanja za pregled ................................................................ ............................................
2. MATERIJALI ZA KONTROLU
PO MODULU ................................................................ ...................................................
SAMOSTALNI RAD UČENIKA ..............................
4. ZAHTJEVI ZA PROJEKT UPRAVLJANJA
RADOVI ZA REDOVNE I DOPISNE STUDENTE
OBLICI TRENINGA .................................................. ........................................................
5. POPIS PRIPREMNIH PITANJA
NA ISPIT (STUDIJ) STUDENATA
REDOVNO I DOPISNO OBRAZOVANJE................................................. ......
6. POPIS REFERENCE ................................................ .. ............

UVOD

Teorijska mehanika – znanost o općim zakonima mehaničko kretanje, ravnoteža i interakcija materijalnih tijela.

Ovo je jedna od temeljnih općeznanstvenih fizikalno-matematičkih disciplina. To je teorijska osnova moderne tehnologije.

Proučavanje teorijske mehanike, uz ostale fizikalno-matematičke discipline, pridonosi širenju znanstvenih horizonata, formira sposobnost betoniranja i apstraktno mišljenje te pridonosi poboljšanju opće tehničke kulture budućeg specijalista.

Teorijska mehanika, kao znanstvena osnova svega tehničkim disciplinama, doprinosi razvoju vještina racionalne odluke inženjerski zadaci povezan s radom, popravkom i projektiranjem poljoprivrednih i meliorativnih strojeva i opreme.

Prema prirodi zadataka koji se razmatraju, mehanika se dijeli na statiku, kinematiku i dinamiku. Dinamika je dio teorijske mehanike koji proučava gibanje materijalnih tijela pod djelovanjem primijenjenih sila.

NA obrazovni i metodički kompleksa (UMK) predstavlja materijale o proučavanju odjeljka "Dinamika" koji uključuje tečaj predavanja, osnovne materijale za izvođenje praktični rad, zadaci i uzorci izvođenja za samostalan rad te kontrolu odgojno-obrazovne djelatnosti redovitih izvanrednih studenata.

NA kao rezultat proučavanja odjeljka "Dinamika" učenik mora učiti teorijske osnove dinamiku i ovladati osnovnim metodama rješavanja problema dinamike:

Poznavati metode rješavanja zadataka dinamike, opće teoreme dinamike, principe mehanike;

Znati odrediti zakone gibanja tijela ovisno o silama koje na njega djeluju; primjenjivati ​​zakone i teoreme mehanike za rješavanje problema; odrediti statičke i dinamičke reakcije veza koje ograničavaju kretanje tijela.

Nastavnim planom i programom discipline "Teorijska mehanika" predviđen je ukupan broj sati u učionici - 136, uključujući 36 sati za proučavanje odjeljka "Dinamika".

1. ZNANSTVENI I TEORIJSKI SADRŽAJ NASTAVNO-METODIČKOG KOMPLEKSA

1.1. Glosar

Statika je dio mehanike koji ocrtava opću doktrinu sila, proučava se redukcija složeni sustavi sile do najjednostavnijeg oblika i uspostavljeni su uvjeti ravnoteže razni sustavi snage.

Kinematika je dio teorijske mehanike u kojem se proučava kretanje materijalnih objekata, bez obzira na uzroke koji uzrokuju to kretanje, tj. bez obzira na sile koje djeluju na te objekte.

Dinamika je grana teorijske mehanike koja proučava gibanje materijalnih tijela (točaka) pod djelovanjem primijenjenih sila.

Materijalna točka- materijalno tijelo čija je razlika u kretanju točaka beznačajna.

Masa tijela je skalarna pozitivna vrijednost koja ovisi o količini tvari sadržanoj u danom tijelu i određuje njegovu mjeru inercije pri kretanje naprijed.

Referentni sustav - koordinatni sustav povezan s tijelom, u odnosu na koji se proučava gibanje drugog tijela.

inercijski sustav- sustav u kojem su ispunjeni prvi i drugi zakon dinamike.

Moment sile je vektorska mjera djelovanja sile tijekom nekog vremena.

Količina kretanja materijalne točke je vektorska mjera njezina gibanja, koja je jednaka umnošku mase točke i vektora njezine brzine.

Kinetička energija je skalarna mjera mehaničkog gibanja.

Elementarni rad sile je infinitezimalna skalarna vrijednost jednaka točkasti proizvod vektor sile na vektor beskonačno malog pomaka točke primjene sile.

Kinetička energija je skalarna mjera mehaničkog gibanja.

Kinetička energija materijalne točke je skalar

pozitivna vrijednost jednaka polovici umnoška mase točke i kvadrata njezine brzine.

Kinetička energija mehaničkog sustava je aritme-

kinetički zbroj kinetičkih energija svih materijalnih točaka ovog sustava.

Sila je mjera mehaničke interakcije tijela koja karakterizira njezin intenzitet i smjer.

1.2. Teme predavanja i njihov sadržaj

Odjeljak 1. Uvod u dinamiku. Osnovni koncepti

klasična mehanika

Tema 1. Dinamika materijalne točke

Zakoni dinamike materijalne točke (zakoni Galilea - Newtona). Diferencijalne jednadžbe gibanja materijalne točke. Dva glavna zadatka dinamike za materijalnu točku. Rješenje drugog problema dinamike; integracijske konstante i njihovo određivanje iz početnih uvjeta.

Literatura:, str. 180-196, , str. 12-26.

Tema 2. Dinamika relativnog gibanja materijala

Relativno gibanje materijalne točke. Diferencijalne jednadžbe relativnog gibanja točke; prijenosne i Coriolisove sile inercije. Načelo relativnosti u klasičnoj mehanici. Slučaj relativnog odmora.

Literatura: , str. 180-196, , str. 127-155.

Tema 3. Geometrija masa. Središte mase mehaničkog sustava

Masa sustava. Središte mase sustava i njegove koordinate.

Literatura:, str. 86-93, str. 264-265

Tema 4. Momenti tromosti krutog tijela

Momenti tromosti krutog tijela oko osi i pola. Radijus inercije. Teorem o momentima tromosti oko paralelnih osi. Aksijalni momenti tromosti nekih tijela.

Centrifugalni momenti inercije kao karakteristika asimetrije tijela.

Literatura: , str. 265-271, , str. 155-173.

Odjeljak 2. Opći teoremi dinamike materijalne točke

i mehanički sustav

Tema 5. Teorem o gibanju središta mase sustava

Teorem o gibanju središta mase sustava. Posljedice iz teorema o gibanju središta mase sustava.

Literatura: , str. 274-277, , str. 175-192.

Tema 6. Količina kretanja materijalne točke

i mehanički sustav

Količina gibanja materijalne točke i mehaničkog sustava. Elementarni impuls i impuls sile za konačan vremenski period. Teorem o promjeni količine gibanja točke i sustava u diferencijalnom i integralnom obliku. Zakon održanja količine gibanja.

Literatura: , str. 280-284, , str. 192-207.

Tema 7. Moment količine gibanja materijalne točke

i mehanički sustav u odnosu na središte i os

Moment momenta točke oko središta i osi. Teorem o promjeni kutnog momenta točke. Kinetički moment mehaničkog sustava oko središta i osi.

Kutni moment rotacije krutog tijela oko osi rotacije. Teorem o promjeni kinetičkog momenta sustava. Zakon održanja količine gibanja.

Literatura: , str. 292-298, , str. 207-258.

Tema 8. Rad i snaga sila

Elementarni rad sile, njezin analitički izraz. Rad sile na konačni put. Rad gravitacije, elastična sila. Jednakost nule zbroja rada unutarnjih sila koje djeluju u tijelu. Rad sila primijenjenih na kruto tijelo koje rotira oko fiksne osi. Vlast. Učinkovitost.

Literatura: , str. 208-213, , str. 280-290.

Tema 9. Kinetička energija materijalne točke

i mehanički sustav

Kinetička energija materijalne točke i mehaničkog sustava. Proračun kinetičke energije krutog tijela u različitim slučajevima njegova gibanja. Koenigov teorem. Teorem o promjeni kinetičke energije točke u diferencijalnom i integralnom obliku. Teorem o promjeni kinetičke energije mehaničkog sustava u diferencijalnom i integralnom obliku.

Literatura: , str. 301-310, , str. 290-344.

Tema 10. Potencijalno polje sila i potencijal

Koncept polja sile. Potencijalno polje sila i funkcija sile. Rad sile na konačnom pomaku točke u potencijalnom polju sila. Potencijalna energija.

Literatura: , str. 317-320, , str. 344-347.

Tema 11. Dinamika krutog tijela

Diferencijalne jednadžbe translacijskog gibanja krutog tijela. Diferencijalna jednadžba rotacijsko gibanje kruto tijelo oko fiksne osi. fizičko visak. Diferencijalne jednadžbe gibanja u ravnini krutog tijela.

Literatura: , str. 323-334, , str. 157-173.

Odjeljak 1. Uvod u dinamiku. Osnovni koncepti

klasična mehanika

Dinamika je grana teorijske mehanike koja proučava gibanje materijalnih tijela (točaka) pod djelovanjem primijenjenih sila.

materijalno tijelo- tijelo koje ima masu.

Materijalna točka- materijalno tijelo čija je razlika u kretanju točaka beznačajna. To može biti ili tijelo čije se dimenzije mogu zanemariti tijekom njegovog kretanja ili tijelo konačnih dimenzija, ako se kreće naprijed.

Čestice se nazivaju i materijalne točke, na koje se čvrsto tijelo mentalno dijeli pri određivanju nekih njegovih dinamičkih karakteristika. Primjeri materijalnih točaka (slika 1): a - kretanje Zemlje oko Sunca. Zemlja je materijalna točka; b je translacijsko gibanje krutog tijela. Čvrsto- majka-

al točka, budući da V B \u003d V A; a B = a A; c - rotacija tijela oko osi.

Čestica tijela je materijalna točka.

Inercija je svojstvo materijalnih tijela da pod djelovanjem primijenjenih sila mijenjaju brzinu svog kretanja brže ili sporije.

Masa tijela je skalarna pozitivna vrijednost koja ovisi o količini tvari sadržanoj u danom tijelu i određuje njegovu mjeru inercije tijekom translacijskog gibanja. U klasičnoj mehanici masa je konstanta.

sila - kvantitativna mjera mehanička interakcija između tijela ili između tijela (točke) i polja (električnog, magnetskog itd.).

Sila je vektorska veličina koju karakteriziraju veličina, točka primjene i smjer (linija djelovanja) (slika 2: A - točka primjene; ​​AB - linija djelovanja sile).

Riža. 2

U dinamici, uz stalne sile, postoje i promjenjive sile koje mogu ovisiti o vremenu t, brzini ϑ, udaljenosti r ili o kombinaciji ovih veličina, t.j.

F = konst;

F = F(t);

F = F(ϑ) ;

F = F(r) ;

F = F(t, r, ϑ) .

	Primjeri takvih sila prikazani su na sl. 3: a										- tjelesna težina;
			(ϑ) – sila otpora zraka; b −		T =						- vučna sila

električna lokomotiva; c − F = F (r) je sila odbijanja od središta O ili privlačenja prema njemu.

Referentni sustav - koordinatni sustav povezan s tijelom, u odnosu na koji se proučava gibanje drugog tijela.

Inercijski sustav je sustav u kojem su ispunjeni prvi i drugi zakon dinamike. Ovo je fiksni koordinatni sustav ili sustav koji se kreće jednoliko i pravocrtno.

Kretanje u mehanici je promjena položaja tijela u prostoru i vremenu u odnosu na druga tijela.

Prostor u klasičnoj mehanici je trodimenzionalan, u skladu s euklidskom geometrijom.

Vrijeme je skalarna veličina koja teče na isti način u bilo kojem referentnom sustavu.

Sustav jedinica je skup mjernih jedinica fizičke veličine. Za mjerenje svih mehaničkih veličina dovoljne su tri osnovne jedinice: jedinice duljine, vremena, mase ili sile.

Mehanički	Dimenzija		Notacija	Dimenzija	Notacija
veličina
				centimetar
	kilogram-

Sve ostale mjerne jedinice mehaničkih veličina su njihove izvedenice. Koriste se dvije vrste sustava jedinica: međunarodni sustav Jedinice SI (ili manje - CGS) i tehnički sustav jedinica - MKGSS.

Tema 1. Dinamika materijalne točke

1.1. Zakoni dinamike materijalne točke (zakoni Galilea - Newtona)

Prvi zakon (tromnosti).

izoliran od vanjski utjecaji materijalna točka održava svoje stanje mirovanja ili se kreće jednoliko i pravocrtno sve dok je primijenjene sile ne prisile da promijeni ovo stanje.

Gibanje koje vrši točka u odsutnosti sila ili pod djelovanjem uravnoteženog sustava sila naziva se gibanje inercije.

Na primjer, kretanje tijela po glatkoj (sila trenja je nula)

horizontalna površina (slika 4: G - tjelesna težina; N - normalna reakcija ravnine).

Budući da je G = − N , onda je G + N = 0.

Kada je ϑ 0 ≠ 0 tijelo se kreće istom brzinom; kod ϑ 0 = 0 tijelo miruje (ϑ 0 je početna brzina).

Drugi zakon (osnovni zakon dinamike).

Umnožak mase točke i akceleracije koju ona prima pod djelovanjem dane sile jednak je po apsolutnoj vrijednosti toj sili, a njezin se smjer poklapa sa smjerom akceleracije.

a b

Matematički se ovaj zakon izražava vektorskom jednakošću

Za F = const,

a = const - gibanje točke je jednoliko. EU-

je li a ≠ const, α

- usporeno snimanje (slika 5, ali);

a ≠ const,

a -

– ubrzano gibanje (slika 5, b);m – masa točke;

vektor ubrzanja;

– vektorska sila; ϑ 0 je vektor brzine).

Kod F = 0,a 0 = 0 = ϑ 0 = const - točka se giba jednoliko i pravocrtno, ili kod ϑ 0 = 0 - miruje (zakon inercije). Drugi

zakon vam omogućuje da uspostavite odnos između mase m tijela koje se nalazi u blizini Zemljina površina, a njegova težina G .G = mg , gdje je g

ubrzanje gravitacije.

Treći zakon (zakon jednakosti djelovanja i reakcije). Dvije materijalne točke djeluju jedna na drugu silama jednakim po veličini i usmjerenim duž ravne linije koja spaja

ove točke, u suprotnim smjerovima.

Budući da se sile F 1 = − F 2 primjenjuju na različite točke, tada sustav sila (F 1 , F 2 ) nije uravnotežen, tj. (F 1 , F 2 )≈ 0 (slika 6.).

Zauzvrat

m a = m a

- stav

mase međudjelujućih točaka obrnuto su proporcionalne njihovim akceleracijama.

Četvrti zakon (zakon neovisnosti djelovanja sila). Ubrzanje koje je primila točka pod djelovanjem simultane

ali nekoliko sila, jednak je geometrijskom zbroju onih ubrzanja koje bi točka primila pod djelovanjem svake sile posebno na nju.

Objašnjenje (slika 7).

t a n

a 1 a kF n

Rezultantne R sile (F 1 ,...F k ,...F n ) .

Budući da je ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = ma n , tada

a = a 1 + ...+ a k + ...+ a n = ∑ a k , tj. četvrti zakon je ekvivalentan

k = 1

pravilo zbrajanja sila.

1.2. Diferencijalne jednadžbe gibanja materijalne točke

Neka više sila istovremeno djeluje na materijalnu točku, među kojima postoje i konstante i varijable.

Drugi zakon dinamike zapisujemo u obliku

= ∑

(t ,

k = 1

, ϑ=

r je radijus vektor kretanja

točka, tada (1.2) sadrži derivacije od r i predstavlja diferencijalnu jednadžbu gibanja materijalne točke u vektorskom obliku ili osnovna jednadžba dinamike materijalne točke.

Projekcije vektorske jednakosti (1.2): - na os kartezijanskih koordinata (sl. 8, ali)

max=md
					= ∑Fkx;
					k = 1
svibanj=md
					= ∑Fky;	(1.3)
					k = 1
maz=m					= ∑Fkz;
					k = 1

Na prirodnoj osi (slika 8, b)

mat				= ∑ Fk τ ,
				k = 1
				= ∑ F k n ;
				k = 1

mab = m0 = ∑ Fk b

k = 1

M t oM oa

b na o

Jednadžbe (1.3) i (1.4) su diferencijalne jednadžbe gibanja materijalne točke u kartezijanskim koordinatnim osi i prirodnim osi, tj. prirodne diferencijalne jednadžbe koje se obično koriste za krivuljasto gibanje točke ako je putanja točke i poznati su njezini polumjeri zakrivljenosti.

1.3. Dva glavna problema dinamike za materijalnu točku i njihovo rješenje

Prvi (izravni) zadatak.

Poznavajući zakon gibanja i masu točke, odredite silu koja djeluje na točku.

Da biste riješili ovaj problem, morate znati ubrzanje točke. U problemima ovog tipa može se izravno specificirati, ili se specificira zakon gibanja točke prema kojem se može odrediti.

1. Dakle, ako je kretanje točke zadano u kartezijanskim koordinatama

x \u003d f 1 (t) , y \u003d f 2 (t) i z \u003d f 3 (t) tada se određuju projekcije ubrzanja

na koordinatnoj osi x =		d2x			d2y			d2z		A onda - projekt-
F x , F y i F z sile na ove osi:
				,k ) = F F z . (1.6) 2. Ako točka obvezuje krivolinijsko gibanje a poznat je zakon gibanja s = f (t), putanja točke i njezin polumjer zakrivljenosti ρ, tada prikladno je koristiti prirodne osi, a projekcije ubrzanja na te osi određene su poznatim formulama: Tangencijalna os a τ = d ϑ = d 2 2 s – tangencijalno ubrzanje;dt dt HomeNormal ds 2 a n = ϑ 2 = dt je normalno ubrzanje. Projekcija akceleracije na binormalu je nula. Zatim projekcije sile na prirodne osi F=m F=m Modul i smjer sile određuju se formulama: F \u003d F τ 2 + F n 2; cos( ; cos( Drugi (obrnuti) zadatak. Poznavajući sile koje djeluju na točku, njezinu masu i početni uvjeti gibanje, odrediti zakon gibanja točke ili bilo koju drugu njezinu kinematičku karakteristiku. Početni uvjeti za kretanje točke u kartezijanskim osi su koordinate točke x 0, y 0, z 0 i projekcija početne brzine ϑ 0 na te osi ϑ 0 x \u003d x 0, ϑ 0 y \u003d y 0 i ϑ 0 z = z 0 u vrijeme koje odgovara dajući početak gibanja točke i uzet jednak nuli. Rješavanje problema ovog tipa svodi se na sastavljanje diferencijala diferencijalne jednadžbe (ili jedna jednadžba) gibanja materijalne točke i njihovo naknadno rješavanje po izravna integracija ili korištenjem teorije diferencijalnih jednadžbi. Pregledajte pitanja 1. Što proučava dinamika? 2. Kakvo se gibanje naziva inercijalno gibanje? 3. Pod kojim će se uvjetima materijalna točka mirovati ili kretati jednoliko i pravocrtno? 4. Koja je bit prvog glavnog problema dinamike materijalne točke? Drugi zadatak? 5. Zapišite prirodne diferencijalne jednadžbe gibanja materijalne točke. Zadaci za samostalno učenje 1. Točka mase m = 4 kg giba se vodoravnom ravnom crtom akceleracijom a = 0,3 t. Odredite modul sile koja djeluje na točku u smjeru njezina gibanja u trenutku t = 3 s. 2. Dio mase m = 0,5 kg klizi niz pladanj. Pod kojim kutom u odnosu na vodoravnu ravninu treba postaviti ladicu tako da se dio giba ubrzanjem a = 2 m / s 2? Angle express u stupnjevima. 3. Točka mase m = 14 kg giba se duž osi Ox akceleracijom a x = 2 t . Odredite modul sile koja djeluje na točku u smjeru gibanja u trenutku t = 5 s.

(MEHANIČKI SUSTAVI) - IV opcija

1. Osnovna jednadžba dinamike materijalne točke, kao što je poznato, izražava se jednadžbom . Diferencijalne jednadžbe gibanja proizvoljne točke neslobodnog mehaničkog sustava prema dva načina dijeljenja sila može se zapisati u dva oblika:

(1) , gdje je k=1, 2, 3, … , n broj točaka materijalnog sustava.

(2)

gdje je masa k-te točke; - radijus vektor k-te točke, - zadana (aktivna) sila koja djeluje na k-tu točku ili rezultanta svih aktivnih sila koje djeluju na k-tu točku. - rezultanta reakcijskih sila veza koje djeluju na k-tu točku; - rezultanta unutarnjih sila koje djeluju na k-tu točku; - rezultanta vanjskih sila koje djeluju na k-tu točku.

Jednadžbe (1) i (2) mogu se koristiti za rješavanje i prvog i drugog problema dinamike. Međutim, rješenje drugog problema dinamike za sustav postaje vrlo komplicirano ne samo s matematička točka viziju, ali i zato što se suočavamo s temeljnim poteškoćama. Oni leže u činjenici da je i za sustav (1) i za sustav (2) broj jednadžbi značajno manje od broja nepoznato.

Dakle, ako koristimo (1), tada će poznati za drugi (inverzni) problem dinamike biti i , a nepoznanice će biti i . Vektorske jednadžbe bit će " n", a nepoznato - "2n".

Ako polazimo od sustava jednadžbi (2), tada su poznate i dio vanjskih sila . Zašto dio? Činjenica je da broj vanjskih sila uključuje vanjske reakcije veze koje su nepoznate. Osim toga, bit će i nepoznanica.

Dakle, i sustav (1) i sustav (2) su OTVORENI. Moramo dodati jednadžbe, uzimajući u obzir jednadžbe odnosa, a možda još trebamo nametnuti neka ograničenja na same odnose. Što uraditi?

Ako pođemo od (1), onda možemo slijediti put sastavljanja Lagrangeovih jednadžbi prve vrste. Ali ovaj način nije racionalan jer lakši zadatak(manje stupnjeva slobode), to je teže riješiti s gledišta matematike.

Zatim obratimo pozornost na sustav (2), gdje su - uvijek nepoznati. Prvi korak u rješavanju sustava je uklanjanje ovih nepoznanica. Treba imati na umu da nas u pravilu ne zanimaju unutarnje sile tijekom kretanja sustava, odnosno kada se sustav kreće nije potrebno znati kako se kreće svaka točka sustava, ali dovoljno je znati kako se sustav u cjelini kreće.

Dakle, ako različiti putevi isključiti iz sustava (2) nepoznate sile, tada dobivamo neke relacije, tj. neke Opće karakteristike za sustav, čije poznavanje omogućuje prosuđivanje kako se sustav općenito kreće. Ove karakteristike uvode se pomoću tzv opći teoremi dinamike. Postoje četiri takva teorema:

1. Teorem o kretanje središta mase mehaničkog sustava;

2. Teorem o promjena količine gibanja mehaničkog sustava;

3. Teorem o promjena kutnog momenta mehaničkog sustava;

4. Teorem o promjena kinetičke energije mehaničkog sustava.