Hoe vectoren worden opgeteld en afgetrokken. Eigenschappen van vermenigvuldiging van een vector met een getal

Voor de juiste weergave van de natuurwetten in de natuurkunde zijn geschikte wiskundige hulpmiddelen nodig.

In meetkunde en natuurkunde zijn er grootheden die worden gekarakteriseerd en numerieke waarde, en richting.

Het is raadzaam om ze weer te geven als gerichte segmenten of vectoren.

Dergelijke waarden hebben een begin (weergegeven door een punt) en een einde, aangegeven door een pijl. De lengte van het segment wordt (lengte) genoemd.

snelheid;
versnelling;
pols;
kracht;
moment;
kracht;
in beweging;
veldsterkte, enz.

vliegtuig coördinaten

Laten we een segment definiëren op het vlak gericht van punt A (x1, y1) naar punt B (x2, y2). De coördinaten a (a1, a2) zijn getallen a1=x2-x1, a2=y2-y1.

De module wordt berekend met behulp van de stelling van Pythagoras:

De nulvector heeft het begin en het einde. Coördinaten en lengte zijn 0.

Som van vectoren

Bestaan verschillende regels voor het berekenen van het bedrag

driehoeksregel;
veelhoek regel;
parallellogram regel.

De vectoroptellingsregel kan worden verklaard aan de hand van problemen uit de dynamica en mechanica. Beschouw de optelling van vectoren volgens de driehoeksregel aan de hand van het voorbeeld van krachten die op een puntlichaam werken en opeenvolgende verplaatsingen van het lichaam in de ruimte.

Stel dat het lichaam eerst van punt A naar punt B bewoog en vervolgens van punt B naar punt C. De uiteindelijke verplaatsing is een segment gericht van het beginpunt A naar het eindpunt C.

Het resultaat van twee verplaatsingen of hun som s = s1+ s2. Zo'n methode heet driehoeksregel.

Pijlen staan in een ketting achter elkaar, indien nodig, om een parallelle overdracht uit te voeren. Het totale segment sluit de reeks af. Het begin valt samen met het begin van de eerste, het einde - met het einde van de laatste. In buitenlandse studieboeken deze methode genaamd "kop tegen kop".

De coördinaten van het resultaat c = a + b zijn gelijk aan de som van de overeenkomstige coördinaten van de termen c (a1+ b1, a2+ b2).

De som van parallelle (collineaire) vectoren wordt ook bepaald door de driehoeksregel.

Als twee beginsegmenten loodrecht op elkaar staan, dan is het resultaat van hun toevoeging de hypotenusa van de rechthoekige driehoek. De lengte van de som wordt berekend met behulp van de stelling van Pythagoras.

Voorbeelden:

De snelheid van een horizontaal gegooid lichaam loodrecht versnelling vrije val.
Met uniform roterende beweging lijnsnelheid lichaam staat loodrecht op de centripetale versnelling.

Drie of meer vectoren toevoegen produceren volgens veelhoek regel, "kop tegen kop"

Laten we aannemen dat krachten F1 en F2 op een puntlichaam worden uitgeoefend.

De ervaring leert dat het gecombineerde effect van deze krachten gelijk is aan de werking van één kracht die diagonaal langs het daarop gebouwde parallellogram is gericht. Deze resulterende kracht is gelijk aan hun som F \u003d F1 + F 2. De bovenstaande methode van optellen wordt genoemd parallellogram regel.

De lengte wordt in dit geval berekend met de formule

Waarbij θ de hoek tussen de zijden is.

De driehoeks- en parallellogramregels zijn onderling uitwisselbaar. In de natuurkunde wordt de parallellogramregel vaker gebruikt, omdat de gerichte hoeveelheden krachten, snelheden en versnellingen meestal worden toegepast op één puntlichaam. In een 3D-coördinatensysteem is de boxregel van toepassing.

Algebra elementen

Optellen is een binaire bewerking: u kunt slechts een paar tegelijk toevoegen.
commutativiteit: de som van de permutatie van de termen verandert niet a + b = b + a. Dit blijkt duidelijk uit de parallellogramregel: de diagonaal is altijd hetzelfde.
Associativiteit: de som van een willekeurig aantal vectoren is niet afhankelijk van de volgorde van hun optelling (a + b) + c = a + (b + c).
Optellen met een nulvector verandert niet van richting of lengte: a +0= a .
Voor elke vector is er tegenover. Hun som is gelijk aan nul a +(-a)=0, en de lengtes zijn hetzelfde.

Het aftrekken van een gericht segment is gelijk aan het optellen van het tegenovergestelde. De coördinaten zijn gelijk aan het verschil van de corresponderende coördinaten. De lengte is:

Voor aftrekken kunt u een aangepaste driehoeksregel gebruiken.

Vermenigvuldiging met een scalair

Het resultaat van vermenigvuldiging met een scalair is een vector.

De productcoördinaten worden verkregen door de overeenkomstige coördinaten van de bron te vermenigvuldigen met een scalair.

scalair - numerieke waarde met een plus- of minteken, groter of kleiner dan één.

Voorbeelden scalairen in de natuurkunde:

gewicht;
tijd;
aanval;
lengte;
plein;
volume;
dikte;
temperatuur;
energie.

Voorbeelden:

De verplaatsing van een eenparig bewegend lichaam is gelijk aan het product van tijd en snelheid s = vt.
Het momentum van een lichaam is de massa vermenigvuldigd met de snelheid p = mv.
De tweede wet van Newton. Het product van lichaamsgewicht en versnelling is gehecht resulterende kracht ma=F.
De kracht die werkt op een geladen deeltje in een elektrisch veld is evenredig met de lading F = qE.

Het scalaire product van de gerichte segmenten a en b is gelijk aan het product van de modules en de cosinus van de hoek ertussen. Het scalaire product van onderling loodrechte segmenten is gelijk aan nul.

Voorbeeld:

Werk is scalair product krachten en verplaatsingen A = Fs .

X en ja genaamd vector z zoals dat z+y=x.

Optie 1. De startpunten van alle vectoren vallen samen met de oorsprong.

Laten we het verschil van vectoren en . construeren .

Het verschil van vectoren plotten z=x-y, je moet de vector toevoegen x met tegengesteld aan ja vector jij". tegenovergestelde vector jij" is eenvoudig gebouwd:

Vector jij" is tegengesteld aan de vector ja, als y+y"= 0, waarbij 0 een nulvector van de juiste grootte is. Vervolgens wordt de optelling van vectoren uitgevoerd x en jij":

Uit uitdrukking (1) blijkt dat om het verschil van vectoren te construeren, het voldoende is om de verschillen van de corresponderende coördinaten van de vectoren te berekenen x en ja.

Rijst. een

In afb. 1 in tweedimensionale ruimte vertegenwoordigt het verschil van vectoren x=(10,3) en ja=(2,4).

Berekenen z=x-y=(10-3,3-4)=(7,-1). Laten we het verkregen resultaat vergelijken met de geometrische interpretatie. Inderdaad, na het construeren van de vector jij" en parallelle beweging van het startpunt van de vector jij" naar het eindpunt van de vector x, we krijgen de vector jij"", en na het toevoegen van de vectoren x en jij"", we krijgen de vector z.

Optie 2. De uitgangspunten van de vectoren zijn willekeurig.

Rijst. 2

In afb. 2 in tweedimensionale ruimte is het verschil van vectoren x=AB en ja=CD, waar EEN(1,0), B(11,3), C(1,2), D(3.6). Om de vector te berekenen z=x-y, geconstrueerd tegengesteld aan de vector ja vector jij":

Vervolgens moet je de vectoren toevoegen x en jij". Vector jij" beweegt evenwijdig zodat het punt C" viel samen met het punt B. Hiervoor worden de verschillen in de coördinaten van de punten berekend B en Met.

ov, eerst moet je een concept begrijpen als het uitstellen van een vector vanaf een bepaald punt.

Definitie 1

Als het punt $A$ het begin is van een vector $\overrightarrow(a)$, dan wordt gezegd dat de vector $\overrightarrow(a)$ gescheiden is van het punt $A$ (Fig. 1).

Figuur 1. $\overrightarrow(a)$ uitgezet vanaf punt $A$

We introduceren de volgende stelling:

Stelling 1

Vanaf elk punt $K$ kan men een vector $\overrightarrow(a)$ tekenen en slechts één.

Bewijs.

Bestaan: Er zijn hier twee gevallen om te overwegen:

De vector $\overrightarrow(a)$ is nul.

In dit geval is het duidelijk dat de gewenste vector de vector $\overrightarrow(KK)$ is.

De vector $\overrightarrow(a)$ is niet nul.

Laat het punt $A$ het begin van de vector $\overrightarrow(a)$ aangeven, en het punt $B$ het einde van de vector $\overrightarrow(a)$. Laten we een lijn $b$ trekken door het punt $K$ evenwijdig aan de vector$\overrechterpijl(a)$. Laten we de segmenten $\left|KL\right|=|AB|$ en $\left|KM\right|=|AB|$ op deze rechte lijn plotten. Beschouw de vectoren $\overrightarrow(KL)$ en $\overrightarrow(KM)$. Van deze twee vectoren zal de gewenste de vector zijn die samen met de $\overrightarrow(a)$ vector wordt gestuurd (Fig. 2)

Figuur 2. Illustratie van Stelling 1

uniciteit: uniciteit volgt onmiddellijk uit de constructie die is uitgevoerd in de subsectie "bestaan".

De stelling is bewezen.

Aftrekken van vectoren. Regel één:

Laten we vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ krijgen.

definitie 2

Het verschil van twee vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ is een vector $\overrightarrow(c)$ die, wanneer toegevoegd aan de vector $\overrightarrow(b)$, de vector $\ geeft overrightarrow(a)$ , d.w.z

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Aanwijzing:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

We zullen de constructie van het verschil van twee vectoren bekijken met behulp van het probleem.

voorbeeld 1

Laat de vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ gegeven worden. Construeer de vector $\overrightarrow(a)-\overrightarrow(b)$.

Beslissing.

Laten we een willekeurig punt $O$ construeren en daaruit de vectoren $\overrightarrow(OA)=\overrightarrow(a)$ en $\overrightarrow(OB)=\overrightarrow(b)$ plotten. Als we het punt $B$ verbinden met het punt $A$, krijgen we de vector $\overrightarrow(BA)$ (Fig. 3).

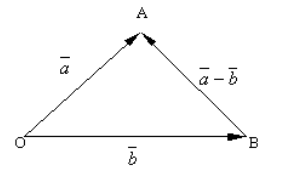
Figuur 3. Verschil van twee vectoren

Volgens de driehoeksregel voor het construeren van de som van twee vectoren, zien we dat

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Uit definitie 2 halen we dat:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Antwoord:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Uit dit probleem krijgen we de volgende regel voor het vinden van het verschil van twee vectoren. Om het verschil $\overrightarrow(a)-\overrightarrow(b)$ te vinden, heb je nodig van willekeurig punt$O$ zet de vectoren $\overrightarrow(OA)=\overrightarrow(a)$ en $\overrightarrow(OB)=\overrightarrow(b)$ opzij en verbindt het einde van de tweede vector met het einde van de eerste vector.

Aftrekken van vectoren. Regel twee:

Denk aan het volgende begrip dat we nodig hebben.

Definitie 3

De vector $\overrightarrow(a_1)$ wordt arbitrair genoemd voor de vector $\overrightarrow(a)$ als deze vectoren tegengesteld gericht zijn en dezelfde lengte hebben.

Aanwijzing: De vector $(-\overrightarrow(a))$ is het tegenovergestelde van de vector $\overrightarrow(a)$.

Om de tweede regel voor het verschil van twee vectoren in te voeren, moeten we eerst de volgende stelling introduceren en bewijzen.

Stelling 2

Voor elke twee vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ geldt de volgende gelijkheid:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Bewijs.

Volgens definitie 2 hebben we:

Voeg aan beide delen de vector $\left(-\overrightarrow(b)\right)$ toe, we krijgen

Aangezien de vectoren $\overrightarrow(b)$ en $\left(-\overrightarrow(b)\right)$ tegengesteld zijn, is $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ overrightarrow (0)$. We hebben

De stelling is bewezen.

Uit deze stelling krijgen we de volgende regel voor het verschil van twee vectoren: Om het verschil $\overrightarrow(a)-\overrightarrow(b)$ te vinden, moeten we de vector $\overrightarrow(OA)=\overrightarrow( uitstellen) a)$ vanaf een willekeurig punt $O$, leg dan vanaf het verkregen punt $A$ de vector $\overrightarrow(AB)=-\overrightarrow(b)$ opzij en verbind het begin van de eerste vector met het einde van de tweede vector.

Een voorbeeld van een probleem over het concept van het verschil van vectoren

Voorbeeld 2

Laat $ADCD$ een parallellogram zijn waarvan de diagonalen elkaar snijden op $O$. $\overrightarrow(AB)=\overrightarrow(a)$, $\overrightarrow(AD)=\overrightarrow(b)$ (Fig. 4). Druk de volgende vectoren uit in termen van $\overrightarrow(a)$ en $\overrightarrow(b)$:

a) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

Afbeelding 4. Parallellogram

Beslissing.

a) We voegen toe volgens de driehoeksregel, we krijgen

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Uit de eerste regel voor het verschil van twee vectoren, verkrijgen we

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) Aangezien $\overrightarrow(OC)=\overrightarrow(AO)$, krijgen we

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Volgens Stelling 2 hebben we:

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Met behulp van de driehoeksregel hebben we eindelijk

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

ov, eerst moet je een concept begrijpen als het uitstellen van een vector vanaf een bepaald punt.

Definitie 1

Als het punt $A$ het begin is van een vector $\overrightarrow(a)$, dan wordt gezegd dat de vector $\overrightarrow(a)$ gescheiden is van het punt $A$ (Fig. 1).

Figuur 1. $\overrightarrow(a)$ uitgezet vanaf punt $A$

We introduceren de volgende stelling:

Stelling 1

Vanaf elk punt $K$ kan men een vector $\overrightarrow(a)$ tekenen en slechts één.

Bewijs.

Bestaan: Er zijn hier twee gevallen om te overwegen:

De vector $\overrightarrow(a)$ is nul.

In dit geval is het duidelijk dat de gewenste vector de vector $\overrightarrow(KK)$ is.

De vector $\overrightarrow(a)$ is niet nul.

Laat het punt $A$ het begin van de vector $\overrightarrow(a)$ aangeven, en het punt $B$ het einde van de vector $\overrightarrow(a)$. Laten we een lijn $b$ trekken evenwijdig aan de vector $\overrightarrow(a)$ door het punt $K$. Laten we de segmenten $\left|KL\right|=|AB|$ en $\left|KM\right|=|AB|$ op deze rechte lijn plotten. Beschouw de vectoren $\overrightarrow(KL)$ en $\overrightarrow(KM)$. Van deze twee vectoren zal de gewenste de vector zijn die samen met de $\overrightarrow(a)$ vector wordt gestuurd (Fig. 2)

Figuur 2. Illustratie van Stelling 1

uniciteit: uniciteit volgt onmiddellijk uit de constructie die is uitgevoerd in de subsectie "bestaan".

De stelling is bewezen.

Aftrekken van vectoren. Regel één:

Laten we vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ krijgen.

definitie 2

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Aanwijzing:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

We zullen de constructie van het verschil van twee vectoren bekijken met behulp van het probleem.

voorbeeld 1

Laat de vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ gegeven worden. Construeer de vector $\overrightarrow(a)-\overrightarrow(b)$.

Beslissing.

Figuur 3. Verschil van twee vectoren

Volgens de driehoeksregel voor het construeren van de som van twee vectoren, zien we dat

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Uit definitie 2 halen we dat:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Antwoord:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Uit dit probleem krijgen we de volgende regel voor het vinden van het verschil van twee vectoren. Om het verschil $\overrightarrow(a)-\overrightarrow(b)$ te vinden, moet je vanaf een willekeurig punt $O$ de vectoren $\overrightarrow(OA)=\overrightarrow(a)$ en $\overrightarrow( opzij zetten OB)=\overrightarrow(b )$ en verbind het einde van de tweede vector met het einde van de eerste vector.

Aftrekken van vectoren. Regel twee:

Denk aan het volgende begrip dat we nodig hebben.

Definitie 3

De vector $\overrightarrow(a_1)$ wordt arbitrair genoemd voor de vector $\overrightarrow(a)$ als deze vectoren tegengesteld gericht zijn en dezelfde lengte hebben.

Aanwijzing: De vector $(-\overrightarrow(a))$ is het tegenovergestelde van de vector $\overrightarrow(a)$.

Om de tweede regel voor het verschil van twee vectoren in te voeren, moeten we eerst de volgende stelling introduceren en bewijzen.

Stelling 2

Voor elke twee vectoren $\overrightarrow(a)$ en $\overrightarrow(b)$ geldt de volgende gelijkheid:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Bewijs.

Volgens definitie 2 hebben we:

Voeg aan beide delen de vector $\left(-\overrightarrow(b)\right)$ toe, we krijgen

Aangezien de vectoren $\overrightarrow(b)$ en $\left(-\overrightarrow(b)\right)$ tegengesteld zijn, is $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ overrightarrow (0)$. We hebben

De stelling is bewezen.

Een voorbeeld van een probleem over het concept van het verschil van vectoren

Voorbeeld 2

a) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

Afbeelding 4. Parallellogram

Beslissing.

a) We voegen toe volgens de driehoeksregel, we krijgen

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Uit de eerste regel voor het verschil van twee vectoren, verkrijgen we

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) Aangezien $\overrightarrow(OC)=\overrightarrow(AO)$, krijgen we

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Volgens Stelling 2 hebben we:

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Met behulp van de driehoeksregel hebben we eindelijk

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

Hoe vectoren worden opgeteld is niet altijd duidelijk voor leerlingen. Kinderen hebben geen idee wat er achter hen zit. Je hoeft alleen de regels te onthouden en niet na te denken over de essentie. Juist over de principes van optellen en aftrekken van vectorgrootheden is daarom veel kennis nodig.

Het toevoegen van twee of meer vectoren resulteert altijd in een andere. Bovendien zal het altijd hetzelfde zijn, ongeacht de ontvangst van de locatie.

Meestal in schoolcursus geometrie beschouwt de toevoeging van twee vectoren. Het kan worden uitgevoerd volgens de regel van een driehoek of een parallellogram. Deze tekeningen zien er anders uit, maar het resultaat van de actie is hetzelfde.

Hoe wordt optellen gedaan volgens de regel van een driehoek?

Het wordt gebruikt wanneer de vectoren niet-collineair zijn. Dat wil zeggen, ze liggen niet op dezelfde lijn of evenwijdig.

In dit geval moet de eerste vector vanaf een willekeurig punt worden uitgesteld. Vanaf het einde is het nodig om evenwijdig en gelijk aan de tweede te tekenen. Het resultaat is een vector die begint bij het begin van de eerste en eindigt aan het einde van de tweede. De tekening lijkt op een driehoek. Vandaar de naam van de regel.

Als de vectoren collineair zijn, kan deze regel ook worden toegepast. Alleen de tekening wordt langs één lijn geplaatst.

Hoe wordt parallellogramoptelling uitgevoerd?

Nogmaals? is alleen van toepassing op collineaire vectoren. De constructie wordt uitgevoerd volgens een ander principe. Hoewel het begin hetzelfde is. We moeten de eerste vector uitstellen. En vanaf het begin - de tweede. Op basis daarvan, voltooi het parallellogram en teken een diagonaal vanaf het begin van beide vectoren. Zij zal het resultaat zijn. Zo worden vectoren opgeteld volgens de parallellogramregel.

Tot nu toe zijn dat er twee geweest. Maar wat als het er 3 of 10 zijn? Gebruik de volgende truc.

Hoe en wanneer wordt de polygoonregel toegepast?

Als u vectoren moet optellen, waarvan het aantal meer dan twee is, moet u niet bang zijn. Het is voldoende om ze achtereenvolgens allemaal opzij te leggen en het begin van de ketting met het einde te verbinden. Deze vector is de gewenste som.

Welke eigenschappen zijn geldig voor operaties op vectoren?

Over de nulvector. Die beweert dat wanneer toegevoegd, de originele wordt verkregen.

Over de tegenovergestelde vector. Dat wil zeggen, ongeveer een die de tegenovergestelde richting en gelijke waarde in absolute waarde heeft. Hun som zal nul zijn.

Over de commutativiteit van optellen. Wat is er sindsdien bekend? lagere school. Het veranderen van de plaatsen van de termen verandert het resultaat niet. Met andere woorden, het maakt niet uit welke vector eerst moet worden uitgesteld. Het antwoord zal nog steeds correct en uniek zijn.

Over de associatie van optellen. Met deze wet kun je vectoren van een triple in paren optellen en er een derde bij optellen. Als we dit met symbolen schrijven, krijgen we het volgende:

eerste + (tweede + derde) = tweede + (eerste + derde) = derde + (eerste + tweede).

Wat is er bekend over het verschil van vectoren?

Er is geen aparte aftrekbewerking. Dit komt doordat het in feite een toevoeging is. Alleen de tweede van hen krijgt de tegenovergestelde richting. En dan wordt alles gedaan alsof de toevoeging van vectoren is overwogen. Daarom praten ze praktisch niet over hun verschil.

Om het werk met hun aftrekking te vereenvoudigen, is de driehoeksregel aangepast. Nu (bij aftrekken) moet de tweede vector worden uitgesteld vanaf het begin van de eerste. Het antwoord zal degene zijn die het eindpunt van de minuend ermee verbindt. Hoewel het mogelijk is om uit te stellen zoals eerder beschreven, gewoon door de richting van de tweede te veranderen.

Hoe de som en het verschil van vectoren in coördinaten te vinden?

In het probleem worden de coördinaten van de vectoren gegeven en is het nodig om hun waarden voor de laatste te achterhalen. In dit geval hoeven de constructies niet te worden uitgevoerd. Dat wil zeggen, u kunt eenvoudige formules gebruiken die de regel voor het optellen van vectoren beschrijven. Ze zien er zo uit:

a(x, y, z) + b(k, l, m) = c(x+k, y+l, z+m);

a (x, y, z) -in (k, l, m) \u003d c (x-k, y-l, z-m).

Het is gemakkelijk te zien dat de coördinaten alleen moeten worden opgeteld of afgetrokken, afhankelijk van de specifieke taak.

Eerste voorbeeld met oplossing

Voorwaarde. Gegeven een rechthoek ABCD. De zijden zijn 6 en 8 cm. Het snijpunt van de diagonalen is gemarkeerd met de letter O. Het is nodig om het verschil tussen de vectoren AO en VO te berekenen.

Beslissing. Eerst moet je deze vectoren tekenen. Ze zijn gericht van de hoekpunten van de rechthoek naar het snijpunt van de diagonalen.

Als je goed naar de tekening kijkt, kun je zien dat de vectoren al zijn uitgelijnd, zodat de tweede in contact is met het einde van de eerste. Het is gewoon dat zijn richting verkeerd is. Het moet vanaf dit punt beginnen. Dit is als de vectoren worden opgeteld, en in het probleem - aftrekken. Stop. Deze actie betekent dat je de tegenovergestelde vector moet toevoegen. Dus VO moet worden vervangen door OB. En het blijkt dat twee vectoren al een paar zijden hebben gevormd uit de driehoeksregel. Daarom is het resultaat van hun toevoeging, dat wil zeggen het gewenste verschil, de vector AB.

En het valt samen met de zijkant van de rechthoek. Om een numeriek antwoord vast te leggen, heeft u het volgende nodig. Teken een rechthoek in de lengte zodat de langste zijde horizontaal is. De nummering van de hoekpunten begint linksonder en gaat tegen de klok in. Dan is de lengte van de vector AB gelijk aan 8 cm.

Antwoord. Het verschil tussen AO en VO is 8 cm.

Het tweede voorbeeld en zijn gedetailleerde oplossing

Voorwaarde. De ruit ABCD heeft diagonalen van 12 en 16 cm Het snijpunt is gemarkeerd met de letter O. Bereken de lengte van de vector gevormd door het verschil tussen de vectoren AO en BO.

Beslissing. Laat de aanduiding van de hoekpunten van de ruit hetzelfde zijn als in het vorige probleem. Net als bij de oplossing van het eerste voorbeeld blijkt het gewenste verschil gelijk te zijn aan de vector AB. En de lengte is onbekend. De oplossing van het probleem werd teruggebracht tot het berekenen van een van de zijden van de ruit.

Hiervoor moet je rekening houden met de driehoek ABO. Het is rechthoekig omdat de diagonalen van de ruit elkaar onder een hoek van 90 graden snijden. En zijn poten zijn gelijk aan de helft van de diagonalen. Dat wil zeggen, 6 en 8 cm De gezochte zijde in het probleem valt samen met de hypotenusa in deze driehoek.

Om het te vinden, heb je de stelling van Pythagoras nodig. Het kwadraat van de hypotenusa wordt is gelijk aan de som nummers 6 2 en 8 2 . Na het kwadrateren worden de waarden verkregen: 36 en 64. Hun som is 100. Hieruit volgt dat de hypotenusa 10 cm is.

Antwoord. Het verschil tussen de vectoren AO en VO is 10 cm.

Derde voorbeeld met gedetailleerde oplossing

Voorwaarde. Bereken het verschil en de som van twee vectoren. Hun coördinaten zijn bekend: de eerste heeft 1 en 2, de tweede heeft 4 en 8.

Beslissing. Om de som te vinden, moet u de eerste en tweede coördinaten in paren optellen. Het resultaat zijn de getallen 5 en 10. Het antwoord is een vector met coördinaten (5; 10).

Voor het verschil moet je de coördinaten aftrekken. Na het uitvoeren van deze actie worden de nummers -3 en -6 verkregen. Dit zijn de coördinaten van de gewenste vector.

Antwoord. De som van de vectoren is (5; 10), hun verschil is (-3; -6).

vierde voorbeeld

Voorwaarde. De lengte van de vector AB is 6 cm, BC - 8 cm De tweede wordt opzij gezet van het einde van de eerste in een hoek van 90 graden. Bereken: a) het verschil tussen de modules van de vectoren BA en BC en de module van het verschil tussen BA en BC; b) de som van dezelfde modules en de modulus van de som.

Oplossing: a) De lengtes van de vectoren staan al in de opgave. Daarom is het niet moeilijk om hun verschil te berekenen. 6 - 8 = -2. De situatie met de verschilmodulus is iets gecompliceerder. Eerst moet je uitzoeken welke vector het resultaat is van de aftrekking. Voor dit doel moet de vector BA opzij worden gezet, die is gericht op andere kant AB. Teken vervolgens de vector BC vanaf het uiteinde en richt deze in de richting tegengesteld aan de oorspronkelijke. Het resultaat van de aftrekking is de CA-vector. De modulus kan worden berekend met behulp van de stelling van Pythagoras. Eenvoudige berekeningen leiden tot een waarde van 10 cm.

b) De som van de modules van de vectoren is 14 cm Om het tweede antwoord te vinden is enige transformatie nodig. De vector BA is tegengesteld aan de gegeven - AB. Beide vectoren zijn gericht vanuit hetzelfde punt. In deze situatie kunt u de parallellogramregel gebruiken. Het resultaat van de optelling is een diagonaal, en niet alleen een parallellogram, maar een rechthoek. De diagonalen zijn gelijk, wat betekent dat de modulus van de som hetzelfde is als in de vorige paragraaf.

Antwoord: a) -2 en 10 cm; b) 14 en 10 cm.