Формула дисперсії довільної величини. Дисперсія та стандартне відхилення у MS EXCEL

Однак цієї характеристики ще мало для дослідження випадкової величини. Уявимо двох стрільців, які стріляють по мішені. Один стріляє влучно і потрапляє близько до центру, а інший просто розважається і навіть не цілиться. Але що кумедно, його середнійрезультат буде таким самим, як і в першого стрілка! Цю ситуацію умовно ілюструють такі випадкові величини:

«Снайперське» математичне очікуванняоднаково, однак і у « цікавої особистості»: - Воно теж нульове!

Таким чином, виникає потреба кількісно оцінити, наскільки далеко розпорошенікулі (значення випадкової величини) щодо центру мішені (математичного очікування). Ну а розсіюванняз латині перекладається не інакше, як дисперсія .

Подивимося, як визначається ця числова характеристика одному з прикладів 1-ї частини уроку:

Там ми знайшли невтішне математичне очікування цієї гри, і зараз ми маємо обчислити її дисперсію, яка позначаєтьсячерез.

З'ясуємо, наскільки далеко розкидані виграші/програші щодо середнього значення. Очевидно, що для цього потрібно вирахувати різниціміж значеннями випадкової величиниі її математичним очікуванням:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Тепер начебто потрібно підсумувати результати, але цей шлях не годиться – тому, що коливання вліво взаємознижуватимуться з коливаннями вправо. Так, наприклад, у стрільця-«любителя» (Приклад вище)різниці складуть , і при додаванні дадуть нуль, тому ніякої оцінки розсіювання його стрілянини ми не отримаємо.

Щоб обійти цю неприємність, можна розглянути модулірізниць, але з технічних причин прижився підхід, коли їх зводять у квадрат. Рішення зручніше оформити таблицею:

І тут напрошується вирахувати середньозваженезначення квадратів відхилень. А це що таке? Це їх математичне очікування, яке і є мірилом розсіювання:

– визначеннядисперсії. З визначення одразу зрозуміло, що дисперсія не може бути негативною- Візьміть на замітку для практики!

Згадуємо, як знаходити матожидання. Розмножуємо квадрати різниць на відповідні ймовірності (продовження таблиці):
– образно кажучи, це «сила тяги»,
та підсумовуємо результати:

Чи не здається вам, що на тлі виграшів результат вийшов завеликим? Все вірно - ми зводили в квадрат, і щоб повернутися до розмірності нашої гри, потрібно витягти квадратний корінь. Ця величинаназивається середнім квадратичним відхиленням і позначається грецькою літерою "сигма":

Іноді це значення називають стандартним відхиленням .

У чому його зміст? Якщо ми відхилимося від математичного очікування вліво та вправо на середнє квадратичне відхилення:

– то цьому інтервалі будуть «сконцентровані» найімовірніші значення випадкової величини. Що ми, власне, і спостерігаємо:

Проте так склалося, що з аналізі розсіювання майже завжди оперують поняттям дисперсії. Давайте розберемося, що вона означає стосовно ігор. Якщо у випадку зі стрілками йдеться про «купність» попадань щодо центру мішені, то дисперсія характеризує дві речі:

По-перше, очевидно, що зі збільшенням ставок, дисперсія теж зростає. Так, наприклад, якщо ми збільшимо у 10 разів, то математичне очікування збільшиться у 10 разів, а дисперсія – у 100 разів (якщо це квадратична величина). Але, зауважте, що самі правила гри не змінилися! Змінилися лише ставки, грубо кажучи, раніше ми ставили 10 карбованців, тепер 100.

Другий, більше цікавий моментполягає в тому, що дисперсія характеризує стиль гри. Подумки зафіксуємо ігрові ставки на якомусь певному рівні, і подивимося, що тут до чого:

Гра з низькою дисперсією – це обережна гра. Гравець схильний вибирати найнадійніші схеми, де за 1 раз він не програє/виграє занадто багато. Наприклад, система «червоне/чорне» в рулетці (див. Приклад 4 статті Випадкові величини) .

Гра із високою дисперсією. Її часто називають дисперсійноїгрою. Це авантюрний чи агресивний стиль гри, де гравець обирає "адреналінові" схеми. Згадаймо хоча б «Мартінгейл», в якому на кону виявляються суми, що на порядки перевершують «тиху» гру попереднього пункту.

Показовою є ситуація в покері: тут є так звані тайтовігравці, які схильні обережно і «труситися» над своїми ігровими засобами (Банкролом). Не дивно, що їхній банкрол не піддається значним коливанням (низька дисперсія). Навпаки, якщо у гравця висока дисперсія, це агресор. Він часто ризикує, робить великі ставки і може, як зірвати величезний банк, так і програтися вщент.

Те саме відбувається на Форексі, і так далі – прикладів маса.

Причому, у всіх випадках не важливо – чи на копійки йде гра, чи на тисячі доларів. На будь-якому рівні є свої низько- та високодисперсійні гравці. Ну, а за середній виграш, як ми пам'ятаємо, «відповідає» математичне очікування.

Напевно, ви помітили, що знаходження дисперсії – процес тривалий і копіткий. Але математика щедра:

Формула для знаходження дисперсії

Ця формулавиводиться безпосередньо з визначення дисперсії, і ми негайно пускаємо її в обіг. Скопіюю зверху табличку з нашою грою:

і знайдене маточування.

Обчислимо дисперсію другим способом. Спочатку знайдемо математичне очікування – квадрата випадкової величини. за визначення математичного очікування:

У даному випадку:

Таким чином, за формулою:

Як кажуть, відчуйте різницю. І на практиці, звичайно, краще застосовувати формулу (якщо іншого не потребує умова).

Освоюємо техніку рішення та оформлення:

Приклад 6

Знайти її математичне очікування, дисперсію та середнє квадратичне відхилення.

Це завдання зустрічається повсюдно, і, зазвичай, йде без змістовного сенсу.
Можете уявляти кілька лампочок з числами, які загоряються в дурдомі з певними ймовірностями:)

Рішення: Основні обчислення зручно звести до таблиці Спочатку у верхні два рядки записуємо вихідні дані. Потім розраховуємо твори, потім і, нарешті, суми у правому стовпці:

Власне, майже все готове. У третьому рядку намалювалося готове математичне очікування: .

Дисперсію обчислимо за такою формулою:

І, нарешті, середнє квадратичне відхилення:
- особисто я зазвичай округляю до 2 знаків після коми.

Усі обчислення можна провести на калькуляторі, а ще краще – в Екселі:

ось тут вже важко помилитися:)

Відповідь:

Бажаючі можуть ще більше спростити своє життя та скористатися моїм калькулятором (Демо), який не тільки вмить вирішить дане завдання, але й збудує тематичні графіки (скоро дійдемо). Програму можна скачати в бібліотеці- якщо ви завантажили хоча б один навчальний матеріал, або отримати іншим способом. Дякуємо за підтримку проекту!

Пара завдань для самостійного рішення:

Приклад 7

Обчислити дисперсію випадкової величини попереднього прикладу визначення.

І аналогічний приклад:

Приклад 8

Дискретна випадкова величина задана своїм законом розподілу:

Так, значення випадкової величини бувають досить великими (Приклад з реальної роботи) , і тут, по можливості, використовуйте Ексель. Як, до речі, і в Прімері 7 – це швидше, надійніше та приємніше.

Рішення та відповіді внизу сторінки.

На закінчення 2-ї частини уроку розберемо ще одну типове завдання, можна навіть сказати, невеликий ребус:

Приклад 9

Дискретна випадкова величина може набувати лише два значення: і , причому . Відома ймовірність, математичне очікування та дисперсія.

Рішення: почнемо з невідомої ймовірності Так як випадкова величина може прийняти лише два значення, то сума ймовірностей відповідних подій:

і оскільки, то.

Залишилося знайти …, легко сказати:) Але так гаразд, понеслося. За визначенням математичного очікування:
- Підставляємо відомі величини:

- І більше з цього рівняння нічого не вичавити, хіба що можна переписати його у звичному напрямку:

або:

Про подальших діяхДумаю, ви здогадуєтеся. Складемо і вирішимо систему:

Десяткові дроби- це, звичайно, повне неподобство; множимо обидва рівняння на 10:

і ділимо на 2:

Ось так то краще. З 1-го рівняння виражаємо:
(Це більш простий шлях)- Підставляємо в 2-е рівняння:

Зводимо у квадратта проводимо спрощення:

Помножуємо на:

В результаті отримано квадратне рівняння, знаходимо його дискримінант:
- Чудово!

і у нас виходить два рішення:

1) якщо , то ;

2) якщо , то.

Умові задовольняє перша пара значень. З високою ймовірністю все правильно, проте запишемо закон розподілу:

і виконаємо перевірку, а саме, знайдемо матожидання:

У багатьох випадках виникає потреба ввести ще одну числову характеристикудля вимірювання ступеня розсіювання, розкидання значень, що приймаються випадковою величиною ξ навколо її математичного очікування.

Визначення.Дисперсією випадкової величини ξ називається число.

D ξ= M(ξ-M ξ) 2 . (1)

Іншими словами, дисперсія є математичним очікуванням квадрата відхилення значень випадкової величини від її середнього значення.

називається середнім квадратичнимвідхиленням

величини ξ .

Якщо дисперсія характеризує середній розмірквадрата відхилення ξ від Mξ, то можна розглядати як деяку середню характеристикусамого відхилення, точніше, величини | ξ-Mξ |.

З визначення (1) випливають такі дві властивості дисперсії.

1. Дисперсія постійної величинидорівнює нулю. Це цілком відповідає наочному сенсі дисперсії як «заходи розкиду».

Справді, якщо

ξ = С,то Mξ = Cі, значить Dξ = M(C-C) 2 = M 0 = 0.

2. При множенні випадкової величини ξ на постійне числоЗ її дисперсія множиться на C2

D(Cξ) = C 2 Dξ . (3)

Дійсно

D(Cξ) = M(C

= M(C .

3. Має місце наступна формула для обчислення дисперсії:

. (4)

Доказ цієї формули випливає із властивостей математичного очікування.

Ми маємо:

4. Якщо величини ξ 1 та ξ 2 незалежні, то дисперсія їх суми дорівнює сумі їх дисперсій:

Доведення . Для підтвердження використовуємо властивості математичного очікування. Нехай Mξ 1 = m 1 , Mξ 2 = m 2 тоді.

Формулу (5) доведено.

Оскільки дисперсія випадкової величини є за визначенням математичне очікування величини ( ξ -m) 2 , де m = Mξ ,то обчислення дисперсії можна скористатися формулами, отриманими в §7 гл.II.

Так, якщо ξ є ДСВ із законом розподілу

x 1	x 2	...
p 1	p 2	...

то матимемо:

. (7)

Якщо ξ безперервна випадкова величина із щільністю розподілу p(x), Тоді отримаємо:

Dξ= . (8)

Якщо використовувати формулу (4) для обчислення дисперсії, можна отримати інші формули, а саме:

, (9)

якщо величина ξ дискретна, та

Dξ= , (10)

якщо ξ розподілена із щільністю p(x).

приклад 1 . Нехай величина ξ рівномірно розподілена на відрізку [ a,b]. Скориставшись формулою (10) отримаємо:

Можна показати, що дисперсія випадкової величини, розподіленої за нормальним законом із щільністю

p(x)= , (11)

дорівнює σ 2 .

Тим самим з'ясовується значення параметра σ, що входить у вираз щільності (11) для нормального закону; σ є середнє квадратичне відхиленнявеличини ξ.

Приклад 2 . Знайти дисперсію випадкової величини ξ , розподіленою за біноміальним законом.

Рішення . Скориставшись поданням ξ у вигляді

ξ = ξ 1 + ξ 2 + ξ n(див. приклад 2 §7 гл. II) і застосовуючи формулу складання дисперсій для незалежних величин, отримаємо

Dξ = Dξ 1 + Dξ 2 + Dξ n .

Дисперсія будь-якої з величин ξ i (i= 1,2, n) підраховується безпосередньо:

Dξ i = M(ξ i) 2 - (Mξ i) 2 = 0 2 · q+ 1 2 p- p 2 = p(1-p) = pq.

Остаточно отримуємо

Dξ= npq, де q = 1 - p.

Для згрупованих даних залишкова дисперсія - середня з внутрішньогрупових дисперсій:

Де σ 2 j - внутрішньогрупова дисперсія j-ї групи.

Для не згрупованих даних залишкова дисперсія– міра точності апроксимації, тобто. наближення лінії регресії до вихідних даних:
де y(t) – прогноз рівняння тренда; yt – вихідний ряд динаміки; n - кількість точок; p – число коефіцієнтів рівняння регресії (кількість змінних, що пояснюють).
У цьому прикладі вона називається незміщена оцінка дисперсії.

Приклад №1. Розподіл робітників трьох підприємств одного об'єднання за тарифними розрядами характеризується такими даними:

Тарифний розряд робітника	Чисельність робітників на підприємстві
Тарифний розряд робітника	підприємство 1	підприємство 2	підприємство 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Визначити:
1. дисперсію по кожному підприємству (внутрішньогрупові дисперсії);
2. середню із внутрішньогрупових дисперсій;
3. міжгрупову дисперсію;
4. загальну дисперсію.

Рішення.
Перш ніж приступити до вирішення завдання необхідно з'ясувати, яка ознака є результативною, а якою є факторною. У прикладі результативною ознакою є «Тарифний розряд», а факторною ознакою – «Номер (назва) підприємства».
Тоді маємо три групи (підприємства), для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії:

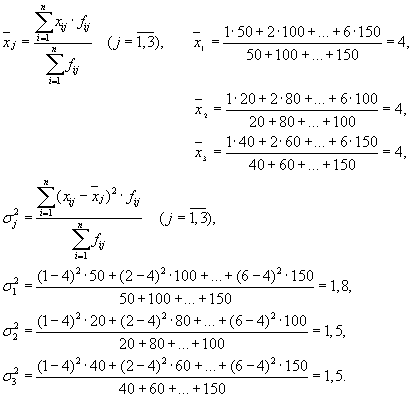
Підприємство	Групова середня,	Внутрішньогрупова дисперсія,
1	4	1,8

Середня з внутрішньогрупових дисперсій ( залишкова дисперсія) розрахуємо за формулою:

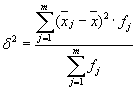
де можна розрахувати:

або:

тоді:
Загальна дисперсія дорівнюватиме: s 2 = 1,6 + 0 = 1,6.
Загальну дисперсію також можна розрахувати і за однією з наступних двох формул:

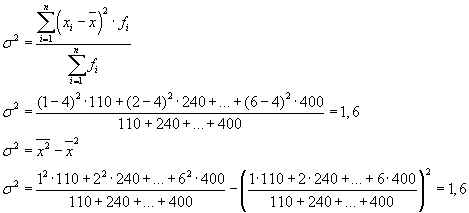
При вирішенні практичних завдань часто доводиться мати справу з ознакою, яка приймає лише два альтернативні значення. У цьому випадку говорять не про вагу того чи іншого значення ознаки, а про його частку в сукупності. Якщо частку одиниць сукупності, які мають досліджувану ознаку, позначити через « р», а не володіють – через « q», то дисперсію можна розрахувати за такою формулою:
s 2 = p×q

Приклад №2. За даними про вироблення шести робочих бригади визначити міжгрупову дисперсію та оцінити вплив робочої зміни на їх продуктивність праці, якщо загальна дисперсія дорівнює 12,2.

№ робітника бригади	Вироблення робітника, шт.
№ робітника бригади	в I зміну	у II зміну
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Рішення. Початкові дані

X	f 1	f 2	f 3	f 4	f 5	f 6	Разом
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Разом	31	33	37	37	40	38

Тоді маємо 6 групи, для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії.
1. Знаходимо середні значення кожної групи.

2. Знаходимо середнє квадратичне кожної групи.

Результати розрахунку зведемо до таблиці:

Номер групи	Групова середня	Внутрішньогрупова дисперсія
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Внутрішньогрупова дисперсіяхарактеризує зміну (варіацію) досліджуваної (результативної) ознаки в межах групи під впливом на нього всіх факторів, крім фактора, покладеного в основу угруповання:
Середню із внутрішньогрупових дисперсій розрахуємо за формулою:

4. Міжгрупова дисперсіяхарактеризує зміну (варіацію) досліджуваного (результативного) ознаки під впливом нього чинника (факторного ознаки), покладеного в основу угруповання.
Міжгрупову дисперсію визначимо як:

де

Тоді

Загальна дисперсіяхарактеризує зміна (варіацію) досліджуваного (результативного) ознаки під впливом нею всіх без винятку чинників (факторних ознак). За умовою завдання вона дорівнює 12.2.
Емпіричне кореляційне ставленнявимірює, яку частину загальної коливання результативної ознаки викликає фактор, що вивчається. Це відношення факторної дисперсії до загальної дисперсії:

Визначаємо емпіричне кореляційне відношення:

Зв'язки між ознаками можуть бути слабкими та сильними (тісними). Їхні критерії оцінюються за шкалою Чеддока:
0.1 0.3 0.5 0.7 0.9 У нашому прикладі зв'язок між ознакою Y фактором X слабкий
Коефіцієнт детермінації.

Визначимо коефіцієнт детермінації:

Таким чином, на 0.67% варіація обумовлена відмінностями між ознаками, а на 99.37% іншими факторами.
Висновок: у разі вироблення робочих залежить від роботи у конкретну зміну, тобто. вплив робочої зміни з їхньої продуктивність праці не значний і зумовлено іншими чинниками.

Приклад №3. На основі даних про середню заробітної платиі квадратах відхилень від її величини по двох групах робітників знайти загальну дисперсію, застосувавши правило додавання дисперсій:

Рішення:
Середня із внутрішньогрупових дисперсій

Міжгрупову дисперсію визначимо як:

Загальна дисперсія дорівнюватиме: 480 + 13824 = 14304

Основними узагальнюючими показниками варіації у статистиці є дисперсії та середнє квадратичне відхилення.

Дисперсія це середня арифметична квадратів відхилень кожного значення ознаки від загальної середньої. Дисперсія називається середнім квадратом відхилень і позначається  2 . Залежно від вихідних даних дисперсія може обчислюватися за середньою арифметичною простою або зваженою:

 дисперсія незважена (проста);

 дисперсія зважена.

Середнє квадратичне відхилення це узагальнююча характеристика абсолютних розмірів варіації ознаки у сукупності. Виражається воно у тих самих одиницях виміру, як і ознака (в метрах, тоннах, відсотках, гектарах тощо. буд.).

Середнє квадратичне відхилення являє собою квадратний корінь з дисперсії і позначається :

 середнє квадратичне відхилення незважене;

 середнє квадратичне відхилення зважене.

Середнє квадратичне відхилення є мірилом середньої надійності. Чим менше середнє квадратичне відхилення, тим краще середня арифметична відбиває всю сукупність, що представляється.

Обчислення середнього квадратичного відхилення передує розрахунок дисперсії.

Порядок розрахунку дисперсії зваженої наступний:

1) визначають середню арифметичну зважену:

2) розраховують відхилення варіантів від середньої:

3) зводять у квадрат відхилення кожного варіанта від середньої:

4) множать квадрати відхилень на ваги (частоти):

5) підсумовують отримані твори:

6) отриману суму ділять на суму ваг:

Приклад 2.1

Обчислимо середню арифметичну зважену:

Значення відхилень від середньої та його квадратів представлені у таблиці. Визначимо дисперсію:

Середнє квадратичне відхилення дорівнюватиме:

Якщо вихідні дані представлені у вигляді інтервального ряду розподілу , спочатку потрібно визначити дискретне значення ознаки, а потім застосувати викладений метод.

Приклад 2.2

Покажемо розрахунок дисперсії для інтервального ряду даних про розподіл посівної площі колгоспу за врожайністю пшениці.

Середня арифметична дорівнює:

Обчислимо дисперсію:

6.3. Розрахунок дисперсії за формулою за індивідуальними даними

Техніка обчислення дисперсії складна, а при великих значенняхваріантів та частот може бути громіздкою. Розрахунки можна спростити, використовуючи властивості дисперсії.

Дисперсія має такі властивості.

1. Зменшення або збільшення ваг (частот) варіюючої ознаки в кілька разів дисперсію не змінює.

2. Зменшення або збільшення кожного значення ознаки на ту саму постійну величину Адисперсію не змінює.

3. Зменшення або збільшення кожного значення ознаки в якесь число разів kвідповідно зменшує або збільшує дисперсію в k 2 рази середнє квадратичне відхилення  в kразів.

4. Дисперсія ознаки щодо довільної величини завжди більше дисперсії щодо середньої арифметичної на квадрат різниці між середньою та довільною величинами:

Якщо А 0, то приходимо до наступної рівності:

тобто дисперсія ознаки дорівнює різниці між середнім квадратом значень ознаки та квадратом середньої.

Кожна властивість при розрахунку дисперсії може бути застосована самостійно або у поєднанні з іншими.

Порядок розрахунку дисперсії простий:

1) визначають середню арифметичну :

2) зводять у квадрат середню арифметичну:

3) зводять у квадрат відхилення кожного варіанта ряду:

х i 2 .

4) знаходять суму квадратів варіантів:

5) ділять суму квадратів варіантів з їхньої число, т. е. визначають середній квадрат:

6) визначають різницю між середнім квадратом ознаки та квадратом середньої:

Приклад 3.1Є такі дані про продуктивність праці робочих:

Зробимо такі розрахунки:

Дисперсія випадкової величини є мірою розкиду значень цієї величини. Мала дисперсія означає, що значення згруповані близько одне до одного. Велика дисперсія свідчить про сильний розкид значень. Поняття дисперсії випадкової величини застосовується у статистиці. Наприклад, якщо порівняти дисперсію значень двох величин (таких як результати спостережень за пацієнтами чоловічої та жіночої статі), можна перевірити значущість певної змінної. Також дисперсія використовується при побудові статистичних моделей, тому що мала дисперсія може бути ознакою того, що ви надмірно підганяєте значення.

Кроки

Обчислення дисперсії вибірки

Запишіть значення вибірки.Найчастіше статистикам доступні лише вибірки певних генеральних сукупностей. Наприклад, як правило, статистики не аналізують витрати на утримання сукупності всіх автомобілів у Росії – вони аналізують випадкову вибіркуіз кількох тисяч автомобілів. Така вибірка допоможе визначити середні витрати на автомобіль, але швидше за все отримане значення буде далеко від реального.
- Наприклад, проаналізуємо кількість булочок, проданих у кафе за 6 днів, взятих у випадковому порядку. Вибірка має наступний вигляд: 17, 15, 23, 7, 9, 13. Це вибірка, а не сукупність, тому що у нас немає даних про продані булочки за кожен день роботи кафе.
- Якщо вам дано сукупність, а не вибірка значень, перейдіть до наступного розділу.
Запишіть формулу обчислення дисперсії вибірки.Дисперсія є мірою розкиду значень певної величини. Чим ближче значення дисперсії до нуля, тим ближчі значення згруповані один до одного. Працюючи з вибіркою значень, використовуйте таку формулу для обчислення дисперсії:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))– це дисперсія. Дисперсія вимірюється в квадратних одиницяхвимірювання.
- x i (\displaystyle x_(i))– кожне значення у вибірці.
- x i (\displaystyle x_(i))треба відняти x̅, звести у квадрат, та був скласти отримані результати.
- x̅ – вибіркове середнє (середнє значення вибірки).
- n – кількість значень вибірці.
Обчисліть середнє значення вибірки.Воно позначається як x. Середнє значення вибірки обчислюється як звичайне середнє арифметичне: складіть усі значення у вибірці, а потім отриманий результат поділіть на кількість значень у вибірці.
- У нашому прикладі складіть значення у вибірці: 15 + 17 + 23 + 7 + 9 + 13 = 84
  Тепер результат поділіть на кількість значень у вибірці (у нашому прикладі їх 6): 84 ÷ 6 = 14.
  Вибіркове середнє x = 14.
- Вибіркове середнє – це центральне значення, навколо якого розподілені значення вибірці. Якщо значення вибірці групуються навколо вибіркового середнього, то дисперсія мала; інакше дисперсія велика.
Відніміть середнє вибіркове з кожного значення у вибірці.Тепер обчисліть різницю x i (\displaystyle x_(i))- x̅, де x i (\displaystyle x_(i))– кожне значення у вибірці. Кожен отриманий результат свідчить про відхилення конкретного значення від вибіркового середнього, тобто як далеко це значення перебуває від середнього значення вибірки.
- У нашому прикладі:
  x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
  x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
  x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
  x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
  x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
  x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
- Правильність отриманих результатів легко перевірити, оскільки їх сума має дорівнювати нулю. Це з визначенням середнього значення, оскільки від'ємні значення(відстань від середнього значення до менших значень) повністю компенсуються позитивними значеннями(Відстанями від середнього значення до великих значень).
Як зазначалося вище, сума різниць x i (\displaystyle x_(i))- x̅ повинна дорівнювати нулю. Це означає, що середня дисперсіязавжди дорівнює нулю, що дає уявлення про розкид значень деякої величини. Для вирішення цієї проблеми зведіть у квадрат кожну різницю x i (\displaystyle x_(i))- x̅. Це призведе до того, що ви отримаєте лише позитивні числа, які при додаванні ніколи не дадуть 0.
- У нашому прикладі:
  (x 1 (\displaystyle x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
  (x 2 (\displaystyle (x_(2)))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
  9 2 = 81
  (-7) 2 = 49
  (-5) 2 = 25
  (-1) 2 = 1
- Ви знайшли квадрат різниці - x̅) 2 (\displaystyle ^(2))для кожного значення у вибірці.
Обчисліть суму квадратів різниці.Тобто знайдіть ту частину формули, яка записується так: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))]. Тут знак Σ означає суму квадратів різниць для кожного значення x i (\displaystyle x_(i))у вибірці. Ви вже знайшли квадрати різниць (x i (\displaystyle (x_(i)))- x̅) 2 (\displaystyle ^(2))для кожного значення x i (\displaystyle x_(i))у вибірці; Тепер просто складіть ці квадрати.
- У нашому прикладі: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
Отриманий результат розділіть на n - 1, де n – кількість значень вибірки.Якийсь час тому для обчислення дисперсії вибірки статистики ділили результат просто на n; у цьому випадку ви отримаєте середнє значення квадрата дисперсії, що ідеально підходить для опису дисперсії даної вибірки. Але пам'ятайте, що будь-яка вибірка – це лише невелика частина генеральної сукупностізначень. Якщо взяти іншу вибірку і виконати такі самі обчислення, ви отримаєте інший результат. Як з'ясувалося, розподіл на n - 1 (а не просто на n) дає більше точну оцінкудисперсії генеральної сукупності, у чому ви зацікавлені. Розподіл на n – 1 став загальноприйнятим, тому воно включено до формули для обчислення дисперсії вибірки.
- У прикладі вибірка включає 6 значень, тобто n = 6.
  Дисперсія вибірки = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
Відмінність дисперсії стандартного відхилення.Зауважте, що у формулі є показник ступеня, тому дисперсія вимірюється у квадратних одиницях вимірювання аналізованої величини. Іноді такою величиною досить складно оперувати; у таких випадках користуються стандартним відхиленням, яке дорівнює квадратного кореняіз дисперсії. Саме тому дисперсія вибірки позначається як s 2 (\displaystyle s^(2)), а стандартне відхиленнявибірки – як s (\displaystyle s).
- У прикладі стандартне відхилення вибірки: s = √33,2 = 5,76.
Обчислення дисперсії сукупності
1. Проаналізуйте деяку сукупність значень.Сукупність включає всі значення аналізованої величини. Наприклад, якщо ви вивчаєте вік мешканців Ленінградської області, Сукупність включає вік всіх жителів цієї області. У разі роботи із сукупністю рекомендується створити таблицю та внести до неї значення сукупності. Розглянемо наступний приклад:
  - У деякій кімнаті є 6 акваріумів. У кожному акваріумі мешкає така кількість риб:
    x 1 = 5 (\displaystyle x_(1)=5)
    x 2 = 5 (\displaystyle x_(2)=5)
    x 3 = 8 (\displaystyle x_(3)=8)
    x 4 = 12 (\displaystyle x_(4)=12)
    x 5 = 15 (\displaystyle x_(5)=15)
    x 6 = 18 (\displaystyle x_(6)=18)
2. Запишіть формулу обчислення дисперсії генеральної сукупності.Так як сукупність входять всі значення деякої величини, то наведена нижче формула дозволяє отримати точне значення дисперсії сукупності. Для того щоб відрізнити дисперсію сукупності від дисперсії вибірки (значення якої є лише оцінним), статистики використовують різні змінні:
  - σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n
  - σ 2 (\displaystyle ^(2))- Дисперсія сукупності (читається як "сигма в квадраті"). Дисперсія вимірюється у квадратних одиницях виміру.
  - x i (\displaystyle x_(i))- Кожне значення в сукупності.
  - Σ – знак суми. Тобто з кожного значення x i (\displaystyle x_(i))потрібно відняти μ, звести у квадрат, та був скласти отримані результати.
  - μ – середнє значення сукупності.
  - n – кількість значень у генеральній сукупності.
3. Обчисліть середнє значення сукупності.Працюючи з генеральною сукупністю її середнє значення позначається як μ (мю). Середнє значення сукупності обчислюється як звичайне середнє арифметичне: складіть усі значення в генеральній сукупності, а потім отриманий результат розділіть на кількість значень у генеральній сукупності.
  - Майте на увазі, що середні величини не завжди обчислюються як середнє арифметичне.
  - У прикладі середнє значення сукупності: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
4. Відніміть середнє значення сукупності з кожного значення в генеральній сукупності.Чим ближче значення різниці нанівець, тим ближче конкретне значення до середнього значення сукупності. Знайдіть різницю між кожним значенням у сукупності та її середнім значенням, і ви отримаєте перше уявлення про розподіл значень.
  - У нашому прикладі:
    x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
    x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
    x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
    x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
    x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
    x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
5. Зведіть у квадрат кожен отриманий результат.Значення різниць будуть як позитивними, і негативними; якщо нанести ці значення на числову пряму, всі вони лежатимуть праворуч і ліворуч від середнього значення сукупності. Це не годиться для обчислення дисперсії, так як позитивні та негативні числакомпенсують одне одного. Тому зведіть у квадрат кожну різницю, щоб отримати винятково позитивні числа.
  - У нашому прикладі:
    (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))для кожного значення сукупності (від i = 1 до i = 6):
    (-5,5)2 (\displaystyle ^(2)) = 30,25
    (-5,5)2 (\displaystyle ^(2)), де x n (\displaystyle x_(n)) – останнє значенняу генеральній сукупності.
  - Для обчислення середнього значення отриманих результатів потрібно знайти їхню суму та розділити її на n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/n
  - Тепер запишемо наведене пояснення з використанням змінних: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n і отримаємо формулу для обчислення дисперсії сукупності.