Σχεδιάστε το γράφημα κατάστασης για την αλυσίδα Markov. Ομογενείς αλυσίδες Markov
1. μήτρα P2μετάβαση του κυκλώματος από την κατάσταση Εγώσε μια πολιτεία ισε δυο
βήμα;
2. κατανομή πιθανοτήτων σε καταστάσεις αυτή τη στιγμή t=2;
3. η πιθανότητα ότι αυτή τη στιγμή t=1 κατάσταση του κυκλώματος θα είναι Α2;
4. στάσιμη κατανομή.
Λύση.Για μια διακριτή αλυσίδα Markov στην περίπτωση της ομοιογένειάς της, ισχύει η ακόλουθη σχέση:
όπου P1 είναι ο πίνακας των πιθανοτήτων μετάβασης σε ένα βήμα.
Рn - πίνακας πιθανοτήτων μετάβασης για n βήματα.
1. Βρείτε τον πίνακα μετάβασης P2 σε δύο βήματα
Αφήστε την κατανομή πιθανοτήτων σε καταστάσεις ενεργή μικρότο βήμα καθορίζεται από το διάνυσμα
.
Γνωρίζοντας τη μήτρα Πνμετάβαση σε n βήματα, μπορούμε να προσδιορίσουμε την κατανομή πιθανότητας σε καταστάσεις στις (S+ιδ)-ο βήμα ![]() . (5)
. (5)
2. Ας βρούμε την κατανομή πιθανοτήτων στις καταστάσεις του συστήματος αυτή τη στιγμή t=2. Ας βάλουμε (5) μικρό=0 και n=2. Επειτα ![]() .
.
Θα το πάρουμε.
3. Ας βρούμε την κατανομή πιθανοτήτων στις καταστάσεις του συστήματος αυτή τη στιγμή t=1.
Ας βάλουμε (5) μικρό=0 και n=1, τότε .
Πώς μπορούμε να δούμε ότι η πιθανότητα ότι αυτή τη στιγμή t=1 κατάσταση του κυκλώματος θα είναι Α2,ίσος р2(1)=0,69.
Η κατανομή πιθανότητας στις καταστάσεις ονομάζεται στάσιμη εάν δεν αλλάζει από βήμα σε βήμα, δηλαδή
Στη συνέχεια από τη σχέση (5) στο n=1 παίρνουμε
4. Ας βρούμε τη στατική κατανομή. Αφού =2 έχουμε =(p1; p2). Ας γράψουμε το σύστημα γραμμικές εξισώσεις(6) σε μορφή συντεταγμένων

Η τελευταία κατάσταση ονομάζεται κανονικοποίηση. Στο σύστημα (6) μια εξίσωση είναι πάντα ένας γραμμικός συνδυασμός άλλων. Επομένως, μπορεί να διαγραφεί. Ας λύσουμε μαζί την πρώτη εξίσωση του συστήματος και την εξίσωση κανονικοποίησης. Έχουμε 0,6 p1=0,3p2, αυτό είναι p2=2p1. Επειτα p1+2p1=1 ή , δηλαδή . Ως εκ τούτου, .
Απάντηση:
1) ο πίνακας μετάβασης σε δύο βήματα για μια δεδομένη αλυσίδα Markov έχει τη μορφή ![]() ;
;
2) κατανομή πιθανοτήτων σε καταστάσεις αυτή τη στιγμή t=2 ίσον ![]() ;
;
3) η πιθανότητα ότι αυτή τη στιγμή t=1 κατάσταση του κυκλώματος θα είναι Α2, είναι ίσο p2(t)=0,69;
4) η στατική κατανομή έχει τη μορφή
Δόθηκε η μήτρα  εντάσεις μετάβασης μιας συνεχούς αλυσίδας Markov. Δημιουργήστε ένα γράφημα κατάστασης με ετικέτα που αντιστοιχεί στον πίνακα Λ. δημιουργήσετε ένα σύστημα διαφορικές εξισώσεις Kolmogorov για πιθανότητες κατάστασης. βρείτε την περιοριστική κατανομή πιθανοτήτων. Λύση.Ομογενής αλυσίδα Markov με πεπερασμένος αριθμόςπολιτείες Α'1, Α2,…ΕΝΑχαρακτηρίζεται από τη μήτρα των εντάσεων μετάβασης
εντάσεις μετάβασης μιας συνεχούς αλυσίδας Markov. Δημιουργήστε ένα γράφημα κατάστασης με ετικέτα που αντιστοιχεί στον πίνακα Λ. δημιουργήσετε ένα σύστημα διαφορικές εξισώσεις Kolmogorov για πιθανότητες κατάστασης. βρείτε την περιοριστική κατανομή πιθανοτήτων. Λύση.Ομογενής αλυσίδα Markov με πεπερασμένος αριθμόςπολιτείες Α'1, Α2,…ΕΝΑχαρακτηρίζεται από τη μήτρα των εντάσεων μετάβασης  ,
,
Οπου ![]() - ένταση μετάβασης της αλυσίδας Markov από το κράτος Аiσε μια πολιτεία Аj; рij(Δt)- πιθανότητα μετάβασης Ai→Ajανά χρονικό διάστημα Δ
t.
- ένταση μετάβασης της αλυσίδας Markov από το κράτος Аiσε μια πολιτεία Аj; рij(Δt)- πιθανότητα μετάβασης Ai→Ajανά χρονικό διάστημα Δ
t.
Οι μεταβάσεις του συστήματος από κατάσταση σε κατάσταση καθορίζονται εύκολα χρησιμοποιώντας ένα γράφημα κατάστασης με ετικέτα, στο οποίο σημειώνονται τόξα που αντιστοιχούν στις εντάσεις λ
ij>0. Ας δημιουργήσουμε ένα γράφημα κατάστασης με ετικέτα για δεδομένης μήτραςεντάσεις μετάβασης 
Έστω ένα διάνυσμα πιθανοτήτων Rj(t),
ι=1, 2,…,, το σύστημα είναι σε κατάσταση ΕΝΑιστη στιγμή t.
Προφανώς 0≤ Rj(t)≤1 και . Στη συνέχεια, με τον κανόνα της διαφοροποίησης διανυσματική συνάρτηση κλιμακωτό επιχείρημαπαίρνουμε ![]() . Πιθανότητες Rj(t)ικανοποιεί το σύστημα των διαφορικών εξισώσεων Kolmogorov (SDEK), το οποίο σε μορφή πίνακα έχει τη μορφή . (7)
. Πιθανότητες Rj(t)ικανοποιεί το σύστημα των διαφορικών εξισώσεων Kolmogorov (SDEK), το οποίο σε μορφή πίνακα έχει τη μορφή . (7)
Αν την αρχική στιγμή το σύστημα ήταν στην κατάσταση Аj, τότε το SDUK θα πρέπει να επιλυθεί υπό τις αρχικές συνθήκες
RΕγώ(0)=1, рj(0)=0, j≠i,j=1, 2,…,.
(8)
Το σύνολο του SDEK (7) και των αρχικών συνθηκών (8) περιγράφει μοναδικά μια ομοιογενή αλυσίδα Markov με συνεχόμενος χρόνοςκαι έναν πεπερασμένο αριθμό καταστάσεων.
Ας συνθέσουμε ένα SDEK για μια δεδομένη αλυσίδα Markov. Αφού =3, λοιπόν ι=1, 2, 3.
Από τη σχέση (7) προκύπτει  .
.
Από εδώ θα έχουμε 
Η τελευταία κατάσταση ονομάζεται κανονικοποίηση.
Η κατανομή πιθανοτήτων σε καταστάσεις ονομάζεται ακίνητος, αν δεν αλλάζει με την πάροδο του χρόνου, δηλαδή που Rj=συνθ, ι=1,2,…,. Από εδώ ![]() .
.
Στη συνέχεια από το SDUK (7) παίρνουμε ένα σύστημα για την εύρεση της σταθερής κατανομής ![]() (9)
(9)
Για αυτό το πρόβλημα, από το SDUK θα έχουμε 
Από την συνθήκη κανονικοποίησης λαμβάνουμε 3р2+р2+р2=1ή ![]() . Επομένως, η κατανομή ορίου έχει τη μορφή .
. Επομένως, η κατανομή ορίου έχει τη μορφή .
Σημειώστε ότι αυτό το αποτέλεσμα μπορεί να ληφθεί απευθείας από το γράφημα κατάστασης με ετικέτα εάν χρησιμοποιήσουμε τον κανόνα: για μια σταθερή κατανομή, το άθροισμα των γινομένων λ
jiπι, j≠Εγώ, για βέλη που προέρχονται από Εγώ-η κατάσταση ισούται με το άθροισμα των γινομένων λ
jiπι, j≠Εγώ, για τα βέλη που περιλαμβάνονται στο Εγώ-η πολιτεία. Πραγματικά, 
Είναι προφανές ότι το προκύπτον σύστημα είναι ισοδύναμο με αυτό που μεταγλωττίστηκε χρησιμοποιώντας το SDUK. Επομένως έχει την ίδια λύση.
Απάντηση: η σταθερή κατανομή έχει τη μορφή .
Μια αλυσίδα Markov είναι μια σειρά γεγονότων στα οποία κάθε επόμενο γεγονός εξαρτάται από το προηγούμενο. Σε αυτό το άρθρο θα εξετάσουμε αυτή την έννοια με περισσότερες λεπτομέρειες.
Η αλυσίδα Markov είναι ένας κοινός και αρκετά απλός τρόπος μοντελοποίησης τυχαία γεγονότα. Χρησιμοποιείται σε διάφορους τομείς, από τη δημιουργία κειμένου έως την οικονομική μοντελοποίηση. Το περισσότερο διάσημο παράδειγμαείναι το SubredditSimulator. ΣΕ σε αυτήν την περίπτωσηΗ αλυσίδα Markov χρησιμοποιείται για την αυτοματοποίηση της δημιουργίας περιεχομένου σε όλο το subreddit.
Η αλυσίδα Markov είναι σαφής και εύκολη στη χρήση γιατί μπορεί να εφαρμοστεί χωρίς τη χρήση στατιστικών ή μαθηματικών εννοιών. Η αλυσίδα Markov είναι ιδανική για εκμάθηση πιθανοτικών μοντέλων και επιστήμης δεδομένων.
Σενάριο
Φανταστείτε ότι υπάρχουν μόνο δύο καιρικές συνθήκες: Μπορεί να έχει ήλιο ή συννεφιά. Μπορείτε πάντα να προσδιορίσετε με ακρίβεια τον καιρό αυτή τη στιγμή. Εγγυημένα θα είναι καθαρός ή νεφελώδης.
Τώρα θέλετε να μάθετε πώς να προβλέψετε τον καιρό για αύριο. Διαισθητικά, καταλαβαίνεις ότι ο καιρός δεν μπορεί να αλλάξει δραματικά σε μια μέρα. Αυτό επηρεάζεται από πολλούς παράγοντες. Ο αυριανός καιρός εξαρτάται άμεσα από τον τωρινό κ.λπ. Έτσι, για να προβλέψετε τον καιρό, συλλέγετε δεδομένα για αρκετά χρόνια και καταλήγετε στο συμπέρασμα ότι μετά από μια συννεφιασμένη μέρα, η πιθανότητα μιας ηλιόλουστης ημέρας είναι 0,25. Είναι λογικό να υποθέσουμε ότι η πιθανότητα δύο συνεχόμενων συννεφιασμένων ημερών είναι 0,75, αφού έχουμε μόνο δύο πιθανές καιρικές συνθήκες.

Τώρα μπορείτε να προβλέψετε τον καιρό αρκετές ημέρες νωρίτερα με βάση τον τρέχοντα καιρό.
Αυτό το παράδειγμα δείχνει βασικές έννοιεςΑλυσίδες Markov. Μια αλυσίδα Markov αποτελείται από ένα σύνολο μεταβάσεων που καθορίζονται από μια κατανομή πιθανοτήτων, οι οποίες με τη σειρά τους ικανοποιούν την ιδιότητα Markov.
Σημειώστε ότι στο παράδειγμα η κατανομή πιθανοτήτων εξαρτάται μόνο από τις μεταβάσεις από την τρέχουσα ημέρα στην επόμενη. Αυτό μοναδική ιδιοκτησίαΔιαδικασία Markov - το κάνει αυτό χωρίς τη χρήση μνήμης. Συνήθως, αυτή η προσέγγιση δεν είναι σε θέση να δημιουργήσει μια ακολουθία στην οποία παρατηρείται οποιαδήποτε τάση. Για παράδειγμα, ενώ μια αλυσίδα Markov μπορεί να προσομοιώσει το στυλ γραφής με βάση τη συχνότητα χρήσης μιας λέξης, δεν μπορεί να δημιουργήσει κείμενα με βαθύ νόημα, αφού μπορεί να λειτουργήσει μόνο με μεγάλα κείμενα. Αυτός είναι ο λόγος για τον οποίο μια αλυσίδα Markov δεν μπορεί να παράγει περιεχόμενο που εξαρτάται από το πλαίσιο.
Μοντέλο
Τυπικά, μια αλυσίδα Markov είναι ένα πιθανό αυτόματο. Η κατανομή πιθανότητας μετάβασης συνήθως αναπαρίσταται ως πίνακας. Εάν μια αλυσίδα Markov έχει N πιθανές καταστάσεις, τότε ο πίνακας θα έχει τη μορφή N x N, στην οποία η καταχώρηση (I, J) θα είναι η πιθανότητα μετάβασης από την κατάσταση I στην κατάσταση J. Επιπλέον, ένας τέτοιος πίνακας πρέπει να είναι στοχαστική, δηλαδή σειρές ή στήλες το άθροισμα πρέπει να είναι μία. Σε έναν τέτοιο πίνακα, κάθε σειρά θα έχει τη δική της κατανομή πιθανοτήτων.

Γενική άποψη μιας αλυσίδας Markov με καταστάσεις με τη μορφή κύκλων και άκρες με τη μορφή μεταβάσεων.

Ένα παράδειγμα πίνακα μετάβασης με τρεις πιθανές καταστάσεις.
Μια αλυσίδα Markov έχει ένα διάνυσμα αρχικής κατάστασης, που αναπαρίσταται ως πίνακας N x 1. Περιγράφει τις κατανομές πιθανοτήτων της αρχής σε καθεμία από τις N δυνατές καταστάσεις. Το λήμμα I περιγράφει την πιθανότητα να ξεκινήσει η αλυσίδα στην κατάσταση I.
Αυτές οι δύο δομές είναι αρκετά επαρκείς για να αναπαραστήσουν μια αλυσίδα Markov.
Έχουμε ήδη συζητήσει πώς να λάβουμε την πιθανότητα μετάβασης από τη μια κατάσταση στην άλλη, αλλά τι γίνεται με τη λήψη αυτής της πιθανότητας σε λίγα βήματα; Για να γίνει αυτό, πρέπει να προσδιορίσουμε την πιθανότητα μετάβασης από την κατάσταση I στην κατάσταση J σε βήματα M. Στην πραγματικότητα είναι πολύ απλό. Ο πίνακας μετάβασης P μπορεί να προσδιοριστεί με τον υπολογισμό (I, J) αυξάνοντας το P στην ισχύ M. Για μικρές τιμές του M, αυτό μπορεί να γίνει χειροκίνητα χρησιμοποιώντας επαναλαμβανόμενο πολλαπλασιασμό. Αλλά μεγάλες αξίεςΜ, αν είστε εξοικειωμένοι με τη γραμμική άλγεβρα, περισσότερα αποτελεσματικός τρόποςανεβάζοντας μια μήτρα σε μια ισχύ θα διαγώνιαζε πρώτα αυτή τη μήτρα.
Markov αλυσίδα: συμπέρασμα
Τώρα, γνωρίζοντας τι είναι μια αλυσίδα Markov, μπορείτε εύκολα να την εφαρμόσετε σε μία από τις γλώσσες προγραμματισμού. Οι απλές αλυσίδες Markov είναι το θεμέλιο για περισσότερη μελέτη πολύπλοκες μεθόδουςπρίπλασμα.
Όλες οι πιθανές καταστάσεις του συστήματος σε μια ομοιογενή αλυσίδα Markov, και είναι ο στοχαστικός πίνακας που ορίζει αυτήν την αλυσίδα, που αποτελείται από πιθανότητες μετάβασης ![]() (βλ. σελίδα 381).
(βλ. σελίδα 381).
Ας υποδηλώσουμε με την πιθανότητα το σύστημα να βρίσκεται σε κατάσταση τη χρονική στιγμή, εάν είναι γνωστό ότι τη στιγμή του χρόνου το σύστημα ήταν στην κατάσταση (,). Προφανώς, ![]() . Χρησιμοποιώντας θεωρήματα για την πρόσθεση και τον πολλαπλασιασμό των πιθανοτήτων, μπορούμε εύκολα να βρούμε:
. Χρησιμοποιώντας θεωρήματα για την πρόσθεση και τον πολλαπλασιασμό των πιθανοτήτων, μπορούμε εύκολα να βρούμε:
![]()
![]()
ή σε σημειογραφία μήτρας
![]()
Από εδώ, δίνοντας τις τιμές διαδοχικά, παίρνουμε τον σημαντικό τύπο
Αν υπάρχουν όρια
![]()
ή σε σημειογραφία μήτρας
![]()
μετά οι αξίες ![]() ονομάζονται οριακές ή τελικές πιθανότητες μετάβασης.
ονομάζονται οριακές ή τελικές πιθανότητες μετάβασης.
Για να μάθουμε σε ποιες περιπτώσεις υπάρχουν περιοριστικές πιθανότητες μετάβασης και να αντλήσουμε τους αντίστοιχους τύπους, εισάγουμε την παρακάτω ορολογία.
Θα ονομάσουμε έναν στοχαστικό πίνακα και την αντίστοιχη ομοιογενή αλυσίδα Markov κανονική εάν ο πίνακας δεν έχει χαρακτηριστικούς αριθμούς διαφορετικούς από τη μονάδα και ίσους σε συντελεστή με ένα, και κανονικό εάν επιπλέον μονάδα είναι απλή ρίζα χαρακτηριστική εξίσωσημήτρες
Ένας κανονικός πίνακας χαρακτηρίζεται από το γεγονός ότι στην κανονική του μορφή (69) (σελ. 373) οι πίνακες είναι πρωτόγονοι. Για έναν κανονικό πίνακα επιπλέον.
Επιπλέον, μια ομοιογενής αλυσίδα Markov ονομάζεται αδιάσπαστη, αποσυνθέσιμη, άκυκλη, κυκλική εάν για αυτήν την αλυσίδα η στοχαστική μήτρα είναι, αντίστοιχα, αδιάσπαστη, αποσυνθέσιμη, πρωτόγονη, πρωταρχική.
Δεδομένου ότι μια πρωτόγονη στοχαστική μήτρα είναι ένας ειδικός τύπος μιας κανονικής μήτρας, μια ακυκλική αλυσίδα Markov είναι ένας ειδικός τύπος κανονικής αλυσίδας.
Θα δείξουμε ότι περιοριστικές πιθανότητες μετάβασης υπάρχουν μόνο για κανονικές ομοιογενείς αλυσίδες Markov.
Πράγματι, έστω το ελάχιστο πολυώνυμο ενός κανονικού πίνακα . Επειτα
Σύμφωνα με το Θεώρημα 10, μπορούμε να υποθέσουμε ότι
Με βάση τον τύπο (24) Κεφ. V (σελίδα 113)
 (96)
(96)
Οπου ![]() είναι ο ανηγμένος συνημμένος πίνακας και
είναι ο ανηγμένος συνημμένος πίνακας και

Αν είναι κανονικός πίνακας, τότε
και επομένως, στη δεξιά πλευρά του τύπου (96), όλοι οι όροι εκτός από τον πρώτο τείνουν στο μηδέν. Επομένως, για έναν κανονικό πίνακα υπάρχει ένας πίνακας που αποτελείται από τις περιοριστικές πιθανότητες μετάβασης, και
Η αντίθετη κατάσταση είναι προφανής. Αν υπάρχει πρόβλημα
τότε ο πίνακας δεν μπορεί να έχει χαρακτηριστικός αριθμός, για το οποίο , a , από τότε το όριο δεν θα υπήρχε [Το ίδιο όριο πρέπει να υπάρχει λόγω της ύπαρξης του ορίου (97").]
Έχουμε αποδείξει ότι για μια κανονική (και μόνο κανονική) ομοιογενή αλυσίδα Markov υπάρχει ένας πίνακας. Αυτός ο πίνακας προσδιορίζεται από τον τύπο (97).
Ας δείξουμε πώς μπορεί να εκφραστεί ο πίνακας μέσω του χαρακτηριστικού πολυωνύμου
και τον συνημμένο πίνακα ![]() .
.
Από ταυτότητα
Δυνάμει των (95), (95") και (98) έχει ως εξής:

Επομένως, ο τύπος (97) μπορεί να αντικατασταθεί από τον τύπο
 (97)
(97)
Για μια κανονική αλυσίδα Markov, δεδομένου ότι είναι ένας συγκεκριμένος τύπος κανονικής αλυσίδας, η μήτρα υπάρχει και καθορίζεται από οποιονδήποτε από τους τύπους (97), (97"). Σε αυτήν την περίπτωση, ο τύπος (97") έχει επίσης τη μορφή
2. Θεωρήστε μια κανονική αλυσίδα γενικού τύπου (ακανόνιστη). Γράφουμε τον αντίστοιχο πίνακα σε κανονική μορφή
 (100)
(100)
όπου είναι οι πρωτόγονοι στοχαστικοί πίνακες και οι αδιάσπαστοι πίνακες έχουν μέγιστους χαρακτηριστικούς αριθμούς. πιστεύοντας
 ,
, 
ας το γράψουμε στη φόρμα

 (101)
(101)

Αλλά ![]() , αφού όλοι οι χαρακτηριστικοί αριθμοί του πίνακα είναι μικρότεροι του ενός σε απόλυτη τιμή. Να γιατί
, αφού όλοι οι χαρακτηριστικοί αριθμοί του πίνακα είναι μικρότεροι του ενός σε απόλυτη τιμή. Να γιατί
 (102)
(102)
Εφόσον είναι πρωτόγονοι στοχαστικοί πίνακες, οι πίνακες σύμφωνα με τους τύπους (99) και (35) (σελ. 362) είναι θετικοί
![]()
και σε κάθε στήλη οποιουδήποτε από αυτούς τους πίνακες όλα τα στοιχεία είναι ίσα μεταξύ τους:
![]() .
.
Σημειώστε ότι η κανονική μορφή (100) του στοχαστικού πίνακα αντιστοιχεί στη διαίρεση των καταστάσεων του συστήματος σε ομάδες:
Κάθε ομάδα στο (104) αντιστοιχεί στη δική της ομάδα σειρών στο (101). Σύμφωνα με την ορολογία του L.N. Kolmogorov, οι καταστάσεις του συστήματος που περιλαμβάνονται ονομάζονται ουσιώδεις και οι καταστάσεις που περιλαμβάνονται στις υπόλοιπες ομάδες ονομάζονται ασήμαντες.
Από τη μορφή (101) του πίνακα προκύπτει ότι για οποιονδήποτε πεπερασμένο αριθμό βημάτων (από στιγμή σε στιγμή), είναι δυνατή μόνο η μετάβαση του συστήματος: α) από ουσιώδη κατάσταση σε ουσιώδη κατάσταση της ίδιας ομάδας, β. ) από μια ασήμαντη κατάσταση σε μια ουσιαστική κατάσταση, και γ) από μια ασήμαντη κατάσταση σε μια ασήμαντη κατάσταση της ίδιας ή προηγούμενης ομάδας.
Από τη μορφή (102) του πίνακα προκύπτει ότι στην περίπτωση της μετάβασης είναι δυνατή μόνο από οποιαδήποτε κατάσταση σε μια ουσιαστική κατάσταση, δηλ., η πιθανότητα μετάβασης σε οποιαδήποτε μη ουσιαστική κατάσταση τείνει στο μηδέν με τον αριθμό των βημάτων. Επομένως, οι ουσιώδεις καταστάσεις μερικές φορές ονομάζονται οριακές καταστάσεις.
3. Από τον τύπο (97) προκύπτει:
![]() .
.
Αυτό δείχνει ότι κάθε στήλη του πίνακα είναι ένα ιδιοδιάνυσμα του στοχαστικού πίνακα για τον χαρακτηριστικό αριθμό.
Για έναν κανονικό πίνακα, ο αριθμός 1 είναι μια απλή ρίζα της χαρακτηριστικής εξίσωσης και αυτός ο αριθμός αντιστοιχεί μόνο σε ένα (μέχρι βαθμωτό παράγοντα) ιδιοδιανύσμα του πίνακα. Επομένως, σε οποιαδήποτε στήλη του πίνακα, όλα τα στοιχεία είναι ίσα με τον ίδιο μη αρνητικό αριθμό:
Έτσι, σε μια κανονική αλυσίδα, οι περιοριστικές πιθανότητες μετάβασης δεν εξαρτώνται από την αρχική κατάσταση.
Αντίθετα, εάν σε κάποια κανονική ομοιογενή αλυσίδα Markov οι πιθανότητες μετάβασης prodel δεν εξαρτώνται από την αρχική κατάσταση, δηλ. οι τύποι (104) ισχύουν, τότε στο σχήμα (102) για τον πίνακα είναι απαραίτητο. Αλλά τότε η αλυσίδα είναι κανονική.
Για μια ακυκλική αλυσίδα, η οποία είναι μια ειδική περίπτωση μιας κανονικής αλυσίδας, είναι μια πρωτόγονη μήτρα. Επομένως, για κάποιους (βλ. Θεώρημα 8 στη σελίδα 377). Αλλά στη συνέχεια ![]() .
.
Αντίθετα, προκύπτει ότι για κάποιους, και αυτό, από το Θεώρημα 8, σημαίνει ότι ο πίνακας είναι πρωτόγονος και, επομένως, η δεδομένη ομοιογενής αλυσίδα Markov είναι άκυκλη.
Διατυπώνουμε τα αποτελέσματα που προκύπτουν με τη μορφή του παρακάτω θεωρήματος:
Θεώρημα 11. 1. Για να υπάρχουν όλες οι περιοριστικές πιθανότητες μετάβασης σε μια ομοιογενή αλυσίδα Markov, είναι απαραίτητο και αρκετό η αλυσίδα να είναι κανονική. Στην περίπτωση αυτή, ο πίνακας που αποτελείται από περιοριστικές πιθανότητες μετάβασης προσδιορίζεται από τον τύπο (95) ή (98).
2. Προκειμένου οι περιοριστικές πιθανότητες μετάβασης σε μια κανονική ομοιογενή αλυσίδα Markov να είναι ανεξάρτητες από την αρχική κατάσταση, είναι απαραίτητο και αρκετό η αλυσίδα να είναι κανονική. Σε αυτή την περίπτωση, ο πίνακας καθορίζεται από τον τύπο (99).
3. Προκειμένου όλες οι περιοριστικές πιθανότητες μετάβασης σε μια κανονική ομοιογενή αλυσίδα Markov να είναι διαφορετικές από το μηδέν, είναι απαραίτητο και αρκετό η αλυσίδα να είναι άκυκλη.
4. Ας εισαγάγουμε στήλες απόλυτων πιθανοτήτων
![]() (105)
(105)
πού είναι η πιθανότητα το σύστημα να βρίσκεται σε κατάσταση (,) αυτή τη στιγμή. Χρησιμοποιώντας τα θεωρήματα της πρόσθεσης και του πολλαπλασιασμού των πιθανοτήτων, βρίσκουμε:
![]() (,),
(,),
ή σε σημειογραφία μήτρας
όπου είναι ο μετατιθέμενος πίνακας για τον πίνακα .
Όλες οι απόλυτες πιθανότητες (105) προσδιορίζονται από τον τύπο (106), εάν είναι γνωστές οι αρχικές πιθανότητες και ο πίνακας πιθανοτήτων μετάβασης
Ας εισαγάγουμε τις περιοριστικές απόλυτες πιθανότητες
![]()
Περνώντας και στις δύο πλευρές της ισότητας (106) στο όριο στο , παίρνουμε:
Σημειώστε ότι η ύπαρξη πίνακα περιοριστικών πιθανοτήτων μετάβασης συνεπάγεται την ύπαρξη περιοριστικών απόλυτων πιθανοτήτων ![]() για τυχόν αρχικές πιθανότητες
για τυχόν αρχικές πιθανότητες ![]() και αντίστροφα.
και αντίστροφα.
Από τον τύπο (107) και από τη μορφή (102) του πίνακα προκύπτει ότι οι περιοριστικές απόλυτες πιθανότητες που αντιστοιχούν σε ασήμαντες καταστάσεις είναι ίσες με μηδέν.
Πολλαπλασιάζοντας και τις δύο πλευρές της ισότητας του πίνακα
στα δεξιά στο , λαμβάνουμε δυνάμει του (107):
δηλ. η στήλη των οριακών απόλυτων πιθανοτήτων είναι ένα ιδιοδιάνυσμα του πίνακα για τον χαρακτηριστικό αριθμό.
Αν αυτό το κύκλωμαΟ Markov είναι κανονικός, τότε είναι μια απλή ρίζα της χαρακτηριστικής εξίσωσης του πίνακα . Στην περίπτωση αυτή, η στήλη των περιοριστικών απόλυτων πιθανοτήτων προσδιορίζεται μοναδικά από το (108) (από και ).
Ας δοθεί μια κανονική αλυσίδα Markov. Στη συνέχεια από (104) και από (107) προκύπτει:
![]() (109)
(109)
Στην περίπτωση αυτή, οι περιοριστικές απόλυτες πιθανότητες δεν εξαρτώνται από τις αρχικές πιθανότητες.
Αντίθετα, μπορεί να μην εξαρτάται από την παρουσία του τύπου (107) εάν και μόνο εάν όλες οι σειρές του πίνακα είναι πανομοιότυπες, δηλ.
![]() ,
,
και επομένως (σύμφωνα με το Θεώρημα 11) είναι ένας κανονικός πίνακας.
Αν είναι ένας πρωτόγονος πίνακας, τότε , και ως εκ τούτου δυνάμει του (109)
Αντίθετα, αν όλα δεν εξαρτώνται από τις αρχικές πιθανότητες, τότε σε κάθε στήλη του πίνακα όλα τα στοιχεία είναι πανομοιότυπα και σύμφωνα με το (109), και αυτό, σύμφωνα με το Θεώρημα 11, σημαίνει ότι είναι ένας πρωτόγονος πίνακας, δηλαδή αυτή η αλυσίδα είναι άκυκλο.
Από τα παραπάνω προκύπτει ότι το Θεώρημα 11 μπορεί να διατυπωθεί ως εξής:
Θεώρημα 11". 1. Για να υπάρχουν όλες οι περιοριστικές απόλυτες πιθανότητες σε μια ομοιογενή αλυσίδα Markov για οποιεσδήποτε αρχικές πιθανότητες, είναι απαραίτητο και αρκετό η αλυσίδα να είναι κανονική.
2. Για να υπάρχουν περιοριστικές απόλυτες πιθανότητες σε μια ομοιογενή αλυσίδα Markov για οποιεσδήποτε αρχικές πιθανότητες και να μην εξαρτώνται από αυτές τις αρχικές πιθανότητες, είναι απαραίτητο και αρκετό η αλυσίδα να είναι κανονική.
3. Για να έχει μια ομοιογενής αλυσίδα Markov θετικές οριακές απόλυτες πιθανότητες για οποιεσδήποτε αρχικές πιθανότητες και αυτές οι περιοριστικές πιθανότητες να είναι ανεξάρτητες από τις αρχικές, είναι απαραίτητο και αρκετό η αλυσίδα να είναι άκυκλη.
5. Τώρα σκεφτείτε μια ομοιογενή αλυσίδα Markov γενικού τύπουμε τον πίνακα πιθανοτήτων μετάβασης.
Ας πάρουμε την κανονική μορφή (69) του πίνακα και ας τη συμβολίσουμε με τους δείκτες αυθεντικότητας των πινάκων στο (69). Έστω το ελάχιστο κοινό πολλαπλάσιο των ακεραίων. Τότε ο πίνακας δεν έχει χαρακτηριστικούς αριθμούς ίσους σε συντελεστή με ένα, αλλά διαφορετικούς από έναν, δηλαδή είναι ένας κανονικός πίνακας. σε αυτήν την περίπτωση - ο μικρότερος δείκτης στον οποίο - ο σωστός πίνακας. Ονομάζουμε τον αριθμό περίοδο μιας δεδομένης ομοιογενούς αλυσίδας Markov και... Αντίθετα, αν και ![]() , που ορίζεται από τους τύπους (110) και (110").
, που ορίζεται από τους τύπους (110) και (110").
Οι μέσες οριακές απόλυτες πιθανότητες που αντιστοιχούν σε ασήμαντες καταστάσεις είναι πάντα μηδενικές.
Εάν η κανονική μορφή του πίνακα είναι ένας αριθμός (και μόνο σε αυτήν την περίπτωση), οι μέσες οριακές απόλυτες πιθανότητες δεν εξαρτώνται από τις αρχικές πιθανότητες και καθορίζονται μοναδικά από την εξίσωση (111).
Αυτό το άρθρο δίνει γενική ιδέασχετικά με τον τρόπο δημιουργίας κειμένων χρησιμοποιώντας τη μοντελοποίηση της διαδικασίας Markov. Συγκεκριμένα, θα εισαγάγουμε τις αλυσίδες Markov και, ως πρακτική, θα εφαρμόσουμε μια μικρή γεννήτρια κειμένου στην Python.
Αρχικά, ας γράψουμε τους απαραίτητους, αλλά όχι ακόμη πολύ σαφείς, ορισμούς από τη σελίδα της Wikipedia για να κατανοήσουμε τουλάχιστον κατά προσέγγιση τι έχουμε να κάνουμε:
διαδικασία Markov t t
Αλυσίδα Markov
Τι σημαίνουν όλα αυτά; Ας το καταλάβουμε.
Βασικά
Το πρώτο παράδειγμα είναι εξαιρετικά απλό. Χρησιμοποιώντας μια πρόταση από ένα παιδικό βιβλίο, θα κατακτήσουμε τη βασική έννοια της αλυσίδας Markov και θα ορίσουμε επίσης τι είναι στο πλαίσιο μας σώμα, συνδέσμους, κατανομή πιθανοτήτων και ιστογράμματα. Αν και η πρόταση δίνεται στις αγγλική γλώσσα, η ουσία της θεωρίας θα είναι εύκολο να κατανοηθεί.
Αυτή η πρόταση είναι πλαίσιο, δηλαδή τη βάση βάσει της οποίας θα δημιουργηθεί το κείμενο στο μέλλον. Αποτελείται από οκτώ λέξεις, αλλά ταυτόχρονα μοναδικές λέξειςμόνο πέντε είναι συνδέσεις(μιλάμε για Markovian αλυσίδες). Για λόγους σαφήνειας, ας χρωματίσουμε κάθε σύνδεσμο με το δικό του χρώμα:

Και σημειώνουμε τον αριθμό των εμφανίσεων κάθε συνδέσμου στο κείμενο:

Στην παραπάνω εικόνα μπορείτε να δείτε ότι η λέξη "ψάρι"εμφανίζεται στο κείμενο 4 φορές πιο συχνά από καθεμία από τις άλλες λέξεις ( "Ένα", "δύο", "κόκκινο", "μπλε"). Δηλαδή την πιθανότητα να συναντήσουμε τη λέξη στο σώμα μας "ψάρι" 4 φορές μεγαλύτερη από την πιθανότητα να συναντήσετε κάθε άλλη λέξη που φαίνεται στο σχήμα. Μιλώντας στη γλώσσα των μαθηματικών, μπορούμε να προσδιορίσουμε τον νόμο κατανομής μιας τυχαίας μεταβλητής και να υπολογίσουμε με ποια πιθανότητα θα εμφανιστεί μία από τις λέξεις στο κείμενο μετά την τρέχουσα. Η πιθανότητα υπολογίζεται ως εξής: πρέπει να διαιρέσουμε τον αριθμό των εμφανίσεων της λέξης που χρειαζόμαστε στο σώμα με συνολικός αριθμόςόλες οι λέξεις σε αυτό. Για τη λέξη "ψάρι"αυτή η πιθανότητα είναι 50% αφού εμφανίζεται 4 φορές σε μια πρόταση 8 λέξεων. Για κάθε έναν από τους υπόλοιπους συνδέσμους, αυτή η πιθανότητα είναι 12,5% (1/8).
Παριστάνουν γραφικά την κατανομή τυχαίες μεταβλητέςδυνατή χρήση ιστογράμματα. Σε αυτήν την περίπτωση, η συχνότητα εμφάνισης κάθε συνδέσμου στην πρόταση είναι σαφώς ορατή:

Έτσι, το κείμενό μας αποτελείται από λέξεις και μοναδικούς συνδέσμους και εμφανίσαμε την κατανομή πιθανότητας της εμφάνισης κάθε συνδέσμου σε μια πρόταση σε ένα ιστόγραμμα. Εάν πιστεύετε ότι δεν αξίζει να ασχοληθείτε με τα στατιστικά, διαβάστε παρακάτω. Και ίσως θα σώσει τη ζωή σας.
Η ουσία του ορισμού
Τώρα ας προσθέσουμε στο κείμενό μας στοιχεία που πάντα υπονοούνται, αλλά δεν εκφράζονται στην καθημερινή ομιλία - την αρχή και το τέλος της πρότασης:

Οποιαδήποτε πρόταση περιέχει αυτά τα αόρατα "αρχή" και "τέλος", ας τα προσθέσουμε ως συνδέσμους στη διανομή μας:

Ας επιστρέψουμε στον ορισμό που δόθηκε στην αρχή του άρθρου:
διαδικασία Markov- μια τυχαία διαδικασία, η εξέλιξη της οποίας μετά από οποιαδήποτε καθορισμένη τιμήπαράμετρος χρόνου tδεν εξαρτάται από την εξέλιξη που προηγήθηκε t, με την προϋπόθεση ότι η αξία της διαδικασίας αυτή τη στιγμή είναι σταθερή.
Αλυσίδα Markov - ειδική περίπτωσηΗ διαδικασία Markov, όταν ο χώρος των καταστάσεων της είναι διακριτός (δηλ. όχι περισσότερο από μετρήσιμος).
Λοιπόν, τι σημαίνει αυτό; Σε γενικές γραμμές, μοντελοποιούμε μια διαδικασία στην οποία η κατάσταση του συστήματος την επόμενη χρονική στιγμή εξαρτάται μόνο από την κατάστασή του την τρέχουσα στιγμή και δεν εξαρτάται σε καμία περίπτωση από όλες τις προηγούμενες καταστάσεις.
Φανταστείτε τι έχετε μπροστά σας παράθυρο, το οποίο εμφανίζει μόνο την τρέχουσα κατάσταση του συστήματος (στην περίπτωσή μας, είναι μία λέξη) και πρέπει να καθορίσετε ποια θα είναι η επόμενη λέξη με βάση μόνο τα δεδομένα που παρουσιάζονται σε αυτό το παράθυρο. Στο σώμα μας, οι λέξεις διαδέχονται η μία την άλλη σύμφωνα με το ακόλουθο μοτίβο:

Έτσι, σχηματίζονται ζεύγη λέξεων (ακόμη και το τέλος της πρότασης έχει το δικό του ζευγάρι - ένα κενό νόημα):

Ας ομαδοποιήσουμε αυτά τα ζευγάρια με βάση την πρώτη λέξη. Θα δούμε ότι κάθε λέξη έχει το δικό της σύνολο συνδέσμων, που στα πλαίσια της πρότασης μας μπορώακολούθα τον:

Ας παρουσιάσουμε αυτές τις πληροφορίες με άλλο τρόπο - για κάθε σύνδεσμο εκχωρούμε έναν πίνακα με όλες τις λέξεις που μπορεί να εμφανίζονται στο κείμενο μετά από αυτόν τον σύνδεσμο:

Ας ρίξουμε μια πιο προσεκτική ματιά. Βλέπουμε ότι κάθε σύνδεσμος έχει λέξεις που μπορώ μετά από αυτό σε μια πρόταση. Αν δείχναμε το παραπάνω διάγραμμα σε κάποιον άλλο, αυτό το άτομο θα μπορούσε, με κάποια πιθανότητα, να ανακατασκευάσει το δικό μας αρχική προσφορά, δηλαδή το σώμα.
Παράδειγμα.Ας ξεκινήσουμε με τη λέξη "Αρχή". Στη συνέχεια, επιλέξτε τη λέξη "Ενας", αφού σύμφωνα με το σχήμα μας αυτό είναι η μόνη λέξη, που μπορεί να ακολουθεί την αρχή μιας πρότασης. Πίσω από τον Λόγο "Ενας"επίσης μόνο μια λέξη μπορεί να ακολουθήσει - "ψάρι". Τώρα η νέα πρόταση στην ενδιάμεση έκδοση μοιάζει "Ενα ψάρι". Περαιτέρω η κατάσταση γίνεται πιο περίπλοκη - για "ψάρι"μπορεί να υπάρχουν λέξεις με ίση πιθανότητα 25% "δύο", "κόκκινο", "μπλε"και τέλος της πρότασης "Τέλος". Αν υποθέσουμε ότι η επόμενη λέξη είναι "δύο", η ανοικοδόμηση θα συνεχιστεί. Μπορούμε όμως να επιλέξουμε έναν σύνδεσμο "Τέλος". Σε αυτήν την περίπτωση, με βάση το σχήμα μας, θα δημιουργηθεί τυχαία μια πρόταση που είναι πολύ διαφορετική από το σώμα - "Ενα ψάρι".
Μόλις προσομοιώσαμε μια διαδικασία Markov - προσδιορίσαμε κάθε επόμενη λέξη μόνο με βάση τη γνώση για την τρέχουσα. Για να κατανοήσουμε πλήρως το υλικό, ας δημιουργήσουμε διαγράμματα που δείχνουν τις εξαρτήσεις μεταξύ των στοιχείων μέσα στο σώμα μας. Τα οβάλ αντιπροσωπεύουν συνδέσμους. Τα βέλη οδηγούν σε πιθανούς συνδέσμους που μπορούν να ακολουθήσουν τη λέξη στο οβάλ. Δίπλα σε κάθε βέλος είναι η πιθανότητα με την οποία θα εμφανιστεί ο επόμενος σύνδεσμος μετά τον τρέχοντα:

Εξαιρετική! Έχουμε μάθει απαραίτητες πληροφορίεςνα προχωρήσουμε και να αναλύσουμε πιο σύνθετα μοντέλα.
Διεύρυνση της βάσης του λεξιλογίου
Σε αυτό το μέρος του άρθρου θα κατασκευάσουμε ένα μοντέλο σύμφωνα με την ίδια αρχή όπως πριν, αλλά στην περιγραφή θα παραλείψουμε κάποια βήματα. Εάν αντιμετωπίζετε δυσκολίες, επιστρέψτε στη θεωρία στο πρώτο μπλοκ.
Ας πάρουμε άλλα τέσσερα αποσπάσματα από τον ίδιο συγγραφέα (επίσης στα αγγλικά, δεν θα μας βλάψει):
«Σήμερα είσαι εσύ. Αυτό είναι πιο αληθινό παρά αληθινό. Δεν υπάρχει κανένας ζωντανός που να είναι περισσότερο από σένα».
«Έχεις μυαλό στο κεφάλι σου. Έχεις τα πόδια στα παπούτσια σου. Μπορείτε να κατευθύνετε τον εαυτό σας όποια κατεύθυνση επιλέξετε. Είσαι μόνος σου."
"Περισσότερο ότι εσυανάγνωση περισσότεροπράγματα που θα ξέρεις. Όσο περισσότερα μαθαίνεις, τόσο περισσότερα μέρη θα πας».
«Σκέψου αριστερά και σκέψου δεξιά, σκέψου χαμηλά και σκέψου ψηλά. Ω, πιστεύουν ότι μπορείς να σκεφτείς αν προσπαθήσεις».
Η πολυπλοκότητα του σώματος έχει αυξηθεί, αλλά στην περίπτωσή μας αυτό είναι μόνο ένα πλεονέκτημα - τώρα η δημιουργία κειμένου θα μπορεί να παράγει πιο ουσιαστικές προτάσεις. Το γεγονός είναι ότι σε οποιαδήποτε γλώσσα υπάρχουν λέξεις που εμφανίζονται στην ομιλία πιο συχνά από άλλες (για παράδειγμα, χρησιμοποιούμε την πρόθεση "in" πολύ πιο συχνά από τη λέξη "cryogenic"). Πως περισσότερες λέξειςστο σώμα μας (και επομένως τις εξαρτήσεις μεταξύ τους), τόσο περισσότερες πληροφορίες έχει η γεννήτρια σχετικά με το ποια λέξη είναι πιο πιθανό να εμφανιστεί στο κείμενο μετά την τρέχουσα.
Ο ευκολότερος τρόπος για να το εξηγήσετε αυτό είναι από την άποψη του προγράμματος. Γνωρίζουμε ότι για κάθε σύνδεσμο υπάρχει ένα σύνολο λέξεων που μπορούν να τον ακολουθήσουν. Και επίσης, κάθε λέξη χαρακτηρίζεται από τον αριθμό των εμφανίσεών της στο κείμενο. Χρειαζόμαστε κάποιον τρόπο για να καταγράψουμε όλες αυτές τις πληροφορίες σε ένα μέρος. Για το σκοπό αυτό, ένα λεξικό που αποθηκεύει ζεύγη "(κλειδί, τιμή)" ταιριάζει καλύτερα. Το πλήκτρο λεξικού θα καταγράψει την τρέχουσα κατάσταση του συστήματος, δηλαδή έναν από τους συνδέσμους του σώματος (για παράδειγμα, "ο"στην παρακάτω εικόνα). και ένα άλλο λεξικό θα αποθηκευτεί στην τιμή του λεξικού. Στο ένθετο λεξικό, τα κλειδιά θα είναι λέξεις που μπορούν να εμφανίζονται στο κείμενο μετά τον τρέχοντα σύνδεσμο του σώματος ( "σκέφτεται"Και "περισσότερο"μπορεί να ακολουθήσει στο κείμενο "ο"), και οι τιμές είναι ο αριθμός των εμφανίσεων αυτών των λέξεων στο κείμενο μετά τον σύνδεσμό μας (τη λέξη "σκέφτεται"εμφανίζεται στο κείμενο μετά τη λέξη "ο" 1 φορά, λέξη "περισσότερο"μετά τη λέξη "ο"- 4 φορές):

Ξαναδιάβασε την παραπάνω παράγραφο πολλές φορές για να βεβαιωθείς ότι την κατανοείς ακριβώς. Λάβετε υπόψη ότι το ένθετο λεξικό σε αυτήν την περίπτωση είναι το ίδιο ιστόγραμμα· μας βοηθά να παρακολουθούμε συνδέσμους και τη συχνότητα εμφάνισής τους στο κείμενο σε σχέση με άλλες λέξεις. Πρέπει να σημειωθεί ότι ακόμη και μια τέτοια βάση λεξιλογίου είναι πολύ μικρή για τη σωστή δημιουργία κειμένων φυσική γλώσσα- Θα πρέπει να περιέχει περισσότερες από 20.000 λέξεις, ή ακόμα καλύτερα, περισσότερες από 100.000. Και ακόμα καλύτερα, περισσότερες από 500.000. Ας δούμε όμως τη βάση λεξιλογίου που έχουμε.
Η αλυσίδα Markov σε αυτή την περίπτωση κατασκευάζεται παρόμοια με το πρώτο παράδειγμα - κάθε επόμενη λέξη επιλέγεται μόνο με βάση τη γνώση για την τρέχουσα λέξη, όλες οι άλλες λέξεις δεν λαμβάνονται υπόψη. Αλλά χάρη στην αποθήκευση στο λεξικό δεδομένων σχετικά με το ποιες λέξεις εμφανίζονται πιο συχνά από άλλες, μπορούμε να δεχθούμε κατά την επιλογή ενημερωμένη απόφαση. Ας δούμε ένα συγκεκριμένο παράδειγμα:
Περισσότερο:
Αν δηλαδή η τρέχουσα λέξη είναι η λέξη "περισσότερο", μετά από αυτό μπορεί να υπάρχουν λέξεις με ίση πιθανότητα 25% "πράγματα"Και "μέρη", και με πιθανότητα 50% - η λέξη "ότι". Αλλά οι πιθανότητες μπορεί να είναι όλες ίσες:
Νομίζω:
Εργασία με Windows
Μέχρι τώρα, θεωρούσαμε παράθυρα μόνο στο μέγεθος μιας λέξης. Μπορείτε να αυξήσετε το μέγεθος του παραθύρου έτσι ώστε η δημιουργία κειμένου να παράγει περισσότερες «επαληθευμένες» προτάσεις. Αυτό σημαίνει ότι όσο μεγαλύτερο είναι το παράθυρο, τόσο μικρότερες είναι οι αποκλίσεις από το σώμα κατά τη διάρκεια της παραγωγής. Η αύξηση του μεγέθους του παραθύρου αντιστοιχεί στη μετάβαση της αλυσίδας Markov σε περισσότερα υψηλή τάξη. Προηγουμένως, κατασκευάζαμε ένα κύκλωμα πρώτης τάξης· για ένα παράθυρο, δύο λέξεις θα παράγουν ένα κύκλωμα δεύτερης τάξης, τρεις θα παράγουν ένα κύκλωμα τρίτης τάξης και ούτω καθεξής.
Παράθυρο- αυτά είναι τα δεδομένα τωρινή κατάστασησυστήματα που χρησιμοποιούνται για τη λήψη αποφάσεων. Αν συνδυάσουμε ένα μεγάλο παράθυρο και ένα μικρό σύνολο δεδομένων, πιθανότατα θα λαμβάνουμε την ίδια πρόταση κάθε φορά. Ας πάρουμε τη βάση του λεξιλογίου από το πρώτο μας παράδειγμα και ας επεκτείνουμε το παράθυρο στο μέγεθος 2:

Η επέκταση σημαίνει ότι κάθε παράθυρο έχει πλέον μόνο μία επιλογή για την επόμενη κατάσταση του συστήματος - ανεξάρτητα από το τι κάνουμε, θα λαμβάνουμε πάντα την ίδια πρόταση, πανομοιότυπη με την περίπτωσή μας. Επομένως, για να πειραματιστείτε με τα παράθυρα και για να επιστρέψει μοναδικό περιεχόμενο από το πρόγραμμα δημιουργίας κειμένου, εφοδιαστείτε με λεξιλόγιο τουλάχιστον 500.000 λέξεων.
Υλοποίηση σε Python
Δομή δεδομένων δικτόγραμμα
Ένα Δικτόγραμμα (το dict είναι ένας ενσωματωμένος τύπος δεδομένων λεξικού στην Python) θα εμφανίζει τη σχέση μεταξύ των συνδέσμων και τη συχνότητα εμφάνισής τους στο κείμενο, δηλαδή την κατανομή τους. Αλλά ταυτόχρονα, θα έχει την ιδιότητα λεξικού που χρειαζόμαστε - ο χρόνος εκτέλεσης του προγράμματος δεν θα εξαρτάται από την ποσότητα των δεδομένων εισόδου, πράγμα που σημαίνει ότι δημιουργούμε έναν αποτελεσματικό αλγόριθμο.
Εισαγωγή τυχαίας κλάσης Dictogram(dict): def __init__(self, iterable=None): # Αρχικοποίηση της διανομής μας ως νέο αντικείμενο κλάσης, # προσθήκη υπαρχόντων στοιχείων super(Dictogram, self).__init__() self.types = 0 # αριθμός μοναδικά κλειδιά στη διανομή self.tokens = 0 # σύνολοόλες οι λέξεις στη διανομή αν επαναλαμβανόμενες: self.update(iterable) def update(self, iterable): # Ενημέρωση της διανομής με στοιχεία από το υπάρχον # επαναλαμβανόμενο σύνολο δεδομένων για στοιχείο σε iterable: if item in self: self += 1 self .tokens += 1 else: self = 1 self.types += 1 self.tokens += 1 def count(self, item): # Επιστρέψτε την μετρητή τιμή του στοιχείου ή 0 εάν το στοιχείο στον εαυτό του: επιστροφή εαυτό επιστρέφει 0 def return_random_word (self): random_key = random.sample(self, 1) # Ένας άλλος τρόπος: # random.choice(histogram.keys()) return random_key def return_weighted_random_word(self): # Δημιουργήστε έναν ψευδοτυχαίο αριθμό μεταξύ 0 και (n- 1), # όπου n είναι ο γενικός αριθμός λέξεων random_int = random.randint(0, self.tokens-1) index = 0 list_of_keys = self.keys() # print "random index:", random_int for i in range(0 , self.types): index += self] # print the index if(index > random_int): # print list_of_keys[i] return list_of_keys[i]
Στον κατασκευαστή της δομής Δικτόγραμμα μπορεί να περάσει οποιοδήποτε αντικείμενο που μπορεί να επαναληφθεί. Τα στοιχεία αυτού του αντικειμένου θα είναι οι λέξεις για να αρχικοποιήσετε το Δικτόγραμμα, για παράδειγμα, όλες τις λέξεις από ένα βιβλίο. Σε αυτήν την περίπτωση, μετράμε τα στοιχεία έτσι ώστε για να έχουμε πρόσβαση σε κάποιο από αυτά δεν χρειάζεται να εξετάζουμε ολόκληρο το σύνολο δεδομένων κάθε φορά.
Κάναμε επίσης δύο λειτουργίες για επιστροφή τυχαία λέξη. Η μία συνάρτηση επιλέγει ένα τυχαίο πλήκτρο στο λεξικό και η άλλη, λαμβάνοντας υπόψη τον αριθμό των εμφανίσεων κάθε λέξης στο κείμενο, επιστρέφει τη λέξη που χρειαζόμαστε.
Δομή αλυσίδας Markov
από ιστογράμματα εισαγωγή Δικτόγραμμα def make_markov_model(data): markov_model = dict() για i στο range(0, len(data)-1): if data[i] in markov_model: # Απλώς προσαρτήστε σε μια υπάρχουσα διανομή markov_model].update( ]) else: markov_model] = Dictogram() επιστρέφει το markov_modelΣτην παραπάνω υλοποίηση, έχουμε ένα λεξικό που αποθηκεύει τα παράθυρα ως κλειδί σε ένα ζεύγος "(κλειδί, τιμή)" και διανομές ως τιμές σε αυτό το ζεύγος.
Δομή αλυσίδας Markov Ν-ης τάξης
από ιστογράμματα εισαγωγή Δικτόγραμμα def make_higher_order_markov_model(order, data): markov_model = dict() for i in range(0, len(data)-order): # Create a window window = tuple(data) # Προσθήκη στο λεξικό if window in markov_model: # Επισύναψη σε υπάρχουσα διανομή markov_model.update() else: markov_model = Dictogram() return markov_modelΠολύ παρόμοια με μια αλυσίδα Markov πρώτης παραγγελίας, αλλά σε αυτήν την περίπτωση αποθηκεύουμε παράλαση αυτοκινήτωνως κλειδί σε ένα ζεύγος "(κλειδί, τιμή)" σε ένα λεξικό. Το χρησιμοποιούμε αντί για λίστα, καθώς η πλειάδα προστατεύεται από οποιεσδήποτε αλλαγές και αυτό είναι σημαντικό για εμάς - τελικά, τα κλειδιά στο λεξικό δεν πρέπει να αλλάζουν.
Ανάλυση μοντέλων
Ωραία, έχουμε εφαρμόσει το λεξικό. Πώς μπορούμε όμως τώρα να δημιουργήσουμε περιεχόμενο με βάση την τρέχουσα κατάσταση και το βήμα προς την επόμενη κατάσταση; Ας δούμε το μοντέλο μας:
Από ιστογράμματα εισαγωγή Δικτόγραμμα εισαγωγή τυχαία από συλλογές εισαγωγή deque import re def generate_random_start(model): # Για να δημιουργήσετε οποιαδήποτε αρχική λέξη, αφαιρέστε το σχόλιο της γραμμής: # return random.choice(model.keys()) # Για να δημιουργήσετε τη "σωστή" αρχική λέξη , χρησιμοποιήστε τον παρακάτω κωδικό: # Σωστό αρχικές λέξεις- αυτές είναι αυτές που ήταν η αρχή των προτάσεων στο σώμα εάν "END" στο μοντέλο: seed_word = "END" ενώ seed_word == "END": seed_word = model["END"].return_weighted_random_word() επιστρέφει seed_word επιστρέφει τυχαία. option(model .keys()) def generate_random_sentence(length, markov_model): τρέχουσα_λέξη = δημιουργώ_τυχαία_έναρξη(markov_model) πρόταση = για i στο εύρος(0, μήκος): τρέχον_δικτόγραμμα = τυχαίο_μοντέλο τυχαία_λέξη_μάρκο = τρέχον_δικτογράμμα.return_λέξη_συνήθης_τυχαία_σύμβαση (current_word) πρόταση = πρόταση.capitalize() return " ".join(sentence) + "." επιστροφή πρότασης
Τι έπεται?
Προσπαθήστε να σκεφτείτε πού μπορείτε να χρησιμοποιήσετε μόνοι σας μια συσκευή δημιουργίας κειμένου που βασίζεται σε αλυσίδες Markov. Απλώς μην ξεχνάτε ότι το πιο σημαντικό είναι πώς αναλύετε το μοντέλο και ποιους ειδικούς περιορισμούς θέτετε στη γενιά. Ο συγγραφέας αυτού του άρθρου, για παράδειγμα, κατά τη δημιουργία της δημιουργίας tweet, χρησιμοποίησε ένα μεγάλο παράθυρο, περιόρισε το παραγόμενο περιεχόμενο σε 140 χαρακτήρες και χρησιμοποίησε μόνο «σωστές» λέξεις για να ξεκινήσει προτάσεις, δηλαδή αυτές που ήταν η αρχή των προτάσεων στο το σώμα.
Μέθοδοι μαθηματικές περιγραφέςΟι τυχαίες διεργασίες Markov σε ένα σύστημα με διακριτές καταστάσεις (DS) εξαρτώνται από το ποια χρονικά σημεία (προηγουμένως γνωστά ή τυχαία) μπορούν να συμβούν μεταβάσεις του συστήματος από κατάσταση σε κατάσταση.
Εάν η μετάβαση ενός συστήματος από κατάσταση σε κατάσταση είναι δυνατή σε προκαθορισμένες χρονικές στιγμές, έχουμε να κάνουμε με τυχαίος διαδικασία Markovμε διακριτό χρόνο.Εάν η μετάβαση είναι δυνατή σε οποιαδήποτε τυχαία χρονική στιγμή, τότε έχουμε να κάνουμε τυχαία διαδικασία Markov με συνεχή χρόνο.
Ας υπάρχει φυσικό σύστημα μικρό, που μπορεί να είναι μέσα nπολιτείες μικρό 1 , μικρό 2 , …, S n. Οι μεταβάσεις από κατάσταση σε κατάσταση είναι δυνατές μόνο σε στιγμές του χρόνου t 1 , t 2 , …, tk, ας ονομάσουμε αυτές τις στιγμές σε χρονικά βήματα. Θα εξετάσουμε την κοινοπραξία στο σύστημα μικρόως συνάρτηση του ακέραιου ορίσματος 1, 2, ..., κ, όπου το όρισμα είναι ο αριθμός βήματος.
Παράδειγμα: μικρό 1 → μικρό 2 → μικρό 3 → μικρό 2 .
Ας συμφωνήσουμε να ορίσουμε S i (κ) – γεγονός που συνίσταται στο γεγονός ότι μετά κβήματα το σύστημα βρίσκεται στην κατάσταση S Εγώ.
Για κάθε κσυμβάντα S 1 ( κ), S 2 ( κ),…, Σ n (κ) μορφή πλήρη ομάδα εκδηλώσεωνκαι είναι ασύμβατες.
Μια διαδικασία σε ένα σύστημα μπορεί να αναπαρασταθεί ως μια αλυσίδα γεγονότων.
Παράδειγμα: μικρό 1 (0) , μικρό 2 (1) , S 3 (2) , S 5 (3) ,….
Αυτή η ακολουθία ονομάζεται Αλυσίδα Markov
, εάν για κάθε βήμα η πιθανότητα μετάβασης από οποιαδήποτε κατάσταση S iσε οποιαδήποτε κατάσταση Sjδεν εξαρτάται από το πότε και πώς το σύστημα έφτασε στην κατάσταση S i.
Αφήστε ανά πάσα στιγμή μετά από οποιαδήποτε κ-ο σύστημα βημάτων μικρόμπορεί να βρίσκεται σε μία από τις πολιτείες μικρό 1 , μικρό 2 , …, S n, δηλαδή ένα συμβάν από μια πλήρη ομάδα γεγονότων μπορεί να συμβεί: μικρό 1 (κ), S 2 ( κ) , …, S n (κ) . Ας υποδηλώσουμε τις πιθανότητες αυτών των γεγονότων:
Π 1 (1) = Π(μικρό 1 (1)); Π 2 (1) = Π(μικρό 2 (1)); …; Πν(1) = Π(S n (κ));
Π 1 (2) = Π(μικρό 1 (2)); Π 2 (2) = Π(S 2 (2)); ...; Πν(2) = Π(S n (2));
Π 1 (κ) = Π(μικρό 1 (κ)); Π 2 (κ) = Π(μικρό 2 (κ)); …; Πν(κ) = Π(S n (κ)).
Είναι εύκολο να δούμε ότι για κάθε αριθμό βήματος η συνθήκη ικανοποιείται
Π 1 (κ) + Π 2 (κ) +…+ Πν(κ) = 1.
Ας ονομάσουμε αυτές τις πιθανότητες πιθανότητες κατάστασηςΕπομένως, η εργασία θα ακούγεται ως εξής: βρείτε τις πιθανότητες καταστάσεων συστήματος για οποιαδήποτε κ.
Παράδειγμα.Ας υπάρχει κάποιο είδος συστήματος που μπορεί να βρίσκεται σε οποιαδήποτε από τις έξι καταστάσεις. τότε οι διεργασίες που συμβαίνουν σε αυτό μπορούν να απεικονιστούν είτε ως γράφημα αλλαγών στην κατάσταση του συστήματος (Εικ. 7.9, ΕΝΑ), ή με τη μορφή γραφήματος κατάστασης συστήματος (Εικ. 7.9, σι).
ΕΝΑ) 
Ρύζι. 7.9
Επίσης, οι διεργασίες στο σύστημα μπορούν να απεικονιστούν ως μια ακολουθία καταστάσεων: μικρό 1 , μικρό 3 , μικρό 2 , μικρό 2 , μικρό 3 , μικρό 5 , μικρό 6 , μικρό 2 .
Πιθανότητα κατάστασης σε ( κ+ 1)ο βήμα εξαρτάται μόνο από την κατάσταση στο κ-μ βήμα.
Για οποιοδήποτε βήμα κυπάρχουν κάποιες πιθανότητες το σύστημα να μεταβεί από οποιαδήποτε κατάσταση σε οποιαδήποτε άλλη κατάσταση, ας τις ονομάσουμε πιθανότητες πιθανότητες μετάβασης μιας αλυσίδας Markov.
Μερικές από αυτές τις πιθανότητες θα είναι 0 εάν η μετάβαση από τη μια κατάσταση στην άλλη δεν είναι δυνατή σε ένα βήμα.
Η αλυσίδα Markov ονομάζεται ομοιογενής, εάν οι καταστάσεις μετάβασης δεν εξαρτώνται από τον αριθμό βήματος, αλλιώς καλείται ετερογενής.
Ας υπάρξει μια ομοιογενής αλυσίδα Markov και αφήστε το σύστημα μικρόΕχει nπιθανές καταστάσεις: μικρό 1 , …, S n. Αφήστε την πιθανότητα μετάβασης σε μια άλλη κατάσταση σε ένα βήμα να είναι γνωστή για κάθε κατάσταση, δηλ. P ij(από S i V Sjσε ένα βήμα), τότε μπορούμε να γράψουμε τις πιθανότητες μετάβασης ως πίνακα.
 . (7.1)
. (7.1)
Κατά μήκος της διαγώνιου αυτού του πίνακα είναι οι πιθανότητες να μεταβεί το σύστημα από την κατάσταση S iστην ίδια κατάσταση S i.
Χρήση συμβάντων που έχετε καταχωρίσει προηγουμένως ![]() , μπορούμε να γράψουμε τις πιθανότητες μετάβασης ως πιθανότητες υπό όρους:
, μπορούμε να γράψουμε τις πιθανότητες μετάβασης ως πιθανότητες υπό όρους: ![]() .
.
Προφανώς, το άθροισμα των όρων ![]() σε κάθε γραμμή του πίνακα (1) ισούται με ένα, αφού τα συμβάντα
σε κάθε γραμμή του πίνακα (1) ισούται με ένα, αφού τα συμβάντα ![]() σχηματίζουν μια πλήρη ομάδα ασυμβίβαστων γεγονότων.
σχηματίζουν μια πλήρη ομάδα ασυμβίβαστων γεγονότων.
Κατά την εξέταση των αλυσίδων Markov, καθώς και κατά την ανάλυση του Markov τυχαία διαδικασία, χρησιμοποιούνται διάφορα γραφήματα κατάστασης (Εικ. 7.10). 
Ρύζι. 7.10
Αυτό το σύστημα μπορεί να βρίσκεται σε οποιαδήποτε από τις έξι καταστάσεις, ενώ P ijείναι η πιθανότητα μετάβασης του συστήματος από την κατάσταση S iσε μια πολιτεία Sj. Για αυτό το σύστημα, γράφουμε τις εξισώσεις ότι το σύστημα ήταν σε κάποια κατάσταση και εκτός αυτής κατά τη διάρκεια του χρόνου tδεν βγήκε: 
ΣΕ γενική περίπτωσηη αλυσίδα Markov είναι ανομοιογενής, δηλαδή η πιθανότητα P ijαλλάζει από βήμα σε βήμα. Ας υποθέσουμε ότι δίνεται ένας πίνακας πιθανοτήτων μετάβασης σε κάθε βήμα, τότε η πιθανότητα ότι το σύστημα μικρόεπί κ-ο βήμα θα είναι στο κράτος S i, μπορεί να βρεθεί χρησιμοποιώντας τον τύπο ![]()
Γνωρίζοντας τον πίνακα πιθανοτήτων μετάβασης και αρχική κατάστασησύστημα, μπορεί κανείς να βρει τις πιθανότητες των καταστάσεων ![]() μετά από οποιαδήποτε κ-ο βήμα. Αφήστε την αρχική στιγμή το σύστημα να είναι σε κατάσταση S m. Τότε για t = 0
μετά από οποιαδήποτε κ-ο βήμα. Αφήστε την αρχική στιγμή το σύστημα να είναι σε κατάσταση S m. Τότε για t = 0
.
Ας βρούμε τις πιθανότητες μετά το πρώτο βήμα. Από το κράτος S mτο σύστημα θα πάει σε πολιτείες μικρό 1 , μικρό 2, κλπ. με πιθανότητες Μετα μεσημβριας 1 , Μετα μεσημβριας 2 , …, μμμ, …, P mn. Τότε μετά το πρώτο βήμα οι πιθανότητες θα είναι ίσες
. (7.2)
Ας βρούμε τις πιθανότητες της κατάστασης μετά το δεύτερο βήμα: . Θα υπολογίσουμε αυτές τις πιθανότητες χρησιμοποιώντας τον τύπο πλήρη πιθανότηταμε υποθέσεις: ![]() .
.
Οι υποθέσεις θα είναι οι ακόλουθες δηλώσεις:
- Μετά το πρώτο βήμα το σύστημα ήταν στην κατάσταση S 1 - H 1.
- Μετά το δεύτερο βήμα το σύστημα ήταν στην κατάσταση S2-H2.
- μετά nτου ου βήματος, το σύστημα ήταν στην κατάσταση S n -H n.

Πιθανότητα οποιασδήποτε κατάστασης μετά το δεύτερο βήμα:
![]() (7.3)
(7.3)
Ο τύπος (7.3) συνοψίζει όλες τις πιθανότητες μετάβασης P ij, αλλά λαμβάνονται υπόψη μόνο μη μηδενικά. Πιθανότητα οποιασδήποτε κατάστασης μετά κ-ο βήμα:
![]() (7.4)
(7.4)
Έτσι, η πιθανότητα μιας κατάστασης μετά κ-το βήμα καθορίζεται από επαναλαμβανόμενη φόρμουλα(7.4) μέσω των πιθανοτήτων ( κ - 1)ο βήμα.
Εργασία 6.Δίνεται ένας πίνακας πιθανοτήτων μετάβασης για μια αλυσίδα Markov σε ένα βήμα. Βρείτε τον πίνακα μετάβασης ενός δεδομένου κυκλώματος σε τρία βήματα  .
.
Λύση.Ο πίνακας μετάβασης ενός συστήματος είναι ένας πίνακας που περιέχει όλες τις πιθανότητες μετάβασης αυτού του συστήματος: 
Κάθε γραμμή του πίνακα περιέχει τις πιθανότητες γεγονότων (μετάβαση από την κατάσταση Εγώσε μια πολιτεία ι), που σχηματίζουν μια πλήρη ομάδα, οπότε το άθροισμα των πιθανοτήτων αυτών των γεγονότων είναι ίσο με ένα: ![]()
Ας συμβολίσουμε με p ij (n) την πιθανότητα ότι ως αποτέλεσμα n βημάτων (δοκιμών) το σύστημα θα μετακινηθεί από την κατάσταση i στην κατάσταση j. Για παράδειγμα, το p 25 (10) είναι η πιθανότητα μετάβασης από τη δεύτερη κατάσταση στην πέμπτη σε δέκα βήματα. Σημειώστε ότι για n=1 λαμβάνουμε πιθανότητες μετάβασης p ij (1)=p ij .
Μας δίνεται μια εργασία: γνωρίζοντας τις πιθανότητες μετάβασης p ij, βρείτε τις πιθανότητες p ij (n) της μετάβασης του συστήματος από την κατάσταση Εγώσε μια πολιτεία ιπίσω nβήματα. Για να γίνει αυτό, εισάγουμε ένα ενδιάμεσο (μεταξύ ΕγώΚαι ι) κατάσταση r. Με άλλα λόγια, θα υποθέσουμε ότι από την αρχική κατάσταση Εγώπίσω Μβήματα το σύστημα θα πάει σε μια ενδιάμεση κατάσταση rμε πιθανότητα p ij (n-m), μετά την οποία, για το υπόλοιπο n-m βήματααπό την ενδιάμεση κατάσταση r θα πάει στην τελική κατάσταση j με πιθανότητα p ij (n-m) . Χρησιμοποιώντας τον τύπο συνολικής πιθανότητας παίρνουμε: ![]() .
.
Αυτός ο τύπος ονομάζεται ισότητα του Markov. Χρησιμοποιώντας αυτόν τον τύπο, μπορείτε να βρείτε όλες τις πιθανότητες p ij (n) και, κατά συνέπεια, τον ίδιο τον πίνακα P n. Εφόσον ο λογισμός πίνακα οδηγεί στον στόχο πιο γρήγορα, γράφουμε τη σχέση πίνακα που προκύπτει από τον προκύπτοντα τύπο σε γενική μορφή.
Ας υπολογίσουμε τον πίνακα μετάβασης της αλυσίδας Markov σε τρία βήματα χρησιμοποιώντας τον προκύπτον τύπο: 
Απάντηση: .
.
Εργασία Νο. 1. Ο πίνακας πιθανοτήτων μετάβασης της αλυσίδας Markov έχει τη μορφή:  .
.
Η κατανομή στις καταστάσεις τη χρονική στιγμή t=0 προσδιορίζεται από το διάνυσμα:
π 0 =(0,5; 0,2; 0,3)
Εύρημα:α) κατανομή ανά κατάσταση σε στιγμές t=1,2,3,4.
γ) σταθερή κατανομή.
 Δείτε τι είναι το "Legion (αριθμός)" σε άλλα λεξικά
Δείτε τι είναι το "Legion (αριθμός)" σε άλλα λεξικά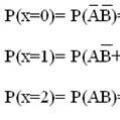 Παραδείγματα επίλυσης προβλημάτων στο θέμα "Τυχαίες μεταβλητές"
Παραδείγματα επίλυσης προβλημάτων στο θέμα "Τυχαίες μεταβλητές" Διαβάζω το ποίημα "Frost, Red Nose" του Nekrasov
Διαβάζω το ποίημα "Frost, Red Nose" του Nekrasov