Ο άμεσος μετασχηματισμός Fourier σας επιτρέπει να προσδιορίσετε. Μετασχηματισμός Fourier

Μετασχηματισμός Fourierείναι μια οικογένεια μαθηματικών μεθόδων που βασίζονται στην αποσύνθεση της αρχικής συνεχούς συνάρτησης του χρόνου σε ένα σύνολο βασικών αρμονικών συναρτήσεων (οι οποίες είναι ημιτονοειδείς συναρτήσεις) διαφορετικής συχνότητας, πλάτους και φάσης. Μπορεί να φανεί από τον ορισμό ότι η κύρια ιδέα του μετασχηματισμού είναι ότι οποιαδήποτε συνάρτηση μπορεί να αναπαρασταθεί ως ένα άπειρο άθροισμα ημιτονοειδών, καθένα από τα οποία θα χαρακτηρίζεται από το πλάτος, τη συχνότητα και την αρχική του φάση.

Ο μετασχηματισμός Fourier είναι ο ιδρυτής της φασματικής ανάλυσης. Η φασματική ανάλυση είναι μια μέθοδος επεξεργασίας σήματος που σας επιτρέπει να χαρακτηρίσετε το περιεχόμενο συχνότητας του μετρούμενου σήματος. Ανάλογα με το πώς αναπαρίσταται το σήμα, χρησιμοποιούνται διαφορετικοί μετασχηματισμοί Fourier. Υπάρχουν διάφοροι τύποι μετασχηματισμού Fourier:

– Continuous Fourier Transform (στην αγγλική λογοτεχνία Continue Time Fourier Transform – CTFTή εν συντομία, FT);

– Discrete Fourier Transform (στην αγγλική λογοτεχνία Discrete Fourier Transform – DFT);

– Γρήγορος μετασχηματισμός Fourier (στην αγγλική λογοτεχνία Fast Fourier transform – FFT).

Συνεχής μετασχηματισμός Fourier

Ο μετασχηματισμός Fourier είναι ένα μαθηματικό εργαλείο που χρησιμοποιείται σε διάφορα επιστημονικά πεδία. Σε ορισμένες περιπτώσεις, μπορεί να χρησιμοποιηθεί ως μέσο επίλυσης σύνθετων εξισώσεων που περιγράφουν δυναμικές διεργασίες που συμβαίνουν υπό την επίδραση ηλεκτρικής, θερμικής ή φωτεινής ενέργειας. Σε άλλες περιπτώσεις, σας επιτρέπει να επισημάνετε τα κανονικά στοιχεία σε ένα σύνθετο ταλαντευόμενο σήμα, ώστε να μπορείτε να ερμηνεύσετε σωστά τις πειραματικές παρατηρήσεις στην αστρονομία, την ιατρική και τη χημεία. Ένας συνεχής μετασχηματισμός είναι στην πραγματικότητα μια γενίκευση της σειράς Fourier, με την προϋπόθεση ότι η περίοδος της διευρυμένης συνάρτησης τείνει στο άπειρο. Έτσι, ο κλασικός μετασχηματισμός Fourier ασχολείται με το φάσμα του σήματος που λαμβάνεται σε όλο το εύρος της ύπαρξης της μεταβλητής.

Υπάρχουν διάφοροι τύποι γραφής του συνεχούς μετασχηματισμού Fourier, οι οποίοι διαφέρουν μεταξύ τους ως προς την τιμή του συντελεστή μπροστά από το ολοκλήρωμα (δύο μορφές γραφής):

ή

όπου και είναι η εικόνα Fourier της συνάρτησης ή το φάσμα συχνοτήτων της συνάρτησης.

- κυκλική συχνότητα.

Θα πρέπει να σημειωθεί ότι διαφορετικοί τύποι ηχογράφησης συναντώνται σε διάφορους τομείς της επιστήμης και της τεχνολογίας. Ο συντελεστής κανονικοποίησης είναι απαραίτητος για τη σωστή κλιμάκωση του σήματος από το πεδίο συχνότητας στο πεδίο του χρόνου. Ο παράγοντας κανονικοποίησης μειώνει το πλάτος του σήματος στην έξοδο του αντίστροφου μετασχηματισμού έτσι ώστε να ταιριάζει με το πλάτος του αρχικού σήματος. Στη μαθηματική βιβλιογραφία, ο άμεσος και ο αντίστροφος μετασχηματισμός Fourier πολλαπλασιάζονται με τον παράγοντα , ενώ στη φυσική, τις περισσότερες φορές, ο παράγοντας δεν ορίζεται για τον άμεσο μετασχηματισμό, αλλά ο παράγοντας ορίζεται για τον αντίστροφο. Εάν υπολογίσουμε διαδοχικά τον άμεσο μετασχηματισμό Fourier ενός συγκεκριμένου σήματος και στη συνέχεια πάρουμε τον αντίστροφο μετασχηματισμό Fourier, τότε το αποτέλεσμα του αντίστροφου μετασχηματισμού θα πρέπει να συμπίπτει πλήρως με το αρχικό σήμα.

Εάν η συνάρτηση είναι περιττή στο διάστημα (−∞, +∞), τότε ο μετασχηματισμός Fourier μπορεί να αναπαρασταθεί ως ημιτονική συνάρτηση:

Εάν η συνάρτηση είναι άρτια στο διάστημα (−∞, +∞), τότε ο μετασχηματισμός Fourier μπορεί να αναπαρασταθεί με όρους συνημίτονο:

Έτσι, ο συνεχής μετασχηματισμός Fourier μας επιτρέπει να αναπαραστήσουμε μια μη περιοδική συνάρτηση ως ολοκλήρωμα μιας συνάρτησης που αντιπροσωπεύει σε κάθε σημείο της τον συντελεστή της σειράς Fourier για μια μη περιοδική συνάρτηση.

Ο μετασχηματισμός Fourier είναι αναστρέψιμος, δηλαδή, εάν η εικόνα Fourier του υπολογίστηκε από τη συνάρτηση, τότε η αρχική συνάρτηση μπορεί να αποκατασταθεί μοναδικά από την εικόνα Fourier. Ο αντίστροφος μετασχηματισμός Fourier νοείται ως ολοκλήρωμα της μορφής (δύο μορφές γραφής):

ή

πού είναι η εικόνα Fourier της συνάρτησης ή το φάσμα συχνοτήτων της συνάρτησης;

- κυκλική συχνότητα.

Εάν η συνάρτηση είναι περιττή στο διάστημα (−∞, +∞), τότε ο αντίστροφος μετασχηματισμός Fourier μπορεί να αναπαρασταθεί ως ημιτονική συνάρτηση:

Εάν η συνάρτηση είναι άρτια στο διάστημα (−∞, +∞), τότε ο αντίστροφος μετασχηματισμός Fourier μπορεί να αναπαρασταθεί ως προς τη συνημίτονο:

Ως παράδειγμα, εξετάστε την ακόλουθη συνάρτηση . Το γράφημα της εκθετικής συνάρτησης υπό μελέτη παρουσιάζεται παρακάτω.

Εφόσον η συνάρτηση είναι άρτια συνάρτηση, τότε ο συνεχής μετασχηματισμός Fourier θα οριστεί ως εξής:

Ως αποτέλεσμα, λάβαμε την εξάρτηση της μεταβολής της μελετημένης εκθετικής συνάρτησης από το διάστημα συχνοτήτων (βλ. παρακάτω).

Ο συνεχής μετασχηματισμός Fourier χρησιμοποιείται συνήθως στη θεωρία όταν εξετάζουμε σήματα που αλλάζουν σύμφωνα με δεδομένες συναρτήσεις, αλλά στην πράξη συνήθως ασχολούνται με μετρήσεις που είναι διακριτά δεδομένα. Τα αποτελέσματα των μετρήσεων καταγράφονται σε τακτά χρονικά διαστήματα με μια συγκεκριμένη συχνότητα δειγματοληψίας, για παράδειγμα, 16000 Hz ή 22000 Hz. Ωστόσο, στη γενική περίπτωση, οι διακριτές μετρήσεις μπορεί να πάνε άνισα, αλλά αυτό περιπλέκει τη μαθηματική συσκευή ανάλυσης, επομένως συνήθως δεν χρησιμοποιείται στην πράξη.

Υπάρχει ένα σημαντικό θεώρημα του Kotelnikov (στην ξένη βιβλιογραφία υπάρχει το όνομα "θεώρημα Nyquist-Shannon", "θεώρημα δείγματος"), το οποίο δηλώνει ότι ένα αναλογικό περιοδικό σήμα με πεπερασμένο (περιορισμένο σε πλάτος) φάσμα (0 ... fmax) μπορούν να αποκατασταθούν μοναδικά χωρίς παραμορφώσεις και απώλειες στις διακριτές τους μετρήσεις, που λαμβάνονται με συχνότητα μεγαλύτερη ή ίση με το διπλάσιο της ανώτερης συχνότητας του φάσματος - συχνότητα δειγματοληψίας (fdisc >= 2*fmax). Με άλλα λόγια, σε ρυθμό δειγματοληψίας 1000 Hz, ένα σήμα με συχνότητα έως και 500 Hz μπορεί να ανακτηθεί από ένα αναλογικό περιοδικό σήμα. Πρέπει να σημειωθεί ότι η διακριτοποίηση μιας συνάρτησης στο χρόνο οδηγεί στην περιοδοποίηση του φάσματος της και η διακριτοποίηση του φάσματος στη συχνότητα οδηγεί στην περιοδοποίηση της συνάρτησης.

Αυτός είναι ένας από τους μετασχηματισμούς Fourier που χρησιμοποιούνται ευρέως στους αλγόριθμους επεξεργασίας ψηφιακών σημάτων.

Ο άμεσος διακριτός μετασχηματισμός Fourier συσχετίζει μια συνάρτηση χρόνου, η οποία ορίζεται από N-σημεία μέτρησης σε ένα δεδομένο χρονικό διάστημα, με μια άλλη συνάρτηση, η οποία ορίζεται σε ένα διάστημα συχνότητας. Θα πρέπει να σημειωθεί ότι η συνάρτηση στο χρονικό διάστημα καθορίζεται με τη χρήση δειγμάτων N και η συνάρτηση στον τομέα συχνότητας καθορίζεται χρησιμοποιώντας το φάσμα K-fold.

k ˗ δείκτης συχνότητας.

Η συχνότητα του kth σήματος καθορίζεται από την έκφραση

όπου T είναι η χρονική περίοδος κατά την οποία ελήφθησαν τα δεδομένα εισόδου.

Ο άμεσος διακριτός μετασχηματισμός μπορεί να ξαναγραφτεί με όρους πραγματικών και φανταστικών συνιστωσών. Το πραγματικό συστατικό είναι ένας πίνακας που περιέχει τις τιμές των συνημιτονικών συνιστωσών και το φανταστικό στοιχείο είναι ένας πίνακας που περιέχει τις τιμές των ημιτονοειδών συνιστωσών.

Από τις τελευταίες εκφράσεις φαίνεται ότι ο μετασχηματισμός αποσυνθέτει το σήμα σε ημιτονοειδείς συνιστώσες (που ονομάζονται αρμονικές) με συχνότητες από μία ταλάντωση ανά περίοδο έως Ν ταλαντώσεις ανά περίοδο.

Ο διακριτός μετασχηματισμός Fourier έχει ένα χαρακτηριστικό, αφού μια διακριτή ακολουθία μπορεί να ληφθεί από το άθροισμα των συναρτήσεων με διαφορετική σύνθεση του αρμονικού σήματος. Με άλλα λόγια, μια διακριτή ακολουθία αποσυντίθεται σε αρμονικές μεταβλητές - διφορούμενα. Επομένως, κατά την επέκταση μιας διακριτής συνάρτησης χρησιμοποιώντας έναν διακριτό μετασχηματισμό Fourier, στο δεύτερο μισό του φάσματος εμφανίζονται στοιχεία υψηλής συχνότητας, τα οποία δεν ήταν στο αρχικό σήμα. Αυτό το φάσμα υψηλής συχνότητας είναι μια κατοπτρική εικόνα του πρώτου μέρους του φάσματος (όσον αφορά τη συχνότητα, τη φάση και το πλάτος). Συνήθως δεν λαμβάνεται υπόψη το δεύτερο μισό του φάσματος και τα πλάτη του σήματος του πρώτου μέρους του φάσματος διπλασιάζονται.

Θα πρέπει να σημειωθεί ότι η επέκταση μιας συνεχούς συνάρτησης δεν οδηγεί στην εμφάνιση ενός εφέ κατοπτρισμού, αφού μια συνεχής συνάρτηση αποσυντίθεται μοναδικά σε αρμονικές μεταβλητές.

Το πλάτος της συνιστώσας DC είναι η μέση τιμή της συνάρτησης για μια επιλεγμένη χρονική περίοδο και προσδιορίζεται ως εξής:

Τα πλάτη και οι φάσεις των συνιστωσών συχνότητας του σήματος καθορίζονται από τις ακόλουθες σχέσεις:

Οι προκύπτουσες τιμές πλάτους και φάσης ονομάζονται πολική σημειογραφία. Το διάνυσμα σήματος που προκύπτει θα οριστεί ως εξής:

Εξετάστε τον αλγόριθμο για τον μετασχηματισμό μιας διακριτά δεδομένης συνάρτησης σε ένα δεδομένο διάστημα (σε μια δεδομένη περίοδο) με τον αριθμό των αρχικών σημείων

Μετασχηματισμός D σπινθήρα Fourier

Ως αποτέλεσμα του μετασχηματισμού, λαμβάνουμε τις πραγματικές και τις φανταστικές τιμές της συνάρτησης, η οποία ορίζεται στο εύρος συχνοτήτων.

Ο αντίστροφος διακριτός μετασχηματισμός Fourier συσχετίζει μια συνάρτηση συχνότητας , η οποία ορίζεται από ένα φάσμα K-fold στο πεδίο συχνοτήτων, με μια άλλη συνάρτηση, η οποία ορίζεται στο πεδίο του χρόνου.

N ˗ ο αριθμός των τιμών σήματος που μετρήθηκαν ανά περίοδο, καθώς και η πολλαπλότητα του φάσματος συχνοτήτων.

k ˗ δείκτης συχνότητας.

Όπως ήδη αναφέρθηκε, ο διακριτός μετασχηματισμός Fourier αντιστοιχίζει τα Ν-σημεία ενός διακριτού σήματος σε φασματικά δείγματα μιγαδικών Ν του σήματος. Ο υπολογισμός ενός φασματικού δείγματος απαιτεί N πράξεις μιγαδικού πολλαπλασιασμού και πρόσθεσης. Έτσι, η υπολογιστική πολυπλοκότητα του διακριτού αλγόριθμου μετασχηματισμού Fourier είναι τετραγωνική, με άλλα λόγια, απαιτούνται μιγαδικές πράξεις πολλαπλασιασμού και πρόσθεσης.

Μετασχηματισμός Fourier - ένας μετασχηματισμός που συγκρίνει τις συναρτήσεις κάποιας πραγματικής μεταβλητής. Αυτή η λειτουργία εκτελείται κάθε φορά που αντιλαμβανόμαστε διαφορετικούς ήχους. Το αυτί εκτελεί έναν αυτόματο «υπολογισμό», τον οποίο η συνείδησή μας είναι ικανή να εκτελέσει μόνο αφού μελετήσει το αντίστοιχο τμήμα των ανώτερων μαθηματικών. Το ανθρώπινο όργανο ακοής δημιουργεί έναν μετασχηματισμό, ως αποτέλεσμα του οποίου ο ήχος (ταλαντωτική κίνηση σωματιδίων υπό όρους σε ένα ελαστικό μέσο που διαδίδονται σε μορφή κύματος σε στερεό, υγρό ή αέριο μέσο) παρέχεται με τη μορφή φάσματος διαδοχικών τιμών του επιπέδου έντασης των τόνων διαφορετικών υψών. Μετά από αυτό, ο εγκέφαλος μετατρέπει αυτές τις πληροφορίες σε έναν ήχο οικείο σε όλους.

Μαθηματικός μετασχηματισμός Fourier

Ο μετασχηματισμός των ηχητικών κυμάτων ή άλλων ταλαντωτικών διεργασιών (από την ακτινοβολία φωτός και την παλίρροια των ωκεανών σε κύκλους αστρικής ή ηλιακής δραστηριότητας) μπορεί επίσης να πραγματοποιηθεί χρησιμοποιώντας μαθηματικές μεθόδους. Έτσι, χρησιμοποιώντας αυτές τις τεχνικές, είναι δυνατή η αποσύνθεση συναρτήσεων αναπαραστώντας τις ταλαντωτικές διεργασίες ως ένα σύνολο ημιτονοειδών συνιστωσών, δηλαδή κυματιστές καμπύλες που πηγαίνουν από το ελάχιστο στο μέγιστο και μετά πάλι στο ελάχιστο, όπως ένα κύμα θάλασσας. Μετασχηματισμός Fourier - ένας μετασχηματισμός του οποίου η συνάρτηση περιγράφει τη φάση ή το πλάτος κάθε ημιτονοειδούς που αντιστοιχεί σε μια ορισμένη συχνότητα. Η φάση είναι το σημείο εκκίνησης της καμπύλης και το πλάτος είναι το ύψος της.

Ο μετασχηματισμός Fourier (τα παραδείγματα φαίνονται στη φωτογραφία) είναι ένα πολύ ισχυρό εργαλείο που χρησιμοποιείται σε διάφορους τομείς της επιστήμης. Σε ορισμένες περιπτώσεις, χρησιμοποιείται ως μέσο επίλυσης μάλλον πολύπλοκων εξισώσεων που περιγράφουν δυναμικές διεργασίες που συμβαίνουν υπό την επίδραση του φωτός, της θερμικής ή ηλεκτρικής ενέργειας. Σε άλλες περιπτώσεις, σας επιτρέπει να προσδιορίσετε τα κανονικά στοιχεία σε πολύπλοκα ταλαντευτικά σήματα, χάρη στα οποία μπορείτε να ερμηνεύσετε σωστά διάφορες πειραματικές παρατηρήσεις στη χημεία, την ιατρική και την αστρονομία.

Ιστορική αναφορά

Ο πρώτος άνθρωπος που εφάρμοσε αυτή τη μέθοδο ήταν ο Γάλλος μαθηματικός Jean Baptiste Fourier. Ο μετασχηματισμός, που αργότερα πήρε το όνομά του, χρησιμοποιήθηκε αρχικά για να περιγράψει τον μηχανισμό της αγωγιμότητας της θερμότητας. Ο Φουριέ πέρασε ολόκληρη την ενήλικη ζωή του μελετώντας τις ιδιότητες της θερμότητας. Συνέβαλε τεράστια στη μαθηματική θεωρία του προσδιορισμού των ριζών των αλγεβρικών εξισώσεων. Ο Φουριέ ήταν καθηγητής ανάλυσης στην Πολυτεχνική Σχολή, γραμματέας του Ινστιτούτου Αιγυπτιολογίας, ήταν στην αυτοκρατορική υπηρεσία, στην οποία διακρίθηκε κατά την κατασκευή του δρόμου προς Τορίνο (υπό την ηγεσία του, περισσότερα από 80 χιλιάδες τετραγωνικά χιλιόμετρα ελονοσίας βάλτοι αποξηράνθηκαν). Ωστόσο, όλη αυτή η έντονη δραστηριότητα δεν εμπόδισε τον επιστήμονα να κάνει μαθηματική ανάλυση. Το 1802, έβγαλε μια εξίσωση που περιγράφει τη διάδοση της θερμότητας στα στερεά. Το 1807, ο επιστήμονας ανακάλυψε μια μέθοδο για την επίλυση αυτής της εξίσωσης, η οποία ονομάστηκε "μετασχηματισμός Fourier".

Ανάλυση θερμικής αγωγιμότητας

Ο επιστήμονας εφάρμοσε μια μαθηματική μέθοδο για να περιγράψει τον μηχανισμό αγωγιμότητας της θερμότητας. Ένα βολικό παράδειγμα, στο οποίο δεν υπάρχουν δυσκολίες στον υπολογισμό, είναι η διάδοση της θερμικής ενέργειας μέσω ενός σιδερένιου δακτυλίου, ένα μέρος βυθισμένο στη φωτιά. Για να πραγματοποιήσει πειράματα, ο Φουριέ θέρμανε ένα μέρος αυτού του δακτυλίου καυτό και το έθαψε σε ψιλή άμμο. Μετά από αυτό, έκανε μετρήσεις θερμοκρασίας στην αντίθετη πλευρά του. Αρχικά, η κατανομή της θερμότητας είναι ακανόνιστη: ένα μέρος του δακτυλίου είναι κρύο και το άλλο είναι ζεστό, και μπορεί να παρατηρηθεί μια απότομη διαβάθμιση θερμοκρασίας μεταξύ αυτών των ζωνών. Ωστόσο, κατά τη διαδικασία διάδοσης της θερμότητας σε ολόκληρη την επιφάνεια του μετάλλου, γίνεται πιο ομοιόμορφο. Έτσι, σύντομα αυτή η διαδικασία παίρνει τη μορφή ημιτονοειδούς. Στην αρχή, το γράφημα αυξάνεται ομαλά και επίσης μειώνεται ομαλά, ακριβώς σύμφωνα με τους νόμους της αλλαγής της συνάρτησης συνημιτόνου ή ημιτόνου. Το κύμα σταδιακά ισοπεδώνεται και, ως αποτέλεσμα, η θερμοκρασία γίνεται ίδια σε ολόκληρη την επιφάνεια του δακτυλίου.

Ο συγγραφέας αυτής της μεθόδου πρότεινε ότι η αρχική ακανόνιστη κατανομή μπορεί να αποσυντεθεί σε μια σειρά στοιχειωδών ημιτονοειδών. Κάθε ένα από αυτά θα έχει τη δική του φάση (αρχική θέση) και το δικό του μέγιστο θερμοκρασίας. Επιπλέον, κάθε τέτοιο στοιχείο αλλάζει από το ελάχιστο στο μέγιστο και πίσω σε μια πλήρη περιστροφή γύρω από τον δακτύλιο ακέραιο αριθμό φορές. Μια συνιστώσα με μία περίοδο ονομαζόταν θεμελιώδης αρμονική και μια τιμή με δύο ή περισσότερες περιόδους ονομαζόταν δεύτερη και ούτω καθεξής. Έτσι, η μαθηματική συνάρτηση που περιγράφει τη μέγιστη θερμοκρασία, τη φάση ή τη θέση ονομάζεται μετασχηματισμός Fourier της συνάρτησης κατανομής. Ο επιστήμονας μείωσε ένα μόνο συστατικό, το οποίο είναι δύσκολο να περιγραφεί μαθηματικά, σε ένα εύχρηστο εργαλείο - σειρά συνημίτονου και ημιτόνου, που μαζί δίνουν την αρχική κατανομή.

Η ουσία της ανάλυσης

Εφαρμόζοντας αυτή την ανάλυση στον μετασχηματισμό της διάδοσης της θερμότητας μέσω ενός στερεού αντικειμένου που έχει δακτυλιοειδές σχήμα, ο μαθηματικός συλλογίστηκε ότι η αύξηση των περιόδων του ημιτονοειδούς συστατικού θα οδηγούσε στην ταχεία διάσπασή του. Αυτό φαίνεται καθαρά στις θεμελιώδεις και δεύτερες αρμονικές. Στο δεύτερο, η θερμοκρασία φθάνει τη μέγιστη και την ελάχιστη τιμή δύο φορές σε ένα πέρασμα και στο πρώτο, μόνο μία φορά. Αποδεικνύεται ότι η απόσταση που καλύπτεται από τη θερμότητα στη δεύτερη αρμονική θα είναι η μισή από αυτήν στην κύρια. Επιπλέον, η κλίση στο δεύτερο θα είναι επίσης δύο φορές πιο απότομη από το πρώτο. Επομένως, δεδομένου ότι η πιο έντονη ροή θερμότητας διανύει μια απόσταση δύο φορές μικρότερη, αυτή η αρμονική θα διασπαστεί τέσσερις φορές πιο γρήγορα από τη θεμελιώδη σε συνάρτηση με το χρόνο. Στο μέλλον, αυτή η διαδικασία θα είναι ακόμη πιο γρήγορη. Ο μαθηματικός πίστευε ότι αυτή η μέθοδος σας επιτρέπει να υπολογίσετε τη διαδικασία της αρχικής κατανομής της θερμοκρασίας με την πάροδο του χρόνου.

Πρόκληση για τους σύγχρονους

Ο αλγόριθμος μετασχηματισμού Fourier έγινε μια πρόκληση για τα θεωρητικά θεμέλια των μαθηματικών εκείνης της εποχής. Στις αρχές του δέκατου ένατου αιώνα, οι περισσότεροι εξέχοντες επιστήμονες, συμπεριλαμβανομένων των Lagrange, Laplace, Poisson, Legendre και Biot, δεν αποδέχτηκαν τη δήλωσή του ότι η αρχική κατανομή θερμοκρασίας αποσυντίθεται σε συστατικά με τη μορφή θεμελιώδους αρμονικής και υψηλότερων συχνοτήτων. Ωστόσο, η Ακαδημία Επιστημών δεν μπορούσε να αγνοήσει τα αποτελέσματα που έλαβε ο μαθηματικός και του απένειμε βραβείο για τη θεωρία των νόμων της αγωγιμότητας της θερμότητας, καθώς και για τη σύγκρισή της με φυσικά πειράματα. Στην προσέγγιση του Fourier, η κύρια ένσταση ήταν το γεγονός ότι η ασυνεχής συνάρτηση αντιπροσωπεύεται από το άθροισμα πολλών ημιτονοειδών συναρτήσεων που είναι συνεχείς. Εξάλλου, περιγράφουν σκισμένες ευθείες και καμπύλες γραμμές. Οι σύγχρονοι του επιστήμονα δεν αντιμετώπισαν ποτέ παρόμοια κατάσταση, όταν οι ασυνεχείς συναρτήσεις περιγράφονταν με συνδυασμό συνεχών, όπως τετραγωνικών, γραμμικών, ημιτονοειδών ή εκθετικών. Σε περίπτωση που ο μαθηματικός είχε δίκιο στις δηλώσεις του, τότε το άθροισμα μιας άπειρης σειράς μιας τριγωνομετρικής συνάρτησης θα πρέπει να μειωθεί σε μια ακριβή βαθμιαία. Τότε, μια τέτοια δήλωση φαινόταν παράλογη. Ωστόσο, παρά τις αμφιβολίες, ορισμένοι ερευνητές (π.χ. Claude Navier, Sophie Germain) έχουν διευρύνει το πεδίο της έρευνας και τις έχουν ξεπεράσει την ανάλυση της κατανομής της θερμικής ενέργειας. Εν τω μεταξύ, οι μαθηματικοί συνέχισαν να αγωνιούν για το ερώτημα εάν το άθροισμα πολλών ημιτονοειδών συναρτήσεων μπορεί να αναχθεί σε μια ακριβή αναπαράσταση μιας ασυνεχούς.

200 χρόνια ιστορίας

Αυτή η θεωρία αναπτύχθηκε σε δύο αιώνες, σήμερα τελικά έχει διαμορφωθεί. Με τη βοήθειά του, οι χωρικές ή χρονικές λειτουργίες χωρίζονται σε ημιτονοειδείς συνιστώσες, οι οποίες έχουν τη δική τους συχνότητα, φάση και πλάτος. Αυτός ο μετασχηματισμός επιτυγχάνεται με δύο διαφορετικές μαθηματικές μεθόδους. Η πρώτη από αυτές χρησιμοποιείται όταν η αρχική συνάρτηση είναι συνεχής και η δεύτερη - όταν αντιπροσωπεύεται από ένα σύνολο διακριτών μεμονωμένων αλλαγών. Εάν η έκφραση λαμβάνεται από τιμές που ορίζονται από διακριτά διαστήματα, τότε μπορεί να χωριστεί σε πολλές ημιτονοειδείς εκφράσεις με διακριτές συχνότητες - από τη χαμηλότερη και στη συνέχεια δύο φορές, τρεις φορές και ούτω καθεξής υψηλότερη από την κύρια. Ένα τέτοιο άθροισμα ονομάζεται σειρά Fourier. Εάν δοθεί στην αρχική παράσταση μια τιμή για κάθε πραγματικό αριθμό, τότε μπορεί να αποσυντεθεί σε πολλές ημιτονοειδείς από όλες τις πιθανές συχνότητες. Ονομάζεται κοινώς ολοκλήρωμα Fourier και η λύση συνεπάγεται ολοκληρωτικούς μετασχηματισμούς της συνάρτησης. Ανεξάρτητα από το πώς επιτυγχάνεται η μετατροπή, πρέπει να καθοριστούν δύο αριθμοί για κάθε συχνότητα: πλάτος και συχνότητα. Αυτές οι τιμές εκφράζονται με τη μορφή μιας ενιαίας Θεωρίας εκφράσεων μιγαδικών μεταβλητών, μαζί με τον μετασχηματισμό Fourier, κατέστησαν δυνατή τη διενέργεια υπολογισμών στο σχεδιασμό διαφόρων ηλεκτρικών κυκλωμάτων, την ανάλυση των μηχανικών δονήσεων, τη μελέτη του μηχανισμός διάδοσης κυμάτων και πολλά άλλα.

Μετασχηματισμός Fourier σήμερα

Σήμερα, η μελέτη αυτής της διαδικασίας περιορίζεται κυρίως στην εύρεση αποτελεσματικών μεθόδων για τη μετάβαση από μια συνάρτηση στη μετασχηματισμένη μορφή της και αντίστροφα. Αυτή η λύση ονομάζεται άμεσος και αντίστροφος μετασχηματισμός Fourier. Τι σημαίνει? Για να παραχθεί ένας άμεσος μετασχηματισμός Fourier, μπορεί κανείς να χρησιμοποιήσει μαθηματικές μεθόδους ή αναλυτικές. Παρά το γεγονός ότι προκύπτουν ορισμένες δυσκολίες κατά τη χρήση τους στην πράξη, τα περισσότερα ολοκληρώματα έχουν ήδη βρεθεί και συμπεριληφθεί σε μαθηματικά βιβλία αναφοράς. Με τη βοήθεια αριθμητικών μεθόδων, μπορεί κανείς να υπολογίσει εκφράσεις των οποίων η μορφή βασίζεται σε πειραματικά δεδομένα ή συναρτήσεις των οποίων τα ολοκληρώματα δεν βρίσκονται στους πίνακες και είναι δύσκολο να παρουσιαστούν σε αναλυτική μορφή.

Πριν από την έλευση της τεχνολογίας των υπολογιστών, οι υπολογισμοί τέτοιων μετασχηματισμών ήταν πολύ κουραστικοί, απαιτούσαν τη χειροκίνητη εκτέλεση ενός μεγάλου αριθμού αριθμητικών πράξεων, οι οποίες εξαρτιόνταν από τον αριθμό των σημείων που περιγράφουν τη συνάρτηση κύματος. Για τη διευκόλυνση των υπολογισμών, σήμερα υπάρχουν ειδικά προγράμματα που επέτρεψαν την εφαρμογή νέων.Έτσι, το 1965, ο James Cooley και ο John Tukey δημιούργησαν λογισμικό που έγινε γνωστό ως "Fast Fourier Transform". Σας επιτρέπει να εξοικονομήσετε χρόνο για υπολογισμούς μειώνοντας τον αριθμό των πολλαπλασιασμών στην ανάλυση της καμπύλης. Η μέθοδος γρήγορου μετασχηματισμού Fourier βασίζεται στη διαίρεση της καμπύλης σε μεγάλο αριθμό ομοιόμορφων τιμών δείγματος. Αντίστοιχα, ο αριθμός των πολλαπλασιασμών μειώνεται στο μισό με την ίδια μείωση στον αριθμό των πόντων.

Εφαρμογή του μετασχηματισμού Fourier

Αυτή η διαδικασία χρησιμοποιείται σε διάφορους τομείς της επιστήμης: στη φυσική, την επεξεργασία σήματος, τη συνδυαστική, τη θεωρία πιθανοτήτων, την κρυπτογραφία, τη στατιστική, την ωκεανολογία, την οπτική, την ακουστική, τη γεωμετρία και άλλα. Οι πλούσιες δυνατότητες εφαρμογής του βασίζονται σε μια σειρά από χρήσιμα χαρακτηριστικά, τα οποία ονομάζονται «Ιδιότητες μετασχηματισμού Fourier». Ας τα εξετάσουμε.

1. Ο μετασχηματισμός μιας συνάρτησης είναι γραμμικός τελεστής και, με την κατάλληλη κανονικοποίηση, είναι ενιαίος. Αυτή η ιδιότητα είναι γνωστή ως θεώρημα Parseval, ή γενικά θεώρημα Plancherel, ή δυϊσμός του Pontryagin.

2. Ο μετασχηματισμός είναι αναστρέψιμος. Επιπλέον, το αντίστροφο αποτέλεσμα έχει σχεδόν την ίδια μορφή όπως στην άμεση λύση.

3. Οι ημιτονοειδείς βασικές εκφράσεις είναι δικές τους διαφοροποιημένες συναρτήσεις. Αυτό σημαίνει ότι μια τέτοια αναπαράσταση αλλάζει με σταθερό συντελεστή σε συνηθισμένους αλγεβρικούς.

4. Σύμφωνα με το θεώρημα της «συνέλιξης», αυτή η διαδικασία μετατρέπει μια σύνθετη πράξη σε στοιχειώδη πολλαπλασιασμό.

5. Ο διακριτός μετασχηματισμός Fourier μπορεί να υπολογιστεί γρήγορα σε έναν υπολογιστή χρησιμοποιώντας τη μέθοδο "γρήγορη".

Ποικιλίες του μετασχηματισμού Fourier

1. Τις περισσότερες φορές, αυτός ο όρος χρησιμοποιείται για να δηλώσει έναν συνεχή μετασχηματισμό που παρέχει οποιαδήποτε τετραγωνικά ολοκληρωμένη έκφραση ως άθροισμα σύνθετων εκθετικών παραστάσεων με συγκεκριμένες γωνιακές συχνότητες και πλάτη. Αυτός ο τύπος έχει πολλές διαφορετικές μορφές, οι οποίες μπορεί να διαφέρουν σε σταθερούς συντελεστές. Η συνεχής μέθοδος περιλαμβάνει έναν πίνακα μετατροπών, ο οποίος βρίσκεται σε βιβλία μαθηματικών αναφορών. Μια γενικευμένη περίπτωση είναι ένας κλασματικός μετασχηματισμός, μέσω του οποίου η δεδομένη διαδικασία μπορεί να αυξηθεί στην απαιτούμενη πραγματική ισχύ.

2. Η συνεχής μέθοδος είναι μια γενίκευση της πρώιμης τεχνικής των σειρών Fourier, που ορίζεται για διάφορες περιοδικές συναρτήσεις ή εκφράσεις που υπάρχουν σε μια περιορισμένη περιοχή και τις αναπαριστούν ως μια σειρά ημιτονοειδών.

3. Διακριτός μετασχηματισμός Fourier. Αυτή η μέθοδος χρησιμοποιείται στην τεχνολογία των υπολογιστών για επιστημονικούς υπολογισμούς και για την επεξεργασία ψηφιακού σήματος. Για να πραγματοποιηθεί αυτός ο τύπος υπολογισμού, απαιτείται να υπάρχουν συναρτήσεις που ορίζουν μεμονωμένα σημεία, περιοδικές ή περιορισμένες περιοχές σε ένα διακριτό σύνολο αντί για συνεχή ολοκληρώματα Fourier. Ο μετασχηματισμός σήματος σε αυτή την περίπτωση αντιπροσωπεύεται ως το άθροισμα των ημιτονοειδών. Παράλληλα, η χρήση της «γρήγορης» μεθόδου επιτρέπει τη χρήση διακριτών λύσεων για τυχόν πρακτικά προβλήματα.

4. Ο μετασχηματισμός Fourier με παράθυρο είναι μια γενικευμένη μορφή της κλασικής μεθόδου. Σε αντίθεση με την τυπική λύση, όταν χρησιμοποιείται, η οποία λαμβάνεται σε όλο το εύρος ύπαρξης μιας δεδομένης μεταβλητής, εδώ μόνο η τοπική κατανομή συχνότητας έχει ιδιαίτερο ενδιαφέρον, με την προϋπόθεση ότι διατηρείται η αρχική μεταβλητή (χρόνος).

5. Δισδιάστατος μετασχηματισμός Fourier. Αυτή η μέθοδος χρησιμοποιείται για εργασία με δισδιάστατους πίνακες δεδομένων. Σε αυτή την περίπτωση, ο μετασχηματισμός πραγματοποιείται πρώτα προς τη μία κατεύθυνση και στη συνέχεια προς την άλλη.

συμπέρασμα

Σήμερα, η μέθοδος Fourier είναι σταθερά εδραιωμένη σε διάφορους τομείς της επιστήμης. Για παράδειγμα, το 1962, το σχήμα της διπλής έλικας του DNA ανακαλύφθηκε χρησιμοποιώντας ανάλυση Fourier σε συνδυασμό με την τελευταία να εστιάζει σε κρυστάλλους ινών DNA, με αποτέλεσμα η εικόνα που ελήφθη από τη διάθλαση της ακτινοβολίας να καταγραφεί σε φιλμ. Αυτή η εικόνα έδωσε πληροφορίες σχετικά με την τιμή του πλάτους κατά τη χρήση του μετασχηματισμού Fourier σε μια δεδομένη κρυσταλλική δομή. Τα δεδομένα φάσης ελήφθησαν συγκρίνοντας τον χάρτη περίθλασης DNA με χάρτες που προέκυψαν από την ανάλυση παρόμοιων χημικών δομών. Ως αποτέλεσμα, οι βιολόγοι έχουν αποκαταστήσει την κρυσταλλική δομή - την αρχική λειτουργία.

Οι μετασχηματισμοί Fourier παίζουν τεράστιο ρόλο στη μελέτη του διαστήματος, της φυσικής των ημιαγωγών και του πλάσματος, της ακουστικής μικροκυμάτων, της ωκεανογραφίας, του ραντάρ, της σεισμολογίας και των ιατρικών εξετάσεων.

Αυτοί οι μετασχηματισμοί είναι λειτουργικοί επειδή μετατρέπουν κάποια συνάρτηση μιας μεταβλητής σε μια εντελώς διαφορετική συνάρτηση μιας μεταβλητής και το αντίστροφο.

Οι μετασχηματισμοί Fourier έχουν τη μορφή:

Η ολοκληρωτική εξίσωση (4.34) ονομάζεται άμεση και η εξίσωση (4.35) ονομάζεται αντίστροφος μετασχηματισμός Fourier. Συντομογραφία για αυτές τις εξισώσεις

Το ολοκλήρωμα Fourier (άμεσος μετασχηματισμός Fourier) σας επιτρέπει να επεκτείνετε μια μη περιοδική συνάρτηση που έχει την ιδιότητα της απόλυτης ολοκλήρωσης εντός δεδομένων ορίων σε μια άπειρη σειρά αρμονικών που σχηματίζουν ένα συνεχές φάσμα συχνοτήτων στην περιοχή από έως με ένα απειροελάχιστο διάστημα συχνοτήτων μεταξύ γειτονικών αρμονικών (δηλαδή στο όριο

Η μέθοδος μετασχηματισμού Fourier είναι ακατάλληλη για μη μηδενικές αρχικές (ή οριακές) συνθήκες. Αυτή η μέθοδος μπορεί να εφαρμοστεί μόνο όταν οι επιθυμητές συναρτήσεις έχουν εικόνα Fourier, δηλ. για απόλυτα ενσωματωμένες συναρτήσεις χρόνου που ικανοποιούν την ανισότητα

Οι πιο κοινές συναρτήσεις στη θεωρία ελέγχου είναι η συνάρτηση μοναδιαίου βήματος (1.44) και το γινόμενο μιας ημιτονοειδούς συνάρτησης και η συνάρτηση μονάδας (1.51). Ο μετασχηματισμός Fourier δεν είναι εφαρμόσιμος σε καμία από αυτές τις συναρτήσεις, καθώς η συνθήκη (4.38) δεν ικανοποιείται.

Αυτές οι αδυναμίες περιορίζουν τη χρήση της μεθόδου μετασχηματισμού Fourier.

Για να εφαρμοστεί το ολοκλήρωμα Fourier, είναι απαραίτητο να επιλέξετε μια συνάρτηση που να είναι αρκετά κοντά σε αυτήν που μελετάται, για παράδειγμα, σε μια συνάρτηση βήματος σε πεπερασμένες τιμές, αλλά ταυτόχρονα να ικανοποιεί την συνθήκη (4.38). Αυτή η συνάρτηση μπορεί να ληφθεί πολλαπλασιάζοντας

συνάρτηση βήματος όπου c είναι μια αρκετά μικρή θετική τιμή. Η πρόσφατα αποκτηθείσα βοηθητική λειτουργία

Αφήνοντας το c να τείνει στο μηδέν και περνώντας στο όριο, μπορούμε να περάσουμε από τη βοηθητική συνάρτηση στην κύρια.Επιπλέον, αν περιοριστούμε σε συναρτήσεις που είναι πανομοιότυπα ίσες με το μηδέν, τότε η συνθήκη (4.38) θα ισχύει για μια μεγάλη κλάση των συναρτήσεων και μπορούμε να βρούμε το φάσμα συχνοτήτων της συνάρτησης χρησιμοποιώντας την έκφραση (4.34) . Αντίθετα, εισάγουμε μια νέα σημείωση, καθώς αυτή η ποσότητα εξαρτάται πλέον και από το c:

Βάζοντας με βρείτε

Αυτός ο τύπος συμπίπτει με τον άμεσο μετασχηματισμό Laplace (4.9).

Από αυτό προκύπτει ότι ο μετασχηματισμός Fourier μπορεί να θεωρηθεί ως ειδική περίπτωση του μετασχηματισμού Laplace.

Οι μέθοδοι μετασχηματισμού που περιγράφονται παραπάνω μας επιτρέπουν να βγάλουμε τα ακόλουθα συμπεράσματα:

1) Οι ολοκληρωτικές-διαφορικές εξισώσεις αντικαθίστανται από αλγεβρικές εξισώσεις.

2) η λειτουργία του προσδιορισμού των σταθερών ολοκλήρωσης εξαλείφεται, καθώς οι αρχικές συνθήκες λαμβάνονται υπόψη από την αρχή κατά την εύρεση της εικόνας της επιθυμητής τιμής.

3) η λειτουργία του προσδιορισμού των ριζών της χαρακτηριστικής εξίσωσης διατηρείται πλήρως.

Το πιο βολικό για την επίλυση πρακτικών προβλημάτων είναι η μέθοδος μετασχηματισμού Laplace. Σε ελαφρώς τροποποιημένη μορφή, μπορεί να εφαρμοστεί στη μελέτη διακριτών ACS (βλ. Κεφάλαιο 7).

Εξετάστε τη χρήση της μεθόδου μετασχηματισμού Laplace για την επίλυση μιας διαφορικής εξίσωσης της μορφής

Μετασχηματίζουμε αυτή τη διαφορική εξίσωση χρησιμοποιώντας τον άμεσο μετασχηματισμό Laplace (4.9) και τα θεωρήματα 1 και 2. Ως αποτέλεσμα, λαμβάνουμε μια αλγεβρική εξίσωση γραμμένη για εικόνες:

όπου είναι το άθροισμα όλων των όρων που περιέχουν τις αρχικές προϋποθέσεις.

Από εδώ είναι η εικόνα της επιθυμητής συνάρτησης

Για μηδενικές αρχικές συνθήκες, οι εκφράσεις (4.41) και (4.42) απλοποιούνται:

Γνωρίζοντας την εικόνα της επιθυμητής συνάρτησης, μπορείτε να βρείτε το πρωτότυπο, για παράδειγμα, από πίνακες εικόνων.

Εάν η εικόνα της επιθυμητής τιμής είναι ένα ορθολογικό αλγεβρικό κλάσμα, τότε προσπαθούν να το γράψουν ως άθροισμα απλών κλασμάτων με σταθερούς συντελεστές. Ο αντίστροφος μετασχηματισμός για καθένα από αυτά τα απλά κλάσματα μπορεί να ληφθεί από τους πίνακες και η τελική έκφραση του πρωτοτύπου παρουσιάζεται ως το άθροισμα των μεμονωμένων τιμών που βρέθηκαν. Μπορείτε επίσης να χρησιμοποιήσετε το θεώρημα αποσύνθεσης για να προσδιορίσετε το αρχικό.

Αν η εικόνα Laplace είναι ένα ορθολογικό αλγεβρικό κλάσμα της μορφής

Εξετάστε τις βασικές ιδιότητες του μετασχηματισμού Fourier.

Γραμμικότητα. Εξετάστε τις συναρτήσεις και
με φάσματα
και
:

(12)

Τότε το φάσμα του γραμμικού συνδυασμού τους θα είναι:

Χρονοκαθυστερηση. Υποθέτουμε ότι το φάσμα είναι γνωστό
σήμα

(14)

Ας υπολογίσουμε το φάσμα του σήματος με χρονική μετατόπιση:
. Δηλώστε το όρισμα συνάρτησης της νέας μεταβλητής
, έπειτα
και

Παρουσιάστηκε καθυστέρηση σήματος για λίγο οδηγεί στον πολλαπλασιασμό του φάσματος με
.

Αλλαγή κλίμακας.Υποθέτουμε ότι το φάσμα είναι γνωστό
σήμα
όπως μέσω
εκφράζεται το φάσμα του σήματος
. Εισάγουμε μια νέα μεταβλητή
, αλλάζουμε τη μεταβλητή ολοκλήρωσης
.

(16)

Πολλαπλασιασμός με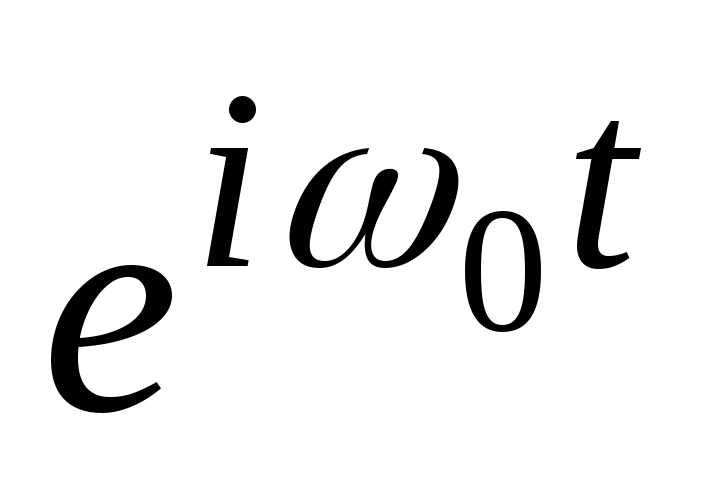
. Όπως και στην προηγούμενη περίπτωση, υποθέτουμε ότι το φάσμα είναι γνωστό
σήμα
. Βρείτε το φάσμα αυτού του σήματος, πολλαπλασιασμένο επί
.

Έτσι, πολλαπλασιάζοντας το σήμα επί
οδηγεί σε μετατόπιση του φάσματος κατά .

Παράγωγο φάσμα.Σε αυτή την περίπτωση, το βασικό σημείο είναι η απόλυτη ενσωμάτωση της συνάρτησης. Από το γεγονός ότι το ολοκλήρωμα του συντελεστή συνάρτησης πρέπει να είναι οριοθετημένο, προκύπτει ότι στο άπειρο η συνάρτηση πρέπει να τείνει στο μηδέν. Το ολοκλήρωμα της παραγώγου της συνάρτησης λαμβάνεται σε μέρη, οι μη ολοκληρωτικοί όροι που προκύπτουν είναι ίσοι με μηδέν, αφού η συνάρτηση τείνει στο μηδέν στο άπειρο.

(18)

Φάσμα του ολοκληρώματος.Ας βρούμε το φάσμα του σήματος
. Και θα το υποθέσουμε
, δηλαδή το σήμα δεν έχει σταθερή συνιστώσα. Αυτή η απαίτηση είναι απαραίτητη ώστε οι όροι εκτός του ολοκληρώματος να είναι ίσοι με μηδέν όταν το ολοκλήρωμα λαμβάνεται από μέρη.

(19)

Θεώρημα συνέλιξης.Είναι γνωστό ότι
και
φάσματα συνάρτησης
και
αντίστοιχα. Απαιτείται να εκφραστεί το φάσμα συνέλιξης
διά μέσου
και
. Για να γίνει αυτό, στο ολοκλήρωμα Fourier της συνέλιξης, μία από τις συναρτήσεις θα αντικατασταθεί από τη μεταβλητή
, τότε ο εκθέτης μπορεί να αντικατασταθεί
. Ως αποτέλεσμα μιας τέτοιας αντικατάστασης, το διπλό ολοκλήρωμα θα είναι ίσο με το γινόμενο δύο ολοκληρωμάτων Fourier.

(20)

Ο μετασχηματισμός Fourier της συνέλιξης δύο σημάτων δίνει το γινόμενο των φασμάτων αυτών των σημάτων.

Παραγωγή σημάτων.Είναι γνωστό ότι
και
είναι τα φάσματα των συναρτήσεων
και
αντίστοιχα. Απαιτείται η έκφραση του φάσματος του προϊόντος
μέσω φασμάτων
και
. Ας αντικαταστήσουμε το ολοκλήρωμα Fourier αντί για ένα από τα σήματα, για παράδειγμα
, η έκφρασή του με όρους του αντιστρόφου μετασχηματισμού Fourier και στη συνέχεια αλλάζει τη σειρά ολοκλήρωσης.

(21)

Το φάσμα του γινομένου των σημάτων είναι η συνέλιξη των φασμάτων αυτών των σημάτων.

Διακριτό φάσμα σήματος

Ιδιαίτερη προσοχή πρέπει να δοθεί στα διακριτά σήματα, καθώς αυτά τα σήματα χρησιμοποιούνται στην ψηφιακή επεξεργασία. Ένα διακριτό σήμα, σε αντίθεση με ένα συνεχές, είναι μια ακολουθία αριθμών που αντιστοιχεί στις τιμές ενός συνεχούς σήματος σε ορισμένα χρονικά σημεία. Ένα υπό όρους διακριτό σήμα μπορεί να θεωρηθεί ως ένα συνεχές σήμα, το οποίο σε ορισμένες χρονικές στιγμές παίρνει κάποιες τιμές και άλλες φορές είναι ίσο με μηδέν. Έτσι, για παράδειγμα, διακριτή
το σήμα μπορεί να δοθεί ως το γινόμενο ενός συνεχούς σήματος
σε μια ακολουθία περιοδικών επαναλαμβανόμενων ορθογώνιων παλμών
- παλμοί χρονισμού (Εικ. 1).

Ρύζι. 1. Διακριτικοποίηση σήματος.

(22)

Οι ορθογώνιοι παλμοί έχουν διάρκεια , περίοδος επανάληψης :

(23)

Το πλάτος του παλμού επιλέγεται έτσι ώστε το ολοκλήρωμα του παλμού κατά τη διάρκεια της περιόδου να είναι ίσο με . Σε αυτή την περίπτωση, οι παλμοί του ρολογιού είναι αδιάστατοι. Επεκτείνουμε την ακολουθία τέτοιων παλμών σε μια τριγωνομετρική σειρά:

(24)

Για να λαμβάνετε άμεσες μετρήσεις σήματος
, είναι απαραίτητο να κατευθύνετε τη διάρκεια του παλμού στο μηδέν:
. Ένα τέτοιο σήμα ρολογιού ονομάζουμε ιδανικό. Σε αυτή την περίπτωση, οι συντελεστές διαστολής
στη σειρά Fourier όλα θα είναι ίσα με 1.

(25)

Ακριβώς η ίδια μορφή έχει την επέκταση στη σειρά Fourier της συνάρτησης:

(26)

Συντελεστές επέκτασης σε τριγωνομετρική σειρά του σήματος ρολογιού
:

(27)

Τότε το διακριτό σήμα θα μοιάζει με:

Κατά τον υπολογισμό του μετασχηματισμού Fourier ενός διακριτού σήματος, ανταλλάσσουμε τη λειτουργία άθροισης και ολοκλήρωσης και στη συνέχεια χρησιμοποιούμε την ιδιότητα δ - Λειτουργίες:

Το φάσμα ενός διακριτού σήματος είναι μια περιοδική συνάρτηση. Εξετάστε τον εκθέτη στον όρο του ξενοδοχείου
ως συνάρτηση της συχνότητας. Η περίοδος επανάληψης του είναι . Η μεγαλύτερη περίοδος επανάληψης για όρους με αριθμούς
, και αυτή, κατά συνέπεια, θα είναι η περίοδος επανάληψης ολόκληρου του φάσματος. Αυτό είναι το φάσμα ενός διακριτού σήματος έχει περίοδο επανάληψης ίση με τη συχνότητα κβαντοποίησης
.

Ας δούμε άλλη παράσταση
. Εξαιτίας του γεγονότος ότι
είναι προϊόν συναρτήσεων
και
, το φάσμα του διακριτού σήματος
υπολογίζεται ως συνέλιξη των φασμάτων ενός συνεχούς σήματος
και το φάσμα του σήματος ρολογιού
.

(30)

Υπολογίζω
χρησιμοποιώντας (25). Επειδή
περιοδική συνάρτηση, το φάσμα της είναι διακριτό.

Συνέλιξη λοιπόν (30)

Από την έκφραση (32) προκύπτει ότι το φάσμα του διακριτού σήματος είναι μια περιοδικά επαναλαμβανόμενη συνάρτηση
.

Το ίδιο το γεγονός ότι συμβαίνουν ποιοτικές αλλαγές στο φάσμα του σήματος ως αποτέλεσμα της δειγματοληψίας υποδηλώνει ότι το αρχικό σήμα μπορεί να παραμορφωθεί, καθώς καθορίζεται πλήρως από το φάσμα του. Ωστόσο, από την άλλη πλευρά, η περιοδική επανάληψη του ίδιου φάσματος από μόνη της δεν εισάγει τίποτα νέο στο φάσμα, επομένως, υπό ορισμένες προϋποθέσεις, γνωρίζοντας τις τιμές του σήματος σε μεμονωμένα χρονικά σημεία, μπορείτε να βρείτε ποια τιμή είναι αυτό το σήμα πήρε σε οποιαδήποτε άλλη χρονική στιγμή, δηλαδή, λάβετε το αρχικό συνεχές σήμα. Αυτό είναι το νόημα του θεωρήματος Kotelnikov, το οποίο επιβάλλει μια προϋπόθεση για την επιλογή της συχνότητας κβαντισμού σύμφωνα με τη μέγιστη συχνότητα στο φάσμα του σήματος.

Εάν αυτή η συνθήκη παραβιαστεί, τότε μετά την ψηφιοποίηση του σήματος, θα υπερτεθεί ένα περιοδικά επαναλαμβανόμενο φάσμα (Εικ. 2). Το φάσμα που προκύπτει από την επικάλυψη θα αντιστοιχεί σε άλλο σήμα.

Ρύζι. 2. Επικάλυψη φασμάτων.

Αυτή η σειρά μπορεί επίσης να γραφτεί ως:

(2),
όπου , k-ο μιγαδικό πλάτος.

Η σχέση μεταξύ των συντελεστών (1) και (3) εκφράζεται με τους ακόλουθους τύπους:

Σημειώστε ότι και οι τρεις αυτές αναπαραστάσεις της σειράς Fourier είναι απολύτως ισοδύναμες. Μερικές φορές, όταν εργάζεστε με σειρές Fourier, είναι πιο βολικό να χρησιμοποιείτε τους εκθέτες του φανταστικού ορίσματος αντί για ημίτονο και συνημίτονο, δηλαδή να χρησιμοποιείτε τον μετασχηματισμό Fourier σε σύνθετη μορφή. Αλλά είναι βολικό για εμάς να χρησιμοποιήσουμε τον τύπο (1), όπου η σειρά Fourier αντιπροσωπεύεται ως άθροισμα συνημιτονικών κυμάτων με τα αντίστοιχα πλάτη και φάσεις. Σε κάθε περίπτωση, είναι λάθος να πούμε ότι το αποτέλεσμα του μετασχηματισμού Fourier του πραγματικού σήματος θα είναι τα σύνθετα πλάτη των αρμονικών. Όπως λέει σωστά το wiki, "Ο μετασχηματισμός Fourier (;) είναι μια πράξη που αντιστοιχίζει μια συνάρτηση μιας πραγματικής μεταβλητής σε μια άλλη συνάρτηση, επίσης μιας πραγματικής μεταβλητής."

Σύνολο:
Η μαθηματική βάση της φασματικής ανάλυσης των σημάτων είναι ο μετασχηματισμός Fourier.

Ο μετασχηματισμός Fourier μας επιτρέπει να αναπαραστήσουμε μια συνεχή συνάρτηση f(x) (σήμα) που ορίζεται στο τμήμα (0, T) ως το άθροισμα ενός άπειρου αριθμού (άπειρης σειράς) τριγωνομετρικών συναρτήσεων (ημιτονοειδές ή/και συνημίτονο) με συγκεκριμένα πλάτη και φάσεις, που λαμβάνονται επίσης υπόψη στο τμήμα (0, T). Μια τέτοια σειρά ονομάζεται σειρά Fourier.

Σημειώνουμε μερικά ακόμη σημεία, η κατανόηση των οποίων απαιτείται για τη σωστή εφαρμογή του μετασχηματισμού Fourier σε ανάλυση σήματος. Αν θεωρήσουμε τη σειρά Fourier (το άθροισμα των ημιτονοειδών) σε ολόκληρο τον άξονα Χ, τότε μπορούμε να δούμε ότι έξω από το τμήμα (0, T), η συνάρτηση που αντιπροσωπεύεται από τη σειρά Fourier θα επαναλαμβάνει περιοδικά τη συνάρτησή μας.

Για παράδειγμα, στο γράφημα στο Σχ. 7, η αρχική συνάρτηση ορίζεται στο τμήμα (-T \ 2, + T \ 2) και η σειρά Fourier αντιπροσωπεύει μια περιοδική συνάρτηση που ορίζεται σε ολόκληρο τον άξονα x.

Αυτό συμβαίνει επειδή τα ίδια τα ημιτονοειδή είναι περιοδικές συναρτήσεις, αντίστοιχα, και το άθροισμά τους θα είναι περιοδική συνάρτηση.

εικ.7 Αναπαράσταση μη περιοδικής αρχικής συνάρτησης με σειρά Fourier

Με αυτόν τον τρόπο:

Η αρχική μας συνάρτηση είναι συνεχής, μη περιοδική, που ορίζεται σε κάποιο διάστημα μήκους T.
Το φάσμα αυτής της συνάρτησης είναι διακριτό, δηλαδή παρουσιάζεται ως μια άπειρη σειρά αρμονικών συνιστωσών - η σειρά Fourier.
Στην πραγματικότητα, μια ορισμένη περιοδική συνάρτηση ορίζεται από τη σειρά Fourier, η οποία συμπίπτει με τη δική μας στο τμήμα (0, T), αλλά αυτή η περιοδικότητα δεν είναι απαραίτητη για εμάς.

Οι περίοδοι των αρμονικών συνιστωσών είναι πολλαπλάσια του τμήματος (0, T) στο οποίο ορίζεται η αρχική συνάρτηση f(x). Με άλλα λόγια, οι αρμονικές περίοδοι είναι πολλαπλάσιες της διάρκειας της μέτρησης του σήματος. Για παράδειγμα, η περίοδος της πρώτης αρμονικής της σειράς Fourier είναι ίση με το διάστημα T στο οποίο ορίζεται η συνάρτηση f(x). Η περίοδος της δεύτερης αρμονικής της σειράς Fourier είναι ίση με το διάστημα T/2. Και ούτω καθεξής (βλ. Εικ. 8).

εικ.8 Περίοδοι (συχνότητες) των αρμονικών συνιστωσών της σειράς Fourier (εδώ T = 2;)

Αντίστοιχα, οι συχνότητες των αρμονικών συνιστωσών είναι πολλαπλάσια του 1/Τ. Δηλαδή, οι συχνότητες των αρμονικών συνιστωσών Fk είναι ίσες με Fk= k\T, όπου το k κυμαίνεται από 0 έως?, για παράδειγμα, k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (σε μηδενική συχνότητα - σταθερή συνιστώσα).

Έστω η αρχική μας συνάρτηση ένα σήμα καταγεγραμμένο για T=1 sec. Τότε η περίοδος της πρώτης αρμονικής θα είναι ίση με τη διάρκεια του σήματος μας T1=T=1 sec και η συχνότητα της αρμονικής είναι 1 Hz. Η περίοδος της δεύτερης αρμονικής θα είναι ίση με τη διάρκεια του σήματος διαιρούμενη με 2 (T2=T/2=0,5 sec) και η συχνότητα είναι 2 Hz. Για την τρίτη αρμονική T3=T/3 sec και η συχνότητα είναι 3 Hz. Και ούτω καθεξής.

Το βήμα μεταξύ αρμονικών σε αυτή την περίπτωση είναι 1 Hz.

Έτσι, ένα σήμα με διάρκεια 1 sec μπορεί να αποσυντεθεί σε αρμονικές συνιστώσες (για να ληφθεί ένα φάσμα) με ανάλυση συχνότητας 1 Hz.
Για να αυξήσετε την ανάλυση κατά 2 φορές στα 0,5 Hz, είναι απαραίτητο να αυξήσετε τη διάρκεια μέτρησης κατά 2 φορές - έως και 2 δευτερόλεπτα. Ένα σήμα με διάρκεια 10 δευτερολέπτων μπορεί να αποσυντεθεί σε αρμονικές συνιστώσες (για να ληφθεί ένα φάσμα) με ανάλυση συχνότητας 0,1 Hz. Δεν υπάρχουν άλλοι τρόποι για να αυξήσετε την ανάλυση συχνότητας.

Υπάρχει τρόπος να αυξηθεί τεχνητά η διάρκεια του σήματος προσθέτοντας μηδενικά στη διάταξη των δειγμάτων. Αλλά δεν αυξάνει την ανάλυση της πραγματικής συχνότητας.

3. Διακριτά σήματα και διακριτός μετασχηματισμός Fourier

Με την ανάπτυξη της ψηφιακής τεχνολογίας άλλαξαν και οι τρόποι αποθήκευσης δεδομένων μέτρησης (σήματα). Εάν νωρίτερα το σήμα μπορούσε να εγγραφεί σε μαγνητόφωνο και να αποθηκευτεί σε κασέτα σε αναλογική μορφή, τώρα τα σήματα ψηφιοποιούνται και αποθηκεύονται σε αρχεία στη μνήμη του υπολογιστή ως σύνολο αριθμών (μετρήσεις).

Το συνηθισμένο σχήμα για τη μέτρηση και την ψηφιοποίηση ενός σήματος έχει ως εξής.

εικ.9 Σχέδιο του καναλιού μέτρησης

Το σήμα από τον μορφοτροπέα μέτρησης φτάνει στο ADC κατά τη διάρκεια μιας χρονικής περιόδου T. Τα δείγματα σήματος (δείγμα) που λαμβάνονται κατά τη διάρκεια του χρόνου T μεταφέρονται στον υπολογιστή και αποθηκεύονται στη μνήμη.

εικ.10 Ψηφιοποιημένο σήμα - Λήφθηκαν Ν μετρήσεις σε χρόνο T

Ποιες είναι οι απαιτήσεις για τις παραμέτρους ψηφιοποίησης σήματος; Μια συσκευή που μετατρέπει ένα αναλογικό σήμα εισόδου σε διακριτό κωδικό (ψηφιακό σήμα) ονομάζεται μετατροπέας αναλογικού σε ψηφιακό (ADC, Αγγλικά μετατροπέας αναλογικού σε ψηφιακό, ADC) (Wiki).

Μία από τις κύριες παραμέτρους του ADC είναι ο μέγιστος ρυθμός δειγματοληψίας (ή ρυθμός δειγματοληψίας, ρυθμός δειγματοληψίας στα αγγλικά) - η συχνότητα λήψης δειγμάτων ενός σήματος συνεχούς χρόνου κατά τη δειγματοληψία του. Μετρημένο σε Hertz. ((Wiki))

Σύμφωνα με το θεώρημα Kotelnikov, εάν ένα συνεχές σήμα έχει φάσμα περιορισμένο από τη συχνότητα Fmax, τότε μπορεί να αποκατασταθεί πλήρως και μοναδικά από τα διακριτά δείγματά του που λαμβάνονται σε χρονικά διαστήματα , δηλ. με συχνότητα Fd ; 2*Fmax, όπου Fd - ρυθμός δειγματοληψίας. Fmax - μέγιστη συχνότητα του φάσματος σήματος. Με άλλα λόγια, ο ρυθμός δειγματοληψίας σήματος (ρυθμός δειγματοληψίας ADC) πρέπει να είναι τουλάχιστον 2 φορές η μέγιστη συχνότητα του σήματος που θέλουμε να μετρήσουμε.

Και τι θα συμβεί αν λάβουμε μετρήσεις με χαμηλότερη συχνότητα από αυτή που απαιτεί το θεώρημα Kotelnikov;

Σε αυτή την περίπτωση, εμφανίζεται το φαινόμενο του «aliasing» (γνωστό και ως στροβοσκοπικό φαινόμενο, φαινόμενο moiré), στο οποίο το σήμα υψηλής συχνότητας μετά την ψηφιοποίηση μετατρέπεται σε σήμα χαμηλής συχνότητας που στην πραγματικότητα δεν υπάρχει. Στο σχ. 5 υψηλής συχνότητας κόκκινο ημιτονοειδές κύμα είναι το πραγματικό σήμα. Το μπλε ημιτονοειδές κύμα χαμηλότερης συχνότητας είναι ένα εικονικό σήμα που προκύπτει από το γεγονός ότι περισσότερο από μισή περίοδος σήματος υψηλής συχνότητας έχει χρόνο να περάσει κατά τη διάρκεια του χρόνου δειγματοληψίας.

Ρύζι. 11. Η εμφάνιση ψευδούς σήματος χαμηλής συχνότητας όταν ο ρυθμός δειγματοληψίας δεν είναι αρκετά υψηλός

Για να αποφευχθεί η επίδραση της αλλοίωσης, τοποθετείται ένα ειδικό φίλτρο κατά της παραμόρφωσης μπροστά από το ADC - LPF (χαμηλοπερατό φίλτρο), το οποίο διέρχεται συχνότητες κάτω από τη μισή συχνότητα δειγματοληψίας ADC και διακόπτει τις υψηλότερες συχνότητες.

Για τον υπολογισμό του φάσματος ενός σήματος από τα διακριτά δείγματά του, χρησιμοποιείται ο διακριτός μετασχηματισμός Fourier (DFT). Σημειώνουμε για άλλη μια φορά ότι το φάσμα ενός διακριτού σήματος «εξ ορισμού» περιορίζεται από τη συχνότητα Fmax, η οποία είναι μικρότερη από τη μισή συχνότητα δειγματοληψίας Fd. Επομένως, το φάσμα ενός διακριτού σήματος μπορεί να αναπαρασταθεί από το άθροισμα ενός πεπερασμένου αριθμού αρμονικών, σε αντίθεση με το άπειρο άθροισμα για τη σειρά Fourier ενός συνεχούς σήματος, το φάσμα του οποίου μπορεί να είναι απεριόριστο. Σύμφωνα με το θεώρημα Kotelnikov, η μέγιστη αρμονική συχνότητα πρέπει να είναι τέτοια ώστε να αντιστοιχεί σε τουλάχιστον δύο δείγματα, επομένως ο αριθμός των αρμονικών είναι ίσος με το ήμισυ του αριθμού των δειγμάτων του διακριτού σήματος. Δηλαδή, εάν υπάρχουν Ν δείγματα στο δείγμα, τότε ο αριθμός των αρμονικών στο φάσμα θα είναι ίσος με N/2.

Εξετάστε τώρα τον διακριτό μετασχηματισμό Fourier (DFT).

Συγκρίνοντας με τη σειρά Fourier

Βλέπουμε ότι συμπίπτουν, εκτός από το ότι ο χρόνος στο DFT είναι διακριτός και ο αριθμός των αρμονικών περιορίζεται στο N/2 - ο μισός αριθμός των δειγμάτων.

Οι τύποι DFT γράφονται σε αδιάστατες ακέραιες μεταβλητές k, s, όπου k είναι οι αριθμοί των δειγμάτων σήματος, s είναι οι αριθμοί των φασματικών συνιστωσών.
Η τιμή του s δείχνει τον αριθμό των πλήρων ταλαντώσεων της αρμονικής στην περίοδο T (η διάρκεια της μέτρησης του σήματος). Ο διακριτός μετασχηματισμός Fourier χρησιμοποιείται για να βρεθούν τα πλάτη και οι φάσεις των αρμονικών αριθμητικά, δηλ. "στον υπολογιστη"

Επιστρέφοντας στα αποτελέσματα που ελήφθησαν στην αρχή. Όπως αναφέρθηκε παραπάνω, όταν επεκτείνουμε μια μη περιοδική συνάρτηση (το σήμα μας) σε μια σειρά Fourier, η σειρά Fourier που προκύπτει αντιστοιχεί στην πραγματικότητα σε μια περιοδική συνάρτηση με περίοδο T. (Εικ. 12).

εικ.12 Περιοδική συνάρτηση f(x) με περίοδο Т0, με περίοδο μέτρησης Т>T0

Όπως φαίνεται στο Σχ. 12, η ​​συνάρτηση f(x) είναι περιοδική με περίοδο Т0. Ωστόσο, λόγω του γεγονότος ότι η διάρκεια του δείγματος μέτρησης Τ δεν συμπίπτει με την περίοδο της συνάρτησης T0, η συνάρτηση που λαμβάνεται ως σειρά Fourier έχει ασυνέχεια στο σημείο Τ. Ως αποτέλεσμα, το φάσμα αυτής της συνάρτησης θα περιέχουν μεγάλο αριθμό αρμονικών υψηλής συχνότητας. Εάν η διάρκεια του δείγματος μέτρησης T συνέπιπτε με την περίοδο της συνάρτησης T0, τότε μόνο η πρώτη αρμονική (ημιτονοειδής με περίοδο ίση με τη διάρκεια του δείγματος) θα υπήρχε στο φάσμα που λήφθηκε μετά τον μετασχηματισμό Fourier, αφού η συνάρτηση f Το (x) είναι ένα ημιτονοειδές.

Με άλλα λόγια, το πρόγραμμα DFT "δεν γνωρίζει" ότι το σήμα μας είναι ένα "κομμάτι ημιτονοειδούς κύματος", αλλά προσπαθεί να αναπαραστήσει μια περιοδική συνάρτηση ως σειρά, η οποία έχει ένα κενό λόγω της ασυνέπειας των μεμονωμένων κομματιών του το ημιτονοειδές κύμα.

Ως αποτέλεσμα, εμφανίζονται αρμονικές στο φάσμα, οι οποίες συνολικά θα πρέπει να αντιπροσωπεύουν τη μορφή της συνάρτησης, συμπεριλαμβανομένης αυτής της ασυνέχειας.

Έτσι, για να ληφθεί το «σωστό» φάσμα του σήματος, που είναι το άθροισμα πολλών ημιτονοειδών με διαφορετικές περιόδους, είναι απαραίτητο ένας ακέραιος αριθμός περιόδων κάθε ημιτονοειδούς να ταιριάζει στην περίοδο μέτρησης του σήματος. Στην πράξη, αυτή η προϋπόθεση μπορεί να ικανοποιηθεί για μια αρκετά μεγάλη διάρκεια της μέτρησης του σήματος.

Εικ.13 Ένα παράδειγμα της λειτουργίας και του φάσματος του σήματος του κινηματικού σφάλματος του κιβωτίου ταχυτήτων

Με μικρότερη διάρκεια, η εικόνα θα φαίνεται "χειρότερη":

Εικ.14 Ένα παράδειγμα της λειτουργίας και του φάσματος του σήματος δόνησης του δρομέα

Στην πράξη, μπορεί να είναι δύσκολο να κατανοήσουμε πού βρίσκονται τα «πραγματικά στοιχεία» και πού τα «τεχνουργήματα» που προκαλούνται από τη μη πολλαπλότητα των περιόδων των στοιχείων και τη διάρκεια του δείγματος σήματος ή τα «άλματα και διαλείμματα» του την κυματομορφή. Φυσικά, οι λέξεις «πραγματικά συστατικά» και «τεχνουργήματα» δεν είναι μάταιες. Η παρουσία πολλών αρμονικών στο γράφημα φάσματος δεν σημαίνει ότι το σήμα μας στην πραγματικότητα «αποτελείται» από αυτές. Είναι σαν να νομίζουμε ότι ο αριθμός 7 "αποτελείται" από τους αριθμούς 3 και 4. Ο αριθμός 7 μπορεί να αναπαρασταθεί ως το άθροισμα των αριθμών 3 και 4 - αυτό είναι σωστό.

Το ίδιο είναι και το σήμα μας… ή μάλλον, ούτε καν το «σήμα μας», αλλά μια περιοδική συνάρτηση που συντάσσεται επαναλαμβάνοντας το σήμα μας (δειγματοληψία) μπορεί να αναπαρασταθεί ως άθροισμα αρμονικών (ημιτονοειδών) με συγκεκριμένα πλάτη και φάσεις. Αλλά σε πολλές περιπτώσεις σημαντικές για πρακτική (δείτε τα παραπάνω σχήματα), είναι πράγματι δυνατό να συσχετιστούν οι αρμονικές που λαμβάνονται στο φάσμα με πραγματικές διεργασίες που είναι κυκλικής φύσης και συμβάλλουν σημαντικά στο σχήμα του σήματος.

Μερικά αποτελέσματα

1. Το πραγματικό μετρούμενο σήμα, διάρκεια T sec, ψηφιοποιημένο από το ADC, δηλαδή, που αντιπροσωπεύεται από ένα σύνολο διακριτών δειγμάτων (N τεμάχια), έχει ένα διακριτό μη περιοδικό φάσμα, που αντιπροσωπεύεται από ένα σύνολο αρμονικών (N/2 τεμάχια ).

2. Το σήμα αντιπροσωπεύεται από ένα σύνολο πραγματικών τιμών και το φάσμα του αντιπροσωπεύεται από ένα σύνολο πραγματικών τιμών. Οι αρμονικές συχνότητες είναι θετικές. Το γεγονός ότι είναι πιο βολικό για τους μαθηματικούς να αναπαριστούν το φάσμα σε σύνθετη μορφή χρησιμοποιώντας αρνητικές συχνότητες δεν σημαίνει ότι «είναι σωστό» και «πρέπει πάντα να γίνεται με αυτόν τον τρόπο».

3. Το σήμα που μετράται στο χρονικό διάστημα T προσδιορίζεται μόνο στο χρονικό διάστημα T. Τι συνέβη πριν αρχίσουμε να μετράμε το σήμα και τι θα συμβεί μετά από αυτό - αυτό είναι άγνωστο στην επιστήμη. Και στην περίπτωσή μας - δεν είναι ενδιαφέρον. Το DFT ενός χρονικά περιορισμένου σήματος δίνει το «πραγματικό» του φάσμα, με την έννοια ότι, υπό ορισμένες συνθήκες, σας επιτρέπει να υπολογίσετε το πλάτος και τη συχνότητα των συνιστωσών του.

Μεταχειρισμένα υλικά και άλλα χρήσιμα υλικά.