Κατάταξη μήτρας: ορισμός, μέθοδοι εύρεσης, παραδείγματα, λύσεις. Εύρεση της κατάταξης μιας μήτρας Ποια είναι η κατάταξη μιας μήτρας 1123 5814

Και επίσης εξετάστε μια σημαντική πρακτική εφαρμογή του θέματος: μελέτη συστήματος γραμμικών εξισώσεων για συμβατότητα.

Ποια είναι η κατάταξη ενός πίνακα;

Η χιουμοριστική επιγραφή του άρθρου περιέχει μεγάλη δόση αλήθειας. Η ίδια η λέξη «κατάταξη» συνδέεται συνήθως με κάποιο είδος ιεραρχίας, τις περισσότερες φορές με την κλίμακα σταδιοδρομίας. Όσες περισσότερες γνώσεις, εμπειρία, ικανότητες, διασυνδέσεις κ.λπ. έχει ένας άνθρωπος. - τόσο υψηλότερη είναι η θέση του και το εύρος των ευκαιριών του. Σε όρους νεολαίας, η κατάταξη αναφέρεται στο συνολικό βαθμό "σκληρότητας".

Και τα μαθηματικά μας αδέρφια ζουν με τις ίδιες αρχές. Ας κάνουμε μια βόλτα μερικά αυθαίρετα μηδέν πίνακες:

Ας σκεφτούμε αν στο matrix μόνο μηδενικά, τότε για ποια κατάταξη μπορούμε να μιλήσουμε; Όλοι είναι εξοικειωμένοι με την άτυπη έκφραση «συνολικό μηδέν». Στην κοινωνία του matrix, όλα είναι ακριβώς τα ίδια:

Μηδενική κατάταξη μήτραςοποιοδήποτε μέγεθος είναι μηδέν.

Σημείωση : ο μηδενικός πίνακας συμβολίζεται με το ελληνικό γράμμα "θήτα"

Για να κατανοήσουμε καλύτερα την κατάταξη της μήτρας, στο εξής θα βασιστώ στα υλικά αναλυτική γεωμετρία. Θεωρήστε το μηδέν διάνυσματου τρισδιάστατου χώρου μας, που δεν ορίζει μια συγκεκριμένη κατεύθυνση και είναι άχρηστος για οικοδόμηση συγγενική βάση. Από αλγεβρική άποψη, οι συντεταγμένες ενός δεδομένου διανύσματος γράφονται σε μήτρα«ένα προς τρία» και λογικό (με την καθορισμένη γεωμετρική έννοια)υποθέστε ότι η κατάταξη αυτού του πίνακα είναι μηδέν.

Τώρα ας δούμε μερικά μη μηδενικό διανύσματα στήληςκαι διανύσματα σειρών:

Κάθε στιγμιότυπο έχει τουλάχιστον ένα μη μηδενικό στοιχείο, και αυτό είναι κάτι!

Η κατάταξη οποιουδήποτε διανύσματος μη μηδενικής γραμμής (διάνυσμα στήλης) είναι ίση με ένα

Και γενικά μιλώντας - εάν είναι σε μήτρα αυθαίρετα μεγέθηέχει τουλάχιστον ένα μη μηδενικό στοιχείο, μετά την κατάταξή του όχι λιγότερομονάδες.

Τα αλγεβρικά διανύσματα σειρών και στηλών είναι αφηρημένα σε κάποιο βαθμό, οπότε ας στραφούμε ξανά στον γεωμετρικό συσχετισμό. μη μηδενικό διάνυσμαθέτει μια καλά καθορισμένη κατεύθυνση στο χώρο και είναι κατάλληλο για κατασκευή βάση, οπότε η κατάταξη του πίνακα θα θεωρηθεί ότι είναι ίση με ένα.

Θεωρητικό υπόβαθρο : στη γραμμική άλγεβρα, ένα διάνυσμα είναι ένα στοιχείο ενός διανυσματικού χώρου (που ορίζεται με 8 αξιώματα), το οποίο, συγκεκριμένα, μπορεί να είναι μια διατεταγμένη σειρά (ή στήλη) πραγματικών αριθμών με τις πράξεις της πρόσθεσης και του πολλαπλασιασμού με έναν πραγματικό αριθμό που ορίζονται για αυτούς. Για περισσότερες πληροφορίες σχετικά με τους φορείς, ανατρέξτε στο άρθρο Γραμμικοί μετασχηματισμοί.

γραμμικά εξαρτώμενη(εκφράζονται μεταξύ τους). Από γεωμετρική άποψη, η δεύτερη γραμμή περιέχει τις συντεταγμένες του συγγραμμικού διανύσματος , που δεν προώθησε το θέμα στην οικοδόμηση τρισδιάστατη βάση, όντας περιττός υπό αυτή την έννοια. Έτσι, η κατάταξη αυτού του πίνακα είναι επίσης ίση με ένα.

Ξαναγράφουμε τις συντεταγμένες των διανυσμάτων σε στήλες ( μεταφέρετε τη μήτρα):

Τι έχει αλλάξει ως προς την κατάταξη; Τίποτα. Οι στήλες είναι αναλογικές, που σημαίνει ότι η κατάταξη είναι ίση με μία. Παρεμπιπτόντως, σημειώστε ότι και οι τρεις γραμμές είναι επίσης αναλογικές. Μπορούν να αναγνωριστούν με τις συντεταγμένες τρίασυγγραμμικά διανύσματα του επιπέδου, εκ των οποίων μόνο έναχρήσιμο για την κατασκευή μιας «επίπεδης» βάσης. Και αυτό είναι σε πλήρη συμφωνία με τη γεωμετρική αίσθηση της κατάταξης.

Μια σημαντική δήλωση προκύπτει από το παραπάνω παράδειγμα:

Η κατάταξη μιας μήτρας ανά γραμμές είναι ίση με την κατάταξη μιας μήτρας ανά στήλες. Το ανέφερα ήδη λίγο στο μάθημα για την αποτελεσματικότητα μέθοδοι υπολογισμού της ορίζουσας.

Σημείωση : η γραμμική εξάρτηση σειρών οδηγεί σε γραμμική εξάρτηση στηλών (και αντίστροφα). Αλλά για να εξοικονομήσω χρόνο, και από συνήθεια, θα μιλάω σχεδόν πάντα για τη γραμμική εξάρτηση των χορδών.

Ας συνεχίσουμε να εκπαιδεύουμε το αγαπημένο μας κατοικίδιο. Προσθέστε τις συντεταγμένες ενός άλλου συγγραμμικού διανύσματος στον πίνακα της τρίτης σειράς :

Μας βοήθησε στο χτίσιμο μιας τρισδιάστατης βάσης; Φυσικά και όχι. Και τα τρία διανύσματα περπατούν εμπρός και πίσω κατά μήκος της ίδιας διαδρομής και η κατάταξη του πίνακα είναι ένα. Μπορείτε να πάρετε όσα συγγραμμικά διανύσματα θέλετε, ας πούμε 100, να βάλετε τις συντεταγμένες τους σε έναν πίνακα 100 επί 3, και η κατάταξη ενός τέτοιου ουρανοξύστη θα παραμείνει ακόμη μία.

Ας εξοικειωθούμε με το matrix του οποίου οι σειρές γραμμικά ανεξάρτητη. Ένα ζεύγος μη συγγραμμικών διανυσμάτων είναι κατάλληλο για την κατασκευή μιας τρισδιάστατης βάσης. Η κατάταξη αυτού του πίνακα είναι δύο.

Ποια είναι η κατάταξη του πίνακα; Οι γραμμές δεν φαίνεται να είναι ανάλογες ... άρα θεωρητικά τρεις. Ωστόσο, η κατάταξη αυτού του πίνακα είναι επίσης ίση με δύο. Πρόσθεσα τις δύο πρώτες γραμμές και έγραψα το αποτέλεσμα στο κάτω μέρος, δηλ. εκφράζεται γραμμικάτρίτη γραμμή μέσω των δύο πρώτων. Γεωμετρικά, οι σειρές του πίνακα αντιστοιχούν στις συντεταγμένες των τριών συνεπίπεδα διανύσματα, και ανάμεσα σε αυτό το τριπλό υπάρχει ένα ζευγάρι μη γραμμικών συντρόφων.

Οπως βλέπεις γραμμική εξάρτησηστον εξεταζόμενο πίνακα δεν είναι προφανής και σήμερα θα μάθουμε απλώς πώς να το φέρουμε "σε καθαρό νερό".

Νομίζω ότι πολλοί άνθρωποι μαντεύουν ποια είναι η κατάταξη ενός matrix!

Θεωρήστε έναν πίνακα του οποίου οι σειρές γραμμικά ανεξάρτητη. Μορφή διανυσμάτων συγγενική βάση, και η κατάταξη αυτού του πίνακα είναι τρεις.

Όπως γνωρίζετε, οποιοδήποτε τέταρτο, πέμπτο, δέκατο διάνυσμα του τρισδιάστατου χώρου θα εκφραστεί γραμμικά σε όρους διανυσμάτων βάσης. Επομένως, εάν προστεθεί οποιοσδήποτε αριθμός σειρών στον πίνακα, τότε η κατάταξή του θα είναι ακόμα τρεις.

Παρόμοιος συλλογισμός μπορεί να πραγματοποιηθεί για πίνακες μεγαλύτερων μεγεθών (προφανώς, ήδη χωρίς γεωμετρικό νόημα).

Ορισμός : Η κατάταξη μήτρας είναι ο μέγιστος αριθμός γραμμικά ανεξάρτητων σειρών. Ή: η κατάταξη ενός πίνακα είναι ο μέγιστος αριθμός γραμμικά ανεξάρτητων στηλών. Ναι, πάντα ταιριάζουν.

Από τα παραπάνω προκύπτει μια σημαντική πρακτική οδηγία: η κατάταξη ενός πίνακα δεν υπερβαίνει την ελάχιστη διάστασή του. Για παράδειγμα, στη μήτρα τέσσερις σειρές και πέντε στήλες. Η ελάχιστη διάσταση είναι τέσσερα, επομένως, η κατάταξη αυτού του πίνακα δεν θα υπερβαίνει σίγουρα το 4.

Σημειογραφία: στην παγκόσμια θεωρία και πρακτική δεν υπάρχει γενικά αποδεκτό πρότυπο για τον προσδιορισμό της κατάταξης του πίνακα, το πιο κοινό μπορεί να βρεθεί: - όπως λένε, ένας Άγγλος γράφει ένα πράγμα, ένας Γερμανός άλλο. Επομένως, με βάση το γνωστό ανέκδοτο για την αμερικανική και ρωσική κόλαση, ας ορίσουμε την κατάταξη της μήτρας με μια εγγενή λέξη. Για παράδειγμα: . Και αν ο πίνακας είναι "ανώνυμος", από τους οποίους υπάρχουν πολλά, τότε μπορείτε απλά να γράψετε .

Πώς να βρείτε την κατάταξη ενός πίνακα χρησιμοποιώντας ανηλίκους;

Εάν η γιαγιά μας είχε μια πέμπτη στήλη στη μήτρα, τότε θα έπρεπε να είχε υπολογιστεί μια άλλη δευτερεύουσα 4ης τάξης ("μπλε", "βατόμουρο" + 5η στήλη).

συμπέρασμα: η μέγιστη τάξη ενός μη μηδενικού δευτερεύοντος είναι τρεις, άρα .

Ίσως δεν κατάλαβαν όλοι πλήρως αυτή τη φράση: το δευτερεύον 4ης τάξης είναι ίσο με μηδέν, αλλά μεταξύ των δευτερευόντων 3ης τάξης υπήρχε ένα μη μηδενικό - επομένως, η μέγιστη τάξη μη μηδενικόελάσσονα και ίσο με τρία.

Τίθεται το ερώτημα, γιατί να μην υπολογίσουμε αμέσως την ορίζουσα; Λοιπόν, πρώτον, στις περισσότερες εργασίες ο πίνακας δεν είναι τετράγωνος και δεύτερον, ακόμα κι αν λάβετε μια μη μηδενική τιμή, τότε η εργασία θα απορριφθεί με μεγάλη πιθανότητα, καθώς συνήθως συνεπάγεται μια τυπική "από κάτω προς τα πάνω" λύση. Και στο εξεταζόμενο παράδειγμα, η μηδενική ορίζουσα της 4ης τάξης μας επιτρέπει ακόμη και να ισχυριστούμε ότι η κατάταξη του πίνακα είναι μόνο μικρότερη από τέσσερις.

Οφείλω να ομολογήσω ότι κατέληξα στο πρόβλημα που αναλύθηκε μόνος μου για να εξηγήσω καλύτερα τη μέθοδο της οριοθέτησης ανηλίκων. Στην πραγματική πράξη, όλα είναι πιο απλά:

Παράδειγμα 2

Βρείτε την κατάταξη ενός πίνακα με τη μέθοδο περιθωρίου ανηλίκων

Λύση και απάντηση στο τέλος του μαθήματος.

Πότε ο αλγόριθμος εκτελείται πιο γρήγορα; Ας επιστρέψουμε στον ίδιο πίνακα τέσσερα επί τέσσερα . Προφανώς, η λύση θα είναι η συντομότερη στην περίπτωση του "καλού" γωνιακά ανήλικα: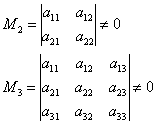

Και, αν , τότε , αλλιώς - .

Η σκέψη δεν είναι καθόλου υποθετική - υπάρχουν πολλά παραδείγματα όπου το όλο θέμα περιορίζεται μόνο σε γωνιακά ανήλικα.

Ωστόσο, σε ορισμένες περιπτώσεις, μια άλλη μέθοδος είναι πιο αποτελεσματική και προτιμότερη:

Πώς να βρείτε την κατάταξη ενός πίνακα χρησιμοποιώντας τη μέθοδο Gauss;

Αυτή η ενότητα προορίζεται για αναγνώστες που είναι ήδη εξοικειωμένοι με Μέθοδος Gaussκαι σιγά σιγά το έπιασαν στα χέρια τους.

Από τεχνική άποψη, η μέθοδος δεν είναι νέα:

1) χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, φέρνουμε τον πίνακα σε μια βαθμιδωτή μορφή.

2) η κατάταξη του πίνακα είναι ίση με τον αριθμό των σειρών.

Είναι απολύτως σαφές ότι Η χρήση της μεθόδου Gauss δεν αλλάζει την κατάταξη του πίνακα, και η ουσία εδώ είναι εξαιρετικά απλή: σύμφωνα με τον αλγόριθμο, κατά τη διάρκεια των στοιχειωδών μετασχηματισμών, εντοπίζονται και αφαιρούνται όλες οι περιττές αναλογικές (γραμμικά εξαρτώμενες) γραμμές, με αποτέλεσμα να παραμένει ένα "ξηρό υπόλειμμα" - ο μέγιστος αριθμός γραμμικά ανεξάρτητες γραμμές.

Ας μετατρέψουμε τον παλιό γνωστό πίνακα με τις συντεταγμένες τριών συγγραμμικών διανυσμάτων:

(1) Η πρώτη σειρά προστέθηκε στη δεύτερη σειρά, πολλαπλασιαζόμενη επί -2. Η πρώτη γραμμή προστέθηκε στην τρίτη γραμμή.

(2) Οι μηδενικές γραμμές αφαιρούνται.

Άρα απομένει μία γραμμή, επομένως . Περιττό να πούμε ότι αυτό είναι πολύ πιο γρήγορο από τον υπολογισμό εννέα μηδενικών ανηλίκων 2ης τάξης και μόνο μετά την εξαγωγή συμπερασμάτων.

Σας το θυμίζω αυτό από μόνο του αλγεβρικός πίνακαςτίποτα δεν μπορεί να αλλάξει και οι μετασχηματισμοί πραγματοποιούνται μόνο για να μάθουμε την κατάταξη! Παρεμπιπτόντως, ας σταθούμε ξανά στο ερώτημα, γιατί όχι; Πηγή Matrix 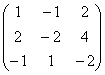μεταφέρει πληροφορίες που είναι θεμελιωδώς διαφορετικές από τις πληροφορίες μήτρας και γραμμής. Σε ορισμένα μαθηματικά μοντέλα (χωρίς υπερβολή), η διαφορά σε έναν αριθμό μπορεί να είναι θέμα ζωής και θανάτου. ... Θυμήθηκα τους δασκάλους των σχολικών μαθηματικών πρωτοβάθμιας και δευτεροβάθμιας τάξης, που έκοψαν ανελέητα τον βαθμό κατά 1-2 μονάδες για την παραμικρή ανακρίβεια ή παρέκκλιση από τον αλγόριθμο. Και ήταν τρομερά απογοητευτικό όταν, αντί για το φαινομενικά εγγυημένο «πέντε», βγήκε «καλό» ή ακόμα χειρότερο. Η κατανόηση ήρθε πολύ αργότερα - πώς αλλιώς να εμπιστευθεί κανείς δορυφόρους, πυρηνικές κεφαλές και σταθμούς ηλεκτροπαραγωγής; Αλλά μην ανησυχείτε, δεν εργάζομαι σε αυτούς τους τομείς =)

Ας περάσουμε σε πιο ουσιαστικές εργασίες, όπου, μεταξύ άλλων, θα εξοικειωθούμε με σημαντικές υπολογιστικές τεχνικές Μέθοδος Gauss:

Παράδειγμα 3

Βρείτε την κατάταξη ενός πίνακα χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς

Λύση: δίνεται ένας πίνακας τέσσερα επί πέντε, που σημαίνει ότι η κατάταξή του σίγουρα δεν είναι μεγαλύτερη από 4.

Στην πρώτη στήλη, δεν υπάρχει 1 ή -1, επομένως, απαιτούνται πρόσθετα βήματα για να ληφθεί τουλάχιστον μία μονάδα. Σε όλη την ύπαρξη του ιστότοπου, μου έχει τεθεί επανειλημμένα η ερώτηση: "Είναι δυνατή η αναδιάταξη των στηλών κατά τη διάρκεια στοιχειωδών μετασχηματισμών;". Εδώ - αναδιάταξη της πρώτης ή της δεύτερης στήλης, και όλα είναι καλά! Στις περισσότερες εργασίες όπου Μέθοδος Gauss, οι στήλες μπορούν πραγματικά να αναδιαταχθούν. ΑΛΛΑ ΜΗΝ. Και το θέμα δεν είναι καν μια πιθανή σύγχυση με τις μεταβλητές, το θέμα είναι ότι στο κλασικό μάθημα της διδασκαλίας των ανώτερων μαθηματικών αυτή η ενέργεια παραδοσιακά δεν λαμβάνεται υπόψη, επομένως, μια τέτοια απότομη θα φανεί ΠΟΛΥ στραβά (ή ακόμα και θα αναγκαστεί να ξανακάνει τα πάντα) .

Το δεύτερο σημείο αφορά τους αριθμούς. Κατά τη διάρκεια της απόφασης, είναι χρήσιμο να καθοδηγηθείτε από τον ακόλουθο εμπειρικό κανόνα: Οι στοιχειώδεις μετασχηματισμοί θα πρέπει, αν είναι δυνατόν, να μειώσουν τους αριθμούς του πίνακα. Πράγματι, είναι πολύ πιο εύκολο να δουλέψεις με ένα-δύο-τρία παρά, για παράδειγμα, με 23, 45 και 97. Και η πρώτη ενέργεια στοχεύει όχι μόνο στην απόκτηση μιας μονάδας στην πρώτη στήλη, αλλά και στην εξάλειψη των αριθμών 7 και 11.

Πρώτα η πλήρης λύση και μετά τα σχόλια:

(1) Η πρώτη σειρά προστέθηκε στη δεύτερη σειρά, πολλαπλασιαζόμενη επί -2. Η πρώτη γραμμή προστέθηκε στην τρίτη γραμμή, πολλαπλασιαζόμενη επί -3. Και στο σωρό: η 1η γραμμή, πολλαπλασιασμένη με -1, προστέθηκε στην 4η γραμμή.

(2) Οι τρεις τελευταίες γραμμές είναι αναλογικές. Διαγράφηκε η 3η και η 4η γραμμή, η δεύτερη γραμμή μετακινήθηκε στην πρώτη θέση.

(3) Η πρώτη σειρά προστέθηκε στη δεύτερη σειρά, πολλαπλασιαζόμενη επί -3.

Ο πίνακας που ανάγεται σε μια κλιμακωτή μορφή έχει δύο σειρές.

Απάντηση:

Τώρα είναι η σειρά σας να βασανίσετε τη μήτρα τέσσερα προς τέσσερα:

Παράδειγμα 4

Βρείτε την κατάταξη ενός πίνακα χρησιμοποιώντας τη μέθοδο Gaussian

Σας το θυμίζω Μέθοδος Gaussδεν συνεπάγεται ξεκάθαρη ακαμψία και η λύση σας πιθανότατα θα είναι διαφορετική από τη δική μου λύση. Ένα σύντομο δείγμα της εργασίας στο τέλος του μαθήματος.

Ποια μέθοδος να χρησιμοποιήσετε για να βρείτε την κατάταξη ενός πίνακα;

Στην πράξη, συχνά δεν λέγεται καθόλου ποια μέθοδος πρέπει να χρησιμοποιηθεί για την εύρεση της κατάταξης. Σε μια τέτοια κατάσταση, θα πρέπει να αναλυθεί η συνθήκη - για ορισμένους πίνακες είναι πιο λογικό να πραγματοποιηθεί η λύση μέσω ανηλίκων, ενώ για άλλους είναι πολύ πιο κερδοφόρο να εφαρμοστούν στοιχειώδεις μετασχηματισμοί:

Παράδειγμα 5

Βρείτε την κατάταξη ενός πίνακα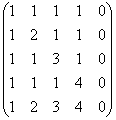

Λύση: ο πρώτος τρόπος με κάποιο τρόπο εξαφανίζεται αμέσως =)

Λίγο ψηλότερα, συμβούλεψα να μην αγγίξετε τις στήλες της μήτρας, αλλά όταν υπάρχει μηδενική στήλη ή αναλογικές / αντίστοιχες στήλες, τότε αξίζει τον ακρωτηριασμό:

(1) Η πέμπτη στήλη είναι μηδέν, την αφαιρούμε από τον πίνακα. Έτσι, η κατάταξη του πίνακα είναι το πολύ τέσσερις. Η πρώτη σειρά πολλαπλασιάζεται με -1. Αυτό είναι ένα άλλο χαρακτηριστικό χαρακτηριστικό της μεθόδου Gaussian, που κάνει την ακόλουθη δράση μια ευχάριστη βόλτα:

(2) Σε όλες τις γραμμές, ξεκινώντας από τη δεύτερη, προστέθηκε η πρώτη γραμμή.

(3) Η πρώτη σειρά πολλαπλασιάστηκε με -1, η τρίτη σειρά διαιρέθηκε με 2, η τέταρτη σειρά διαιρέθηκε με 3. Η δεύτερη σειρά πολλαπλασιασμένη με -1 προστέθηκε στην πέμπτη σειρά.

(4) Η τρίτη γραμμή προστέθηκε στην πέμπτη γραμμή, πολλαπλασιαζόμενη επί -2.

(5) Οι δύο τελευταίες γραμμές είναι αναλογικές, διαγράφουμε την πέμπτη.

Το αποτέλεσμα είναι 4 σειρές.

Απάντηση:

Τυπικό πενταόροφο κτίριο για αυτοεξερεύνηση:

Παράδειγμα 6

Βρείτε την κατάταξη ενός πίνακα

Σύντομη λύση και απάντηση στο τέλος του μαθήματος.

Θα πρέπει να σημειωθεί ότι η φράση "κατάταξη μήτρας" δεν είναι τόσο κοινή στην πράξη και στα περισσότερα προβλήματα μπορείτε να το κάνετε χωρίς αυτήν. Αλλά υπάρχει ένα έργο όπου η υπό εξέταση έννοια είναι ο κύριος χαρακτήρας, και στο τέλος του άρθρου θα εξετάσουμε αυτήν την πρακτική εφαρμογή:

Πώς να διερευνήσετε το σύστημα γραμμικών εξισώσεων για συμβατότητα;

Συχνά, εκτός από την επίλυση συστήματα γραμμικών εξισώσεωνσύμφωνα με την προϋπόθεση, απαιτείται πρώτα να εξεταστεί για συμβατότητα, δηλαδή να αποδειχθεί ότι οποιαδήποτε λύση υπάρχει. Βασικό ρόλο σε αυτή την επαλήθευση διαδραματίζει Θεώρημα Kronecker-Capelli, το οποίο θα διατυπώσω στην απαιτούμενη μορφή:

Αν κατάταξη πίνακες συστήματοςίσο με τον βαθμό σύστημα επαυξημένης μήτρας, τότε το σύστημα είναι συνεπές και αν ο δεδομένος αριθμός συμπίπτει με τον αριθμό των αγνώστων, τότε η λύση είναι μοναδική.

Έτσι, για να μελετήσετε το σύστημα για συμβατότητα, είναι απαραίτητο να ελέγξετε την ισότητα , όπου - μήτρα συστήματος(θυμηθείτε την ορολογία από το μάθημα Μέθοδος Gauss), ένα - σύστημα επαυξημένης μήτρας(δηλ. πίνακας με συντελεστές σε μεταβλητές + στήλη ελεύθερων όρων).

Αυτό το άρθρο θα συζητήσει μια έννοια όπως η κατάταξη μιας μήτρας και οι απαραίτητες πρόσθετες έννοιες. Θα δώσουμε παραδείγματα και αποδείξεις για την εύρεση της κατάταξης μιας μήτρας και επίσης θα σας πούμε τι είναι η δευτερεύουσα μήτρα και γιατί είναι τόσο σημαντική.

Matrix minor

Για να κατανοήσουμε ποια είναι η κατάταξη ενός πίνακα, είναι απαραίτητο να κατανοήσουμε μια τέτοια έννοια ως ελάσσονα πίνακα.

Ορισμός 1

Ανήλικοςκμήτρα ης τάξης - την ορίζουσα ενός τετραγωνικού πίνακα της τάξης k × k, ο οποίος αποτελείται από τα στοιχεία του πίνακα A, που βρίσκεται σε προεπιλεγμένες k-γραμμές και k-στήλες, ενώ διατηρεί τη θέση των στοιχείων του πίνακα A.

Με απλά λόγια, αν στον πίνακα A διαγράψουμε (p-k) σειρές και (n-k) στήλες και από εκείνα τα στοιχεία που παραμένουν, κάνουμε έναν πίνακα, διατηρώντας τη διάταξη των στοιχείων του πίνακα A, τότε η ορίζουσα του πίνακα που προκύπτει είναι το ελάσσονα τάξης k του πίνακα Α.

Από το παράδειγμα προκύπτει ότι τα δευτερεύοντα δευτερεύοντα στοιχεία πρώτης τάξης του πίνακα Α είναι τα ίδια τα στοιχεία του πίνακα.

Μπορούμε να δώσουμε αρκετά παραδείγματα ανηλίκων 2ης τάξης. Ας επιλέξουμε δύο σειρές και δύο στήλες. Για παράδειγμα, 1η και 2η σειρά, 3η και 4η στήλη.

Με αυτήν την επιλογή στοιχείων, το δευτερεύον της δεύτερης τάξης θα είναι - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

Μια άλλη ελάσσονα 2ης τάξης του πίνακα Α είναι 0 0 1 1 = 0

Ας παρέχουμε απεικονίσεις της κατασκευής ανηλίκων δεύτερης τάξης του πίνακα Α:

Το δευτερεύον 3ης τάξης προκύπτει διαγράφοντας την τρίτη στήλη του πίνακα Α:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

Μια απεικόνιση του τρόπου με τον οποίο προκύπτει η ελάσσονα 3ης τάξης του πίνακα Α:

Για έναν δεδομένο πίνακα, δεν υπάρχουν δευτερεύοντα μικρότερα από την 3η τάξη, επειδή

k ≤ m i n (p , n) = m i n (3 , 4) = 3

Πόσα δευτερεύοντα k-ης τάξης υπάρχουν για έναν πίνακα Α τάξης p×n;

Ο αριθμός των ανηλίκων υπολογίζεται με τον ακόλουθο τύπο:

C p k × C n k , g e C p k = p ! κ! (ρ - κ) ! και C nk = n ! κ! (n - k) ! - τον αριθμό των συνδυασμών από p έως k, από n σε k, αντίστοιχα.

Αφού αποφασίσουμε ποια είναι τα δευτερεύοντα στοιχεία του πίνακα Α, μπορούμε να προχωρήσουμε στον προσδιορισμό της κατάταξης του πίνακα Α.

Κατάταξη μήτρας: μέθοδοι εύρεσης

Ορισμός 2

Κατάταξη μήτρας - η υψηλότερη τάξη του πίνακα, εκτός από το μηδέν.

Ονομασία 1

Κατάταξη (Α), Rg(A), Rang(A).

Από τον ορισμό της κατάταξης ενός πίνακα και του ελάσσονος πίνακα ενός πίνακα, γίνεται σαφές ότι η κατάταξη ενός μηδενικού πίνακα είναι ίση με το μηδέν και η κατάταξη ενός μη μηδενικού πίνακα είναι διαφορετική από το μηδέν.

Εύρεση της κατάταξης ενός πίνακα εξ ορισμού

Ορισμός 3

Μέθοδος δευτερεύουσας απαρίθμησης - μια μέθοδος που βασίζεται στον προσδιορισμό της κατάταξης ενός πίνακα.

Αλγόριθμος ενεργειών με απαρίθμηση ανηλίκων :

Είναι απαραίτητο να βρεθεί η κατάταξη του πίνακα Α της τάξης Π× n. Εάν υπάρχει τουλάχιστον ένα μη μηδενικό στοιχείο, τότε η κατάταξη του πίνακα είναι τουλάχιστον ίση με ένα ( επειδή είναι δευτερεύον 1ης τάξης που δεν ισούται με μηδέν).

Στη συνέχεια ακολουθεί η απαρίθμηση ανηλίκων 2ης τάξης. Αν όλα τα δευτερεύοντα 2ης τάξης είναι ίσα με μηδέν, τότε η κατάταξη είναι ίση με ένα. Εάν υπάρχει τουλάχιστον ένα μη μηδενικό δευτερεύον της 2ης τάξης, είναι απαραίτητο να μεταβείτε στην απαρίθμηση ανηλίκων 3ης τάξης και η κατάταξη του πίνακα, σε αυτή την περίπτωση, θα είναι τουλάχιστον δύο.

Ας κάνουμε το ίδιο με την κατάταξη της 3ης τάξης: αν όλα τα δευτερεύοντα στοιχεία του πίνακα είναι ίσα με μηδέν, τότε η κατάταξη θα είναι ίση με δύο. Εάν υπάρχει τουλάχιστον ένα μη μηδενικό δευτερεύον τρίτης τάξης, τότε η κατάταξη του πίνακα είναι τουλάχιστον τρεις. Και ούτω καθεξής, κατ' αναλογία.

Παράδειγμα 2

Βρείτε την κατάταξη ενός πίνακα:

A \u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

Δεδομένου ότι ο πίνακας είναι μη μηδενικός, η κατάταξή του είναι τουλάχιστον ίση με ένα.

Το δευτερεύον 2ης τάξης - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 είναι μη μηδενικό. Αυτό σημαίνει ότι η κατάταξη του πίνακα Α είναι τουλάχιστον δύο.

Ταξινομούμε τα ανήλικα της 3ης τάξης: C 3 3 × C 5 3 \u003d 1 5 ! 3! (5 - 3) ! = 10 τεμάχια.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

Τα ανήλικα 3ης τάξης είναι μηδέν, επομένως η κατάταξη του πίνακα είναι δύο.

Απάντηση : Κατάταξη (Α) = 2.

Εύρεση της κατάταξης ενός πίνακα με τη μέθοδο περιθωρίου ανηλίκων

Ορισμός 3

Μέθοδος Fringing Minor - μια μέθοδος που σας επιτρέπει να έχετε ένα αποτέλεσμα με λιγότερη υπολογιστική εργασία.

Ελάσσονα κρόσσια - ελάσσονος M o k (k + 1) -η τάξη του πίνακα A, που συνορεύει με τον ελάσσονα M της τάξης k του πίνακα A, αν ο πίνακας που αντιστοιχεί στον δευτερεύοντα M o k "περιέχει" τον πίνακα που αντιστοιχεί στον δευτερεύοντα Μ.

Με απλά λόγια, ο πίνακας που αντιστοιχεί στο περιγραμμένο δευτερεύον M λαμβάνεται από τον πίνακα που αντιστοιχεί στο συνοριακό δευτερεύον M o k διαγράφοντας τα στοιχεία μιας γραμμής και μιας στήλης.

Παράδειγμα 3

Βρείτε την κατάταξη ενός πίνακα:

A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

Για να βρούμε την κατάταξη, παίρνουμε το δευτερεύον 2ης τάξης M = 2 - 1 4 1

Καταγράφουμε όλα τα συνοριακά ανήλικα:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

Για να τεκμηριωθεί η μέθοδος οριοθέτησης δευτερευόντων, παρουσιάζουμε ένα θεώρημα του οποίου η διατύπωση δεν απαιτεί αποδεικτική βάση.

Θεώρημα 1

Εάν όλα τα ελάσσονα που συνορεύουν με το μικρότερο της k-ης τάξης ενός πίνακα Α τάξης p επί n είναι ίσα με μηδέν, τότε όλα τα ελάσσονα τάξης (k + 1) του πίνακα A είναι ίσα με μηδέν.

Αλγόριθμος δράσης :

Για να βρείτε την κατάταξη μιας μήτρας, δεν είναι απαραίτητο να περάσετε από όλα τα ανήλικα, απλά κοιτάξτε τα σύνορα.

Εάν τα συνοριακά ανήλικα είναι ίσα με μηδέν, τότε η κατάταξη του πίνακα είναι μηδέν. Εάν υπάρχει τουλάχιστον ένα δευτερεύον που δεν είναι ίσο με μηδέν, τότε θεωρούμε ανηλίκους που συνορεύουν.

Αν είναι όλα μηδέν, τότε η κατάταξη(Α) είναι δύο. Εάν υπάρχει τουλάχιστον ένα μη μηδενικό συνοριακό δευτερεύον, τότε προχωράμε στην εξέταση των συνοριακών ελάσσων του. Και ούτω καθεξής, με παρόμοιο τρόπο.

Παράδειγμα 4

Βρείτε την κατάταξη ενός πίνακα με τη μέθοδο περιθωρίου ανηλίκων

A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

Πώς να αποφασίσετε;

Εφόσον το στοιχείο a 11 του πίνακα Α δεν είναι ίσο με μηδέν, τότε παίρνουμε το δευτερεύον της 1ης τάξης. Ας αρχίσουμε να ψάχνουμε για ένα οριακό μικρότερο εκτός από το μηδέν:

2 1 4 2 = 2 x 2 - 1 x 4 = 0 2 0 4 1 = 2 x 1 - 0 x 4 = 2

Βρήκαμε ένα συνοριακό δευτερεύον 2ης τάξης που δεν ισούται με μηδέν 2 0 4 1 .

Ας απαριθμήσουμε τα συνοριακά ανήλικα - (υπάρχουν (4 - 2) × (5 - 2) = 6 τεμάχια).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

Απάντηση : Κατάταξη(Α) = 2.

Εύρεση της κατάταξης ενός πίνακα με τη μέθοδο Gauss (χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς)

Θυμηθείτε τι είναι οι στοιχειώδεις μετασχηματισμοί.

Στοιχειώδεις μεταμορφώσεις:

με την αναδιάταξη των σειρών (στήλων) του πίνακα.
πολλαπλασιάζοντας όλα τα στοιχεία οποιασδήποτε σειράς (στήλης) του πίνακα με έναν αυθαίρετο μη μηδενικό αριθμό k.

προσθέτοντας στα στοιχεία οποιασδήποτε σειράς (στήλης) στοιχεία που αντιστοιχούν σε μια άλλη σειρά (στήλη) του πίνακα, τα οποία πολλαπλασιάζονται με έναν αυθαίρετο αριθμό k.

Ορισμός 5

Εύρεση της κατάταξης ενός πίνακα με τη μέθοδο Gauss - μια μέθοδος που βασίζεται στη θεωρία της ισοδυναμίας πίνακα: εάν ο πίνακας Β λαμβάνεται από τον πίνακα Α χρησιμοποιώντας έναν πεπερασμένο αριθμό στοιχειωδών μετασχηματισμών, τότε Rank(A) = Rank(B).

Η εγκυρότητα αυτής της δήλωσης προκύπτει από τον ορισμό του πίνακα:

στην περίπτωση μετάθεσης των γραμμών ή στηλών ενός πίνακα, η ορίζοντή του αλλάζει πρόσημο. Εάν είναι ίσο με μηδέν, τότε κατά τη μετάθεση σειρών ή στηλών παραμένει ίσο με μηδέν.
στην περίπτωση πολλαπλασιασμού όλων των στοιχείων οποιασδήποτε σειράς (στήλης) του πίνακα με έναν αυθαίρετο αριθμό k, ο οποίος δεν είναι ίσος με μηδέν, η ορίζουσα του πίνακα που προκύπτει είναι ίση με την ορίζουσα του αρχικού πίνακα, ο οποίος πολλαπλασιάζεται από k?

στην περίπτωση προσθήκης στα στοιχεία μιας συγκεκριμένης γραμμής ή στήλης του πίνακα των αντίστοιχων στοιχείων μιας άλλης γραμμής ή στήλης, τα οποία πολλαπλασιάζονται με τον αριθμό k, δεν αλλάζει ορίζουσα της.

Η ουσία της μεθόδου των στοιχειωδών μετασχηματισμών : ανάγουμε τον πίνακα, του οποίου η κατάταξη πρέπει να βρεθεί, σε τραπεζοειδή χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς.

Για τι?

Η κατάταξη των πινάκων αυτού του είδους είναι αρκετά εύκολο να βρεθεί. Είναι ίσος με τον αριθμό των σειρών που έχουν τουλάχιστον ένα μη μηδενικό στοιχείο. Και επειδή η κατάταξη δεν αλλάζει κατά τη διάρκεια των στοιχειωδών μετασχηματισμών, αυτή θα είναι η κατάταξη του πίνακα.

Ας δείξουμε αυτή τη διαδικασία:

για ορθογώνιους πίνακες Α τάξης p επί n, ο αριθμός των σειρών των οποίων είναι μεγαλύτερος από τον αριθμό των στηλών:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n n - 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k

για ορθογώνιους πίνακες Α τάξης p επί n, ο αριθμός των γραμμών των οποίων είναι μικρότερος από τον αριθμό των στηλών:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ p 1 ⋯ b p n , R a n k (A) = p

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

για τετράγωνους πίνακες Α τάξης n κατά n:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n 0 - 1 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k ,< n

Παράδειγμα 5

Βρείτε την κατάταξη του πίνακα Α χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

Πώς να αποφασίσετε;

Δεδομένου ότι το στοιχείο a 11 είναι μη μηδενικό, είναι απαραίτητο να πολλαπλασιάσουμε τα στοιχεία της πρώτης σειράς του πίνακα A με 1 a 11 \u003d 1 2:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

Προσθέτουμε στα στοιχεία της 2ης σειράς τα αντίστοιχα στοιχεία της 1ης σειράς, τα οποία πολλαπλασιάζονται με (-3). Στα στοιχεία της 3ης σειράς προσθέτουμε τα στοιχεία της 1ης σειράς, τα οποία πολλαπλασιάζονται με (-1):

~ A (1) \u003d 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) \u003d \u003d 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5 ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

Το στοιχείο a 22 (2) είναι μη μηδενικό, επομένως πολλαπλασιάζουμε τα στοιχεία της 2ης σειράς του πίνακα A με A (2) με a 1 a 22 (2) = - 2 3:

A (3) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

Στα στοιχεία της 3ης σειράς του πίνακα που προκύπτει, προσθέτουμε τα αντίστοιχα στοιχεία της 2ης σειράς, τα οποία πολλαπλασιάζονται με 3 2 .
στα στοιχεία της 4ης σειράς - τα στοιχεία της 2ης σειράς, τα οποία πολλαπλασιάζονται με 9 2.
στα στοιχεία της 5ης σειράς - τα στοιχεία της 2ης σειράς, τα οποία πολλαπλασιάζονται με 3 2 .

Όλα τα στοιχεία της σειράς είναι μηδέν. Έτσι, με τη βοήθεια στοιχειωδών μετασχηματισμών, έχουμε αναγάγει τη μήτρα σε τραπεζοειδή μορφή, από την οποία φαίνεται ότι R a n k (A (4)) = 2 . Από αυτό προκύπτει ότι η κατάταξη του αρχικού πίνακα είναι επίσης ίση με δύο.

Σχόλιο

Εάν πραγματοποιήσετε στοιχειώδεις μετασχηματισμούς, τότε δεν επιτρέπονται κατά προσέγγιση τιμές!

Εάν παρατηρήσετε κάποιο λάθος στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Σε κάθε πίνακα, δύο τάξεις μπορούν να συσχετιστούν: μια κατάταξη γραμμής (η κατάταξη του συστήματος σειρών) και μια κατάταξη στήλης (η κατάταξη του συστήματος στηλών).

Θεώρημα

Η κατάταξη της γραμμής ενός πίνακα είναι ίση με την κατάταξη στηλών του.

Κατάταξη μήτρας

Ορισμός

Κατάταξη μήτραςΤο $A$ είναι η κατάταξη του συστήματος γραμμών ή στηλών του.

Υποδηλώνεται με $\operatorname(rang) A$

Στην πράξη, για να βρεθεί η κατάταξη ενός πίνακα, χρησιμοποιείται η ακόλουθη δήλωση: η κατάταξη ενός πίνακα είναι ίση με τον αριθμό των μη μηδενικών σειρών αφού ο πίνακας έχει μειωθεί σε μια κλιμακωτή μορφή.

Οι στοιχειώδεις μετασχηματισμοί σε γραμμές (στήλες) ενός πίνακα δεν αλλάζουν την κατάταξή του.

Η κατάταξη ενός πίνακα βημάτων είναι ίση με τον αριθμό των μη μηδενικών σειρών του.

Παράδειγμα

Ασκηση.Βρείτε την κατάταξη ενός πίνακα $ A=\left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & ( 7) \ \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3)\end(πίνακας)\δεξιά) $

Λύση.Χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς στις σειρές του, μειώνουμε τον πίνακα $A$ σε μια φόρμα βήματος. Για να το κάνετε αυτό, αφαιρέστε πρώτα τα δύο δεύτερα από την τρίτη γραμμή:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3)\end(πίνακας)\δεξιά) $$

Από τη δεύτερη γραμμή αφαιρούμε την τέταρτη γραμμή, πολλαπλασιαζόμενη επί 4. από το τρίτο - δύο τέταρτα:

$$ A \sim \left(\begin(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3)\end(πίνακας)\δεξιά) $$

Προσθέτουμε τα πρώτα πέντε στη δεύτερη γραμμή και τρία τρίτα στην τρίτη:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(πίνακας)\δεξιά) $$

Αλλάξτε την πρώτη και τη δεύτερη γραμμή:

$$ A \sim \left(\begin(array)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(πίνακας)\δεξιά) $$

$$ A \sim \left(\begin(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0)\end(πίνακας)\δεξιά) \Δεξί βέλος \όνομα χειριστή(κύμα) A=2 $$

Απάντηση.$ \όνομα χειριστή(κατάταξη) A=2 $

Μέθοδος μικρής οριοθέτησης

Μια άλλη μέθοδος για την εύρεση της κατάταξης ενός πίνακα βασίζεται σε αυτό το θεώρημα - μέθοδος μικρής οριοθέτησης. Η ουσία αυτής της μεθόδου είναι η εύρεση ανηλίκων, ξεκινώντας από χαμηλότερες τάξεις και μεταβαίνοντας σε υψηλότερες. Εάν η δευτερεύουσα τάξη $n$-th είναι μη μηδενική και όλα τα $n+1$-th ελάσσονα είναι ίσα με μηδέν, τότε η κατάταξη του πίνακα θα είναι ίση με $n$ .

Παράδειγμα

Ασκηση.Βρείτε την κατάταξη ενός πίνακα $ A=\left(\begin(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0 ) \\ (-1) & (-2) & (6) & (6)\end(πίνακας)\δεξιά) $ χρησιμοποιώντας τη μέθοδο ελάσσονος περιγράμματος.

Λύση.Τα δευτερεύοντα στοιχεία της ελάχιστης τάξης είναι τα δευτερεύοντα στοιχεία πρώτης τάξης, τα οποία είναι ίσα με τα στοιχεία του πίνακα $A$ . Θεωρήστε, για παράδειγμα, το δευτερεύον $ M_(1)=1 \neq 0 $ . που βρίσκεται στην πρώτη γραμμή και την πρώτη στήλη. Οριοθετώντας το με τη δεύτερη γραμμή και τη δεύτερη στήλη, παίρνουμε το δευτερεύον $ M_(2)^(1)=\left| \begin(array)(ll)(1) & (2) \\ (2) & (4)\end(array)\right|=0 $ ; θεωρήστε ένα άλλο δευτερεύον της δεύτερης τάξης, για αυτό περιορίζουμε το δευτερεύον $M_1$ με τη βοήθεια της δεύτερης σειράς και της τρίτης στήλης, τότε έχουμε το δευτερεύον $ M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $ , δηλαδή, η κατάταξη του πίνακα είναι τουλάχιστον δύο. Στη συνέχεια, θεωρούμε ανηλίκους τρίτης τάξης που περιβάλλουν το δευτερεύον $ M_(2)^(2) $ . Υπάρχουν δύο τέτοια δευτερεύοντα: ένας συνδυασμός της τρίτης σειράς με τη δεύτερη στήλη ή με την τέταρτη στήλη. Υπολογίζουμε αυτά τα ανήλικα.

§3. Κατάταξη μήτρας

Προσδιορισμός της κατάταξης ενός πίνακα

Γραμμικές εξαρτώμενες σειρές

Μετασχηματισμοί στοιχειώδους πίνακα

Ισοδύναμοι πίνακες

Αλγόριθμος για την εύρεση της κατάταξης ενός πίνακα χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς

§τέσσερα. Ορίζοντες πρώτης, δεύτερης και τρίτης τάξης

Ορίζουσα πρώτης τάξης

Ορίζουσα δεύτερης τάξης

Ορίζουσα τρίτης τάξης

Ο κανόνας του Sarrus

§5. Υπολογισμός καθοριστικών παραγόντων μεγάλων παραγγελιών

Αλγεβρική πρόσθεση

Θεώρημα Laplace

Ορίζουσα τριγωνικής μήτρας

Εφαρμογή. Η έννοια της ορίζουσας Πη τάξη γενικά.

§ 3. Κατάταξη μήτρας

Κάθε πίνακας χαρακτηρίζεται από έναν ορισμένο αριθμό που είναι σημαντικός για την επίλυση συστημάτων γραμμικών εξισώσεων. Αυτός ο αριθμός ονομάζεται κατάταξη μήτρας.

Κατάταξη μήτραςισούται με τον αριθμό των γραμμικά ανεξάρτητων σειρών του (στήλες), μέσω των οποίων εκφράζονται γραμμικά όλες οι άλλες σειρές (στήλες) του.

Οι γραμμές (στήλες) ενός πίνακα καλούνται γραμμικά εξαρτώμενηαν τα αντίστοιχα στοιχεία τους είναι ανάλογα.

Με άλλα λόγια, τα στοιχεία μιας από τις γραμμικά εξαρτώμενες σειρές είναι ίσα με τα στοιχεία της άλλης, πολλαπλασιαζόμενα με τον ίδιο αριθμό. Για παράδειγμα, οι σειρές 1 και 2 του πίνακα ΑΛΛΑεξαρτώνται γραμμικά αν , όπου (λ είναι κάποιος αριθμός).

Παράδειγμα. Βρείτε την κατάταξη ενός πίνακα

Λύση.

Η δεύτερη σειρά λαμβάνεται από την πρώτη εάν τα στοιχεία της πολλαπλασιάζονται με -3, η τρίτη λαμβάνεται από την πρώτη εάν τα στοιχεία της πολλαπλασιάζονται με 0 και η τέταρτη σειρά δεν μπορεί να εκφραστεί ως προς την πρώτη. Αποδεικνύεται ότι ο πίνακας έχει δύο γραμμικά ανεξάρτητες σειρές, επειδή η πρώτη και η τέταρτη σειρά δεν είναι ανάλογες, επομένως η κατάταξη του πίνακα είναι 2.

Κατάταξη μήτρας ΑΛΛΑσυμβολίζεται βαθμός Αή r(ΕΝΑ).

Από τον ορισμό της κατάταξης ενός πίνακα, προκύπτει:

1. Η κατάταξη ενός πίνακα δεν υπερβαίνει τη μικρότερη από τις διαστάσεις του, δηλ. για μήτρα Είμαι × n .

2. Η κατάταξη ενός πίνακα είναι μηδέν μόνο εάν είναι μηδενικός πίνακας.

Στη γενική περίπτωση, ο προσδιορισμός της κατάταξης ενός πίνακα είναι αρκετά επίπονος. Για να διευκολυνθεί αυτή η εργασία, χρησιμοποιούνται μετασχηματισμοί που διατηρούν την κατάταξη του πίνακα, οι οποίοι καλούνται στοιχειώδεις μεταμορφώσεις:

1) απόρριψη μιας μηδενικής σειράς (στήλης).

2) πολλαπλασιασμός όλων των στοιχείων μιας γραμμής (στήλης) με έναν αριθμό διαφορετικό από το μηδέν.

3) αλλαγή της σειράς των σειρών (στήλες).

4) προσθέτοντας στα στοιχεία μιας σειράς (στήλης) τα αντίστοιχα στοιχεία μιας άλλης σειράς (στήλης), πολλαπλασιαζόμενα με οποιονδήποτε αριθμό.

5) μεταφορά μήτρας.

Οι δύο πίνακες ονομάζονται ισοδύναμοςαν το ένα λαμβάνεται από το άλλο με πεπερασμένο αριθμό στοιχειωδών μετασχηματισμών.

Η ισοδυναμία των πινάκων υποδεικνύεται με το σύμβολο "~" (ισοδύναμο).

Με τη βοήθεια στοιχειωδών μετασχηματισμών, οποιοσδήποτε πίνακας μπορεί να μειωθεί σε τριγωνική μορφή, τότε ο υπολογισμός της κατάταξής του δεν είναι δύσκολος.

Η διαδικασία υπολογισμού της κατάταξης ενός πίνακα χρησιμοποιώντας στοιχειώδεις μετασχηματισμούςας δούμε ένα παράδειγμα.

Παράδειγμα. Βρείτε την κατάταξη ενός πίνακα

Α =

Λύση.

Το καθήκον μας είναι να φέρουμε τη μήτρα σε τριγωνική μορφή, δηλ. χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, βεβαιωθείτε ότι μόνο τα μηδενικά βρίσκονται κάτω από την κύρια διαγώνιο στον πίνακα.

1. Εξετάστε την πρώτη γραμμή. Αν στοιχείο ένα 11 = 0, τότε κατά τη μετάθεση σειρών ή στηλών, το επιτυγχάνουμε ένα 11 ¹ 0. Στο παράδειγμά μας, ας ανταλλάξουμε, για παράδειγμα, την πρώτη και τη δεύτερη σειρά του πίνακα:

Α =

Τώρα στοιχείο ένα 11 ¹ 0. Πολλαπλασιάζοντας την πρώτη σειρά με κατάλληλους αριθμούς και προσθέτοντας με άλλες σειρές, θα διασφαλίσουμε ότι όλα τα στοιχεία της πρώτης στήλης (εκτός ένα 11) ήταν ίσα με μηδέν.

2. Σκεφτείτε τώρα τη δεύτερη γραμμή. Αν στοιχείο ένα 22 = 0, τότε κατά τη μετάθεση σειρών ή στηλών, το πετυχαίνουμε ένα 22 ¹ 0. Αν το στοιχείο ένα 22 ¹ 0 (και έχουμε ένα 22 = –1 ¹ 0), στη συνέχεια πολλαπλασιάζοντας τη δεύτερη σειρά με κατάλληλους αριθμούς και προσθέτοντας σε άλλες σειρές, θα διασφαλίσουμε ότι όλα τα στοιχεία της δεύτερης στήλης (εκτός ένα 22) ήταν ίσες με μηδέν.

3. Αν στη διαδικασία των μετασχηματισμών προκύψουν σειρές (στήλες) που αποτελούνται εξ ολοκλήρου από μηδενικά, τότε τις απορρίπτουμε. Στο παράδειγμά μας, θα απορρίψουμε τις γραμμές 3 και 4:

Ο τελευταίος πίνακας έχει μια κλιμακωτή μορφή και περιέχει δύο σειρές. Είναι γραμμικά ανεξάρτητα, επομένως η κατάταξη του πίνακα είναι 2.

§ τέσσερα. Ορίζοντες πρώτης, δεύτερης και τρίτης τάξης

Μεταξύ της ποικιλίας των πινάκων, οι τετράγωνοι πίνακες ξεχωρίζονται ξεχωριστά. Αυτός ο τύπος μήτρας είναι καλός επειδή:

1. Οι πίνακες ταυτότητας είναι τετράγωνοι.

2. Μπορείτε να πολλαπλασιάσετε και να προσθέσετε οποιουσδήποτε τετράγωνους πίνακες της ίδιας σειράς, και παίρνετε έναν πίνακα της ίδιας σειράς.

3. Οι τετράγωνοι πίνακες μπορούν να αυξηθούν σε ισχύ.

Επίσης, μόνο οι τετραγωνικοί πίνακες μπορούν να έχουν ορίζοντα.

Καθοριστική μήτραείναι ένας ειδικός αριθμός που υπολογίζεται σύμφωνα με κάποιον κανόνα. Καθοριστική μήτρα ΑΛΛΑσυμβολίζεται:

Ή με ίσιες αγκύλες: ,

Ή κεφαλαίο ελληνικό γράμμα "δέλτα": Δ( ΕΝΑ),

Ή το σύμβολο "καθοριστικός παράγοντας": det ( ΕΝΑ).

Ορίζουσα πίνακα πρώτης τάξης ΑΛΛΑ= (ένα 11) ή ορίζουσα πρώτης τάξης, είναι ένας αριθμός ίσος με το στοιχείο του πίνακα:

∆1 = =ένα 11

Ορίζουσα μήτρας δεύτερης τάξης ή ορίζουσα δεύτερης τάξης

Παράδειγμα:

Η ορίζουσα ενός πίνακα τρίτης τάξης ή ορίζουσα τρίτης τάξης, είναι ένας αριθμός που υπολογίζεται από τον τύπο:

Η ορίζουσα τρίτης τάξης μπορεί να υπολογιστεί χρησιμοποιώντας Ο κανόνας του Sarrus .

Ο κανόνας του Sarrus. Οι δύο πρώτες στήλες υπογράφονται στην ορίζουσα τρίτης τάξης στα δεξιά και με το σύμβολο συν (+) λαμβάνουν το άθροισμα των γινομένων των τριών στοιχείων που βρίσκονται στην κύρια διαγώνιο της ορίζουσας και στις "ευθείες γραμμές" παράλληλα. στην κύρια διαγώνιο, με αρνητικό πρόσημο (-) παίρνουν το άθροισμα των γινομένων των στοιχείων που βρίσκονται στη δεύτερη διαγώνιο και στις παράλληλες προς αυτήν «ευθείες γραμμές».

Παράδειγμα:

Είναι εύκολο να δούμε ότι ο αριθμός των όρων στην ορίζουσα αυξάνεται με τη σειρά του. Γενικά στην ορίζουσα ΠΗ σειρά, ο αριθμός των όρων είναι 1 2 3 ... Π = Π!.

Ας ελέγξουμε: για το Δ 1 ο αριθμός των όρων είναι ίσος με 1! = 1,

για Δ 2 ο αριθμός των όρων είναι 2! = 1 2 = 2,

για Δ 3 ο αριθμός των όρων είναι 3! = 1 2 3 = 6.

Από αυτό προκύπτει ότι για την ορίζουσα 4ης τάξης, ο αριθμός των όρων είναι 4! = 1 2 3 4 = 24, που σημαίνει ότι ο υπολογισμός μιας τέτοιας ορίζουσας είναι αρκετά επίπονος, για να μην αναφέρουμε ορίζοντες υψηλότερης τάξης. Λαμβάνοντας υπόψη αυτό, προσπαθούν να μειώσουν τον υπολογισμό των καθοριστικών παραγόντων των μεγάλων τάξεων στον υπολογισμό των οριζόντιων παραγόντων της δεύτερης ή τρίτης τάξης.

§ 5. Υπολογισμός καθοριστικών παραγόντων μεγάλων παραγγελιών

Ας εισαγάγουμε μια σειρά από έννοιες.

Ας δοθεί ένας τετραγωνικός πίνακας A n-η σειρά:

Α=

Ανήλικος Μ ij στοιχείο έναΤο ij ονομάζεται ορίζουσα ( Π– 1)η σειρά που λαμβάνεται από τον πίνακα ΑΛΛΑαπεργία Εγώ-η γραμμή και ι-η στήλη.

Για παράδειγμα, το στοιχείο είναι δευτερεύον ένα 12 πίνακες τρίτης τάξης θα είναι:

Αλγεβρική πρόσθεση ΑΛΛΑ ij στοιχείο έναΤο ij είναι το ελάσσονα, λαμβάνεται με το πρόσημο (−1) Εγώ + ι:

ΑΛΛΑ ij = (−1) Εγώ + j M ij

Με άλλα λόγια, ΑΛΛΑ ij = Μ ij αν Εγώ+ιΖυγός αριθμός,

ΑΛΛΑ ij = − Μ ij αν Εγώ+ιπεριττός αριθμός.

Παράδειγμα. Βρείτε αλγεβρικά συμπληρώματα στοιχείων της δεύτερης σειράς ενός πίνακα

Λύση.

Με τη βοήθεια αλγεβρικών συμπληρωμάτων, μπορεί κανείς να υπολογίσει ορίζουσες μεγάλων τάξεων, με βάση το θεώρημα του Laplace.

Θεώρημα Laplace. Η ορίζουσα ενός τετραγωνικού πίνακα ισούται με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε από τις σειρές (στήλες) του και των αλγεβρικών συμπληρωμάτων τους:

– αποσύνθεση στην i-η γραμμή.

( είναι η επέκταση στην jη στήλη).

Παράδειγμα. Υπολογίστε την ορίζουσα μήτρας αποσύνθεση στην πρώτη γραμμή.

Λύση.

Έτσι, μια ορίζουσα οποιασδήποτε τάξης μπορεί να αναχθεί στον υπολογισμό πολλών οριζόντων μικρότερης τάξης. Είναι προφανές ότι για την επέκταση είναι βολικό να επιλέξετε μια γραμμή ή στήλη που περιέχει όσο το δυνατόν περισσότερα μηδενικά.

Ας εξετάσουμε ένα ακόμη παράδειγμα.

Παράδειγμα. Υπολογίστε την ορίζουσα ενός τριγωνικού πίνακα

Λύση.

Το κατάλαβα η ορίζουσα ενός τριγωνικού πίνακα είναι ίση με το γινόμενο των στοιχείων της κύριας διαγωνίου του .

Αυτό το σημαντικό συμπέρασμα καθιστά εύκολο τον υπολογισμό της ορίζουσας οποιουδήποτε τριγωνικού πίνακα. Αυτό είναι ακόμη πιο χρήσιμο επειδή, εάν είναι απαραίτητο, οποιαδήποτε ορίζουσα μπορεί να αναχθεί σε τριγωνική μορφή. Σε αυτή την περίπτωση, χρησιμοποιούνται ορισμένες ιδιότητες καθοριστικών παραγόντων.

Εφαρμογή

Η έννοια της ορίζουσας Πη τάξη γενικά.

Γενικά, μπορεί κανείς να δώσει έναν αυστηρό ορισμό για την ορίζουσα μήτρας Που σειρά, αλλά για αυτό είναι απαραίτητο να εισαγάγουμε μια σειρά από έννοιες.

μετάθεσηαριθμοί 1, 2, ..., nκαλείται οποιαδήποτε διάταξη αυτών των αριθμών με συγκεκριμένη σειρά. Στη στοιχειώδη άλγεβρα, αποδεικνύεται ότι ο αριθμός όλων των μεταθέσεων που μπορούν να σχηματιστούν από nοι αριθμοί είναι 12...n = n!. Για παράδειγμα, τρεις αριθμοί 1, 2, 3 μπορούν να σχηματίσουν 3! = 6 μεταθέσεις: 123, 132, 312, 321, 231, 213.

Λένε ότι σε μια δεδομένη μετάθεση του αριθμού Εγώκαι ιαπαρτίζω αντιστροφή(διαταραχή) αν Εγώ> ι, αλλά Εγώστέκεται σε αυτή τη μετάθεση πριν ι, δηλαδή αν ο μεγαλύτερος αριθμός βρίσκεται στα αριστερά του μικρότερου.

Η μετάθεση ονομάζεται ακόμη και(ή Περιττός) εάν ο συνολικός αριθμός των αντιστροφών είναι άρτιος (μονός), αντίστοιχα.

Μια πράξη μέσω της οποίας περνά κανείς από μια μετάθεση σε μια άλλη, που αποτελείται από την ίδια nκαλούνται αριθμοί υποκατάσταση nου βαθμού.

Μια αντικατάσταση που μετατρέπει μια μετάθεση σε άλλη γράφεται σε δύο γραμμές σε κοινές αγκύλες και οι αριθμοί που καταλαμβάνουν τις ίδιες θέσεις στις υπό εξέταση μεταθέσεις ονομάζονται αντίστοιχοι και γράφονται ο ένας κάτω από τον άλλο. Για παράδειγμα, το σύμβολο

υποδηλώνει μια μετάθεση στην οποία το 3 πηγαίνει στο 4, το 1 στο 2, το 2 στο 1, το 4 στο 3. Μια μετάθεση ονομάζεται άρτια (ή περιττή) εάν ο συνολικός αριθμός αντιστροφών και στις δύο σειρές της αντικατάστασης είναι άρτιος (μονός). Οποιαδήποτε αντικατάσταση nο βαθμός μπορεί να γραφτεί ως

εκείνοι. με τη φυσική διάταξη των αριθμών στην επάνω γραμμή.

Ας μας δοθεί ένας τετραγωνικός πίνακας τάξης n

Εξετάστε όλα τα πιθανά προϊόντα nστοιχεία αυτού του πίνακα, που λαμβάνονται ένα και μόνο από κάθε γραμμή και κάθε στήλη, δηλ. έργα της μορφής:

όπου δείκτες q 1 , q 2 ,..., q nσυνθέτουν κάποια μετάθεση αριθμών
1, 2,..., n. Ο αριθμός τέτοιων προϊόντων είναι ίσος με τον αριθμό των διαφορετικών μεταθέσεων από nχαρακτήρες, δηλ. ισοδυναμεί n!. Σημάδι εργασίας , ισούται με (–1) q, όπου qείναι ο αριθμός των αντιστροφών στη μετάθεση των δεύτερων δεικτών στοιχείων.

καθοριστικός n-η σειράονομάζεται το αλγεβρικό άθροισμα όλων των πιθανών γινομένων πάνω nστοιχεία μήτρας, που λαμβάνονται ένα και μόνο από κάθε γραμμή και κάθε στήλη, δηλ. έργα της μορφής: . Ταυτόχρονα, το σημάδι του έργου ισούται με (–1) q, όπου qείναι ο αριθμός των αντιστροφών στη μετάθεση των δεύτερων δεικτών στοιχείων.

Γραμμική άλγεβρα

Θεωρήστε έναν πίνακα Α μεγέθους .

Α=
Επιλέξτε k σειρές και k στήλες σε αυτό (
).

Ορισμός 26:ΑνήλικοςΗ k-η τάξη του πίνακα Α είναι η ορίζουσα του τετραγωνικού πίνακα, ο οποίος προκύπτει από τον δεδομένο με επιλογή σε αυτόν.

k σειρές και k στήλες.

Ορισμός 27:τάξηΟ πίνακας ονομάζεται η μεγαλύτερη από τις μη μηδενικές τάξεις των δευτερευόντων του, r(A).

Ορισμός 28:Ο ανήλικος του οποίου η σειρά είναι ίδια με τον βαθμό του καλείται βασικό μικρό.

Δήλωση:

1. Η κατάταξη εκφράζεται ως ακέραιος αριθμός.(
)

2.r=0,
όταν το Α είναι μηδέν.

Στοιχειώδεις μετασχηματισμοί πινάκων.

Οι στοιχειώδεις μετασχηματισμοί των πινάκων περιλαμβάνουν τα ακόλουθα:

1) πολλαπλασιασμός όλων των στοιχείων οποιασδήποτε σειράς (στήλης) του πίνακα με τον ίδιο αριθμό.

2) προσθήκη στα στοιχεία οποιασδήποτε σειράς (στήλης) του πίνακα των αντίστοιχων στοιχείων μιας άλλης σειράς (στήλης) πολλαπλασιαζόμενη με τον ίδιο αριθμό.

3) μετάθεση των σειρών (στηλών) του πίνακα.

4) απόρριψη της μηδενικής σειράς (στήλης).

5) αντικατάσταση γραμμών μήτρας με αντίστοιχες στήλες.

Ορισμός 29:Οι πίνακες που λαμβάνονται ο ένας από τον άλλο, κάτω από στοιχειώδεις μετασχηματισμούς, ονομάζονται ισοδύναμοι πίνακες, που συμβολίζονται με "~"

Η κύρια ιδιότητα των ισοδύναμων πινάκων: Οι τάξεις των ισοδύναμων πινάκων είναι ίσες.

Παράδειγμα 18:Υπολογίστε το r(A),

Λύση:Πολλαπλασιάστε την πρώτη γραμμή βήμα προς βήμα με (-4)(-2)

(-7) και στη συνέχεια προσθέστε στη δεύτερη, τρίτη και τέταρτη σειρά αντίστοιχα.

αλλάξτε τη δεύτερη και την τέταρτη γραμμή
πολλαπλασιάστε τη δεύτερη σειρά με (-2) και προσθέστε την στην τέταρτη σειρά. προσθέστε τη δεύτερη και την τρίτη σειρά.

προσθέστε την τρίτη και τέταρτη σειρά.

~
απορρίψτε τη μηδενική γραμμή

~
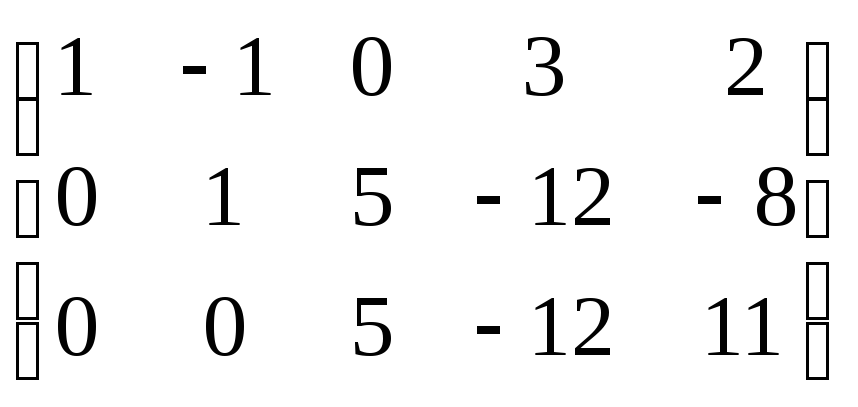r(A)=3
κατάταξη του αρχικού πίνακα

ισούται με τρία.

Ορισμός 30:Ονομάζουμε έναν πίνακα A βηματικό πίνακα εάν όλα τα στοιχεία της κύριας διαγωνίου 0, και τα στοιχεία κάτω από την κύρια διαγώνιο είναι μηδέν.

Πρόταση:

1) η κατάταξη ενός πίνακα βημάτων είναι ίση με τον αριθμό των σειρών του.

2) οποιοσδήποτε πίνακας μπορεί να αναχθεί σε βαθμιδωτή μορφή με τη βοήθεια στοιχειωδών μετασχηματισμών.

Παράδειγμα 19:Σε ποιες τιμές του πίνακα 
έχει βαθμό ίσο με ένα;

Λύση:Η κατάταξη είναι ίση με ένα αν η ορίζουσα δεύτερης τάξης είναι ίση με μηδέν, δηλ.

§6. Συστήματα γραμμικών εξισώσεων γενικής μορφής.

σύστημα προβολής
---(9) ονομάζεται σύστημα γενικής μορφής.

Ορισμός 31:Δύο συστήματα λέγονται ισοδύναμα (ισοδύναμα) αν κάθε λύση του πρώτου συστήματος είναι λύση του δεύτερου και αντίστροφα.

Στο σύστημα (1) ο πίνακας A=
θα ονομάζεται κύριος πίνακας του συστήματος, και =
σύστημα διευρυμένου πίνακα

Θεώρημα. Kronecker-Cappelli

Για να είναι συνεπές το σύστημα (9), είναι απαραίτητο και αρκετό η κατάταξη του κύριου πίνακα του συστήματος να είναι ίση με την κατάταξη του εκτεταμένου πίνακα, δηλ. r(A)=r( )

Θεώρημα 1.Εάν η κατάταξη του πίνακα ενός συνεπούς συστήματος είναι ίση με τον αριθμό των αγνώστων, τότε το σύστημα έχει μια μοναδική λύση.

Θεώρημα 2.Εάν η κατάταξη του πίνακα ενός κοινού συστήματος είναι μικρότερη από τον αριθμό των αγνώστων, τότε το σύστημα έχει άπειρο αριθμό λύσεων.

Ο κανόνας για την επίλυση ενός αυθαίρετου συστήματος γραμμικών εξισώσεων:

1) βρείτε τις τάξεις των κύριων και εκτεταμένων πινάκων του συστήματος. Αν ένα
, τότε το σύστημα είναι ασυνεπές.

2) Αν
=r, τότε το σύστημα είναι συμβατό. Βρείτε κάποιο βασικό δευτερεύον της τάξης r. Θα καλέσουμε το βασικό δευτερεύον, βάσει του οποίου καθορίστηκε η κατάταξη του πίνακα.

Οι άγνωστοι των οποίων οι συντελεστές περιλαμβάνονται στη βασική ελάσσονα ονομάζονται κύριοι (βασικοί) και αριστερά στα αριστερά, ενώ οι υπόλοιποι άγνωστοι ονομάζονται ελεύθεροι και μεταφέρονται στη δεξιά πλευρά της εξίσωσης.

3) Να βρείτε τις εκφράσεις των κύριων αγνώστων ως προς τους ελεύθερους. Λαμβάνεται η γενική λύση του συστήματος.

Παράδειγμα 20:Ερευνήστε το σύστημα και, σε περίπτωση συμβατότητάς του, βρείτε είτε μια μοναδική είτε γενική λύση