Testiranje hipoteze da je prosjek jednak određenoj vrijednosti. Testiranje hipoteze da je prosjek jednak zadanoj vrijednosti a
8.1. Pojam zavisnih i nezavisnih uzoraka.
Odabir kriterija za provjeru hipoteze
primarno određuje jesu li uzorci koji se razmatraju ovisni ili neovisni. Uvedimo odgovarajuće definicije.
Def. Uzorci se nazivaju nezavisna, ako postupak odabira jedinica u prvom uzorku nije ni na koji način povezan s postupkom odabira jedinica u drugom uzorku.
Primjer dva nezavisna uzorka bili bi gore razmotreni uzorci muškaraca i žena koji rade u istom poduzeću (u istoj industriji, itd.).
Napominjemo da neovisnost dvaju uzoraka uopće ne znači da ne postoji zahtjev za određenom vrstom sličnosti tih uzoraka (njihove homogenosti). Stoga, kada proučavamo razinu prihoda muškaraca i žena, malo je vjerojatno da ćemo dopustiti situaciju u kojoj su muškarci odabrani među moskovskim poslovnim ljudima, a žene iz australskih starosjedilaca. I žene bi trebale biti Moskovljanke i, štoviše, “poslovne žene”. Ali ovdje nije riječ o ovisnosti uzoraka, već o zahtjevu homogenosti proučavane populacije objekata, koji mora biti zadovoljen kako pri prikupljanju tako i pri analizi socioloških podataka.
Def. Uzorci se nazivaju ovisni ili upareni, ako je svaka jedinica jednog uzorka "povezana" s određenom jedinicom drugog uzorka.
Ova zadnja definicija vjerojatno će postati jasnija ako damo primjer zavisnih uzoraka.
Pretpostavimo da želimo saznati je li očev društveni status u prosjeku niži društveni status sin (vjerujemo da možemo mjeriti ovo složeno i dvosmisleno shvaćeno društvene karakteristike osoba). Čini se očiglednim da je u takvoj situaciji uputno odabrati parove ispitanika (otac, sin) i pretpostaviti da je svaki element prvog uzorka (jedan od očeva) “vezan” za određeni element drugog uzorka (njegov sin). Ova dva uzorka nazvat ćemo ovisnima.
8.2. Testiranje hipoteza za neovisne uzorke
Za nezavisna uzoraka, izbor kriterija ovisi o tome znamo li opće varijance s 1 2 i s 2 2 karakteristike koja se razmatra za uzorke koji se proučavaju. Smatrat ćemo ovaj problem riješenim, pod pretpostavkom da odstupanja uzorka podudaraju s općim. U ovom slučaju, kriterij je vrijednost:
Prije nego prijeđemo na raspravu o situaciji kada su nam opće varijance (ili barem jedna od njih) nepoznate, napominjemo sljedeće.
Logika korištenja kriterija (8.1) slična je onoj koju smo opisali pri razmatranju "hi-kvadrat" kriterija (7.2). Postoji samo jedna temeljna razlika. Govoreći o značenju kriterija (7.2), razmatrali smo beskonačan broj uzoraka veličine n, “izvučenih” iz naše opće populacije. Ovdje, analizirajući značenje kriterija (8.1), prelazimo na razmatranje beskonačnog broja pare uzorci veličine n 1 i n 2. Za svaki par izračunava se statistika oblika (8.1). Ukupnost dobivenih vrijednosti takve statistike, u skladu s našim oznakama, odgovara normalna distribucija(kao što smo se dogovorili, slovo z se koristi za označavanje takvog kriterija da zadovoljava normalna distribucija).
Dakle, ako su nam opće varijance nepoznate, prisiljeni smo ih koristiti umjesto njih procjene uzorka s 1 2 i s 2 2 . Međutim, u ovom slučaju normalna razdioba mora se zamijeniti Studentovom razdiobom - z se mora zamijeniti s t (kao što je bio slučaj u sličnoj situaciji pri konstruiranju interval pouzdanosti za matematičko očekivanje). Međutim, uz dovoljno velike veličine uzorka (n 1, n 2 ³ 30), kao što već znamo, Studentova distribucija praktički se poklapa s normalnom. Drugim riječima, za velike uzorke možemo nastaviti koristiti kriterij:
Situacija je složenija kada su varijance nepoznate, a veličina barem jednog uzorka je mala. Tada u igru ulazi još jedan faktor. Vrsta kriterija ovisi o tome možemo li nepoznate varijance promatrane karakteristike u dva analizirana uzorka smatrati jednakima. Da bismo to otkrili, moramo testirati hipotezu:
H 0: s 1 2 = s 2 2. (8.3)
Za testiranje ove hipoteze koristi se kriterij
O specifičnostima korištenja ovog kriterija pričati ćemo u nastavku, a sada ćemo nastaviti raspravljati o algoritmu za odabir kriterija koji se koristi za testiranje hipoteza o jednakosti matematičkih očekivanja.
Ako se hipoteza (8.3) odbaci, tada kriterij koji nas zanima ima oblik:
 (8.5)
(8.5)
(tj. razlikuje se od kriterija (8.2), koji je korišten za velike uzorke, po tome što odgovarajuće statistike nemaju normalnu distribuciju, već Studentovu distribuciju). Ako se hipoteza (8.3) prihvati, mijenja se tip korištenog kriterija:
 (8.6)
(8.6)
Sažmimo kako se odabire kriterij za provjeru hipoteze o jednakosti općih matematičkih očekivanja na temelju analize dva neovisna uzorka.
znan
nepoznato
veličina uzorka je velika
H 0: s 1 = s 2 odbijeno

Prihvaćeno

8.3. Testiranje hipoteza za ovisne uzorke
Prijeđimo na razmatranje zavisnih uzoraka. Neka nizovi brojeva
X 1, X 2, …, X n;
Y 1 , Y 2 , … , Y n –
to su vrijednosti razmatranog slučajnog uzorka za elemente dva zavisna uzorka. Uvedimo oznaku:
D i = X i - Y i , i = 1, ... , n.
Za ovisan kriterij uzorka koji vam omogućuje testiranje hipoteze
kako slijedi:

Imajte na umu da upravo navedeni izraz za s D nije ništa više od novog izraza za poznata formula, izražavajući standardnu devijaciju. U u ovom slučaju govorimo o o standardnoj devijaciji vrijednosti D i . Slična formulačesto se u praksi koristi kao jednostavnija (u usporedbi s "direktnim" izračunom zbroja kvadratnih odstupanja vrijednosti razmatrane vrijednosti od odgovarajuće aritmetičke sredine) metoda izračuna disperzije.
Usporedimo li gornje formule s onima koje smo koristili kada smo raspravljali o načelima konstruiranja intervala pouzdanosti, lako je uočiti da je testiranje hipoteze o jednakosti sredina za slučaj zavisnih uzoraka u biti testiranje jednakosti matematičkog očekivanja vrijednosti D i na nulu. Veličina
je standardna devijacija za D i . Stoga je vrijednost upravo opisanog kriterija t n -1 u biti jednaka vrijednosti D i izraženoj u dijelovima prosjeka kvadratno odstupanje. Kao što smo rekli gore (kada raspravljamo o metodama za konstrukciju intervala pouzdanosti), ovaj se pokazatelj može koristiti za procjenu vjerojatnosti razmatrane vrijednosti Di. Razlika je u tome što smo gore govorili o jednostavnoj aritmetičkoj sredini, normalno raspodijeljenoj, a ovdje govorimo o prosječnim razlikama, takvi prosjeci imaju Studentovu distribuciju. Ali razmišljanje o odnosu između vjerojatnosti odstupanja aritmetičke sredine uzorka od nule (s matematičkim očekivanjem jednakim nuli) i koliko jedinica to odstupanje čini ostaje valjano.
Usporedba srednjih vrijednosti dviju populacija je važna praktični značaj. U praksi su česti slučajevi kada prosječan rezultat jedna serija eksperimenata razlikuje se od prosječnog rezultata druge serije. Pritom se postavlja pitanje može li se uočeno odstupanje prosjeka objasniti neizbježnim slučajne greške eksperiment ili je uzrokovan određenim obrascima. U industriji se zadatak usporedbe prosjeka često javlja pri selektivnom praćenju kvalitete proizvoda proizvedenih u različitim postrojenjima ili u različitim tehnološkim uvjetima, u financijskoj analizi pri usporedbi razine profitabilnosti raznih sredstava itd.

Formulirajmo problem. Neka postoje dvije populacije karakterizirane općom sredinom i i poznate disperzije I. Potrebno je provjeriti hipotezu o jednakosti općih sredstava, tj. : =. Za testiranje hipoteze, dva neovisna uzorka volumena i uzeta su iz tih populacija, iz kojih su pronađene aritmetičke sredine i varijance uzorka i. S dovoljno velikim volumenima uzorka, uzorak ima prosjek i ima približno normalan zakon distribucije, odnosno i. Ako hipoteza je točna, razlika ima normalan zakon distribucije s matematičkim očekivanjem i disperzijom.
Dakle, kada je hipoteza ispunjena, statistika

ima standardnu normalnu distribuciju N (0; 1).
Testiranje hipoteza o brojčane vrijednosti parametri
Hipoteze o brojčanim vrijednostima pojavljuju se u raznim problemima. Neka su vrijednosti određenog parametra proizvoda proizvedenih automatskim linijskim strojem, i neka je navedena nominalna vrijednost ovog parametra. Svaki zasebno značenje može, naravno, nekako odstupati od zadane nominalne vrijednosti. Očito, kako biste provjerili ispravne postavke ovog stroja, morate biti sigurni da će prosječna vrijednost parametra za proizvode proizvedene na njemu odgovarati nominalnoj vrijednosti, tj. testirati hipotezu protiv alternative, ili, ili
Prilikom nasumičnog postavljanja stroja, možda će biti potrebno testirati hipotezu da je točnost proizvodnje proizvoda za dani parametar, određen varijancama, jednaka dana vrijednost, tj. ili, na primjer, činjenica da je udio neispravnih proizvoda koje proizvodi stroj jednak zadanoj vrijednosti p 0, tj. itd.
Slični problemi mogu nastati, primjerice, u financijskoj analizi, kada je na temelju uzoraka podataka potrebno utvrditi može li se uzeti u obzir povrat na imovinu određena vrsta ili portfelj vrijednosnih papira, ili njegov rizik jednak određenom broju; ili na temelju rezultata selektivne revizije dokumenata iste vrste, morate se uvjeriti može li se postotak učinjenih pogrešaka smatrati jednakim nominalnoj vrijednosti itd.
U opći slučaj hipoteze sličan tip imaju oblik gdje je određeni parametar distribucije koja se proučava, a područje je njegovih specifičnih vrijednosti, koje se u određenom slučaju sastoji od jedne vrijednosti.
5. studenog 2012. 5. studenog 2012. 5. studenog 2012. 5. studenog 2012. Predavanje 6. Usporedba dva uzorka 6-1. Hipoteza jednakosti sredstava. Upareni uzorci 6-2.Interval pouzdanosti za razliku u sredinama. Upareni uzorci 6-3. Hipoteza jednakosti varijanci 6-4. Hipoteza jednakosti udjela 6-5. Interval pouzdanosti za razliku u proporcijama
2 Ivanov O.V., 2005. U ovom predavanju... U prethodnom predavanju testirali smo hipotezu o jednakosti srednjih vrijednosti dviju općih populacija i konstruirali interval pouzdanosti za razliku srednjih vrijednosti za slučaj neovisnih uzoraka. Sada ćemo razmotriti kriterij za testiranje hipoteze o jednakosti srednjih vrijednosti i konstruirati interval pouzdanosti za razliku srednjih vrijednosti u slučaju uparenih (ovisnih) uzoraka. Zatim će se u odjeljku 6-3 testirati hipoteza o jednakosti varijanci, u odjeljku 6-4 - hipoteza o jednakosti udjela. Na kraju konstruiramo interval pouzdanosti za razliku u proporcijama.

5. studenog 2012. 5. studenog 2012. 5. studenog 2012. 5. studenog 2012. Hipoteza jednakosti sredstava. Upareni uzorci Izjava o problemu Hipoteze i statistika Redoslijed radnji Primjer

4 Ivanov O.V., 2005 Upareni uzorci. Opis problema Što imamo 1. Dva jednostavna slučajni uzorci, dobivenih iz dvije opće populacije. Uzorci su upareni (ovisni). 2. Oba uzorka imaju veličinu n 30. Ako nisu, tada su oba uzorka uzeta iz normalno raspoređenih populacija. Ono što želimo je testirati hipotezu o razlici između srednjih vrijednosti dviju populacija:

5 Ivanov O.V., 2005 Statistika za uparene uzorke Za testiranje hipoteze koristi se statistika: gdje je razlika između dvije vrijednosti u jednom paru - opći prosjek za uparene razlike - prosjek uzorka za uparene razlike - standardna devijacija razlike za uzorak - broj parova

6 Ivanov O.V., 2005 Primjer. Obuka polaznika Grupa od 15 polaznika polagala je test prije i poslije obuke. Rezultati ispitivanja su u tablici. Testirajmo hipotezu za uparene uzorke o nepostojanju utjecaja treninga na pripremu učenika na razini značajnosti od 0,05. Riješenje. Izračunajmo razlike i njihove kvadrate. Student Prije Poslije Σ= 21 Σ= 145

7 Ivanov O.V., 2005 Rješenje Korak 1. Glavna i alternativna hipoteza: Korak 2. Postavljena je razina značajnosti =0,05. Korak 3. Pomoću tablice za df = 15 – 1=14 nalazimo kritičnu vrijednost t = 2,145 i upisujemo kritično područje: t > 2,145. 2.145."> 2.145."> 2.145." title="7 Ivanov O.V., 2005 Rješenje Korak 1. Glavna i alternativna hipoteza: Korak 2. Razina značajnosti postavljena je = 0,05. Korak 3. Po tablici za df = 15 – 1=14 nalazimo kritičnu vrijednost t = 2,145 i upisujemo kritično područje: t > 2,145."> title="7 Ivanov O.V., 2005 Rješenje Korak 1. Glavna i alternativna hipoteza: Korak 2. Postavljena je razina značajnosti =0,05. Korak 3. Pomoću tablice za df = 15 – 1=14 nalazimo kritičnu vrijednost t = 2,145 i upisujemo kritično područje: t > 2,145."> !}

9 Ivanov O.V., 2005 Statistika rješenja uzima vrijednost: Korak 5. Usporedite dobivenu vrijednost s kritičnom regijom. 1.889 
5. studenog 2012. 5. studenog 2012. 5. studenog 2012. 5. studenog 2012. Interval pouzdanosti za razliku u srednjim vrijednostima. Upareni uzorci Izjava problema Metoda za konstruiranje intervala pouzdanosti Primjer

11 Ivanov O.V., 2005. Opis problema Što imamo Imamo dva nasumična uparena (ovisna) uzorka veličine n iz dvije opće populacije. Opće populacije imaju normalan zakon distribucije s parametrima 1, 1 i 2, 2 ili su volumeni oba uzorka 30. Ono što želimo je procijeniti prosječnu vrijednost uparenih razlika za dvije opće populacije. Da biste to učinili, konstruirajte interval pouzdanosti za prosjek u obliku:



5. studenog 2012. 5. studenog 2012. 5. studenog 2012. 5. studenog 2012. Hipoteza o jednakosti varijanci Izjava o problemu Hipoteze i statistika Redoslijed radnji Primjer

15 Ivanov O.V., 2005. Tijekom studije... Istraživač će možda trebati provjeriti pretpostavku da su varijance dviju populacija koje se proučavaju jednake. U slučaju kada te populacije imaju normalnu distribuciju, za to postoji F-test, koji se naziva i Fisherov test. Za razliku od Studenta, Fischer nije radio u pivovari.

16 Ivanov O.V., 2005. Opis problema Što imamo 1. Dva jednostavna slučajna uzorka dobivena iz dvije normalno raspoređene populacije. 2. Uzorci su neovisni. To znači da ne postoji odnos između subjekata uzorka. Ono što želimo je testirati hipotezu o jednakosti varijanci populacije:







23 Ivanov O.V., 2005. Primjer Medicinski istraživač želi provjeriti postoji li razlika između otkucaja srca pušača i nepušača (broj otkucaja u minuti). Rezultati dviju nasumično odabranih skupina prikazani su u nastavku. Pomoću α = 0,05 utvrdite je li liječnik u pravu. Pušači Nepušači

24 Ivanov O.V., 2005 Rješenje Korak 1. Glavna i alternativna hipoteza: Korak 2. Postavljena je razina značajnosti =0,05. Korak 3. Pomoću tablice za broj stupnjeva slobode brojnika 25 i nazivnika 17 nalazimo kritičnu vrijednost f = 2,19 i kritično područje: f > 2,19. Korak 4. Pomoću uzorka izračunavamo statističku vrijednost: 2.19. Korak 4. Pomoću uzorka izračunavamo statističku vrijednost: "> 

5. studenoga 2012. 5. studenoga 2012. 5. studenoga 2012. 5. studenoga 2012. Hipoteza jednakih udjela Izjava o problemu Hipoteze i statistika Slijed radnji Primjer

27 Ivanov O.V., 2005 Pitanje Od 100 nasumično odabranih studenata sociološkog fakulteta, 43 pohađaju posebne kolegije. Od 200 nasumično odabranih studenata ekonomije, njih 90 pohađa posebne kolegije. Razlikuje li se udio studenata koji pohađaju posebne kolegije između odsjeka za sociologiju i ekonomiju? Čini se da nije bitno drugačije. Kako to mogu provjeriti? Udio onih koji pohađaju posebne tečajeve je udio atributa. 43 – broj “uspjeha”. 43/100 – udio uspjeha. Terminologija je ista kao u Bernoullijevoj shemi.

28 Ivanov O.V., 2005. Opis problema Što imamo 1. Dva jednostavna slučajna uzorka dobivena iz dvije normalno raspodijeljene populacije. Uzorci su neovisni. 2. Za uzorke su ispunjeni np 5 i nq 5. To znači da najmanje 5 elemenata uzorka ima ispitivanu karakterističnu vrijednost, a najmanje 5 nema. Ono što želimo je testirati hipotezu o jednakosti udjela neke karakteristike u dvije opće populacije:



31 Ivanov O.V., 2005 Primjer. Specijalni kolegiji dvaju fakulteta Od 100 nasumično odabranih studenata sociološkog fakulteta, 43 pohađa posebne kolegije. Od 200 studenata ekonomije, njih 90 pohađa posebne kolegije. Na razini značajnosti = 0,05 testirati hipotezu da ne postoji razlika između udjela studenata koji pohađaju posebne kolegije na ova dva fakulteta. 33 Ivanov O.V., 2005 Rješenje Korak 1. Glavna i alternativna hipoteza: Korak 2. Postavljena je razina značajnosti =0,05. Korak 3. Pomoću tablice normalne distribucije pronalazimo kritične vrijednosti z = – 1,96 i z = 1,96 i konstruiramo kritično područje: z 1,96. Korak 4. Na temelju uzorka izračunavamo vrijednost statistike.

34 Ivanov O.V., 2005 Rješenje Korak 5. Usporedite dobivenu vrijednost s kritičnim područjem. Rezultirajuća statistička vrijednost nije spadala u kritično područje. Korak 6. Formulirajte zaključak. Nema razloga odbaciti glavnu hipotezu. Udio onih koji pohađaju posebne tečajeve ne razlikuje se statistički značajno.

5. studenog 2012. 5. studenog 2012. 5. studenog 2012. 5. studenog 2012. Interval pouzdanosti za razliku u proporcijama Izjava problema Metoda za konstruiranje intervala pouzdanosti Primjer



Homogenost dvaju uzoraka provjerava se Studentovim testom (odn t– kriterij). Razmotrimo formulaciju problema provjere homogenosti dvaju uzoraka. Neka se naprave dva uzorka volumena i . Treba provjeriti Nulta hipoteza da su opće srednje vrijednosti dva uzorka jednake. Odnosno, i. n 1
Prije razmatranja metoda za rješavanje problema, razmotrimo neke teorijska načela, koristi se za rješavanje problema. Poznati matematičar W.S. Gosset (koji je niz svojih radova objavio pod pseudonimom Student) dokazao je tu statistiku t(6.4) poštuje određeni zakon raspodjele, koji je kasnije nazvan Studentov zakon raspodjele (drugi naziv zakona je “ t– distribucija”).
Prosječna vrijednost slučajne varijable x;
Očekivana vrijednost nasumična varijabla x;
Standardna devijacija prosječnog volumena uzorka n.
Razred standardna devijacija prosjek se izračunava pomoću formule (6.5):
Standardna devijacija slučajne varijable x.
Studentova distribucija ima jedan parametar - broj stupnjeva slobode.
Sada se vratimo na izvornu formulaciju problema s dva uzorka i razmotrimo nasumična varijabla jednaka razlici između prosjeka dva uzorka (6.6):
![]() (6.6)
(6.6)
Pod uvjetom da je hipoteza o jednakosti općih sredstava zadovoljena, (6.7) vrijedi:
![]() (6.7)
(6.7)
Prepišimo relaciju (6.4) u odnosu na naš slučaj:
Procjena standardne devijacije može se izraziti u smislu procjene standardne devijacije kombinirane populacije (6.9):
 (6.9)
(6.9)
Procjena varijance objedinjene populacije može se izraziti u smislu procjena varijance izračunatih iz dva uzorka i:
 (6.10)
(6.10)
Uzimajući u obzir formulu (6.10), relacija (6.9) može se prepisati kao (6.11). Odnos (6.9) je glavni formula za izračun problemi s usporedbom prosjeka:
Kada zamijenimo vrijednost u formulu (6.8), imat ćemo vrijednost uzorka t- kriteriji. Prema Studentovim tablicama raspodjele s brojem stupnjeva slobode ![]() te se može odrediti određena razina značajnosti. Sada, ako je , tada je hipoteza o jednakosti dva sredstva odbačena.
te se može odrediti određena razina značajnosti. Sada, ako je , tada je hipoteza o jednakosti dva sredstva odbačena.
Pogledajmo primjer izvođenja izračuna za testiranje hipoteze o jednakosti dvaju prosjeka u EXCEL-u. Kreirajmo podatkovnu tablicu (sl. 6.22). Generirati ćemo podatke pomoću programa za generiranje slučajni brojevi Paket "Analiza podataka":
X1 uzorak iz normalne distribucije s parametrima ![]()
![]() volumen;
volumen;
X2 uzorak iz normalne distribucije s parametrima volumena;
X3 uzorak iz normalne distribucije s parametrima ![]() volumen;
volumen;
X4 uzorak iz normalne distribucije s parametrima ![]() volumen.
volumen.
Provjerimo hipotezu o jednakosti dvaju prosjeka (X1-X2), (X1-X3), (X1-X4). Prvo, izračunajmo parametre uzoraka značajki X1-X4 (Sl. 6.23). Zatim izračunavamo vrijednost t- kriteriji. Izračuni će se izvesti pomoću formula (6.6) – (6.9) u EXCEL-u. Rezultate izračuna sažimamo u tablici (slika 6.24).

Riža. 6.22. Tablica podataka

Riža. 6.23. Parametri značajki uzoraka X1-X4

Riža. 6.24. Zbirna tablica za izračun vrijednosti t– kriteriji za parove karakteristika (X1-X2), (X1-X3), (X1-X4)
Prema rezultatima prikazanim u tablici na Sl. 6.24 možemo zaključiti da je za par znakova (X1-X2) hipoteza o jednakosti prosjeka dvaju znakova odbačena, a za parove znakova (X1-X3), (X1-X4) hipoteza se može smatrati valjanom .
Isti rezultati mogu se dobiti korištenjem programa Two-Sample. t-test s jednakim varijancama” paketa Data Analysis. Sučelje programa prikazano je na sl. 6.25.

Riža. 6.25. Mogućnosti programa s dva uzorka t- test s jednakim varijancama”
Rezultati izračuna za testiranje hipoteza o jednakosti dva prosječna para karakteristika (X1-X2), (X1-X3), (X1-X4), dobiveni pomoću programa, prikazani su na slici. 6.26-6.28.

Riža. 6.26. Izračun vrijednosti t– kriterij za par karakteristika (X1-X2)

Riža. 6.27. Izračun vrijednosti t– kriterij za par karakteristika (X1-X3)

Riža. 6.28. Izračun vrijednosti t– kriterij za par karakteristika (X1-X4)
Dva uzorka t-test s jednakim varijancama se inače naziva t-test s neovisnim uzorcima. Rašireno također primljeno t- ispitivanje zavisnih uzoraka. Situacija kada je potrebno primijeniti ovaj kriterij nastaje kada se ista slučajna varijabla mjeri dva puta. Broj opažanja u oba slučaja je isti. Uvedimo oznaku za dva uzastopna mjerenja nekog svojstva istih objekata, , i označimo razliku dva uzastopna mjerenja:
U ovom slučaju, formula za vrijednost uzorka kriterija ima oblik:
 , (6.13)
, (6.13)
 (6.15)
(6.15)
U ovom slučaju broj stupnjeva slobode je . Testiranje hipoteza može se izvesti pomoću programa Paired Two-Sample. t-test” paket za analizu podataka (Sl. 6.29).

Riža. 6.29. Parametri programa “Upareni dva uzorka”. t-test"
6.5. Analiza varijance – klasifikacija prema jednom kriteriju (F - kriterij)
U analizi varijance testira se hipoteza koja je generalizacija hipoteze o jednakosti dvaju sredina na slučaj kada se hipoteza o jednakosti više sredina testira istovremeno. Analizom varijance ispituje se stupanj utjecaja jednog ili više faktorskih obilježja na rezultirajuće obilježje. Ideja analiza varijance pripada R. Fischeru. Njime je obrađivao rezultate agronomskih pokusa. Analiza varijance koristi se za utvrđivanje značajnosti utjecaja kvalitativni faktori na vrijednost koja se proučava. Engleski skraćeni naziv za analizu varijance je ANOVA (analysis variation).
Opći obrazac prikaz podataka s klasifikacijom prema jednom kriteriju prikazan je u tablici 6.1.
Tablica 6.1. Obrazac za prikaz podataka s klasifikacijom prema jednom obilježju
Razmotrimo dva neovisna uzorka x 1, x 2, ….., x n i y 1, y 2, …, y n, izvađena iz normalnih populacija s jednakim varijancama, s veličinama uzorka n i m, redom, i prosječnim vrijednostima μ x, μ y i varijanca σ 2 su nepoznate. Potrebno je testirati glavnu hipotezu H 0: μ x = μ y s konkurentskom H 1: μ x μ y.
Kao što je poznato, prosjeci uzoraka će imati sljedeća svojstva: ~N(μ x, σ 2 /n), ~N(μ y, σ 2 /m).
Njihova razlika je normalna vrijednost s prosjekom ![]() i varijanca, dakle
i varijanca, dakle
~ ![]() (23).
(23).
Pretpostavimo na trenutak da je glavna hipoteza H 0 točna: μ x – μ y =0. Zatim ![]() i dijeljenjem vrijednosti s njezinom standardnom devijacijom dobivamo standardnu normalu sl. Veličina
i dijeljenjem vrijednosti s njezinom standardnom devijacijom dobivamo standardnu normalu sl. Veličina ![]() ~N(0,1).
~N(0,1).
Prethodno je navedeno da veličina ![]() raspoređeni prema zakonu s (n-1)-im stupnjem slobode, a
raspoređeni prema zakonu s (n-1)-im stupnjem slobode, a ![]() - prema zakonu s (m-1) stupnjeva slobode. Uzimajući u obzir neovisnost ova dva zbroja, nalazimo da su ukupni iznos
- prema zakonu s (m-1) stupnjeva slobode. Uzimajući u obzir neovisnost ova dva zbroja, nalazimo da su ukupni iznos ![]() raspoređeni prema zakonu s n+m-2 stupnjeva slobode.
raspoređeni prema zakonu s n+m-2 stupnjeva slobode.
Sjećajući se koraka 7, vidimo da je razlomak  pokorava se t-distribuciji (Student) s ν=m+n-2 stupnja slobode: Z=t. Ova činjenica se javlja samo kada je hipoteza H 0 istinita.
pokorava se t-distribuciji (Student) s ν=m+n-2 stupnja slobode: Z=t. Ova činjenica se javlja samo kada je hipoteza H 0 istinita.
Zamjenom ξ i Q njihovim izrazima dobivamo proširenu formulu za Z:
 (24)
(24)
Sljedeća vrijednost Z, koja se naziva statistika kriterija, omogućuje vam donošenje odluke pomoću sljedećeg niza radnji:
1. Utvrđeno je područje D=[-t β,ν , +t β,ν ] koje sadrži β=1–α područja ispod krivulje distribucije t ν (tablica 10).
2. Eksperimentalna vrijednost Z on statistike Z izračunava se pomoću formule (24), za koju su vrijednosti x 1 i y 1 specifičnih uzoraka, kao i njihove srednje vrijednosti uzorka i , zamijenjene umjesto X 1 i Y 1 .
3. Ako je Z na D, tada se smatra da hipoteza H 0 nije u suprotnosti s eksperimentalnim podacima i prihvaća se.
Ako je Z na D, tada je hipoteza H 1 prihvaćena.
Ako je hipoteza H 0 točna, tada se Z pokorava poznatoj t ν -distribuciji s nultom sredinom i s velikom vjerojatnošću β = 1–α spada u D-područje prihvaćanja hipoteze H 0 . Kada opažena, eksperimentalna vrijednost Z on padne u D. Smatramo to dokazom u korist hipoteze H 0.
Kada Z 0 n leži izvan D (kako kažu, leži u kritičnom području K), što je prirodno ako je hipoteza H 1 istinita, ali malo vjerojatno ako je H 0 istinita, tada hipotezu H 0 možemo odbaciti samo prihvaćanjem H 1 .
Primjer 31.
Uspoređuju se dva razreda benzina: A i B. Na 11 vozila iste snage jednom su na kružnoj šasiji ispitani benzini razreda A i B. Jedan automobil se pokvario na putu i za njega na benzinu B nema podataka.
Potrošnja benzina na 100 km
Tablica 12
| ja | ||||||||||||
| X i | 10,51 | 11,86 | 10,5 | 9,1 | 9,21 | 10,74 | 10,75 | 10,3 | 11,3 | 11,8 | 10,9 | n=11 |
| U i | 13,22 | 13,0 | 11,5 | 10,4 | 11,8 | 11,6 | 10,64 | 12,3 | 11,1 | 11,6 | - | m=10 |
Varijanca u potrošnji benzina razreda A i B je nepoznata i pretpostavlja se da je ista. Je li moguće, na razini značajnosti α=0,05, prihvatiti hipotezu da su pravi prosječni troškovi μ A i μ B ovih vrsta benzina isti?
Riješenje. Testiranje hipoteze H 0: μ A -μ B = 0 s konkurentskom. H 1:μ 1 μ 2 učinite sljedeće:
1. Nađite srednje vrijednosti uzorka i zbroj kvadrata odstupanja Q.
![]()
![]() ;
;
![]() ;
;
2. Izračunajte eksperimentalnu vrijednost Z statistike
3. Iz tablice 10 t-distribucije nalazimo granicu t β,ν za broj stupnjeva slobode ν=m+n–2=19 i β=1–α=0,95. Tablica 10 ima t 0,95,20 =2,09 i t 0,95,15 =2,13, ali ne i t 0,95,19. Interpolacijom nalazimo t 0,95,19 =2,09+ =2,10.
4. Provjerite u kojem se od dva područja D ili K nalazi broj Zon. Zon=-2,7 D=[-2,10; -2,10].
Budući da promatrana vrijednost Z on leži u kritičnom području, K = R\D, odbacujemo je. H 0 i prihvatiti hipotezu H 1. U ovom slučaju kažu da je njihova razlika značajna. Da se, pod svim uvjetima ovog primjera, samo Q promijenio, recimo, Q se udvostručio, tada bi se naš zaključak promijenio. Udvostručenje Q dovelo bi do smanjenja vrijednosti Zon za faktor i tada bi broj Zon pao u njega važeće područje D, kako bi hipoteza H 0 izdržala test i bila prihvaćena. U tom bi se slučaju neslaganje između i moglo objasniti prirodnom raspršenošću podataka, a ne činjenicom da je μ A μ B.
Teorija testiranja hipoteza vrlo je opsežna; hipoteze mogu biti o vrsti zakona raspodjele, o homogenosti uzoraka, o neovisnosti sljedećih veličina itd.
KRITERIJ c 2 (PEARSON)
Najčešći kriterij u praksi za testiranje jednostavne hipoteze. Primjenjuje se kada zakon distribucije nije poznat. Razmotrimo slučajnu varijablu X nad kojom je n nezavisni testovi. Dobivena je realizacija x 1 , x 2 ,...,x n. Potrebno je provjeriti hipotezu o zakonu distribucije ove slučajne varijable.
Razmotrimo slučaj jednostavne hipoteze. Jednostavna hipoteza testira dosljednost uzorka s opća populacija, s normalnom distribucijom (poznatom). Gradimo prema uzorku varijacijske serije x (1) , x (2) , ..., x (n) . Interval dijelimo na podintervale. Neka ti intervali budu r. Tada ćemo pronaći vjerojatnost da će X, kao rezultat testa, pasti u interval Di, i=1 ,..., r ako je hipoteza koja se testira točna.
![]()
Kriterij ne provjerava istinitost gustoće vjerojatnosti, već istinitost brojeva
Svakom intervalu Di pridružujemo slučajni događaj A i - pogodak u ovom intervalu (pogodak kao rezultat testiranja preko X njegov rezultat implementacije u Di). Uvedimo slučajne varijable. m i je broj testova od n provedenih u kojima se dogodio događaj A i. m i su raspodijeljeni prema binomnom zakonu i ako je hipoteza točna
Dm i =np i (1-p i)
Kriterij c 2 ima oblik 
p 1 +p 2 +...+p r =1
m 1 +m 2 +...+m r =n
Ako je hipoteza koja se testira točna, tada m i predstavlja učestalost pojavljivanja događaja koji ima vjerojatnost pi u svakom od n pokušaja, prema tome, možemo smatrati m i slučajnom varijablom koja podliježe binomnom zakonu sa središtem u točki npi. Kada je n velik, tada možemo pretpostaviti da je frekvencija asimptotski normalno raspoređena s istim parametrima. Ako je hipoteza točna, treba očekivati da će oni biti asimptotski normalno raspoređeni
međusobno povezani odnosom
![]()
Kao mjeru odstupanja između podataka uzorka m 1 +m 2 +...+m r i teoretskog np 1 +np 2 +...+np r, razmotrite vrijednost

c 2 - zbroj kvadrata asimptotski normalne vrijednosti srodni linearna ovisnost. Već smo se susreli sa sličnim slučajem i znamo da prisutnost linearna veza dovela do smanjenja broja stupnjeva slobode za jedan.
Ako je hipoteza koja se testira točna, tada kriterij c 2 ima distribuciju koja teži kao n®¥ distribuciji c 2 s r-1 stupnjeva slobode.
Pretpostavimo da je hipoteza netočna. Tada postoji tendencija povećanja članova zbroja, tj. ako je hipoteza netočna, tada će ovaj iznos pasti u određeno područje velike vrijednosti c 2 . Uzmimo regiju kao kritičnu regiju pozitivne vrijednosti kriteriji

| |
U slučaju nepoznatih parametara distribucije, svaki parametar smanjuje broj stupnjeva slobode za Pearsonov kriterij za jedan
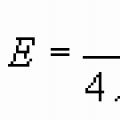 Ostrogradsky–Gaussov teorem
Ostrogradsky–Gaussov teorem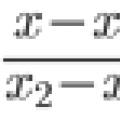 Kako naučiti rješavati probleme iz analitičke geometrije?
Kako naučiti rješavati probleme iz analitičke geometrije? Značenje riječi merkantilan Značenje riječi merkantilan
Značenje riječi merkantilan Značenje riječi merkantilan