Pronađite svojstvene vektore matrice. Sistem homogenih linearnih jednačina

Svojstveni vektor kvadratne matrice je onaj koji, kada se pomnoži sa datom matricom, rezultira kolinearnim vektorom. Jednostavnim riječima, kada se matrica pomnoži s vlastitim vektorom, potonji ostaje isti, ali pomnožen nekim brojem.

Definicija

Svojstveni vektor je vektor V koji nije nula, koji, kada se pomnoži kvadratnom matricom M, postaje sam, uvećan za neki broj λ. U algebarskoj notaciji ovo izgleda ovako:

M × V = λ × V,

gdje je λ vlastita vrijednost matrice M.

Razmislite numerički primjer. Radi lakšeg pisanja, brojevi u matrici će biti odvojeni tačkom i zarezom. Recimo da imamo matricu:

M = 0; 4;
6; 10.

Pomnožimo ga vektorom stupca:

V = -2;

Kada množimo matricu vektorom kolone, dobijamo i vektor kolone. Strogo matematički jezik formula za množenje matrice 2 × 2 vektorom stupca bi izgledala ovako:

M × V = M11 × V11 + M12 × V21;
M21 x V11 + M22 x V21.

M11 označava element matrice M koji stoji u prvom redu i prvoj koloni, a M22 je element koji se nalazi u drugom redu i drugoj koloni. Za našu matricu, ovi elementi su M11 = 0, M12 = 4, M21 = 6, M22 10. Za vektor stupac ove vrijednosti su V11 = –2, V21 = 1. Prema ovoj formuli dobijamo sljedeće rezultat proizvoda kvadratne matrice vektorom:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

Radi praktičnosti, pišemo vektor stupca u red. Dakle, pomnožili smo kvadratnu matricu sa vektorom (-2; 1), što je rezultiralo vektorom (4; -2). Očigledno, ovo je isti vektor pomnožen sa λ = -2. lambda in ovaj slučaj označava sopstvenu vrijednost matrice.

Vlastiti vektor matrice je kolinearni vektor, odnosno objekt koji ne mijenja svoj položaj u prostoru kada se pomnoži sa matricom. Koncept kolinearnosti u vektorska algebra slično terminu paralelizam u geometriji. U geometrijskoj interpretaciji kolinearni vektori- To su paralelno usmjereni segmenti različitih dužina. Još od Euklidovog vremena znamo da jedna prava ima beskonačan broj linija paralelnih sa njom, pa je logično pretpostaviti da svaka matrica ima beskonačan broj sopstveni vektori.

Iz prethodnog primjera, može se vidjeti da oba (-8; 4), i (16; -8), i (32, -16) mogu biti svojstveni vektori. Sve su to kolinearni vektori koji odgovaraju svojstvenoj vrijednosti λ = -2. Kada množimo originalnu matricu ovim vektorima, i dalje ćemo dobiti vektor kao rezultat, koji se razlikuje od originalne 2 puta. Zato je pri rješavanju zadataka za pronalaženje svojstvenog vektora potrebno pronaći samo linearno nezavisne vektorske objekte. Najčešće, za n × n matricu, postoji n-ti broj sopstvenih vektora. Naš kalkulator je dizajniran za analizu kvadratnih matrica drugog reda, tako da će se gotovo uvijek kao rezultat naći dva svojstvena vektora, osim kada se poklapaju.

U gornjem primjeru, unaprijed smo znali svojstveni vektor originalne matrice i vizualno odredili lambda broj. Međutim, u praksi se sve događa obrnuto: na početku postoje svojstvene vrijednosti, a tek onda svojstveni vektori.

Algoritam rješenja

Pogledajmo ponovo originalnu matricu M i pokušajmo pronaći oba njena svojstvena vektora. Dakle, matrica izgleda ovako:

M = 0; 4;
6; 10.

Za početak, moramo odrediti svojstvenu vrijednost λ, za koju trebamo izračunati determinantu sljedeće matrice:

(0 − λ); 4;
6; (10 − λ).

Ova matrica dobijeno oduzimanjem nepoznatog λ od elemenata na glavnoj dijagonali. Determinanta je određena standardnom formulom:

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Pošto naš vektor ne smije biti nula, uzimamo rezultirajuću jednačinu kao linearno zavisnu i izjednačavamo našu determinantu detA sa nulom.

(0 − λ) × (10 − λ) − 24 = 0

Proširimo zagrade i dobijemo karakteristična jednačina matrice:

λ 2 − 10λ − 24 = 0

Ovo je standardno kvadratna jednačina, koji se rješava u smislu diskriminanta.

D \u003d b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 \u003d 196

Koren diskriminanta je sqrt(D) = 14, tako da je λ1 = -2, λ2 = 12. Sada za svaku lambda vrijednost, moramo pronaći svojstveni vektor. Izrazimo koeficijente sistema za λ = -2.

M − λ × E = 2; 4;
6; 12.

U ovoj formuli, E je matrica identiteta. Na osnovu dobijene matrice komponovaćemo sistem linearne jednačine:

2x + 4y = 6x + 12y

gdje su x i y elementi sopstvenog vektora.

Skupimo sve X na lijevoj strani i sve Y na desnoj strani. Očigledno - 4x = 8y. Podijelite izraz sa -4 i dobijete x = -2y. Sada možemo odrediti prvi svojstveni vektor matrice uzimanjem bilo koje vrijednosti nepoznatih (sjetite se beskonačnosti linearno zavisnih svojstvenih vektora). Uzmimo y = 1, a zatim x = -2. Dakle, prvi sopstveni vektor izgleda kao V1 = (–2; 1). Vratite se na početak članka. Upravo smo ovim vektorskim objektom pomnožili matricu da bismo demonstrirali koncept svojstvenog vektora.

Sada pronađimo svojstveni vektor za λ = 12.

M - λ × E = -12; 4
6; -2.

Sastavimo isti sistem linearnih jednačina;

-12x + 4y = 6x − 2y
-18x = -6y
3x=y.

Uzmimo sada x = 1, dakle y = 3. Dakle, drugi svojstveni vektor izgleda kao V2 = (1; 3). Prilikom množenja originalne matrice sa dati vektor, rezultat će uvijek biti isti vektor pomnožen sa 12. Ovo završava algoritam rješenja. Sada znate kako ručno definirati svojstveni vektor matrice.

determinanta;
trag, odnosno zbir elemenata na glavnoj dijagonali;
rang, tj maksimalni iznos linearno nezavisni redovi/kolone.

Program radi prema gore navedenom algoritmu, minimizirajući proces rješenja. Važno je istaći da se u programu lambda označava slovom "c". Pogledajmo brojčani primjer.

Primjer programa

Pokušajmo definirati svojstvene vektore za sljedeću matricu:

M=5; trinaest;
4; 14.

Unesimo ove vrijednosti u ćelije kalkulatora i dobijemo odgovor u sljedećem obliku:

Rang matrice: 2;
Matrična determinanta: 18;
Trag matrice: 19;
Proračun sopstvenog vektora: c 2 − 19.00c + 18.00 (karakteristična jednačina);
Izračun sopstvenog vektora: 18 (prva lambda vrijednost);
Izračun sopstvenog vektora: 1 (druga lambda vrijednost);
Sistem jednačina vektora 1: -13x1 + 13y1 = 4x1 − 4y1;
Sistem jednadžbi vektora 2: 4x1 + 13y1 = 4x1 + 13y1;
Vlastiti vektor 1: (1; 1);
Vlastiti vektor 2: (-3,25; 1).

Tako smo dobili dva linearno nezavisna svojstvena vektora.

Zaključak

Linearna algebra i analitička geometrija standardni su predmeti za svakog brucoša tehnička specijalnost. Veliki broj vektori i matrice je zastrašujuća i lako je pogriješiti u takvim glomaznim proračunima. Naš program će omogućiti studentima da provjere svoje proračune ili automatski riješe problem pronalaženja svojstvenog vektora. U našem katalogu postoje i drugi kalkulatori linearne algebre, koristite ih u svom učenju ili poslu.

Kako zalijepiti matematičke formule na web stranicu?

Ako ikada trebate dodati jednu ili dvije matematičke formule na web stranicu, najlakši način da to učinite je kako je opisano u članku: matematičke formule se lako ubacuju na web stranicu u obliku slika koje Wolfram Alpha automatski generiše. Pored jednostavnosti, ovo univerzalni način pomoći će poboljšanju vidljivosti stranice u tražilice. Radi već dugo (i mislim da će raditi zauvijek), ali je moralno zastario.

Ako stalno koristite matematičke formule na svojoj web stranici, onda preporučujem da koristite MathJax, posebnu JavaScript biblioteku koja prikazuje matematička notacija u web pretraživačima koji koriste oznake MathML, LaTeX ili ASCIIMathML.

Postoje dva načina da počnete koristiti MathJax: (1) koristeći jednostavan kod, možete brzo povezati MathJax skriptu sa svojom web lokacijom, koja će biti u pravi trenutak automatsko preuzimanje sa udaljenog servera (lista servera); (2) prenesite MathJax skriptu sa udaljenog servera na vaš server i povežite ga sa svim stranicama vašeg sajta. Drugi metod je komplikovaniji i dugotrajniji i omogućiće vam da ubrzate učitavanje stranica vašeg sajta, a ako roditeljski MathJax server iz nekog razloga postane privremeno nedostupan, to ni na koji način neće uticati na vašu veb lokaciju. Unatoč ovim prednostima, odabrao sam prvi metod, jer je jednostavniji, brži i ne zahtijeva tehničke vještine. Slijedite moj primjer i u roku od 5 minuta moći ćete koristiti sve mogućnosti MathJaxa na vašoj web stranici.

Možete povezati skriptu MathJax biblioteke sa udaljenog servera koristeći dvije opcije koda preuzete sa glavne MathJax web stranice ili sa stranice dokumentacije:

Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kod vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake . Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako unesete prvi kod, morat ćete ga povremeno ažurirati. Ako zalijepite drugi kod, stranice će se sporije učitavati, ali nećete morati stalno pratiti ažuriranja MathJaxa.

Najlakši način za povezivanje MathJax-a je u Bloggeru ili WordPress-u: u kontrolnu ploču stranice dodajte widget dizajniran za umetanje JavaScript koda treće strane, kopirajte prvu ili drugu verziju koda za učitavanje prikazanu iznad u njega i postavite widget bliže na početak šablona (usput, to uopće nije potrebno, pošto se MathJax skripta učitava asinhrono). To je sve. Sada naučite MathML, LaTeX i ASCIIMathML sintaksu označavanja i spremni ste da ugradite matematičke formule u svoje web stranice.

Svaki fraktal se gradi prema određenom pravilu, koje se dosljedno primjenjuje neograničen broj puta. Svako takvo vrijeme naziva se iteracija.

Iterativni algoritam za konstruisanje Mengerovog sunđera je prilično jednostavan: originalna kocka sa stranom 1 podeljena je ravninama paralelnim sa njenim plohama na 27 jednakih kocki. Iz nje se uklanjaju jedna središnja kocka i 6 susjednih kocki duž lica. Ispada set koji se sastoji od 20 preostalih manjih kockica. Učinivši isto sa svakom od ovih kockica, dobijamo set koji se sastoji od 400 manjih kockica. Nastavljajući ovaj proces u nedogled, dobijamo Menger sunđer.

www.site omogućava vam da pronađete. Sajt vrši kalkulaciju. Za nekoliko sekundi, server će se oglasiti ispravno rješenje. Karakteristična jednačina za matricu bice algebarski izraz, pronađeno po pravilu za izračunavanje determinante matrice matrice, dok će na glavnoj dijagonali biti razlike u vrijednostima dijagonalnih elemenata i varijable. Prilikom izračunavanja karakteristična jednačina za matricu online, svaki element matriceće se pomnožiti sa odgovarajućim drugim elementima matrice. Pronađi u načinu rada online moguće samo za kvadrat matrice. Pronađi operaciju karakteristična jednačina za matricu online svodi se na kalkulaciju algebarski zbir proizvodi elemenata matrice kao rezultat nalaženja determinante matrice, samo u svrhu utvrđivanja karakteristična jednačina za matricu online. Ova operacija traje posebno mjesto u teoriji matrice, omogućava vam da pronađete svojstvene vrijednosti i vektore koristeći korijene. Pronalaženje zadatka karakteristična jednačina za matricu online je množenje elemenata matrice uz naknadno zbrajanje ovih proizvoda prema određenom pravilu. www.site nalazi karakteristična jednačina za matricu datu dimenziju u modu online. proračun karakteristična jednačina za matricu online za datu dimenziju, ovo je pronalaženje polinoma sa numeričkim ili simboličkim koeficijentima koji se nalaze po pravilu za izračunavanje determinante matrice- kao zbir proizvoda odgovarajućih elemenata matrice, samo u svrhu utvrđivanja karakteristična jednačina za matricu online. Pronalaženje polinoma u odnosu na varijablu za kvadrat matrice, kao definicija karakteristična jednačina za matricu, uobičajeno u teoriji matrice. Vrijednost korijena polinoma karakteristična jednačina za matricu online koristi se za definiranje vlastitih vektora i sopstvene vrijednosti za matrice. Međutim, ako je determinanta matrice onda će biti nula matrična karakteristična jednačinaće i dalje postojati, za razliku od obrnutog matrice. Da bi izračunali karakteristična jednačina za matricu ili tražite nekoliko odjednom matrice karakteristične jednačine, potrebno je uložiti puno vremena i truda, dok će naš server pronaći karakteristična jednačina za online matricu. U ovom slučaju, odgovor pronalaženjem karakteristična jednačina za matricu onlineće biti ispravan i sa dovoljnom tačnošću, čak i ako su brojevi prilikom pronalaženja karakteristična jednačina za matricu online biće iracionalno. Online www.site unosi znakova su dozvoljeni u elementima matrice, tj karakteristična jednačina za online matricu može se predstaviti u opštem simboličkom obliku prilikom izračunavanja matrica karakterističnih jednačina na mreži. Korisno je provjeriti dobijeni odgovor prilikom rješavanja zadatka nalaženja karakteristična jednačina za matricu online korištenjem stranice www.site. Prilikom izvođenja operacije izračunavanja polinoma - karakteristična jednačina matrice, potrebno je biti pažljiv i izuzetno koncentrisan u rješavanju ovog problema. Zauzvrat, naša stranica će vam pomoći da provjerite svoju odluku o ovoj temi matrica karakterističnih jednačina na mreži. Ako nemate vremena za duge provjere riješenih problema, onda www.siteće svakako biti zgodan alat za provjeru prilikom pronalaženja i izračunavanja karakteristična jednačina za matricu online.

". U prvom dijelu su navedene odredbe koje su minimalno neophodne za razumijevanje hemometrije, a drugi dio sadrži činjenice koje trebate znati za dublje razumijevanje metoda multivarijantna analiza. Prezentacija je ilustrovana primerima napravljenim u Excel radnoj svesci. Matrix.xls koji prati ovaj dokument.

Veze na primjere se postavljaju u tekst kao Excel objekti. Ovi primjeri su apstraktne prirode, ni na koji način nisu vezani za zadatke. analitička hemija. Pravi primjeri upotreba matrične algebre u hemometriji se raspravlja u drugim tekstovima posvećenim različitim kemometrijskim aplikacijama.

Većina mjerenja u analitičkoj hemiji nisu direktna, ali indirektno. To znači da se u eksperimentu, umjesto vrijednosti željenog analita C (koncentracija), dobije druga vrijednost x(signal) povezan sa, ali nije jednak C, tj. x(C) ≠ C. Po pravilu, vrsta zavisnosti x(C) nije poznato, ali na sreću u analitičkoj hemiji većina mjerenja je proporcionalna. To znači da kao koncentracija C in a puta, signal X će se povećati za isti iznos, tj. x(a C) = sjekira(C). Osim toga, signali su također aditivni, pa će signal iz uzorka koji sadrži dvije supstance sa koncentracijama C 1 i C 2 biti jednak je zbiru signale svake komponente, tj. x(C1 + C2) = x(C1)+ x(C2). Proporcionalnost i aditivnost zajedno daju linearnost. Moglo bi se navesti mnogo primjera koji bi ilustrirali princip linearnosti, ali dovoljno je spomenuti dva najveća jasnim primjerima- hromatografija i spektroskopija. Druga karakteristika inherentna eksperimentu u analitičkoj hemiji je višekanalni. Moderna analitička oprema istovremeno mjeri signale za mnoge kanale. Na primjer, intenzitet propuštanja svjetlosti se mjeri za nekoliko talasnih dužina odjednom, tj. domet. Stoga, u eksperimentu imamo posla sa različitim signalima x 1 , x 2 ,...., x n karakterizira skup koncentracija C 1 ,C 2 , ..., C m supstanci prisutnih u sistemu koji se proučava.

Rice. 1 Spectra

Dakle, analitički eksperiment karakteriše linearnost i višedimenzionalnost. Stoga je zgodno eksperimentalne podatke posmatrati kao vektore i matrice i manipulirati njima pomoću aparata matrične algebre. Plodnost ovog pristupa ilustruje primjer prikazan u , koji prikazuje tri spektra snimljena za 200 valnih dužina od 4000 do 4796 cm–1. Prvi ( x 1) i drugi ( x 2) spektri su dobijeni za standardne uzorke u kojima su poznate koncentracije dvije supstance A i B: u prvom uzorku [A] = 0,5, [B] = 0,1, au drugom uzorku [A] = 0,2, [ B] = 0,6. Šta reći o novom, nepoznatom uzorku, čiji je spektar naznačen x 3 ?

Razmotrimo tri eksperimentalna spektra x 1 , x 2 i x 3 kao tri vektora dimenzije 200. Koristeći linearnu algebru, to se lako može pokazati x 3 = 0.1 x 1 +0.3 x 2 , pa treći uzorak očigledno sadrži samo supstance A i B u koncentracijama [A] = 0,5×0,1 + 0,2×0,3 = 0,11 i [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Osnovne informacije

1.1 Matrice

Matrix nazvana, na primjer, pravokutna tablica brojeva

Rice. 2 Matrix

Matrice su označene velikim podebljanim slovima ( A), a njihovi elementi - odgovarajući mala slova sa indeksima, tj. a ij . Prvi indeks numerira redove, a drugi broj stupaca. U kemometriji je uobičajeno označavati maksimalna vrijednost indeks sa istim slovom kao i sam indeks, ali velikim slovima. Dakle, matrica A može se napisati i kao ( a ij , i = 1,..., I; j = 1,..., J). Za primjer matrice I = 4, J= 3 i a 23 = −7.5.

Par brojeva I i J naziva se dimenzija matrice i označava se kao I× J. Primjer matrice u kemometriji je skup spektra dobivenih za I uzorci na J talasne dužine.

1.2. Najjednostavnije operacije sa matricama

Matrice mogu pomnožiti brojevima. U ovom slučaju, svaki element se množi ovim brojem. Na primjer -

Rice. 3 Množenje matrice brojem

Dvije matrice iste dimenzije mogu biti elementarne fold i oduzimati. Na primjer,

Rice. 4 Sabiranje matrice

Kao rezultat množenja brojem i sabiranja, dobiva se matrica iste dimenzije.

Nulta matrica je matrica koja se sastoji od nula. Određeno je O. Očigledno je da A+O = A, A−A = O i 0 A = O.

Matrica može transponovati. Tokom ove operacije, matrica se okreće, tj. redovi i kolone se zamjenjuju. Transpozicija je označena crticom, A" ili indeks A t . Dakle, ako A = {a ij , i = 1,..., I; j = 1,...,J), onda A t = ( a ji , j = 1,...,J; i = 1,..., I). na primjer

Rice. 5 Matrična transpozicija

Očigledno je da ( A t) t = A, (A+B) t = A t + B t .

1.3. Množenje matrice

Matrice mogu umnožiti, ali samo ako imaju odgovarajuće dimenzije. Zašto je to tako, biće jasno iz definicije. Matrični proizvod A, dimenzija I× K, i matrice B, dimenzija K× J, naziva se matrica C, dimenzija I× J, čiji su elementi brojevi

Dakle, za proizvod AB potrebno je da broj kolona u lijevoj matrici A bio jednak broju redova u desnoj matrici B. Primjer matričnog proizvoda -

Slika 6 Proizvod matrica

Pravilo množenja matrice može se formulirati na sljedeći način. Za pronalaženje elementa matrice C stoji na raskrsnici i-ti red i j-ta kolona ( c ij) mora se pomnožiti element po element i-ti red prve matrice A na j-ti stupac druge matrice B i zbrojite sve rezultate. Dakle, u prikazanom primjeru, element iz trećeg reda i drugog stupca dobija se kao zbir proizvoda trećeg reda po elementima A i druga kolona B

Slika 7 Element proizvoda matrica

Proizvod matrica zavisi od redosleda, tj. AB ≠ BA, barem iz dimenzionalnih razloga. Kaže se da je nekomutativno. Međutim, proizvod matrica je asocijativan. To znači da ABC = (AB)C = A(BC). Štaviše, ona je i distributivna, tj. A(B+C) = AB+AC. Očigledno je da AO = O.

1.4. Kvadratne matrice

Ako je broj stupaca matrice jednak broju njenih redova ( I = J=N), tada se takva matrica naziva kvadratna. U ovom dijelu ćemo razmotriti samo takve matrice. Među tim matricama mogu se izdvojiti matrice sa posebnim svojstvima.

Samica matrica (označeno I i ponekad E) je matrica u kojoj su svi elementi jednaki nuli, osim dijagonalnih, koji su jednaki 1, tj.

Ocigledno AI = IA = A.

Matrica se zove dijagonala, ako su svi njegovi elementi, osim dijagonalnih ( a ii) jednaki su nuli. na primjer

Rice. 8 Dijagonalna matrica

Matrix A zove vrh trouglasti, ako su svi njegovi elementi koji leže ispod dijagonale jednaki nuli, tj. a ij= 0, at i>j. na primjer

Rice. 9 Gornji trouglasta matrica

Donja trokutasta matrica definirana je na sličan način.

Matrix A pozvao simetrično, ako A t = A. Drugim riječima a ij = a ji. na primjer

Rice. 10 Simetrična matrica

Matrix A pozvao ortogonalno, ako

A t A = aa t = I.

Matrica se zove normalno ako

1.5. Trag i determinanta

Praćenje kvadratna matrica A(označeno Tr( A) ili Sp( A)) je zbir njegovih dijagonalnih elemenata,

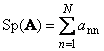
Na primjer,

Rice. 11 Trag matrice

Očigledno je da

Sp(α A) = α Sp( A) i

Sp( A+B) = Sp( A)+ Sp( B).

To se može pokazati

Sp( A) = Sp( A t), Sp( I) = N,

a takođe i to

Sp( AB) = Sp( BA).

Drugi važna karakteristika kvadratna matrica je njegova odrednica(označeno sa det( A)). Definicija determinante u opšti slučaj prilično komplicirano, pa ćemo početi s najjednostavnijom opcijom - matricom A dimenzija (2×2). Onda

Za (3×3) matricu, determinanta će biti jednaka

U slučaju matrice ( N× N) determinanta se izračunava kao zbir 1 2 3 ... N= N! pojmovi, od kojih je svaki jednak

Indeksi k 1 , k 2 ,..., k N definirani su kao sve moguće uređene permutacije r brojevi u skupu (1, 2, ... , N). Izračunavanje determinante matrice je složena procedura, koja se u praksi izvodi pomoću posebnih programa. Na primjer,

Rice. 12 Matrična determinanta

Napominjemo samo očigledna svojstva:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektori

Ako matrica ima samo jedan stupac ( J= 1), onda se takav objekat naziva vektor. Tačnije, vektor kolone. na primjer

Na primjer, mogu se uzeti u obzir i matrice koje se sastoje od jednog reda

Ovaj objekt je također vektor, ali vektor reda. Prilikom analize podataka važno je razumjeti s kojim vektorima imamo posla – stupcima ili redovima. Dakle, spektar uzet za jedan uzorak može se smatrati vektorom reda. Tada skup spektralnih intenziteta na nekoj talasnoj dužini za sve uzorke treba tretirati kao vektor kolone.

Dimenzija vektora je broj njegovih elemenata.

Jasno je da se bilo koji vektor kolone može transformisati u vektor reda transpozicijom, tj.

U onim slučajevima kada oblik vektora nije posebno određen, već se jednostavno kaže vektor, onda oni označavaju vektor stupac. I ovog pravila ćemo se pridržavati. Vektor se označava malim direktnim podebljanim slovom. Nulti vektor je vektor čiji su svi elementi jednaki nuli. To je označeno 0 .

1.7. Najjednostavnije operacije s vektorima

Vektori se mogu sabirati i množiti brojevima na isti način kao i matrice. Na primjer,

Rice. 13 Operacije s vektorima

Dva vektora x i y pozvao kolinearno, ako postoji broj α takav da

1.8. Proizvodi vektora

Dva vektora iste dimenzije N može se umnožiti. Neka postoje dva vektora x = (x 1 , x 2 ,...,x N) t i y = (y 1 , y 2 ,...,y N) t . Vođeni pravilom množenja "red po stupac", od njih možemo napraviti dva proizvoda: x t y i xy t . Prvi rad

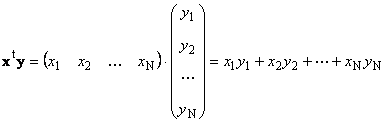
pozvao skalar ili interni. Njegov rezultat je broj. Takođe koristi notaciju ( x,y)= x t y. Na primjer,

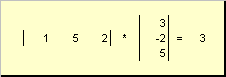
Rice. 14 Unutrašnji (skalarni) proizvod

Drugi rad

pozvao vanjski. Njegov rezultat je matrica dimenzija ( N× N). Na primjer,

Rice. 15 Spoljašnji proizvod

vektori, skalarni proizvod koji je jednak nuli nazivaju se ortogonalno.

1.9. Vektorska norma

Skalarni proizvod vektora sa samim sobom naziva se skalarni kvadrat. Ova vrijednost

definira kvadrat dužina vektor x. Za označavanje dužine (također se naziva norma vektor) koristi se notacija

Na primjer,

Rice. 16 Vektorska norma

Vektor jedinične dužine (|| x|| = 1) naziva se normalizovanim. Nenulti vektor ( x ≠ 0 ) može se normalizirati dijeljenjem dužine, tj. x = ||x|| (x/||x||) = ||x|| e. Evo e = x/||x|| je normalizovani vektor.

Vektori se nazivaju ortonormalni ako su svi normalizirani i po paru ortogonalni.

1.10. Ugao između vektora

Skalarni proizvod definira i injekcijaφ između dva vektora x i y

Ako su vektori ortogonalni, onda je cosφ = 0 i φ = π/2, a ako su kolinearni, onda je cosφ = 1 i φ = 0.

1.11. Vektorska reprezentacija matrice

Svaka matrica A veličina I× J može se predstaviti kao skup vektora

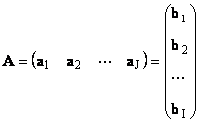
Ovdje svaki vektor a j je j-ta kolona i vektor reda b i je i-ti red matrice A

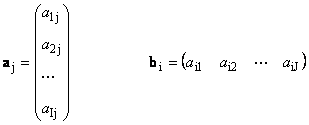
1.12. Linearno zavisni vektori

Vektori iste dimenzije ( N) se može sabirati i množiti brojem, baš kao i matrice. Rezultat je vektor iste dimenzije. Neka postoji nekoliko vektora iste dimenzije x 1 , x 2 ,...,x K i isti broj brojeva α α 1 , α 2 ,...,α K. Vector

y= α 1 x 1 + α 2 x 2 +...+α K x K

pozvao linearna kombinacija vektori x k .

Ako postoje takvi brojevi različiti od nule α k ≠ 0, k = 1,..., K, šta y = 0 , onda takav skup vektora x k pozvao linearno zavisna. Inače, vektori se nazivaju linearno nezavisni. Na primjer, vektori x 1 = (2, 2) t i x 2 = (−1, −1) t su linearno zavisne, jer x 1 +2x 2 = 0

1.13. Matrix rang

Razmotrite skup K vektori x 1 , x 2 ,...,x K dimenzije N. Rang ovog sistema vektora je maksimalni broj linearno nezavisnih vektora. Na primjer u setu

postoje samo dva linearno nezavisna vektora, na primjer x 1 i x 2, pa je njegov rang 2.

Očigledno, ako u skupu ima više vektora od njihove dimenzije ( K>N), onda su oni nužno linearno zavisni.

Matrix rang(označeno rangom ( A)) je rang sistema vektora od kojih se sastoji. Iako se bilo koja matrica može predstaviti na dva načina (vektori stupaca ili vektori reda), to ne utiče na vrijednost ranga, jer

1.14. inverzna matrica

kvadratna matrica A naziva se nedegenerisanim ako ima jedinstvenu obrnuto matrica A-1 , utvrđeno uslovima

aa −1 = A −1 A = I.

Inverzna matrica ne postoji za sve matrice. Neophodan i dovoljan uslov za nedegeneraciju je

det( A) ≠ 0 ili rang ( A) = N.

Inverzija matrice je složena procedura za koju postoje posebni programi. Na primjer,

Rice. 17 Inverzija matrice

Dajemo formule za najjednostavniji slučaj - matrice 2 × 2

Ako matrice A i B su nedegenerisani, dakle

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverzna matrica

Ako je matrica A je degenerisana i inverzna matrica ne postoji, onda se u nekim slučajevima može koristiti pseudo-inverzno matrica, koja je definisana kao takva matrica A+ to

aa + A = A.

Pseudo-inverzna matrica nije jedina i njen oblik zavisi od načina konstrukcije. Na primjer za pravougaone matrice može se koristiti Moore-Penrose metoda.

Ako je broj kolona manje od broja linije, onda

A + =(A t A) −1 A t

Na primjer,

Rice. 17a Inverzija pseudo matrice

Ako je broj kolona više broja linije, onda

A + =A t( aa t) −1

1.16. Množenje vektora matricom

Vector x može se pomnožiti matricom A odgovarajuću dimenziju. U ovom slučaju, vektor stupca se množi na desnoj strani Sjekira, a vektorski niz je na lijevoj strani x t A. Ako je dimenzija vektora J, i dimenziju matrice I× J onda je rezultat vektor dimenzija I. Na primjer,

Rice. 18 Vektorsko-matrično množenje

Ako je matrica A- kvadratni ( I× I), zatim vektor y = Sjekira ima iste dimenzije kao x. Očigledno je da

A(α 1 x 1 + α 2 x 2) = α 1 Sjekira 1 + α 2 Sjekira 2 .

Stoga se matrice mogu smatrati linearnim transformacijama vektora. Posebno x = x, Ox = 0 .

2. Dodatne informacije

2.1. Sistemi linearnih jednačina

Neka bude A- veličina matrice I× J, a b- vektor dimenzija J. Razmotrite jednačinu

Sjekira = b

u odnosu na vektor x, dimenzije I. U suštini, ovo je sistem I linearne jednadžbe sa J nepoznato x 1 ,...,x J. Rješenje postoji ako i samo ako

rang ( A) = rang( B) = R,

gdje B je matrica proširene dimenzije I×( J+1) koji se sastoji od matrice A, podstavljena kolonom b, B = (A b). Inače, jednačine su nekonzistentne.

Ako a R = I = J, onda je rješenje jedinstveno

x = A −1 b.

Ako a R < I, onda ih ima mnogo razna rješenja, što se može izraziti u terminima linearne kombinacije J−R vektori. Sistem homogene jednačine Sjekira = 0 sa kvadratnom matricom A (N× N) nema trivijalno rešenje (x ≠ 0 ) ako i samo ako det( A) = 0. Ako R= rang( A)<N, onda postoje N−R linearno nezavisna rješenja.

2.2. Bilinearni i kvadratni oblici

Ako a A- Ovo kvadratna matrica, a x i y- vektori odgovarajuće dimenzije, zatim skalarni proizvod forme x t Ay pozvao bilinearni oblik definisan matricom A. At x = y izraz x t Sjekira pozvao kvadratni formu.

2.3. Pozitivno određene matrice

kvadratna matrica A pozvao pozitivno definitivno, ako je za bilo koji vektor različit od nule x ≠ 0 ,

x t Sjekira > 0.

The negativan (x t Sjekira < 0), nenegativan (x t Sjekira≥ 0) i nepozitivna (x t Sjekira≤ 0) određene matrice.

2.4. Cholesky decomposition

Ako je simetrična matrica A je pozitivno određen, onda postoji jedinstvena trokutasta matrica U sa pozitivnim elementima, za koje

A = U t U.

Na primjer,

Rice. 19 Cholesky dekompozicija

2.5. polarna dekompozicija

Neka bude A je nedegenerirana kvadratna matrica dimenzija N× N. Zatim postoji jedinstvena polar performanse

A = SR,

gdje S je nenegativna simetrična matrica, i R je ortogonalna matrica. matrice S i R može se eksplicitno definirati:

S 2 = aa t or S = (aa t) ½ i R = S −1 A = (aa t) −½ A.

Na primjer,

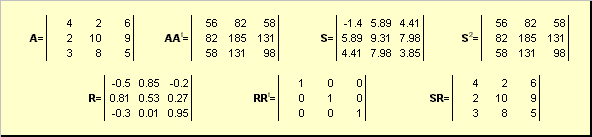
Rice. 20 Polarna dekompozicija

Ako je matrica A je degenerisan, onda dekompozicija nije jedinstvena - naime: S i dalje sam, ali R može biti mnogo. Polarna dekompozicija predstavlja matricu A kao kombinacija kompresije/rastezanja S i okretanje R.

2.6. Svojstveni vektori i sopstvene vrijednosti

Neka bude A je kvadratna matrica. Vector v pozvao sopstveni vektor matrice A, ako

Av = λ v,

gdje se zove broj λ vlastita vrijednost matrice A. Dakle, transformacija koju matrica izvodi A preko vektora v, svodi se na jednostavno rastezanje ili kompresiju s faktorom λ. Svojstveni vektor je određen do množenja konstantom α ≠ 0, tj. ako v je svojstveni vektor, onda je α v je također svojstveni vektor.

2.7. Svojstvene vrijednosti

Na matrici A, dimenzija ( N× N) ne može biti veći od N sopstvene vrijednosti. Oni zadovoljavaju karakteristična jednačina

det( A − λ I) = 0,

biće algebarska jednačina N-th red. Konkretno, za matricu 2×2, karakteristična jednačina ima oblik

Na primjer,

Rice. 21 Sopstvene vrijednosti

Skup svojstvenih vrijednosti λ 1 ,..., λ N matrice A pozvao spektra A.

Spektar ima različita svojstva. Posebno

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

Vlastite vrijednosti proizvoljne matrice mogu biti kompleksni brojevi, ali ako je matrica simetrična ( A t = A), tada su njegove vlastite vrijednosti realne.

2.8. Vlastiti vektori

Na matrici A, dimenzija ( N× N) ne može biti veći od N svojstvene vektore, od kojih svaki odgovara svojoj vrijednosti. Odrediti svojstveni vektor v n potrebno je da rešite sistem homogenih jednačina

(A − λ n I)v n = 0 .

Ima netrivijalno rješenje jer det( A-λ n I) = 0.

Na primjer,

Rice. 22 Sopstveni vektori

Svojstveni vektori simetrične matrice su ortogonalni.

Svojstvene vrijednosti (brojevi) i svojstveni vektori.
Primjeri rješenja

Budi svoj

Iz obje jednačine slijedi da .

Stavimo onda: .

Kao rezultat: je drugi sopstveni vektor.

Hajde da ponovimo važne tačke rješenja:

– rezultirajući sistem svakako jeste zajednička odluka(jednadžbe su linearno zavisne);

- "Y" se bira na način da je cijeli broj, a prva "x" koordinata je cjelobrojna, pozitivna i što manja.

– provjeravamo da li određeno rješenje zadovoljava svaku jednačinu sistema.

Odgovori .

Međusobne "kontrolne tačke" bile su sasvim dovoljne, pa je provjera jednakosti, u principu, suvišna.

U različitim izvorima informacija, koordinate vlastitih vektora često se ne pišu u stupcima, već u redovima, na primjer: (i, da budem iskren, i sam sam ih pisao u redovima). Ova opcija je prihvatljiva, ali u svjetlu teme linearne transformacije tehnički praktičniji za upotrebu vektori stupaca.

Možda vam se rješenje učinilo jako dugim, ali to je samo zato što sam prvi primjer prokomentarisao vrlo detaljno.

Primjer 2

matrice

Treniramo sami! Približan uzorak konačnog dizajna zadatka na kraju lekcije.

Ponekad je potrebno dodatni zadatak, odnosno:

napišite kanonsku dekompoziciju matrice

Šta je to?

Ako se formiraju sopstveni vektori matrice osnovu, onda se može predstaviti kao:

Gdje je matrica sastavljena od koordinata vlastitih vektora, – dijagonala matrica sa odgovarajućim svojstvenim vrijednostima.

Ova matrična dekompozicija se zove kanonski ili dijagonala.

Razmotrimo matricu prvog primjera. Njeni sopstveni vektori linearno nezavisna(nekolinearne) i čine osnovu. Napravimo matricu od njihovih koordinata:

Na glavna dijagonala matrice po propisanom redu locirane su vlastite vrijednosti, a preostali elementi su jednaki nuli:
- još jednom naglašavam važnost reda: "dva" odgovara 1. vektoru i stoga se nalazi u 1. koloni, "tri" - 2. vektoru.

Prema uobičajenom algoritmu za pronalaženje inverzna matrica ili Gauss-Jordan metoda naći . Ne, to nije greška u kucanju! - Pred tobom je rijedak, kao pomračenje sunca događaj kada se inverzni poklapa sa originalnom matricom.

Ostaje napisati kanonsku dekompoziciju matrice:

Sistem se može riješiti sa elementarne transformacije a u sljedećim primjerima ćemo pribjeći ovu metodu. Ali ovdje "školska" metoda djeluje mnogo brže. Iz 3. jednačine izražavamo: - zamjenu u drugu jednačinu:

Pošto je prva koordinata nula, dobijamo sistem , iz svake jednačine iz koje sledi da .

I opet obratite pažnju na obavezno prisustvo linearnog odnosa. Ako se dobije samo trivijalno rješenje , tada je ili svojstvena vrijednost pogrešno pronađena, ili je sistem kompajliran / riješen s greškom.

Kompaktne koordinate daju vrijednost

Vlastiti vektor:

I još jednom provjeravamo da li je pronađeno rješenje zadovoljava svaku jednačinu sistema. U narednim pasusima i narednim zadacima preporučujem da se ova želja prihvati kao obavezno pravilo.

2) Za svojstvenu vrijednost, slijedeći isti princip, dobijamo sledeći sistem:

Iz 2. jednačine sistema izražavamo: - zamjenu u treću jednačinu:

Pošto je koordinata "zeta" jednaka nuli, dobijamo sistem , iz čije jednačine sledi linearna zavisnost.

Neka bude

Provjeravamo da li je rješenje zadovoljava svaku jednačinu sistema.

Dakle, sopstveni vektor: .

3) I, konačno, sistem odgovara vlastitoj vrijednosti:

Druga jednačina izgleda najjednostavnije, pa je iz nje izražavamo i zamjenjujemo u 1. i 3. jednadžbu:

Sve je u redu - otkrivena je linearna ovisnost koju zamjenjujemo u izraz:

Kao rezultat, "X" i "Y" su izraženi kroz "Z": . U praksi nije potrebno postići samo takve odnose, u nekim slučajevima je zgodnije izraziti i kroz ili i kroz . Ili čak "voz" - na primjer, "X" do "Y", i "Y" do "Z"

Stavimo onda:

Provjeravamo da li je pronađeno rješenje zadovoljava svaku jednačinu sistema i napiše treći svojstveni vektor

Odgovori: sopstveni vektori:

Geometrijski, ovi vektori definiraju tri različita prostorna pravca ("Tamo i nazad"), prema kojem linearna transformacija transformira vektore različite od nule (svojstvene vektore) u vektore kolinearne njima.

Ako je po uvjetu bilo potrebno pronaći kanonsku ekspanziju od , onda je to moguće ovdje, jer različite vlastite vrijednosti odgovaraju različitim linearno nezavisnim svojstvenim vektorima. Pravimo matricu iz njihovih koordinata, dijagonalna matrica od relevantan svojstvene vrijednosti i nađi inverzna matrica .

Ako je prema uslovu potrebno napisati matrica linearna transformacija u osnovi sopstvenih vektora, onda dajemo odgovor u obliku . Postoji razlika, i to značajna razlika! Za ovu matricu je matrica "de".

Izazovite sa više jednostavne proračune za nezavisna odluka:

Primjer 5

Naći svojstvene vektore linearne transformacije date matricom

Prilikom pronalaženja vlastitih brojeva pokušajte ne dovesti slučaj do polinoma 3. stepena. Osim toga, vaša sistemska rješenja mogu se razlikovati od mojih rješenja – ovdje nema jednoznačnosti; i vektori koje pronađete mogu se razlikovati od vektora uzorka do proporcionalnosti njihovim odgovarajućim koordinatama. Na primjer, i . Estetski je ugodnije predstaviti odgovor u obliku , ali je u redu ako se zaustavite na drugoj opciji. Međutim, sve ima razumne granice, verzija ne izgleda baš dobro.

Okvirni konačni uzorak zadatka na kraju lekcije.

Kako riješiti problem u slučaju više vlastitih vrijednosti?

Opšti algoritam ostaje isti, ali ima svoje posebnosti, te je preporučljivo zadržati neke dijelove rješenja u strožijem akademskom stilu:

Primjer 6

Pronađite svojstvene vrijednosti i svojstvene vektore

Odluka

Naravno, pišemo velikim slovom fantastičnu prvu kolonu:

I nakon raspadanja kvadratni trinom za množitelje:

Kao rezultat, dobivaju se vlastite vrijednosti, od kojih su dvije višekratne.

Hajde da nađemo svoje vektori:

1) Postupit ćemo sa usamljenim vojnikom prema „pojednostavljenoj“ šemi:

Iz posljednje dvije jednačine jasno je vidljiva jednakost koju, očigledno, treba zamijeniti 1. jednačinom sistema:

Nema bolje kombinacije:
Vlastiti vektor:

2-3) Sada uklanjamo nekoliko stražara. U ovom slučaju može biti ili dva ili jedan svojstveni vektor. Bez obzira na višestrukost korijena, vrijednost zamjenjujemo u determinanti , što nam donosi sljedeće homogeni sistem linearnih jednačina:

Svojstveni vektori su upravo vektori
fundamentalni sistem odlučivanja

Zapravo, tokom čitave lekcije samo smo se bavili pronalaženjem vektora fundamentalnog sistema. Samo za sada ovaj termin nije bila posebno potrebna. Uzgred, oni spretni studenti koji, u kamuflaži homogene jednačine, biće primoran da ga sada popuši.

Jedina akcija bila je uklanjanje dodatnih linija. Rezultat je "jedan po tri" matrica sa formalnim "korakom" u sredini.
– osnovna varijabla, – slobodne varijable. Postoje dvije slobodne varijable, dakle postoje i dva vektora fundamentalnog sistema.

Izrazimo osnovnu varijablu u terminima slobodnih varijabli: . Faktor nule ispred "x" omogućava mu da preuzme apsolutno sve vrijednosti (što je također jasno vidljivo iz sistema jednadžbi).

U kontekstu ovog problema, prikladnije je opće rješenje napisati ne u redu, već u stupcu:

Par odgovara sopstvenom vektoru:
Par odgovara sopstvenom vektoru:

Bilješka : sofisticirani čitaoci mogu da pokupe ove vektore usmeno - samo analizom sistema , ali ovdje je potrebno određeno znanje: postoje tri varijable, rang sistemske matrice- jedinična sredstva fundamentalni sistem odlučivanja sastoji se od 3 – 1 = 2 vektora. Međutim, pronađeni vektori su savršeno vidljivi i bez ovog znanja, čisto na intuitivnom nivou. U ovom slučaju, treći vektor će biti napisan još „ljepše“: . Međutim, riječ opreza, u drugom primjeru jednostavan izbor možda i nije, zbog čega je rezervacija namijenjena iskusnim osobama. Osim toga, zašto ne uzeti kao treći vektor, recimo, ? Na kraju krajeva, njegove koordinate također zadovoljavaju svaku jednačinu sistema i vektore su linearno nezavisne. Ova opcija je, u principu, prikladna, ali "kriva", budući da je "drugi" vektor linearna kombinacija vektora osnovnog sistema.

Odgovori: vlastite vrijednosti: , svojstveni vektori:

Sličan primjer za "uradi sam" rješenje:

Primjer 7

Pronađite svojstvene vrijednosti i svojstvene vektore

Približan uzorak završne obrade na kraju lekcije.

Treba napomenuti da se i u 6. i u 7. primjeru dobija trostruka linearno nezavisnih vlastitih vektora, pa se stoga originalna matrica može predstaviti u kanonska dekompozicija. Ali takve maline se ne dešavaju u svim slučajevima:

Primjer 8