Konstantsete koefitsientidega lineaarsed erinevusvõrrandid. Mannekeenide diferentsiaalvõrrandid

Sageli tekitab ainuüksi diferentsiaalvõrrandite mainimine õpilastes ebameeldiva tunde. Miks see juhtub? Kõige sagedamini seetõttu, et materjali põhitõdede uurimisel tekib teadmiste lünk, mille tõttu difuusorite edasine uurimine muutub lihtsalt piinamiseks. Pole selge, mida teha, kuidas otsustada, kust alustada?

Siiski püüame teile näidata, et difuusorid pole nii keerulised, kui tundub.

Diferentsiaalvõrrandite teooria põhimõisted

Kooliajast teame lihtsamaid võrrandeid, milles peame leidma tundmatu x. Tegelikult diferentsiaalvõrrandid neist vaid veidi erinev – muutuja asemel X peate leidma neis funktsiooni y(x) , mis muudab võrrandi identiteediks.

Diferentsiaalvõrranditel on suur praktiline tähtsus. See ei ole abstraktne matemaatika, millel pole mingit seost meid ümbritseva maailmaga. Paljusid reaalseid looduslikke protsesse kirjeldatakse diferentsiaalvõrrandite abil. Näiteks stringi võnked, harmoonilise ostsillaatori liikumine, kasutades diferentsiaalvõrrandeid mehaanika ülesannetes, leiavad keha kiiruse ja kiirenduse. Samuti DU kasutatakse laialdaselt bioloogias, keemias, majanduses ja paljudes teistes teadustes.

Diferentsiaalvõrrand (DU) on võrrand, mis sisaldab funktsiooni y(x), funktsiooni enda, sõltumatute muutujate ja muude parameetrite tuletisi erinevates kombinatsioonides.

Diferentsiaalvõrrandid on mitut tüüpi: tavalised diferentsiaalvõrrandid, lineaarsed ja mittelineaarsed, homogeensed ja mittehomogeensed, esimest ja kõrgemat järku diferentsiaalvõrrandid, osadiferentsiaalvõrrandid jne.

Diferentsiaalvõrrandi lahendus on funktsioon, mis muudab selle identiteediks. Kaugjuhtimispuldil on üldised ja erilahendused.

Diferentsiaalvõrrandi üldlahendus on lahenduste üldkogum, mis muudab võrrandi identiteediks. Diferentsiaalvõrrandi osalahend on lahendus, mis vastab algselt määratud lisatingimustele.

Diferentsiaalvõrrandi järjekorra määrab selle tuletisi kõrgeim järk.

Tavalised diferentsiaalvõrrandid

Tavalised diferentsiaalvõrrandid on võrrandid, mis sisaldavad ühte sõltumatut muutujat.

Vaatleme lihtsaimat esimest järku tavalist diferentsiaalvõrrandit. See näeb välja nagu:

Sellise võrrandi saab lahendada lihtsalt selle parema külje integreerimisega.

Selliste võrrandite näited:

Eraldatavad võrrandid

Üldiselt näeb seda tüüpi võrrand välja järgmine:

Siin on näide:

Sellise võrrandi lahendamisel peate muutujad eraldama, viies selle vormile:

Pärast seda jääb alles mõlemad osad integreerida ja lahendus leida.

Esimest järku lineaarsed diferentsiaalvõrrandid

Sellised võrrandid näevad välja järgmised:

Siin on p(x) ja q(x) mõned sõltumatu muutuja funktsioonid ning y=y(x) on soovitud funktsioon. Siin on näide sellisest võrrandist:

Sellise võrrandi lahendamisel kasutavad nad enamasti suvalise konstandi muutmise meetodit või esitavad soovitud funktsiooni kahe teise funktsiooni y(x)=u(x)v(x) korrutisena.

Selliste võrrandite lahendamiseks on vaja teatud ettevalmistusi ja neid on üsna keeruline "ühe pilguga" võtta.

Eraldatavate muutujatega diferentsiaalvõrrandi lahendamise näide

Niisiis vaatasime lihtsamaid kaugjuhtimispuldi tüüpe. Vaatame nüüd ühe neist lahendust. Olgu selleks eraldatavate muutujatega võrrand.

Esmalt kirjutame tuletise tuttavamal kujul ümber:

Seejärel jagame muutujad, see tähendab, et võrrandi ühes osas kogume kõik "mina" ja teises - "X":

Nüüd jääb üle mõlemad osad integreerida:

Integreerime ja saame selle võrrandi üldise lahenduse:

Muidugi on diferentsiaalvõrrandite lahendamine omamoodi kunst. Peate suutma aru saada, mis tüüpi võrrandiga on tegu, ning õppima ka nägema, milliseid teisendusi tuleb sellega teha, et viia ühele või teisele vormile, rääkimata lihtsalt eristamis- ja integreerimisvõimest. Ja DE lahendamise õnnestumiseks on vaja harjutamist (nagu kõiges). Ja kui teil pole praegu aega aru saada, kuidas diferentsiaalvõrrandeid lahendatakse, või kui Cauchy probleem on luuna kurku kinni jäänud või te ei tea, kuidas esitlust õigesti ette valmistada, võtke ühendust meie autoritega. Lühikese ajaga pakume Sulle valmis ja detailse lahenduse, mille detailidest saad aru igal Sulle sobival ajal. Seniks soovitame vaadata videot teemal “Kuidas lahendada diferentsiaalvõrrandeid”:

Vaatleme n-ndat järku erinevusvõrrandit

y(k) = F(k) (92)

Nagu diferentsiaalvõrrandite puhul, määratakse lahendus alati esimest järku võrrandite jaoks ja üldiselt ei leia seda kõrgemat järku võrrandite puhul.

Abistav lahendus.

Vaatleme homogeenset esimest järku võrrandit

a 1 (k)y(k+1) + a 0 (k)y(k) = 0, (93)

kus a 0 (k)≠0 ja a 1 (k)≠0. Seda saab vormis ümber kirjutada

y(k+1) = a(k)y(k). (94)

kui k=0,1,2...

y(1)=a(0)y(0),

y(2)=a(1)a(0)y(0)

y(3)=a(2)a(1)a(0)y(0)

või üldiselt

seega on võrrandi (94) üldlahend

Korrutise alumine piir on suvaline, kuna mis tahes fikseeritud arvu tegureid a(0), a(1) ja a(2), ... saab kombineerida suvalise konstandiga C.

Esimest järku kõrgema homogeense võrrandi lahendust üldjuhul ei väljendata elementaarfunktsioonide kujul, kuna võrranditel (81) ja (82) põhinev protseduur, mille koefitsiendid sõltuvad k-st, lakkab kehtimast. Kui on teada kõik võrrandi sõltumatud lahendid peale ühe, saab määrata ülejäänud lahendi. Nagu diferentsiaalvõrrandite puhul, on paljudel üksikjuhtudel võimalik saada selge lahendus. Vormi võrrand

a n f(k + n)y(k + n) + ... + a 1 f (k + 1)y(k + 1) + a n f(k)y(k) = 0,

kus koefitsiendid a i on konstantsed väärtused, asendades z(k)=f(k)y(k), taandatakse see konstantsete koefitsientidega diferentsiaalvõrrandiks. Protseduur on osaliselt sarnane Euleri diferentsiaalvõrrandi jaoks kasutatavaga, kuid sel juhul tuleb sõltuv (mitte sõltumatu) muutuja asendada. Seda meetodit kasutatakse laialdaselt muutuvate koefitsientidega võrrandite lahendamisel.

Automaatjuhtimissüsteemide diferentsiaalvõrrandid. Automaatjuhtimissüsteemide diferentsiaalvõrrandite koostamise metoodika.

Üldised märkused.

Automaatjuhtimissüsteemid on oma eesmärgi ja disaini poolest erinevad. ACS-i käitumist saab kirjeldada tavaliste osadiferentsiaalvõrrandite, diferentsiaalvõrrandite jne abil.

Iga ACS esindab üksikute elementide komplekti, mis suhtlevad üksteisega ja on ühendatud ühendustega. ACS-i diferentsiaalvõrrandite koostamise esimene samm on süsteemi jagamine üksikuteks elementideks ja nende elementide jaoks diferentsiaalvõrrandite koostamine. Elementide võrrandid ja üksikute elementide vaheliste seoste võrrandid kirjeldavad protsessi juhtimissüsteemis, s.t. süsteemi kõigi koordinaatide ajas muutumine. Teades elementide võrrandeid ja seoste võrrandeid, on võimalik koostada ACS-i plokkskeem.

ACS-i struktuuriskeem iseloomustab süsteemi geomeetriat, s.o. näitab, millistest elementidest ATS koosneb ja kuidas need elemendid on omavahel seotud. ACS-i olekut, nagu ka iga selles sisalduvat elementi, iseloomustab teatud arv sõltumatuid muutujaid. Need muutujad võivad olla kas elektrilised suurused (vool, pinge jne) või mehaanilised suurused (kiirus, pöördenurk, liikumine jne). Tavaliselt valitakse süsteemi või selle elemendi oleku iseloomustamiseks üks üldistatud koordinaat süsteemi või elemendi sisendis (g(t)) ja üks väljundis (x(t)). Mõnel juhul on selline esitus võimatu, kuna süsteemil või selle elemendil võib olla mitu sisend- ja väljundkogust. Mitmemõõtmelistes süsteemides võib vaadelda vektori sisend- ja väljundkoguseid, mille mõõtmed ühtivad vastavalt ACS-i sisend- ja väljundkoguste arvuga.

Diferentsiaalvõrrandite koostamine ja lineariseerimine süsteemide elemendid.

ACS-i diferentsiaalvõrrandite koostamisel on põhiülesanne süsteemi üksikute elementide diferentsiaalvõrrandite koostamine. Üksikute elementide võrrandid koostatakse nende füüsikaliste seaduste alusel, mis iseloomustavad elemendi käitumist.

ACS elementide diferentsiaalvõrrandite koostamisel tuleks püüda kirjeldada antud elemendi käitumist võimalikult täpselt. Saadud võrrandite keerukus muudab aga nende lahenduste omaduste uurimise keeruliseks. Seetõttu tuleb diferentsiaalvõrrandite koostamisel püüda saavutada mõistlik kompromiss elemendi käitumise kõige täielikuma kirjelduse ja tekkivate võrrandite ülevaatamise ja uurimise võimaluse vahel.

Kui elemendi dünaamikat kirjeldatakse lineaarse diferentsiaalvõrrandiga, siis seda elementi nimetatakse lineaarne, kui diferentsiaalvõrrand ei ole lineaarne, siis nimetatakse elementi mittelineaarne.

Analüüsi lihtsustamiseks asendatakse võimalusel mittelineaarsed diferentsiaalvõrrandid ligikaudselt lineaarvõrranditega, mille lahendid kattuvad piisava täpsusega mittelineaarsete võrrandite lahenditega. Seda protsessi mittelineaarse diferentsiaalvõrrandi asendamiseks lineaarsega nimetatakse lineariseerimine.

Kui elemendi diferentsiaalvõrrand on selle staatilise karakteristiku mittelineaarsuse tõttu mittelineaarne, siis taandatakse võrrandi lineariseerimine elemendi mittelineaarse karakteristiku asendamisele. x=φ(g) mingi lineaarne funktsioon x= ag+ b. Analüütiliselt on see asendus tehtud funktsiooni Taylori seeria laiendusega x=φ(g) püsiseisundile vastava punkti läheduses ja jättes kõrvale kõik liikmed, mis sisaldavad elemendi sisendväärtuse hälvet ∆g esimesest suurema võimsuseni. Geomeetriliselt tähendab see kõvera asendamist x=φ(g) punktis (x 0 , g 0) kõverale tõmmatud puutuja, mis vastab elemendi töö püsiolekule (joonis 29). Muudel juhtudel teostatakse lineariseerimist funktsioonist vähe hälbiva sekandi joonistamisega x=φ(g) elemendi sisendväärtuse muutuste vajalikus vahemikus.

Koos lineariseeritavate karakteristikutega on ka omadusi, mis sellisele lineariseerimisele ei allu. Nende hulka kuuluvad näiteks omadused, mida ei saa stabiilse oleku punkti läheduses Taylori seeriaks laiendada. Me nimetame selliseid omadusi oluliselt mittelineaarne.

Vaatleme mittelineaarse elemendi võrrandi lineariseerimise protsessi Taylori seeria abil. Kirjeldagu elemendi käitumist mittelineaarne diferentsiaalvõrrand

F(x n , x ' , x, g) = 0 (1). Seejärel iseloomustatakse elemendi püsiseisundit võrrandiga F(0, 0, x, g) = 0 (2). olgu g 0 ja x 0 püsiseisundi väärtused. Siis saab koordinaadid g ja x kirjutada x = x 0 + ∆x, g = g 0 + ∆g, kus ∆g ja ∆x on koordinaatide g ja x kõrvalekalle püsiseisundist. Valem (1) hälvete kujul on järgmine:

F(∆x ’’, ∆x’, x 0 + ∆x, g 0 + ∆g) = 0 (3).

Laiendame võrrandi (3) vasakut poolt Taylori seeriaks püsiseisupunkti (0, 0, x 0, g 0) suhtes:

Võrrandi (4) vasakpoolsed osatuletised esindavad mõningaid numbreid, mille väärtused sõltuvad funktsiooni F(x '', x ', x, g) tüübist ja koordinaatide x väärtustest 0 ja g 0.

Arvestades hälbeid ∆g, ∆x püsiseisundist, samuti nende tuletisi aja suhtes, väikeseks ja eeldades, et funktsioon F(x '' , x ' , x, g) on ​​piisavalt sujuv kõikide argumentide jaoks püsiseisundile vastava punkti läheduses jätame võrrandisse (4) kõrvale kõik liikmed, mis sisaldavad hälbeid ∆g ja ∆x, samuti nende tuletised esimesest kõrgemal määral. Saadud võrrand (5) on konstantsete koefitsientidega lineaarne diferentsiaalvõrrand ,,,ja on võrrandi (1) lineariseerimise tulemus.

Ilmselgelt on lineariseerimise vajalik tingimus funktsiooni F(x ’’ , x ’ , x, g) laiendamise võimalus püsiseisundile vastava punkti läheduses Taylori seeriaks.

Võrrandi (1) lineariseerimisprotsessi saab geomeetriliselt tõlgendada järgmiselt. Muutujate x '' , x ' , x, g ruumis defineerib võrrand (1) teatud pinna. Üleminek võrrandilt (1) lineaarvõrrandile (5) tähendab pinna asendamist kindla puutujatasandiga, mis on tõmmatud pinnale püsiseisundile vastavas punktis. Loomulikult, mida väiksem on erinevus pinna- ja tasapinnapunktide vahel, seda väiksem on sellise asendamise viga. See kehtib ainult püsiseisundi väikeses läheduses.

Kontrollitavuse ja vaadeldavuse mõiste.

Tavaliselt nimetatakse protsessi või objekti täielikult juhitavaks, kui seda saab teatud olekust x(t 0) viia soovitud tasakaaluolekusse x(t 1) piiratud ajaintervalli t 1 – t 0 jooksul. Teisisõnu, protsess on täielikult juhitav, kui on piiratud ajaintervallil t 0 ≤ t ≤ t 1 määratletud juhttoiming m(t), mis viib protsessi algolekust x(t 0) soovitud olekusse. tasakaaluseisund x(t 1) aja jooksul t 1 – t 0 .

Vajalikud ja piisavad tingimused täielikuks juhitavuseks diskreetsete süsteemide puhul võib sõnastada järgmiselt.

Lineaarne diskreetne n-ndat järku protsess on täielikult juhitav siis ja ainult siis, kui vektorid

s 1 = φ(-T)h(T),

s 2 = φ(-T)h(T),

s n = φ(-T)h(T)

lineaarselt sõltumatu.

Need vektorid tekivad järgmiste teisenduste tõttu.

(t) = Ax(t) + d m(t),

milles m(t) on ainus juhttoiming. Ühe juhttoimingu juhtumit peetakse tulemuseks olevate avaldiste tõlgendamise lihtsustamiseks. Protsessi üleminekuolekute võrrandil on vorm

kus φ(T) on protsessi siirdemaatriks ja
.

Kontrollitavuse mõistele võib anda ka teise tõlgenduse, mis aitab kaasa selle paremale mõistmisele. Lineaarset mitmemõõtmelist protsessi kirjeldatakse vektori diferentsiaalvõrrandiga (t) = Ax(t) + D m(t), kus x on n-mõõtmeline olekuvektor;

m – r-mõõtmeline vektor, mis kujutab juhtimistoiminguid;

A – n-ndat järku kordajate ruutmaatriks;

D – kontrollmaatriks suurusega n×r.

Maatriksi A saab taandada diagonaaliks

,

kus λ i on lineaarse protsessi maatriksi A omaväärtused, mis eeldatakse olevat kõik erinevad.

Kasutades asendust x=Tz, kirjutame võrrandi kanoonilisel kujul

(t) = Λz(t) + ∆ m(t),

Kus
. Vektorit nimetatakse kanooniliseks olekuvektoriks.

Võrrandiga kirjeldatud protsess (t) = Ax(t) + D m(t), on juhitav, kui maatriks ∆ ei sisalda ridu, mille kõik elemendid on nullid; nullist erinevatele ridadele ∆ vastavaid koordinaate loetakse kontrollituks.

Näide:

Tuletage tsentrifugaalpendli diferentsiaalvõrrand, mida kasutatakse mõnes automaatjuhtimissüsteemis sensorelemendina. Pendli skeem on näidatud joonisel. Sisendsuurus on nurkkiirus ω ja väljundsuurus on platvormi nihe x. Pöörlemiskiiruse kasvades lähevad kuulid tsentrifugaaljõu mõjul lahku ja liigutavad platvormi. Platvormi mõjutavad ka vedru elastsusjõud, summutusjõud ja inertsjõud.

Toome sisse järgmised tähistused: c – vedru jäikuse koefitsient; k – viskoosne hõõrdetegur; m – kuuli mass; M – piki OX-telge toimuvas translatsioonilises liikumises osalevate osade mass; ω – võlli nurkkiirus; f 0 – vedru eelsurvejõud.

Tsentrifugaalpendli diferentsiaalvõrrandi koostamiseks kasutame teist tüüpi Lagrange'i võrrandit:
(I = 1, 2,…, n) (*). Üldistatud koordinaadiks x i valime väljundkoordinaadi - platvormi x liikumise. Leiame avaldise tsentrifugaalpendli kineetilisele energiale T, potentsiaalsele energiale P ja dissipatiivsele funktsioonile R. Jooniselt on selge, et

ρ = r + l sin α, x = 2a(1 – cos α).

Süsteemi kineetiline energia T = T 1 + T 2 + T 3, kus T 1 on kineetiline energia pöörleval liikumisel ümber OX-telje; T 2 – kuulide kineetiline energia pöördliikumisel ümber punktide A ja A’; Т 3 – masside kineetiline energia translatsioonilises liikumises piki OX-telge. Meil on:

,

,
. (*1)

Pendli potentsiaalne energia P = P 1 + P 2 + P 3, kus P 1 on OX-teljega paralleelselt liikuvate masside potentsiaalne energia; P 2 – potentsiaalne energia; P 3 – vedru potentsiaalne energia. Vaadeldava juhtumi jaoks on meil:

,
,
. (*2)

Leiame üldistatud dissipatiivse jõu Q R . Amortisaatori olemasolu tõttu on kuivhõõrdejõud võrreldes viskoosse hõõrdejõuga väike ja seda võib tähelepanuta jätta. Vastavalt valemile
saab

. (*3)

Arvutame Lagrange'i võrrandis (*) sisalduvate üksikute terminite väärtused:

,

,

.

Asendame saadud avaldised teist tüüpi Lagrange'i võrrandiga (*), siis

Tutvustame järgmist tähistust:

,
,

; (*5)

. (*6)

Võttes arvesse aktsepteeritud tähistust, kirjutatakse tsentrifugaalpendli võrrand kujul

Võrrand (*7) on mittelineaarne diferentsiaalvõrrand. Tasakaaluseisund (x 0, ω 0) on võrrandi lahend

Vaatleme pendli väikeseid võnkumisi tasakaaluseisundi suhtes

x = x 0 + ∆x, ω = ω 0 + ∆ω. (*9)

Laiendame funktsioonid f 1 (x), f 2 (x), f 3 (x, ω) Taylori jadaks tasakaaluseisundi (x 0, ω 0) läheduses.

kus funktsioonide F 1 (∆x), F 2 (∆x), F 3 (∆x, ∆ω) väiksus on suurem kui ∆x ja ∆ω. Arvestades, et x’ = ∆x’ ja x” = ∆x”, ning võttes arvesse avaldisi (*8), (*9), (*10), saab võrrandi (*7) ümber kirjutada järgmiselt.

kus on funktsioon

on võrreldes ajaga kõrgem väiksusaste
. Funktsiooni mahajätmine
, saame pendli võnkumiste lineariseeritud võrrandi tasakaaluoleku suhtes (x 0, ω 0)

, (*11)

,

(*12)

.

Süsteemid, mille sisend- ja väljundjadad on ühendatud konstantsete koefitsientidega lineaarse diferentsiaalvõrrandiga, moodustavad konstantsete parameetritega lineaarsete süsteemide klassi alamhulga. LPP-süsteemide kirjeldamine diferentsiaalvõrranditega on väga oluline, kuna see võimaldab sageli leida tõhusaid viise selliste süsteemide konstrueerimiseks. Veelgi enam, diferentsiaalvõrrandi abil saab määrata palju vaadeldava süsteemi omadusi, sealhulgas omasagedusi ja nende paljusust, süsteemi järjestust, nullvõimendusele vastavaid sagedusi jne.

Kõige üldisemal juhul on füüsiliselt realiseeritava süsteemiga seotud konstantsete koefitsientidega järgu lineaarne erinevusvõrrand järgmine

(2.18)

kus koefitsiendid ja kirjeldavad konkreetset süsteemi ja . Kuidas süsteemi järjekord täpselt iseloomustab diferentsiaalvõrrandi matemaatilisi omadusi, seda näidatakse allpool. Võrrand (2.18) on kirjutatud kujul, mis on mugav otsese asendusmeetodi abil lahendada. Algtingimuste komplekti omamine [näiteks jaoks ] ja sisendjada, kasutades valemit (2.18), saate väljundjada otse arvutada. Näiteks erinevuse võrrand

(2.19)

algtingimusega ja on lahendatav asendusega, mis annab

Kuigi erinevusvõrrandite lahendamine otsese asendamise teel on mõnel juhul kasulik, on palju kasulikum saada võrrandile eksplitsiitne lahendus. Selliste lahenduste leidmise meetodeid käsitletakse üksikasjalikult diferentsiaalvõrrandi käsitlevas kirjanduses ja siin antakse vaid lühike ülevaade. Põhiidee taandub diferentsiaalvõrrandi kahe lahendi saamisele: homogeenne ja osaline. Homogeenne lahendus saadakse, kui asendada kõik sisendjada elemente sisaldavad terminid nullidega ja määrata vastus, kui sisendjada on null. Just see lahenduste klass kirjeldab antud süsteemi põhiomadusi. Konkreetne lahendus saadakse, valides antud sisendjada väljundjada tüübi. Homogeense lahuse suvaliste konstantide määramiseks kasutatakse algtingimusi. Näitena lahendame selle meetodi abil võrrandi (2.19). Homogeensel võrrandil on vorm

(2.20)

On teada, et konstantsete koefitsientidega lineaarsete diferentsiaalvõrranditele vastavate homogeensete võrrandite iseloomulikud lahendid on lahendid kujul . Seega, asendades võrrandis (2.20) asemel, saame

(2.21)

Proovime leida konkreetse lahenduse, mis vastab vormi sisestusjärjestusele

(2.22)

Võrrandist (2.19) saame

Kuna võrdsete astmete koefitsiendid peavad olema samad, peavad B, C ja D olema võrdsed

(2.24)

Seega on üldlahendusel vorm

(2.25)

Koefitsient määratakse algtingimusest, kust ja

(2.26)

Lahenduse (2.26) valikuline kontroll näitab selle täielikku vastavust ülaltoodud otsese lahendusega. Lahenduse (2.26) ilmne eelis on see, et see võimaldab väga lihtsalt määrata mis tahes konkreetse .

Joonis fig. 2.7. Lihtsa esimest järku erinevusvõrrandi rakendamise skeem.

Diferentsiaalvõrrandite tähtsus seisneb selles, et need määravad otseselt digitaalse süsteemi konstrueerimise meetodi. Seega kõige üldisema kujuga esimest järku erinevusvõrrand

saab rakendada joonisel fig. 2.7. Viivituse plokk viibib ühe loendi võrra. Sellist süsteemikujunduse vormi, kus sisend- ja väljundjadade jaoks kasutatakse eraldi viiteelemente, nimetatakse otsevormiks 1. Allpool käsitleme selle ja teiste digitaalsete süsteemide konstrueerimise erinevaid meetodeid.

Kõige üldisema vormi teist järku erinevusvõrrand

Joonis fig. 2.8. Skeem teist järku erinevusvõrrandi rakendamiseks.

saab rakendada joonisel fig. 2.8. See ahel kasutab sisend- ja väljundjadade jaoks ka eraldi viivituselemente.

Selle peatüki materjalide järgnevast esitlemisest selgub, et kõrgemat järku süsteemide realiseerimisel saab kasutada esimest ja teist järku süsteeme, kuna viimaseid saab kujutada jada- või paralleelühendusega esmajärjekorras. ja teist järku süsteemid.

V i r e f e r m o r e l a l i v e n tid kutsutakse. vormi võrrand

kus on soovitud ja F- antud funktsioon. Lõplike erinevuste (2) asendamine nende avaldistega soovitud funktsiooni väärtuste kaudu vastavalt punktile (1) viib vormi võrrandini

Kui , st võrrand (3) sisaldab tõesti nii , kui ka , siis nimetatakse võrrandit (3). m-ndat järku diferentsiaalvõrrand ehk diferentsiaalvõrrand V o r t i c a l e l a l i o n .

(6)

kus on suvalised konstandid.

3) Mittehomogeense lineaarvõrrandi üldlahend. (4) esitatakse selle mis tahes konkreetse lahenduse ja homogeense lineaarvõrrandi üldlahenduse summana. (5).

Mittehomogeense võrrandi (5) konkreetse lahenduse saab koostada homogeense võrrandi üldlahendi (6) põhjal, rakendades suvaliste konstantide muutmise meetodit (vt näiteks). R. u. konstantsete koefitsientidega

võib otseselt leida lineaarselt sõltumatuid osalahendusi. Sel eesmärgil võetakse arvesse iseloomulikke omadusi. võrrand

ja otsitakse selle juuri. Kui kõik juured on lihtsad, siis funktsioonid

moodustavad lineaarselt sõltumatu süsteemi võrrandi (7) lahenditest. Juhul, kui - paljususe juur r, Lahendused on lineaarselt sõltumatud

Kui koefitsiendid on 0 , a 1 , . . ., a t reaal ja võrrandil (8) on näiteks keeruline juur. lihtjuur, siis komplekslahenduste asemel eristatakse kahte lineaarselt sõltumatut reaallahendust

Olgu siis R.u. 2. järk konstantsete reaalkoefitsientidega

(9) Iseloomulik võrrand

on juured

Sel juhul on mugav kirjutada võrrandi (9) üldlahend kujule

(10)

kus c 1 ja c 2 on suvalised konstandid. Kui ja on keerulised konjugeeritud juured:

siis on üldlahenduse teisel esitusel vorm

Mitme juure korral saab üldlahenduse, minnes (10) või (11) piirini. See näeb välja nagu

Nagu suvalise järjestusega võrrandite puhul, on ka R. jaoks at. 2. järku võib käsitleda Cauchy probleemi või erinevaid piirväärtusprobleeme. Näiteks Cauchy probleemi puhul

Tavaliste lineaarsete erinevusvõrrandite lahendamine

konstantsete koefitsientidega

Lineaarse diskreetse süsteemi väljundi ja sisendi suhet saab kirjeldada tavalise lineaarse diferentsiaalvõrrandiga konstantsete koefitsientidega

,

Kus y[n]- väljundsignaal hetkel n,

x[n]- sisendsignaal hetkel n,

ai,b k– konstantsed koefitsiendid.

Selliste võrrandite lahendamiseks saab kasutada kahte meetodit

• Otsene meetod
• Meetod Z – teisendused.

Esiteks kaalume lineaarse erinevuse võrrandi lahendamist otsemeetodi abil.

Mittehomogeense (nullist erineva parema küljega) lineaarse erinevuse võrrandi üldlahend on võrdne üldine lahendus lineaarne homogeense erinevuse võrrand ja privaatne lahendus ebahomogeenne võrrand

Homogeense erinevuse võrrandi üldlahend ( null-sisendvastuseks) a h [n]

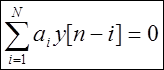
on määratletud kui

.

Asendades selle lahenduse homogeenseks võrrandiks, saame

Sellist polünoomi nimetatakse iseloomulik polünoom süsteemid. Tal on N juured . Juured võivad olla päris või keerulised ning mõned juured võivad olla kokkulangevad (mitu).

Kui juured on reaalsed ja erinevad, siis on homogeense võrrandi lahendil vorm

kus on koefitsiendid

Kui mõni juur, näiteks λ 1 on paljusus m, siis saab vormi vastav lahendustermin

Kui kõik homogeense võrrandi koefitsiendid ja vastavalt ka karakteristlik polünoom on reaalsed, siis on lahenduse kaks liiget, mis vastavad lihtsatele keerukatele konjugaatjuurtele saab esitada (kirjutada) kujul , koefitsientidega A,B määratakse algtingimustega.

Privaatse lahenduse tüüp y p [n] võrrand sõltub paremast küljest (sisendsignaalist) ja määratakse vastavalt allolevale tabelile

Tabel 1. Konkreetse lahenduse tüüp parema külje erineva iseloomu jaoks

Sisendsignaalx[n]	Privaatne lahendusy p [n]
A(pidev)

Lineaarse diferentsiaalvõrrandi lahendamine Z - teisendusmeetodiga seisneb kasutamises Z– teisendused võrrandiks, kasutades lineaarsuse ja ajanihke omadusi. Tulemuseks on lineaarne algebraline võrrand Z- vajaliku funktsiooni pildid. Tagurpidi Z– teisendus annab soovitud lahenduse ajapiirkonnas. Pöördteisendus Z - teisenduse saamiseks kasutatakse kõige sagedamini ratsionaalse avaldise jaotamist lihtsateks (elementaar) murdudeks, kuna pöördteisendusel eraldi elementaarmurdust on lihtne vorm.

Pange tähele, et ajadomeenile liikumiseks saab pöörd-Z-teise arvutamiseks kasutada muid meetodeid.

Näide. Määrame lineaarse erinevuse võrrandiga kirjeldatud süsteemi vastuse (väljundsignaali) sisendsignaalile

Lahendus.

1. Otsene meetod võrrandi lahendamiseks.

Homogeenne võrrand. Sellele iseloomulik polünoom.

Polünoomi juured .

Homogeense võrrandi lahendus.

Kuna me määratleme konkreetse lahenduse vormis .

Asendame selle võrrandisse

Et leida konstant TO võtame vastu n = 2. Siis

Või K = 2,33

Sellest ka konkreetne lahendus ja erinevusvõrrandi (1) üldlahendus

Leiame konstandid C 1 Ja C 2. Selleks paneme n = 0, siis algsest erinevusvõrrandist saame . Antud võrrandi jaoks

Sellepärast . Avaldisest (1)

Seega

.

Avaldisest (1) jaoks n = 1 meil on .
C 1 ja C 2 jaoks saame järgmised kaks võrrandit

.

Selle süsteemi lahendamine annab järgmised väärtused: C 1 = 0,486 ja C 2 = -0,816.

Seetõttu on selle võrrandi üldine lahendus

2. Lahendus Z – teisendusmeetodil.

Võtame Z - teisenduse algsest erinevuse võrrandist, võttes arvesse aja nihke omadust (teoreemi) . Saame