Pronalaženje sin cos. Osnovne trigonometrijske formule
Jedna od grana matematike s kojom se školarci nose s najvećim poteškoćama je trigonometrija. Nije ni čudo: da biste slobodno svladali ovo područje znanja, potrebno vam je prostorno razmišljanje, sposobnost pronalaženja sinusa, kosinusa, tangensa, kotangenata pomoću formula, pojednostavljivanje izraza i sposobnost korištenja broja pi u izračunima. Osim toga, morate znati primijeniti trigonometriju pri dokazivanju teorema, a to zahtijeva ili razvijenu matematičku memoriju ili sposobnost dedukcije složenih logičkih lanaca.
Porijeklo trigonometrije
Upoznavanje s ovom znanošću trebalo bi započeti definicijom sinusa, kosinusa i tangensa kuta, ali prvo morate shvatiti što trigonometrija uopće radi.
Povijesno, glavni predmet proučavanja ovog odjeljka matematička znanost bili pravokutni trokuti. Prisutnost kuta od 90 stupnjeva omogućuje izvođenje različitih operacija koje omogućuju određivanje vrijednosti svih parametara figure koja se razmatra pomoću dvije strane i jednog kuta ili dva kuta i jedne strane. U prošlosti su ljudi primijetili ovaj uzorak i počeli ga aktivno koristiti u izgradnji zgrada, navigaciji, astronomiji, pa čak i umjetnosti.
Prva razina
U početku se o odnosu kutova i stranica govorilo isključivo na primjeru pravokutnog trokuta. Tada su otkrivene posebne formule koje su omogućile proširenje granica uporabe u Svakidašnjica ovu granu matematike.
Učenje trigonometrije u školi danas počinje s pravokutnim trokutima, nakon čega stečeno znanje učenici koriste u fizici i rješavanju apstraktnih problema. trigonometrijske jednadžbe, rad s kojim počinje u srednjoj školi.
Sferna trigonometrija
Kasnije, kad je znanost došla na red sljedeća razina razvoja, formule sa sinusom, kosinusom, tangensom, kotangensom počele su se koristiti u sfernoj geometriji, gdje vrijede druga pravila, a zbroj kutova u trokutu je uvijek veći od 180 stupnjeva. Ovaj odjeljak se ne proučava u školi, ali je potrebno znati za njegovo postojanje, barem zato Zemljina površina, a površina bilo kojeg drugog planeta je konveksna, što znači da će svaka oznaka na površini biti unutra trodimenzionalni prostor"lučni".

Uzmi globus i konac. Pričvrstite konac na bilo koje dvije točke na globusu tako da bude zategnut. Obratite pozornost - dobio je oblik luka. Upravo se takvim oblicima bavi sferna geometrija koja se koristi u geodeziji, astronomiji i drugim teorijskim i primijenjenim područjima.
Pravokutni trokut
Nakon što smo malo naučili o načinima korištenja trigonometrije, vratimo se na osnovnu trigonometriju kako bismo dalje razumjeli što su sinus, kosinus, tangens, koji se proračuni mogu izvesti uz njihovu pomoć i koje formule koristiti.
Prvi korak je razumijevanje pojmova koji se odnose na pravokutni trokut. Prvo, hipotenuza je strana nasuprot kutu od 90 stupnjeva. Ona je najduža. Sjećamo se da je, prema Pitagorinom teoremu, njegova brojčana vrijednost jednaka korijenu zbroja kvadrata druge dvije strane.
Na primjer, ako su dvije strane 3 odnosno 4 centimetra, duljina hipotenuze bit će 5 centimetara. Inače, stari Egipćani su za to znali prije otprilike četiri i pol tisuće godina.
Preostale dvije stranice koje tvore pravi kut zovu se katete. Osim toga, moramo zapamtiti da je zbroj kutova u trokutu u pravokutni sustav koordinata je 180 stupnjeva.
Definicija
Konačno, uz dobro razumijevanje geometrijske osnove, možemo se okrenuti definiciji sinusa, kosinusa i tangensa kuta.
Sinus kuta je omjer suprotnog kraka (tj. strane nasuprot željeni kut) na hipotenuzu. Kosinus kuta je omjer susjedne katete i hipotenuze.

Zapamtite da ni sinus ni kosinus ne mogu biti veći od jedan! Zašto? Budući da je hipotenuza standardno najduža. Bez obzira na to koliko je krak dug, bit će kraći od hipotenuze, što znači da će njihov omjer uvijek biti manji od jedan. Stoga, ako u odgovoru na zadatak dobijete sinus ili kosinus s vrijednošću većom od 1, potražite pogrešku u izračunima ili zaključivanju. Ovaj je odgovor očito pogrešan.
Konačno, tangens kuta je omjer suprotne strane prema susjednoj strani. Isti rezultat će dati dijeljenje sinusa s kosinusom. Pogledajte: u skladu s formulom, duljinu stranice podijelimo s hipotenuzom, nakon čega podijelimo s duljinom druge stranice i pomnožimo s hipotenuzom. Dakle, dobivamo isti omjer kao u definiciji tangente.
Kotangens je, odnosno, omjer stranice koja graniči s kutom i suprotne strane. Isti rezultat dobivamo dijeljenjem jedinice s tangentom.
Dakle, razmotrili smo definicije sinusa, kosinusa, tangensa i kotangensa i možemo se pozabaviti formulama.
Najjednostavnije formule
U trigonometriji se ne može bez formula - kako pronaći sinus, kosinus, tangens, kotangens bez njih? A to je upravo ono što se traži pri rješavanju problema.
Prva formula koju morate znati kada počnete proučavati trigonometriju kaže da je zbroj kvadrata sinusa i kosinusa kuta jednak jedan. Ova formula izravna je posljedica Pitagorinog poučka, ali štedi vrijeme ako želite znati vrijednost kuta, a ne stranice.
Mnogi se učenici ne mogu sjetiti druge formule, koja je također vrlo popularna pri rješavanju školskih zadataka: zbroj jedan i kvadrata tangente kuta jednak je jedinici podijeljen s kvadratom kosinusa kuta. Pogledajte bolje: na kraju krajeva, ovo je ista tvrdnja kao u prvoj formuli, samo su obje strane identiteta podijeljene s kvadratom kosinusa. Ispostavilo se da jednostavna matematička operacija čini trigonometrijsku formulu potpuno neprepoznatljivom. Zapamtite: znati što su sinus, kosinus, tangens i kotangens, pravila pretvorbe i još ponešto osnovne formule u bilo kojem trenutku možete povući traženi više složene formule na komadu papira.
Formule dvostrukog kuta i zbrajanje argumenata
Još dvije formule koje trebate naučiti odnose se na vrijednosti sinusa i kosinusa za zbroj i razliku kutova. Oni su prikazani na donjoj slici. Imajte na umu da se u prvom slučaju sinus i kosinus množe oba puta, au drugom se dodaje umnožak sinusa i kosinusa u paru.

Postoje i formule povezane s argumentima u obrascu dvostruki kut. U potpunosti su izvedeni iz prethodnih - kao praksu, pokušajte ih dobiti sami uzimajući alfa kut jednaka kutu beta.
Konačno, imajte na umu da se formule dvostrukog kuta mogu pretvoriti u niži stupanj sinusa, kosinusa, tangensa alfa.
Teoremi
Dva glavna teorema u osnovnoj trigonometriji su sinusni teorem i kosinusni teorem. Uz pomoć ovih teorema, možete lako razumjeti kako pronaći sinus, kosinus i tangens, a time i površinu figure, veličinu svake strane itd.
Sinusni teorem kaže da kao rezultat dijeljenja duljine svake stranice trokuta s vrijednošću suprotnog kuta, dobivamo isti broj. Štoviše, taj će broj biti jednak dvama radijusima opisane kružnice, odnosno kružnice koja sadrži sve točke zadanog trokuta.

Kosinusni teorem generalizira Pitagorin teorem, projicirajući ga na sve trokute. Ispada da od zbroja kvadrata dviju strana oduzmite njihov umnožak pomnožen s dvostrukim kosinusom susjednog kuta - dobivena vrijednost bit će jednaka kvadratu treće strane. Stoga se Pitagorin teorem ispostavlja kao poseban slučaj kosinusnog teorema.
Pogreške zbog nepažnje
Čak i znajući što su sinus, kosinus i tangens, lako je pogriješiti zbog odsutnosti ili pogreške u najjednostavnijim izračunima. Da bismo izbjegli takve pogreške, upoznajmo se s najpopularnijim od njih.
Prvo, ne biste trebali pretvarati obične razlomke u decimale prije dobivanja konačni rezultat- odgovor možete ostaviti u obrascu obični razlomak osim ako uvjetom nije drugačije navedeno. Takva se transformacija ne može nazvati pogreškom, ali treba imati na umu da se u svakoj fazi problema mogu pojaviti novi korijeni, koji bi se, prema ideji autora, trebali smanjiti. U ovom slučaju ćete gubiti vrijeme na nepotrebno matematičke operacije. To posebno vrijedi za vrijednosti kao što je korijen iz tri ili dva, jer se one pojavljuju u zadacima na svakom koraku. Isto vrijedi i za zaokruživanje "ružnih" brojeva.

Nadalje, imajte na umu da se kosinusni teorem odnosi na bilo koji trokut, ali ne i Pitagorin teorem! Ako greškom zaboravite oduzeti dvostruki proizvod strane pomnožene s kosinusom kuta između njih, ne samo da ćete dobiti potpuno pogrešan rezultat, već ćete također pokazati potpuno nerazumijevanje predmeta. Ovo je gore od greške iz nepažnje.
Treće, nemojte brkati vrijednosti za kutove od 30 i 60 stupnjeva za sinuse, kosinuse, tangente, kotangense. Zapamtite ove vrijednosti, jer je sinus od 30 stupnjeva jednak kosinusu od 60, i obrnuto. Lako ih je pomiješati, zbog čega ćete neizbježno dobiti pogrešan rezultat.
Primjena
Mnogi studenti ne žure početi proučavati trigonometriju, jer ne razumiju njezino primijenjeno značenje. Što je sinus, kosinus, tangens za inženjera ili astronoma? To su koncepti zahvaljujući kojima možete izračunati udaljenost do dalekih zvijezda, predvidjeti pad meteorita, poslati istraživačku sondu na drugi planet. Bez njih je nemoguće izgraditi zgradu, dizajnirati automobil, izračunati opterećenje na površini ili putanju objekta. A ovo su samo najočitiji primjeri! Uostalom, trigonometrija se u ovom ili onom obliku koristi posvuda, od glazbe do medicine.
Konačno
Dakle, vi ste sinus, kosinus, tangens. Možete ih koristiti u izračunima i uspješno rješavati školske zadatke.

Cijela bit trigonometrije svodi se na činjenicu da se nepoznati parametri moraju izračunati iz poznatih parametara trokuta. Postoji ukupno šest opcija: dužine tri strane i veličina tri ugla. Sva razlika u zadacima leži u činjenici da su zadani različiti ulazni podaci.
Kako pronaći sinus, kosinus, tangens na temelju poznate duljine noge ili hipotenuza, sada znate. Budući da ovi izrazi ne znače ništa više od omjera, a omjer je razlomak, Glavni cilj trigonometrijski problem postaje pronalaženje korijena obične jednadžbe ili sustava jednadžbi. I tu će vam pomoći obična školska matematika.
Trigonometrijski identiteti su jednakosti koje uspostavljaju odnos između sinusa, kosinusa, tangensa i kotangensa jednog kuta, što vam omogućuje pronalaženje bilo koje od ovih funkcija, pod uvjetom da je bilo koja druga poznata.
tg \alpha = \frac(\sin \alpha)(\cos \alpha), \enspace ctg \alpha = \frac(\cos \alpha)(\sin \alpha)
tg \alpha \cdot ctg \alpha = 1
Ova identičnost kaže da je zbroj kvadrata sinusa jednog kuta i kvadrata kosinusa jednog kuta jednak jedan, što u praksi omogućuje izračunavanje sinusa jednog kuta kada je poznat njegov kosinus i obrnuto. .
Prilikom pretvaranja trigonometrijski izrazi vrlo često se koristi ova identičnost, koja omogućuje zamjenu zbroja kvadrata kosinusa i sinusa jednog kuta s jedinicom i također izvođenje operacije zamjene obrnutim redoslijedom.
Određivanje tangensa i kotangensa kroz sinus i kosinus
tg \alpha = \frac(\sin \alpha)(\cos \alpha),\enspace
Ti se identiteti formiraju iz definicija sinusa, kosinusa, tangensa i kotangensa. Uostalom, ako pogledate, onda je po definiciji ordinata od y sinus, a apscisa od x je kosinus. Tada će tangens biti jednak omjeru \frac(y)(x)=\frac(\sin \alpha)(\cos \alpha), i omjer \frac(x)(y)=\frac(\cos \alpha)(\sin \alpha)- bit će kotangens.
Dodajemo da će se identiteti dogoditi samo za takve kutove \alpha za koje trigonometrijske funkcije uključene u njih imaju smisla, ctg \alpha=\frac(\cos \alpha)(\sin \alpha).
Na primjer: tg \alpha = \frac(\sin \alpha)(\cos \alpha) vrijedi za \alpha kutove koji se razlikuju od \frac(\pi)(2)+\pi z, A ctg \alpha=\frac(\cos \alpha)(\sin \alpha)- za kut \alpha koji nije \pi z , z je cijeli broj.
Odnos tangensa i kotangensa
tg \alpha \cdot ctg \alpha=1
Ovaj identitet vrijedi samo za kutove \alpha koji su različiti od \frac(\pi)(2) z. U protivnom se neće odrediti ni kotangens ni tangens.
Na temelju gore navedenih točaka, to dobivamo tg \alpha = \frac(y)(x), A ctg\alpha=\frac(x)(y). Otuda slijedi da tg \alpha \cdot ctg \alpha = \frac(y)(x) \cdot \frac(x)(y)=1. Dakle, tangens i kotangens jednog kuta u kojem imaju smisla su međusobno recipročni brojevi.
Odnosi između tangensa i kosinusa, kotangensa i sinusa
tg^(2) \alpha + 1=\frac(1)(\cos^(2) \alpha)- zbroj kvadrata tangensa kuta \alpha i 1 jednak je inverznom kvadratu kosinusa tog kuta. Ovaj identitet vrijedi za sve \alpha osim \frac(\pi)(2)+ \pi z.
1+ctg^(2) \alpha=\frac(1)(\sin^(2)\alpha)- zbroj 1 i kvadrata kotangensa kuta \alpha jednak je inverznom kvadratu sinusa zadanog kuta. Ovaj identitet vrijedi za bilo koji \alpha osim \pi z .
Primjeri s rješenjima zadataka pomoću trigonometrijskih identiteta
Primjer 1
Pronađite \sin \alpha i tg \alpha if \cos \alpha=-\frac12 I \frac(\pi)(2)< \alpha < \pi ;
Prikaži rješenje
Riješenje
Funkcije \sin \alpha i \cos \alpha povezane su formulom \sin^(2)\alpha + \cos^(2) \alpha = 1. Zamjenom u ovu formulu \cos \alpha = -\frac12, dobivamo:
\sin^(2)\alpha + \lijevo (-\frac12 \desno)^2 = 1
Ova jednadžba ima 2 rješenja:
\sin \alpha = \pm \sqrt(1-\frac14) = \pm \frac(\sqrt 3)(2)
Po stanju \frac(\pi)(2)< \alpha < \pi . U drugoj četvrtini sinus je pozitivan, dakle \sin \alpha = \frac(\sqrt 3)(2).
Da bismo pronašli tg \alpha , koristimo formulu tg \alpha = \frac(\sin \alpha)(\cos \alpha)
tg \alpha = \frac(\sqrt 3)(2) : \frac12 = \sqrt 3
Primjer 2
Pronađite \cos \alpha i ctg \alpha ako je i \frac(\pi)(2)< \alpha < \pi .
Prikaži rješenje
Riješenje
Zamjena u formulu \sin^(2)\alpha + \cos^(2) \alpha = 1 uvjetni broj \sin \alpha=\frac(\sqrt3)(2), dobivamo \lijevo (\frac(\sqrt3)(2)\desno)^(2) + \cos^(2) \alpha = 1. Ova jednadžba ima dva rješenja \cos \alpha = \pm \sqrt(1-\frac34)=\pm\sqrt\frac14.
Po stanju \frac(\pi)(2)< \alpha < \pi . U drugoj četvrtini kosinus je negativan, dakle \cos \alpha = -\sqrt\frac14=-\frac12.
Da bismo pronašli ctg \alpha , koristimo formulu ctg \alpha = \frac(\cos \alpha)(\sin \alpha). Znamo odgovarajuće vrijednosti.
ctg \alpha = -\frac12: \frac(\sqrt3)(2) = -\frac(1)(\sqrt 3).
Nositi se sa jednostavni pojmovi: sinus i kosinus i izračun kosinus na kvadrat i sinus na kvadrat.
Sinus i kosinus proučavaju se u trigonometriji (znanost o trokutima s pravim kutom).
Pa počnimo s osnovnim pojmovima. pravokutni trokut:
Hipotenuza- stranica koja uvijek leži nasuprot pravog kuta (kut od 90 stupnjeva). Hipotenuza je najdulja stranica pravokutnog trokuta.
Preostale dvije stranice u pravokutnom trokutu nazivaju se noge.
Također upamtite da zbroj triju kutova u trokutu uvijek iznosi 180°.
Sada prijeđimo na kosinus i sinus kuta alfa (∠α)(tako da svaki nepravi kut u trokutu možete nazvati ili koristiti kao simbol x - "x", što ne mijenja suštinu).
Sinus kuta alfa (sin ∠α)- to je stav suprotan krak (strana nasuprot odgovarajućeg kuta) na hipotenuzu. Ako pogledate sliku, sin ∠ABC = AC / BC
Kosinus kuta alfa (cos ∠α)- stav susjedni na kut katete prema hipotenuzi. Gledajući ponovno gornju sliku, onda cos ∠ABC = AB / BC
I samo da vas podsjetim: kosinus i sinus nikada neće biti veći od jedan, jer je svaki valjak kraći od hipotenuze (a hipotenuza je najdulja stranica svakog trokuta, jer je najdulja stranica smještena nasuprot hipotenuzi visoki kut u trokutu).
Kosinus na kvadrat, sinus na kvadrat
Sada prijeđimo na glavno trigonometrijske formule: izračunajte kosinus na kvadrat i sinus na kvadrat.
Da biste ih izračunali, trebali biste zapamtiti osnovni trigonometrijski identitet:
sin 2 α + cos 2 α = 1(sinus kvadrat plus kosinus kvadrat jednog kuta uvijek je jednak jedan).
Iz trigonometrijskog identiteta izvlačimo zaključke o sinusu:
sin 2 α \u003d 1 - cos 2 α
sinus kvadrat alfa jednako jedan minus kosinus dvostrukog kuta alfa i sve to podijelite s dva.
sin2α = (1 – cos(2α)) / 2
Iz trigonometrijskog identiteta izvlačimo zaključke o kosinusu:
cos 2 α \u003d 1 - sin 2 α
ili više teška opcija formule: kosinus kvadrat alfa jednako je jedan plus kosinus dvostrukog kuta alfa i također sve podijelite s dva.
cos2α = (1 + cos(2α)) / 2
Ove dvije složenije formule sinusa na kvadrat i kosinusa na kvadrat također se nazivaju "smanjenje snage za kvadrate trigonometrijskih funkcija". Oni. bio drugi stupanj, spušten na prvi i izračuni su postali praktičniji.
Koncepti sinusa (), kosinusa (), tangensa (), kotangensa () neraskidivo su povezani s pojmom kuta. Da bismo dobro razumjeli ove, na prvi pogled, složene pojmove (koji kod mnogih školaraca izazivaju stanje užasa) i da bismo se uvjerili da “vrag nije tako strašan kako ga slikaju”, krenimo od samog početka. i razumjeti pojam kuta.
Pojam kuta: radijan, stupanj
Pogledajmo sliku. Vektor se "okrenuo" u odnosu na točku za određeni iznos. Dakle, mjera ove rotacije u odnosu na početni položaj bit će kutak.
Što još trebate znati o pojmu kuta? Pa, jedinice kuta, naravno!
Kut se, kako u geometriji tako iu trigonometriji, može mjeriti u stupnjevima i radijanima.
Poziva se kut od (jedan stupanj). središnji kut u krugu, na temelju kružnog luka jednakog dijelu kruga. Dakle, cijela se kružnica sastoji od "komada" kružnih lukova ili je kut koji opisuje kružnica jednak.

Odnosno, gornja slika prikazuje kut koji je jednak, odnosno taj kut se temelji na kružnom luku veličine opsega.
Kut u radijanima naziva se središnji kut u krugu, koji se temelji na kružnom luku, čija je duljina jednaka polumjeru kruga. Pa, jeste li razumjeli? Ako ne, onda pogledajmo sliku.

Dakle, slika prikazuje kut jednak radijanu, odnosno taj kut se temelji na kružnom luku čija je duljina jednaka polumjeru kruga (duljina je jednaka duljini ili polumjeru jednaka duljini lukovi). Dakle, duljina luka izračunava se formulom:
Gdje je središnji kut u radijanima.
Pa, znajući ovo, možete li odgovoriti koliko radijana sadrži kut opisan kružnicom? Da, za ovo morate zapamtiti formulu za opseg kruga. evo je:
Pa, povežimo sada ove dvije formule i ustanovimo da je kut opisan kružnicom jednak. To jest, korelirajući vrijednost u stupnjevima i radijanima, dobivamo to. Odnosno,. Kao što vidite, za razliku od "stupnjeva", riječ "radijan" je izostavljena, jer je mjerna jedinica obično jasna iz konteksta.
Koliko radijana ima? Tako je!
kužiš Zatim pričvrstite naprijed:
Ima li poteškoća? Onda pogledajte odgovori:
Pravokutni trokut: sinus, kosinus, tangens, kotangens kuta
Dakle, s konceptom kuta smo shvatili. Ali što je sinus, kosinus, tangens, kotangens kuta? Hajdemo shvatiti. U tome će nam pomoći pravokutni trokut.

Kako se zovu stranice pravokutnog trokuta? Tako je, hipotenuza i noge: hipotenuza je stranica koja leži nasuprot pravog kuta (u našem primjeru, ovo je stranica); noge su dvije preostale strane i (one uz pravi kut), osim toga, ako uzmemo u obzir krake u odnosu na kut, tada je krak susjedni krak, a krak suprotni. Dakle, odgovorimo sada na pitanje: što su sinus, kosinus, tangens i kotangens kuta?
Sinus kuta je omjer suprotne (daleke) noge prema hipotenuzi.
u našem trokutu.
Kosinus kuta- ovo je omjer susjedne (bliske) noge prema hipotenuzi.
u našem trokutu.
Kutna tangenta- ovo je omjer suprotne (dalje) noge u odnosu na susjednu (blizu).
u našem trokutu.
Kotangens kuta- ovo je omjer susjedne (bliske) noge prema suprotnoj (daleko).
u našem trokutu.
Ove definicije su neophodne zapamtiti! Da biste lakše zapamtili koju nogu podijeliti na što, morate jasno razumjeti da u tangens I kotangens samo katete sjede, a hipotenuza se pojavljuje samo u sinus I kosinus. A onda možete smisliti lanac asocijacija. Na primjer, ovaj:
kosinus→dodir→dodir→susjedni;
Kotangens→dodir→dodir→susjedni.
Prije svega, potrebno je zapamtiti da sinus, kosinus, tangens i kotangens kao omjeri stranica trokuta ne ovise o duljinama tih stranica (pod jednim kutom). Nemoj vjerovati? Zatim se uvjerite gledajući sliku:

Razmotrimo, na primjer, kosinus kuta. Po definiciji, iz trokuta: , ali možemo izračunati kosinus kuta iz trokuta: . Vidite, duljine stranica su različite, ali vrijednost kosinusa jednog kuta je ista. Dakle, vrijednosti sinusa, kosinusa, tangensa i kotangensa ovise isključivo o veličini kuta.
Ako razumijete definicije, samo naprijed i popravite ih!
Za trokut prikazan na donjoj slici nalazimo.

Pa, jeste li shvatili? Zatim pokušajte sami: izračunajte isto za kut.
Jedinična (trigonometrijska) kružnica
Razumijevajući koncepte stupnjeva i radijana, razmotrili smo krug čiji je polumjer jednak. Takav se krug zove singl. Vrlo je koristan u proučavanju trigonometrije. Stoga se malo detaljnije zadržavamo na njemu.

Kao što vidite, ovaj krug je ugrađen Kartezijanski sustav koordinate. Polumjer kružnice jednak je jedinici, dok središte kružnice leži u ishodištu, početni položaj radijus vektora fiksiran je duž pozitivnog smjera osi (u našem primjeru to je polumjer).
Svakoj točki kruga odgovaraju dva broja: koordinata duž osi i koordinata duž osi. Koji su to koordinatni brojevi? I uopće, kakve oni veze imaju s ovom temom? Da biste to učinili, sjetite se razmatranog pravokutnog trokuta. Na gornjoj slici možete vidjeti dva cijela pravokutna trokuta. Razmotrimo trokut. Pravokutan je jer je okomit na os.
Što je jednako iz trokuta? Tako je. Osim toga, znamo da je polumjer jedinične kružnice, i prema tome, . Zamijenite ovu vrijednost u našu formulu kosinusa. Evo što se događa:
A čemu je jednako iz trokuta? Pa naravno, ! Zamijenite vrijednost polumjera u ovu formulu i dobijte:
Dakle, možete li mi reći koje su koordinate točke koja pripada krugu? Pa nema šanse? A ako to shvatite i samo su brojke? Kojoj koordinati odgovara? Pa, naravno, koordinata! Kojoj koordinati odgovara? Tako je, koordiniraj! Dakle, točka.

I što su onda jednaki i? Tako je, upotrijebimo odgovarajuće definicije tangensa i kotangensa i dobijemo to, a.
Što ako je kut veći? Evo, na primjer, kao na ovoj slici:

Što se promijenilo u ovaj primjer? Hajdemo shvatiti. Da bismo to učinili, ponovno se okrećemo pravokutnom trokutu. Razmotrimo pravokutni trokut: kut (kao susjedni kutu). Kolika je vrijednost sinusa, kosinusa, tangensa i kotangensa kuta? Tako je, držimo se odgovarajućih definicija trigonometrijskih funkcija:
Pa, kao što vidite, vrijednost sinusa kuta još uvijek odgovara koordinati; vrijednost kosinusa kuta - koordinate; i vrijednosti tangensa i kotangensa na odgovarajuće omjere. Dakle, ove relacije su primjenjive na sve rotacije radijus vektora.
Već je spomenuto da je početni položaj radijus vektora duž pozitivnog smjera osi. Do sada smo rotirali ovaj vektor u smjeru suprotnom od kazaljke na satu, ali što se događa ako ga rotiramo u smjeru kazaljke na satu? Ništa neobično, dobit ćete i kut određene veličine, ali samo on će biti negativan. Dakle, kada rotiramo radijus vektor u smjeru suprotnom od kazaljke na satu, dobivamo pozitivni kutovi , a kada se okreće u smjeru kazaljke na satu - negativan.
Dakle, znamo da je cijela revolucija radijus vektora oko kruga ili. Je li moguće rotirati radijus vektor za ili za? Pa naravno da možete! U prvom slučaju, dakle, radijus vektor će činiti jedan puni okret i zaustaviti se na ili.
U drugom slučaju, odnosno, radijus vektor će napraviti tri potpuna kruga i zaustaviti se na poziciji ili.
Dakle, iz gornjih primjera možemo zaključiti da kutovi koji se razlikuju za ili (gdje je bilo koji cijeli broj) odgovaraju istom položaju radijus vektora.
Donja slika prikazuje kut. Ista slika odgovara kutu, i tako dalje. Ovaj popis se može nastaviti na neodređeno vrijeme. Svi ovi kutovi mogu se napisati općom formulom ili (gdje je bilo koji cijeli broj)

Sada, poznavanje definicija osnovnih trigonometrijskih funkcija i korištenje jedinični krug, pokušajte odgovoriti kolike su vrijednosti jednake:
Evo jediničnog kruga koji će vam pomoći:

Ima li poteškoća? Onda idemo shvatiti. Dakle, znamo da:
Odavde određujemo koordinate točaka koje odgovaraju određenim mjerama kuta. Pa, počnimo redom: kut na odgovara točki s koordinatama, dakle:
Ne postoji;
Nadalje, držeći se iste logike, otkrivamo da kutovi u odgovaraju točkama s koordinatama, odnosno. Znajući to, lako je odrediti vrijednosti trigonometrijskih funkcija u odgovarajućim točkama. Prvo pokušajte sami, a zatim provjerite odgovore.
odgovori:
Ne postoji
Ne postoji
Ne postoji
Ne postoji
Dakle, možemo napraviti sljedeću tablicu:

Nema potrebe pamtiti sve te vrijednosti. Dovoljno je zapamtiti korespondenciju između koordinata točaka na jediničnom krugu i vrijednosti trigonometrijskih funkcija:
Ali vrijednosti trigonometrijskih funkcija kutova u i, dane u donjoj tablici, mora se zapamtiti:

Ne bojte se, sada ćemo pokazati jedan od primjera dovoljno memoriranje odgovarajuće vrijednosti:
Da biste koristili ovu metodu, važno je zapamtiti vrijednosti sinusa za sve tri mjere kuta (), kao i vrijednost tangensa kuta u. Poznavajući ove vrijednosti, vrlo je lako vratiti cijelu tablicu - vrijednosti kosinusa se prenose u skladu sa strelicama, to jest:
Znajući to, možete vratiti vrijednosti za. Brojnik " " će odgovarati i nazivnik " " će se podudarati. Vrijednosti kotangensa prenose se u skladu sa strelicama prikazanim na slici. Ako ovo razumijete i zapamtite dijagram sa strelicama, tada će biti dovoljno zapamtiti cijelu vrijednost iz tablice.
Koordinate točke na kružnici
Je li moguće pronaći točku (njene koordinate) na kružnici, poznavanje koordinata središta kruga, njegovog polumjera i kuta zakreta?
Pa naravno da možete! Iznesimo opća formula pronaći koordinate točke.
Evo, na primjer, imamo takav krug:

Zadano nam je da je točka središte kruga. Polumjer kružnice je jednak. Potrebno je pronaći koordinate točke dobivene rotacijom točke za stupnjeve.
Kao što se može vidjeti sa slike, koordinata točke odgovara duljini segmenta. Duljina segmenta odgovara koordinati središta kruga, odnosno jednaka je. Duljina segmenta može se izraziti pomoću definicije kosinusa:
Onda to imamo za koordinatu točke.
Po istoj logici nalazimo vrijednost y koordinate za točku. Tako,
Dakle u opći pogled koordinate točke određuju se formulama:
Koordinate centra kruga,
radijus kruga,
Kut rotacije radijus vektora.
Kao što vidite, za jedinični krug koji razmatramo, ove formule su značajno smanjene, budući da su koordinate središta nula, a radijus je jednak jedan:
Pa, probajmo ove formule za okus, vježbajući pronalaženje točaka na kružnici?
1. Odredite koordinate točke na jediničnoj kružnici dobivenoj okretanjem točke.
2. Odredite koordinate točke na jediničnoj kružnici dobivenoj rotacijom točke na.
3. Odredite koordinate točke na jediničnoj kružnici dobivenoj okretanjem točke.
4. Točka - središte kruga. Polumjer kružnice je jednak. Potrebno je pronaći koordinate točke dobivene rotacijom početnog radijus vektora za.
5. Točka - središte kruga. Polumjer kružnice je jednak. Potrebno je pronaći koordinate točke dobivene rotacijom početnog radijus vektora za.
Imate problema s pronalaženjem koordinata točke na kružnici?
Riješite ovih pet primjera (ili dobro razumite rješenje) i naučit ćete kako ih pronaći!
1.
Vidi se da. A znamo što odgovara punom okretu početne točke. Tako, željenu točku bit će u istom položaju kao i pri uključivanju. Znajući to, nalazimo željene koordinate točke:
2. Krug je jedinica sa središtem u točki, što znači da možemo koristiti pojednostavljene formule:
Vidi se da. Znamo što odgovara dvjema potpunim rotacijama početne točke. Tako će željena točka biti u istom položaju kao kod okretanja. Znajući to, nalazimo željene koordinate točke:
Sinus i kosinus su tablične vrijednosti. Pamtimo njihove vrijednosti i dobivamo:
Dakle, željena točka ima koordinate.
3. Krug je jedinica sa središtem u točki, što znači da možemo koristiti pojednostavljene formule:
Vidi se da. Oslikajmo razmatrani primjer na slici:

Polumjer čini kutove s osi jednake i. Znajući da su tablične vrijednosti kosinusa i sinusa jednake i nakon što smo utvrdili da kosinus ovdje uzima negativno značenje, a sinus je pozitivan, imamo:
Više slični primjeri razumjeti pri proučavanju formula za redukciju trigonometrijskih funkcija u temi.
Dakle, željena točka ima koordinate.
4.
Kut rotacije radijus vektora (po uvjetu)
Da bismo odredili odgovarajuće predznake sinusa i kosinusa, konstruiramo jediničnu kružnicu i kut:

Kao što vidite, vrijednost tj. je pozitivna, a vrijednost tj. negativna. Poznavajući tablične vrijednosti odgovarajućih trigonometrijskih funkcija, dobivamo da je:
Zamijenimo dobivene vrijednosti u našu formulu i pronađimo koordinate:
Dakle, željena točka ima koordinate.
5. Za rješavanje ovog problema koristimo formule u općem obliku, gdje
Koordinate središta kruga (u našem primjeru,
Polumjer kruga (prema uvjetu)
Kut rotacije radijus vektora (po uvjetu).
Zamijenite sve vrijednosti u formulu i dobijte:
i - tablične vrijednosti. Sjećamo se i zamijenimo ih u formulu:
Dakle, željena točka ima koordinate.
SAŽETAK I OSNOVNA FORMULA
Sinus kuta je omjer suprotnog (daljeg) kraka i hipotenuze.
Kosinus kuta je omjer susjedne (bliske) noge i hipotenuze.
Tangens kuta je omjer suprotnog (daljeg) kraka prema susjednom (bliskom).
Kotangens kuta je omjer susjednog (bliskog) kraka prema suprotnom (dalekom).
Primjeri:
\(\cos(30^°)=\)\(\frac(\sqrt(3))(2)\)
\(\cos\)\(\frac(π)(3)\) \(=\)\(\frac(1)(2)\)
\(\cos2=-0,416…\)
Argument i vrijednost
Kosinus oštrog kuta
Kosinus oštrog kuta može se odrediti pomoću pravokutnog trokuta - jednak je omjeru susjedne katete i hipotenuze.
Primjer :
1) Neka je zadan kut i trebate odrediti kosinus tog kuta.

2) Dovršimo bilo koji pravokutni trokut na ovom kutu.

3) Nakon što smo izmjerili potrebne stranice, možemo izračunati kosinus.

Kosinus broja
Brojevni krug vam omogućuje da odredite kosinus bilo kojeg broja, ali obično pronađite kosinus brojeva koji je nekako povezan s: \(\frac(π)(2)\) , \(\frac(3π)(4)\) , \(-2π\ ).
Na primjer, za broj \(\frac(π)(6)\) - kosinus će biti jednak \(\frac(\sqrt(3))(2)\) . A za broj \(-\)\(\frac(3π)(4)\) to će biti jednako \(-\)\(\frac(\sqrt(2))(2)\) (približno \ (-0 ,71\)).

Kosinus za druge brojeve koji se često susreću u praksi, vidi.
Vrijednost kosinusa uvijek se nalazi između \(-1\) i \(1\). U ovom slučaju, kosinus se može izračunati za apsolutno bilo koji kut i broj.
Kosinus bilo kojeg kuta
Zahvaljujući brojčani krug kosinus se može odrediti ne samo oštar kut, ali i tup, negativan, pa čak i veći od \(360°\) (puni okret). Kako to učiniti - lakše je vidjeti jednom nego čuti \(100\) puta, pa pogledajte sliku.

Sada objašnjenje: neka je potrebno odrediti kosinus kuta KOA S stupanjska mjera u \(150°\). Kombiniramo točku OKO sa središtem kruga i bočnom stranom u redu- s osi \(x\). Nakon toga odložite \ (150 ° \) u smjeru suprotnom od kazaljke na satu. Zatim ordinata točke Aće nam pokazati kosinus ovog kuta.
Ako nas zanima kut s mjerom stupnjeva, na primjer, u \ (-60 ° \) (kut KOV), radimo isto, ali \(60°\) odmaknuto u smjeru kazaljke na satu.

I konačno, kut je veći od \(360°\) (kut KOS) - sve je slično tupom, samo nakon punog okretanja u smjeru kazaljke na satu, idemo u drugi krug i "dobijamo nedostatak stupnjeva". Konkretno, u našem slučaju, kut \(405°\) je iscrtan kao \(360° + 45°\).

Lako je pogoditi da za odvajanje kuta, na primjer, u \ (960 ° \), morate napraviti dva zavoja (\ (360 ° + 360 ° + 240 ° \)), a za kut u \ (2640 ° \) - cijelih sedam.
Kao što možete zamijeniti, i kosinus broja i kosinus proizvoljnog kuta definirani su na gotovo isti način. Mijenja se samo način nalaženja točke na kružnici.
Predznaci kosinusa u četvrtinama
Pomoću kosinusne osi (odnosno apscisne osi, označene crvenom bojom na slici), lako je odrediti predznake kosinusa duž numeričke (trigonometrijske) kružnice:
Gdje su vrijednosti na osi od \(0\) do \(1\), kosinus će imati znak plus (I i IV četvrtine su zelena površina),
- gdje su vrijednosti na osi od \(0\) do \(-1\), kosinus će imati znak minus (II i III četvrtine - ljubičasto područje).

Veza s drugim trigonometrijskim funkcijama:
- isti kut (ili broj): osn trigonometrijski identitet\(\sin^2x+\cos^2x=1\)- isti kut (ili broj): po formuli \(1+tg^2x=\)\(\frac(1)(\cos^2x)\)
- i sinus istog kuta (ili broja): \(ctgx=\)\(\frac(\cos(x))(\sinx)\)
Pogledajte ostale najčešće korištene formule.
Rješenje jednadžbe \(\cosx=a\)
Rješenje jednadžbe \(\cosx=a\), gdje je \(a\) broj koji nije veći od \(1\) i nije manji od \(-1\), tj. \(a∈[-1;1]\):
\(\cos x=a\) \(⇔\) \(x=±\arccosa+2πk, k∈Z\)

Ako \(a>1\) ili \(a<-1\), то решений у уравнения нет.
Primjer . Riješite trigonometrijsku jednadžbu \(\cosx=\)\(\frac(1)(2)\).Riješenje:
Riješi jednadžbu pomoću brojčane kružnice. Za ovo:
1) Napravimo sjekire.
2) Izgradimo krug.
3) Na kosinusnoj osi (osi \(y\)) označite točku \(\frac(1)(2)\) .
4) Kroz ovu točku povucite okomicu na kosinusnu os.
5) Označite sjecišta okomice i kružnice.
6) Potpišimo vrijednosti ovih točaka: \(\frac(π)(3)\) ,\(-\)\(\frac(π)(3)\) .
7) Zapišite sve vrijednosti koje odgovaraju tim točkama pomoću formule \(x=t+2πk\), \(k∈Z\):
\(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\);

Odgovor: \(x=±\frac(π)(3)+2πk\) \(k∈Z\)
Funkcija \(y=\cos(x)\)
Ako iscrtamo kutove u radijanima duž osi \(x\), a vrijednosti kosinusa koje odgovaraju tim kutovima duž osi \(y\), dobit ćemo sljedeći grafikon:

Ovaj graf se zove i ima sljedeća svojstva:
Domena definicije je bilo koja vrijednost x: \(D(\cos(x))=R\)
- raspon vrijednosti - od \(-1\) do \(1\) uključujući: \(E(\cos(x))=[-1;1]\)
- parno: \(\cos(-x)=\cos(x)\)
- periodički s periodom \(2π\): \(\cos(x+2π)=\cos(x)\)
- točke presjeka s koordinatnim osima:
apscisa: \((\)\(\frac(π)(2)\) \(+πn\),\(;0)\), gdje \(n ϵ Z\)
y-os: \((0;1)\)
- intervali znakova:
funkcija je pozitivna na intervalima: \((-\)\(\frac(π)(2)\) \(+2πn;\) \(\frac(π)(2)\) \(+2πn) \), gdje \(n ϵ Z\)
funkcija je negativna na intervalima: \((\)\(\frac(π)(2)\) \(+2πn;\)\(\frac(3π)(2)\) \(+2πn)\ ), gdje \(n ϵ Z\)
- intervali povećanja i smanjenja:
funkcija raste na intervalima: \((π+2πn;2π+2πn)\), gdje je \(n ϵ Z\)
funkcija opada na intervalima: \((2πn;π+2πn)\), gdje je \(n ϵ Z\)
- maksimumi i minimumi funkcije:
funkcija ima najveću vrijednost \(y=1\) u točkama \(x=2πn\), gdje \(n ϵ Z\)
funkcija ima minimalnu vrijednost \(y=-1\) u točkama \(x=π+2πn\), gdje je \(n ϵ Z\).
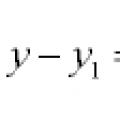 Jednadžbe pravaca i krivulja u ravnini
Jednadžbe pravaca i krivulja u ravnini Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda
Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda Zahvaljujući zarezu Zbog činjenice da u njihovim
Zahvaljujući zarezu Zbog činjenice da u njihovim