Як складаються та віднімаються вектори. Властивості множення вектора на число

Для правильного відображення законів природи у фізиці потрібен відповідний математичний інструментарій.

У геометрії та фізиці є величини, що характеризуються і числовим значенням, та напрямком.

Їх доцільно зображати спрямованими відрізками або векторами.

Такі величини мають початок (відображається точкою) і кінець, що позначається стрілкою. Довжина відрізка називається (довжиною).

швидкість;
прискорення;
імпульс;
сила;
момент;
сили;
переміщення;
напруженість поля та ін.

Координати на площині

Задамо на площині відрізок, спрямований з точки А (x1, y1) в точку В (x2, y2). Його координатами a(a1, a2) є числа а1=x2-x1, а2=y2-y1.

Модуль розраховується за теоремою Піфагора:

У нульового вектора початок збігається з кінцем. Координати та довжина дорівнюють 0.

Сума векторів

Існують кілька правил для розрахунку суми

правило трикутника;
правило багатокутника;
правило паралелограма.

Правило складання векторів можна пояснити задачах з динаміки і механіки. Розглянемо складання векторів за правилом трикутника на прикладі сил, що впливають на точкове тіло та послідовних переміщень тіла у просторі.

Припустимо, тіло перемістилося спочатку з точки A до точки B, а потім з точки B в точку C. Підсумкове переміщення є відрізок, спрямований від початкової точки A до кінцевої точки C.

Результат двох переміщень або їхня сума s = s1+ s2. Такий спосіб називається правилом трикутника.

Стрілки вибудовують у ланцюжок одну за одною, при необхідності здійснюючи паралельне перенесення. Сумарний відрізок замикає послідовність. Його початок збігається з початком першого, кінець – з кінцем останнього. В іноземних підручниках даний методназивається «хвіст до голови».

Координати результату c = a + b дорівнюють сумі відповідних координат доданків c (a1+ b1, a2+ b2).

Сума паралельних (колінеарних) векторів також визначається за правилом трикутника.

Якщо два вихідні відрізки перпендикулярні один одному, то результат їхнього складання являє собою гіпотенузу побудованого на них прямокутного трикутника. Довжина суми обчислюється за теоремою Піфагора.

Приклади:

Швидкість тіла, кинутого горизонтально, перпендикулярнаприскорення вільного падіння.
При рівномірному обертальний рух лінійна швидкістьтіла перпендикулярна доцентрового прискорення.

Додавання трьох і більше векторіввиробляють по правилу багатокутника, «хвіст до голови»

Припустимо, що до точкового тіла прикладені сили F1 та F2.

Досвід доводить, що сукупний вплив цих сил рівнозначний дії однієї сили, спрямованої по діагоналі побудованого на них паралелограма. Ця рівнодіюча сила дорівнює їх сумі F = F1 + F 2. Наведений спосіб додавання називається правилом паралелограма.

Довжина в цьому випадку обчислюється за формулою

Де θ – кут між сторонами.

Правила трикутника та паралелограма взаємозамінні. У фізиці частіше застосовують правило паралелограма, тому що спрямовані величини сил, швидкостей, прискорень зазвичай прикладені до одного точкового тіла. У тривимірній системі координат застосовується правило паралелепіпеда.

Елементи алгебри

Додавання є двійковою операцією: за один раз можна скласти лише пару.
Комутативність: сума від перестановки доданків не змінюється a + b = b + a. Це ясно з правила паралелограма: діагональ завжди одна й та сама.
Асоціативність: сума довільного числа векторів залежить від порядку їх складання (a + b)+ c = a +(b + c).
Підсумовування з нульовим вектором не змінює напрям, ні довжину: a +0= a .
Для кожного вектора є протилежний. Їхня сума дорівнює нулю a +(-a)=0, а довжини збігаються.

Віднімання спрямованого відрізка рівносильне доданню протилежного. Координати рівні різниці відповідних координат. Довжина дорівнює:

Для віднімання можна використовувати видозмінене правило трикутника.

Розмноження на скаляр

Результатом множення на скаляр буде вектор.

Координати твору виходять перемноженням на скаляр відповідних координат вихідного.

Скаляр - числова величиназі знаком плюс чи мінус, більше чи менше одиниці.

Приклади скалярних величину фізиці:

маса;
час;
заряд;
довжина;
площа;
Об `єм;
густина;
температура;
Енергія.

Приклади:

Переміщення тіла, що рівномірно рухається, дорівнює добутку часу і швидкості s = vt .
Імпульс тіла - маса, помножена на швидкість p = mv.
Другий закон Ньютона. Добуток маси тіла на прискорення дорівнює прикладеноїрівнодіючою силою ma=F.
Сила, що діє на заряджену частинку в електричному полі, пропорційна заряду F = qE.

Скалярний добуток спрямованих відрізків a і b дорівнює добутку модулів на косинус кута між ними. Скалярний добуток взаємно перпендикулярних відрізків дорівнює нулю.

приклад:

Робота є скалярним творомсили та переміщення A = Fs.

X та yназивається вектор zтакий, що z+y=x.

Варіант 1.Початкові точки всіх векторів збігаються з початком координат.

Побудуємо різницю векторів і .

Для побудови різниці векторів z=x-yпотрібно скласти вектор xз протилежним до yвектором y". Протилежний вектор y"будується просто:

Вектор y"є протилежним до вектору y, так як y+y"= 0 де 0 - нульовий вектор відповідного розміру. Далі виконується складання векторів xі y":

З виразу (1) видно що для побудови різниці векторів достатньо обчислити різниці відповідних координат векторів xі y.

Рис. 1

Рис. 1 у двовимірному просторі представлений різниця векторів x=(10,3) та y=(2,4).

Обчислимо z=x-y= (10-3,3-4) = (7,-1). Порівняємо отриманий результат із геометричною інтерпретацією. Справді, після побудови вектора y"та паралельного переміщення початкової точки вектора y"на кінцеву точку вектора x, отримаємо вектор y"", а після складання векторів xі y"", отримаємо вектор z.

Варіант 2.Початкові точки векторів довільні.

Рис. 2

Рис. 2 у двовимірному просторі представлений різниця векторів x=ABі y=CD, де A(1,0), B(11,3), C(1,2), D(3,6). Для обчислення вектора z=x-y, побудований протилежний до вектору yвектор y":

Далі потрібно скласти вектори xі y". Вектор y"переміщається паралельно так, щоб точка C"збіглася з точкою B. Для цього обчислюються різниці координат точок Bі З.

ов, спочатку необхідно розібратися у такому понятті, як відкладання вектора від цієї точки.

Визначення 1

Якщо точка $A$ почала якогось вектора $\overrightarrow(a)$, то кажуть, що вектор $\overrightarrow(a)$ відкладено від точки $A$ (рис. 1).

Малюнок 1. $\overrightarrow(a)$ відкладений від точки $A$

Введемо таку теорему:

Теорема 1

Від будь-якої точки $K$ можна відкласти вектор $\overrightarrow(a)$ і лише один.

Доведення.

Існування:Тут потрібно розглянути два випадки:

Вектор $\overrightarrow(a)$ - нульовий.

В цьому випадку, очевидно, що вектор, що шукається - вектор $ \ overrightarrow (KK) $.

Вектор $\overrightarrow(a)$ - ненульовий.

Позначимо точкою $A$ - початок вектора $\overrightarrow(a)$, а точкою $B$ - кінець вектора $\overrightarrow(a)$. Проведемо через точку $K$ пряму $b$ паралельну вектору$\overrightarrow(a)$. Відкладемо на цій прямій відрізки $\left|KLright|=|AB|$ і $\left|KMright|=|AB|$. Розглянемо вектори $\overrightarrow(KL)$ і $\overrightarrow(KM)$. З цих двох векторів шуканим буде той, який буде направлений із вектором $\overrightarrow(a)$ (рис. 2)

Рисунок 2. Ілюстрація теореми 1

Єдиність:єдиність відразу випливає з побудови, проведеної у пункті «існування».

Теорему доведено.

Віднімання векторів. Правило перше

Нехай нам дано вектори $\overrightarrow(a)$ і $\overrightarrow(b)$.

Визначення 2

Різницею двох векторів $\overrightarrow(a)$ і $\overrightarrow(b)$ називається такий вектор $\overrightarrow(c)$, який при складанні з вектором $\overrightarrow(b)$ дає вектор $\overrightarrow(a)$ , тобто

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Позначення:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Побудову різниці двох векторів розглянемо за допомогою завдання.

Приклад 1

Нехай дані вектори $\overrightarrow(a)$ і $\overrightarrow(b)$. Побудувати вектор $\overrightarrow(a)-\overrightarrow(b)$.

Рішення.

Побудуємо довільну точку $O$ і відкладемо від неї вектори $\overrightarrow(OA)=\overrightarrow(a)$ і $\overrightarrow(OB)=\overrightarrow(b)$. Поєднавши точку $B$ з точкою $A$, отримаємо вектор $overrightarrow(BA)$ (рис. 3).

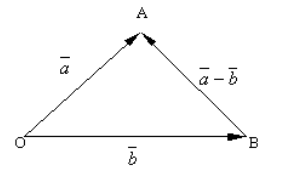
Рисунок 3. Різниця двох векторів

За правилом трикутника для побудови суми двох векторів бачимо, що

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

З визначення 2 отримуємо, що

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Відповідь:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

З цього завдання отримуємо таке правило для знаходження різниці двох векторів. Щоб знайти різницю $\overrightarrow(a)-\overrightarrow(b)$ потрібно від довільної точки$O$ відкласти вектори $\overrightarrow(OA)=\overrightarrow(a)$ і $\overrightarrow(OB)=\overrightarrow(b)$ і з'єднати кінець другого вектора з кінцем першого вектора.

Віднімання векторів. Правило друге

Згадаймо таке необхідне нам поняття.

Визначення 3

Вектор $\overrightarrow(a_1)$ називається довільним для вектора $\overrightarrow(a)$, якщо ці вектори протилежно спрямовані та мають рівну довжину.

Позначення:Вектор $(-\overrightarrow(a))$ протилежний для вектора $\overrightarrow(a)$.

Для того щоб ввести друге правило для різниці двох векторів, нам необхідно спочатку ввести і довести наступну теорему.

Теорема 2

Для будь-яких двох векторів $\overrightarrow(a)$ і $\overrightarrow(b)$ справедлива наступна рівність:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Доведення.

За визначенням 2, маємо

Додамо до обох частин вектор $\left(-\overrightarrow(b)\right)$, отримаємо

Оскільки вектори $\overrightarrow(b)$ і $\left(-\overrightarrow(b)\right)$ протилежні, то $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\overrightarrow (0) $. Маємо

Теорему доведено.

З цієї теореми отримуємо наступне правило для різниці двох векторів: Щоб знайти різницю $\overrightarrow(a)-\overrightarrow(b)$ потрібно від довільної точки $O$ відкласти вектор $\overrightarrow(OA)=\overrightarrow(a)$, потім від отриманої точки $A$ відкласти вектор $\overrightarrow(AB)=-\overrightarrow(b)$ і з'єднати початок першого вектора з кінцем другого вектора.

Приклад завдання поняття різниці векторів

Приклад 2

Нехай дано паралелограм $ADCD$, діагоналі якого перетинаються у точці $O$. $ \ overrightarrow (AB) = \ overrightarrow (a) $, $ \ overrightarrow (AD) = \ overrightarrow (b) $ (рис. 4). Виразити через вектори $\overrightarrow(a)$ і $\overrightarrow(b)$ наступні вектори:

а) $\overrightarrow(DC)+\overrightarrow(CB)$

б) $\overrightarrow(BO)-\overrightarrow(OC)$

Малюнок 4. Паралелограм

Рішення.

а) Зробимо додавання за правилом трикутника, отримаємо

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

З першого правила різниці двох векторів, отримуємо

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

б) Так як $ \ overrightarrow (OC) = \ overrightarrow (AO) $, отримаємо

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

По теоремі 2, маємо

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Використовуючи правило трикутника, маємо остаточно

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

ов, спочатку необхідно розібратися у такому понятті, як відкладання вектора від цієї точки.

Визначення 1

Малюнок 1. $\overrightarrow(a)$ відкладений від точки $A$

Введемо таку теорему:

Теорема 1

Від будь-якої точки $K$ можна відкласти вектор $\overrightarrow(a)$ і лише один.

Доведення.

Існування:Тут потрібно розглянути два випадки:

Вектор $\overrightarrow(a)$ - нульовий.

В цьому випадку, очевидно, що вектор, що шукається - вектор $ \ overrightarrow (KK) $.

Вектор $\overrightarrow(a)$ - ненульовий.

Позначимо точкою $A$ - початок вектора $\overrightarrow(a)$, а точкою $B$ - кінець вектора $\overrightarrow(a)$. Проведемо через точку $K$ пряму $b$ паралельну вектору $\overrightarrow(a)$. Відкладемо на цій прямій відрізки $\left|KLright|=|AB|$ і $\left|KMright|=|AB|$. Розглянемо вектори $\overrightarrow(KL)$ і $\overrightarrow(KM)$. З цих двох векторів шуканим буде той, який буде направлений із вектором $\overrightarrow(a)$ (рис. 2)

Рисунок 2. Ілюстрація теореми 1

Єдиність:єдиність відразу випливає з побудови, проведеної у пункті «існування».

Теорему доведено.

Віднімання векторів. Правило перше

Нехай нам дано вектори $\overrightarrow(a)$ і $\overrightarrow(b)$.

Визначення 2

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Позначення:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Побудову різниці двох векторів розглянемо за допомогою завдання.

Приклад 1

Нехай дані вектори $\overrightarrow(a)$ і $\overrightarrow(b)$. Побудувати вектор $\overrightarrow(a)-\overrightarrow(b)$.

Рішення.

Рисунок 3. Різниця двох векторів

За правилом трикутника для побудови суми двох векторів бачимо, що

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

З визначення 2 отримуємо, що

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Відповідь:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

З цього завдання отримуємо таке правило для знаходження різниці двох векторів. Щоб знайти різницю $\overrightarrow(a)-\overrightarrow(b)$ потрібно від довільної точки $O$ відкласти вектори $\overrightarrow(OA)=\overrightarrow(a)$ і $\overrightarrow(OB)=\overrightarrow(b )$ і з'єднати кінець другого вектора з кінцем першого вектора.

Віднімання векторів. Правило друге

Згадаймо таке необхідне нам поняття.

Визначення 3

Позначення:Вектор $(-\overrightarrow(a))$ протилежний для вектора $\overrightarrow(a)$.

Теорема 2

Для будь-яких двох векторів $\overrightarrow(a)$ і $\overrightarrow(b)$ справедлива наступна рівність:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Доведення.

За визначенням 2, маємо

Додамо до обох частин вектор $\left(-\overrightarrow(b)\right)$, отримаємо

Теорему доведено.

Приклад завдання поняття різниці векторів

Приклад 2

а) $\overrightarrow(DC)+\overrightarrow(CB)$

б) $\overrightarrow(BO)-\overrightarrow(OC)$

Малюнок 4. Паралелограм

Рішення.

а) Зробимо додавання за правилом трикутника, отримаємо

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

З першого правила різниці двох векторів, отримуємо

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

б) Так як $ \ overrightarrow (OC) = \ overrightarrow (AO) $, отримаємо

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

По теоремі 2, маємо

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Використовуючи правило трикутника, маємо остаточно

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

Як відбувається складання векторів, який завжди зрозуміло учням. Діти не уявляють того, що за ними ховається. Доводиться просто запам'ятовувати правила, а не вдумуватись у суть. Тому саме про принципи складання та віднімання векторних величин потрібно багато знань.

У результаті додавання двох і більше векторів завжди виходить ще один. Причому він завжди обов'язково буде однаковим незалежно від прийому його знаходження.

Найчастіше в шкільному курсігеометрії розглядається додавання двох векторів. Воно може бути виконане за правилом трикутника чи паралелограма. Ці малюнки виглядають по-різному, але результат від дії один.

Як відбувається додавання за правилом трикутника?

Воно застосовується тоді, коли вектори неколінеарні. Тобто не лежать на одній прямій чи паралельних.

У цьому випадку від певної довільної точки необхідно відкласти перший вектор. З його кінця потрібно провести паралельний та рівний другому. Результатом стане вектор, що виходить із початку першого і завершується наприкінці другого. Малюнок нагадує трикутник. Звідси й назва правила.

Якщо вектори колінеарні, це правило теж можна застосовувати. Лише малюнок буде розташований вздовж однієї лінії.

Як виконується додавання за правилом паралелограма?

Знову ж? застосовується тільки для не колінеарних векторів. Побудова виконується за іншим принципом. Хоча початок такий самий. Потрібно відкласти перший вектор. І від його початку – другий. На їх основі добудувати паралелограм та провести діагональ із початку обох векторів. Вона буде результатом. Так виконується складання векторів за правилом паралелограма.

Досі їх було дві. А як бути, якщо їх 3 чи 10? Використовувати наступний прийом.

Як і коли застосовується правило багатокутника?

Якщо потрібно виконати складання векторів, число яких більше двох, лякатися не варто. Достатньо послідовно відкласти їх усі і з'єднати початок ланцюжка з її кінцем. Цей вектор і буде шуканою сумою.

Які властивості дійсні для дій із векторами?

Про нульовий вектор.Яке стверджує, що при додаванні з ним виходить вихідний.

Про протилежний вектор.Тобто про таке, що має протилежний напрямок і рівне за модулем значення. Їх сума дорівнюватиме нулю.

Про комутативність складання.Те, що відомо ще з початкової школи. Зміна місць доданків не призводить до зміни результату. Іншими словами, будь-який вектор відкладати спочатку. Відповідь все одно буде вірною і єдиною.

Про асоціативність складання.Цей закон дозволяє складати попарно будь-які вектори із трійки та до них додавати третій. Якщо записати це за допомогою знаків, то вийде таке:

перший + (другий + третій) = другий + (перший + третій) = третій + (перший + другий).

Що відомо про різницю векторів?

Окремої операції віднімання немає. Це з тим, що його, власне, є додаванням. Тільки другому з них задається протилежний напрямок. А потім все виконується так, ніби розглядалося складання векторів. Тому про їх різницю практично не говорять.

Для того щоб спростити роботу з їх відніманням, видозмінено правило трикутника. Тепер (при відніманні) другий вектор потрібно відкласти з початку першого. Відповіддю буде те, що з'єднує кінцеву точку зменшуваного з нею ж віднімається. Хоча можна і відкладати так, як було описано раніше, просто змінивши напрямок другого.

Як знайти суму та різницю векторів у координатах?

У задачі дані координати векторів і потрібно дізнатися їх значення для підсумкового. При цьому побудов виконувати не потрібно. Тобто можна скористатися нескладними формулами, які описують правило додавання векторів. Вони виглядають так:

а (х, у, z) + (k, l, m) = з (х + k, y + l, z + m);

а (х, у, z) - (k, l, m) = з (х-k, y-l, z-m).

Легко помітити, що координати потрібно просто скласти чи відняти залежно від конкретного завдання.

Перший приклад із рішенням

Умови. Дано прямокутник АВСД. Його сторони дорівнюють 6 і 8 см. Точка перетину діагоналей позначена буквою О. Потрібно обчислити різницю векторів АТ і ВО.

Рішення. Спочатку слід зобразити ці вектори. Вони спрямовані від вершин прямокутника до точки перетину діагоналей.

Якщо уважно подивитися на креслення, то можна побачити, що вектори вже поєднані так, щоб другий з них стикався з кінцем першого. Ось тільки його напрямок неправильний. Він має з цієї точки починатися. Це якщо вектори складаються, а задачі — віднімання. Стоп. Ця дія означає, що потрібно додати протилежний вектор. Значить, ВО потрібно замінити на ВВ. І вийде, що два вектори вже утворили пару сторін із правила трикутника. Тому результат від їхнього складання, тобто різниця, що шукається, — вектор АВ.

А він збігається із стороною прямокутника. Для того щоб записати числову відповідь, знадобиться таке. Накреслити прямокутник вздовж так, щоб більша сторона йшла горизонтально. Нумерацію вершин починати з лівої нижньої та йти проти годинникової стрілки. Тоді довжина вектора АВ дорівнюватиме 8 см.

Відповідь. Різниця АТ і ВО дорівнює 8 см.

Другий приклад та його докладне рішення

Умови. У ромба АВСД діагоналі дорівнюють 12 і 16 см. Точка їх перетину позначена літерою О. Обчисліть довжину вектора, утвореного різницею векторів АТ і ВО.

Рішення. Нехай позначення вершин ромба буде таким самим, як у попередній задачі. Аналогічно рішенню першого прикладу виходить, що різниця, що шукається, дорівнює вектору АВ. А його довжина невідома. Розв'язання задачі звелося до того, щоб обчислити одну із сторін ромба.

Для цього потрібно розглянути трикутник АВО. Він прямокутний, тому що діагоналі ромба перетинаються під кутом 90 градусів. А його катети дорівнюють половинам діагоналей. Тобто 6 і 8 см. сторона, що шукається в задачі, збігається з гіпотенузою в цьому трикутнику.

Для її знаходження потрібно теорема Піфагора. Квадрат гіпотенузи буде дорівнює сумічисел 6 2 та 8 2 . Після зведення у квадрат вийдуть значення: 36 і 64. Їх сума — 100. Звідси випливає, що гіпотенуза дорівнює 10 див.

Відповідь. Різниця векторів АТ і ВО становить 10 см.

Третій приклад із детальним рішенням

Умови. Обчислити різницю та суму двох векторів. Відомі їх координати: у першого - 1 і 2, у другого - 4 і 8.

Рішення. Для знаходження суми потрібно скласти попарно перші та другі координати. Результатом будуть числа 5 та 10. Відповіддю буде вектор з координатами (5; 10).

Для різниці потрібно виконати віднімання координат. Після виконання цієї дії вийдуть числа -3 та -6. Вони будуть координатами шуканого вектора.

Відповідь. Сума векторів - (5; 10), їх різниця - (-3; -6).

Четвертий приклад

Умови. Довжина вектора АВ дорівнює 6 см, НД - 8 см. Другий відкладений від кінця першого під кутом в 90 градусів. Обчислити: а) різницю модулів векторів ВА і ПС і модуль різниці ВА та ПС; б) суму цих модулів і модуль суми.

Рішення: а) Довжини векторів вже дано завдання. Тому обчислити їх різницю не складе труднощів. 6 – 8 = -2. Дещо складніше ситуація з модулем різниці. Спочатку потрібно дізнатися, який вектор буде результатом віднімання. Для цієї мети слід відкласти вектор ВА, який спрямований у протилежний бікАВ. Потім від кінця провести вектор ВС, направивши його у бік, протилежну вихідному. Результатом віднімання вийде вектор СА. Його модуль можна визначити по теоремі Піфагора. Прості обчислення призводять до значення 10 см.

б) Сума модулів векторів виходить дорівнює 14 см. Для пошуку другої відповіді знадобиться деяке перетворення. Вектор ВА протилежно спрямований до того, що дано — АВ. Обидва вектори спрямовані з однієї точки. У цій ситуації можна використовувати правило паралелограма. Результатом додавання буде діагональ, причому не просто паралелограма, а прямокутника. Його діагоналі рівні, отже, модуль суми такий самий, як у попередньому пункті.

Відповідь: а) -2 та 10 см; б) 14 та 10 см.