Cực trị của một hàm - nói một cách đơn giản về phức. Cách tìm điểm cực trị của hàm số

Điểm cực trị của hàm là điểm trong miền của hàm mà giá trị của hàm nhận giá trị nhỏ nhất hoặc lớn nhất. Các giá trị của hàm tại các điểm này được gọi là cực trị (cực tiểu và cực đại) của hàm.

Sự định nghĩa. Chấm x1 phạm vi chức năng f(x) được gọi là điểm tối đa của chức năng , nếu giá trị của hàm tại thời điểm này lớn hơn giá trị của hàm tại các điểm đủ gần với nó, nằm ở bên phải và bên trái của nó (nghĩa là, bất đẳng thức f(x0 ) > f(x 0 + Δ x) x1 tối đa.

Sự định nghĩa. Chấm x2 phạm vi chức năng f(x) được gọi là điểm tối thiểu của hàm, nếu giá trị của hàm tại điểm này nhỏ hơn giá trị của hàm tại các điểm đủ gần với nó, nằm ở bên phải và bên trái của nó (nghĩa là bất đẳng thức f(x0 ) < f(x 0 + Δ x) ). Trong trường hợp này, hàm được cho là có x2 tối thiểu.

Hãy nói điểm x1 - điểm tối đa của chức năng f(x). Sau đó, trong khoảng thời gian lên đến x1 chức năng tăng lên, do đó, đạo hàm của hàm lớn hơn 0 ( f "(x)> 0), và trong khoảng thời gian sau x1 chức năng đang giảm, vì vậy đạo hàm hàm nhỏ hơn 0 ( f "(x) < 0 ). Тогда в точке x1

Chúng tôi cũng giả định rằng điểm x2 - điểm tối thiểu của hàm f(x). Sau đó, trong khoảng thời gian lên đến x2 hàm giảm và đạo hàm của hàm nhỏ hơn 0 ( f "(x) < 0 ), а в интервале после x2 hàm tăng và đạo hàm của hàm lớn hơn 0 ( f "(x)> 0). Trong trường hợp này cũng tại điểm x2 đạo hàm của hàm bằng 0 hoặc không tồn tại.

Định lý Fermat (một tiêu chí cần thiết cho sự tồn tại của cực trị của một hàm). Nếu điểm x0 - điểm cực trị của hàm f(x), thì tại thời điểm này đạo hàm của hàm bằng 0 ( f "(x) = 0) hoặc không tồn tại.

Sự định nghĩa. Các điểm mà tại đó đạo hàm của một hàm số bằng 0 hoặc không tồn tại được gọi là điểm quan trọng .

ví dụ 1 Hãy xem xét một chức năng.

Tại điểm x= 0 đạo hàm của hàm số bằng 0, do đó, điểm x= 0 là điểm tới hạn. Tuy nhiên, như có thể thấy trên đồ thị của hàm, nó tăng trong toàn bộ miền xác định, vì vậy điểm x= 0 không phải là điểm cực trị của hàm này.

Do đó, các điều kiện để đạo hàm của một hàm tại một điểm bằng 0 hoặc không tồn tại là các điều kiện cần để có cực trị, nhưng không đủ, vì có thể đưa ra các ví dụ khác về hàm mà các điều kiện này được thỏa mãn, nhưng hàm không có cực trị tại điểm tương ứng. Đó là lý do tại sao phải có đầy đủ các chỉ dẫn, giúp bạn có thể đánh giá liệu có điểm cực trị tại một điểm tới hạn cụ thể hay không và điểm nào - cực đại hay cực tiểu.

Định lý (tiêu chí đủ đầu tiên cho sự tồn tại của cực trị của một hàm).Điểm quan trọng x0 f(x), nếu đạo hàm của hàm thay đổi dấu khi đi qua điểm này và nếu dấu chuyển từ "cộng" thành "trừ", thì điểm lớn nhất, và nếu từ "trừ" thành "cộng", thì điểm nhỏ nhất .

Nếu gần điểm x0 , ở bên trái và bên phải của nó, đạo hàm giữ nguyên dấu của nó, điều này có nghĩa là hàm hoặc chỉ giảm hoặc chỉ tăng trong một số vùng lân cận của điểm x0 . Trong trường hợp này, tại điểm x0 không có cực đoan.

Vì thế, để xác định điểm cực trị của hàm số, bạn cần thực hiện như sau :

Tìm đạo hàm của một hàm số.
Lập phương trình đạo hàm bằng 0 và xác định các điểm tới hạn.
Nhẩm hoặc trên giấy, đánh dấu các điểm tới hạn trên trục số và xác định dấu của đạo hàm của hàm số trong các khoảng kết quả. Nếu dấu của đạo hàm chuyển từ "cộng" thành "trừ", thì điểm tới hạn là điểm tối đa, và nếu từ "trừ" thành "cộng", thì điểm tới hạn là điểm cực tiểu.
Tính giá trị của hàm số tại các điểm cực trị.

Ví dụ 2 Tìm cực trị của một hàm .

Dung dịch. Hãy tìm đạo hàm của hàm số:

Lập phương trình đạo hàm bằng 0 để tìm các điểm tới hạn:

Vì đối với bất kỳ giá trị nào \ u200b \ u200bof "x", mẫu số không bằng 0, khi đó chúng ta cân bằng tử số bằng 0:

Có một điểm quan trọng x= 3. Chúng tôi xác định dấu của đạo hàm trong các khoảng được giới hạn bởi điểm này:

trong phạm vi từ trừ vô cùng đến 3 - dấu trừ, nghĩa là, hàm giảm,

trong phạm vi từ 3 đến cộng vô cùng - một dấu cộng, nghĩa là, hàm tăng.

Đó là, điểm x= 3 là điểm cực tiểu.

Tìm giá trị của hàm số tại điểm cực tiểu:

Như vậy, tìm được điểm cực trị của hàm số là: (3; 0) và nó là điểm cực tiểu.

Định lý (tiêu chí đủ thứ hai cho sự tồn tại của điểm cực trị của một hàm số).Điểm quan trọng x0 là điểm cực trị của hàm f(x), nếu đạo hàm cấp hai của hàm tại điểm này không bằng 0 ( f ""(x) ≠ 0), hơn nữa, nếu đạo hàm cấp hai lớn hơn 0 ( f ""(x)> 0), thì điểm cực đại và nếu đạo hàm cấp hai nhỏ hơn 0 ( f ""(x) < 0 ), то точкой минимума.

Nhận xét 1. Nếu tại một điểm x0 cả đạo hàm thứ nhất và thứ hai đều biến mất, khi đó tại thời điểm này không thể đánh giá sự có mặt của một điểm cực trị trên cơ sở dấu hiệu đủ thứ hai. Trong trường hợp này, bạn cần sử dụng tiêu chí đủ đầu tiên cho điểm cực trị của hàm.

Nhận xét 2. Tiêu chí đủ thứ hai cho cực trị của một hàm số cũng không áp dụng được khi đạo hàm thứ nhất không tồn tại tại điểm đứng yên (khi đó đạo hàm cấp hai cũng không tồn tại). Trong trường hợp này, cũng cần sử dụng tiêu chuẩn đầu tiên đủ cho điểm cực trị của hàm.

Bản chất cục bộ của cực trị của hàm

Từ các định nghĩa trên, ta thấy rằng cực trị của một hàm có tính chất cục bộ - đây là giá trị lớn nhất và nhỏ nhất của hàm so với các giá trị gần nhất.

Giả sử bạn xem xét thu nhập của mình trong khoảng thời gian một năm. Nếu vào tháng 5, bạn kiếm được 45.000 rúp và vào tháng 4 là 42.000 rúp và vào tháng 6 là 39.000 rúp, thì thu nhập của tháng 5 là mức tối đa của hàm thu nhập so với các giá trị gần nhất. Nhưng vào tháng 10, bạn đã kiếm được 71.000 rúp, vào tháng 9 là 75.000 rúp và vào tháng 11 là 74.000 rúp, vì vậy thu nhập của tháng 10 là mức tối thiểu của hàm thu nhập so với các giá trị lân cận. Và bạn có thể dễ dàng nhận thấy rằng giá trị lớn nhất trong số các giá trị của Tháng 4-Tháng 5-Tháng 6 nhỏ hơn giá trị tối thiểu của Tháng 9-Tháng 10-Tháng 11.

Nói chung, một hàm có thể có một số cực trị trên một khoảng và nó có thể hóa ra rằng bất kỳ điểm cực tiểu nào của hàm số này đều lớn hơn bất kỳ điểm cực đại nào. Vì vậy, đối với chức năng được hiển thị trong hình trên,.

Có nghĩa là, người ta không nên nghĩ rằng giá trị lớn nhất và nhỏ nhất của hàm tương ứng là giá trị lớn nhất và nhỏ nhất của nó trên toàn bộ đoạn đang xét. Tại điểm cực đại, hàm có giá trị lớn nhất chỉ so với các giá trị mà nó có tại tất cả các điểm đủ gần với điểm cực đại và tại điểm cực tiểu, hàm có giá trị nhỏ nhất chỉ so với các giá trị đó nó có ở tất cả các điểm đủ gần với điểm tối thiểu.

Do đó, chúng ta có thể tinh chỉnh khái niệm điểm cực trị của một hàm số đã cho ở trên và gọi các điểm cực tiểu là điểm cực tiểu địa phương, và điểm cực đại - điểm cực đại địa phương.

Chúng ta cùng nhau tìm kiếm cực trị của hàm

Ví dụ 3

Lời giải. Hàm số xác định và liên tục trên toàn bộ trục số. Dẫn xuất của nó cũng tồn tại trên toàn bộ dãy số. Do đó, trong trường hợp này, chỉ những điểm mà tại đó, tức là, đóng vai trò là điểm tới hạn. , từ khi nào và. Điểm tới hạn và chia toàn bộ miền của hàm số thành ba khoảng đơn điệu:. Chúng tôi chọn một điểm điều khiển trong mỗi điểm và tìm dấu của đạo hàm tại điểm này.

Đối với khoảng thời gian, điểm tham chiếu có thể là: chúng tôi tìm thấy. Lấy một điểm trong khoảng thời gian, chúng ta nhận được, và lấy một điểm trong khoảng thời gian, chúng ta có. Vì vậy, trong khoảng thời gian và, và trong khoảng thời gian. Theo dấu hiệu đủ đầu tiên của một điểm cực trị, không có điểm cực trị nào (vì đạo hàm giữ nguyên dấu của nó trong khoảng), và hàm số có cực tiểu tại điểm (vì đạo hàm đổi dấu từ trừ sang cộng khi đi qua thông qua điểm này). Tìm các giá trị tương ứng của hàm:, và. Trong khoảng thời gian, hàm giảm, kể từ trong khoảng thời gian này, và trong khoảng thời gian nó tăng lên, kể từ trong khoảng thời gian này.

Để làm rõ việc xây dựng đồ thị, chúng ta tìm các giao điểm của nó với các trục tọa độ. Khi chúng ta thu được một phương trình có nghiệm nguyên và nghĩa là hai điểm (0; 0) và (4; 0) của đồ thị hàm số được tìm thấy. Sử dụng tất cả thông tin nhận được, chúng tôi xây dựng một biểu đồ (xem ở phần đầu của ví dụ).

Ví dụ 4 Tìm cực trị của hàm số và dựng đồ thị của nó.

Miền của hàm là toàn bộ dòng số, ngoại trừ điểm, tức là .

Để rút ngắn nghiên cứu, chúng ta có thể sử dụng thực tế là hàm này là số chẵn, vì . Do đó, đồ thị của nó đối xứng qua trục Oy và nghiên cứu chỉ có thể được thực hiện trong khoảng thời gian.

Tìm đạo hàm và các điểm quan trọng của chức năng:

1) ;

2) ,

nhưng hàm bị phá vỡ tại điểm này, vì vậy nó không thể là một điểm cực trị.

Do đó, hàm đã cho có hai điểm tới hạn: và. Tính đến tính chẵn lẻ của hàm, chúng tôi chỉ kiểm tra điểm bằng dấu đủ thứ hai của điểm cực trị. Để làm điều này, chúng tôi tìm đạo hàm cấp hai và xác định dấu hiệu của nó tại: we get. Vì và, khi đó là điểm cực tiểu của hàm, trong khi .

Để có một bức tranh đầy đủ hơn về đồ thị của hàm số, chúng ta hãy tìm hiểu hành vi của nó trên các ranh giới của miền xác định:

(ở đây biểu tượng cho thấy mong muốn x về 0 ở bên phải, và x vẫn tích cực; tương tự có nghĩa là khát vọng x về 0 ở bên trái, và x vẫn âm). Vì vậy, nếu, sau đó. Tiếp theo, chúng tôi tìm thấy

những thứ kia. nếu, sau đó.

Đồ thị của hàm số không có giao điểm với các trục. Hình ảnh ở đầu ví dụ.

Chúng ta cùng nhau tiếp tục tìm kiếm các điểm cực trị của hàm

Ví dụ 8 Tìm cực trị của hàm số.

Dung dịch. Tìm miền của hàm. Vì bất bình đẳng phải giữ, chúng tôi nhận được từ.

Hãy tìm đạo hàm cấp một của hàm số:

Hãy tìm các điểm tới hạn của hàm.

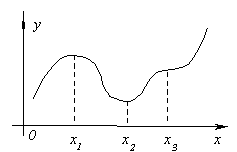
Xét đồ thị của một hàm số liên tục y = f (x)được hiển thị trong hình.

Giá trị hàm tại điểm x 1 sẽ lớn hơn các giá trị của hàm tại tất cả các điểm lân cận cả bên trái và bên phải của x một . Trong trường hợp này, hàm được cho là có x 1 tối đa Tại điểm x 3 chức năng rõ ràng cũng có một tối đa. Nếu chúng ta xem xét điểm x 2, thì giá trị của hàm trong nó nhỏ hơn tất cả các giá trị lân cận. Trong trường hợp này, hàm được cho là có x 2 tối thiểu. Tương tự cho điểm x 4 .

Hàm số y = f (x) tại điểm x 0 có tối đa, nếu giá trị của hàm tại thời điểm này lớn hơn giá trị của nó tại tất cả các điểm của khoảng nào đó chứa điểm x 0, tức là nếu có một vùng lân cận của điểm x 0, dành cho tất cả mọi người x≠x 0 , thuộc khu vực lân cận này, chúng tôi có sự bất bình đẳng f (x)<f (x 0 ) .

Hàm số y = f (x) Nó có tối thiểu tại điểm x 0 , nếu có một vùng lân cận của điểm x 0 , cái gì dành cho mọi người x≠x 0 thuộc vùng lân cận này, chúng ta có bất đẳng thức f (x)>f (x0.

Các điểm mà tại đó hàm số đạt cực đại và cực tiểu được gọi là điểm cực trị và các giá trị của hàm số tại các điểm này là điểm cực trị của hàm số.

Chúng ta hãy chú ý đến thực tế là một hàm được xác định trên một đoạn có thể đạt cực đại và cực tiểu chỉ tại các điểm nằm trong đoạn đang xét.

Lưu ý rằng nếu một hàm có giá trị cực đại tại một điểm, điều này không có nghĩa là tại thời điểm này hàm có giá trị lớn nhất trong toàn bộ miền. Trong hình đã thảo luận ở trên, hàm tại điểm x 1 có giá trị cực đại, mặc dù có những điểm mà tại đó giá trị của hàm lớn hơn tại điểm x 1 . Đặc biệt, f(x 1) < f(x 4) tức là cực tiểu của hàm lớn hơn cực đại. Từ định nghĩa của giá trị cực đại, ta chỉ suy ra rằng đây là giá trị lớn nhất của hàm số tại các điểm đủ gần với điểm cực đại.

Định lý 1. (Điều kiện cần thiết để tồn tại một điểm cực trị.) Nếu chức năng có thể phân biệt y = f (x) có ở điểm x = x 0 cực trị, thì đạo hàm của nó tại thời điểm này biến mất.

Bằng chứng. Hãy để, cho rõ ràng, tại điểm x 0, hàm có giá trị cực đại. Sau đó, cho các gia số vừa đủ nhỏ Δ x chúng ta có f (x 0 + Δ x) 0 ) , I E. Nhưng sau đó

Chuyển các bất đẳng thức này đến giới hạn là Δ x→ 0 và có tính đến đạo hàm f "(x 0) tồn tại, và do đó giới hạn bên trái không phụ thuộc vào cách Δ x→ 0, chúng tôi nhận được: cho Δ x → 0 – 0 f "(x 0) ≥ 0 và tại Δ x → 0 + 0 f "(x 0) ≤ 0. Kể từ f "(x 0) xác định một số, khi đó hai bất đẳng thức này chỉ tương thích với nhau khi f "(x 0) = 0.

Định lý đã được chứng minh nói rằng các điểm cực đại và cực tiểu chỉ có thể nằm trong số các giá trị của đối số mà đạo hàm biến mất.

Chúng ta đã xét trường hợp một hàm có đạo hàm tại tất cả các điểm thuộc một đoạn nào đó. Điều gì xảy ra khi đạo hàm không tồn tại? Hãy xem xét các ví dụ.

Các ví dụ.

y=|x|.
Hàm số không có đạo hàm tại một điểm x= 0 (tại thời điểm này, đồ thị của hàm số không có tiếp tuyến xác định), nhưng tại thời điểm này, hàm số có cực tiểu, vì y(0) = 0 và cho tất cả x≠ 0y > 0.

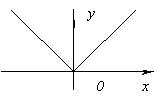
Hàm không có đạo hàm tại x= 0, vì nó tiến đến vô cùng khi x= 0. Nhưng tại thời điểm này, chức năng đã đạt mức tối đa.

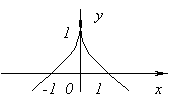
Hàm không có đạo hàm tại x= 0 vì tại x→ 0. Tại thời điểm này, hàm không có cực đại cũng không có cực tiểu. Có thật không, f (x)= 0 và lúc x<0f (x)<0, а при x>0f (x)>0.

Như vậy, từ các ví dụ đã cho và định lý được xây dựng, rõ ràng là hàm chỉ có thể có cực trị trong hai trường hợp: 1) tại các điểm mà đạo hàm tồn tại và bằng 0; 2) tại điểm mà đạo hàm không tồn tại.

Tuy nhiên, nếu một lúc nào đó x 0 chúng tôi biết điều đó f "(x 0 ) = 0, thì từ đó không thể kết luận rằng tại thời điểm x 0 thì hàm số có cực trị.

Ví dụ. .

Nhưng điểm x= 0 không phải là điểm cực trị, vì ở bên trái của điểm này, các giá trị hàm nằm bên dưới trục Con bò và ở trên bên phải.

Các giá trị của một đối số từ miền của một hàm, mà đạo hàm của hàm biến mất hoặc không tồn tại, được gọi là điểm quan trọng.

Từ những điều đã nói ở trên, các điểm cực trị của một hàm nằm trong số các điểm tới hạn, và tuy nhiên, không phải mọi điểm tới hạn đều là điểm cực trị. Do đó, để tìm cực trị của hàm, bạn cần tìm tất cả các điểm tới hạn của hàm, sau đó kiểm tra từng điểm riêng biệt để tìm cực đại và cực tiểu. Đối với điều này, định lý sau đây phục vụ.

Định lý 2. (Điều kiện đủ để tồn tại một điểm cực trị.)Để hàm liên tục trên khoảng nào đó có chứa điểm tới hạn x 0 và có thể phân biệt được ở tất cả các điểm của khoảng thời gian này (ngoại trừ, có lẽ, chính điểm x 0). Nếu khi đi từ trái sang phải qua điểm này, đạo hàm đổi dấu từ cộng sang trừ, thì tại điểm x = x 0, hàm có giá trị cực đại. Nếu, khi đi qua x 0 từ trái sang phải, đạo hàm đổi dấu từ trừ sang cộng thì lúc này hàm số có cực tiểu.

Do đó, nếu

Bằng chứng. Trước tiên, chúng ta hãy giả định rằng khi đi qua x 0, đạo hàm thay đổi dấu từ cộng sang trừ, tức là cho tất cả x gần đến điểm x 0 f "(x)> 0 cho x< x 0 , f "(x)< 0 cho x> x 0. Hãy để chúng tôi áp dụng định lý Lagrange cho sự khác biệt f (x) - f (x 0 ) = f "(c) (x- x 0), ở đâu c nằm giữa x và x 0 .

Để cho x< x 0. sau đó c< x 0 và f "(c)> 0. Đó là lý do tại sao f "(c) (x-x 0)< 0 và do đó,
f (x) - f (x 0 )< 0, tức là f (x)< f(x 0 ).

Để cho x> x 0. sau đó c> x 0 và f "(c)< 0. Có nghĩa f "(c) (x-x 0)< 0. Đó là lý do tại sao f (x) - f (x 0 ) <0,т.е.f (x)< f (x 0 ) .

Do đó, đối với tất cả các giá trị xđủ gần để x 0 f (x)< f (x 0 ) . Và điều này có nghĩa là tại thời điểm x 0, hàm có giá trị cực đại.

Phần thứ hai của định lý cực tiểu cũng được chứng minh tương tự.

Hãy để chúng tôi minh họa ý nghĩa của định lý này trong hình. Để cho f "(x 1 ) = 0 và cho bất kỳ x,đủ gần để x 1, sự bất bình đẳng

f "(x)< 0 lúc x< x 1 , f "(x)> 0 lúc x> x 1 .

Sau đó, bên trái của điểm x 1 hàm đang tăng và giảm ở bên phải, do đó, khi x = x 1 hàm đi từ tăng đến giảm, tức là nó có cực đại.

Tương tự, người ta có thể xem xét các điểm x 2 và x 3 .

Sơ đồ, tất cả những điều trên có thể được mô tả trong hình:

Quy tắc để nghiên cứu hàm y = f (x) cho cực trị

Tìm phạm vi của một hàm f (x).

Tìm đạo hàm cấp một của một hàm số f "(x).

Xác định các điểm quan trọng, cho điều này:
tìm nghiệm nguyên của phương trình f "(x)=0;

tìm tất cả các giá trị x theo đó đạo hàm f "(x) không tồn tại.

Xác định dấu của đạo hàm bên trái và bên phải của điểm tới hạn. Vì dấu của đạo hàm không đổi giữa hai điểm tới hạn, nên chỉ cần xác định dấu của đạo hàm tại một điểm bất kỳ ở bên trái và tại một điểm ở bên phải của điểm tới hạn.

Tính giá trị của hàm số tại các điểm cực trị.

Các ví dụ. Khám phá các chức năng cho mức tối thiểu và tối đa.

CÁC GIÁ TRỊ CHỨC NĂNG TỐI THIỂU VÀ TỐI ƯU NHẤT TRÊN QUAN TÂM

vĩ đại nhất giá trị của một hàm trên một đoạn là giá trị lớn nhất trong số tất cả các giá trị của nó trên đoạn này và ít nhất là giá trị nhỏ nhất trong tất cả các giá trị của nó.

Xem xét chức năng y = f (x) liên tục trên khoảng [ a, b]. Như đã biết, một hàm như vậy đạt đến giá trị lớn nhất và nhỏ nhất của nó, trên ranh giới của đoạn hoặc bên trong nó. Nếu giá trị lớn nhất hoặc nhỏ nhất của hàm đạt được tại điểm bên trong của đoạn, thì giá trị này là giá trị lớn nhất hoặc nhỏ nhất của hàm, nghĩa là nó đạt được tại các điểm tới hạn.

Do đó, chúng tôi nhận được những điều sau quy tắc tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [ a, b] :

Tìm tất cả các điểm tới hạn của một hàm trong khoảng ( a, b) và tính các giá trị của hàm tại các điểm này.

Tính các giá trị của hàm số ở hai đầu đoạn thẳng cho x = a, x = b.

Trong tất cả các giá trị thu được, hãy chọn giá trị lớn nhất và nhỏ nhất.

Cho hàm $ z = f (x, y) $ được xác định trong một vùng lân cận nào đó của điểm $ (x_0, y_0) $. Người ta nói rằng $ (x_0, y_0) $ là một điểm của (cục bộ) cực đại nếu với tất cả các điểm $ (x, y) $ trong một vùng lân cận của $ (x_0, y_0) $ thì bất đẳng thức $ f (x, y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f (x_0, y_0) $ thì điểm $ (x_0, y_0) $ được gọi là điểm cực tiểu (cục bộ).

Điểm cao và điểm thấp thường được gọi bằng thuật ngữ chung là điểm cực đại.

Nếu $ (x_0, y_0) $ là điểm cực đại thì giá trị của hàm $ f (x_0, y_0) $ tại thời điểm này được gọi là điểm cực đại của hàm $ z = f (x, y) $. Theo đó, giá trị của hàm số tại điểm cực tiểu gọi là điểm cực tiểu của hàm số $ z = f (x, y) $. Cực tiểu và cực đại của một hàm được kết hợp bởi một thuật ngữ chung - cực trị của một hàm.

Thuật toán nghiên cứu hàm $ z = f (x, y) $ có cực trị

Tìm các đạo hàm riêng của $ \ frac (\ một phần z) (\ một phần x) $ và $ \ frac (\ một phần z) (\ một phần y) $. Soạn và giải hệ phương trình $ \ left \ (\ begin (căn chỉnh) & \ frac (\ một phần z) (\ một phần x) = 0; \\ & \ frac (\ một phần z) (\ một phần y) = 0 . \ end (align) \ right. $ Các điểm có tọa độ thỏa mãn hệ thống được chỉ định được gọi là điểm dừng.

Tìm $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2) $, $ \ frac (\ một phần ^ 2z) (\ một phần x \ một phần y) $, $ \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) $ và tính giá trị $ \ Delta = \ frac (\ một phần ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) - \ left (\ frac (\ một phần ^ 2z) (\ một phần x \ một phần y) \ phải) ^ 2 $ tại mọi điểm đứng yên. Sau đó, sử dụng lược đồ sau:
Nếu $ \ Delta> 0 $ và $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2)> 0 $ (hoặc $ \ frac (\ một phần ^ 2z) (\ một phần y ^ 2)> 0 $), thì tại điểm đang học là điểm tối thiểu.

Nếu $ \ Delta> 0 $ và $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.

Nếu $ \ Delta< 0$, то в расматриваемой стационарной точке экстремума нет.

Nếu $ \ Delta = 0 $, thì không có gì xác định được về sự hiện diện của một điểm cực trị; nghiên cứu bổ sung là cần thiết.

Lưu ý (mong muốn hiểu rõ hơn về văn bản): show \ hide

Nếu $ \ Delta> 0 $ thì $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) - \ left (\ frac (\ một phần ^ 2z) (\ một phần x \ một phần y) \ phải) ^ 2> 0 $. Và từ đó nó theo sau rằng $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2)> \ left (\ frac (\ một phần ^ 2z ) (\ một phần x \ một phần y) \ phải) ^ 2 ≥ 0 $. Những thứ kia. $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2)> 0 $. Nếu tích của một số đại lượng lớn hơn 0 thì các đại lượng này cùng dấu. Ví dụ: nếu $ \ frac (\ một phần ^ 2z) (\ một phần x ^ 2)> 0 $, thì $ \ frac (\ một phần ^ 2z) (\ một phần y ^ 2)> 0 $. Tóm lại, nếu $ \ Delta> 0 $ thì các dấu hiệu của $ \ frac (\ part ^ 2z) (\ một phần x ^ 2) $ và $ \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) $ là như nhau.

Ví dụ 1

Khảo sát hàm $ z = 4x ^ 2-6xy-34x + 5y ^ 2 + 42y + 7 $ có cực trị.

$$ \ frac (\ một phần z) (\ một phần x) = 8x-6y-34; \ frac (\ một phần z) (\ một phần y) = - 6x + 10y + 42. $$
$$ \ left \ (\ begin (căn chỉnh) & 8x-6y-34 = 0; \\ & -6x + 10y + 42 = 0. \ end (căn chỉnh) \ phải. $$
Hãy giảm mỗi phương trình của hệ này đi $ 2 $ và chuyển các số sang vế phải của phương trình:
$$ \ left \ (\ begin (căn chỉnh) & 4x-3y = 17; \\ & -3x + 5y = -21. \ end (căn chỉnh) \ phải. $$
Ta đã thu được một hệ phương trình đại số tuyến tính. Trong tình huống này, đối với tôi, có vẻ như ứng dụng thuận tiện nhất của phương pháp Cramer để giải quyết hệ thống kết quả.
$$ \ begin (căn chỉnh) & \ Delta = \ left | \ begin (array) (cc) 4 & -3 \\ -3 & 5 \ end (array) \ right | = 4 \ cdot 5 - (- 3) \ cdot (-3) = 20-9 = 11; \ \ & \ Delta_x = \ trái | \ begin (array) (cc) 17 & -3 \\ -21 & 5 \ end (array) \ right | = 17 \ cdot 5 - (- 3) \ cdot (-21) = 85-63 = 22; \ \ & \ Delta_y = \ trái | \ begin (array) (cc) 4 & 17 \\ -3 & -21 \ end (array) \ right | = 4 \ cdot (-21) -17 \ cdot (-3) = - 84 + 51 = -33 . \ end (căn chỉnh) \\ x = \ frac (\ Delta_ (x)) (\ Delta) = \ frac (22) (11) = 2; \ U0026 y = \ frac (\ Delta_ (y)) (\ Delta) = \ frac (-33) (11) = - 3. $$
Các giá trị $ x = 2 $, $ y = -3 $ là tọa độ của điểm đứng yên $ (2; -3) $.
$$ \ frac (\ một phần ^ 2 z) (\ một phần x ^ 2) = 8; \ frac (\ một phần ^ 2 z) (\ một phần y ^ 2) = 10; \ frac (\ một phần ^ 2 z) (\ một phần x \ một phần y) = - 6. $$
Hãy tính giá trị của $ \ Delta $:
$$ \ Delta = \ frac (\ part ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) - \ left (\ frac (\ một phần ^ 2z) ( \ một phần x \ một phần y) \ phải) ^ 2 = 8 \ cdot 10 - (- 6) ^ 2 = 80-36 = 44. $$
Vì $ \ Delta> 0 $ và $ \ frac (\ một phần ^ 2 z) (\ một phần x ^ 2)> 0 $, nên theo điểm $ (2; -3) $ là điểm nhỏ nhất của hàm $ z $. Ta tìm điểm cực tiểu của hàm $ z $ bằng cách thay tọa độ của điểm $ (2; -3) $ vào hàm đã cho:
$$ z_ (min) = z (2; -3) = 4 \ cdot 2 ^ 2-6 \ cdot 2 \ cdot (-3) -34 \ cdot 2 + 5 \ cdot (-3) ^ 2 + 42 \ cdot (-3) + 7 = -90. $$
Câu trả lời: $ (2; -3) $ - điểm cực tiểu; $ z_ (tối thiểu) = - 90 $.

Ví dụ số 2

Khảo sát hàm $ z = x ^ 3 + 3xy ^ 2-15x-12y + 1 $ có cực trị.

Chúng ta sẽ theo dõi phần trên. Đầu tiên, chúng ta hãy tìm các đạo hàm riêng của bậc đầu tiên:
$$ \ frac (\ một phần z) (\ một phần x) = 3x ^ 2 + 3y ^ 2-15; \ frac (\ một phần z) (\ một phần y) = 6xy-12. $$
Soạn hệ phương trình $ \ left \ (\ begin (căn chỉnh) & \ frac (\ một phần z) (\ một phần x) = 0; \\ & \ frac (\ một phần z) (\ một phần y) = 0. \ end (căn chỉnh) \ right. $:
$$ \ left \ (\ begin (căn chỉnh) & 3x ^ 2 + 3y ^ 2-15 = 0; \\ & 6xy-12 = 0. \ end (căn chỉnh) \ phải. $$
Rút gọn phân thức thứ nhất đi 3 và phương trình thứ hai đi 6.
$$ \ left \ (\ begin (căn chỉnh) & x ^ 2 + y ^ 2-5 = 0; \\ & xy-2 = 0. \ end (căn chỉnh) \ phải. $$
Nếu $ x = 0 $, thì phương trình thứ hai sẽ dẫn chúng ta đến một mâu thuẫn: $ 0 \ cdot y-2 = 0 $, $ -2 = 0 $. Do đó kết luận: $ x \ neq 0 $. Khi đó từ phương trình thứ hai ta có: $ xy = 2 $, $ y = \ frac (2) (x) $. Thay $ y = \ frac (2) (x) $ vào phương trình đầu tiên, ta có:
$$ x ^ 2 + \ left (\ frac (2) (x) \ right) ^ 2-5 = 0; \\ x ^ 2 + \ frac (4) (x ^ 2) -5 = 0; \\ x ^ 4-5x ^ 2 + 4 = 0. $$
Chúng ta có một phương trình bậc hai. Chúng tôi thực hiện phép thay thế $ t = x ^ 2 $ (chúng tôi lưu ý rằng $ t> 0 $):
$$ t ^ 2-5t + 4 = 0; \\ \ begin (căn chỉnh) & D = (- 5) ^ 2-4 \ cdot 1 \ cdot 4 = 9; \\ & t_1 = \ frac (- (- 5) - \ sqrt (9)) (2) = \ frac (5-3) (2) = 1; \\ & t_2 = \ frac (- (- 5) + \ sqrt (9)) (2) = \ frac (5 + 3) (2) = 4. \ end (căn chỉnh) $$
Nếu $ t = 1 $ thì $ x ^ 2 = 1 $. Do đó, chúng ta có hai giá trị $ x $: $ x_1 = 1 $, $ x_2 = -1 $. Nếu $ t = 4 $, thì $ x ^ 2 = 4 $, tức là $ x_3 = 2 $, $ x_4 = -2 $. Nhớ rằng $ y = \ frac (2) (x) $, chúng ta nhận được:
\ begin (căn chỉnh) & y_1 = \ frac (2) (x_1) = \ frac (2) (1) = 2; \\ & y_2 = \ frac (2) (x_2) = \ frac (2) (- 1 ) = - 2; \\ & y_3 = \ frac (2) (x_3) = \ frac (2) (2) = 1; \\ & y_4 = \ frac (2) (x_4) = \ frac (2) ( -2) = - 1. \ end (căn chỉnh)
Vì vậy, chúng ta có bốn điểm đứng yên: $ M_1 (1; 2) $, $ M_2 (-1; -2) $, $ M_3 (2; 1) $, $ M_4 (-2; -1) $. Điều này hoàn thành bước đầu tiên của thuật toán.

Bây giờ chúng ta hãy đi xuống thuật toán. Hãy tìm đạo hàm riêng của bậc hai:
$$ \ frac (\ một phần ^ 2 z) (\ một phần x ^ 2) = 6x; \ frac (\ một phần ^ 2 z) (\ một phần y ^ 2) = 6x; \ frac (\ một phần ^ 2 z) (\ một phần x \ một phần y) = 6y. $$
Tìm $ \ Delta $:
$$ \ Delta = \ frac (\ part ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) - \ left (\ frac (\ một phần ^ 2z) ( \ một phần x \ một phần y) \ phải) ^ 2 = 6x \ cdot 6x- (6y) ^ 2 = 36x ^ 2-36y ^ 2 = 36 (x ^ 2-y ^ 2). $$
Bây giờ chúng ta sẽ tính giá trị của $ \ Delta $ tại mỗi điểm cố định được tìm thấy trước đó. Hãy bắt đầu từ điểm $ M_1 (1; 2) $. Lúc này chúng ta có: $ \ Delta (M_1) = 36 (1 ^ 2-2 ^ 2) = - 108 $. Kể từ $ \ Delta (M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

Hãy khám phá điểm $ M_2 (-1; -2) $. Lúc này chúng ta có: $ \ Delta (M_2) = 36 ((- 1) ^ 2 - (- 2) ^ 2) = - 108 $. Kể từ $ \ Delta (M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

Hãy kiểm tra điểm $ M_3 (2; 1) $. Tại thời điểm này, chúng tôi nhận được:
$$ \ Delta (M_3) = 36 (2 ^ 2-1 ^ 2) = 108; \; \; \ left. \ frac (\ part ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_3) = 6 \ cdot 2 = 12. $$
Vì $ \ Delta (M_3)> 0 $ và $ \ left. \ Frac (\ part ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_3)> 0 $, thì theo $ M_3 (2; 1) $ là điểm cực tiểu của hàm $ z $. Chúng ta tìm điểm cực tiểu của hàm $ z $ bằng cách thay tọa độ của điểm $ M_3 $ vào hàm đã cho:
$$ z_ (min) = z (2; 1) = 2 ^ 3 + 3 \ cdot 2 \ cdot 1 ^ 2-15 \ cdot 2-12 \ cdot 1 + 1 = -27. $$
Nó vẫn còn để khám phá điểm $ M_4 (-2; -1) $. Tại thời điểm này, chúng tôi nhận được:
$$ \ Delta (M_4) = 36 ((- 2) ^ 2 - (- 1) ^ 2) = 108; \; \; \ left. \ frac (\ part ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_4) = 6 \ cdot (-2) = - 12. $$
Vì $ \ Delta (M_4)> 0 $ và $ \ left. \ Frac (\ một phần ^ 2 z) (\ một phần x ^ 2) \ phải | _ (M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_ (max) = z (-2; -1) = (- 2) ^ 3 + 3 \ cdot (-2) \ cdot (-1) ^ 2-15 \ cdot (-2) -12 \ cdot (-1) + 1 = 29. $$
Nghiên cứu cực trị đã hoàn thành. Nó vẫn chỉ để viết ra câu trả lời.

Câu trả lời:

$ (2; 1) $ - điểm cực tiểu, $ z_ (tối thiểu) = - 27 $;

$ (- 2; -1) $ - điểm tối đa, $ z_ (max) = 29 $.

Ghi chú

Trong trường hợp chung, không cần tính giá trị của $ \ Delta $, vì chúng ta chỉ quan tâm đến dấu chứ không quan tâm đến giá trị cụ thể của tham số này. Ví dụ, với ví dụ số 2 đã xét ở trên, tại điểm $ M_3 (2; 1) $ chúng ta có $ \ Delta = 36 \ cdot (2 ^ 2-1 ^ 2) $. Ở đây rõ ràng là $ \ Delta> 0 $ (vì cả hai hệ số $ 36 $ và $ (2 ^ 2-1 ^ 2) $ đều dương) và không thể tìm thấy giá trị cụ thể của $ \ Delta $. Đúng, nhận xét này vô dụng đối với các phép tính thông thường - chúng yêu cầu đưa các phép tính về một số :)

Ví dụ # 3

Khảo sát hàm $ z = x ^ 4 + y ^ 4-2x ^ 2 + 4xy-2y ^ 2 + 3 $ có cực trị.

Chúng tôi sẽ làm theo. Đầu tiên, chúng ta hãy tìm các đạo hàm riêng của bậc đầu tiên:
$$ \ frac (\ một phần z) (\ một phần x) = 4x ^ 3-4x + 4y; \ frac (\ một phần z) (\ một phần y) = 4y ^ 3 + 4x-4y. $$
Soạn hệ phương trình $ \ left \ (\ begin (căn chỉnh) & \ frac (\ một phần z) (\ một phần x) = 0; \\ & \ frac (\ một phần z) (\ một phần y) = 0. \ end (căn chỉnh) \ right. $:
$$ \ left \ (\ begin (căn chỉnh) & 4x ^ 3-4x + 4y = 0; \\ & 4y ^ 3 + 4x-4y = 0. \ end (căn chỉnh) \ phải. $$
Hãy giảm cả hai phương trình đi $ 4 $:
$$ \ left \ (\ begin (căn chỉnh) & x ^ 3-x + y = 0; \\ & y ^ 3 + x-y = 0. \ end (căn chỉnh) \ phải. $$
Hãy thêm phương trình đầu tiên vào phương trình thứ hai và biểu thị $ y $ theo $ x $:
$$ y ^ 3 + x-y + (x ^ 3-x + y) = 0; \\ y ^ 3 + x ^ 3 = 0; y ^ 3 = -x ^ 3; y = -x. $$
Thay $ y = -x $ vào phương trình đầu tiên của hệ, ta sẽ có:
$$ x ^ 3-x-x = 0; \\ x ^ 3-2x = 0; \\ x (x ^ 2-2) = 0. $$
Từ phương trình kết quả ta có: $ x = 0 $ hoặc $ x ^ 2-2 = 0 $. Theo phương trình $ x ^ 2-2 = 0 $ mà $ x = - \ sqrt (2) $ hoặc $ x = \ sqrt (2) $. Vì vậy, ba giá trị của $ x $ được tìm thấy, đó là: $ x_1 = 0 $, $ x_2 = - \ sqrt (2) $, $ x_3 = \ sqrt (2) $. Vì $ y = -x $ nên $ y_1 = -x_1 = 0 $, $ y_2 = -x_2 = \ sqrt (2) $, $ y_3 = -x_3 = - \ sqrt (2) $.

Bước đầu tiên của giải pháp đã kết thúc. Chúng tôi có ba điểm cố định: $ M_1 (0; 0) $, $ M_2 (- \ sqrt (2), \ sqrt (2)) $, $ M_3 (\ sqrt (2), - \ sqrt (2)) $ .

Bây giờ chúng ta hãy đi xuống thuật toán. Hãy tìm đạo hàm riêng của bậc hai:
$$ \ frac (\ một phần ^ 2 z) (\ một phần x ^ 2) = 12x ^ 2-4; \ frac (\ một phần ^ 2 z) (\ một phần y ^ 2) = 12y ^ 2-4; \ frac (\ một phần ^ 2 z) (\ một phần x \ một phần y) = 4. $$
Tìm $ \ Delta $:
$$ \ Delta = \ frac (\ part ^ 2z) (\ một phần x ^ 2) \ cdot \ frac (\ một phần ^ 2z) (\ một phần y ^ 2) - \ left (\ frac (\ một phần ^ 2z) ( \ một phần x \ một phần y) \ phải) ^ 2 = (12x ^ 2-4) (12y ^ 2-4) -4 ^ 2 = \\ = 4 (3x ^ 2-1) \ cdot 4 (3y ^ 2 -1) -16 = 16 (3x ^ 2-1) (3y ^ 2-1) -16 = 16 \ cdot ((3x ^ 2-1) (3y ^ 2-1) -1). $$
Bây giờ chúng ta sẽ tính giá trị của $ \ Delta $ tại mỗi điểm cố định được tìm thấy trước đó. Hãy bắt đầu từ điểm $ M_1 (0; 0) $. Tại thời điểm này, chúng ta có: $ \ Delta (M_1) = 16 \ cdot ((3 \ cdot 0 ^ 2-1) (3 \ cdot 0 ^ 2-1) -1) = 16 \ cdot 0 = 0 $. Vì $ \ Delta (M_1) = 0 $, nghiên cứu bổ sung là cần thiết, vì không thể nói rõ điều gì về sự hiện diện của một điểm cực trị tại điểm được xem xét. Tạm thời chúng ta hãy để nguyên điểm này và chuyển sang các điểm khác.

Hãy kiểm tra điểm $ M_2 (- \ sqrt (2), \ sqrt (2)) $. Tại thời điểm này, chúng tôi nhận được:
\ begin (căn chỉnh) & \ Delta (M_2) = 16 \ cdot ((3 \ cdot (- \ sqrt (2)) ^ 2-1) (3 \ cdot (\ sqrt (2)) ^ 2-1) - 1) = 16 \ cdot 24 = 384; \\ & \ left. \ Frac (\ part ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_2) = 12 \ cdot (- \ sqrt (2) ) ^ 2-4 = 24-4 = 20. \ end (căn chỉnh)
Vì $ \ Delta (M_2)> 0 $ và $ \ left. \ Frac (\ một phần ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_2)> 0 $, thì theo $ M_2 (- \ sqrt (2), \ sqrt (2)) $ là điểm cực tiểu của hàm $ z $. Chúng ta tìm điểm cực tiểu của hàm $ z $ bằng cách thay tọa độ của điểm $ M_2 $ vào hàm đã cho:
$$ z_ (min) = z (- \ sqrt (2), \ sqrt (2)) = (- \ sqrt (2)) ^ 4 + (\ sqrt (2)) ^ 4-2 (- \ sqrt ( 2)) ^ 2 + 4 \ cdot (- \ sqrt (2)) \ sqrt (2) -2 (\ sqrt (2)) ^ 2 + 3 = -5. $$
Tương tự như điểm trước, chúng ta kiểm tra điểm $ M_3 (\ sqrt (2), - \ sqrt (2)) $. Tại thời điểm này, chúng tôi nhận được:
\ begin (căn chỉnh) & \ Delta (M_3) = 16 \ cdot ((3 \ cdot (\ sqrt (2)) ^ 2-1) (3 \ cdot (- \ sqrt (2)) ^ 2-1) - 1) = 16 \ cdot 24 = 384; \\ & \ left. \ Frac (\ part ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_3) = 12 \ cdot (\ sqrt (2)) ^ 2-4 = 24-4 = 20. \ end (căn chỉnh)
Vì $ \ Delta (M_3)> 0 $ và $ \ left. \ Frac (\ một phần ^ 2 z) (\ một phần x ^ 2) \ right | _ (M_3)> 0 $, thì theo $ M_3 (\ sqrt (2), - \ sqrt (2)) $ là điểm cực tiểu của hàm $ z $. Chúng ta tìm điểm cực tiểu của hàm $ z $ bằng cách thay tọa độ của điểm $ M_3 $ vào hàm đã cho:
$$ z_ (min) = z (\ sqrt (2), - \ sqrt (2)) = (\ sqrt (2)) ^ 4 + (- \ sqrt (2)) ^ 4-2 (\ sqrt (2) )) ^ 2 + 4 \ cdot \ sqrt (2) (- \ sqrt (2)) - 2 (- \ sqrt (2)) ^ 2 + 3 = -5. $$
Đã đến lúc quay lại điểm $ M_1 (0; 0) $, nơi $ \ Delta (M_1) = 0 $. Nghiên cứu bổ sung là cần thiết. Cụm từ lảng tránh này có nghĩa là "hãy làm những gì bạn muốn" :). Không có cách chung nào để giải quyết những tình huống như vậy - và điều này có thể hiểu được. Nếu có một phương pháp như vậy, thì nó đã đi vào tất cả các sách giáo khoa từ lâu. Trong thời gian chờ đợi, chúng tôi phải tìm cách tiếp cận đặc biệt cho từng điểm mà $ \ Delta = 0 $. Vâng, hãy điều tra hoạt động của hàm trong vùng lân cận của điểm $ M_1 (0; 0) $. Chúng ta lưu ý ngay rằng $ z (M_1) = z (0; 0) = 3 $. Giả sử rằng $ M_1 (0; 0) $ là một điểm nhỏ nhất. Sau đó, với bất kỳ điểm nào $ M $ từ một vùng lân cận nào đó của điểm $ M_1 (0; 0) $, chúng ta nhận được $ z (M)> z (M_1) $, tức là $ z (M)> 3 $. Điều gì sẽ xảy ra nếu bất kỳ vùng lân cận nào chứa các điểm tại đó $ z (M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Xem xét các điểm mà $ y = 0 $, tức là điểm có dạng $ (x, 0) $. Tại những điểm này, hàm $ z $ sẽ nhận các giá trị sau:
$$ z (x, 0) = x ^ 4 + 0 ^ 4-2x ^ 2 + 4x \ cdot 0-2 \ cdot 0 ^ 2 + 3 = x ^ 4-2x ^ 2 + 3 = x ^ 2 (x ^ 2-2) +3. $$
Trong tất cả các vùng lân cận đủ nhỏ $ M_1 (0; 0) $, chúng ta có $ x ^ 2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Nhưng có thể điểm $ M_1 (0; 0) $ là một điểm cực đại? Nếu đúng như vậy, thì với bất kỳ điểm nào $ M $ từ một vùng lân cận nào đó của điểm $ M_1 (0; 0) $ chúng ta nhận được $ z (M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3 đô la? Khi đó chắc chắn sẽ không có giá trị tối đa tại điểm $ M_1 $.

Xem xét các điểm mà $ y = x $, tức là điểm có dạng $ (x, x) $. Tại những điểm này, hàm $ z $ sẽ nhận các giá trị sau:
$$ z (x, x) = x ^ 4 + x ^ 4-2x ^ 2 + 4x \ cdot x-2 \ cdot x ^ 2 + 3 = 2x ^ 4 + 3. $$
Vì trong vùng lân cận bất kỳ của điểm $ M_1 (0; 0) $ chúng ta có $ 2x ^ 4> 0 $, khi đó $ 2x ^ 4 + 3> 3 $. Kết luận: bất kỳ vùng lân cận nào của điểm $ M_1 (0; 0) $ đều chứa các điểm mà $ z> 3 $, do đó điểm $ M_1 (0; 0) $ không thể là điểm cực đại.

Điểm $ M_1 (0; 0) $ không phải là điểm cực đại cũng không phải là điểm cực tiểu. Kết luận: $ M_1 $ hoàn toàn không phải là một điểm cực trị.

Câu trả lời: $ (- \ sqrt (2), \ sqrt (2)) $, $ (\ sqrt (2), - \ sqrt (2)) $ - điểm tối thiểu của hàm $ z $. Tại cả hai điểm $ z_ (min) = - 5 $.

Điểm cực trị của hàm số là gì và điều kiện cần để có điểm cực trị là gì?

Điểm cực trị của một hàm số là điểm cực đại và cực tiểu của hàm số.

Điều kiện cần để đạt cực đại và cực tiểu (cực trị) của hàm số như sau: nếu hàm số f (x) có cực trị tại điểm x = a thì tại thời điểm này đạo hàm bằng 0 hoặc vô hạn hoặc bằng không tồn tại.

Điều kiện này là cần, nhưng chưa đủ. Đạo hàm tại điểm x = a có thể biến mất, đi đến vô cùng hoặc không tồn tại khi hàm số có cực trị tại điểm này.

Điều kiện đủ để hàm số đạt cực trị (cực đại hoặc cực tiểu) là gì?

Điều kiện đầu tiên:

Nếu, trong một khoảng gần đủ với điểm x = a, đạo hàm f? (X) dương bên trái a và âm bên phải a, thì tại điểm x = a, hàm số f (x) có tối đa

Nếu, trong một khoảng gần đủ với điểm x = a, đạo hàm f? (X) âm bên trái a và dương bên phải a, thì tại điểm x = a, hàm số f (x) có tối thiểu với điều kiện là hàm f (x) liên tục ở đây.

Thay vào đó, bạn có thể sử dụng điều kiện đủ thứ hai cho cực trị của hàm:

Để tại điểm x = và đạo hàm cấp một f? (X) biến mất; nếu đạo hàm cấp hai f ?? (а) âm thì hàm số f (x) đạt cực đại tại điểm x = a, nếu dương thì cực tiểu.

Điểm tới hạn của một hàm là gì và làm thế nào để tìm nó?

Đây là giá trị của đối số hàm mà tại đó hàm có cực trị (tức là cực đại hoặc cực tiểu). Để tìm thấy nó, bạn cần tìm đạo hàm hàm f? (x) và, cho nó bằng 0, giải phương trình f? (x) = 0. Các gốc của phương trình này, cũng như các điểm mà tại đó đạo hàm của hàm này không tồn tại, là các điểm tới hạn, tức là các giá trị của đối số mà tại đó có thể có cực trị . Chúng có thể dễ dàng được xác định bằng cách nhìn vào đồ thị đạo hàm: chúng tôi quan tâm đến những giá trị của đối số mà tại đó đồ thị của hàm số cắt trục abscissa (trục Ox) và những giá trị mà tại đó đồ thị bị đứt.

Ví dụ, chúng ta hãy tìm cực đại của parabol.

Hàm số y (x) = 3x2 + 2x - 50.

Đạo hàm hàm số: y? (X) = 6x + 2

Ta giải phương trình: y? (X) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

Trong trường hợp này, điểm tới hạn là x0 = -1 / 3. Chính vì giá trị này của đối số mà hàm có cực đoan. Để có được nó tìm thấy, chúng tôi thay thế số tìm được trong biểu thức cho hàm thay vì "x":

y0 = 3 * (- 1/3) 2 + 2 * (- 1/3) - 50 = 3 * 1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Cách xác định giá trị lớn nhất và nhỏ nhất của một hàm, tức là giá trị lớn nhất và nhỏ nhất của nó?

Nếu dấu của đạo hàm thay đổi từ “cộng” thành “trừ” khi đi qua điểm tới hạn x0, thì x0 là điểm tối đa; nếu dấu của đạo hàm chuyển từ trừ sang cộng, thì x0 là điểm tối thiểu; nếu dấu không thay đổi thì tại điểm x0 không có cực đại hay cực tiểu.

Đối với ví dụ được xem xét:

Chúng tôi lấy một giá trị tùy ý của đối số ở bên trái của điểm tới hạn: x = -1

Khi x = -1, giá trị của đạo hàm sẽ là y? (-1) = 6 * (-1) + 2 = -6 + 2 = -4 (tức là dấu trừ).

Bây giờ chúng ta lấy một giá trị tùy ý của đối số ở bên phải của điểm tới hạn: x = 1

Với x = 1, giá trị của đạo hàm sẽ là y (1) = 6 * 1 + 2 = 6 + 2 = 8 (tức là dấu cộng).

Như bạn thấy, khi đi qua điểm tới hạn, đạo hàm đổi dấu từ trừ sang cộng. Điều này có nghĩa là tại giá trị tới hạn của x0, chúng ta có một điểm cực tiểu.

Giá trị lớn nhất và nhỏ nhất của hàm số trong khoảng thời gian(trên phân đoạn) được tìm thấy bằng cùng một quy trình, chỉ tính đến thực tế là có lẽ không phải tất cả các điểm tới hạn đều nằm trong khoảng thời gian xác định. Những điểm quan trọng nằm ngoài khoảng thời gian phải được loại trừ khỏi việc xem xét. Nếu chỉ có một điểm tới hạn trong khoảng thời gian, nó sẽ có giá trị cực đại hoặc cực tiểu. Trong trường hợp này, để xác định giá trị lớn nhất và nhỏ nhất của hàm số, chúng ta cũng tính đến các giá trị của hàm số ở hai đầu khoảng.

Ví dụ, hãy tìm giá trị lớn nhất và nhỏ nhất của hàm

y (x) \ u003d 3 sin (x) - 0,5x

trong khoảng thời gian:

Vậy đạo hàm của hàm số là

y? (x) = 3cos (x) - 0,5

Ta giải phương trình 3cos (x) - 0,5 = 0

cos (x) = 0,5 / 3 = 0,16667

x \ u003d ± arccos (0,16667) + 2πk.

Chúng tôi tìm thấy các điểm tới hạn trên khoảng [-9; 9]:

x \ u003d arccos (0,16667) - 2π * 2 \ u003d -11,163 (không bao gồm trong khoảng thời gian)

x \ u003d -arccos (0,16667) - 2π * 1 \ u003d -7,687

x \ u003d arccos (0,16667) - 2π * 1 \ u003d -4,88

x \ u003d -arccos (0,16667) + 2π * 0 \ u003d -1,403

x \ u003d arccos (0,16667) + 2π * 0 \ u003d 1,403

x \ u003d -arccos (0,16667) + 2π * 1 \ u003d 4,88

x \ u003d arccos (0,16667) + 2π * 1 \ u003d 7,687

x \ u003d -arccos (0,16667) + 2π * 2 \ u003d 11,163 (không bao gồm trong khoảng thời gian)

Chúng tôi tìm các giá trị của hàm tại các giá trị quan trọng của đối số:

y (-7,687) = 3cos (-7,687) - 0,5 = 0,885

y (-4,88) = 3cos (-4,88) - 0,5 = 5,398

y (-1,403) = 3cos (-1,403) - 0,5 = -2,256

y (1,403) = 3cos (1,403) - 0,5 = 2,256

y (4,88) = 3cos (4,88) - 0,5 = -5,398

y (7.687) = 3cos (7.687) - 0.5 = -0.885

Có thể thấy rằng trên khoảng [-9; 9] hàm có giá trị lớn nhất tại x = -4,88:

x = -4,88, y = 5,398,

và nhỏ nhất - tại x = 4,88:

x = 4,88, y = -5,398.

Trên khoảng [-6; -3] chúng ta chỉ có một điểm tới hạn: x = -4,88. Giá trị của hàm số tại x = -4,88 là y = 5,398.

Ta tìm giá trị của hàm số ở hai đầu khoảng:

y (-6) = 3cos (-6) - 0,5 = 3,838

y (-3) = 3cos (-3) - 0,5 = 1,077

Trên khoảng [-6; -3] chúng ta có giá trị lớn nhất của hàm

y = 5.398 tại x = -4,88

giá trị nhỏ nhất là

y = 1,077 tại x = -3

Làm thế nào để tìm điểm uốn của đồ thị hàm số và xác định các cạnh của lồi và lõm?

Để tìm tất cả các điểm uốn của đường thẳng y \ u003d f (x), bạn cần tìm đạo hàm cấp hai, cho nó bằng 0 (giải phương trình) và kiểm tra tất cả các giá trị đó của x mà đạo hàm cấp hai bằng 0 , vô hạn hoặc không tồn tại. Nếu khi đi qua một trong các giá trị này mà đạo hàm cấp hai đổi dấu thì lúc này đồ thị của hàm số có một góc uốn. Nếu nó không thay đổi, thì không có uốn.

Các nghiệm nguyên của phương trình f? (x) = 0, cũng như các điểm gián đoạn có thể có của hàm và đạo hàm cấp hai, chia miền của hàm thành một số khoảng. Độ lồi tại mỗi khoảng của chúng được xác định bởi dấu của đạo hàm cấp hai. Nếu đạo hàm cấp hai tại một điểm trên khoảng đang nghiên cứu là dương, thì đường thẳng y = f (x) lõm lên tại đây, và nếu nó là âm thì hướng xuống dưới.

Làm thế nào để tìm cực trị của một hàm hai biến?

Để tìm cực trị của hàm f (x, y), có thể phân biệt được trong vùng gán của nó, bạn cần:

1) tìm các điểm tới hạn và giải hệ phương trình

fx? (x, y) = 0, fy? (x, y) = 0

2) đối với mỗi điểm tới hạn P0 (a; b), điều tra xem dấu hiệu của sự khác biệt có không thay đổi

với mọi điểm (x; y) đủ gần P0. Nếu sự khác biệt giữ nguyên dấu dương thì tại điểm P0 ta có cực tiểu, nếu âm thì cực đại. Nếu sự khác biệt không giữ nguyên dấu của nó thì không có cực trị tại điểm Р0.

Tương tự, cực trị của hàm được xác định cho số lượng đối số lớn hơn.

Trang web chính thức của ca sĩ Mika Newton và ban nhạc của cô ấy là gì
Phép màu mới của Ukraine - Mika Newton! Đây là một nhóm gồm 5 người chơi pop-rock, tận hưởng cuộc sống, cống hiến và nhìn nhận một cách tích cực về cuộc sống này. Các chàng trai đã tập trung tại Kyiv, nơi họ hiện đang sống. Các chàng trai không đồng ý với những nền tảng tiêu chuẩn trong âm nhạc và cuộc sống, khám phá ra âm thanh mới của họ và phá vỡ mọi tiêu chuẩn. Trưởng nhóm -
Làm thế nào để chuyển đổi từ mililit sang mét khối
Đơn vị đo độ dài cơ bản trong hệ SI là mét. Dựa trên điều này, đơn vị thể tích cơ bản nên được coi là mét khối, hay còn được gọi là mét khối hay mét khối. Đây là thể tích của một khối lập phương có các cạnh bằng một mét. Tuy nhiên, trong thực tế không phải lúc nào cũng thuận tiện để biểu thị thể tích bằng mét khối. Ví dụ, thuận tiện để thể hiện thể tích của một căn phòng theo mét khối: nhân chiều dài của
Hàm lượng calo của bột báng là gì
Thực phẩm calorie, bảng calorie. Nhu cầu năng lượng của con người được đo bằng kilocalories (kcal). Từ "calorie" bắt nguồn từ ngôn ngữ Latinh và có nghĩa là "sự ấm áp". Trong vật lý, năng lượng được đo bằng calo. Một kilocalorie là lượng năng lượng
Các giai đoạn phát triển của chủ nghĩa hiện thực trong văn học là gì
Chủ nghĩa hiện thực (lat. Real, real) là một trào lưu trong văn học, nghệ thuật nhằm tái hiện một cách trung thực hiện thực ở những nét đặc trưng của nó. Đặc điểm chung: Nghệ thuật miêu tả cuộc sống bằng hình ảnh, tương ứng với bản chất sự vật hiện tượng của đời sống. Thực tế là phương tiện giúp con người hiểu biết về bản thân và thế giới xung quanh. Đánh máy
Mối quan hệ giữa berkeli và nguyên tố thứ 117 trong bảng tuần hoàn là gì
Berkelium, Berkelium, Bk - nguyên tố thứ 97 trong bảng tuần hoàn. Được phát hiện vào tháng 12 năm 1949 bởi Thompson, Ghiorso và Seaborg tại Đại học California ở Berkeley. Bằng cách chiếu xạ 241Am với các hạt alpha, họ thu được đồng vị Berkelium 243Bk. Bởi vì Bk có cấu trúc tương tự như terbi, lấy tên từ ông Ytterby trong
Yaroslav the Wise nổi tiếng vì điều gì?
Yaroslav the Wise (980-1054), Đại công tước Kyiv (1019). Con trai của Vladimir I Svyatoslavovich. Ông trục xuất Svyatopolk I the Accursed, chiến đấu với anh trai Mstislav, phân chia bang với anh ta (1025), và năm 1035 thống nhất nó một lần nữa. Một số chiến thắng đã bảo đảm biên giới phía nam và phía tây của Nga. Thiết lập quan hệ triều đại với nhiều quốc gia của Ev
Làm thế nào mà truyền thống hét lên "Đắng!"
Từ xa xưa đã có truyền thống hét lên trong tiệc cưới: "Đắng quá!", Buộc đôi tân hôn phải đứng dậy và hôn nhau. Ngày nay, nhiều người thậm chí còn không đoán được ý nghĩa của lễ này là gì, ngày xưa trong các đám cưới, họ hét lên “Đắng!”, Rõ ràng là rượu trong bát được cho là không có đường. NHƯNG
Các triệu chứng của viêm thanh quản là gì
Viêm thanh quản (từ tiếng Hy Lạp khác là λ? Ρυγξ - larynx) là tình trạng viêm thanh quản, thường liên quan đến cảm lạnh hoặc các bệnh truyền nhiễm như sởi, ban đỏ, ho gà. Sự phát triển của bệnh được tạo điều kiện thuận lợi cho việc hạ thân nhiệt, thở bằng miệng, bụi bẩn.
Liệu giới tính và sự giảm dần có được xác định cho các danh từ chỉ có dạng số nhiều hay không
Số là một phạm trù ngữ pháp biểu thị đặc điểm số lượng của vật. 1. Hầu hết các danh từ thay đổi theo số, tức là Nó có hai dạng - số ít và số nhiều. Ở dạng số ít, danh từ chỉ một đối tượng, ở dạng số nhiều, một số đối tượng:
Cháo Nga hữu ích là gì
Cháo kiều mạch Kiều mạch là một loại ngũ cốc đặc biệt. Từ đó, có lẽ, nó là một trong những loại ngũ cốc hữu ích nhất. Không có gì ngạc nhiên khi chúng tôi gọi nó là người đầu tiên. Kiều mạch có chứa chất xơ, một loạt các vitamin - E, PP, B1, B2, folic và axit hữu cơ, cũng như một tỷ lệ lớn tinh bột, góp phần vào việc tiêu thụ đúng lượng tân

Bản đồ tương tác của thành phố Arkhangelsk có thể được xem trên các trang web sau: Map1 - bản đồ vệ tinh và tiêu chuẩn; Map2 - bản đồ tiêu chuẩn (1: 350,000); Map3 - có tên đường, số nhà, có thể tìm kiếm theo đường phố; Map4 - bản đồ có tên đường; Map5 - bản đồ tương tác của thành phố; Map6 - bản đồ tương tác của thành phố.

Điểm x 0 được gọi là điểm tối đa(tối thiểu) của hàm f (х) nếu trong một vùng lân cận nào đó của điểm x 0, bất đẳng thức f (х) ≤f (х 0) (f (х) ≥f (х 0)) được thỏa mãn.
Giá trị của hàm tại thời điểm này được gọi là tối đa hoặc tối thiểu chức năng. Giá trị tối đa và tối thiểu của một hàm được kết hợp bởi một tên chung cực đoan chức năng.
Cực trị của một hàm theo nghĩa này thường được gọi là cực đoan địa phương, nhấn mạnh thực tế rằng khái niệm này chỉ được kết hợp với một vùng lân cận đủ nhỏ của điểm x 0. Trên cùng một khoảng thời gian, một hàm có thể có một số cực đại và cực tiểu cục bộ, không nhất thiết phải trùng với tối đa toàn cầu hoặc tối thiểu(tức là giá trị lớn nhất hoặc nhỏ nhất của hàm trên toàn bộ khoảng thời gian).
Điều kiện cần thiết cho một cực đại. Để một hàm số có cực trị tại một điểm, thì đạo hàm của nó tại điểm đó phải bằng 0 hoặc không tồn tại.
Đối với các hàm phân biệt, điều kiện này tuân theo định lý Fermat. Ngoài ra, nó cung cấp cho trường hợp khi hàm có cực trị tại một điểm mà nó không thể phân biệt được.
Các điểm thỏa mãn điều kiện cực đại cần thiết được gọi là phê bình(hoặc đứng im cho một chức năng khác biệt). Các điểm này phải nằm trong phạm vi của chức năng.
Vì vậy, nếu có một điểm cực trị tại bất kỳ điểm nào, thì điểm này là tới hạn (điều kiện cần). Lưu ý rằng điều ngược lại không đúng. Điểm tới hạn không nhất thiết phải là điểm cực trị, tức là điều kiện đã nêu là không đủ.
Điều kiện đủ đầu tiên cho một điểm cực trị. Nếu khi đi qua một điểm nào đó, đạo hàm của một hàm số phân biệt đổi dấu từ cộng sang trừ thì đây là điểm cực đại của hàm số, còn nếu từ trừ thành cộng thì là điểm cực tiểu.
Việc chứng minh điều kiện này xuất phát từ điều kiện đủ của tính đơn điệu (khi dấu của đạo hàm thay đổi thì chuyển từ hàm tăng sang hàm giảm hoặc từ giảm thành tăng).
Điều kiện đủ thứ hai cho một điểm cực trị. Nếu tại một thời điểm nào đó đạo hàm cấp một của hàm hai phân biệt bằng 0 và đạo hàm cấp hai là dương thì đây là điểm cực tiểu của hàm; và nếu đạo hàm cấp hai là số âm, thì đây là điểm cực đại.
Việc chứng minh điều kiện này cũng dựa trên điều kiện đơn điệu đủ. Thật vậy, nếu đạo hàm cấp hai là dương, thì đạo hàm cấp một là một hàm tăng. Vì nó bằng 0 tại điểm đang xét, do đó, khi đi qua nó, nó đổi dấu từ trừ sang cộng, điều này đưa chúng ta về điều kiện đủ đầu tiên cho cực tiểu cục bộ. Tương tự, nếu đạo hàm thứ hai âm, thì đạo hàm đầu tiên giảm và đổi dấu từ cộng sang trừ, đó là điều kiện đủ để có cực đại cục bộ.
Điều tra một chức năng đến một cực trị phù hợp với các định lý đã xây dựng, nó bao gồm các bước sau:
1. Tìm đạo hàm cấp một của hàm số f` (x).
2. Kiểm tra việc đáp ứng các điều kiện tối đa cần thiết, tức là tìm các điểm tới hạn của hàm f (x) mà tại đó đạo hàm f` (x) = 0 hoặc không tồn tại.
3. Kiểm tra sự đáp ứng của điều kiện tối đa đủ, tức là hoặc kiểm tra dấu của đạo hàm bên trái và bên phải của mỗi điểm tới hạn, hoặc tìm đạo hàm cấp hai f`` (x) và xác định dấu của nó tại mỗi điểm tới hạn. Đưa ra kết luận về sự có mặt của các cực trị của hàm số.
4. Tìm cực trị (các giá trị cực trị) của hàm số.
Tìm tổng thể tối đa và tối thiểu của một hàm trong một khoảng thời gian nhất định cũng có tầm quan trọng thực tế lớn. Lời giải của bài toán này trên một đoạn dựa trên định lý Weierstrass, theo đó một hàm liên tục nhận các giá trị lớn nhất và nhỏ nhất trên một đoạn. Chúng có thể đạt được cả ở điểm cực trị và điểm cuối của đoạn. Do đó, giải pháp bao gồm các bước sau:
1. Tìm đạo hàm của hàm số f` (x).
2. Tìm các điểm tới hạn của hàm số f (x) mà tại đó đạo hàm f` (x) = 0 hoặc không tồn tại.
3. Tìm các giá trị của hàm số tại các điểm tới hạn và cuối đoạn thẳng và chọn giá trị lớn nhất và nhỏ nhất trong số đó.