Ako susjedni uglovi. Susjedni i okomiti kutovi, njihova svojstva

1. Susjedni uglovi.

Nastavimo li stranicu nekog kuta preko njegova vrha, dobit ćemo dva kuta (sl. 72): ∠ABC i ∠CBD, u kojima je jedna stranica BC zajednička, a druge dvije, AB i BD, tvore ravnu crtu .

Dva kuta kojima je jedna stranica zajednička, a druge dvije tvore ravnu crtu nazivaju se susjednim kutovima.

Susjedni kutovi mogu se dobiti i na ovaj način: ako povučemo zraku iz neke točke na pravoj liniji (koja ne leži na danoj pravoj liniji), tada ćemo dobiti susjedne kutove.

Na primjer, ∠ADF i ∠FDV su susjedni kutovi (slika 73).

Susjedni kutovi mogu imati različite položaje (slika 74).

Susjedni kutovi zbrajaju ravni kut, pa zbroj dvaju susjednih kutova je 180°

Stoga se pravi kut može definirati kao kut jednak svom susjednom kutu.

Znajući vrijednost jednog od susjednih kutova, možemo pronaći vrijednost drugog susjednog kuta.

Na primjer, ako je jedan od susjednih kutova 54°, tada će drugi kut biti:

180° - 54° = l26°.

2. Vertikalni kutovi.

Produžimo li stranice kuta izvan njegova vrha, dobit ćemo okomiti kutovi. Na slici 75. kutovi EOF i AOC su okomiti; kutovi AOE i COF su također okomiti.

Dva se kuta nazivaju okomitima ako su stranice jednog kuta produžeci stranica drugog kuta.

Neka je ∠1 = \(\frac(7)(8)\) ⋅ 90° (slika 76). ∠2 uz njega bit će jednak 180° - \(\frac(7)(8)\) ⋅ 90°, tj. 1\(\frac(1)(8)\) ⋅ 90°.

Na isti način možete izračunati koliko su ∠3 i ∠4.

∠3 = 180° - 1\(\frac(1)(8)\) ⋅ 90° = \(\frac(7)(8)\) ⋅ 90°;

∠4 = 180° - \(\frac(7)(8)\) ⋅ 90° = 1\(\frac(1)(8)\) ⋅ 90° (Slika 77).

Vidimo da je ∠1 = ∠3 i ∠2 = ∠4.

Možete riješiti još nekoliko istih zadataka i svaki put ćete dobiti isti rezultat: okomiti kutovi su međusobno jednaki.

Međutim, kako bi bili sigurni da su vertikalni kutovi uvijek jednaki jedan drugome, nije dovoljno uzeti u obzir pojedinačne brojčani primjeri, jer zaključci izvedeni na temelju pojedinih primjera ponekad mogu biti pogrešni.

Valjanost svojstva okomitih kutova potrebno je provjeriti dokazom.

Dokaz se može provesti na sljedeći način (slika 78):

∠a +∠c= 180°;

∠b+∠c= 180°;

(budući da je zbroj susjednih kutova 180°).

∠a +∠c = ∠b+∠c

(budući da je lijeva strana ove jednakosti 180°, a desna također 180°).

Ova jednakost uključuje isti kut S.

Ako smo iz jednake vrijednosti oduzeti jednako, onda će ostati jednako. Rezultat će biti: ∠a = ∠b, tj. vertikalni kutovi su međusobno jednaki.

3. Zbroj kutova koji imaju zajednički vrh.

Na crtežu 79, ∠1, ∠2, ∠3 i ∠4 nalaze se na istoj strani pravca i imaju zajednički vrh na ovom pravcu. U zbroju, ovi kutovi čine ravni kut, tj.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

Na crtežu 80 ∠1, ∠2, ∠3, ∠4 i ∠5 imaju zajednički vrh. Zbroj tih kutova je puni kut, tj. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

Ostali materijali

Susjedni uglovi- dva ugla kojima je jedna stranica zajednička, a druga dva se nastavljaju jedan na drugi.

Zbroj susjednih kutova je 180°

Vertikalni kutovi su dva kuta u kojima su stranice jednog kuta nastavak stranica drugog kuta.

Vertikalni kutovi su jednaki.

2. Znakovi jednakosti trokuta:

potpisujem: Ako su dvije stranice i kut između njih jednog trokuta jednaki dvjema stranicama i kutu između njih drugog trokuta, tada su takvi trokuti sukladni.

II znak: Ako su stranice i dva uz nju susjedna kuta jednog trokuta jednaki stranici i dva uz nju susjedna kuta drugog trokuta, tada su takvi trokuti sukladni.

III znak: Ako su tri stranice jednog trokuta jednake trima stranicama drugog trokuta, tada su ti trokuti sukladni

3. Znakovi paralelnosti dviju linija: jednostrani kutovi, koji leže unakrsno i odgovaraju:

Dva pravca u ravnini nazivaju se paralelno ako se ne sijeku.

Unakrsno ležeći kutovi: 3 i 5, 4 i 6;

Jednostrani kutovi: 4 i 5, 3 i 6; riža. Stranica55

Odgovarajući kutovi: 1 i 5, 4 i 8, 2 i 6, 3 i 7;

Teorema: Ako su u sjecištu dviju pravaca transverzale kutovi jednaki, tada su pravci paralelni.

Teorema: Ako su u sjecištu dviju pravaca sekante odgovarajući kutovi jednaki, tada su pravci paralelni.

Teorema: Ako je u sjecištu dviju pravaca sekante zbroj jednostranih kutova jednak 180°, tada su pravci paralelni.

Teorema: ako su dva paralelna pravca presječena sekantom, tada su poprečno ležeći kutovi jednaki.

Teorema: ako su dva paralelna pravca presječena sekantom, tada su odgovarajući kutovi jednaki

Teorema: ako su dva paralelna pravca presječena sekantom, tada je zbroj jednostraničkih kutova 180°

4. Zbroj kutova trokuta:

Zbroj kutova trokuta je 180°

5. Svojstva jednakokračnog trokuta:

Teorem: B jednakokračan trokut bazni kutovi su jednaki.

Teorem: U jednakokračnom trokutu simetrala povučena na osnovicu je središnja i visina (srednja je obrnuto), (simetrala raspolavlja kut, središnja stranica raspolavlja stranicu, visina čini kut od 90°)

Znak: Ako su dva kuta trokuta jednaka, tada je trokut jednakokračan.

6. Pravokutni trokut:

Pravokutni trokut je trokut u kojem je jedan kut pravi kut (to jest, iznosi 90 stupnjeva)

U pravokutnom trokutu hipotenuza je duža od katete

1. Zbroj dva šiljasta kuta pravokutni trokut jednak 90°

2. Noga pravokutnog trokuta, koja leži nasuprot kutu od 30 °, jednaka je polovici hipotenuze

3. Ako je noga pravokutnog trokuta jednaka polovici hipotenuze, tada je kut nasuprot ove noge 30 °

7. Jednakostraničan trokut:

JEDNAKOSTRANIČAN TROKUT, ravna figura sa tri strane jednake dužine; tri unutarnji kutovi koje tvore strane također su jednake i jednake 60 °C.

8. Sin, cos, tg, ctg:

Sin= , Cos= , tg= , ctg= , tg= ,ctg=

9. Znakovi četverokuta^

Zbroj kutova četverokuta je 2 π = 360°.

Četverokut se može upisati u krug ako i samo ako je zbroj nasuprotnih kutova 180°

10. Znakovi sličnosti trokuta:

potpisujem: ako su dva kuta jednog trokuta jednaka dvama kutovima drugog, tada su ti trokuti slični

II znak: ako su dvije stranice jednog trokuta proporcionalne dvjema stranicama drugog trokuta i ako su kutovi između tih stranica jednaki, tada su ti trokuti slični.

III znak: ako su tri stranice jednog trokuta proporcionalne trima stranicama drugog, onda su takvi trokuti slični

11. Formule:

· Pitagorin poučak: a 2 +b 2 =c 2

· Teorem o grijehu:

· cos teorem:

· 3 formule površine trokuta:

· Površina pravokutnog trokuta: S= S=

· Površina jednakostraničnog trokuta:

· Površina paralelograma: S=ah

· Površina kvadrata: S = a2

· Površina trapeza:

· Površina romba:

· Površina pravokutnika: S=ab

· Jednakostraničan trokut. Visina: h=

· Trigonometrijska jedinica: sin 2 a+cos 2 a=1

· središnja linija trokut: S=

· Srednja linija trapeza:MK=

©2015-2019 stranica
Sva prava pripadaju njihovim autorima. Ova stranica ne polaže pravo na autorstvo, ali omogućuje besplatnu upotrebu.
Datum izrade stranice: 2017-12-12

POGLAVLJE I.

OSNOVNI KONCEPTI.

§jedanaest. SUSJEDNI I OKOMITI KUTOVI.

1. Susjedni uglovi.

Nastavimo li stranicu nekog kuta izvan njegova vrha, dobit ćemo dva kuta (slika 72): / Sunce i / SVD, u kojem je jedna stranica BC zajednička, a druge dvije AB i BD čine ravnu liniju.

Dva kuta kojima je jedna stranica zajednička, a druge dvije tvore ravnu crtu nazivaju se susjednim kutovima.

Susjedni kutovi mogu se dobiti i na ovaj način: ako povučemo zraku iz neke točke na pravoj liniji (koja ne leži na danoj pravoj liniji), tada ćemo dobiti susjedne kutove.
Na primjer, / ADF i / FDV - susjedni kutovi (slika 73).

Susjedni kutovi mogu imati različite položaje (slika 74).

Susjedni kutovi zbrajaju ravni kut, pa umma dva susjedna ugla je 2d.

Stoga se pravi kut može definirati kao kut jednak svom susjednom kutu.

Znajući vrijednost jednog od susjednih kutova, možemo pronaći vrijednost drugog susjednog kuta.

Na primjer, ako je jedan od susjednih kutova 3/5 d, tada će drugi kut biti jednak:

2d- 3 / 5 d= l 2 / 5 d.

2. Vertikalni kutovi.

Produžimo li stranice kuta izvan njegova vrha, dobit ćemo okomite kutove. Na crtežu 75 kutovi EOF i AOC su okomiti; kutovi AOE i COF su također okomiti.

Dva se kuta nazivaju okomitima ako su stranice jednog kuta produžeci stranica drugog kuta.

Neka / 1 = 7 / 8 d(Slika 76). Uz njega / 2 će biti jednako 2 d- 7 / 8 d, tj. 1 1/8 d.

Na isti način možete izračunati čemu su jednaki / 3 i / 4.
/ 3 = 2d - 1 1 / 8 d = 7 / 8 d; / 4 = 2d - 7 / 8 d = 1 1 / 8 d(Slika 77).

Vidimo to / 1 = / 3 i / 2 = / 4.

Možete riješiti još nekoliko istih zadataka i svaki put ćete dobiti isti rezultat: okomiti kutovi su međusobno jednaki.

Međutim, da bismo bili sigurni da su okomiti kutovi uvijek međusobno jednaki, nije dovoljno razmatrati pojedinačne numeričke primjere, jer zaključci izvedeni iz pojedinih primjera ponekad mogu biti pogrešni.

Valjanost svojstva okomitih kutova potrebno je provjeriti zaključivanjem, dokazom.

Dokaz se može provesti na sljedeći način (slika 78):

/ a +/ c = 2d;
/ b+/ c = 2d;

(jer je zbroj susjednih kutova 2 d).

/ a +/ c = / b+/ c

(pošto je lijeva strana ove jednakosti jednaka 2 d, a njegova desna strana također je jednaka 2 d).

Ova jednakost uključuje isti kut S.

Ako od jednakih vrijednosti oduzmemo jednako, onda će ostati jednako. Rezultat će biti: / a = / b, tj. vertikalni kutovi su međusobno jednaki.

Razmatrajući pitanje okomitih kutova, najprije smo objasnili koji se kutovi nazivaju okomitima, tj. dali smo definicija okomiti uglovi.

Zatim smo iznijeli sud (tvrdnju) o jednakosti okomitih kutova i dokazom smo se uvjerili u valjanost tog suda. Takve presude, čija se valjanost mora dokazati, nazivaju se teoremi. Stoga smo u ovom odjeljku dali definiciju okomitih kutova, a također smo naveli i dokazali teorem o njihovom svojstvu.

U budućnosti, proučavajući geometriju, stalno ćemo se morati susretati s definicijama i dokazima teorema.

3. Zbroj kutova koji imaju zajednički vrh.

Na crtežu 79 / 1, / 2, / 3 i / 4 nalaze se na istoj strani pravca i imaju zajednički vrh na tom pravcu. U zbroju, ovi kutovi čine ravni kut, tj.
/ 1+ / 2+/ 3+ / 4 = 2d.

Na crtežu 80 / 1, / 2, / 3, / 4 i / 5 imaju zajednički vrh. Zbrojeno, ovi kutovi čine puni kut, tj. / 1 + / 2 + / 3 + / 4 + / 5 = 4d.

Vježbe.

1. Jedan od susjednih kutova je 0,72 d. Izračunajte kut koji čine simetrale ovih susjednih kutova.

2. Dokaži da simetrale dvaju susjednih kutova tvore pravi kut.

3. Dokažite da ako su dva kuta jednaka, onda su im jednaki i susjedni kutovi.

4. Koliko je pari susjednih uglova na crtežu 81?

5. Može li se par susjednih kutova sastojati od dva šiljasta kuta? iz dva tupa kuta? iz pravog i tupog kuta? iz pravog i oštrog kuta?

6. Ako je jedan od susjednih kutova pravi, što se onda može reći o vrijednosti kuta koji mu je pridružen?

7. Ako u sjecištu dviju ravnih linija postoji jedan pravi kut, što se onda može reći o veličini preostala tri kuta?

Na ovu lekciju sami ćemo razmotriti i razumjeti koncept susjednih kutova. Razmotrimo teorem koji ih se tiče. Uvedimo pojam "okomiti kutovi". Razmotrite potkrepljujuće činjenice u vezi s ovim kutovima. Zatim ćemo formulirati i dokazati dvije korolare o kutu između simetrala okomitih kutova. Na kraju lekcije razmotrit ćemo nekoliko problema posvećenih ovoj temi.

Započnimo našu lekciju konceptom "susjedni kutovi". Slika 1 prikazuje razvijeni kut ∠AOC i polupravu OB koja taj kut dijeli na 2 kuta.

Riža. 1. Kut ∠AOC

Promotrimo kutove ∠AOB i ∠BOC. Posve je očito da imaju zajedničku stranicu VO, dok su stranice AO i OS suprotne. Zrake OA i OS se međusobno nadopunjuju, što znači da leže na istoj ravnoj liniji. Kutovi ∠AOB i ∠BOC su susjedni.

Definicija: Ako dva kuta imaju zajedničku stranicu, a druge dvije stranice su komplementarne zrake, tada se ti kutovi nazivaju srodni.

Teorem 1: Zbroj susjednih kutova je 180 o.

Riža. 2. Crtež za teorem 1

∠MOL + ∠LON = 180o. Ova tvrdnja je točna jer zraka OL dijeli ravni kut ∠MON na dva susjedna kuta. Odnosno, ne znamo stupnjeve mjere niti jednog od susjednih kutova, već znamo samo njihov zbroj - 180 o.

Razmotrimo sjecište dviju linija. Na slici je prikazano sjecište dviju pravaca u točki O.

Riža. 3. Vertikalni kutovi ∠BOA i ∠COD

Definicija: Ako su stranice jednog kuta nastavak drugog kuta, onda se takvi kutovi nazivaju okomitima. Zato su na slici prikazana dva para okomitih kutova: ∠AOB i ∠COD, kao i ∠AOD i ∠BOC.

Teorem 2: Vertikalni kutovi su jednaki.

Poslužimo se slikom 3. Promotrimo razvijeni kut ∠AOC. ∠AOB \u003d ∠AOC - ∠BOC \u003d 180 o - β. Promotrimo razvijeni kut ∠BOD. ∠COD = ∠BOD - ∠BOC = 180 o - β.

Iz ovih razmatranja zaključujemo da je ∠AOB = ∠COD = α. Slično, ∠AOD = ∠BOC = β.

Posljedica 1: Kut između simetrala susjednih kutova je 90°.

Riža. 4. Crtež za posljedicu 1

Kako je OL simetrala kuta ∠BOA, onda je kut ∠LOB = , slično kao i ∠BOK = . ∠LOK = ∠LOB + ∠BOK = + = . Zbroj kutova α + β jednak je 180 o jer su ti kutovi susjedni.

Posljedica 2: Kut između simetrala okomitih kutova je 180°.

Riža. 5. Crtež za posljedicu 2

KO je simetrala ∠AOB, LO je simetrala ∠COD. Očito je ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Zbroj kutova α + β jednak je 180 o jer su ti kutovi susjedni.

Razmotrimo neke zadatke:

Odredite kut uz ∠AOC ako je ∠AOC = 111 o.

Napravimo crtež za zadatak:

Riža. 6. Crtanje na primjer 1

Kako su ∠AOC = β i ∠COD = α susjedni kutovi, tada je α + β = 180 o. Odnosno, 111 o + β \u003d 180 o.

Dakle, β = 69 o.

Ova vrsta problema iskorištava teorem o zbroju susjednih kutova.

Jedan od susjednih kutova je pravi kut, koji (oštar, tupi ili pravi) je drugi kut?

Ako je jedan od kutova prav, a zbroj ta dva kuta iznosi 180°, tada je i drugi kut prav. Ovim se zadatkom provjerava znanje o zbroju susjednih kutova.

Je li točno da su susjedni kutovi pravi kutovi ako su jednaki?

Napravimo jednadžbu: α + β = 180 o, ali kako je α = β, onda je β + β = 180 o, što znači β = 90 o.

Odgovor: Da, izjava je točna.

S obzirom na dva jednaki kutovi. Je li istina da će i njima susjedni kutovi biti jednaki?

Riža. 7. Crtanje na primjer 4

Ako su dva kuta jednaka α, tada će njihovi odgovarajući susjedni kutovi biti 180 o - α. Odnosno, oni će biti jednaki jedni drugima.

Odgovor: Izjava je istinita.

Aleksandrov A.D., Werner A.L., Ryzhik V.I. itd. Geometrija 7. - M.: Prosvjeta.
Atanasjan L.S., Butuzov V.F., Kadomcev S.B. i dr. Geometrija 7. 5. izd. - M.: Prosvjeta.
\Butuzov V.F., Kadomcev S.B., Prasolova V.V. Geometrija 7 / V.F. Butuzova, S.B. Kadomcev, V.V. Prasolov, uredio V.A. Sadovnichy. - M.: Obrazovanje, 2010.

Mjerenje segmenata ().
Opća lekcija o geometriji u 7. razredu ().
Ravna linija, segment ().

Broj 13, 14. Butuzov V.F., Kadomcev S.B., Prasolova V.V. Geometrija 7 / V.F. Butuzova, S.B. Kadomcev, V.V. Prasolov, uredio V.A. Sadovnichy. - M.: Obrazovanje, 2010.
Nađi dva susjedna kuta ako je jedan od njih 4 puta veći od drugog.
S obzirom na kut. Izgradite susjedne i okomite kutove za to. Koliko se takvih uglova može izgraditi?
* U kojem slučaju se dobiva više parova okomitih kutova: kada se tri pravca sijeku u jednoj točki ili u tri točke?

na temu: Susjedni i okomiti kutovi, njihova svojstva.

(3 lekcije)

Kao rezultat proučavanja teme potrebno vam je:

BITI U MOGUĆNOSTI:

Pojmovi: susjedni i okomiti kutovi, okomiti pravci

Razlikovati susjedne i okomite kutove

Teoremi o susjednim i okomitim kutovima

Rješavanje problema korištenjem svojstava susjednih i okomitih kutova

Svojstva susjednih i okomitih kutova

Konstruirajte susjedne i okomite kutove okomite na pravce

KNJIŽEVNOST:

1. Geometrija. 7. razred. Zh.Kaidasov, G. Dosmagambetova, V. Abdiev. Almaty "Mektep". 2012

2. Geometrija. 7. razred. K.O. Bukubaeva, A.T. Mirazov. AlmatyAtamura". 2012

3. Geometrija. 7. razred. Metodičko uputstvo. K.O. Bukubaeva. AlmatyAtamura". 2012

4. Geometrija. 7. razred. Didaktički materijal. A.N.Shynybekov. AlmatyAtamura". 2012

5. Geometrija. 7. razred. Zbirka zadataka i vježbi. K. O. Bukubaeva, A. T. Mirazova. AlmatyAtamura". 2012

Zapamtite da morate raditi prema algoritmu!

Ne zaboravite položiti test, bilježite na marginama,

Molimo ne ostavljajte pitanja koja imate bez odgovora.

Budite objektivni tijekom recenzije, pomoći će i vama i onom

koga provjeravaš.

ŽELIM TI USPJEH!

ZADATAK №1.

Pročitajte definiciju i naučite (2b):

Definicija. Kutovi kojima je jedna stranica zajednička, a druge dvije stranice su dodatne zrake, nazivaju se susjednim.

2) Naučite i zapišite teorem u bilježnicu: (2b)

Zbroj susjednih kutova je 180.

dano:

∠ ANM i∠ DOV - zadani susjedni kutovi

OD - zajednička strana

Dokazati:

∠ AOD+∠ DOV = 180

Dokaz:

Na temelju aksiomaIII 4:

∠ AOD+∠ DOV =∠ AOW.

∠ AOV - raspoređen. Posljedično,

∠ AOD+∠ DOV = 180

Teorem je dokazan.

3) Iz teorema slijedi: (2b)

1) Ako su dva kuta jednaka, jednaki su im i susjedni kutovi;

2) ako su susjedni kutovi jednaki, tada stupanjska mjera svaki od njih je jednak 90°.

Zapamtiti!

Kut jednak 90° naziva se pravim kutom.

Kut manji od 90° naziva se oštar kut.

Kut veći od 90°, a manji od 180° naziva se tupi kut.

Pravi kut Oštri kut Tupi kut

Kako je zbroj susjednih kutova 180°, onda

1) kut uz pravi kut, pravo;

2) kut uz oštar kut je tup;

3) kut pridružen tupom kutu je oštar.

4) Razmotrimo rješenje uzorka hadachi:

a) Dano:∠ hki∠ kl- susjedni;∠ hkviše∠ klna 50°.

Pronaći:∠ hki∠ kl.

Rješenje: Neka∠ kl= x, tada∠ hk= x + 50°. Po svojstvu o zbroju susjednih kutova∠ kl + ∠ hk= 180°.

x + x + 50° = 180°;

2x = 180° - 50°;

2x = 130°;

x = 65°.

∠ kl= 65°;∠ hk= 65°+ 50° = 115°.

Odgovor: 115° i 65°.

b) Neka∠ kl= x, tada∠ hk= 3x

x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.

Odgovor: 135° i 45°.

5) Radite s definicijom susjednih uglova: (2 b)

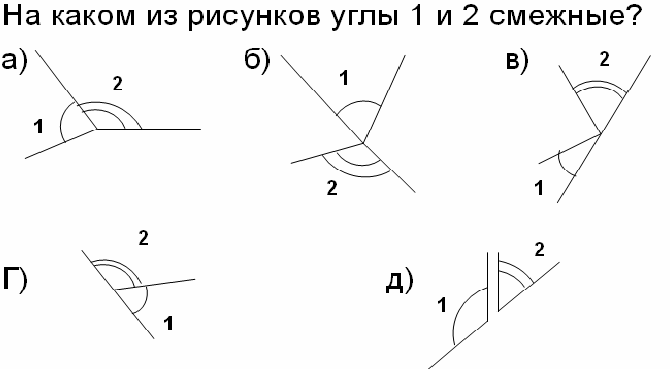
6) Pronađite pogreške u definicijama: (2b)

Proći test #1

Zadatak broj 2

1) Konstruiraj 2 susjedna kuta tako da im zajednička stranica prolazi kroz točku C, a stranica jednog od kutova poklapa se sa zrakom AB. (2b)

2). Praktični rad otkriti svojstva susjednih uglova: (5b)

Napredak

1. Izgradite kutsusjedni kuta , akoa : oštro, ravno, tupo.

2. Izmjerite kutove.

3. Unesite podatke mjerenja u tablicu.

4. Odredite omjer između vrijednosti kutovaa i.

5. Zaključite o svojstvu susjednih kutova.

Proći test #2

Zadatak broj 3

Nacrtaj neprošireno∠ AOB i imenuj zrake koje su stranice tog kuta.

Nacrtaj gredu O koja je nastavak grede OA i gredu OD koja je nastavak grede OB.

Napiši u bilježnicu: kutove∠ AOB i∠ SOD se nazivaju vertikalni. (3b)

Nauči i zapiši u bilježnicu: (4b)

Definicija: Nazivaju se kutovi čije su stranice jedne od njih komplementarne zrake drugeokomiti uglovi.

< 1 i<2, <3 и <4 okomiti kutovi

zrakeODiOA , OCiOEsu po paru komplementarne zrake.

Teorem: Vertikalni kutovi su jednaki.

Dokaz.

Okomiti kutovi nastaju kada se dvije linije sijeku. Neka su pravci a ibsijeku se u točki O.∠ 1 i∠ 2 - okomiti kutovi.

∠ AOC-razmještena sredstva∠ AOC= 180°. Međutim∠ 1+ ∠ 2= ∠ AOC, tj.

∠ 3+ ∠ 1= 180°, pa imamo:

∠ 1= 180 - ∠ 3. (1)

Imamo i to∠ DOV= 180°, dakle∠ 2+ ∠ 3= 180° ili∠ 2= 180°- ∠ 3. (2)

Kako su u jednakosti (1) i (2) izravni dijelovi jednaki, onda∠ 1= ∠ 2.

Teorem je dokazan.

5). Rad s definicijom okomitih kutova: (2b)

6) Pronađite grešku u definiciji: (2b).

Proći test #3

Zadatak broj 4

1) Praktičan rad na otkrivanju svojstava okomitih kutova: (5b)

Napredak:

1. Konstruiraj kut β okomiti kutα , akoα :

oštar, ravan, tup.

2. Izmjerite kutove.

3. Unesite podatke mjerenja u tablicu

4. Pronađite odnos između vrijednosti kutova α i β.

5. Zaključite o svojstvu okomitih kutova.

2) Dokaz svojstava susjednih i okomitih kutova. (3b)

2) Razmotrite primjer rješenjapakao.

Zadatak. Pravci AB i CD sijeku se u točki O tako da je∠ AOD = 35°. Odredite kutove AOC i BOC.

Riješenje:

1) Kutovi AOD i AOC su susjedni, dakle∠ BOC= 180° - 35° = 145°.

2) Kutovi AOC i BOC su također susjedni, dakle∠ BOC= 180° - 145° = 35°.

Sredstva,∠ BOC = ∠ AOD = 35°, a ti su kutovi okomiti. Pitanje: Je li istina da su svi okomiti kutovi jednaki?

3) Rješavanje zadataka na gotovim crtežima: (3b)

1. Odredite kutove AOB, AOD, COD.

3) Nađite kutove BOC, FOA.: (3b)

3. Pronađite susjedne i okomite kutove na slici. Neka su poznate vrijednosti dva kuta označena na crtežu, 28? i 90?. Je li moguće pronaći vrijednosti preostalih kutova bez mjerenja (2b)

Proći test #4

Zadatak broj 5

Provjerite svoje znanje ispunjavanjemverifikacijski rad br. 1

Zadatak broj 6

1) Dokažite samostalno svojstva okomitih kutova i te dokaze zapišite u bilježnicu. (3b)

Učenici samostalno, koristeći svojstva okomitih i susjednih kutova, moraju obrazložiti činjenicu da ako je u sjecištu dviju pravaca jedan od formiranih kutova pravi, onda su i ostali kutovi pravi.

2) Riješite dva problema na izbor:

1. Mjere stupnjeva susjednih kutova odnose se kao 7:2. Pronađite ove kutove. (2b)

2. Jedan od kutova nastalih u sjecištu dvaju pravaca je 11 puta manji od drugog. Odredi svaki od kutova (3b)

3. Nađi susjedne kutove ako se njihova razlika i zbroj odnose kao 2 : 9. (3b)

Zadatak broj 7

Dobro napravljeno! Možete prijeći na testni rad broj 2.

Verifikacijski rad br. 1.

Odlučite se za izbor bilo koje od opcija (10b)

opcija 1

<1 и <2,

<3 и <2,

G)<1 и <3. Какие это углы?

Povezano

e) Nacrtajte (na oko) kut od 30° i< ABC, susjedna datoj

f) Koliki su okomiti kutovi?

Dva se kuta nazivaju okomitima ako su orni jednaki.

g) Iz točke A povuci dva pravca okomita na pravaca

Može se povući samo jedna ravna linija.

opcija 2

1. Učenik je, odgovarajući na pitanja nastavnika, dao odgovarajuće odgovore. Provjerite jesu li točni označavanjem u trećem stupcu riječima "DA", "NE", "NE ZNAM". Ako je “NE”, napišite točan odgovor ili dodajte onaj koji nedostaje.

<1 и <4,

<2 и <4

D)<1 и < 3 смежные?

Ne. Oni su okomiti

E) Koji se pravci nazivaju okomitima?

Dva se pravca nazivaju okomitima ako se sijeku pod pravim kutom.

G) Nacrtajte okomite kutove tako da su im stranice okomite crte.