Ontbinding van getallen in priemfactoren, methoden en voorbeelden van ontleding. Krijg de canonieke ontleding van een getal in priemfactoren

College 14 Willekeurige processen Canonieke uitbreiding van willekeurige processen. Spectrale expansie van een stationair willekeurig proces. SluLezing 14
willekeurige processen
Canonieke uitbreiding van willekeurige processen.
Spectrale ontleding van een stationaire willekeurige
werkwijze. Willekeurige processen met onafhankelijke
secties. Markov-processen en Markov-ketens.
Normale willekeurige processen. Periodiek
niet-stationaire willekeurige processen
(Akhmetov SK)

Canonieke ontleding van stochastische processen

Elke SP X(t) kan zijn gepresenteerd in
de vorm van zijn expansie, d.w.z. als een som
elementaire processen:
Vk - willekeurige variabelen
φk(t) zijn niet-willekeurige functies (sinusoïden, exponenten, macht)
functies, enz.)
Een speciaal geval van een dergelijke decompositie is de Canonical
ontleding
SP X(t) met de vorm
mx(t) = M – wiskundige verwachting van SP X(t)
V1, V2...Vk – ongecorreleerde en gecentreerde SW
D1, D2 …Dk- SW-dispersies V1, V2…Vk
φk(t) zijn niet-willekeurige functies van het argument t
Willekeurige variabelen V1, V2…Vk heten de coëfficiënten van de canonieke
ontleding,
en niet-willekeurige functies φ1(t), φ2(t) φk(t) - coördinaatfuncties
canonieke ontbinding

De belangrijkste kenmerken van de SP gegeven door de canonieke uitbreiding

M - wiskundige verwachting van SP X(t)
Kx(t,t') – correlatiefunctie van SP X(t)
Uitdrukking
- canonieke uitbreiding van de correlatie
functies
Als t=t', dan in overeenstemming met de eerste
eigenschap van de correlatiefunctie
Uitdrukking
Dk(t) -
spreiding
canonieke uitbreiding van de variantie van de SP X(t)

Spectrale ontleding van stationaire SP

Stationaire joint venture kan zijn. vertegenwoordigd door de canonieke ontbinding
Vk en Uk zijn niet-gecorreleerde en gecentreerde SW's met dispersies
D=D=Dk
ω - niet-willekeurige waarde (frequentie)
In dit geval is de canonieke uitbreiding van de correlatiefunctie
wordt gedefinieerd door de uitdrukking
Vertegenwoordigd
canoniek
ontleding
joint venture
X(t)
genaamd
spectrale ontleding van de SP en
uitgedrukt als
Θk - fase van de harmonische oscillatie van de elementaire stationaire SP,
dat is de SW uniform verdeeld in het interval (0, 2π);
Zk - SW, wat de amplitude is van de harmonische oscillatie
elementaire stationaire joint venture

Spectrale ontleding van stationaire SP (2)

De willekeurige variabelen Θk en Zk zijn afhankelijk en daarvoor geldt het volgende:
Vk = Zk cos k
Uk = Zk sin Θk
Stationaire joint venture kan zijn. gepresenteerd als een som van harmonische
oscillaties met willekeurige amplitudes Zk en willekeurige fasen Θk on
verschillende niet-willekeurige frequenties ωk
De correlatiefunctie van de stationaire SP X(t) is even
functie van zijn argument, d.w.z. kx(τ) = kx(-τ). Daarom is het op het interval (-T,
T) kan worden uitgebreid in een Fourier-reeks in even (cosinus) harmonischen:
De variantie van de stationaire SP X(t) is gelijk aan
som
varianties
allemaal
harmonischen
zijn
spectrale ontleding
De afhankelijkheid Dk = f(wk) wordt het discrete spectrum van varianties genoemd of
discrete spectrum van de stationaire SP.

Spectrale ontleding van stationaire SP (3)

bij
→ 0 er zal een overgang zijn naar een continu spectrum
Sx(ω) - spectrale dichtheid
Dus de correlatiefunctie en spectrale dichtheid
zijn gerelateerd door de cosinus Fourier-transformatie. Daarom is de spectrale
de dichtheid van een stationaire joint venture kan zijn: uitgedrukt door de correlatie
functie op formule

Stochastische processen met onafhankelijke secties

In de hydrologie wordt aangenomen dat een reeks overeenkomt met een model van willekeurige
waarden als er geen significante correlatie is tussen leden van deze serie
voor elke dienst τ.
Een willekeurig proces met onafhankelijke secties is een SP waarvoor:
voor t en t'
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx voor τ = 0 en 0 voor τ ≠ 0)
Een dergelijk proces is stationair en heeft een ergodic
eigendom
Voor dergelijke processen zijn de kenmerken van de eendimensionale distributiewet
kan zowel voor elke sectie als voor elke (het is genoeg) worden geschat
continue) implementatie
Dergelijke processen hebben geen correlatie tussen leden binnen enige
implementatie
Bij aanvaarding van een dergelijk model wordt aangenomen dat een aantal hydrologische grootheden
vertegenwoordigt één implementatie van de joint venture
Een willekeurig proces met onafhankelijke secties wordt soms genoemd
"witte ruis" naar analogie met wit licht

Markov-processen en Markov-ketens

willekeurig proces
heet Markov als voor enige
moment van tijd t de waarschijnlijkheid van elk van de toestanden van het systeem in de toekomst
(voor t > t0) hangt alleen af ​​van zijn toestand in het heden (voor t = t0) en niet
hangt af van de staat in het verleden (bij t< t0)
Een Markov-keten of een eenvoudige Markov-keten wordt genoemd
Markov-proces met discrete toestand en discrete tijd
De Markov SP wordt volledig beschreven door de tweedimensionale wet
verdeling. Als het Markov-proces stationair is en
ergodisch, dan kunnen de kenmerken ervan worden geschat vanaf één
implementatie.
Een keten waarin de voorwaardelijke kansen van staten in de toekomst afhangen van
van zijn toestand in verschillende eerdere stappen, wordt complex genoemd
Markov-keten.

Normale (Gaussiaanse) willekeurige processen

Een normaal (Gaussiaans) willekeurig proces X(t) heet
SP, waarin in alle secties de SW X(ti) een normaal heeft
verdeling
Periodiek niet-stationaire SP
Bij het studeren van jaarlijks, maandelijks, dagelijks, enz. processen, meestal
er zijn intra-jaarlijkse, enz. fluctuaties. In dit geval, zoals
wiskundig model, u kunt het model periodiek gebruiken
niet-stationair stochastisch proces (PNSP)
Van een willekeurig proces wordt gezegd dat het periodiek niet-stationair is als
zijn probabilistische kenmerken zijn invariant onder verschuivingen van
positief getal T. Bijvoorbeeld met een discrete stap van één maand
de invariantie moet behouden blijven in ploegen 12, 24, 36, enz.

Dit artikel geeft antwoord op de vraag over het ontbinden van een getal in bladen. Overweeg een algemeen idee van ontbinding met voorbeelden. Laten we de canonieke vorm van de decompositie en zijn algoritme analyseren. Alle alternatieve methoden zullen worden overwogen met behulp van de tekens van deelbaarheid en de tafel van vermenigvuldiging.

Yandex.RTB RA-339285-1

Wat betekent het om een ​​getal in priemfactoren te ontbinden?

Laten we eens kijken naar het concept van priemfactoren. Het is bekend dat elke priemfactor een priemgetal is. In een product van de vorm 2 7 7 23 hebben we dat we 4 priemfactoren hebben in de vorm 2 , 7 , 7 , 23 .

Factoring omvat de weergave ervan als producten van priemgetallen. Als je het getal 30 moet ontleden, krijgen we 2, 3, 5. De invoer heeft de vorm 30 = 2 3 5 . Het is mogelijk dat de vermenigvuldigers herhaald kunnen worden. Een getal als 144 heeft 144 = 2 2 2 2 3 3 .

Niet alle getallen zijn vatbaar voor ontbinding. Getallen die groter zijn dan 1 en gehele getallen zijn, kunnen worden ontbonden. Priemgetallen zijn alleen deelbaar door 1 en zichzelf wanneer ze worden ontbonden, dus het is onmogelijk om deze getallen als een product weer te geven.

Wanneer z verwijst naar gehele getallen, wordt het weergegeven als een product van a en b, waarbij z wordt gedeeld door a en b. Samengestelde getallen worden ontleed in priemfactoren met behulp van de basisstelling van de rekenkunde. Als het getal groter is dan 1, dan is het ontbinden in factoren p 1 , p 2 , … , p n heeft de vorm a = p 1 , p 2 , … , p n . Ontbinding wordt aangenomen in een enkele variant.

Canonieke ontleding van een getal in priemfactoren

Factoren kunnen tijdens de ontbinding worden herhaald. Ze zijn compact geschreven met behulp van een graad. Als we bij het ontbinden van het getal a een factor p 1 hebben, die s 1 keer voorkomt en zo verder p n - s n keer. Dus de ontleding heeft de vorm a=p 1 s 1 a = p 1 s 1 p 2 s 2 … p n s n. Deze invoer wordt de canonieke ontleding van een getal in priemfactoren genoemd.

Wanneer we het getal 609840 ontleden, krijgen we dat 609 840 = 2 2 2 2 3 3 5 7 11 11 , de canonieke vorm zal 609 840 = 2 4 3 2 5 7 11 2 zijn. Met behulp van de canonieke uitbreiding kun je alle delers van een getal en hun getal vinden.

Om goed te ontbinden in factoren, moet u kennis hebben van priemgetallen en samengestelde getallen. Het gaat erom een ​​opeenvolgend aantal delers te krijgen van de vorm p 1 , p 2 , … , p n nummers een , een 1 , een 2 , … , een n - 1, dit maakt het mogelijk om a = p 1 een 1, waarbij a 1 \u003d a: p 1, a \u003d p 1 a 1 \u003d p 1 p 2 a 2, waarbij a 2 \u003d a 1: p 2, ..., a \u003d p 1 p 2 . .. ... p n a n , waar een n = een n - 1: p n. Op vertoning van de bon een n = 1, dan de gelijkheid a = p 1 p 2 … p n we verkrijgen de vereiste ontleding van het getal a in priemfactoren. Let erop dat p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Om de kleinste gemene delers te vinden, moet je de priemgetallentabel gebruiken. Dit wordt gedaan aan de hand van het voorbeeld van het vinden van de kleinste priemdeler van het getal z. Als we priemgetallen 2, 3, 5, 11 enzovoort nemen, en we delen het getal z erdoor. Aangezien z geen priemgetal is, moet u er rekening mee houden dat de kleinste priemdeler niet groter zal zijn dan z . Te zien is dat er geen delers van z zijn, dan is het duidelijk dat z een priemgetal is.

voorbeeld 1

Beschouw het voorbeeld van het getal 87. Wanneer het wordt gedeeld door 2, hebben we dat 87: 2 \u003d 43 met een rest van 1. Hieruit volgt dat 2 geen deler kan zijn, de deling moet volledig worden gemaakt. Wanneer gedeeld door 3, krijgen we dat 87: 3 = 29. Vandaar de conclusie - 3 is de kleinste priemdeler van het getal 87.

Bij het ontbinden in priemfactoren is het noodzakelijk om een ​​tabel met priemgetallen te gebruiken, waarbij a. Bij het ontleden van 95 moeten ongeveer 10 priemgetallen worden gebruikt en bij het ontleden van 846653 ongeveer 1000.

Overweeg het priemfactorisatie-algoritme:

• de kleinste factor vinden met een deler p 1 van een getal a door de formule a 1 \u003d a: p 1, wanneer een 1 \u003d 1, dan is a een priemgetal en is opgenomen in de factorisatie, indien niet gelijk aan 1, dan a \u003d p 1 a 1 en volg het punt hieronder;
• het vinden van een priemdeler p 2 van een 1 door opeenvolgende optelling van priemgetallen, met a 2 = a 1: p 2 , wanneer een 2 = 1 , dan heeft de expansie de vorm a = p 1 p 2 , wanneer een 2 \u003d 1, dan een \u003d p 1 p 2 a 2 , en we maken de overstap naar de volgende stap;
• itereren over priemgetallen en een priemdeler vinden p 3 nummers een 2 volgens de formule a 3 \u003d a 2: p 3 wanneer een 3 \u003d 1 , dan krijgen we dat a = p 1 p 2 p 3 , indien niet gelijk aan 1 dan a = p 1 p 2 p 3 a 3 en ga verder met de volgende stap;
• vind een priemdeler p nee nummers een n - 1 door optelling van priemgetallen met p n - 1, net zoals een n = een n - 1: p n, waarbij a n = 1 , de stap definitief is, als resultaat krijgen we dat a = p 1 p 2 … p n .

Het resultaat van het algoritme wordt geschreven in de vorm van een tabel met ontbonden factoren met een verticale balk achtereenvolgens in een kolom. Beschouw de onderstaande figuur.

Het resulterende algoritme kan worden toegepast door getallen te ontbinden in priemfactoren.

Bij het in rekening brengen van priemfactoren moet het basisalgoritme worden gevolgd.

Voorbeeld 2

Ontleed het getal 78 in priemfactoren.

Oplossing

Om de kleinste priemdeler te vinden, is het nodig om alle priemgetallen in 78 op te sommen. Dat wil zeggen, 78: 2 = 39. Delen zonder rest, dus dit is de eerste priemdeler, die we aanduiden als p 1. We krijgen dat a 1 = a: p 1 = 78: 2 = 39. We kwamen tot een gelijkheid van de vorm a = p 1 a 1 , waarbij 78 = 2 39 . Dan is een 1 = 39 , dat wil zeggen dat u naar de volgende stap moet gaan.

Laten we ons concentreren op het vinden van een priemdeler p2 nummers een 1 = 39. Je moet priemgetallen sorteren, dat wil zeggen 39: 2 = 19 (resterende 1). Aangezien deling een rest heeft, is 2 geen deler. Bij het kiezen van het getal 3 krijgen we dat 39: 3 = 13. Dit betekent dat p 2 = 3 de kleinste priemdeler is van 39 door a 2 = a 1: p 2 = 39: 3 = 13 . We verkrijgen een gelijkheid van de vorm a = p 1 p 2 een 2 in de vorm 78 = 2 3 13 . We hebben dat een 2 = 13 niet gelijk is aan 1 , dan moeten we verder gaan.

De kleinste priemdeler van het getal a 2 = 13 wordt gevonden door getallen te tellen, beginnend bij 3 . We krijgen dat 13: 3 = 4 (rest. 1). Hieruit blijkt dat 13 niet deelbaar is door 5, 7, 11, omdat 13: 5 = 2 (rest. 3), 13: 7 = 1 (rest. 6) en 13: 11 = 1 (rest. 2). Je kunt zien dat 13 een priemgetal is. De formule ziet er als volgt uit: a 3 \u003d a 2: p 3 \u003d 13: 13 \u003d 1. We hebben dat een 3 = 1 , wat het einde van het algoritme betekent. Nu worden de factoren geschreven als 78 = 2 3 13 (a = p 1 p 2 p 3) .

Antwoorden: 78 = 2 3 13 .

Voorbeeld 3

Ontleed het getal 83.006 in priemfactoren.

Oplossing

De eerste stap omvat factoring p 1 = 2 en a 1 \u003d a: p 1 \u003d 83 006: 2 \u003d 41 503, waarbij 83 006 = 2 41 503 .

De tweede stap gaat ervan uit dat 2 , 3 en 5 geen priemdelers zijn voor a 1 = 41503 maar 7 is een priemdeler omdat 41503: 7 = 5929 . We krijgen dat p 2 \u003d 7, a 2 \u003d a 1: p 2 \u003d 41 503: 7 \u003d 5 929. Het is duidelijk dat 83 006 = 2 7 5 929 .

Het vinden van de kleinste priemdeler p 4 tot het getal a 3 = 847 is 7 . Het is te zien dat een 4 \u003d a 3: p 4 \u003d 847: 7 \u003d 121, dus 83 006 \u003d 2 7 7 7 121.

Om de priemdeler van het getal a 4 = 121 te vinden, gebruiken we het getal 11, dat wil zeggen p 5 = 11. Dan krijgen we een uitdrukking van de vorm een 5 \u003d een 4: p 5 \u003d 121: 11 \u003d 11, en 83 006 = 2 7 7 7 11 11 .

Voor nummer een 5 = 11 nummer p6 = 11 is de kleinste priemdeler. Vandaar een 6 \u003d a 5: p 6 \u003d 11: 11 \u003d 1. Dan een 6 = 1. Dit geeft het einde van het algoritme aan. De vermenigvuldigers worden geschreven als 83006 = 2 7 7 7 11 11 .

De canonieke notatie van het antwoord zal de vorm aannemen 83 006 = 2 7 3 11 2 .

Antwoorden: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2 .

Voorbeeld 4

Factoriseer het getal 897 924 289.

Oplossing

Om de eerste priemfactor te vinden, herhaalt u de priemgetallen, beginnend met 2. Het einde van de telling valt op het nummer 937. Dan p 1 = 937, een 1 = a: p 1 = 897 924 289: 937 = 958 297 en 897 924 289 = 937 958 297.

De tweede stap van het algoritme is het opsommen van kleinere priemgetallen. Dat wil zeggen, we beginnen met het nummer 937. Het getal 967 kan als priemgetal worden beschouwd, omdat het een priemdeler is van het getal a 1 = 958 297. Vanaf hier krijgen we dat p 2 \u003d 967, dan een 2 \u003d a 1: p 1 \u003d 958 297: 967 \u003d 991 en 897 924 289 \u003d 937 967 991.

De derde stap zegt dat 991 een priemgetal is, omdat het geen priemdeler heeft die kleiner is dan of gelijk is aan 991 . De geschatte waarde van de radicale uitdrukking is 991< 40 2 . Иначе запишем как 991 < 40 2 . Hieruit blijkt dat p 3 \u003d 991 en a 3 \u003d a 2: p 3 \u003d 991: 991 \u003d 1. We krijgen dat de ontleding van het getal 897 924 289 in priemfactoren wordt verkregen als 897 924 289 \u003d 937 967 991.

Antwoorden: 897 924 289 = 937 967 991 .

Deelbaarheidstests gebruiken voor priemfactorisatie

Om een ​​getal op te splitsen in priemfactoren, moet u het algoritme volgen. Bij kleine getallen is het toegestaan ​​om de tafel van vermenigvuldiging en deelbaarheidstekens te gebruiken. Laten we dit bekijken met voorbeelden.

Voorbeeld 5

Als het nodig is om 10 te factoriseren, toont de tabel: 2 5 \u003d 10. De resulterende getallen 2 en 5 zijn priemgetallen, dus het zijn priemfactoren voor het getal 10.

Voorbeeld 6

Als het nodig is om het getal 48 te ontbinden, toont de tabel: 48 \u003d 6 8. Maar 6 en 8 zijn geen priemfactoren, omdat ze ook kunnen worden ontleed als 6 = 2 3 en 8 = 2 4 . Dan wordt de volledige ontbinding vanaf hier verkregen als 48 = 6 · 8 = 2 · 3 · 2 · 4 . De canonieke notatie heeft de vorm 48 = 2 4 3 .

Voorbeeld 7

Bij het ontleden van het getal 3400 kun je de tekens van deelbaarheid gebruiken. In dit geval zijn de tekens van deelbaarheid door 10 en door 100 relevant. Vanaf hier krijgen we die 3400 \u003d 34 100, waarbij 100 kan worden gedeeld door 10, dat wil zeggen, geschreven als 100 \u003d 10 10, wat betekent dat 3400 \u003d 34 10 10. Op basis van het teken van deelbaarheid krijgen we dat 3400 = 34 10 10 = 2 17 2 5 2 5 . Alle factoren zijn eenvoudig. De canonieke uitbreiding neemt de vorm aan: 3400 = 2 3 5 2 17.

Wanneer we priemfactoren vinden, is het noodzakelijk om de tekens van deelbaarheid en de vermenigvuldigingstabel te gebruiken. Als je het getal 75 weergeeft als een product van factoren, dan moet je rekening houden met de regel van deelbaarheid door 5. We krijgen dat 75 = 5 15 , en 15 = 3 5 . Dat wil zeggen, de gewenste ontleding is een voorbeeld van de vorm van het product 75 = 5 · 3 · 5 .

Als u een fout in de tekst opmerkt, markeer deze dan en druk op Ctrl+Enter

De willekeurige variabele V heet gecentreerd , als zijn wiskundige verwachting gelijk is aan 0. Een elementair gecentreerd willekeurig proces is een product van een gecentreerde willekeurige variabele V en een niet-willekeurige functie φ(t):X(t)=Vφ(t). Een elementair gecentreerd willekeurig proces heeft de volgende kenmerken:

Uitdrukking van de vorm
, waar k ( t ), k =1;2;…-niet-willekeurige functies; , k =1;2;… - ongecorreleerde gecentreerde willekeurige variabelen, wordt de canonieke uitbreiding van een willekeurig proces genoemdX ( t ), terwijl de willekeurige variabelen worden de coëfficiënten van de canonieke expansie genoemd; terwijl niet-willekeurige functies φ k ( t ) - coördinaatfuncties van de canonieke uitbreiding.

Overweeg de kenmerken van een willekeurig proces

Aangezien volgens de voorwaarde
dan

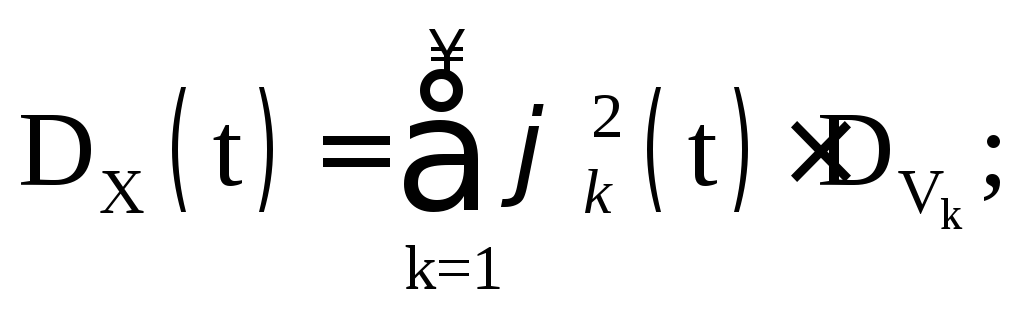
Het is duidelijk dat hetzelfde willekeurige proces verschillende soorten canonieke expansie heeft, afhankelijk van de keuze van de coördinaatfuncties. Bovendien is er zelfs bij de keuze van coördinaatfuncties willekeur in de verdeling van willekeurige variabelen V k. In de praktijk worden op basis van de resultaten van experimenten schattingen verkregen voor de wiskundige verwachting en de correlatiefunctie:
. Na ontbinding
in een dubbele Fourierreeks in coördinaatfuncties φ tot (t):

verkrijg de waarden van de varianties
willekeurige variabelen V k .

4.2. Het concept van een gegeneraliseerde functie. De Dirac-deltafunctie. Integrale canonieke weergave van willekeurige processen.

gegeneraliseerde functie wordt de limiet van een reeks van een familie van continue functies met één parameter genoemd.

Dirac delta-functie
- is een gegeneraliseerde functie die het resultaat is van het passeren van de limiet op
in de familie van functies

Onder de eigenschappen -kenmerken let op het volgende:

2.

3. Als f(t) een continue functie is, dan

Willekeurig proces X( t ), waarvan de correlatiefunctie de vorm heeft die niet-stationaire "witte ruis" wordt genoemd. Als een W ( t 1 )= W - const , dan X( t )-stationaire "witte ruis".

Zoals uit de definitie volgt, zijn geen twee, zelfs willekeurig dicht bij elkaar liggende, secties van "witte ruis" niet gecorreleerd. De uitdrukking W(t) heet intensiteit van witte ruis.

De integrale canonieke weergave van het willekeurige proces X( t ) wordt een uitdrukking van de vorm genoemd
waar
- willekeurig gecentreerde functie;
- niet-willekeurige functie van continue argumenten

De correlatiefunctie van zo'n willekeurig proces heeft de vorm:

Er kan worden aangetoond dat er een niet-willekeurige functie G(λ) bestaat zodat

waarbij G(λ 1) de dispersiedichtheid is; δ(x) - Dirac-deltafunctie. We krijgen

Daarom is de variantie van het willekeurige proces X(t):

.

4.3. Lineaire en niet-lineaire transformaties van stochastische processen

Het volgende probleem wordt beschouwd: een "ingangssignaal" met het karakter van een willekeurig proces X(t) wordt toegevoerd aan de ingang van het systeem (apparaat, omzetter) S. Het systeem zet het om in een "uitgangssignaal" Y(t):

.

Formeel kan de transformatie van een willekeurig proces X(t) in Y(t) worden beschreven met behulp van de zogenaamde systeemoperator A t:

Y(t)=At (X(t)).

De index t geeft aan dat deze operator een transformatie in de tijd uitvoert. De volgende formuleringen van het probleem van de transformatie van een willekeurig proces zijn mogelijk.

De verdelingswetten of algemene kenmerken van het willekeurige proces X(t) aan de ingang van het systeem S zijn bekend, de operator A t van het systeem S is gegeven, het is nodig om de verdelingswet of de algemene kenmerken van de willekeurige proces Y(t) aan de uitgang van systeem S.

De verdelingswetten (algemene kenmerken) van het toevalsproces X(t) en de vereisten voor het toevalsproces Y(t) zijn bekend; het is noodzakelijk om de vorm van de operator A t van het systeem S te bepalen die het beste voldoet aan de gegeven eisen kY(t).

De verdelingswetten (algemene kenmerken) van het willekeurige proces Y(t) zijn bekend en de operator A t van het systeem S wordt gegeven; het is nodig om de verdelingswetten of algemene kenmerken van het willekeurige proces X(t) te bepalen.

P De volgende classificatie van operators А t van het systeem S wordt aangenomen:

Systeembeheerders

Lineair LNlineairN

Lineair homogeen L 0 Lineair inhomogeen L n

Overweeg de impact van een lineair inhomogeen systeem

L n (...) \u003d L 0 (...) + φ (t)

op een willekeurig proces X(t) met de volgende canonieke expansie:

.

We krijgen:

we introduceren de notatie

dan heeft de canonieke ontleding van Y(t) de vorm:

.

Wiskundige verwachting van een willekeurig proces Y(t):

correlatiefunctie van het willekeurige proces Y(t):

Vervolgens,

Aan de andere kant

Verspreiding van willekeurig proces Y(t):

Ter afsluiting van deze sectie merken we op dat de operatoren van differentiatie en integratie van willekeurige processen lineair homogeen zijn.

2. Een kwadratische transformatie wordt beschouwd:

Y(t)=(X(t)) 2 ,

Vk-gecentreerde willekeurige variabelen met een verdeling die symmetrisch is rond nul; vier van hen zijn collectief onafhankelijk. Dan

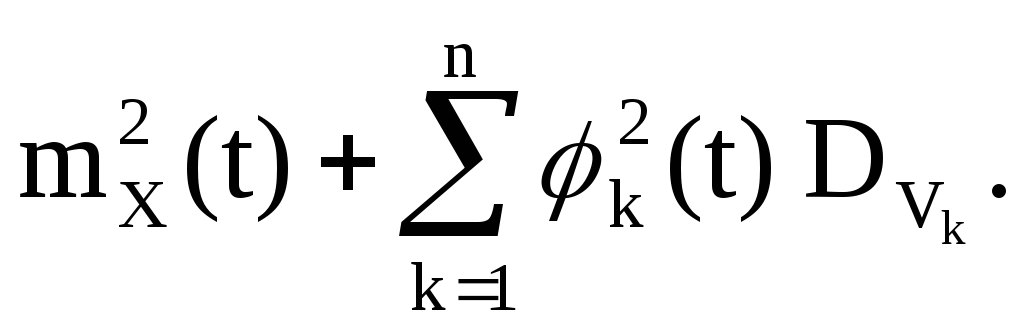
We introduceren niet-willekeurige functies

en willekeurige variabelen

dan heeft het willekeurige proces Y(t) de vorm

Een canonieke ontleding van het willekeurige proces Y(t) wordt verkregen. Correlatiefunctie Y(t):

Formulering. Gegeven een natuurlijk getal n (n > 1). Krijg zijn canonieke ontbinding in priemfactoren, dat wil zeggen, representeer het als een product van priemfactoren. In dit geval is het toegestaan ​​om in de decompositie een factor 1 aan te geven, bijvoorbeeld 264 = 2 * 2 * 2 * 3 * 11 (het programma mag het antwoord 264 = 1 * 2 * 2 * 2 * 3 * 11).

Oplossing. Dit probleem heeft een nogal mooie oplossing.

Van fundamentele stelling van de rekenkunde het is bekend dat voor elk natuurlijk getal groter dan 1 er zijn canonieke ontleding in priemfactoren is, en deze ontleding is uniek tot in de volgorde van de factoren. Dat wil zeggen, bijvoorbeeld 12 = 2 * 2 * 2 en 12 = 3 * 2 * 2 zijn dezelfde uitbreidingen.

Overweeg de canonieke vorm van een willekeurig getal aan de hand van een specifiek voorbeeld. Bijvoorbeeld 264 = 2 * 2 * 2 * 3 * 11. Hoe kan deze structuur worden onthuld? Om deze vraag te beantwoorden, laten we ons de regels herinneren voor het delen van monomials die in elke schoolalgebracursus zijn uiteengezet, waarbij we ons voorstellen dat de getallen in de canonieke decompositie variabelen zijn. Zoals u weet, wordt, als u een uitdrukking opsplitst in een variabele die tot op zekere hoogte in dezelfde mate in deze uitdrukking zit, deze uit zijn record verwijderd.

Dat wil zeggen, als we 264 delen door 2, dan zal één deuce verdwijnen in zijn canonieke expansie. Dan kunnen we controleren of het resulterende quotiënt weer deelbaar is door 2. Het antwoord is ja, maar de derde deling geeft de rest. Dan moet u rekening houden met het volgende natuurlijke getal 3 - het quotiënt wordt er eenmaal in verdeeld. Als gevolg hiervan zullen we, als we de getallenlijn in een positieve richting passeren, het getal 11 bereiken en na delen door 11 n wordt gelijk aan 1, wat aangeeft dat de procedure moet worden beëindigd.

Waarom krijgen we met zo'n "verwijdering" van de gevonden factoren geen deelbaarheid door samengestelde getallen? In feite is alles hier eenvoudig - elk samengesteld getal is het product van priemfactoren die kleiner zijn dan dat. Als gevolg hiervan blijkt dat we zullen verwijderen uit n alle factoren van elk samengesteld getal, totdat we bij zichzelf in een keten van onderverdelingen komen. Bijvoorbeeld, met zo'n iteratie n zal nooit worden gedeeld door 4, aangezien "op weg" naar dit nummer zullen we doorstrepen van n alle factoren zijn tweeën.

Algoritme in natuurlijke taal:

1) Invoer n;

2) Variabele toewijzing p nummers 2;

3) Nummeruitgang n, een gelijkteken en een eenheid voor het verfraaien van de ontbinding;

4) Een lus uitvoeren met een voorwaarde n< > 1 . In een lus:

1. Als een mmodp = 0, geef dan het vermenigvuldigingsteken en de variabele p weer, en deel dan n op de p, verhoog anders de waarde i met 1;

1. programma PrimeFactors;
2. n, p: woord;
3. beginnen
4. p:= 2;
5. leesln(n);
6. schrijf(n, '=1');
7. terwijl n<>1 begin
8. als (n mod p) = 0 begin dan
9. schrijven('*', p);
10. n:= n div p
11. anders beginnen
12. inc(p)