Безперервність елементарних функцій

Теореми про безперервність функцій випливають безпосередньо з відповідних теорем про межі.

Теорема.Сума, твір і приватне двох безперервних функцій є безперервна функція (для приватного за винятком тих значень аргументу, в яких дільник дорівнює нулю).

Теорема.Нехай функції u= φ (x) безперервна в точці х 0 , а функція y = f(u) безперервна в точці u 0 = φ (х 0). Тоді складна функція f(φ (x)) що складається з безперервних функцій, безперервна в точці x 0 .

Теорема.Якщо функція у = f(х) безперервна і суворо монотонна на [ а; b] осі Ох, то зворотна функція у = φ (х) також безперервна і монотонна на відповідному відрізку [ c;d] осі Оу(Без доказу).

Безперервні на відрізку функції мають низку важливих властивостей. Сформулюємо їх як теорем, не наводячи доказів.

Теорема (Вейєрштрасса). Якщо функція безперервна на відрізку, вона досягає цьому відрізку свого найбільшого і найменшого значень.

Зображена на малюнку 5 функція у = f(x) безперервна на відрізку [ а; b], приймає своє найбільше значення Му точці x 1 , а найменше m -у точці х 2 . Для будь-кого х [а; b] має місце нерівність m ≤ f(x) ≤ М.

Наслідок.Якщо функція безперервна на відрізку, вона обмежена на цьому відрізку.

Теорема (Больцано – Коші).Якщо функція у= f(x) безперервна на відрізку [ a; b] і набирає на його кінцях нерівні значення f(a) = Aі f(b) = =В, то на цьому відрізку вона набуває і всіх проміжних значень між Аі В.

Геометрично теорема очевидна (див. рис. 6).

Для будь-якого числа З, укладеного між Аі В, знайдеться точка звсередині цього відрізка така, що f(з) = З. Пряма у = Зперетне графік функції принаймні в одній точці.

Наслідок.Якщо функція у = f(x) безперервна на відрізку [ а; b] і його кінцях приймає значення різних знаків, то всередині відрізка [ а; b] знайдеться хоча б одна точка з, в якій дана функція f(x) звертається в нуль: f(з) = 0.

Геометричний сенс теореми: якщо графік безперервної функції переходить із одного боку осі Охна іншу, то він перетинає вісь Ox(Див. мал. 7).

Рис. 7.

Визначення 4. Функція називається безперервною на відрізку, якщо вона безперервна в кожній точці цього відрізка (у точці a безперервна справа, тобто, а в точці b безперервна зліва, тобто).

Усі основні елементарні функції безперервні у сфері визначення.

Властивості функцій, безперервних на відрізку:

• 1) Якщо функція безперервна на відрізку, вона обмежена у цьому відрізку (перша теорема Вейерштрасса).
• 2) Якщо функція безперервна на відрізку, то на цьому відрізку вона досягає свого найменшого значення та найбільшого значення (друга теорема Вейєрштрасса) (див. рис. 2).
• 3) Якщо функція безперервна на відрізку і його кінцях приймає значення різних знаків, то всередині відрізка існує хоча б одна точка така, що (теорема Больцано-Коші).

Точки розриву функції та їх класифікація

функція безперервність точка відрізок

Точки, у яких умова безперервності не виконується, називаються точками розриву цієї функції. Якщо - точка розриву функції, то в ній не виконується хоча б одна з трьох умов безперервності функції, зазначених у визначеннях 1, 2, а саме:

1) Функція визначена на околиці точки, але не визначена в самій точці. Так функція, розглянута у прикладі 2 а) має розрив у точці, тому що не визначена у цій точці.

2) Функція визначена в точці та її околиці, існують односторонні межі, але вони не рівні між собою: . Наприклад, функція з прикладу 2 б) визначена в точці та її околиці, але, оскільки, а.

3) Функція визначена в точці та її околиці, існують односторонні межі і вони рівні між собою, але не рівні значення функції в точці: . Наприклад, функція. Тут - точка розриву: у цій точці функція визначена, існують односторонні межі і рівні між собою, але, тобто.

Точки розриву функції класифікуються в такий спосіб.

Визначення 5. Точка називається точкою розриву першого роду функції, якщо в цій точці існують кінцеві межі і, але вони не є між собою: . Величина називається при цьому стрибком функції у точці.

Визначення 6 . Точка називається точкою усувного розриву функції, якщо в цій точці існують кінцеві межі і вони рівні між собою: , але сама функція не визначена в точці, або визначена, але.

Визначення 7. Точка називається точкою розриву другого роду функції, якщо в цій точці хоча б одна з односторонніх меж (або) не існує або дорівнює нескінченності.

Приклад 3. Знайти точки розриву наступних функцій та визначити їх тип: а) б)

Рішення. а) Функція визначена і безперервна на інтервалах, і, оскільки кожному з цих інтервалів вона задана безперервними елементарними функціями. Отже, точками розриву цієї функції може лише ті точки, у яких функція змінює своє аналітичне завдання, тобто. точки в. Знайдемо односторонні межі функції у точці:

Оскільки односторонні межі є і кінцеві, але з рівні між собою, точка є точкою розриву першого роду. Стрибок функції:

Для точки знаходимо.

ВЛАСТИВОСТІ ФУНКЦІЙ, НЕПРЕРИВНИХ НА ВІДРІЗКУ

Розглянемо деякі властивості безперервних функцій на відрізку. Ці властивості наведемо без підтвердження.

Функцію y = f(x)називають безперервний на відрізку [a, b], якщо вона безперервна у всіх внутрішніх точках цього відрізка, але в його кінцях, тобто. у точках aі b, безперервна відповідно праворуч і ліворуч.

Теорема 1.Функція безперервна на відрізку [ a, b], хоча в одній точці цього відрізка приймає найбільше значення і хоча б у одній – найменше.

Теорема стверджує, що якщо функція y = f(x)безперервна на відрізку [ a, b], то знайдеться хоча б одна точка x 1 Î [ a, b] така, що значення функції f(x)у цій точці буде найбільшим із усіх її значень на цьому відрізку: f(x 1) ≥ f(x). Аналогічно знайдеться така точка x 2, в якій значення функції буде найменшим із усіх значень на відрізку: f(x 1) ≤ f(x).

Ясно, що таких точок може бути і кілька, наприклад, на малюнку показано, що функція f(x)набуває найменшого значення у двох точках x 2і x 2 ".

Зауваження. Твердження теореми можна стати неправильним, якщо розглянути значення функції на інтервалі ( a, b). Справді, якщо розглянути функцію y = xна (0, 2), то вона безперервна на цьому інтервалі, але не досягає в ньому ні найбільшого, ні найменшого значень: вона досягає цих значень на кінцях інтервалу, але кінці не належать до нашої області.

Також теорема перестає бути вірною для розривних функцій. Наведіть приклад.

Наслідок.Якщо функція f(x)безперервна на [ a, b], вона обмежена у цьому відрізку.

Теорема 2.Нехай функція y = f(x)безперервна на відрізку [ a, b] і кінцях цього відрізка приймає значення різних знаків, тоді всередині відрізка знайдеться, по крайнього заходу, одна точка x = C, в якій функція звертається в нуль: f(C)= 0 де а< C< b

Ця теорема має простий геометричний сенс: якщо точки графіка безперервної функції y = f(x), що відповідають кінцям відрізка [ a, b] лежать по різні боки від осі Ox, то цей графік хоча б в одній точці відрізка перетинає вісь Ox. Розривні функції цією властивістю можуть не мати.

Ця теорема припускає таке узагальнення.

Теорема 3 (теорема про проміжні значення).Нехай функція y = f(x)безперервна на відрізку [ a, b] та f(a) = A, f(b) = B. Тоді для будь-якого числа C, укладеного між Aі B, знайдеться всередині цього відрізку така точка CÎ [ a, b], що f(c) = C.

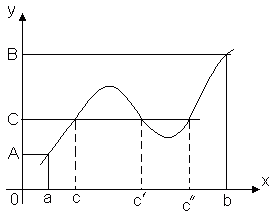
Ця теорема геометрично очевидна. Розглянемо графік функції y = f(x). Нехай f(a) = A, f(b) = B. Тоді будь-яка пряма y = C, де C– будь-яке число, укладене між Aі B, перетне графік функції, принаймні, в одній точці. Абсцис точки перетину і буде тим значенням x = C, за якого f(c) = C.

Таким чином, безперервна функція, переходячи від одного свого значення до іншого, обов'язково проходить через усі проміжні значення. Зокрема:

Наслідок.Якщо функція y = f(x)безперервна на певному інтервалі і приймає найбільше і найменше значення, то цьому інтервалі вона приймає, по крайнього заходу, один раз будь-яке значення, укладене між її найменшим і найбільшим значеннями.

ВИРОБНИЧА І ЇЇ ДОДАТКИ. ВИЗНАЧЕННЯ ВИРОБНИЧОЇ

Нехай маємо деяку функцію y=f(x),визначену на деякому проміжку. Для кожного значення аргументу xз цього проміжку функція y=f(x)має певне значення.

Розглянемо два значення аргументу: вихідне x 0 та нове x.

Різниця x-x 0 називається збільшенням аргументу xу точці x 0 і позначається Δx. Таким чином, Δx = x – x 0 (приріст аргументу то, можливо як позитивним, і негативним). З цієї рівності випливає, що x=x 0 +Δx, тобто. первісне значення змінної набуло деякого збільшення. Тоді, якщо у точці x 0 значення функції було f(x 0 ), то в новій точці xфункція прийматиме значення f(x) = f(x 0 +Δx).

Різниця y – y 0 = f(x) – f(x 0 ) називається збільшенням функції y = f(x)у точці x 0 і позначається символом Δy. Таким чином,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Зазвичай вихідне значення аргументу x 0 вважається фіксованим, а нове значення x- Змінним. Тоді y 0 = f(x 0 ) виявляється постійною, а y = f(x)- Змінною. Прирощення Δyі Δxтакож будуть змінними та формула (1) показує, що Dyє функцією змінної Δx.

Складемо відношення збільшення функції до збільшення аргументу

Знайдемо межу цього відношення при Δx→0. Якщо ця межа існує, то її називають похідною цієї функції f(x)у точці x 0 і позначають f "(x 0). Отже,

Похіднийданої функції y = f(x)у точці x 0 називається межа відношення збільшення функції Δ yдо збільшення аргументу Δ xколи останнє довільним чином прагне до нуля.

Зауважимо, що для однієї і тієї ж функції похідна у різних точках xможе набувати різні значення, тобто. похідну можна розглядати як функцію аргументу x. Ця функція позначається f "(x)

Похідна позначається символами f "(x),y", . Конкретне значення похідної при x = aпозначається f "(a) або y "| x=a.

Операція знаходження похідної від функції f(x)називається диференціюванням цієї функції.

Для безпосереднього знаходження похідної за визначенням можна застосувати таке практичне правило:

приклади.

МЕХАНІЧНИЙ ДУМКА ВИРОБНИЧОЇ

З фізики відомо, що закон рівномірного руху має вигляд s = v·t, де s– шлях, пройдений на момент часу t, v- Швидкість рівномірного руху.

Проте, т.к. більшість рухів, що відбуваються в природі, нерівномірно, то в загальному випадку швидкість, а, отже, і відстань sбуде залежати від часу t, тобто. буде функцією часу.

Отже, нехай матеріальна точка рухається прямою в одному напрямку за законом s = s (t).

Зазначимо деякий момент часу t 0 . До цього моменту точка пройшла шлях s = s (t 0 ). Визначимо швидкість vматеріальної точки в момент часу t 0 .

Для цього розглянемо якийсь інший момент часу t 0 + Δ t. Йому відповідає пройдений шлях s =s(t 0 + Δ t). Тоді за проміжок часу Δ tточка пройшла шлях Δs =s(t 0 + Δ t)–s(t).

Розглянемо ставлення. Воно називається середньою швидкістю у проміжку часу Δ t. Середня швидкість не може точно охарактеризувати швидкість переміщення точки в момент t 0 (т.к. рух нерівномірний). Для того, щоб точніше виразити цю дійсну швидкість за допомогою середньої швидкості, потрібно взяти менший проміжок часу Δ t.

Отже, швидкістю руху на даний момент часу t 0 (миттєвою швидкістю) називається межа середньої швидкості в проміжку від t 0 до t 0 +Δ t, коли Δ t→0:

,

тобто. швидкість нерівномірного рухуце похідна від пройденого шляху за часом.

ГЕОМЕТРИЧНИЙ ДУМКА ВИРОБНИЧОЇ

Введемо спочатку визначення дотичної до кривої у цій точці.

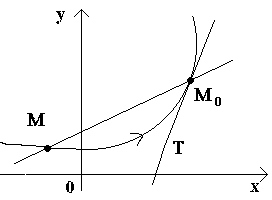
Нехай маємо криву та на ній фіксовану точку М 0(див. малюнок). Розглянемо іншу точку Мцією кривою і проведемо січну M 0 M. Якщо точка Мпочинає переміщатися по кривій, а точка М 0залишається нерухомою, то січна змінює своє становище. Якщо при необмеженому наближенні точки Мпо кривій до точки М 0з будь-якої сторони січка прагне зайняти становище певної прямої М 0 Т, то пряма М 0 Тназивається дотичною до кривої в даній точці М 0.

В.о., дотичноїдо кривої в даній точці М 0називається граничне положення сіючої М 0 М, коли точка Мпрагне вздовж кривої до точки М 0.

Розглянемо тепер безперервну функцію y=f(x)та відповідну цій функції криву. При певному значенні х 0 функція набуває значення y 0 = f (x 0).Цим значенням x 0 та y 0 на кривій відповідає точка М 0 (x 0; y 0).Дамо аргументу x 0приріст Δ х. Новому значенню аргументу відповідає нарощене значення функції y 0 +Δ y=f(x 0 –Δ x). Отримуємо точку М(x 0+Δ x; y 0+Δ y).Проведемо січну М 0 Мі позначимо через φ кут, утворений січною з позитивним напрямком осі Ox. Складемо відношення та зауважимо, що .

Якщо тепер Δ x→0, то через безперервність функції Δ у→0, і тому точка М, переміщаючись кривою, необмежено наближається до точки М 0. Тоді січна М 0 Мбуде прагнути зайняти положення дотичної до кривої в точці М 0, а кут φ→α при Δ x→0, де через α позначили кут між дотичною та позитивним напрямком осі Ox. Оскільки функція tg φ безперервно залежить від φ при φ≠π/2 то при φ→α tg φ → tg α і, отже, кутовий коефіцієнт дотичної буде:

тобто. f "(x)= tg α.

В.о., геометрично у "(x 0)представляє кутовий коефіцієнт, що стосується графіка цієї функції в точці. x 0, тобто. при даному значенні аргументу x, похідна дорівнює тангенсукута, утвореного щодо графіку функції f(x)у відповідній точці М 0 (x; y)з позитивним напрямком осі Ox.

приклад.Знайти кутовий коефіцієнт щодо кривої у = х 2 у точці М(-1; 1).

Раніше ми вже бачили, що ( x 2)" = 2х. Але кутовий коефіцієнт, що стосується кривої є tg α = y"| x = -1 = - 2.

ДИФЕРЕНЦІЙНІСТЬ ФУНКЦІЙ. НЕПРЕРИВНІСТЬ ДИФЕРЕНЦІЙНОЇ ФУНКЦІЇ

Функція y=f(x)називається диференційованау певній точці x 0 якщо вона має в цій точці певну похідну, тобто. якщо межа відношення існує і кінцевий.

Якщо функція диференційована у кожній точці деякого відрізка [ а; b] або інтервалу ( а; b), то кажуть, що вона диференційованана відрізку [ а; b] або відповідно в інтервалі ( а; b).

Справедлива наступна теорема, що встановлює зв'язок між диференційованими та безперервними функціями.

Теорема.Якщо функція y=f(x)диференційована в деякій точці x 0, то вона у цій точці безперервна.

Таким чином, з диференційованості функції випливає її безперервність.

Доведення. Якщо , то

,

де α нескінченно мала величина, тобто. величина, що прагне нуля при Δ x→0. Але тоді

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 при Δ x→0, тобто f(x) – f(x 0)→0 при x→x 0 , а це означає, що функція f(x)безперервна у точці x 0 . Що й потрібно було довести.

Таким чином, у точках розриву функція не може мати похідну. Зворотне твердження неправильне: існують безперервні функції, які у деяких точках є диференційованими (тобто. не мають у цих точках похідної).

Розглянемо малюнку точки а, b, c.

У точці aпри Δ x→0 відношення не має межі (бо односторонні межі різні при Δ x→0–0 та Δ x→0+0). У точці Aграфіка немає певної дотичної, але є дві різні односторонні дотичні з кутовими коефіцієнтами до 1 та до 2 . Такий тип точок називають кутовими точками.

У точці bпри Δ x→0 відношення є знакопостійною нескінченно великою величиною. Функція має нескінченну похідну. У цій точці графік має вертикальну дотичну. Тип точки - "точка перегину" вертикальної дотичної.

У точці cодносторонні похідні є нескінченно більшими величинами різних знаків. У цій точці графік має дві вертикальні дотичні, що злилися. Тип - "точка повернення" з вертикальної дотичної - окремий випадок кутової точки.

З практичної погляду найбільший інтерес представляє використання похідної знаходження найбільшого і найменшого значення функції. З чим це пов'язано? Максимізація прибутку, мінімізація витрат, визначення оптимального завантаження устаткування... Інакше кажучи, у багатьох сферах життя доводиться вирішувати завдання оптимізації будь-яких параметрів. А це є завдання на знаходження найбільшого і найменшого значення функції.

Слід зазначити, що найбільше і найменше значення функції зазвичай шукається на деякому інтервалі X , який є всією областю визначення функції або частиною області визначення. Сам інтервал X може бути відрізком, відкритим інтервалом , нескінченним проміжком.

У цій статті ми говоритимемо про знаходження найбільшого та найменшого значень явно заданої функції однієї змінної y=f(x) .

Навігація на сторінці.

Найбільше та найменше значення функції – визначення, ілюстрації.

Стисло зупинимося на основних визначеннях.

Найбільшим значенням функції , що для будь-кого справедлива нерівність.

Найменшим значенням функції y=f(x) на проміжку X називають таке значення , що для будь-кого справедлива нерівність.

Ці визначення інтуїтивно зрозумілі: найбільше (найменше) значення функції – це найбільше (маленьке) значення на аналізованому інтервалі при абсцисі.

Стаціонарні точки– це значення аргументу, у яких похідна функції перетворюється на нуль.

Для чого нам стаціонарні точки при знаходженні найбільшого та найменшого значень? Відповідь це питання дає теорема Ферма. З цієї теореми випливає, що якщо функція, що диференціюється, має екстремум (локальний мінімум або локальний максимум) в деякій точці, то ця точка є стаціонарною. Таким чином, функція часто приймає своє найбільше (найменше) значення на проміжку X в одній зі стаціонарних точок цього проміжку.

Також часто найбільше та найменше значення функція може приймати у точках, у яких не існує перша похідна цієї функції, а сама функція визначена.

Відразу відповімо на одне з найпоширеніших питань на цю тему: "Чи завжди можна визначити найбільше (найменше) значення функції"? Ні не завжди. Іноді межі проміжку X збігаються з межами області визначення функції або інтервал X нескінченний. А деякі функції на нескінченності та на межах області визначення можуть набувати як нескінченно великі, так і нескінченно малі значення. У цих випадках нічого не можна сказати про найбільше та найменше значення функції.

Для наочності дамо графічну ілюстрацію. Подивіться малюнки – і багато проясниться.

На відрізку

На першому малюнку функція приймає найбільше (max y) і найменше (min y) значення в стаціонарних точках, що знаходяться всередині відрізка [-6; 6].

Розглянемо випадок, зображений другого малюнку. Змінимо відрізок на . У цьому прикладі найменше значення функції досягається в стаціонарній точці, а найбільше - у точці з абсцисою, що відповідає правій межі інтервалу.

На малюнку №3 граничні точки відрізка [-3;2] є абсцисами точок, що відповідають найбільшому та найменшому значенню функції.

На відкритому інтервалі

На четвертому малюнку функція приймає найбільше (max y ) і найменше (min y ) значення стаціонарних точках, що усередині відкритого інтервалу (-6;6) .

На інтервалі про найбільше значення ніяких висновків зробити не можна.

На нескінченності

У прикладі, представленому на сьомому малюнку, функція приймає найбільше значення (max y) у стаціонарній точці з абсцисою x=1, а найменше значення (min y) досягається на правій межі інтервалу. На мінус нескінченності значення функції асимптотично наближаються до y=3.

На інтервалі функція не досягає найменшого, ні найбільшого значення. При прагненні до x=2 праворуч значення функції прагнуть мінус нескінченності (пряма x=2 є вертикальною асимптотою), а при прагненні абсциси до плюс нескінченності, значення функції асимптотично наближаються до y=3 . Графічна ілюстрація цього прикладу наведено малюнку №8.

Алгоритм знаходження найбільшого та найменшого значення безперервної функції на відрізку.

Запишемо алгоритм, що дозволяє знаходити найбільше та найменше значення функції на відрізку.

1. Знаходимо область визначення функції та перевіряємо, чи міститься у ній весь відрізок .
2. Знаходимо всі точки, в яких не існує перша похідна і які містяться у відрізку (зазвичай такі точки збігаються у функцій з аргументом під знаком модуля та у статечних функцій з дробно-раціональним показником). Якщо таких точок немає, переходимо до наступного пункту.
3. Визначаємо всі стаціонарні точки, що у відрізок . Для цього, прирівнюємо її до нуля, вирішуємо отримане рівняння і вибираємо відповідне коріння. Якщо стаціонарних точок немає або жодна з них не потрапляє у відрізок, переходимо до наступного пункту.
4. Обчислюємо значення функції у відібраних стаціонарних точках (якщо такі є), у точках, у яких не існує перша похідна (якщо такі є), а також при x=a та x=b .
5. З отриманих значень функції вибираємо найбільше і найменше - вони будуть шуканими найбільшим і найменшим значеннями функції відповідно.

Розберемо алгоритм при вирішенні прикладу на знаходження найбільшого та найменшого значення функції на відрізку.

приклад.

Знайти найбільше та найменше значення функції

• на відрізку;
• на відрізку [-4;-1].

Рішення.

Областью визначення функції є безліч дійсних чисел, крім нуля, тобто . Обидва відрізки потрапляють у область визначення.

Знаходимо похідну функції по:

Очевидно, похідна функції існує у всіх точках відрізків та [-4;-1].

Стаціонарні точки визначимо з рівняння. Єдиним дійсним коренем є x=2. Ця стаціонарна точка потрапляє у перший відрізок.

Для першого випадку обчислюємо значення функції на кінцях відрізка та в стаціонарній точці, тобто при x=1, x=2 і x=4:

Отже, найбільше значення функції досягається при x=1 а найменше значення - При x = 2.

Для другого випадку обчислюємо значення функції лише на кінцях відрізка [-4;-1] (оскільки він не містить жодної стаціонарної точки):

Рішення.

Почнемо з області визначення функції. Квадратний тричлен у знаменнику дробу не повинен звертатися до нуля:

Легко перевірити, що всі інтервали з умови завдання належать області визначення функції.

Продиференціюємо функцію:

Очевидно, похідна існує по всій області визначення функції.

Знайдемо стаціонарні точки. Похідна звертається в нуль при . Ця стаціонарна точка потрапляє в інтервали (-3; 1) та (-3; 2).

А тепер можна зіставити отримані у кожному пункті результати із графіком функції. Синіми пунктирними лініями позначені асимптоти.

На цьому можна закінчити із знаходженням найбільшого та найменшого значення функції. Алгоритми, розібрані у цій статті, дозволяють отримати результати при мінімумі дій. Однак буває корисно спочатку визначити проміжки зростання та зменшення функції і тільки після цього робити висновки про найбільше і найменше значення функції на якомусь інтервалі. Це дає більш ясну картину та суворе обґрунтування результатів.

Безперервність функції на відрізку.

Поряд із безперервністю функції у точці розглядають її безперервність на різних проміжках.

Функція f (x) називається безперервною на інтервалі (a, b), якщо вона безперервна у кожній точці цього інтервалу.

Функція f (x) називається безперервною на відрізку [a, b], якщо вона безперервна на інтервалі (a, b), безперервна справа в точці a і безперервна зліва в точці b.

Функція називається безперервний на відрізкуякщо вона є безперервною в інтервалі, безперервної праворуч у точці, тобто і безперервної зліва в точці, тобто .

Зауваження.Функція, безперервна на відрізку [a, b] може бути розривною в точках a та b (рис. 1)

Багато функцій, безперервних на відрізку [ a , b ] позначається символом C [ a , b ].

Основні теореми про функції, безперервні на відрізку.

Теорема 1(Про обмеженість безперервної функції). Якщо функція f (x) безперервна на відрізку [ a , b ], вона обмежена у цьому відрізку, тобто. існує таке число C > 0, що x О [ a , b ] виконується нерівність | f (x) | ≤ C .

Теорема 2(Вейєрштрас). Якщо функція f (x) безперервна на відрізку [ a , b ], вона досягає цьому відрізку свого найбільшого значення M і найменшого значення m , тобто. існують точки ?

Найбільше значення M позначається символом max x Про [ a , b ] f (x), а найменше значення m символом min x Про [ a , b ] f(x).
Теорема 3(Про існування нуля). Якщо функція f (x) безперервна на відрізку [ a , b ] і на кінцях відрізка набуває ненульових значень різних знаків, то на інтервалі (a , b) знайдеться принаймні одна точка ξ у якій f (ξ) = 0.
Геометричний сенс теореми полягає в тому, що графік функції, яка відповідає умовам теореми, обов'язково перетне вісь OX(Рис.3).

Зауваження.На цій теоремі заснований метод наближеного вирішення рівняння

f(x) = 0,

(1)

званий методом бісекції (дихотомії), або методом половинного поділу.

Теорема 4(Больцано-Коші). Якщо функція f (x) безперервна на відрізку [ a , b ], вона приймає на (a , b) всі проміжні значення між f (a) і f (b).
Існування безперервної зворотної функції
Нехай функція y = f (x) визначена, суворо монотонна та безперервна на відрізку [a, b]. Тоді на відрізку [ , ] (α = f (a), β = f (b)) існує зворотна функція x = g (y), також суворо монотонна і безперервна на відрізку (α, β).