"застосування властивостей функції під час вирішення рівнянь і нерівностей". «Рішення рівнянь нестандартними методами, використовуючи властивості функцій
Тема: Методи використання обмеженості функцій.
Життя хороше тим, що в ньому
можна займатися математикою.
(Леонард Ейлер)Цілі: розвиток нового нешаблонного мислення, яке можна успішно застосовувати і в інших сферах людської діяльності(Кібернетика, обчислювальна техніка, економіка, радіофізика, хімія та ін).
Завдання: - навчання оцінки об'єктивної та суб'єктивної проблеми завдань і, розумному вибору цих завдань на іспиті;
Створення «скарбнички» нетрадиційних та незвичайних міркувань.
Хід уроку:
Орг. момент. Формулювання учнями теми уроку за допомогою виконання завдань ЄДІ частини А та В та розшифровування теми щодо спадання отриманих відповідей. (Як передбачуваних слів зашифрувати 12 карток під номерами від -2 до 10) (додаток 1 та 2)
обмеженості
2. Розділити учнів на 2 групи, вручити їм набір «Теорія + 10 завдань» (додатки 3 і 4), попросити вибрати ті завдання, які можна виконати з даної теоретичної частини, обґрунтувати свій вибір.3. Показати хід виконання цих завдань на дошці учнями: Носкова К., Дедевшин І., Веселов І.4. Розділити завдання з картки на 2 групи для вирішення їх із подальшою самоперевіркою по листу готових рішень. (Додаток 5)5. Роздати групам листи з описом нових нестандартних методів розв'язання рівнянь та нерівностей для вибору наступної теми(як будинок. завдання знайти у збірниках ЄДІ завдання, які можна вирішувати цим методом) (додаток 6)6. Рефлексія учнів (заповнення таблички)Ф.І. учняДодаток 1.
Розв'яжіть ці завдання та розмістіть відповіді в порядку спадання, зберіть за відповідями тему нашого заняття.
Знайти абсцис точки графіка функції у=3х 2 -7х+7, в якій тангенс кута дотичної дорівнює -1.
Додаток 2.
9 2 0 7Дослідження функцій за допомогою похідної. 10 5 1 -1Метод використання обмеженості функцій. 4 -2 8 12Розв'язання нерівностей графічним способом.
3 11 6Рішення функціональних рівнянь.
Дослідження
Додаток 3.
Одним із ефективних методівВирішення рівнянь або нерівностей є метод, заснований на використанні обмеженості функцій. До найвідоміших обмеженим функціямналежать, наприклад, деякі тригонометричні; зворотні тригонометричні функції; функції, що містять модуль, ступінь, корінь з парним ступенемта інші.
Найбільш поширеними нерівностями є такі:
│f(x) │≥
0, -1
≤
sinx ≤
1, -1
≤
cosx ≤
1, -

 -
-

 ,
a f (x) >0, (f(x) ±
g(x)) 2 n ≥
0,
,
a f (x) >0, (f(x) ±
g(x)) 2 n ≥
0,
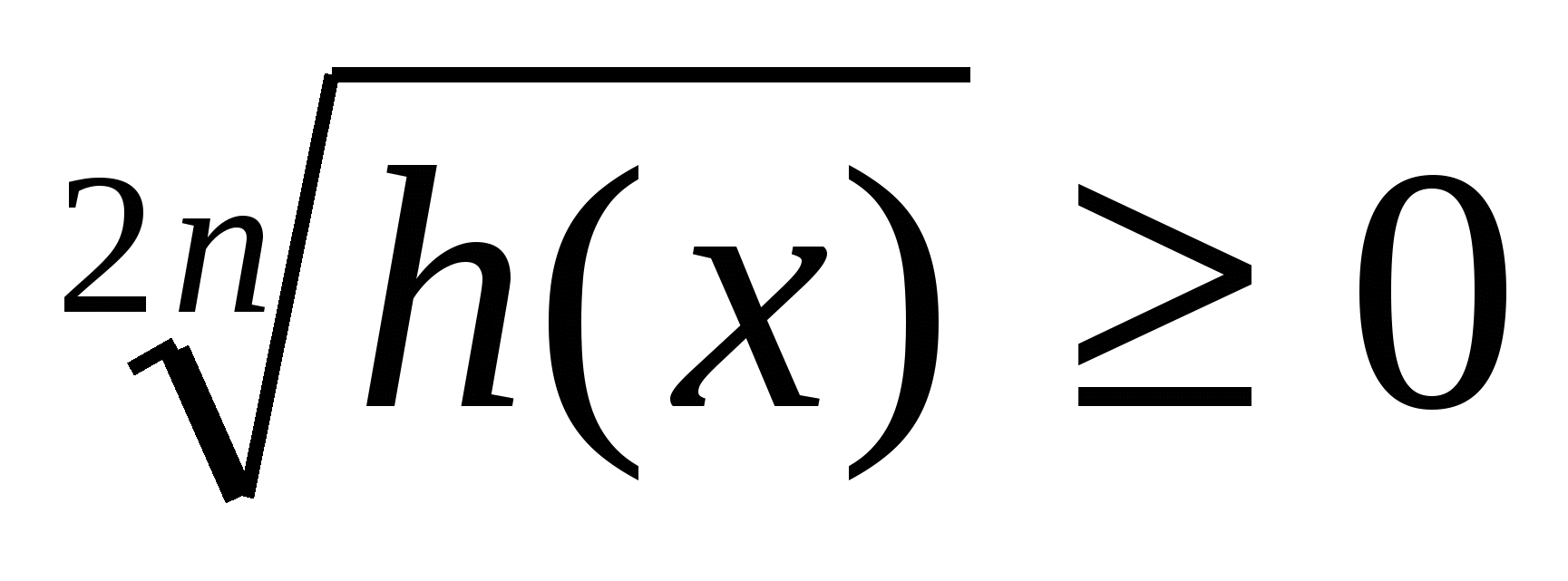 ,
a+
≥
2,
b+
≤
-2
і багато інших. Тут n -натуральне число,
h(x) ≥
0,
a>0,
b
0.
,
a+
≥
2,
b+
≤
-2
і багато інших. Тут n -натуральне число,
h(x) ≥
0,
a>0,
b
0.
Крім наведених найпростіших нерівностей є і складніші, зокрема, тригонометричні нерівності -,
 ,
,
та нерівності з модулями виду 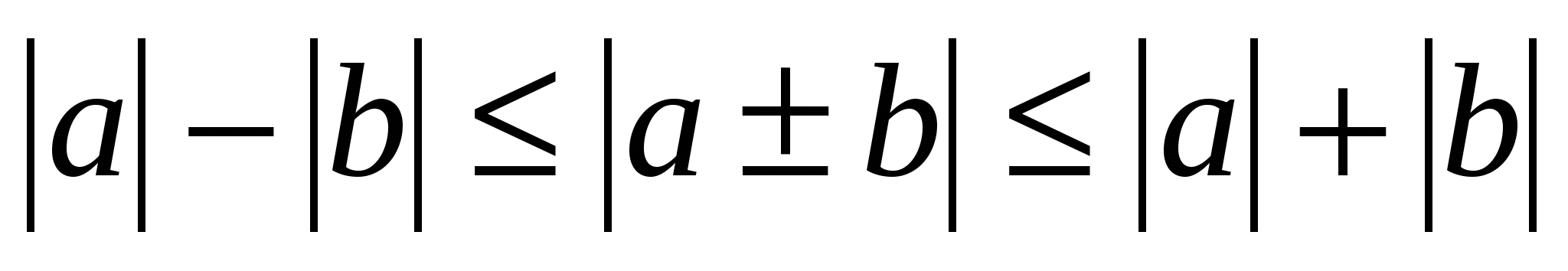 .
.
приклад 1.Вирішити рівняння: 
Рішення:
виділимо повний квадрату правій частині рівняння, тобто. . Звідси слідує що  . Бо при цьому sinπ x ≤
1, то отримуємо систему рівнянь
. Бо при цьому sinπ x ≤
1, то отримуємо систему рівнянь 
Вирішуючи друге рівняння системи, отримуємо що х =. Підстановкою в перше рівняння переконуємося, що знайдене значення х є розв'язком системи, отже, є рішенням вихідного рівняння.
Відповідь:х =.
приклад 2.Вирішити рівняння: 

Рішення: оскільки Sin2 π x ≤
1. Тому, 5+4 sin2 π x ≤
9. Таким чином, отримуємо систему рівнянь: 
Звідси отримуємо систему рівнянь  , З першого рівняння знайдемо х =. Підставимо його у друге рівняння системи та переконаємося, що х= є розв'язком системи, а отже, є розв'язком вихідного рівняння.
, З першого рівняння знайдемо х =. Підставимо його у друге рівняння системи та переконаємося, що х= є розв'язком системи, а отже, є розв'язком вихідного рівняння.
Відповідь:х=
Додаток 4.
Виберіть із запропонованого списку завдань ті, які можна вирішити і за допомогою методу обмеженості функцій.
1. Розв'язати рівняння х 2 -4 x=(2-cos  2. Знайти кількість цілих рішеньнерівності х 2 ctg 2
2. Знайти кількість цілих рішеньнерівності х 2 ctg 2 3. Розв'язати рівняння
3. Розв'язати рівняння 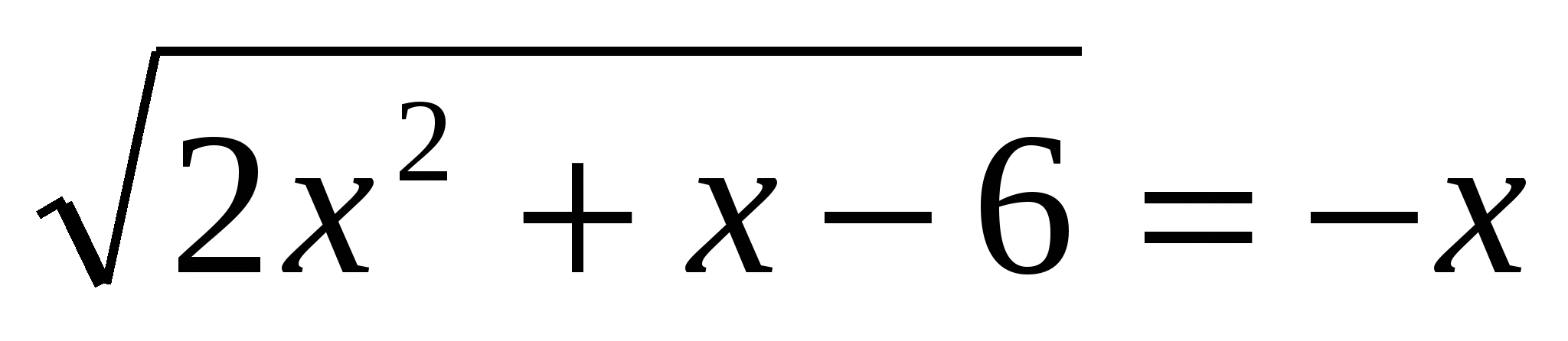 4. Розв'язати рівняння 3-(5. Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2
4. Розв'язати рівняння 3-(5. Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2  6. Розв'язати рівняння
6. Розв'язати рівняння  7. Розв'язати рівняння -25х2+40х-23=( cos
7. Розв'язати рівняння -25х2+40х-23=( cos  8. Знайти добуток коренів рівняння х
8. Знайти добуток коренів рівняння х  9. Розв'язати рівняння
9. Розв'язати рівняння  10. Розв'язати рівняння 3- cos 2
10. Розв'язати рівняння 3- cos 2 
Аркуш самоперевірки.
Додаток 5.
1. Вирішити рівняння
Рішення: т.к. , То т.к. і то
отримуємо систему рівнянь
вирішуємо перше рівняння, отримуємо х = , підставимо це значення у друге рівняння
2 . Вирішити рівняння 3-
cos 2 Рішення: т.к. , То т.к. і то
отримуємо систему рівнянь
вирішуємо друге рівняння, отримуємо х = , підставимо це значення у перше рівняння
отже х= є рішенням вихідного рівняння. Відповідь: х=
3 . Знайти кількість цілих рішень нерівності х 2
+7х-8≤0, що задовольняють умові ctg 2 Рішення: т.к. і то за будь-яких допустимих значень хЗнайдемо нулі квадратного тричлена, за теоремою ВієтаРешим нерівність методом інтервалів
т.ч. хзнаємо, що
цілочисельні значення х - це числа виключаємо Відповідь: 8 цілих рішень 4 . Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2 Рішення: т.к. і то за будь-яких допустимих значень хЗнайдемо нулі вирази, х= і х=Розв'яжемо нерівність методом інтервалів
т.ч. хзнаємо, що
цілочисельні значення х - це числа виключаємо Відповідь: 7 цілих рішень
Додаток 6.
Метод використання монотонності функцій. При вирішенні рівняння типу f(x)=g(x) у ряді випадків ефективним є метод, який використовує монотонність функцій у = f (x) і у = g (x). Якщо функція у = f (x) безперервна і зростає (зменшується) на відрізку a≤ x ≤ b, а функція у = g(x) безперервна і зменшується (зростає) цьому ж відрізку, то рівняння f(x)=g(x) на відрізку a≤ x ≤ b може мати не більше одного кореня, отже необхідно або спробувати підбір знайти єдиний корінь рівняння, або показати, що такого кореня не існує. Особливо цей метод ефективний у тому випадку, коли обидві частини рівняння f(x)=g(x) є «незручними» для спільного дослідження функції. Примітка:Якщо функція у = f(x) зростає, а функція у = g(x) зменшується для a≤ x ≤ b і при цьому f(а)>g(а), то коріння рівняння серед a≤ x ≤ bні.
приклад: Вирішити рівнянняРішення: Областю допустимих значень рівняння є х  . Неважко бачити, що у цій галузі ліва частина рівняння зростає, а права - зменшується, тобто. функціяf(x)=
. Неважко бачити, що у цій галузі ліва частина рівняння зростає, а права - зменшується, тобто. функціяf(x)= є зростаючою, а функціяg(x)=
є зростаючою, а функціяg(x)= - спадна. У зв'язку з цим вихідне рівняння може мати лише один корінь (якщо він є). Підбором знаходимо цей корінь рівняння х = 2.Відповідь: х = 2
- спадна. У зв'язку з цим вихідне рівняння може мати лише один корінь (якщо він є). Підбором знаходимо цей корінь рівняння х = 2.Відповідь: х = 2
Метод розв'язання функціональних рівнянь.
До найбільш складних завданьна ЄДІ відносяться завдання, вирішення яких зводиться до розгляду функціональних рівнянь виду f(f(….f(x)…))=x або f(g(x))=f(h(x)), де f(x),g(x),h(x)- деякі функції та n≥ 2
Методи розв'язання цих функціональних рівнянь ґрунтуються на застосуванні багатьох теорем, розглянемо одну з них.
Теорема1. Коріння рівняння
f(x)=0 є корінням рівняння f(f(….f(x)…))=x
приклад: Розв'язати рівняння х=  ,
де квадратний коріньберетьсяnраз іn≥
1
Рішення: З умови завдання випливає, що х>
0. Нехайf(x)=
,
де квадратний коріньберетьсяnраз іn≥
1
Рішення: З умови завдання випливає, що х>
0. Нехайf(x)=
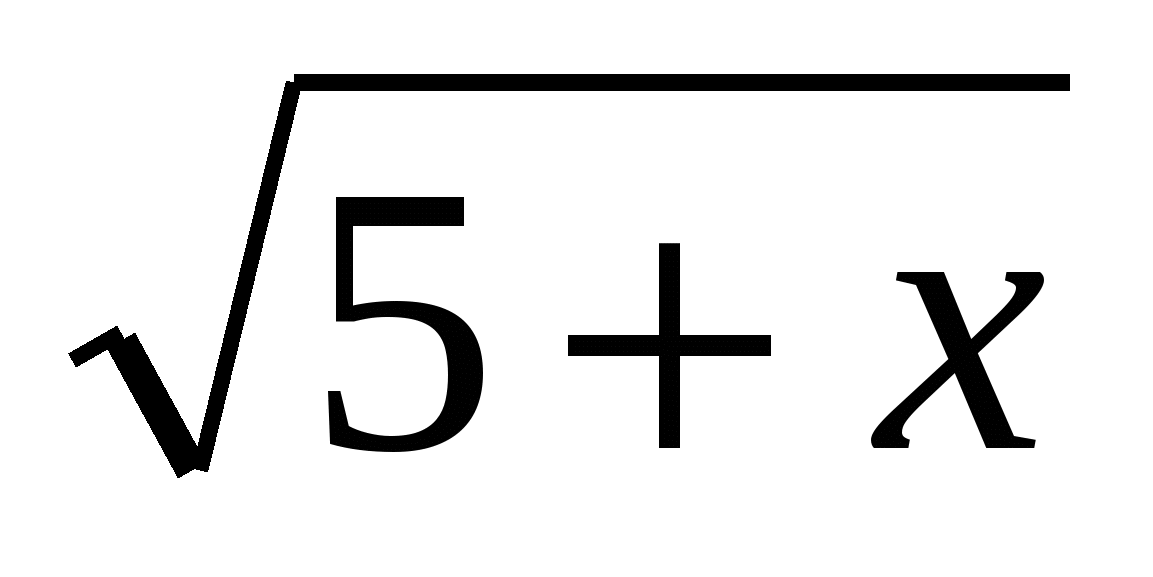 тоді наше рівняння можна представити у вигляді функціонального
f(
f(….
f(
x)…))=
x.
Бо при х>
0 функціяf(x)=
зростає іf(x)
>
0, то рівняння х = рівносильне рівняннюf(x)=
x, тобто.
=х, позитивним рішенням якого є х=
тоді наше рівняння можна представити у вигляді функціонального
f(
f(….
f(
x)…))=
x.
Бо при х>
0 функціяf(x)=
зростає іf(x)
>
0, то рівняння х = рівносильне рівняннюf(x)=
x, тобто.
=х, позитивним рішенням якого є х=  Відповідь:х=
Відповідь:х=
Підготував та провів вчитель математики
МКОУ «ЗОШ №1» м. Поворине
Карташова С. А.
2014р.
Тема урока:«Рішення рівнянь нестандартними методами, використовуючи властивості функцій»
Форма уроку – лекція із наступним закріпленням. Розрахований на 2 уроки
(Слайд №1)
Цілі уроку:
Повторити та узагальнити знання на тему: «Властивості функцій»
Навчити застосовувати функціональний метод розв'язання рівнянь
Розвивати логічне мислення, спостережливість
Виховувати активність, творчу ініціативу.
(слайд №2)
Обладнання: Інтерактивна дошка, комп'ютер із презентацією.
План уроку:
Організаційний момент.
Мотивація навчальної діяльності(повідомлення теми, цілей уроку).
Актуалізація опорних знань (повторення властивостей основних функций).
Вивчення нового матеріалу (функціональний метод розв'язування рівнянь).
Закріплення знань (рішення вправ).
Підведення підсумків. Оцінка.
Хід уроку.
Вчитель:
Для вирішення більшості рівнянь, що зустрічаються на іспитах, достатньо володіти шкільним курсом математики, але при цьому необхідно вміти вирішувати не лише за допомогою стандартних прийомів, призначених для цілком певних типіврівнянь, а й «нестандартними» методами, про які ми й поговоримо сьогодні на уроці. Одним з таких методів розв'язання рівнянь є функціональний, що базується на використанні властивостей функцій. На відміну від графічного методузнання властивостей функцій дозволяє знаходити точні корені рівняння, при цьому не потрібно побудови графіків функцій. Використання властивостей функцій сприяє раціоналізації розв'язування рівнянь.
(слайд №3)
Відповімо на запитання:
Що називається рівнянням?
Що називається коренем рівняння?
Що означає розв'язати рівняння?
Що називається функцією?
Що називається областю визначення функції?
Що називається областю значень функції?
(Слайд №4)
Розглянемо(Слайд №5)
ПРИКЛАД 1. Розв'яжіть рівняння:
Рішення: ОДЗ:
Відповідь: рішень немає.
(Слайд №6)
ПРИКЛАД 2. Розв'яжіть рівняння:
Рішення: ОДЗ:
ОДЗ складається з однієї точки х = 1. Залишається перевірити, чи є х = 1 коренем рівняння. Підставивши, бачимо, що х=1 – корінь рівняння.
Відповідь: х = 1.
Вчитель:
Іноді виявляється достатнім розглянути не всю область визначення функції, а лише її підмножина, на якому функція набуває значень, що задовольняють деяким умовам (наприклад, лише невід'ємні значення)
(Слайд № 7 )
ПРИКЛАД 3.
Рішення. Знайдемо перетин областей визначення функцій у правій та лівій частинах рівняння:
D 1
Обмежимо безлічD, враховуючи, що ліва частина рівняння невід'ємна, і, отже, такою ж має бути права частинаюДля цього потрібно розглянути перетин множиниDз безліччю розв'язків нерівності , тобто з безліччю . Отже, достатньо розглянути рівняння на множині .
Підстановкою переконуємося, що обидва елементи є рішенням рівняння.
Відповідь: -3; 2.
(Слайд № 8 )
ПРИКЛАД 4.
Рішення.
З урахуванням того що коренем рівняння є х = 4.
Відповідь: 4.
Вчитель:
Перейдемо до розв'язання рівнянь із використанням поняття області значень функції.
(Слайд №9-№10)
(Слайд №11)
ПРИКЛАД 1.
Рішення. Так як , то рівняння немає рішення.
Відповідь: немає рішень.
ПРИКЛАД 2.
Рішення. ОДЗ:
Відповідь: немає рішень.
Вчитель:
Якщо функція f ( x ) на проміжку Х обмежена зверху, а функція g ( x ) обмежена знизу, то рівняння f ( x ) = g ( x ) рівносильно системі
(Слайд №12)
ПРИКЛАД 3.
Рішення. За визначенням,
Рівність досягається, якщо
Вирішимо перше рівняння системи:
arccos (x-1) = π, x-1 = -1, x = 0.
При х=0 друге рівняння звертається у правильну числову рівність.
Отже, рішенням системи та даного рівняння є х = 0.
Відповідь: 0.
(Слайд №13-14)
ПРИКЛАД 4.
Рішення.
Знайдемо максимум цієї функції на проміжку (2; 4) за допомогою похідної.
= 0,
g' + -
g 2 3 4 x
Max
g(3)=2.Маємо
Тоді дане рівняннярівносильно системі
Розв'язавши перше рівняння системи, отримаємо х=3, перевіркою, підставивши друге рівняння переконаємося, що х=3 – рішення системи та цього рівняння.
Відповідь: 3.
(Слайд №15)
Вчитель:
Цей метод часто зустрічається на ЄДІ з математики. Цей методполягає в тому, що одна частина рівняння обмежена зверху деяким числом М, а інша частина рівняння обмежена знизу тим самим числом М. Число М прийнято називатимажорантою , а цей метод -методом мажорант . У методі мажорант, як ви вже здогадалися, треба добре розуміти, що таке функція, вміти досліджувати властивості функцій.
(Слайд №16)
Вправи для закріплення, вироблення вмінь та навичок.
Клас поділяється на 2 групи за варіантами.
1 варіант.
Доведіть, що рівняння не має коріння.
Розв'язати рівняння: Відповідь:2,6.
Відповідь: 2.
Вчитель:
Ми сьогодні розглянули нестандартний метод розв'язання рівнянь, використовуючи властивості функцій, який можна застосувати і для розв'язання нерівностей, але про це ми поговоримо на кількох наступних заняттях.
Підбиття підсумків, оцінки.
(Слайд №17)
Домашнє завдання:
«Область визначення функції» - Область визначення квадратичні функції– будь-яке дійсне число. Функція називається логарифмічною, якщо змінна величинастоїть під знаком логарифму. Логарифмічна функція. Функція, змінна величина якої перебуває у показнику ступеня, називається показовою. Квадратична функція.
"Загальні властивості функцій" - Загальні властивостіфункцій. Знайти область визначення функції. Парна функція. Чи є ця функція парною чи непарною. За графіком визначте безліч значень функції. За графіком визначте значення Х. За графіком визначте проміжки зменшення функції. Функція f(x) зростаюча. Дано функцію y=f(x).
«Зростання та зменшення функції» - Зростання та зменшення функції синус. Розглянемо ще один приклад. Проміжками зменшення косинуса є відрізки , n - ціле. Нехай, наприклад, функція f парна і зростає на проміжку , де a?0. Зростання та зменшення функцій. Зростання та зменшення функції косинус. На малюнку нижче зображено графік функції, визначеної на відрізку [-1; 10].
«Застосування безперервності» - значення виразу. Геометричний змістпохідною. Метод інтервалів. Скласти рівняння щодо графіку функції. Дотична до графіка функції. Графік близький до дотичної. Формули. Обчислимо за такою формулою. Стосовною кривою в даній точці M називається граничне положення січної NM. Гіперболу.
"Екстремум функції" - Залежність тиску газу від температури. Тема уроку: «Ознаки зростання та зменшення функції. Тест. Зміна сили струму під час розмикання ланцюга. Дослідження функції на екстремум». Зміна змінного струму. План: Залежність сили струму від напруги. Залежність тиску газу від об'єму. Тема: «Ознаки зростання та зменшення функції.
«Функції та його властивості» - Незалежну змінну називають - аргумент. Зростаюча функція. Визначення функції. Парні та непарні функції. Монотонність функції. Значення залежної змінної називають значеннями функції. Усі значення незалежної змінної утворюють область визначення функції -D(f). 1. Значення функції позитивні.
Всього у темі 23 презентації
Факультативне заняття«Застосування якості обмеженості функцій»
Матеріал, пов'язаний з рівняннями та нерівностями, становить значну частину шкільного курсу математики, але тимчасові рамки уроку не дозволяють розглянути всі питання.
Крім того, обов'язковим мінімумом змісту навчання математики, заданим державним стандартом для основної школи, визначено навчальний матеріалдля обов'язкового розгляду, але не обов'язкового засвоєння (наприклад, нестандартні методи розв'язання рівнянь і нерівностей, методи розв'язання рівнянь і нерівностей з параметром тощо. буд.).
Зважаючи на важливість і широкість матеріалу, пов'язаного з поняттями рівнянь і нерівностей, їх вивчення в сучасною методикоюматематики організовано у змістовно-методичну лінію – лінію рівнянь та нерівностей. Існує три основні напрямки розгортання даної лінії шкільному курсіматематики.
Прикладна спрямованість лінії рівнянь та нерівностей розкривається головним чином щодо алгебраїчного методурішення текстових завдань. Рівняння та нерівності є основною частиною математичних засобів, що використовуються під час вирішення текстових завдань.
Теоретико-математична спрямованість розкривається у двох аспектах: у вивченні найважливіших класів рівнянь, нерівностей та його систем, й у вивченні узагальнених понять і методів які стосуються лінії загалом.
Лінія рівнянь та нерівностей також тісно пов'язана з функціональною лінією. З одного боку - застосування методів, що розробляються в лінії рівнянь та нерівностей, до дослідження функції. З іншого боку, функціональна лінія істотно впливає як утримання лінії рівнянь і нерівностей, і стиль її вивчення. Зокрема, функціональні уявлення є основою залучення графічної наочності до розв'язання та дослідження рівнянь, нерівностей.
У курсі алгебри, що вивчається нами за редакцією Мордковича, функціонально-графічна лінія обрана пріоритетною. Весь матеріал будується за жорсткою схемою: функція-рівняння-перетворення.
У ЄДІ досить часто зустрічаються завдання, які вирішуються за допомогою застосування властивостей функцій. Тому доцільно цей матеріал винести на курси на вибір. Але все-таки я волію деякі такі завдання розглядати на уроках, починаючи з 9 класу.
Застосування властивостей функцій під час вирішення рівнянь і нерівностей
Використання якості обмеженості.
Використання області визначення функції.
Використання монотонності функцій під час вирішення рівнянь і нерівностей.
Використання поняття області зміни функції.
- Використання властивостей парності чи непарності та періодичності функцій.
СЛАЙД 2
Мій виступ виявлено лише одному з нестандартних методів розв'язання рівнянь і нерівностей, заснованому на властивості обмеженості функцій, що входять до рівняння (нерівність). Пропоновані мною завдання можна розглядати на уроках, відведених для підготовки учнів до ЄДІ (три-чотири уроки), або використовувати по одному – два завдання на уроці, також даний матеріалможна використовувати на факультативному занятті (або занятті елективного курсу).
Вже в 9 класі при вивченні якості обмеженості звертаю увагу на важливість цієї властивості та можливість її використання при
Знаходження найменшого та найбільшого значення функції;
Знаходження множини значень функції.
СЛАЙД3.
Розглядаються рішення деяких завдань. Попередньо слід повторити основні визначення. СЛАЙД 4.
На СЛАЙДАХ 5-9 розглядаються завдання знаходження найменшого чи найбільшого значень функції.
СЛАЙД 10.
Застосування якості обмеженості функцій вирішення рівнянь і нерівностей.
1. МЕТОД МАЖОРАНТ (МЕТОД ОЦІНКИ)
Основна ідея методу мажоранту полягає в наступному:
Нехай ми маємо рівняння та існує таке число М, що для будь-кого хз області визначення https://pandia.ru/text/78/376/images/image003_26.gif" width="160". Тоді рівняння рівносильне системі https://pandia.ru/text/78 /376/images/image005_16.gif" width="96" height="35 src=">.
Рішення. Оцінимо обидві частини рівняння.
При всіх значеннях хправильні нерівності https://pandia.ru/text/78/376/images/image007_10.gif"
Отримана система не має рішень, тому що width="20" height="20">
Приклад 1.2 ..gif" width="157" height="20">.gif" width="75" height="51 src=">.
Рішенням першого рівняння системи є значення.
Отже, ![]() вирішення системи.
вирішення системи.
Відповідь: ![]() .
.
приклад 1.3. Вирішити нерівність https://pandia.ru/text/78/376/images/image016_0.gif" width="56" width="84" width="156 height=61" height="61">.
Зворотна заміна: х + 1 = 0 .
Відповідь: - 1.
приклад 1.4. Знайти всі значення параметра апри кожному з яких рівняння має рішення. Знайдіть ці рішення.
Рішення.
Перепишемо рівняння у вигляді. При всіх значеннях хвираз ![]() тому https://pandia.ru/text/78/376/images/image026_0.gif" width="87" і ..gif" width="405"
тому https://pandia.ru/text/78/376/images/image026_0.gif" width="87" і ..gif" width="405"
Відповідь: https://pandia.ru/text/78/376/images/image031_0.gif" width="51" height="41 src=">
2. «ЗУСТРІЧ НА КРАЮ»
Різновидом методу мажорант є завдання (« зустріч на краю») у яких безлічі значень лівої та правої частин рівняння чи нерівності мають єдину загальну точку, що є найбільшим значенням для однієї частини та найменшим для іншої.
Як розпочинати вирішувати такі завдання? Насамперед – привести задані рівнянняабо нерівності до більш простому вигляду: шляхом розкладання на множники, рятуванням від модулів, логарифмів і т. д. Потім необхідно ще раз уважно прочитати завдання, спробувати намалювати графічний образ функцій, що входять до завдання.
 приклад 2.1.
Вирішити рівняння .
приклад 2.1.
Вирішити рівняння .
Рішення. Корінь рівняння легко вгадати – це x= 1. Але довести його єдиність з міркувань монотонності не вдається, оскільки ні ліва, ні права частини рівняння є монотонними функціями. Тут використовується інша ідея..gif" width="191" height="51">. Найбільше значення правої частини отриманого рівняння дорівнює 1 і приймається в точці x= 1..gif" width="185" height="52 src=">). Тому ліва частина досягає при x= 1 свого найменшого значення, Яке також дорівнює 1. Висновок: рівність виконується тоді і тільки тоді, коли обидві частини одночасно дорівнюють 1, тобто при x = 1.
приклад 2.2. Вирішити рівняння .
1 спосіб.
Рішення:Зауважимо, що ліва частина рівняння не перевищує одиниці, тоді як права частина не менше одиниці. Отже, вихідне рівняння має рішення, тільки якщо обидві його частини дорівнюють одиниці. Це можливо лише за .
Відповідь: .
2 спосіб.Це рівняння можна вирішити графічно. Для цього побудуємо в одній системі координат графіки правої та лівої частин рівняння, тобто графік функції та графік функції width="37" height=" 19 ">.
Відповідь: .
Приклад 2. 3. Вирішити рівняння https://pandia.ru/text/78/376/images/image042_0.gif" Width="301"
то дане рівняння виконується лише у тому випадку, якщо виконується система  . Перше рівняння системи має єдиний корінь х= 1, але це корінь не задовольняє другому рівнянню. Тож система рішень не має.
. Перше рівняння системи має єдиний корінь х= 1, але це корінь не задовольняє другому рівнянню. Тож система рішень не має.
Відповідь: Æ
Приклад 2. 4. Вирішити рівняння https://pandia.ru/text/78/376/images/image045_0.gif" width="105" height="21">, то ліва частина рівняння набуває значення від до 2..gif" width=" 137" ..gif" width="217" height="24"> має рішення.
Рішення.
 |
Оцінимо обидві частини нерівності. Для цього перетворимо праву частину нерівності, виділивши повний квадрат ..gif" width="71" height="19">.gif" width="121" ="41">(тобто відбувається «зустріч на краю»).
Відповідь:
приклад 2.6. Знайдіть усі значення параметра апри яких рівняння
Галаєва Катерина, учениця 11 класу МАОУ ЗОШ №149 м Нижнього Новгорода
Робота носить одночасно і прикладний та дослідницький характер. Для повноти дослідження було розглянуто наступні питання:
– Як відображаються властивості функції під час вирішення рівнянь і нерівностей?
– Які рівняння та нерівності вирішуються через визначення властивостей галузі визначення, безлічі значень, інваріантності?
– Який алгоритм розв'язання?
– Розглянуто завдання з параметром, пропонованим у матеріалах КІМ під час підготовки до ЄДІ.
У роботі Катерина досліджувала велике коло завдань і систематизувала їх по зовнішньому вигляду.
Завантажити:
Попередній перегляд:
https://accounts.google.com
Підписи до слайдів:
Розв'язати нерівність Розв'язання. Функція f(х) = монотонно зростає на всій числовій прямій, а функція g(x) = монотонно зменшується на всій ділянці визначення. Тому нерівність f(х) > g(x) виконується, якщо х >
Дякую за увагу!
Попередній перегляд:
Щоб скористатися попереднім переглядом презентацій, створіть собі обліковий запис Google і увійдіть до нього: https://accounts.google.com
Підписи до слайдів:
Використання властивостей функції при розв'язанні рівнянь та нерівностей Виконала роботу: Галаєва Катерина МБОУ ЗОШ №149 Московського району Учениці 11 «А» класу Науковий керівник: Фадєєва І. А. Вчитель математики
Основні напрямки: Вивчення властивостей функції: монотонність, обмеженість, область визначення та інваріантність Дізнатись основні твердження, які найчастіше використовуються при вирішенні рівнянь, нерівностей та систем
Монотонність Функція зростає, якщо більшого значенняаргумент відповідає більшого значення функції. Функція зменшується, якщо більшому значенню аргументу відповідає менше значення функції. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Твердження 1. Якщо функція у = f(x) монотонна, то рівняння f(x) = с має не більше одного кореня. x =2 f(x) = - монотонно спадаюча, отже, інших рішень немає. Відповідь: x = 2
Твердження 2. Якщо функція у = f(x) монотонно зростає, а функція у = g(x) монотонно зменшується, то рівняння f(x) = g(x) має не більше одного кореня. 2 - x = lg (x +11) + 1 g (x) = 2 - x є монотонно спадаючою, а функція f (x) = lg (x + 11) + 1 монотонно зростаючою на області визначення означає рівняння f (х ) = g(x) має не більше одного кореня. Підбором визначаємо, що х = -1. Вище викладене твердження доводить єдиність рішення.
а) f (х) ≤ g (x) у тому і тільки в тому випадку, коли х ϵ (- ∞ ; x 0 ]; б) f (х) ≥ g (x) у тому і тільки в тому випадку, х ϵ [х 0; +∞). Наочний зміст цього твердження очевидний Твердження 3. Якщо функція у = f (х) монотонно зростає на всій числовій прямій, функція у = g (x) монотонно зменшується на всій числовій прямій і f (х 0) = g (x 0), то справедливі такі твердження:
Розв'язати нерівність Розв'язання. Функція f(х) = монотонно зростає на всій числовій прямій, а функція g(x) = монотонно зменшується на всій ділянці визначення. Тому нерівність f(х) > g(x) виконується, якщо х > 2. Додамо область визначення нерівності. Отже, отримаємо систему Ответ: (2; 5).
Твердження 4. Якщо функція у = f(х) монотонно зростає, то рівняння f(х)=х і f(f(х))=х мають одну й ту саму безліч коренів, незалежно від кількості вкладень. Слідство. Якщо n - натуральне число, а функція у = f (х) монотонно зростає, то рівняння f (х) = х і n разів мають одне й те саме безліч коренів.
Вирішити рівняння. Відповідь: Рішення. При x ≥1 права частина рівняння не менше 1, а ліва частина менше 1. Отже, якщо рівняння має коріння, то будь-який з них менше 1. При x ≤0 права частина рівняння непозитивна, а ліва частина позитивна, тому що . Таким чином, будь-який корінь даного рівняння належить інтервалу (0; 1) Помноживши обидві частини даного рівняння на х, розділивши на x чисельник і знаменник лівої частини, отримаємо
Звідки =. Позначивши через t де t 0, отримаємо рівняння = t . Розглянемо зростаючу у своїй області визначення функцію f (t)= 1+ . Отримане рівняння можна записати як f (f (f (f (t))))= t , і за наслідком затвердження 4 воно має таку ж безліч рішень, як і рівняння f (t)= t , тобто. рівняння 1 + = t, звідки. Єдиним позитивним коренемцього квадратного щодо рівняння є. Отже, звідки, тобто. , або. Відповідь:
Твердження 1. Якщо max f (x) = с і min g (x) = с, то рівняння f (x) = g (x) має те ж безліч рішень, що і система Обмеженість Максимальне значення лівої частини дорівнює 1 мінімальне значенняправої частини 1 , отже, рішення рівняння зводитися до системи рівнянь: , з другого рівняння знаходимо можливий претендент x = 0 і переконуємося, що він є рішенням і першого рівняння. Відповідь: x=1.
Розв'язати рівняння Розв'язання. Так як sin3x≤1 і cos4x≤1, ліва частина даного рівняння не перевищує 7. Рівною 7 вона може бути в тому і тільки тому випадку, якщо звідки де k n Z Z . Залишається встановити, чи існують такі цілі k і n, за яких остання системамає рішення. Відповідь: Z
У задачах з невідомими x і параметром a під областю визначення розуміють безліч всіх упорядкованих пар чисел (x ; a) , кожна з яких така, що після підстановки відповідних значень x і a у всі співвідношення співвідношення будуть визначені. Приклад 1. При кожному значення параметра a усуньте нерівність Рішення. Знайдемо область визначення цієї нерівності. З яких видно, що система не має рішень. Отже, область визначення нерівності немає жодних пар чисел x і a , тому нерівність немає рішень. Область визначення Відповідь:
Інваріантність, тобто. незмінність рівняння чи нерівності щодо заміни змінної будь-яким алгебраїчним виразомвід цієї змінної. Найпростішим прикладом інваріантності є парність: якщо – парна функція, то рівняння інваріантне щодо заміни x і - x, оскільки = 0. Інваріантність
Знайти коріння рівняння. Рішення. Зауважимо, що пара інваріанту щодо заміни. Замінивши на рівність, отримаємо. Помноживши обидві частини даної рівності на 2 і віднімаючи з отриманої рівності почленно рівність, знаходимо 3 звідки. Тепер залишилося вирішити рівняння, звідки корінням рівняння є числа. Відповідь: .
Знайти всі значення a для кожного з яких рівняння має більше трьох різних рішень. Розв'язання задач із параметром Властивість монотонності
|x|= позитивно X= |x|= Для двох коренів чисельник може бути позитивний. Тому при корені першого та другого рівняння збігаються, що не відповідає вимогі умови: наявність більше трьох коренів. Відповідь: .
Знайти всі значення a, при кожному з яких рівняння має два корені. Перетворимо рівняння до виду І розглянемо функцію f(x)= певну та безперервну на всій числовій прямій. Графік цієї функції є ламаною, що складається з відрізків прямих і променів, кожна ланка якої є частиною прямої виду y= kt+l . f(x)= При будь-якому розкриття модуля першого виразу k не перевищує 8, тому зростання та зменшення функції f(x) буде залежати від розкриття другого модуля. При x f (x) буде спадати, а за x зростати. Тобто, при x=3 функція прийматиме найбільше значення. Для того, щоб рівняння мало два корені, необхідно, щоб f(3) Властивість монотонності
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Відповідь: a
Знайти всі значення параметра а, при кожному з яких для будь-якого дійсного значення х виконано нерівність Перепишемо нерівність у вигляді, введемо нову змінну t = і розглянемо функцію f (t) = , визначену і безперервну на всій числовій прямій. Графік цієї функції є ламаною, що складається з відрізків прямих і променів, кожна ланка якої є частиною прямого виду, де до
Оскільки, то t ϵ [-1; 1]. В силу монотонного зменшення функції у = f (t) достатньо перевірити лівий край даного відрізка. З. А істинним є значить, що можливе, тільки якщо числа і і v одного знака або якесь з них дорівнює нулю. , = () () 0. Розклавши квадратні тричлени на множники, отримаємо нерівність (з якої знаходимо, що а ϵ (-∞; -1] U (2) U [ 4; +∞).Відповідь: (-∞; - 1] U (2) U )
 Ораторське мистецтво як прообраз публіцистики
Ораторське мистецтво як прообраз публіцистики Цитати про Наполеона - dslinkov — LiveJournal
Цитати про Наполеона - dslinkov — LiveJournal Мені помста Людина на бульдозері зруйнувала місто
Мені помста Людина на бульдозері зруйнувала місто