Tìm góc giữa các mặt phẳng bằng phương pháp tọa độ. Góc giữa các mặt phẳng

Nhiệm vụ 1. Đáy của lăng trụ tứ giác thẳng ABCD 1 B 1 C 1 D 1 là hình chữ nhật ABCD, trong đó AB \u003d 5, AD \u003d 11. Tìm tang của góc giữa mặt phẳng đáy của lăng trụ và mặt phẳng đi qua trung điểm của cạnh AD vuông góc với đường thẳng BD 1 nếu khoảng cách giữa hai đường thẳng AC và B 1 D 1 là 12. Lời giải. Chúng tôi giới thiệu một hệ tọa độ. B(0;0;0), A(5;0;0), C(0;11;0), D 1 (5;11;12) Tọa độ của pháp tuyến với mặt phẳng tiết diện: Tọa độ của pháp tuyến với mặt phẳng cơ sở: – góc nhọn, thì D A B C D1D1 A1A1 B1B1 C1C1 x y z N Góc giữa các mặt phẳng Đáp số: 0,5. Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Nhiệm vụ 2. Tại cơ sở Kim tự tháp hình tam giác SABC nằm trong tam giác vuông ABC. Góc A thẳng. AC \u003d 8, BC \u003d 219. Chiều cao của hình chóp SA là 6. Trên cạnh AC lấy một điểm M sao cho AM \u003d 2. Vẽ mặt phẳng α đi qua điểm M, đỉnh B và điểm N - trung điểm của cạnh SC. Tìm góc nhị diện tạo bởi mặt phẳng α và mặt phẳng đáy của hình chóp. A S x B C M N y z Lời giải. Chúng tôi giới thiệu một hệ tọa độ. Khi đó A(0;0;0), C(0;8;0), M(0;2;0), N(0;4;3), S(0;0;6), Pháp tuyến với mặt phẳng vectơ ( ABC) Pháp tuyến với mặt phẳng (BMN) Góc giữa các mặt phẳng Đáp số: 60°. Phương trình mặt phẳng (ВМN): N.G. Nenasheva giáo viên toán trường trung học GBOU 985

Bài 3. Đáy của hình chóp tứ giác PABCD là hình vuông có cạnh bên bằng 6, cạnh bên PD vuông góc với mặt phẳng của mặt đáy và bằng 6. Tìm góc giữa hai mặt phẳng (BDP) và (BCP). Phán quyết. 1. Vẽ trung tuyến DF của tam giác cân CDP (BC = PD = 6) Vậy DF PC. Và từ BC (CDP) suy ra DF BC nghĩa là DF (PCB) A D C B P F 2. Vì AC DB và AC DP nên AC (BDP) 3. Do đó, góc giữa hai mặt phẳng (BDP) và (BCP) ) được tìm từ điều kiện: Góc giữa các mặt phẳng Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 3. Đáy của hình chóp tứ giác PABCD là hình vuông có cạnh bên bằng 6, cạnh bên PD vuông góc với mặt phẳng của mặt đáy và bằng 6. Tìm góc giữa hai mặt phẳng (BDP) và (BCP). Giải pháp.4. Hãy chọn một hệ tọa độ. Tọa độ của các điểm: 5. Khi đó các vectơ sẽ có tọa độ như sau: 6. Tính các giá trị, ta tìm được: , thì A D C B P F z x y Góc giữa các mặt phẳng Trả lời: Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 4. Trong hình lập phương ABCDA 1 B 1 C 1 D 1, tìm góc giữa hai mặt phẳng (AD 1 E) và (D 1 FC), trong đó E và F là trung điểm của các cạnh A 1 B 1 và B 1 C 1 tương ứng. Giải pháp: 1. Nhập hệ chữ nhật tọa độ và xác định tọa độ của các điểm: 2. Lập phương trình mặt phẳng (AD 1 E): 3. Lập phương trình mặt phẳng (D 1 FC): - vectơ pháp tuyến của mặt phẳng (AD 1 E). - vectơ pháp tuyến của mặt phẳng (D 1 FС). Góc giữa các mặt phẳng x y z Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 4. Trong hình lập phương ABCDA 1 B 1 C 1 D 1, tìm góc giữa hai mặt phẳng (AD 1 E) và (D 1 FC), trong đó E và F là trung điểm của các cạnh A 1 B 1 và B 1 C 1 tương ứng. Giải: 4. Tìm cosin của góc giữa các mặt phẳng bằng công thức Trả lời: Góc giữa các mặt phẳng x y z Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 5. Đoạn thẳng nối tâm đáy của một hình chóp tam giác đều với trung điểm của cạnh bên, bằng bên căn cứ. Tìm góc giữa các mặt bên kề của hình chóp. Bài giải: x y z 1. Cho hệ trục tọa độ vuông góc và xác định tọa độ các điểm A, B, C: K Gọi cạnh đáy là 1. Để xác định, xét các mặt SAC và SBC 2. Tìm tọa độ điểm S: E Góc giữa các mặt phẳng Nenasheva N.G . giáo viên toán trường trung học GBOU 985

Bài 5. Đoạn nối tâm đáy của một hình chóp tam giác đều với trung điểm của cạnh bên bằng cạnh đáy. Tìm góc giữa các mặt bên kề của hình chóp. Lời giải: x y z K E SO ta tìm được từ OSB: Góc giữa hai mặt phẳng Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 5. Đoạn nối tâm đáy của một hình chóp tam giác đều với trung điểm của cạnh bên bằng cạnh đáy. Tìm góc giữa các mặt bên kề của hình chóp. Lời giải: x y z K E 3. Phương trình của mặt phẳng (SAC): - vectơ pháp tuyến của mặt phẳng (SAC). 4. Phương trình của mặt phẳng (SBC): - vectơ pháp tuyến của mặt phẳng (SBC). Góc giữa các mặt phẳng Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bài 5. Đoạn nối tâm đáy của một hình chóp tam giác đều với trung điểm của cạnh bên bằng cạnh đáy. Tìm góc giữa các mặt bên kề của hình chóp. Lời giải: x y z K E 5. Tìm cosin của góc giữa các mặt phẳng theo công thức Trả lời: Góc giữa các mặt phẳng Nenasheva N.G. giáo viên toán trường trung học GBOU 985

Bàn thắng:

• phát triển khả năng xem xét các cách tiếp cận khác nhau để giải quyết vấn đề và phân tích “hiệu quả” của việc áp dụng các phương pháp giải quyết này;
• phát triển khả năng của học sinh trong việc lựa chọn một phương pháp giải quyết vấn đề phù hợp với sở thích toán học của họ, dựa trên kiến ​​​​thức vững chắc hơn và kỹ năng tự tin;
• phát triển khả năng lập kế hoạch cho các giai đoạn liên tiếp để đạt được kết quả;
• phát triển khả năng biện minh cho tất cả các bước và tính toán đã thực hiện;
• lặp lại và sửa chữa chủ đề khác nhau và các vấn đề về phép đo lập thể và phép đo phẳng, các cấu trúc lập thể tiêu biểu liên quan đến việc giải các bài toán hiện nay;
• phát triển tư duy không gian.

• phân tích Các phương pháp khác nhau giải toán: phương pháp véc tơ tọa độ, ứng dụng định lý côsin, ứng dụng định lý ba đường vuông góc;
• so sánh ưu nhược điểm của từng phương pháp;
• nhắc lại các tính chất của hình lập phương, lăng trụ tam giác, lục giác đều;
• chuẩn bị cho kỳ thi;
• phát triển tính độc lập trong việc ra quyết định.

đề cương bài học

khối lập phương A B C D A 1 B 1 C 1 D 1 có cạnh 1 điểm O - tâm mặt A B C D.

a) góc giữa các đường thẳng một 1 d và BO;

b) khoảng cách từ điểm bđến giữa vết cắt một 1 d.

Điểm quyết định a).

Hãy đặt khối lập phương của chúng ta trong một hệ trục tọa độ hình chữ nhật như trong hình, các đỉnh A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Vectơ chỉ phương của đường thẳng một 1 d và B1O:

(0; 1; -1) và (½; ½; -1);

góc φ mong muốn giữa chúng được tìm thấy theo công thức:

cos∠φ = ,
từ đó ∠φ = 30°.

2 cách. Chúng tôi sử dụng định lý cosin.

1) Vẽ đường thẳng ở 1 độ C song song với một đường thẳng một 1 d. Góc phố CB1O sẽ được mong muốn.

2) Từ tam giác vuông BB 1O theo định lý Pitago:

3) Theo định luật cosin của một tam giác CB1O tính góc CB1O:

cos CB 1 O = , góc mong muốn là 30°.

Nhận xét. Khi giải bài toán theo cách 2 có thể thấy, theo định lý ba đường vuông góc COB 1 = 90°, do đó từ hình chữ nhật ∆ CB1O nó cũng dễ dàng tính toán cosin của góc mong muốn.

Quyết định điểm b).

1 chiều. Hãy sử dụng công thức cho khoảng cách giữa hai điểm

hãy để điểm e- tên đệm một 1 d, thì tọa độ E(1;1/2;½), B(0;0;0).

B.E.= .

2 cách. Theo định lý Pitago

Từ hình chữ nhật ∆ CƯNG với trực tiếp CƯNG tìm thấy THÌ LÀ Ở = .

ở bên phải lăng kính tam giác ABCA 1 B 1 C 1 tất cả các cạnh đều bằng nhau một. Tìm góc giữa các đường thẳng AB và một 1C.

1 chiều. Phương pháp vectơ tọa độ

Tọa độ của các đỉnh của lăng kính trong một hệ hình chữ nhật khi lăng kính được định vị, như trong hình: A(0;0;0), B(a; ;0), A 1(0;0;a), C(0;a;0).

Vectơ chỉ phương của đường thẳng một 1C và AB:

(0; a; -a) và (một; ; 0} ;

cos φ = ;

2 cách. Ta sử dụng định luật cosin

Chúng tôi xem xét ∆ A 1 B 1 C, trong đó A 1 B 1 || AB. Chúng ta có

cos φ = .

(Từ Tuyển tập đề thi THTN-2012. Môn Toán: tiêu biểu lựa chọn thi biên tập A.L. Semenova, I.V. Yashchenko)

Trong lăng trụ lục giác đều ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, tất cả các cạnh đều bằng 1, tìm khoảng cách từ điểm e Thẳng B 1 C 1.

1 chiều. Phương pháp vectơ tọa độ

1) Đặt lăng kính trong hệ trục tọa độ vuông góc, đặt các trục tọa độ như hình vẽ. SS1, SW và CE vuông góc với nhau, vì vậy bạn có thể định hướng dọc theo chúng trục tọa độ. Ta có tọa độ:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) Tìm tọa độ các vectơ chỉ phương của các đường thẳng Từ 1 đến 1 và C 1 E:

(0;1;0), (;0;-1).

3) Tìm cosin của góc giữa Từ 1 đến 1 và C 1 E sử dụng tích vô hướng vectơ và :

cos β = = 0 => β = 90° => C 1 E là khoảng cách cần thiết.

4)C 1 E \u003d \u003d 2.

Kết luận: kiến ​​thức phương pháp tiếp cận khác nhauđể giải các bài toán lập thể cho phép bạn chọn phương pháp ưa thích cho bất kỳ học sinh nào, tức là một cách mà học sinh tự tin, giúp tránh mắc lỗi, dẫn đến giải thành công bài toán và đạt điểm cao trong kỳ thi. Phương pháp tọa độ có lợi thế hơn các phương pháp khác ở chỗ nó yêu cầu ít cân nhắc và tầm nhìn lập thể hơn, đồng thời dựa trên việc sử dụng các công thức có nhiều phép loại suy phẳng và đại số quen thuộc hơn với học sinh.

Hình thức bài dạy là sự kết hợp giữa lời giải thích của giáo viên với hoạt động tập thể trực tiếp của học sinh.

Các khối đa diện đang được xem xét được hiển thị trên màn hình bằng máy chiếu video, giúp so sánh nhiều cách khác nhau các giải pháp.

Bài tập về nhà: giải bài 3 theo cách khác, chẳng hạn sử dụng định lí ba đường vuông góc .

Văn

1. Ershova A.P., Goloborodko V.V. Độc lập và bài kiểm tra trong hình học lớp 11. - M.: ILEKSA, - 2010. - 208 tr.

2. Hình học, 10-11: sách giáo khoa cho cơ sở giáo dục: cấp độ cơ bản và hồ sơ / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev và những người khác - M.: Giáo dục, 2007. - 256 tr.

3. SỬ DỤNG-2012. Toán học: các lựa chọn kiểm tra điển hình: 10 lựa chọn / ed. A.L. Semenova, I.V. Yashchenko. – M.: giáo dục quốc dân, 2011. - 112 tr. - (SỬ DỤNG-2012. FIPI - trường học).

Bài báo nói về tìm góc giữa các mặt phẳng. Sau khi đưa ra định nghĩa, chúng tôi sẽ thiết lập một minh họa đồ họa, xem xét cách dài dòng tìm bằng phương pháp tọa độ. Chúng ta thu được một công thức cho các mặt phẳng cắt nhau, bao gồm tọa độ của các vectơ pháp tuyến.

Yandex.RTB R-A-339285-1

Tài liệu sẽ sử dụng dữ liệu và khái niệm đã được nghiên cứu trước đây trong các bài viết về mặt phẳng và đường thẳng trong không gian. Để bắt đầu, cần chuyển sang lý luận cho phép một người có một cách tiếp cận nhất định để xác định góc giữa hai mặt phẳng cắt nhau.

Cho hai mặt phẳng cắt nhau γ 1 và γ 2 . Giao điểm của chúng sẽ có ký hiệu là c . Việc xây dựng mặt phẳng χ được kết nối với giao tuyến của các mặt phẳng này. Mặt phẳng χ đi qua điểm M là đường thẳng c. Các mặt phẳng γ 1 và γ 2 sẽ cắt nhau bằng mặt phẳng χ. Chúng tôi chấp nhận các ký hiệu của đường thẳng cắt γ 1 và χ cho đường thẳng a và giao nhau γ 2 và χ cho đường thẳng b. Ta nhận được rằng giao điểm của các đường thẳng a và b cho điểm M .

Vị trí của điểm M không ảnh hưởng đến góc giữa hai đường thẳng a và b, và điểm M nằm trên đường thẳng c mà mặt phẳng χ đi qua.

Cần dựng mặt phẳng χ 1 vuông góc với đường thẳng c và khác mặt phẳng χ . Giao tuyến của các mặt phẳng γ 1 và γ 2 với sự trợ giúp của χ 1 sẽ có ký hiệu là các đường thẳng a 1 và b 1 .

Có thể thấy rằng khi dựng χ và χ 1 thì các đường thẳng a, b vuông góc với đường thẳng c thì a 1, b 1 vuông góc với đường thẳng c. Tìm các đường thẳng a và a 1 trong mặt phẳng γ 1 vuông góc với đường thẳng c thì có thể coi chúng song song với nhau. Tương tự, vị trí của b và b 1 trong mặt phẳng γ 2 với đường thẳng c vuông góc với nhau biểu thị tính song song của chúng. Điều này có nghĩa là cần thực hiện phép dời hình song song mặt phẳng χ 1 sang χ , tại đó ta được hai đường thẳng trùng nhau a và a 1 , b và b 1 . Ta được rằng góc giữa hai đường thẳng cắt nhau a và b 1 bằng góc giao tuyến a và b.

Hãy xem xét hình dưới đây.

Phán đoán này được chứng minh bằng thực tế là giữa các đường thẳng cắt nhau a và b có một góc không phụ thuộc vào vị trí của điểm M, đó là giao điểm. Các đường thẳng này nằm trong các mặt phẳng γ 1 và γ 2 . Trên thực tế, góc tạo thành có thể được coi là góc giữa hai mặt phẳng cắt nhau.

Hãy chuyển sang xác định góc giữa các mặt phẳng giao nhau hiện có γ 1 và γ 2 .

định nghĩa 1

Góc giữa hai mặt phẳng cắt nhau γ 1 và γ 2 gọi là góc tạo bởi giao tuyến của hai đường thẳng a và b, trong đó các mặt phẳng γ 1 và γ 2 cắt nhau với mặt phẳng χ vuông góc với đường thẳng c.

Hãy xem xét hình dưới đây.

Định nghĩa có thể được gửi dưới dạng khác. Tại giao tuyến của các mặt phẳng γ 1 và γ 2, trong đó c là đường thẳng mà chúng cắt nhau, đánh dấu điểm M, qua đó kẻ các đường thẳng a và b, vuông góc với đường thẳng c và nằm trong các mặt phẳng γ 1 và γ 2 thì góc giữa hai đường thẳng a và b sẽ là góc giữa hai mặt phẳng. Trong thực tế, điều này có thể áp dụng để dựng một góc giữa các mặt phẳng.

Tại giao điểm, một góc được hình thành có giá trị nhỏ hơn 90 độ, nghĩa là độ đo góc có giá trị trên một khoảng thuộc loại này (0, 90]. Đồng thời, các mặt phẳng này được gọi là vuông góc nếu tại giao tuyến tạo thành một góc vuông. Góc giữa mặt phẳng song songđược coi là bằng không.

Cách thông thường để tìm góc giữa các mặt phẳng giao nhau là thực hiện các phép dựng bổ sung. Điều này giúp xác định nó một cách chính xác và điều này có thể được thực hiện bằng cách sử dụng các dấu bằng hoặc đồng dạng của tam giác, sin, cosin của góc.

Xem xét giải quyết vấn đề bằng cách sử dụng một ví dụ từ nhiệm vụ SỬ DỤNG khối C2 .

ví dụ 1

Cho một hình chữ nhật song song A B C D A 1 B 1 C 1 D 1, trong đó cạnh A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, điểm E cách cạnh A A 1 theo tỷ lệ 4: 3. Tìm góc giữa các mặt phẳng A B C và B E D 1 .

Phán quyết

Để rõ ràng, bạn cần vẽ một bản vẽ. Chúng tôi hiểu điều đó

Một biểu diễn trực quan là cần thiết để thuận tiện hơn khi làm việc với góc giữa các mặt phẳng.

Ta lập định nghĩa đường thẳng cắt nhau của các mặt phẳng A B C và B E D 1 . Điểm B là điểm chung. Cần tìm thêm một điểm giao nhau nữa. Xét các đường thẳng D A và D 1 E , chúng nằm trong cùng một mặt phẳng A D D 1 . Vị trí của chúng không biểu thị tính song song, có nghĩa là chúng có một giao điểm chung.

Tuy nhiên, đường thẳng D A nằm trong mặt phẳng A B C, và D 1 E thuộc B E D 1 . Do đó, chúng tôi nhận được rằng các dòng D A và D 1 E có giao điểm chung là giao điểm chung của các mặt phẳng A B C và B E D 1 . Cho biết giao điểm của các đường D A và D 1 E chữ F Từ đây ta có B F là đường thẳng cắt các mặt phẳng A B C và B E D 1 .

Hãy xem xét hình dưới đây.

Để có câu trả lời cần dựng các đường thẳng nằm trong các mặt phẳng A B C và B E D 1 đi qua một điểm nằm trên đường thẳng B F và vuông góc với nó. Sau đó, góc kết quả giữa các đường này được coi là góc mong muốn giữa các mặt phẳng A B C và B E D 1.

Từ đó có thể thấy rằng điểm A là hình chiếu của điểm E trên mặt phẳng A B C. Cần vẽ một đường thẳng cắt đường thẳng B F vuông góc tại điểm M. Có thể thấy rằng đường thẳng A M là hình chiếu của đường thẳng E M lên mặt phẳng A B C, dựa vào định lý về các đường vuông góc A M ⊥ B F . Hãy xem xét hình dưới đây.

∠ A M E là góc tạo bởi các mặt phẳng A B C và B E D 1 . Từ tam giác A E M thu được, chúng ta có thể tìm sin, cosin hoặc tang của góc, sau đó là chính góc đó, chỉ với hai cạnh đã biết của nó. Theo điều kiện, chúng ta có độ dài của A E được tìm theo cách này: đoạn thẳng A A 1 được chia cho điểm E theo tỷ lệ 4: 3, nghĩa là tổng chiều dài của đoạn thẳng là 7 phần, sau đó A E \u003d 4 phần. Chúng tôi tìm thấy A.M.

Cần xét tam giác vuông A B F . Chúng ta có một góc vuông A với chiều cao A M. Từ điều kiện A B \u003d 2, sau đó chúng ta có thể tìm thấy độ dài A F bằng sự đồng dạng của các tam giác D D 1 F và A E F. Ta có A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Cần phải tìm độ dài của cạnh B F từ tam giác A B F bằng định lý Pythagore. Ta có B F   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Tính độ dài cạnh A M qua diện tích tam giác A B F . Ta có diện tích có thể bằng cả S A B C = 1 2 · A B · A F và S A B C = 1 2 · B F · A M .

Ta có A M = A B A F B F = 2 4 2 5 = 4 5 5

Sau đó, chúng ta có thể tìm thấy giá trị của tiếp tuyến của góc của tam giác A E M. Chúng ta nhận được:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Góc mong muốn thu được bởi giao tuyến của các mặt phẳng A B C và B E D 1 bằng a r c t g 5, sau đó, khi đơn giản hóa, chúng ta nhận được a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Câu trả lời: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Một số trường hợp tìm góc giữa các đường thẳng cắt nhau được đưa ra bằng cách sử dụng mặt phẳng tọa độ Giới thiệu x y z và phương toạ độ. Hãy xem xét chi tiết hơn.

Nếu một vấn đề được đưa ra trong đó cần tìm góc giữa các mặt phẳng giao nhau γ 1 và γ 2, chúng ta ký hiệu góc mong muốn là α.

sau đó hệ thống nhất định tọa độ cho thấy rằng chúng ta có tọa độ của các vectơ pháp tuyến của các mặt phẳng cắt nhau γ 1 và γ 2 . Sau đó, chúng ta biểu thị rằng n 1 → = n 1 x , n 1 y , n 1 z là một vectơ pháp tuyến của mặt phẳng γ 1 và n 2 → = (n 2 x , n 2 y , n 2 z) - đối với mặt phẳng γ 2 . Xem xét một phát hiện chi tiết về góc nằm giữa các mặt phẳng này theo tọa độ của các vectơ.

Cần chỉ định đường thẳng dọc theo đó các mặt phẳng γ 1 và γ 2 cắt nhau bằng chữ c. Trên đường thẳng có điểm M, qua điểm đó vẽ mặt phẳng χ vuông góc với c. Mặt phẳng χ dọc theo các đường thẳng a và b cắt các mặt phẳng γ 1 và γ 2 tại điểm M . suy ra từ định nghĩa rằng góc giữa các mặt phẳng cắt nhau γ 1 và γ 2 tương ứng bằng góc của các đường thẳng cắt nhau a và b thuộc các mặt phẳng này.

Trong mặt phẳng χ vẽ từ điểm M vectơ bình thường và biểu thị chúng n 1 → và n 2 → . Vectơ n 1 → nằm trên đường vuông góc với đường thẳng a và vectơ n 2 → nằm trên đường vuông góc với đường thẳng b. Do đó chúng tôi nhận được rằng mặt phẳng đã choχ có vectơ pháp tuyến của đường thẳng a bằng n 1 → và của đường thẳng b bằng n 2 → . Hãy xem xét hình dưới đây.

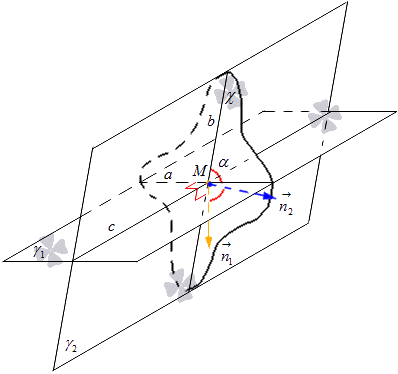
Từ đây, chúng ta có được một công thức mà chúng ta có thể tính sin của góc của các đường thẳng cắt nhau bằng cách sử dụng tọa độ của các vectơ. Ta thấy rằng cosin của góc giữa hai đường thẳng a và b bằng cosin giữa hai mặt phẳng cắt nhau γ 1 và γ 2 suy ra từ công thức cosα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , trong đó chúng ta có n 1 → = (n 1 x , n 1 y , n 1 z) và n 2 → = (n 2 x , n 2 y , n 2 z) là tọa độ của vectơ của các mặt phẳng biểu diễn.

Góc giữa các đường thẳng cắt nhau được tính theo công thức

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

ví dụ 2

Theo điều kiện, một hình bình hành А В С D A 1 B 1 C 1 D 1 được cho , trong đó A B \u003d 2, A D \u003d 3, A A 1 \u003d 7 và điểm E cách cạnh A A 1 4: 3. Tìm góc giữa các mặt phẳng A B C và B E D 1 .

Phán quyết

Nó có thể được nhìn thấy từ điều kiện là các cạnh của nó vuông góc với nhau. Điều này có nghĩa là cần phải giới thiệu một hệ tọa độ O x y z có đỉnh tại điểm C và các trục tọa độ O x, O y, O z. Nó là cần thiết để đặt hướng trên các mặt thích hợp. Hãy xem xét hình dưới đây.

giao nhau của mặt phẳng A B C và B E D 1 tạo thành một góc có thể tìm được theo công thức 2 x 2 + n 2 y 2 + n 2 z 2 , trong đó n 1 → = (n 1 x , n 1 y , n 1 z) và n 2 → = (n 2 x , n 2 y , n 2 z ) là các vectơ pháp tuyến của các mặt phẳng này. Nó là cần thiết để xác định tọa độ. Từ hình bên ta thấy trục tọa độ O x y trùng trong mặt phẳng A B C nghĩa là tọa độ của vectơ pháp tuyến k → bằng giá trị n 1 → = k → = (0, 0, 1) .

Vectơ pháp tuyến của mặt phẳng B E D 1 là tích vectơ của B E → và B D 1 → , trong đó tọa độ của chúng được tìm bởi tọa độ điểm cực trị B, E, D 1 , được xác định dựa vào điều kiện của bài toán.

Chúng tôi nhận được rằng B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Vì A E E A 1 = 4 3 , từ tọa độ các điểm A 2 , 3 , 0 , A 1 2 , 3 , 7 ta tìm được E 2 , 3 , 4 . Ta có B E → = (2 , 0 , 4 ) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Cần thay tọa độ tìm được vào công thức tính góc qua cung cosin. Chúng tôi nhận được

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Phương pháp tọa độ cho kết quả tương tự.

Câu trả lời: r c cos 6 6 .

Vấn đề cuối cùng được xem xét để tìm góc giữa các mặt phẳng giao nhau với các phương trình đã biết có sẵn của các mặt phẳng.

ví dụ 3

Tính sin, cosin của góc và giá trị của góc tạo bởi hai đường thẳng cắt nhau xác định trong hệ tọa độ O x y z và cho bởi các phương trình 2 x - 4 y + z + 1 = 0 và 3 y - z-1 = 0 .

Phán quyết

Khi nghiên cứu một chủ đề phương trình tổng quátđường thẳng có dạng A x + B y + C z + D = 0 tiết lộ rằng A, B, C là các hệ số bằng tọa độ của vectơ pháp tuyến. Do đó n 1 → = 2 , - 4 , 1 và n 2 → = 0 , 3 , - 1 là các vectơ pháp tuyến của các đường thẳng đã cho.

Cần thay tọa độ của các vectơ pháp tuyến của các mặt phẳng vào công thức tính góc mong muốn của các mặt phẳng cắt nhau. Sau đó, chúng tôi nhận được rằng

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Do đó, chúng ta có cosin của góc có dạng cos α = 13 210 . Khi đó góc của các đường cắt nhau không tù. thay thế trong nhận dạng lượng giác, ta được rằng giá trị của sin của góc bằng biểu thức. Chúng tôi tính toán và nhận được điều đó

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Câu trả lời: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Nếu bạn nhận thấy một lỗi trong văn bản, hãy đánh dấu nó và nhấn Ctrl + Enter

\(\blacktriangleright\) Góc nhị diện là góc tạo bởi hai nửa mặt phẳng và đường thẳng \(a\) , là ranh giới chung của chúng.

\(\blacktriangleright\) Để tìm góc giữa hai mặt phẳng \(\xi\) và \(\pi\) , bạn cần tìm góc pháp tuyến cay hoặc là dài) Góc nghiêng tạo bởi các mặt phẳng \(\xi\) và \(\pi\) :

Bước 1: Cho \(\xi\cap\pi=a\) (giao tuyến của các mặt phẳng). Trong mặt phẳng \(\xi\) ta lưu ý điểm tùy ý\(F\) và vẽ \(FA\perp a\) ;

Bước 2: vẽ \(FG\perp \pi\) ;

Bước 3: theo TTP (\(FG\) - vuông góc, \(FA\) - xiên, \(AG\) - phép chiếu) ta có: \(AG\perp a\) ;

Bước 4: Góc \(\angle FAG\) được gọi là góc pháp tuyến của góc nhị diện tạo bởi các mặt phẳng \(\xi\) và \(\pi\) .

Lưu ý rằng tam giác \(AG\) là tam giác vuông.
Cũng lưu ý rằng mặt phẳng \(AFG\) được dựng theo cách này vuông góc với cả hai mặt phẳng \(\xi\) và \(\pi\) . Do đó, có thể nói theo một cách khác: góc giữa các mặt phẳng\(\xi\) và \(\pi\) là góc giữa hai đường thẳng cắt nhau \(c\in \xi\) và \(b\in\pi\) , tạo thành một mặt phẳng vuông góc với \(\xi\ ) và \(\pi\) .

Nhiệm vụ 1 #2875

Mức độ nhiệm vụ: Khó hơn kỳ thi

dana kim tự tháp tứ giác, tất cả các cạnh của nó bằng nhau và đáy là một hình vuông. Tìm \(6\cos \alpha\) , trong đó \(\alpha\) là góc giữa các mặt bên liền kề của nó.

Cho \(SABCD\) là một hình chóp đã cho (\(S\) là một đỉnh) có các cạnh bằng \(a\) . Vì vậy, tất cả mặt bên là các tam giác đều bằng nhau. Tìm góc giữa các mặt \(SAD\) và \(SCD\) .

Hãy vẽ \(CH\perp SD\) . Như \(\tam giác SAD=\tam giác SCD\), thì \(AH\) cũng sẽ có chiều cao là \(\triangle SAD\) . Do đó, theo định nghĩa, \(\angle AHC=\alpha\) là góc nhị diện tuyến tính giữa các mặt \(SAD\) và \(SCD\) .
Vì đáy là hình vuông nên \(AC=a\sqrt2\) . Cũng lưu ý rằng \(CH=AH\) là chiều cao Tam giác đều với bên \(a\) , do đó \(CH=AH=\frac(\sqrt3)2a\) .
Sau đó, theo định lý cosin từ \(\triangle AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Trả lời: -2

Nhiệm vụ 2 #2876

Mức độ nhiệm vụ: Khó hơn kỳ thi

Các mặt phẳng \(\pi_1\) và \(\pi_2\) cắt nhau theo một góc có cosin bằng \(0,2\) . Các mặt phẳng \(\pi_2\) và \(\pi_3\) cắt nhau tại một góc vuông và giao tuyến của các mặt phẳng \(\pi_1\) và \(\pi_2\) song song với giao tuyến của các mặt phẳng \(\pi_2\) và \(\ pi_3\) . Tìm sin của góc giữa hai mặt phẳng \(\pi_1\) và \(\pi_3\) .

Gọi giao tuyến của \(\pi_1\) và \(\pi_2\) là đường thẳng \(a\) , giao tuyến của \(\pi_2\) và \(\pi_3\) là đường thẳng \ (b\) , và đường giao nhau \(\pi_3\) và \(\pi_1\) là đường thẳng \(c\) . Vì \(a\parallel b\) , nên \(c\parallel a\parallel b\) (theo định lý từ phần tài liệu tham khảo lý thuyết “Hình học trong không gian” \(\rightarrow\) “Giới thiệu về hình học lập thể, song song”).

Đánh dấu các điểm \(A\in a, B\in b\) sao cho \(AB\perp a, AB\perp b\) (điều này khả thi vì \(a\parallel b\) ). Lưu ý \(C\in c\) sao cho \(BC\perp c\) , do đó \(BC\perp b\) . Sau đó \(AC\perp c\) và \(AC\perp a\) .
Thật vậy, vì \(AB\perp b, BC\perp b\) , nên \(b\) vuông góc với mặt phẳng \(ABC\) . Vì \(c\parallel a\parallel b\) , nên các đường \(a\) và \(c\) cũng vuông góc với mặt phẳng \(ABC\) , và do đó, cụ thể là bất kỳ đường nào từ mặt phẳng này, dòng \(AC\) .

Do đó nó theo sau đó \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Hóa ra \(\tam giác ABC\) là hình chữ nhật, nghĩa là \[\sin \angle BCA=\cos \angle BAC=0,2.\]

Trả lời: 0,2

Nhiệm vụ 3 #2877

Mức độ nhiệm vụ: Khó hơn kỳ thi

Cho các đường thẳng \(a, b, c\) cắt nhau tại một điểm và góc giữa hai đường thẳng bất kỳ bằng \(60^\circ\) . Tìm \(\cos^(-1)\alpha\) , trong đó \(\alpha\) là góc giữa mặt phẳng tạo bởi các đường \(a\) và \(c\) và mặt phẳng tạo bởi các đường \(b\ ) và \(c\) . Đưa ra câu trả lời của bạn trong độ.

Để các đường cắt nhau tại điểm \(O\) . Vì góc giữa hai đường thẳng bất kỳ bằng \(60^\circ\) , nên cả ba đường thẳng không thể cùng nằm trong một mặt phẳng. Hãy để chúng tôi đánh dấu một điểm \(A\) trên dòng \(a\) và vẽ \(AB\perp b\) và \(AC\perp c\) . sau đó \(\tam giác AOB=\tam giác AOC\) như hình chữ nhật trong cạnh huyền và góc nhọn. Do đó \(OB=OC\) và \(AB=AC\) .
Hãy làm \(AH\perp (BOC)\) . Sau đó, theo định lý ba đường vuông góc \(HC\perp c\) , \(HB\perp b\) . Vì \(AB=AC\) , nên \(\tam giác AHB=\tam giác AHC\) như hình chữ nhật dọc theo cạnh huyền và chân. Do đó, \(HB=HC\) . Do đó \(OH\) ​​là tia phân giác của góc \(BOC\) (vì điểm \(H\) cách đều các cạnh của góc).

Lưu ý rằng theo cách này, chúng ta cũng đã xây dựng góc tuyến tính của góc nhị diện tạo bởi mặt phẳng tạo bởi các đường \(a\) và \(c\) và mặt phẳng tạo bởi các đường \(b\) và \( c\) . Đây là góc \(ACH\) .

Hãy tìm góc này. Vì chúng ta đã chọn tùy ý điểm \(A\) nên chúng ta hãy chọn điểm đó sao cho \(OA=2\) . Sau đó, trong hình chữ nhật \(\triangle AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Vì \(OH\) ​​là tia phân giác nên \(\angle HOC=30^\circ\) , do đó, trong hình chữ nhật \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Sau đó, từ hình chữ nhật \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Trả lời: 3

Nhiệm vụ 4 #2910

Mức độ nhiệm vụ: Khó hơn kỳ thi

Các mặt phẳng \(\pi_1\) và \(\pi_2\) cắt nhau dọc theo đường thẳng \(l\) , chứa các điểm \(M\) và \(N\) . Các đoạn thẳng \(MA\) và \(MB\) lần lượt vuông góc với đường thẳng \(l\) và nằm trong các mặt phẳng \(\pi_1\) và \(\pi_2\) và \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Tìm \(3\cos\alpha\) , trong đó \(\alpha\) là góc giữa hai mặt phẳng \(\pi_1\) và \(\pi_2\) .

Tam giác \(AMN\) là tam giác vuông, \(AN^2 = AM^2 + MN^2\) , từ đâu \ Tam giác \(BMN\) là tam giác vuông, \(BN^2 = BM^2 + MN^2\) , do đó \ Ta viết định lý cosin cho tam giác \(AMB\): \ sau đó \ Vì góc \(\alpha\) giữa các mặt phẳng là một góc nhọn và \(\angle AMB\) hóa ra là một góc tù, nên \(\cos\alpha=\dfrac5(12)\) . sau đó \

Đáp số: 1,25

Nhiệm vụ 5 #2911

Mức độ nhiệm vụ: Khó hơn kỳ thi

\(ABCDA_1B_1C_1D_1\) là hình bình hành, \(ABCD\) là hình vuông có cạnh \(a\) , điểm \(M\) là đáy của đường vuông góc hạ từ điểm \(A_1\) xuống mặt phẳng \ ((ABCD)\) , hơn nữa, \(M\) là giao điểm của các đường chéo của hình vuông \(ABCD\) . được biết rằng \(A_1M = \dfrac(\sqrt(3))(2)a\). Tìm góc giữa hai mặt phẳng \((ABCD)\) và \((AA_1B_1B)\) . Đưa ra câu trả lời của bạn trong độ.

Ta dựng \(MN\) vuông góc với \(AB\) như hình vẽ.

Vì \(ABCD\) là hình vuông có cạnh \(a\) và \(MN\perp AB\) và \(BC\perp AB\) , nên \(MN\song song BC\) . Vì \(M\) là giao điểm của các đường chéo của hình vuông nên \(M\) là trung điểm của \(AC\) , do đó, \(MN\) là đường giữa và \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) là hình chiếu của \(A_1N\) lên mặt phẳng \((ABCD)\) , và \(MN\) vuông góc với \(AB\) , khi đó, theo định lý ba đường vuông góc, \( A_1N\) vuông góc với \(AB \) và góc giữa hai mặt phẳng \((ABCD)\) và \((AA_1B_1B)\) là \(\góc A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Đáp án: 60

Nhiệm vụ 6 #1854

Mức độ nhiệm vụ: Khó hơn kỳ thi

Trong hình vuông \(ABCD\): \(O\) là giao điểm của hai đường chéo; \(S\) không nằm trong mặt phẳng của hình vuông, \(SO \perp ABC\) . Tìm góc giữa hai mặt phẳng \(ASD\) và \(ABC\) nếu \(SO = 5\) và \(AB = 10\) .

Các tam giác vuông \(\triangle SAO\) và \(\triangle SDO\) có hai cạnh và góc xen giữa bằng nhau (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , bởi vì \(O\) là giao điểm của hai đường chéo của hình vuông, \(SO\) là mặt chung) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\tam giác ASD\) là cân. Điểm \(K\) là trung điểm của \(AD\) , thì \(SK\) là chiều cao trong tam giác \(\triangle ASD\) , và \(OK\) là chiều cao trong tam giác \ Mặt phẳng (AOD\) \(\ Rightarrow\) \(SOK\) vuông góc với các mặt phẳng \(ASD\) và \(ABC\) \(\Rightarrow\) \(\angle SKO\) là một góc pháp tuyến bằng đến góc nhị diện cần thiết.

Trong \(\triangle SKO\) : \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) là tam giác vuông cân \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Đáp án: 45

Nhiệm vụ 7 #1855

Mức độ nhiệm vụ: Khó hơn kỳ thi

Trong hình vuông \(ABCD\): \(O\) là giao điểm của hai đường chéo; \(S\) không nằm trong mặt phẳng của hình vuông, \(SO \perp ABC\) . Tìm góc giữa hai mặt phẳng \(ASD\) và \(BSC\) nếu \(SO = 5\) và \(AB = 10\) .

Các tam giác vuông \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) và \(\triangle SOC\) có hai cạnh và góc giữa chúng bằng nhau (\(SO \perp ABC \) \(\Mũi tên phải\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) , vì \(O\) là giao điểm của các đường chéo của hình vuông, \(SO\) là cạnh chung) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\tam giác ASD\) và \(\tam giác BSC\) là các tam giác cân. Điểm \(K\) là trung điểm của \(AD\) , thì \(SK\) là chiều cao trong tam giác \(\triangle ASD\) , và \(OK\) là chiều cao trong tam giác \ (AOD\) \(\ Rightarrow\) mặt phẳng \(SOK\) vuông góc với mặt phẳng \(ASD\) . Điểm \(L\) là trung điểm của \(BC\) , thì \(SL\) là chiều cao trong tam giác \(\triangle BSC\) , và \(OL\) là chiều cao trong tam giác \ (BOC\) \(\ Rightarrow\) mặt phẳng \(SOL\) (hay còn gọi là mặt phẳng \(SOK\) ) vuông góc với mặt phẳng \(BSC\) . Do đó, chúng tôi thu được rằng \(\góc KSL\) là một góc tuyến tính bằng với góc nhị diện mong muốn.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – chiều cao bằng nhau tam giác cân, có thể được tìm thấy bằng cách sử dụng định lý Pythagore: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Có thể thấy rằng \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) cho tam giác \(\triangle KSL\) định lý đảo ngược Pythagore \(\Rightarrow\) \(\triangle KSL\) – tam giác vuông \(\Rightarrow\) \(\angle KSL = 90^\circ\) .

Đáp án: 90

Theo quy luật, việc chuẩn bị cho học sinh tham gia kỳ thi toán học bắt đầu bằng việc lặp lại các công thức cơ bản, bao gồm cả những công thức cho phép bạn xác định góc giữa các mặt phẳng. Mặc dù thực tế là phần hình học này được đề cập đầy đủ chi tiết trong khuôn khổ của chương trình giáo dục, nhiều sinh viên tốt nghiệp cần lặp lại các tài liệu cơ bản. Nắm được cách tìm góc giữa các mặt phẳng, học sinh THPT sẽ có thể nhanh chóng tính ra đáp án đúng trong quá trình giải bài tập và tin tưởng đạt điểm khá theo kỳ thi thống nhất của nhà nước.

Sắc thái chính

Vì vậy, câu hỏi làm thế nào để tìm góc nhị diện không gây khó khăn, chúng tôi khuyên bạn nên làm theo thuật toán giải pháp sẽ giúp bạn đối phó với các nhiệm vụ của kỳ thi.

Trước tiên, bạn cần xác định đường mà các mặt phẳng cắt nhau.

Sau đó, trên dòng này, bạn cần chọn một điểm và vẽ hai đường vuông góc với nó.

Bước tiếp theo là tìm hàm lượng giác góc nhị diện, được hình thành bởi các đường vuông góc. Cách thuận tiện nhất là thực hiện việc này với sự trợ giúp của tam giác thu được, trong đó góc là một phần.

Câu trả lời sẽ là giá trị của góc hoặc hàm lượng giác của nó.

Chuẩn bị cho kỳ thi cùng với Shkolkovo là chìa khóa thành công của bạn

Trong giờ học hôm trước vượt qua kỳ thi nhiều học sinh gặp phải vấn đề tìm định nghĩa và công thức tính góc giữa 2 mặt phẳng. Sách giáo khoa ở trường không phải lúc nào cũng có sẵn khi cần thiết. Và để tìm công thức cần thiết và các ví dụ về ứng dụng chính xác của chúng, bao gồm tìm góc giữa các mặt phẳng trên Internet trực tuyến, đôi khi mất rất nhiều thời gian.

Cổng toán học "Shkolkovo" cung cấp cách tiếp cận mớiđể chuẩn bị cho kỳ thi cấp bang. Các lớp học trên trang web của chúng tôi sẽ giúp sinh viên xác định những phần khó khăn nhất cho bản thân và lấp đầy những lỗ hổng kiến ​​thức.

Chúng tôi đã chuẩn bị và trình bày rõ ràng tất cả các tài liệu cần thiết. Định nghĩa cơ bản và các công thức được trình bày trong phần "Tài liệu tham khảo lý thuyết".

Để tiếp thu tài liệu tốt hơn, chúng tôi cũng khuyên bạn nên thực hành các bài tập tương ứng. Nhiều lựa chọn nhiệm vụ mức độ khác nhauđộ phức tạp, ví dụ, trên, được trình bày trong phần "Danh mục". Tất cả các nhiệm vụ đều chứa một thuật toán chi tiết để tìm câu trả lời đúng. Danh sách bài tập trên trang được bổ sung và cập nhật liên tục.

Thực hành giải các bài toán yêu cầu tìm góc giữa hai mặt phẳng, học sinh có cơ hội lưu bất kỳ bài tập nào trực tuyến vào mục "Yêu thích". Nhờ vậy, họ sẽ có thể quay lại với anh ta. khối lượng bắt buộc thời gian và thảo luận về quá trình quyết định của mình với giáo viên trường học hoặc một gia sư.

Bài này nói về góc giữa các mặt phẳng và cách tìm nó. Đầu tiên, đưa ra định nghĩa góc giữa hai mặt phẳng và đưa ra hình vẽ minh họa. Sau đó, nguyên tắc tìm góc giữa hai mặt phẳng cắt nhau bằng phương pháp tọa độ đã được tháo rời, người ta đã rút ra được công thức cho phép tính góc giữa hai mặt phẳng cắt nhau theo tọa độ đã biết các vectơ pháp tuyến của các mặt phẳng này. Tóm lại, nó cho thấy giải pháp chi tiết nhiệm vụ điển hình.

Điều hướng trang.

Góc giữa các mặt phẳng - định nghĩa.

Hãy để chúng tôi đưa ra các lập luận cho phép chúng tôi dần dần tiếp cận định nghĩa về góc giữa hai mặt phẳng cắt nhau.

Cho chúng ta hai mặt phẳng cắt nhau và . Các mặt phẳng này cắt nhau theo một đường thẳng mà chúng ta ký hiệu bằng chữ c. Hãy dựng mặt phẳng đi qua điểm M thuộc đường thẳng c và vuông góc với đường thẳng c. Trong trường hợp này, mặt phẳng sẽ cắt các mặt phẳng và . Biểu thị đường thẳng mà các mặt phẳng cắt nhau và là a, và đường thẳng mà các mặt phẳng cắt nhau và là b. Hiển nhiên, các đường thẳng a và b cắt nhau tại điểm M.

Dễ dàng chứng minh được rằng góc giữa hai đường thẳng cắt nhau a và b không phụ thuộc vào vị trí của điểm M trên đường thẳng c mà mặt phẳng đi qua.

Hãy dựng một mặt phẳng vuông góc với đường thẳng c và khác với mặt phẳng . Mặt phẳng cắt bởi các mặt phẳng và dọc theo các đường thẳng mà ta kí hiệu lần lượt là a 1 và b 1 .

Từ phương pháp dựng các mặt phẳng và suy ra các đường thẳng a, b vuông góc với đường thẳng c, và các đường thẳng a 1, b 1 vuông góc với đường thẳng c. Vì hai đường thẳng a và a 1 cùng nằm trong một mặt phẳng và vuông góc với đường thẳng c nên chúng song song với nhau. Tương tự, các đường thẳng b và b 1 cùng nằm trong một mặt phẳng và vuông góc với đường thẳng c nên chúng song song với nhau. Như vậy có thể thực hiện phép dời hình song song với mặt phẳng trong đó đường thẳng a 1 trùng với đường thẳng a , đường thẳng b trùng với đường thẳng b 1 . Do đó, góc giữa hai đường thẳng cắt nhau a 1 và b 1 bằng góc giữa hai đường thẳng cắt nhau a và b .

Điều này chứng tỏ góc giữa hai đường thẳng a và b nằm trong hai mặt phẳng cắt nhau và không phụ thuộc vào cách chọn điểm M mà mặt phẳng đi qua. Do đó, thật hợp lý khi coi góc này là góc giữa hai mặt phẳng cắt nhau.

Bây giờ bạn có thể đọc định nghĩa góc giữa hai mặt phẳng cắt nhau và .

Sự định nghĩa.

Góc giữa hai mặt phẳng cắt nhau theo đường thẳng và là góc giữa hai đường thẳng cắt nhau a và b mà mặt phẳng đó cắt nhau và vuông góc với đường thẳng c.

Định nghĩa góc giữa hai mặt phẳng có thể được đưa ra hơi khác một chút. Nếu trên đường thẳng c mà các mặt phẳng cắt nhau, lấy điểm M và vẽ các đường thẳng a và b đi qua nó, vuông góc với đường thẳng c và lần lượt nằm trong các mặt phẳng và thì góc giữa hai đường thẳng a và b là góc giữa các mặt phẳng và . Thông thường, trong thực tế, các cấu trúc như vậy được thực hiện để có được góc giữa các mặt phẳng.

Vì góc giữa hai đường thẳng cắt nhau không vượt quá , nên theo định nghĩa trên, số đo độ của góc giữa hai mặt phẳng cắt nhau được biểu thị bằng số thực từ khoảng. Trong trường hợp này, các mặt phẳng cắt nhau được gọi là vuông góc nếu góc giữa chúng là chín mươi độ. Góc giữa các mặt phẳng song song hoàn toàn không được xác định hoặc được coi là bằng không.

Tìm góc giữa hai mặt phẳng cắt nhau.

Thông thường, khi tìm góc giữa hai mặt phẳng giao nhau, trước tiên bạn phải thực hiện các phép dựng bổ sung để xem các đường giao nhau, góc giữa chúng bằng góc mong muốn, sau đó nối góc này với dữ liệu gốc bằng dấu đẳng thức, dấu hiệu đồng dạng, định lý cosin hay định nghĩa sin, cosin, tang của góc. Trong môn hình học Trung học phổ thông nhiệm vụ tương tự xảy ra.

Ví dụ: hãy đưa ra lời giải cho bài toán C2 từ Kỳ thi thống nhất của bang về toán học năm 2012 (điều kiện được cố ý thay đổi, nhưng điều này không ảnh hưởng đến nguyên tắc của lời giải). Trong đó, chỉ cần tìm góc giữa hai mặt phẳng cắt nhau.

Thí dụ.

Phán quyết.

Đầu tiên, hãy vẽ một bức tranh.

Hãy thực hiện các phép dựng bổ sung để "thấy" góc giữa các mặt phẳng.

Đầu tiên, hãy xác định một đường thẳng mà các mặt phẳng ABC và BED 1 cắt nhau. Điểm B là một trong những điểm chung của chúng. Tìm điểm chung thứ hai của các mặt phẳng này. Các đường thẳng DA và D 1 E nằm trong cùng một mặt phẳng ADD 1 và chúng không song song với nhau nên cắt nhau. Mặt khác, đường thẳng DA nằm trong mặt phẳng ABC, đường thẳng D 1 E nằm trong mặt phẳng BED 1 nên giao điểm của hai đường thẳng DA và D 1 E sẽ là điểm chung của các mặt phẳng ABC và GIƯỜNG 1. Vì vậy, chúng tôi tiếp tục các dòng DA và D 1 E cho đến khi chúng giao nhau, chúng tôi biểu thị giao điểm của chúng bằng chữ F. Khi đó BF là đường thẳng cắt nhau của hai mặt phẳng ABC và BED 1.

Nó vẫn còn để dựng hai đường thẳng nằm trong các mặt phẳng ABC và BED 1, lần lượt đi qua một điểm trên đường thẳng BF và vuông góc với đường thẳng BF - theo định nghĩa, góc giữa các đường thẳng này sẽ bằng góc mong muốn giữa hai đường thẳng mặt phẳng ABC và BED 1 . Hãy làm nó.

chấm A là hình chiếu của điểm E lên mặt phẳng ABC. Vẽ đường thẳng cắt đường thẳng BF vuông góc tại điểm M. Khi đó đường thẳng AM là hình chiếu của đường thẳng EM lên mặt phẳng ABC và theo định lý ba đường vuông góc.

Do đó, góc mong muốn giữa các mặt phẳng ABC và BED 1 là .

Ta có thể xác định sin, cosin hoặc tang của góc này (và do đó là chính góc đó) từ tam giác vuông AEM nếu biết độ dài hai cạnh của nó. Từ điều kiện, có thể dễ dàng tìm được độ dài AE: vì điểm E chia cạnh AA 1 theo tỷ lệ 4 thành 3, tính từ điểm A và độ dài cạnh AA 1 là 7, nên AE \u003d 4. Hãy tìm độ dài của AM.

Để làm điều này, hãy xem xét một tam giác vuông ABF với góc vuông A, trong đó AM là chiều cao. Với điều kiện AB=2. Chúng ta có thể tìm độ dài của cạnh AF từ sự đồng dạng của các tam giác vuông DD 1 F và AEF :

Theo định lý Pitago, từ tam giác ABF ta tìm được . Ta tìm độ dài AM qua diện tích tam giác ABF: một cạnh, diện tích tam giác ABF bằng , Mặt khác , ở đâu .

Như vậy, từ tam giác vuông AEM ta có .

Sau đó, góc mong muốn giữa các mặt phẳng ABC và BED 1 là (lưu ý rằng ).

Câu trả lời:

Trong một số trường hợp, để tìm góc giữa hai mặt phẳng cắt nhau, ta có thể thuận tiện chỉ định Oxyz và dùng phương pháp tọa độ. Hãy dừng lại ở đó.

Hãy đặt nhiệm vụ: tìm góc giữa hai mặt phẳng cắt nhau và . Hãy biểu thị góc mong muốn là .

Ta giả sử rằng trong hệ tọa độ vuông góc Oxyz cho trước, ta biết tọa độ của các vectơ pháp tuyến của các mặt phẳng cắt nhau và hoặc có thể tìm được chúng. Cho phép là vectơ pháp tuyến của mặt phẳng và là vectơ pháp tuyến của mặt phẳng . Hãy để chúng tôi trình bày cách tìm góc giữa các mặt phẳng cắt nhau và thông qua tọa độ của các vectơ pháp tuyến của các mặt phẳng này.

Chúng ta hãy biểu thị đường thẳng mà các mặt phẳng cắt nhau và là c . Qua điểm M trên đường thẳng c vẽ mặt phẳng vuông góc với đường thẳng c. Mặt phẳng cắt các mặt phẳng và dọc theo các đường thẳng a, b lần lượt các đường thẳng a, b cắt nhau tại điểm M . Theo định nghĩa, góc giữa các mặt phẳng cắt nhau và bằng góc giữa các đường thẳng cắt nhau a và b.

Chúng ta hãy đặt sang một bên điểm M trong mặt phẳng các vectơ pháp tuyến và của các mặt phẳng và . Trong trường hợp này, vectơ nằm trên đường thẳng vuông góc với đường thẳng a và vectơ nằm trên đường thẳng vuông góc với đường thẳng b. Như vậy, trong mặt phẳng, vectơ là vectơ pháp tuyến của đường thẳng a, là vectơ pháp tuyến của đường thẳng b.

Trong bài viết Tìm góc giữa các đường thẳng cắt nhau, chúng tôi đã thu được một công thức cho phép bạn tính cosin của góc giữa các đường thẳng cắt nhau bằng cách sử dụng tọa độ của các vectơ pháp tuyến. Do đó, cosin của góc giữa các đường thẳng a và b, và do đó, và cosin của góc giữa hai mặt phẳng cắt nhau và được tìm thấy theo công thức , trong đó và lần lượt là các vectơ pháp tuyến của các mặt phẳng và . Sau đó, nó được tính như .

Hãy giải ví dụ trước bằng phương pháp tọa độ.

Thí dụ.

Cho một hình chữ nhật song song ABCDA 1 B 1 C 1 D 1, trong đó AB \u003d 2, AD \u003d 3, AA 1 \u003d 7 và điểm E chia cạnh AA 1 theo tỷ lệ 4 trên 3, tính từ điểm A . Tìm góc giữa hai mặt phẳng ABC và BED 1.

Phán quyết.

Kể từ khi các bên hình khối tại một đỉnh đôi một vuông góc với nhau, để tiện giới thiệu hệ trục tọa độ vuông góc Oxyz như sau: điểm đầu thẳng hàng với đỉnh C, các trục tọa độ Ox, Oy, Oz hướng dọc theo các cạnh CD, CB, CC 1, tương ứng.

Có thể tìm góc giữa các mặt phẳng ABC và BED 1 thông qua tọa độ của các vectơ pháp tuyến của các mặt phẳng này bằng công thức , trong đó và lần lượt là các vectơ pháp tuyến của các mặt phẳng ABC và BED 1. Hãy xác định tọa độ của các vectơ pháp tuyến.