Očekivanje šah-mata x y. Matematičko očekivanje, definicija, matematičko očekivanje diskretnih i kontinuiranih slučajnih varijabli, selektivno, uvjetno očekivanje, izračun, svojstva, zadaci, procjena očekivanja, varijanca, funkcija distribucije, formule, primjeri

Matematičko očekivanje je definicija

Mat čekanje je jedan od najvažnijih pojmova u matematičkoj statistici i teoriji vjerojatnosti, karakterizira distribuciju vrijednosti ili vjerojatnosti nasumična varijabla. Obično se izražava kao ponderirani prosjek svih mogućih parametara slučajne varijable. Široko se koristi u tehničkoj analizi, proučavanju serija brojeva, proučavanju kontinuiranih i dugotrajnih procesa. Važan je u procjeni rizika, predviđanju cjenovnih pokazatelja pri trgovanju na financijskim tržištima te se koristi u razvoju strategija i metoda taktike igre u teorija kockanja.

Šah-mat čeka- ovo je srednja vrijednost slučajne varijable, distribucija vjerojatnosti slučajna varijabla se razmatra u teoriji vjerojatnosti.

Mat čekanje je mjera srednje vrijednosti slučajne varijable u teoriji vjerojatnosti. Matematičko očekivanje slučajne varijable x označeno M(x).

Matematičko očekivanje (srednja vrijednost populacije) je

Mat čekanje je

Mat čekanje je u teoriji vjerojatnosti, ponderirani prosjek svih mogućih vrijednosti koje ova slučajna varijabla može poprimiti.

Mat čekanje je zbroj umnožaka svih mogućih vrijednosti slučajne varijable s vjerojatnostima tih vrijednosti.

Matematičko očekivanje (srednja vrijednost populacije) je

Mat čekanje je prosječna korist od određene odluke, pod uvjetom da se takva odluka može razmatrati u okviru teorije velikih brojeva i velike udaljenosti.

Mat čekanje je u teoriji kockanja, iznos dobitka koji špekulant može zaraditi ili izgubiti, u prosjeku, za svaku okladu. Jezikom kockanja špekulantima ovo se ponekad naziva "prednošću". špekulant” (ako je pozitivna za špekulanta) ili “house edge” (ako je negativna za špekulanta).

Matematičko očekivanje (srednja vrijednost populacije) je

Mat čekanje je profit po pobjedi pomnožen s prosjekom dobit, minus gubitak pomnožen s prosječnim gubitkom.

Matematičko očekivanje slučajne varijable u matematičkoj teoriji

Jedna od važnih numeričkih karakteristika slučajne varijable je očekivanje. Uvedimo pojam sustava slučajnih varijabli. Razmotrite skup slučajnih varijabli koje su rezultati istog slučajnog eksperimenta. Ako je jedna od mogućih vrijednosti sustava, tada događaj odgovara određenoj vjerojatnosti koja zadovoljava Kolmogorovljev aksiom. Funkcija definirana za sve moguće vrijednosti slučajnih varijabli naziva se zajedničkim zakonom raspodjele. Ova vam funkcija omogućuje izračunavanje vjerojatnosti bilo kojeg događaja iz. Konkretno, zglob zakon distribucija slučajnih varijabli i, koje uzimaju vrijednosti iz skupa i, dana je vjerojatnostima.

Izraz "mat. očekivanje" uveo je Pierre Simon Marquis de Laplace (1795.), a proizašao je iz koncepta "očekivane vrijednosti isplate", koji se prvi put pojavio u 17. stoljeću u teoriji kockanja u djelima Blaisea Pascala i Christiana Huygensa. Međutim, prvo cjelovito teoretsko razumijevanje i ocjenu ovog pojma dao je Pafnuty Lvovich Chebyshev (sredina 19. stoljeća).

Zakon distribucije slučajnih numeričkih varijabli (funkcija distribucije i serija distribucije ili gustoća vjerojatnosti) potpuno opisuju ponašanje slučajne varijable. Ali u nizu problema dovoljno je znati neke numeričke karakteristike veličine koja se proučava (na primjer, njezina prosječna vrijednost i moguće odstupanje od nje) kako bi se odgovorilo na postavljeno pitanje. Glavne numeričke karakteristike slučajnih varijabli su očekivanje, varijanca, mod i medijan.

Matematičko očekivanje diskretne slučajne varijable je zbroj proizvoda njenih mogućih vrijednosti i njihovih odgovarajućih vjerojatnosti. Ponekad mat. očekivanje se naziva ponderirani prosjek, budući da je približno jednako aritmetičkoj sredini opaženih vrijednosti slučajne varijable tijekom velikog broja eksperimenata. Iz definicije prostirke očekivanja proizlazi da njezina vrijednost nije manja od najmanje moguće vrijednosti slučajne varijable niti veća od najveće. Matematičko očekivanje slučajne varijable je neslučajna (konstantna) varijabla.

Matematičko očekivanje ima jednostavno fizičko značenje: ako se jedinica mase postavi na ravnu crtu, stavljajući neku masu u neke točke (za diskretnu distribuciju), ili je "razmazujući" određenom gustoćom (za apsolutno kontinuiranu distribuciju), tada točka koja odgovara očekivanju strunjače bit će koordinatna ravna "težišta".

Prosječna vrijednost slučajne varijable je određeni broj koji je, takoreći, njen “predstavnik” i zamjenjuje je u grubim približnim izračunima. Kada kažemo: "prosječno vrijeme rada lampe je 100 sati" ili "prosječna točka udara je pomaknuta u odnosu na metu za 2 m udesno", time označavamo određenu numeričku karakteristiku slučajne varijable koja opisuje njenu položaj na numeričkoj osi, tj. opis položaja.

Od karakteristika situacije u teoriji vjerojatnosti najvažniju ulogu ima očekivanje slučajne varijable, koje se ponekad jednostavno naziva prosječna vrijednost slučajne varijable.

Razmotrimo slučajnu varijablu x, koji ima moguće vrijednosti x1, x2, …, xn s vjerojatnostima p1, p2, …, pn. Moramo nekim brojem karakterizirati položaj vrijednosti slučajne varijable na x-osi s uzeti u obzir da te vrijednosti imaju različite vjerojatnosti. U tu svrhu prirodno je koristiti takozvani "ponderirani prosjek" vrijednosti xi, a svaku vrijednost xi tijekom usrednjavanja treba uzeti u obzir s "težinom" proporcionalnom vjerojatnosti te vrijednosti. Stoga ćemo izračunati srednju vrijednost slučajne varijable x, koje ćemo označiti M|X|:

Ovaj ponderirani prosjek naziva se mat očekivanje slučajne varijable. Tako smo u razmatranje uveli jedan od najvažnijih pojmova teorije vjerojatnosti - pojam mat. očekivanja. Mat. Očekivanje slučajne varijable je zbroj umnožaka svih mogućih vrijednosti slučajne varijable i vjerojatnosti tih vrijednosti.

Mat. očekivanje slučajne varijable x zbog osebujne ovisnosti o aritmetičkoj sredini opaženih vrijednosti slučajne varijable s velikim brojem eksperimenata. Ova ovisnost je istog tipa kao i ovisnost između frekvencije i vjerojatnosti, naime: s velikim brojem eksperimenata, aritmetička sredina opaženih vrijednosti slučajne varijable približava se (konvergira u vjerojatnosti) svojoj matici. čekajući. Iz prisutnosti odnosa između učestalosti i vjerojatnosti, može se zaključiti kao posljedica postojanja sličnog odnosa između aritmetičke sredine i matematičkog očekivanja. Doista, razmotrite slučajnu varijablu x, karakteriziran nizom distribucija:

Neka se proizvodi N nezavisni eksperimenti, u svakom od njih vrijednost x poprima određenu vrijednost. Pretpostavimo vrijednost x1 pojavio se m1 puta, vrijednost x2 pojavio se m2 vremena, opće značenje xi pojavio se mi puta. Izračunajmo aritmetičku sredinu opaženih vrijednosti X, koja za razliku od očekivanih mata M|X| označit ćemo M*|X|:

S porastom broja pokusa N frekvencije pi približit će se (konvergirati u vjerojatnosti) odgovarajućim vjerojatnostima. Dakle, aritmetička sredina promatranih vrijednosti slučajne varijable M|X| s povećanjem broja eksperimenata približit će se (konvergirati u vjerojatnosti) svom očekivanju. Gore formuliran odnos između aritmetičke sredine i mat. očekivanje je sadržaj jednog od oblika zakona velikih brojeva.

Već znamo da svi oblici zakona velikih brojeva navode činjenicu da su određeni prosjeci stabilni tijekom velikog broja eksperimenata. Ovdje je riječ o stabilnosti aritmetičke sredine iz niza opažanja iste vrijednosti. S malim brojem eksperimenata, aritmetička sredina njihovih rezultata je slučajna; s dovoljnim povećanjem broja eksperimenata, postaje "gotovo ne slučajan" i stabilizirajući se približava konstantnoj vrijednosti - mat. čekajući.

Svojstvo stabilnosti prosjeka za veliki broj eksperimenata lako je eksperimentalno provjeriti. Na primjer, vaganje bilo kojeg tijela u laboratoriju na preciznim vagama, kao rezultat vaganja svaki put dobivamo novu vrijednost; da bismo smanjili pogrešku opažanja, tijelo važemo nekoliko puta i koristimo aritmetičku sredinu dobivenih vrijednosti. Lako je vidjeti da s daljnjim povećanjem broja pokusa (vaganja) aritmetička sredina sve manje reagira na taj porast, a s dovoljno velikim brojem pokusa praktički se prestaje mijenjati.

Treba napomenuti da je najvažnija karakteristika položaja slučajne varijable mat. očekivanje – ne postoji za sve slučajne varijable. Moguće je napraviti primjere takvih slučajnih varijabli za koje mat. nema očekivanja, budući da odgovarajući zbroj ili integral divergiraju. Međutim, za praksu takvi slučajevi nisu od velikog interesa. Obično slučajne varijable s kojima imamo posla imaju ograničen raspon mogućih vrijednosti i, naravno, imaju mat očekivanja.

Uz najvažniju karakteristiku položaja slučajne varijable, prostirku očekivanja, u praksi se ponekad koriste i druge karakteristike položaja, posebice modus i medijan slučajne varijable.

Modus slučajne varijable je njezina najvjerojatnija vrijednost. Izraz "najvjerojatnija vrijednost", strogo govoreći, odnosi se samo na diskontinuirane količine; za kontinuiranu količinu, mod je vrijednost pri kojoj je gustoća vjerojatnosti najveća. Slike prikazuju način rada za diskontinuirane i kontinuirane slučajne varijable.

Ako poligon distribucije (krivulja distribucije) ima više od jednog maksimuma, kaže se da je distribucija "polimodalna".

Ponekad postoje distribucije koje u sredini nemaju maksimum, već minimum. Takve se raspodjele nazivaju "antimodalne".

U općem slučaju modus i očekivanje slučajne varijable se ne poklapaju. U posebnom slučaju kada je distribucija simetrična i modalna (tj. ima mod) i postoji mat. očekivanja, onda se podudara s modom i središtem simetrije distribucije.

Često se koristi još jedna karakteristika položaja - takozvani medijan slučajne varijable. Ova se karakteristika obično koristi samo za kontinuirane slučajne varijable, iako se može formalno definirati i za diskontinuiranu varijablu. Geometrijski, medijan je apscisa točke u kojoj je područje omeđeno krivuljom distribucije prepolovljeno.

U slučaju simetrične modalne distribucije, medijan se poklapa s mat. očekivanje i moda.

Matematičko očekivanje je prosječna vrijednost, slučajna varijabla - numerička karakteristika distribucije vjerojatnosti slučajne varijable. U najopćenitijem smislu, mat očekivanje slučajne varijable X(w) definira se kao Lebesgueov integral s obzirom na mjeru vjerojatnosti R u izvornom prostoru vjerojatnosti:

Mat. očekivanje se također može izračunati kao Lebesgueov integral od x distribucijom vjerojatnosti px količinama x:

Na prirodan način može se definirati koncept slučajne varijable s beskonačnim očekivanjem. Tipičan primjer su vremena povratka u domovinu u nekim slučajnim šetnjama.

Uz pomoć mat. očekivanja su definirana mnogim numeričkim i funkcionalnim karakteristikama distribucije (kao očekivanje odgovarajućih funkcija slučajne varijable), na primjer, generirajuća funkcija, karakteristična funkcija, momenti bilo kojeg reda, posebno varijanca, kovarijanca.

Matematičko očekivanje (srednja vrijednost populacije) je

Matematičko očekivanje je karakteristika položaja vrijednosti slučajne varijable (prosječna vrijednost njezine distribucije). U tom svojstvu matematičko očekivanje služi kao neki "tipični" parametar distribucije i njegova je uloga slična ulozi statičkog momenta - koordinate težišta distribucije mase - u mehanici. Od ostalih karakteristika lokacije, uz pomoć kojih se raspodjela opisuje općenito - medijani, modusi, očekivanje se razlikuje po većoj vrijednosti koju ono i odgovarajuća karakteristika raspršenja - varijanca - imaju u graničnim teoremima teorije vjerojatnosti. S najvećom cjelovitošću smisao očekivanih prostirača otkrivaju zakon velikih brojeva (Čebiševljeva nejednakost) i pojačani zakon velikih brojeva.

Matematičko očekivanje (srednja vrijednost populacije) je

Matematičko očekivanje diskretne slučajne varijable

Neka postoji neka slučajna varijabla koja može poprimiti jednu od nekoliko numeričkih vrijednosti (na primjer, broj bodova u bacanju kocke može biti 1, 2, 3, 4, 5 ili 6). Često se u praksi za takvu vrijednost postavlja pitanje: koju vrijednost uzima "u prosjeku" s velikim brojem testova? Koliki će biti naš prosječni povrat (ili gubitak) od svake od rizičnih transakcija?

Recimo, postoji neka vrsta lutrije. Želimo razumjeti je li isplativo ili ne sudjelovati u tome (ili čak sudjelovati više puta, redovito). Recimo da svaka četvrta karta pobjeđuje, nagrada će biti 300 rubalja, a bilo koja karta - 100 rubalja. Uz beskonačan broj sudjelovanja, to se događa. U tri četvrtine slučajeva izgubit ćemo, svaka tri gubitka koštat će 300 rubalja. U svakom četvrtom slučaju dobit ćemo 200 rubalja. (nagrada minus trošak), odnosno za četiri sudjelovanja gubimo u prosjeku 100 rubalja, za jedno - u prosjeku 25 rubalja. Ukupno će prosječna stopa naše propasti biti 25 rubalja po karti.

Bacamo kocku. Ako nije varanje (bez pomicanja težišta i sl.), koliko ćemo onda bodova prosječno imati odjednom? Budući da je svaka opcija jednako vjerojatna, uzimamo glupu aritmetičku sredinu i dobivamo 3,5. Budući da je ovo PROSJEK, ne treba se ljutiti što niti jedno bacanje neće dati 3,5 boda - pa ova kocka nema lice s takvim brojem!

Sada rezimiramo naše primjere:

Pogledajmo gornju sliku. S lijeve strane nalazi se tablica distribucije slučajne varijable. Vrijednost X može poprimiti jednu od n mogućih vrijednosti (danih u gornjem redu). Ne može biti drugih vrijednosti. Ispod svake moguće vrijednosti dolje je potpisana njezina vjerojatnost. Desno je formula, gdje se M(X) naziva mat. čekajući. Značenje ove vrijednosti je da će s velikim brojem pokusa (s velikim uzorkom) prosječna vrijednost težiti upravo ovom očekivanju.

Vratimo se istoj igraćoj kocki. Mat. očekivani broj bodova pri bacanju je 3,5 (ako ne vjerujete izračunajte sami pomoću formule). Recimo da si ga bacio nekoliko puta. Ispale su 4 i 6. U prosjeku je ispalo 5, odnosno daleko od 3,5. Opet su bacili, ispalo je 3, odnosno u prosjeku (4 + 6 + 3) / 3 = 4,3333 ... Nekako daleko od strunjače. očekivanja. Sada napravite ludi eksperiment - kotrljajte kocku 1000 puta! A ako prosjek nije baš 3,5, onda će biti blizu toga.

Brojimo mat. čeka gore opisanu lutriju. Tablica će izgledati ovako:

Tada će očekivani mat biti, kao što smo gore utvrdili:

Druga je stvar što je i to "na prste", bez formule, teško da ima više opcija. Pa, recimo da je bilo 75% izgubljenih listića, 20% dobitnih listića i 5% dobitnih listića.

Sada neka svojstva prostirke očekivanja.

Mat. čekanje je linearno. Lako je to dokazati:

Konstantni množitelj dopušteno je izvaditi iz znaka za mat. očekivanja, odnosno:

Ovo je poseban slučaj svojstva linearnosti prostirača očekivanja.

Još jedna posljedica linearnosti mat. očekivanja:

to je mat. očekivanje zbroja slučajnih varijabli jednako je zbroju matematičkih očekivanja slučajnih varijabli.

Neka su X, Y nezavisne slučajne varijable, zatim:

Ovo je također lako dokazati) XY sama je slučajna varijabla, dok bi početne vrijednosti mogle poprimiti n i m vrijednosti, odnosno, tada XY može poprimiti nm vrijednosti. svaka od vrijednosti izračunava se na temelju činjenice da se množe vjerojatnosti neovisnih događaja. Kao rezultat, dobivamo ovo:

Matematičko očekivanje kontinuirane slučajne varijable

Kontinuirane slučajne varijable imaju takvu karakteristiku kao što je gustoća distribucije (gustoća vjerojatnosti). Zapravo, karakterizira situaciju da slučajna varijabla uzima neke vrijednosti iz skupa realnih brojeva češće, neke - rjeđe. Na primjer, razmotrite ovaj grafikon:

Ovdje x- zapravo slučajna varijabla, f(x)- gustoća distribucije. Sudeći po ovom grafikonu, tijekom eksperimenata vrijednost xće često biti broj blizak nuli. šanse premašiti 3 ili biti manje -3 nego čisto teorijski.

Ako je poznata gustoća distribucije, tada se prostirka očekivanja pretražuje na sljedeći način:

Neka, na primjer, postoji jednolika raspodjela:

Nađimo prostirku. očekivanje:

Ovo je sasvim u skladu s intuitivnim razumijevanjem. Recimo, ako dobijemo puno slučajnih realnih brojeva s uniformnom distribucijom, svaki segment |0; 1| , tada bi aritmetička sredina trebala biti oko 0,5.

Svojstva prostirki očekivanja - linearnost itd., primjenjiva za diskretne slučajne varijable, vrijede i ovdje.

Odnos matematičkog očekivanja s drugim statističkim pokazateljima

NA statistički analiza, uz mat očekivanja, postoji sustav međuovisnih pokazatelja koji odražavaju homogenost pojava i stabilnost procesima. Indikatori varijacije često nemaju samostalno značenje i koriste se za daljnju analizu podataka. Iznimka je koeficijent varijacije, koji karakterizira homogenost podaci ono što je vrijedno statistički karakteristika.

Stupanj varijabilnosti ili stabilnosti procesima u statističkoj znanosti može se mjeriti pomoću nekoliko pokazatelja.

Najvažniji pokazatelj koji karakterizira varijabilnost slučajna varijabla, je Disperzija, koji je najuže i neposredno povezan s mat. čekajući. Ovaj se parametar aktivno koristi u drugim vrstama statističke analize (testiranje hipoteza, analiza uzročno-posljedičnih odnosa itd.). Kao i srednje linearno odstupanje, varijanca također odražava mjeru širenja podaci oko prosjeka.

Korisno je prevesti jezik znakova na jezik riječi. Ispada da je varijanca prosječni kvadrat odstupanja. To jest, prvo se izračuna prosječna vrijednost, zatim se razlika između svake izvorne i prosječne vrijednosti uzima, kvadrira, zbraja i zatim dijeli s brojem vrijednosti u ovoj populaciji. Razlika između jedne vrijednosti i prosjeka odražava mjeru odstupanja. Kvadrira se kako bi se osiguralo da sva odstupanja postanu isključivo pozitivni brojevi i kako bi se izbjeglo međusobno poništavanje pozitivnih i negativnih odstupanja kada se zbroje. Zatim, s obzirom na kvadrat odstupanja, jednostavno izračunamo aritmetičku sredinu. Prosjek - na kvadrat - odstupanja. Odstupanja se kvadriraju, a uzima se u obzir prosjek. Odgovor na čarobnu riječ "disperzija" su samo tri riječi.

Međutim, u svom čistom obliku, kao što je, na primjer, aritmetička sredina ili , disperzija se ne koristi. To je više pomoćni i posredni pokazatelj koji se koristi za druge vrste statističkih analiza. Ona nema ni normalnu jedinicu mjere. Sudeći po formuli, ovo je kvadrat izvorne podatkovne jedinice.

Matematičko očekivanje (srednja vrijednost populacije) je

Izmjerimo slučajnu varijablu N puta, na primjer, deset puta mjerimo brzinu vjetra i želimo pronaći prosječnu vrijednost. Kako je srednja vrijednost povezana s funkcijom distribucije?

Ili ćemo bacati kocku veliki broj puta. Broj bodova koji će pasti na kockicu tijekom svakog bacanja je slučajna varijabla i može poprimiti bilo koju prirodnu vrijednost od 1 do 6. N teži vrlo određenom broju – mat. očekivanje Mx. U ovom slučaju je Mx = 3,5.

Kako je nastala ova vrijednost? Pustiti unutra N suđenja n1 kada padne 1 bod, n2 puta - 2 boda i tako dalje. Zatim broj ishoda u kojima je pao jedan bod:

Slično je i za ishode kada je ispalo 2, 3, 4, 5 i 6 bodova.

Pretpostavimo sada da su nam poznate raspodjele slučajne varijable x, odnosno znamo da slučajna varijabla x može poprimiti vrijednosti x1, x2,..., xk s vjerojatnostima p1, p2,... , pak.

Mat očekivanje Mx slučajne varijable x je:

Matematičko očekivanje nije uvijek razumna procjena neke slučajne varijable. Dakle, za procjenu prosječne plaće razumnije je koristiti koncept medijana, odnosno takvu vrijednost da broj ljudi koji primaju manje od medijana plaća i velika, utakmica.

Vjerojatnost p1 da je slučajna varijabla x manja od x1/2 i vjerojatnost p2 da je slučajna varijabla x veća od x1/2 iste su i jednake 1/2. Medijan nije jednoznačno određen za sve distribucije.

Standardna ili standardna devijacija u statistici se naziva stupanj odstupanja opažačkih podataka ili skupova od PROSJEČNE vrijednosti. Označava se slovima s ili s. Mala standardna devijacija označava da su podaci grupirani oko srednje vrijednosti, a velika standardna devijacija ukazuje da su početni podaci daleko od nje. Standardna devijacija jednaka je kvadratnom korijenu veličine koja se naziva varijanca. To je prosjek zbroja kvadrata razlika početnih podataka koji odstupaju od srednje vrijednosti. Standardna devijacija slučajne varijable je kvadratni korijen varijance:

Primjer. U uvjetima ispitivanja kada se gađa u metu, izračunajte varijancu i standardnu ​​devijaciju slučajne varijable:

Varijacija- fluktuacija, varijabilnost vrijednosti atributa u jedinicama populacije. Odvojene numeričke vrijednosti značajke koje se javljaju u proučavanoj populaciji nazivaju se varijantama vrijednosti. Nedovoljnost prosječne vrijednosti za potpunu karakterizaciju populacije čini nužnim dopunjavanje prosječnih vrijednosti pokazateljima koji omogućuju procjenu tipičnosti tih prosjeka mjerenjem fluktuacije (varijacije) osobine koja se proučava. Koeficijent varijacije izračunava se po formuli:

Varijacija raspona(R) je razlika između maksimalne i minimalne vrijednosti svojstva u proučavanoj populaciji. Ovaj pokazatelj daje najopćenitiju ideju o fluktuaciji osobine koja se proučava, kao što pokazuje razlika samo između graničnih vrijednosti varijanti. Ovisnost o ekstremnim vrijednostima atributa daje rasponu varijacije nestabilan, slučajan karakter.

Prosječno linearno odstupanje je aritmetička sredina apsolutnih (modulo) odstupanja svih vrijednosti analizirane populacije od njihove prosječne vrijednosti:

Matematičko očekivanje u teoriji kockanja

Mat čekanje je prosječan iznos novca koji kockarski špekulant može dobiti ili izgubiti na određenoj okladi. Ovo je vrlo značajan koncept za špekulanta, jer je temeljan za procjenu većine situacija u igrama. Očekivanje mate također je najbolji alat za analizu osnovnih rasporeda karata i situacija u igri.

Recimo da igrate novčiće s prijateljem, ulažući jednaku okladu od 1 USD svaki put, bez obzira što iskrsne. Repovi - pobijedili ste, glave - izgubili ste. Šanse da dođe do tails-a su jedan prema jedan, a vi se kladite 1 do 1 dolar. Dakle, vaše očekivanje šah-mata je nula, jer matematički govoreći, ne možete znati hoćete li voditi ili izgubiti nakon dva bacanja ili nakon 200.

Vaša dobit po satu je nula. Isplata po satu je iznos novca koji očekujete da ćete osvojiti u jednom satu. Možete baciti novčić 500 puta unutar sat vremena, ali nećete pobijediti niti izgubiti jer vaši izgledi nisu ni pozitivni ni negativni. Ako pogledate, sa stajališta ozbiljnog špekulanta, takav sustav stopa nije loš. Ali to je samo gubljenje vremena.

Ali pretpostavimo da se netko želi kladiti 2 USD protiv vaših 1 USD u istoj igri. Tada odmah imate pozitivno očekivanje od 50 centi od svake oklade. Zašto 50 centi? U prosjeku jednu okladu dobijete, a drugu izgubite. Uložite prvo i izgubite 1 $, uložite drugo i osvojite 2 $. Uložili ste $1 dva puta i vodite za $1. Dakle, svaka vaša oklada od jednog dolara dala vam je 50 centi.

Ako novčić padne 500 puta u jednom satu, vaš će dobitak po satu biti već 250 dolara, jer. u prosjeku ste izgubili jednu dolar 250 puta i osvojio dva dolar 250 puta. 500$ minus 250$ jednako je 250$, što je ukupni dobitak. Imajte na umu da je očekivana vrijednost, odnosno iznos koji u prosjeku osvojite na jednoj okladi, 50 centi. Osvojili ste 250 dolara ulažući dolar 500 puta, što je jednako 50 centi vaše oklade.

Matematičko očekivanje (srednja vrijednost populacije) je

Mat. očekivanje nema nikakve veze s kratkoročnim rezultatima. Vaš protivnik, koji je odlučio uložiti 2 dolara protiv vas, mogao bi vas pobijediti u prvih deset bacanja zaredom, ali vi, s prednošću klađenja 2 prema 1, ako su svi ostali jednaki, zaradite 50 centi na svaki ulog od 1 dolara pod bilo kojim okolnosti. Nije bitno hoćete li dobiti ili izgubiti jednu okladu ili više oklada, ali samo pod uvjetom da imate dovoljno novca da lako nadoknadite troškove. Ako se nastavite kladiti na isti način, tada će se tijekom dugog vremenskog razdoblja vaši dobici približiti zbroju očekivanih vrijednosti u pojedinačnim bacanjima.

Svaki put kada napravite bolju okladu (okladu koja dugoročno može biti isplativa) kada su izgledi u vašu korist, sigurno ćete nešto osvojiti, bez obzira na to izgubite li ili ne u određenoj ruci. Suprotno tome, ako ste sklopili okladu s lošijim ishodom (okladu koja je dugoročno neisplativa) kada vam izgledi nisu naklonjeni, nešto gubite, bez obzira jeste li dobili ili izgubili u ovoj ruci.

Matematičko očekivanje (srednja vrijednost populacije) je

Kladite se s najboljim ishodom ako je vaše očekivanje pozitivno, a pozitivno je ako su izgledi u vašu korist. Klađenjem s najgorim ishodom imate negativna očekivanja, što se događa kada su izgledi protiv vas. Ozbiljni špekulanti klade se samo s najboljim ishodom, s najgorim - odustaju. Što znače izgledi u vašu korist? Na kraju možete osvojiti više nego što stvarni izgledi donose. Stvarni izgledi za pogađanje repova su 1 prema 1, ali vi dobivate 2 prema 1 zbog omjera klađenja. U ovom slučaju izgledi su u vašu korist. Definitivno dobivate najbolji ishod s pozitivnim očekivanjem od 50 centi po okladi.

Evo složenijeg primjera. očekivanja. Prijatelj zapisuje brojeve od jedan do pet i kladi se u 5 USD u odnosu na tvojih 1 USD da nećeš odabrati taj broj. Pristajete li na takvu okladu? Što je ovdje očekivanje?

U prosjeku ćete pogriješiti četiri puta. Na temelju toga, izgledi protiv toga da pogodite broj bit će 4 prema 1. Izgledi su da ćete izgubiti dolar u jednom pokušaju. Ipak, dobivate 5 prema 1, s mogućnošću gubitka 4 prema 1. Dakle, izgledi su vam naklonjeni, možete prihvatiti okladu i nadati se najboljem ishodu. Ako ovu okladu napravite pet puta, u prosjeku ćete izgubiti četiri puta po $1 i jednom osvojiti $5. Na temelju toga, za svih pet pokušaja zaradit ćete 1 $ s pozitivnim matematičkim očekivanjem od 20 centi po okladi.

Špekulant koji će dobiti više nego što se kladi, kao u gornjem primjeru, hvata izglede. Suprotno tome, on uništava šanse kada očekuje da će dobiti manje nego što se kladi. Kladioničar može imati pozitivna ili negativna očekivanja ovisno o tome hvata li ili uništava izglede.

Ako se uložite u 50 USD da biste osvojili 10 USD s šansama za dobitak 4 prema 1, dobit ćete negativno očekivanje od 2 USD, jer u prosjeku ćete dobiti četiri puta po 10 dolara i jednom izgubiti 50 dolara, što pokazuje da će gubitak po okladi biti 10 dolara. Ali ako se uložite u 30$ da dobijete 10$, s istim izgledima za pobjedu 4 prema 1, tada u ovom slučaju imate pozitivno očekivanje od 2$, jer ponovno dobivate četiri puta po 10 dolara i jednom gubite 30 dolara, što je dobit po 10 dolara. Ovi primjeri pokazuju da je prva oklada loša, a druga dobra.

Mat. očekivanje je središte svake situacije u igri. Kada kladionica potiče ljubitelje nogometa da se klade na 11 dolara kako bi osvojili 10 dolara, oni imaju pozitivno očekivanje od 50 centi za svakih 10 dolara. Ako kockarnica isplaćuje čak i novac iz Craps Pass linije, tada je pozitivno očekivanje kuće otprilike 1,40 USD za svakih 100 USD; ova je igra strukturirana tako da svi koji se klade na ovu liniju gube 50,7% u prosjeku i dobivaju 49,3% vremena. Bez sumnje, upravo to naizgled minimalno pozitivno očekivanje donosi ogromne zarade vlasnicima kasina diljem svijeta. Kao što je vlasnik kasina Vegas World Bob Stupak primijetio: “Jedna tisućinka postotak negativna vjerojatnost na dovoljno velikoj udaljenosti će bankrotirati najbogatijeg čovjeka na svijetu.

Matematičko očekivanje pri igranju pokera

Igra Poker je najilustrativniji i najilustrativniji primjer u smislu korištenja teorije i svojstava podloge za čekanje.

Mat. očekivanje (engleski Expected Value) u pokeru - prosječna korist od određene odluke, pod uvjetom da se takva odluka može razmatrati u okviru teorije velikih brojeva i velike udaljenosti. Uspješan poker podrazumijeva uvijek prihvaćanje poteza s pozitivnim matematičkim očekivanjem.

Matematičko očekivanje (srednja vrijednost populacije) je

Matematičko značenje. očekivanja kod igranja pokera leži u činjenici da se često susrećemo sa slučajnim varijablama pri donošenju odluke (ne znamo koje karte protivnik ima u ruci, koje će karte doći u sljedećim rundama trgovina). Svako od rješenja moramo razmotriti sa stajališta teorije velikih brojeva, koja kaže da će s dovoljno velikim uzorkom prosječna vrijednost slučajne varijable težiti svojoj sredini.

Među određenim formulama za izračun očekivanih prostirki, sljedeća je najprimjenjivija u pokeru:

Kada igrate poker mat. očekivanje se može izračunati i za oklade i za pozive. U prvom slučaju treba uzeti u obzir fold equity, u drugom, vlastite izglede u potu. Prilikom ocjenjivanja mat. očekivanja ovog ili onog poteza, treba imati na umu da fold uvijek ima nulto očekivanje. Stoga će odbacivanje karata uvijek biti unosnija odluka od bilo kojeg negativnog poteza.

Matematičko očekivanje (srednja vrijednost populacije) je

Očekivanje vam govori što možete očekivati ​​(ili izgubiti) za svaki rizik koji preuzmete. Kockarnice zarađuju novac jer očekivanje šah-mata od svih igara koje se u njima prakticiraju ide u korist kasina. S dovoljno dugim nizom igara može se očekivati ​​da će klijent izgubiti svoje novac jer je "vjerojatnost" u korist kasina. Međutim, profesionalni kasino špekulanti ograničavaju svoje igre na kratka vremenska razdoblja, čime povećavaju izglede u svoju korist. Isto vrijedi i za investiranje. Ako su vaša očekivanja pozitivna, možete zaraditi više novca sklapanjem mnogih trgovina u kratkom vremenskom razdoblju. razdoblje vrijeme. Očekivanje je vaš postotak dobiti po pobjedi pomnožen s vašom prosječnom dobiti minus vaša vjerojatnost gubitka pomnožena s vašim prosječnim gubitkom.

Poker se također može promatrati u smislu šah-mata. Možete pretpostaviti da je određeni potez isplativ, ali u nekim slučajevima možda nije najbolji, jer je drugi potez isplativiji. Recimo da ste pogodili full house u pet card draw pokeru. Vaš protivnik se kladi. Znaš da ako podigneš ulog, on će zvati. Stoga se podizanje čini najboljom taktikom. Ali ako povisite ulog, preostala dva špekulanta sigurno će odustati. Ali ako platite okladu, bit ćete potpuno sigurni da će druga dva špekulanta nakon vas učiniti isto. Kada podignete ulog, dobivate jednu jedinicu, a jednostavnim pozivom - dvije. Dakle, poziv vam daje veću pozitivnu očekivanu vrijednost i najbolja je taktika.

Mat. čekanje također može dati ideju o tome koje su poker taktike manje isplative, a koje više. Na primjer, ako igrate određenu ruku i mislite da je vaš prosječni gubitak 75 centi uključujući ante, tada biste trebali igrati tu ruku jer ovo je bolje od odustajanja kada je ante $1.

Još jedan važan razlog za razumijevanje suštine mat. očekivanje je da vam daje osjećaj mira bez obzira jeste li dobili okladu ili ne: ako ste dobro uložili ili odustali na vrijeme, znat ćete da ste zaradili ili uštedjeli određenu količinu novca koju bi slabiji špekulant mogao ne spremiti. Puno je teže odustati ako ste frustrirani što vaš protivnik ima bolju ruku na ždrijebu. Uz sve to, ono što uštedite neigranjem, umjesto klađenjem, dodaje se vašim dobicima po noći ili mjesecu.

Samo zapamtite da ako zamijenite ruke, protivnik će vas pratiti, a kao što ćete vidjeti u članku Fundamental Theorem of Poker, to je samo jedna od vaših prednosti. Trebali biste se radovati kada se to dogodi. Možete čak naučiti uživati ​​u izgubljenoj karti, jer znate da bi drugi špekulanti na vašem mjestu izgubili puno više.

Kao što je spomenuto u primjeru s novčićima na početku, omjer profita po satu povezan je s matematičkim očekivanjima, a ovaj je koncept posebno važan za profesionalne špekulante. Kada ćete igrati poker, morate mentalno procijeniti koliko možete osvojiti u sat vremena igre. U većini slučajeva morat ćete se osloniti na svoju intuiciju i iskustvo, ali možete se poslužiti i nekim matematičkim izračunima. Na primjer, ako igrate draw lowball i vidite da tri igrača ulažu 10 dolara, a zatim izvuku dvije karte, što je vrlo loša taktika, možete sami izračunati da svaki put kada ulože 10 dolara izgube oko 2 dolara. Svaki od njih to radi osam puta na sat, što znači da sva trojica gube oko 48 dolara po satu. Vi ste jedan od preostala četiri špekulanta, koji su približno jednaki, pa ova četiri špekulanta (i vi među njima) morate podijeliti 48 dolara, a svaki će zaraditi 12 dolara po satu. Vaša satnica u ovom slučaju jednostavno je vaš udio u iznosu novca koji su izgubila tri loša špekulanta u jednom satu.

Matematičko očekivanje (srednja vrijednost populacije) je

Tijekom dugog vremenskog razdoblja, ukupni profit špekulanta je zbroj njegovih matematičkih očekivanja u zasebnim raspodjelama. Što više igrate s pozitivnim očekivanjima, više dobivate, i obrnuto, što više ruku igrate s negativnim očekivanjima, više gubite. Kao rezultat toga, trebali biste dati prednost igri koja može maksimizirati vaša pozitivna očekivanja ili poništiti vaša negativna očekivanja kako biste mogli maksimizirati svoj dobitak po satu.

Pozitivno matematičko očekivanje u strategiji igre

Ako znate brojati karte, možda ste u prednosti u odnosu na kasino ako vas ne primijete i izbace. Kockarnice vole pijane špekulante i mrze brojače karata. Prednost će vam omogućiti da pobijedite više puta nego što izgubite tijekom vremena. Dobro upravljanje novcem korištenjem mat kalkulacija može vam pomoći da bolje iskoristite svoju prednost i smanjite svoje gubitke. Bez prednosti, bolje je dati novac u dobrotvorne svrhe. U igri na burzi prednost daje sustav igre koji stvara više dobiti nego gubitka, razlika cijene i provizije. nikakav upravljanje kapitalom neće spasiti loš sustav igranja.

Pozitivno očekivanje definirano je vrijednošću većom od nule. Što je taj broj veći, statistička očekivanja su veća. Ako je vrijednost manja od nule, tada očekivanje će također biti negativno. Što je veći modul negativne vrijednosti, to je situacija gora. Ako je rezultat nula, tada je očekivanje bezuvjetno. Možete pobijediti samo ako imate pozitivno matematičko očekivanje, razuman sustav igre. Igranje intuicijom vodi u katastrofu.

Matematičko očekivanje i

Matematičko očekivanje prilično je tražen i popularan statistički pokazatelj u provedbi burzovnog trgovanja na financijskim tržištima. tržišta. Prije svega, ovaj parametar se koristi za analizu uspjeha trgovina. Nije teško pogoditi da što je ta vrijednost veća, to je više razloga za smatrati trgovinu koja se proučava uspješnom. Naravno, analiza raditi trgovac se ne može napraviti samo uz pomoć ovog parametra. Međutim, izračunata vrijednost u kombinaciji s drugim metodama procjene kvalitete raditi, može značajno poboljšati točnost analize.

Mat očekivanja često se izračunavaju u uslugama praćenja računa za trgovanje, što vam omogućuje brzu procjenu obavljenog posla na depozitu. Kao iznimke, možemo navesti strategije koje koriste "overstaying" gubitničke trgovine. Trgovac sreća ga može pratiti neko vrijeme, i stoga, možda neće biti nikakvih gubitaka u njegovom radu. U ovom slučaju neće biti moguće kretati se samo prema očekivanju, jer se rizici koji se koriste u radu neće uzeti u obzir.

U trgovanju na tržište mat očekivanja se najčešće koriste kada se predviđa profitabilnost strategije trgovanja ili kada se predviđa prihod trgovac na temelju statistike njegovih prethodnih nadmetanje.

Matematičko očekivanje (srednja vrijednost populacije) je

U vezi s upravljanjem novcem, vrlo je važno razumjeti da kod trgovanja s negativnim očekivanjima ne postoji shema upravljanje novca, što svakako može donijeti visoku zaradu. Ako nastavite igrati burza pod tim uvjetima, bez obzira na metodu upravljanje novca, izgubit ćete cijeli račun, bez obzira koliko velik bio na početku.

Ovaj aksiom ne vrijedi samo za igre s negativnim očekivanjima ili trgovanja, nego vrijedi i za igre s jednakim izgledima. Stoga je jedini slučaj u kojem imate dugoročnu priliku imati koristi kada sklapate poslove s pozitivnim matematičkim očekivanjima.

Razlika između negativnog i pozitivnog očekivanja je razlika između života i smrti. Nije važno koliko je očekivanje pozitivno ili koliko negativno; bitno je da li je pozitivno ili negativno. Stoga prije razmatranja pitanja upravljanja kapital morate pronaći igru ​​s pozitivnim očekivanjima.

Ako nemate tu igru, onda vas nikakvo upravljanje novcem na svijetu neće spasiti. S druge strane, ako imate pozitivna očekivanja, tada ih je moguće, pravilnim upravljanjem novcem, pretvoriti u funkciju eksponencijalnog rasta. Nije važno koliko je malo pozitivno očekivanje! Drugim riječima, nije važno koliko je isplativ sustav trgovanja temeljen na jednom ugovoru. Ako imate sustav koji osvaja 10 USD po ugovoru na jednoj trgovini (nakon provizija i proklizavanja), mogu se koristiti tehnike upravljanja kapital na način da bude profitabilniji od sustava koji pokazuje prosječnu dobit od 1000 USD po trgovini (nakon naknada i proklizavanja).

Nije bitno koliko je sustav bio profitabilan, nego koliko se sigurno može reći da će sustav u budućnosti pokazati barem minimalnu dobit. Stoga je najvažnija priprema koja se može napraviti jest osigurati da sustav pokazuje pozitivnu očekivanu vrijednost u budućnosti.

Kako biste imali pozitivnu očekivanu vrijednost u budućnosti, vrlo je važno ne ograničavati stupnjeve slobode vašeg sustava. To se postiže ne samo eliminacijom ili smanjenjem broja parametara koje treba optimizirati, već i smanjenjem što je više moguće sistemskih pravila. Svaki parametar koji dodate, svako pravilo koje napravite, svaka sićušna promjena koju napravite u sustavu smanjuje broj stupnjeva slobode. U idealnom slučaju, želite izgraditi prilično primitivan i jednostavan sustav koji će stalno donositi mali profit na gotovo svakom tržištu. Opet, važno je da shvatite da nije važno koliko je sustav isplativ, sve dok je profitabilan. koji zaradite u trgovanju zaradit ćete učinkovitim upravljanjem novcem.

Matematičko očekivanje (srednja vrijednost populacije) je

Sustav trgovanja jednostavno je alat koji vam daje pozitivno matematičko očekivanje kako biste mogli koristiti upravljanje novcem. Sustavi koji rade (pokazuju barem minimalnu dobit) na samo jednom ili nekoliko tržišta, ili imaju različita pravila ili parametre za različita tržišta, najvjerojatnije neće dugo raditi u stvarnom vremenu. Problem s većinom tehnički orijentiranih trgovaca je taj što troše previše vremena i truda optimizirajući različita pravila i parametre trgovinskog sustava. To daje potpuno suprotne rezultate. Umjesto da gubite energiju i vrijeme računala na povećanje profita trgovinskog sustava, svoju energiju usmjerite na povećanje razine pouzdanosti dobivanja minimalnog profita.

Znajući da upravljanje kapitalom- ovo je samo igra brojeva koja zahtijeva korištenje pozitivnih očekivanja, trgovac može prestati tražiti "sveti gral" trgovanja na burzi. Umjesto toga, može početi testirati svoju metodu trgovanja, saznati koliko je ta metoda logična, daje li pozitivna očekivanja. Ispravne metode upravljanja novcem primijenjene na bilo koje, čak i vrlo osrednje metode trgovanja, obavit će ostatak posla.

Da bi svaki trgovac bio uspješan u svom poslu, mora riješiti tri najvažnija zadatka: Osigurati da broj uspješnih transakcija premašuje neizbježne pogreške i pogrešne procjene; Postavite svoj sustav trgovanja tako da prilika za zaradu bude što je moguće češća; Ostvarite stabilan pozitivan rezultat svog poslovanja.

I ovdje, za nas, zaposlene trgovce, šah-mat može biti dobra pomoć. očekivanje. Ovaj pojam u teoriji vjerojatnosti jedan je od ključnih. Pomoću njega možete dati prosječnu procjenu neke slučajne vrijednosti. Matematičko očekivanje slučajne varijable slično je težištu, ako sve moguće vjerojatnosti zamislimo kao točke različitih masa.

U odnosu na strategiju trgovanja, za procjenu njezine učinkovitosti, najčešće se koristi očekivanje dobiti (ili gubitka). Ovaj se parametar definira kao zbroj umnožaka zadanih razina dobiti i gubitka i vjerojatnosti njihove pojave. Na primjer, razvijena strategija trgovanja pretpostavlja da će 37% svih operacija donijeti dobit, a ostatak - 63% - bit će neprofitabilan. Istovremeno, prosjek prihod od uspješne transakcije bit će 7 dolara, a prosječni gubitak će biti jednak 1,4 dolara. Izračunajmo mat. očekivanja trgovanja na takvom sustavu:

Što ovaj broj znači? Kaže da ćemo, prema pravilima ovog sustava, u prosjeku od svake zaključene transakcije dobiti 1.708 dolara. Budući da je rezultat učinkovitosti veći od nule, takav se sustav može koristiti za stvarni rad. Ako se, kao rezultat izračuna mat, očekivanje pokaže negativnim, onda to već ukazuje na prosječni gubitak i to će dovesti do propasti.

Iznos dobiti po trgovini također se može izraziti kao relativna vrijednost u obliku %. Na primjer:

Postotak prihoda po 1 transakciji - 5%;

Postotak uspješnih trgovačkih operacija - 62%;

Postotak gubitka po 1 trgovini - 3%;

Postotak neuspješnih transakcija - 38%;

U ovom slučaju, mat. očekivanje će biti:

To jest, prosječna transakcija će donijeti 1,96%.

Moguće je razviti sustav koji će, unatoč prevladavanju gubitnih poslova, dati pozitivan rezultat, budući da je njegov MO>0.

Međutim, samo čekanje nije dovoljno. Teško je zaraditi ako sustav daje vrlo malo signala za trgovanje. U ovom će slučaju biti usporediva s bankovnim kamatama. Neka svaka operacija u prosjeku donosi samo 0,5 dolara, ali što ako sustav pretpostavlja 1000 transakcija godišnje? To će biti vrlo ozbiljan iznos u relativno kratkom vremenu. Iz ovoga logično proizlazi da se još jednim obilježjem dobrog sustava trgovanja može smatrati kratko razdoblje držanja.

Izvori i poveznice

dic.academic.ru - akademski online rječnik

mathematics.ru - obrazovna stranica o matematici

nsu.ru - obrazovna web stranica Državnog sveučilišta Novosibirsk

webmath.ru - obrazovni portal za studente, kandidate i školsku djecu.

exponenta.ru obrazovna matematička web stranica

ru.tradimo.com - besplatna online škola trgovanja

crypto.hut2.ru - multidisciplinarni izvor informacija

poker-wiki.ru - besplatna enciklopedija pokera

sernam.ru - Znanstvena biblioteka odabranih prirodoslovnih publikacija

reshim.su - web stranica

unfx.ru - Forex na UNFX-u: obuka, signali trgovanja, upravljanje povjerenjem

- - matematičko očekivanje Jedna od numeričkih karakteristika slučajne varijable, često se naziva njezin teorijski prosjek. Za diskretnu slučajnu varijablu X, matematički ... ... Tehnički prevoditeljski priručnik

OČEKIVANA VRIJEDNOST- (očekivana vrijednost) Prosječna vrijednost distribucije ekonomske varijable koju ona može uzeti. Ako je pt cijena dobra u trenutku t, njegovo matematičko očekivanje je označeno s Ept. Za označavanje vremenske točke do koje ... ... Ekonomski rječnik

Očekivana vrijednost- prosječna vrijednost slučajne varijable. Matematičko očekivanje je deterministička vrijednost. Aritmetička sredina realizacija slučajne varijable je procjena matematičkog očekivanja. Prosječno…… Službena terminologija je (srednja vrijednost) slučajne varijable numerička karakteristika slučajne varijable. Ako je slučajna varijabla dana na prostoru vjerojatnosti (vidi Teorija vjerojatnosti), tada je njezin M. o. MX (ili EX) je definiran kao Lebesgueov integral: gdje je... Fizička enciklopedija

OČEKIVANA VRIJEDNOST- slučajna varijabla je njegova numerička karakteristika. Ako slučajna varijabla X ima funkciju raspodjele F(x), tada njezin M. o. bit će: . Ako je distribucija X diskretna, tada M.o.: , gdje su x1, x2, ... moguće vrijednosti diskretne slučajne varijable X; p1 ... Geološka enciklopedija

OČEKIVANA VRIJEDNOST- Engleski. očekivana vrijednost; njemački Erwartung mathematische. Stohastička sredina ili centar disperzije slučajne varijable. Antinazi. Enciklopedija sociologije, 2009 ... Enciklopedija sociologije

Očekivana vrijednost- Vidi također: Uvjetno očekivanje Matematičko očekivanje je srednja vrijednost slučajne varijable, distribucija vjerojatnosti slučajne varijable, razmatra se u teoriji vjerojatnosti. U engleskoj književnosti iu matematičkoj ... ... Wikipediji

Očekivana vrijednost- 1.14 Matematičko očekivanje E (X) gdje je xi vrijednosti diskretne slučajne varijable; p = P (X = xi); f(x) je gustoća kontinuirane slučajne varijable * Ako ovaj izraz postoji u smislu apsolutne konvergencije Izvor ... Rječnik-priručnik pojmova normativne i tehničke dokumentacije

Wir verwenden Cookies für die best Presentation unserer Website. Wenn Sie diese Website weiterhin nutzen, stimmen Sie dem zu. u redu

Budite strpljivi i pročitajte ovo..

Igra pozitivnih očekivanja vitalan je koncept za sve špekulante, to je koncept na kojem se gradi sustav vjerovanja, ali sam koncept ne može se graditi na vjeri. Kockarnice ne rade na temelju vjere. Casino posluje upravljajući svojim poslovanjem na temelju čiste matematike. Kasino zna da će zakoni ruleta i kocke na kraju prevladati. Stoga kasino ne dopušta prekid igre. Kasinu ne smeta čekanje, ali kasino ne staje i igra 24 sata na dan, jer što duže igrate njihovu igru ​​negativnog matematičkog očekivanja, to su organizatori kasina sigurniji da će dobiti vaš novac.

Trgovac treba razumjeti matematička očekivanja. Ovisno o tome tko ima matematičku prednost u igri, to se naziva ili prednost igrača - pozitivno očekivanje, ili prednost kockarnice - negativno očekivanje. Recimo da igramo na glavu ili na rep. Ni ti ni ja nemamo prednost, svaki ima 50% šanse za pobjedu. Ali ako ovu igru ​​odnesemo u kockarnicu koja uzima 10% popusta na svaki okretaj, tada dobivate samo 90 centi za svaki izgubljeni dolar. Ova prednost kockarnice pretvara se u snažno negativno matematičko očekivanje za vas kao igrača. I nikakav sustav kontrole kapitala, nikakva strategija ne može pobijediti igru ​​negativnih očekivanja.

U igrama s negativnim matematičkim očekivanjem ne postoji shema (strategija) upravljanja novcem koja će vas učiniti pobjednikom.

Zanimljivost je rulet, predvodnik svih kockarskih igara, uzmimo ga kao osnovu. Dakle, kasino, vriska, buka, emocije i blještava predstava, ali mi ćemo se fokusirati na rulet. Izračunajmo matematičko očekivanje igranja ruleta ako igrate samo na crveno-crno (u trgovanju, usput, ovo je dugo ili kratko). Dakle, na stolu za rulet postoji samo 38 igraćih polja - 36 brojeva (18 crvenih i 18 crnih polja), kao i dvije nule (uzmimo rulet s dvije nule). Dakle, vjerojatnost dobitka kada se kladite na crveno ili crno je otprilike 0,45 (18/38). U slučaju pozitivnog ishoda oklade, udvostručujemo svoj ulog, a u slučaju neuspjeha gubimo sve uloženo. O da, u slučaju nule gubimo i novac. Stoga imamo negativno matematičko očekivanje. Ova se igra može nazvati neprofitabilnom zbog prisutnosti dvije nule među igraćim poljima, u slučaju kojih kasino uzima našu okladu u svoju korist. Jedna ćelija je oko 2,6% kotača ruleta, dvije ćelije su više od 5%, to je postotak koji vlasnici kockarnica u prosjeku stave u svoje džepove od svake transakcije, tako da kasino polako izbacuje novac iz kupaca, zarađujući za mnoge desetljeća.

Naravno, za casino ova igra ima pozitivno matematičko očekivanje, s dvije nule casino će primiti novac igrača u dvadeset slučajeva od 38. I što dulje igra traje, to će casino dobiti više profita.

A što je matematičko očekivanje financijskih igara? Oklade na financijske instrumente imaju sve vanjske atribute kockanja, financijske igre na burzi sprej zero rulet na veliki broj komponenti vjerojatnosti - spread, provizije burzi, brokerske provizije, pretplate za korištenje terminala mjenjačnice, naknade za prijenos sredstva na račune i, zapravo, 13% poreza na buduću dobit u zbiru svojevrsni su analogni zero ruletu. To daje temelj govoriti o negativnom, u početku nepovoljnom matematičkom očekivanju za igrača (tradera).

Želim da shvatite - nijedna metoda upravljanja novcem, nijedna strategija ne može pretvoriti negativna očekivanja u pozitivna. Ovo je apsolutno točna primjedba. Nema matematičkih dokaza za ovu tvrdnju. Međutim, to ne znači da se to ne može dogoditi. Naravno, u kockanju, sudionik može ući u niz dobitaka, slučajnosti i jednostavno prestati igrati, kao rezultat toga, takva će osoba u biti biti pobjednik. Ali koliko će dugo odustati od igre?

Stoga je jedini slučaj u kojem dugoročno imate šanse pobijediti igra s pozitivnim matematičkim očekivanjem.. Mislim da obično možete pobijediti korištenjem iste veličine oklade više puta i samo ako nema gornja upijajuća barijera. Kockar koji počne sa 100$ prestat će igrati ako njegov račun naraste na 101$. Ovaj gornji cilj (101 USD) naziva se apsorpcijska barijera. Recimo da se igrač uvijek kladi 1 dolar na crvenu boju ruleta gdje je 18 pruga crveno, 18 crnih pruga, 2 pruge su nula, pri nuli novac ide u kasino. Dakle, igra se igra s malim negativnim matematičkim očekivanjem. Veća je vjerojatnost da će njegov račun porasti na 101 USD i da će igrač prestati igrati nego da će njegov račun pasti na nulu i igrač neće imati za što igrati. Ako igrač uvijek iznova igra rulet, bit će žrtva negativnog matematičkog očekivanja. Ako takvu igru ​​igrate samo jednom, onda aksiom neizbježnog bankrota, naravno, ne vrijedi, ako je igrate jednom, recimo snaga negativnog matea. očekivanja će biti što slabija. Razlika između negativnog očekivanja i pozitivnog očekivanja je razlika između života i smrti vašeg depozita.

Kada shvatite da igra ima negativno matematičko očekivanje, onda je najbolja oklada bez oklade. Zapamti to ne postoji strategija upravljanja novcem koja može pretvoriti izgubljenu igru ​​u dobitnu. Recimo da se i dalje morate kladiti u igri negativnog očekivanja, tada bi najbolja strategija bila " strategija maksimalne hrabrosti » . Drugim riječima, želite se što manje kladiti (za razliku od igre s pozitivnim očekivanjima, gdje se treba kladiti što češće, poželjno je uopće ne napuštati igru). Dakle, što više pokušaja napravite, veća je vjerojatnost da ćete izgubiti ako imate negativna očekivanja. Stoga, s negativnim očekivanjem, manje su šanse za gubitak ako se duljina igre skrati (to jest, kako se broj pokušaja približava 1). Ako igrate igru ​​u kojoj postoji 49% šanse da osvojite $1 i 51% šanse da izgubite $1, najbolje je da igrate samo jednom. Što više oklada položite, to je veća vjerojatnost da ćete izgubiti (pri čemu se vjerojatnost gubitka približava 100% sigurnosti kako se igra približava beskonačnosti s negativnim očekivanjem).

Organizatori igre, kockarnica - neće reći trgovcu o matematičkom očekivanju, "oni" će reći trgovcu o mogućnosti dobitka i pronaći razne razloge za trgovca da se kladi. Slušajući organizatore igre i ogroman broj igrača blizu tržišta koji primaju proviziju ne riskirajući svoj novac, trgovac smatra da je za uspješnu igru ​​važno analizirati grafikon, vijesti, podvlačiti crte na pseudoznanosti onih analize i time pronaći pravi trenutak za otvaranje pozicija i time navodno povećati pouzdanost svog sustava - strategije (ako postoji) i pobijediti tržište. Ali istina je da najmanje 97% ljudi koji pokušavaju izmisliti sustave trgovinske strategije samo pokušavaju pronaći idealan unos. Ovaj ulazni signal je nemoćan protiv izvornog matematički negativnog očekivanja. Zapravo, trgovci gotovo uvijek govore o tome da njihovi sustavi imaju najmanje 60% sigurnosni faktor. Ali u isto vrijeme se pitaju zašto ne zarađuju, na duge staze trgovci gube novac! Shvatite da je čak i sustav s visokim postotkom dobitaka s negativnim matematičkim očekivanjem put u nikamo, najbolja stvar koju trgovac može učiniti je zaustaviti se na pobjedničkom nizu i više ne ulaziti na tržište.

Još jedan zanimljiv detalj, recimo da igru ​​započnete s jednim dolarom, pobijedite na prvom bacanju i zaradite dolar. Pri sljedećem bacanju ulažete cijeli svoj račun (2 USD), ali ovaj put gubite i gubite ih. Izgubili ste početni iznos od $1 i profit od $1. Činjenica je da ako iskoristite 100% računa, izaći ćete iz igre čim naiđete na gubitak, što je neizbježan događaj. Iz ovoga proizlazi važno pravilo, ako ste ipak započeli igru, onda igrajte s istim okladama, a dobitak uzmite sebi. Ne ulazite na tržište s velikim okladama s negativnom matematičkom vrijednošću

Kratkoročni trgovci stalno govore stvari kao da sam uspješan dnevni trgovac. Na tržnicu ulazim i izlazim nekoliko puta dnevno. I zarađujem gotovo svaki dan. Ali jučer sam izgubio gotovo godinu dana i jako sam uzrujan zbog toga. Takve pogreške nastaju kao rezultat promjene oklade, upadanja u zamku korištenja poluge i emocionalnog trgovanja. Odabir unosa, zarada neko vrijeme i pražnjenje računa kao rezultat, to je sudbina velike većine trgovaca koji igraju samo na polju negativnog partnera. očekivanja.

Kako se trgovci bore s tržištem? Pokušaji razbijanja negativnog matematičkog očekivanja su iste serije oklada na iste "događaje". Ovo je klasičan primjer kockanja gdje igrači pokušavaju iskoristiti nizove. Jedini slučaj koji ih dovodi do gubitka ovim pristupom je kada postoji mnogo identičnih pogodaka u nizu u nizu. Serije, što manje to bolje - učinkovitije od igre na slijepo, međutim serije ne daju pozitivno matematičko očekivanje.

Svi ste sigurno čuli za Martingale, ovo je poboljšana serijska strategija. Ovdje igrač počinje s minimalnim ulogom, obično $1, i udvostručuje ulog nakon svakog gubitka. Teoretski, prije ili kasnije mora pobijediti i onda vratiti sve što je izgubio plus jedan dolar. Nakon toga ponovno može napraviti minimalni ulog i krenuti ispočetka. Osnovni koncept Martingale metode temelji se na činjenici da kako se iznos smanjuje kao posljedica gubitaka, mogućnost kompenzacije gubitaka raste ili ostaje ista. Ovo je popularna vrsta upravljanja novcem za kockare. Sustav udvostručavanja izgleda kao win-win sve dok ne shvatite da će dugi niz poraza uništiti svakog igrača, koliko god on bio bogat. Igrač koji počne s 1 $ i izgubi 46 puta mora položiti svoju 47. okladu od 70 trilijuna $, a to je više od cijene cijelog svijeta (oko 50 trilijuna). Jasno je da će puno prije ostati bez novca ili će naići na ograničenja u pogledu svog depozita ili kasina. Mislim da je sustav udvostručenja beskoristan ako imate negativno matematičko očekivanje i previše je riskantno koristiti ovaj sustav za vlastiti novac.

U beskonačnom nastavku igra s negativnim matematičkim očekivanjem je uzaludna. Ali s ograničenim brojem serija, postoji šansa za pobjedu. Ili trebate potražiti prostirku. pozitivna igra u kojoj će mogući dobitak biti veći od mogućeg gubitka po 1 okladi.

Većina trgovaca umire od jednog od dva metka – neznanja i emocija. Laici igraju na slutnju, upuštajući se u obrte koji su - zbog negativnog matematičkog očekivanja - trebali propustiti. Ako prežive, tada, nakon što su naučili, počinju razvijati pametnije sustave. Zatim, sigurni u sebe, izbace glavu iz rova ​​– i padnu pod drugi metak. Previše samouvjereni, klade se previše na jednu trgovinu i ispadaju iz igre nakon kratkog niza gubitaka. Emocionalnost ima najizravniji utjecaj na financijski rezultat koji ostvaruje investitor – u većoj mjeri igrač iz financijskih špekulacija. A što je ponašanje osobe emotivnije, to će odstupanje matematičkog očekivanja financijskih rezultata njezina trgovanja biti značajnije od stvarnosti. Za kockanje s negativnim matematičkim očekivanjem, financijski rezultati dobiveni pod utjecajem emocija smrt su depozita.

U pravilu, sve igre s novčanim dobitkom, bilo da se radi o lutriji, okladama na hipodromu i kladionicama, automatima i sl., igre su s negativnim matematičkim očekivanjem za igrača. Kockarnice ne organiziraju samo ove igre za vas. Posebnost prosječnog trgovca je u tome što nije u stanju izračunati sve sitnice koje ga čekaju u budućnosti, te je stoga budućnost njegove igre gotova stvar.

Želim da shvatite da se sudjelovanje u bilo kojoj od igara s negativnim matematičkim očekivanjem ne može smatrati izvorom stabilnog prihoda.

Što učiniti? Svatko odlučuje za sebe, ja sam pronašao matematički pozitivno očekivanje na dioničkim opcijama, ali i tamo stalne promjene pravila igre od strane brokera i burzi dovode do snažnog pada konačnog prihoda. Zamazana nula ruleta na spreadove, rekvizicije, brokere i ostale sitnice ozbiljno umanjuje konačnu zaradu, ali samo uz korištenje opcija možete izgraditi sustav šah-mat + u ovom “kazinu 21. stoljeća”.

Potražite matematičko pozitivno očekivanje na bilo koji način!

Mislim da je tako, ključ za zarađivanje novca na financijskom tržištu je imati sustav s visokim pozitivnim matematičkim očekivanjem, korištenjem ovog sustava izuzetno je važno koristiti početno utvrđenu veličinu pozicije, raditi strogo u skladu s pravilima i opetovano i kao što je dulje moguće nastaviti igru ​​i zaraditi boreći se s nestašlucima organizatora ovog "kazina".

Svaka pojedinačna vrijednost u potpunosti je određena svojom funkcijom raspodjele. Također, za rješavanje praktičnih problema dovoljno je poznavati nekoliko numeričkih karakteristika, zahvaljujući kojima postaje moguće predstaviti glavne značajke slučajne varijable u sažetom obliku.

Ove količine su prvenstveno očekivana vrijednost i disperzija .

Očekivana vrijednost- prosječna vrijednost slučajne varijable u teoriji vjerojatnosti. Označeno kao .

Na najjednostavniji način, matematičko očekivanje slučajne varijable X(w), nalaze se kao sastavniLebesgue s obzirom na mjeru vjerojatnosti R početni prostor vjerojatnosti

Također možete pronaći matematičko očekivanje vrijednosti kao Lebesgueov integral iz x distribucijom vjerojatnosti R X količinama x:

gdje je skup svih mogućih vrijednosti x.

Matematičko očekivanje funkcije od slučajne varijable x je kroz distribuciju R X. Na primjer, ako x- slučajna varijabla s vrijednostima u i f(x)- nedvosmislen Borelfunkcija x , zatim:

Ako a F(x)- distribucijska funkcija x, tada je matematičko očekivanje reprezentativno sastavniLebesgue - Stieltjes (ili Riemann - Stieltjes):

dok je integrabilnost x u kojem smislu ( * ) odgovara konačnosti integrala

U posebnim slučajevima, ako x ima diskretnu distribuciju s vjerojatnim vrijednostima x k, k=1, 2, . , i vjerojatnosti , dakle

ako x ima apsolutno kontinuiranu distribuciju s gustoćom vjerojatnosti p(x), onda

u ovom slučaju, postojanje matematičkog očekivanja je ekvivalentno apsolutnoj konvergenciji odgovarajućeg niza ili integrala.

Svojstva matematičkog očekivanja slučajne varijable.

• Matematičko očekivanje konstantne vrijednosti jednako je ovoj vrijednosti:

C- konstantno;

• M=C.M[X]

• Matematičko očekivanje zbroja nasumično uzetih vrijednosti jednako je zbroju njihovih matematičkih očekivanja:

• Matematičko očekivanje umnoška neovisnih slučajnih varijabli = umnožak njihovih matematičkih očekivanja:

M=M[X]+M[Y]

ako x i Y nezavisna.

ako niz konvergira:

Algoritam za izračun matematičkog očekivanja.

Svojstva diskretnih slučajnih varijabli: sve njihove vrijednosti mogu se prenumerirati prirodnim brojevima; izjednačite svaku vrijednost s vjerojatnošću različitom od nule.

1. Redom pomnožite parove: x i na pi.

2. Dodajte umnožak svakog para x i p i.

Na primjer, za n = 4 :

Funkcija distribucije diskretne slučajne varijable korak po korak, naglo raste u onim točkama čije vjerojatnosti imaju pozitivan predznak.

Primjer: Nađite matematičko očekivanje pomoću formule.

- broj dječaka među 10 novorođenčadi.

Sasvim je jasno da taj broj nije unaprijed poznat, au sljedećih deset rođene djece može biti:

Ili dečki - jedan i jedini od navedenih opcija.

I, kako biste ostali u formi, malo tjelesnog odgoja:

- daljina skoka u dalj (u nekim jedinicama).

Čak ni majstor sporta to ne može predvidjeti :)

Međutim, koje su vaše hipoteze?

2) Kontinuirana slučajna varijabla - uzima svi numeričke vrijednosti iz nekog konačnog ili beskonačnog raspona.

Bilješka : kratice DSV i NSV popularne su u obrazovnoj literaturi

Prvo, analizirajmo diskretnu slučajnu varijablu, zatim - stalan.

Zakon distribucije diskretne slučajne varijable

- ovo je usklađenost između mogućih vrijednosti ove količine i njihovih vjerojatnosti. Najčešće je zakon napisan u tablici:

Izraz je dosta uobičajen red distribucija, ali u nekim situacijama zvuči dvosmisleno, i stoga ću se držati "zakona".

A sada vrlo važna točka: budući da je slučajna varijabla nužno prihvatit će jedna od vrijednosti, tada se formiraju odgovarajući događaji puna grupa a zbroj vjerojatnosti njihove pojave jednak je jedinici:

ili, ako je napisano presavijeno:

Tako, na primjer, zakon raspodjele vjerojatnosti bodova na kockici ima sljedeći oblik:

Bez komentara.

Možda ste pod dojmom da diskretna slučajna varijabla može poprimiti samo "dobre" cjelobrojne vrijednosti. Otklonimo iluziju - oni mogu biti bilo što:

Primjer 1

Neka igra ima sljedeći zakon raspodjele isplate:

…vjerojatno ste dugo sanjali o ovakvim zadacima :) Da vam otkrijem tajnu - i ja. Pogotovo nakon završetka rada na teorija polja.

Riješenje: budući da slučajna varijabla može poprimiti samo jednu od tri vrijednosti, formiraju se odgovarajući događaji puna grupa, što znači da je zbroj njihovih vjerojatnosti jednak jedan:

Razotkrivamo "partizana":

– dakle, vjerojatnost dobitka konvencionalnih jedinica je 0,4.

Kontrola: što trebate osigurati.

Odgovor:

Nije neuobičajeno kada zakon raspodjele treba samostalno sastaviti. Za ovu upotrebu klasična definicija vjerojatnosti, teoremi množenja/zbrajanja za vjerojatnosti događaja i drugi čips tervera:

Primjer 2

U kutiji je 50 srećki, od kojih je 12 dobitnih, od kojih 2 osvajaju po 1000 rubalja, a ostale po 100 rubalja. Napravite zakon raspodjele slučajne varijable - veličine dobitka, ako je iz kutije nasumično izvučen jedan listić.

Riješenje: kao što ste primijetili, uobičajeno je smjestiti vrijednosti slučajne varijable uzlazni redoslijed. Stoga počinjemo s najmanjim dobicima, odnosno rubljama.

Ukupno je takvih karata 50 - 12 = 38, a prema klasična definicija:
je vjerojatnost da nasumično izvučeni listić neće dobiti.

Ostali slučajevi su jednostavni. Vjerojatnost dobitka u rubljama je:

Provjera: - a ovo je posebno ugodan trenutak takvih zadataka!

Odgovor: zahtijevani zakon raspodjele isplate:

Sljedeći zadatak za samostalno odlučivanje:

Primjer 3

Vjerojatnost da će strijelac pogoditi metu je . Napravite zakon raspodjele za slučajnu varijablu - broj pogodaka nakon 2 hica.

...znala sam da ti nedostaje :) Sjećamo se teoremi množenja i zbrajanja. Rješenje i odgovor na kraju lekcije.

Zakon raspodjele u potpunosti opisuje slučajnu varijablu, ali u praksi je korisno (a ponekad i korisnije) poznavati samo neke od njih. numeričke karakteristike .

Matematičko očekivanje diskretne slučajne varijable

Jednostavnim rječnikom rečeno, ovo prosječna očekivana vrijednost uz ponovljeno testiranje. Neka slučajna varijabla ima vrijednosti s vjerojatnostima odnosno. Tada je matematičko očekivanje ove slučajne varijable jednako zbroj radova sve njegove vrijednosti prema odgovarajućim vjerojatnostima:

ili u presavijenom obliku:

Izračunajmo, na primjer, matematičko očekivanje slučajne varijable - broja bodova ispuštenih na kocki:

Sada se prisjetimo naše hipotetske igre:

Postavlja se pitanje je li uopće isplativo igrati ovu igru? ... tko ima dojmove? Dakle, ne možete reći "na brzinu"! Ali na ovo se pitanje može lako odgovoriti izračunavanjem matematičkog očekivanja, u biti - prosječne težine vjerojatnosti dobitka:

Dakle, matematičko očekivanje ove igre gubljenje.

Ne vjerujte dojmovima - vjerujte brojkama!

Da, ovdje možete pobijediti 10 ili čak 20-30 puta zaredom, ali na duge staze neizbježno ćemo propasti. I ne bih vam savjetovao da igrate takve igre :) Pa, možda samo Za zabavu.

Iz svega navedenog proizlazi da matematičko očekivanje NIJE SLUČAJNA vrijednost.

Kreativni zadatak za samostalno istraživanje:

Primjer 4

Gospodin X igra europski rulet prema sljedećem sustavu: stalno ulaže 100 rubalja na crveno. Sastavite zakon raspodjele slučajne varijable – njen dobitak. Izračunajte matematičko očekivanje dobitka i zaokružite ga na kopejke. Kako prosjek gubi li igrač za svakih sto uloženih?

Referenca : Europski rulet sadrži 18 crvenih, 18 crnih i 1 zeleni sektor ("nula"). U slučaju ispadanja "crvenog", igraču se isplaćuje dvostruki ulog, inače ide u prihod kasina

Postoje mnogi drugi sustavi ruleta za koje možete izraditi vlastite tablice vjerojatnosti. Ali to je slučaj kada nam ne trebaju nikakvi zakoni raspodjele i tablice, jer je sigurno utvrđeno da će matematičko očekivanje igrača biti potpuno isto. Mijenja se samo od sustava do sustava

Očekivana vrijednost. matematičko očekivanje diskretna slučajna varijabla x, koji ima konačan broj vrijednosti xja s vjerojatnostima Rja, naziva se suma:

matematičko očekivanje kontinuirana slučajna varijabla x naziva se integral umnoška njegovih vrijednosti x na gustoću distribucije vjerojatnosti f(x):

(6b)

Nepravilan integral (6 b) pretpostavlja se da je apsolutno konvergentan (inače kažemo da je očekivanje M(x) ne postoji). Matematičko očekivanje karakterizira značiti nasumična varijabla x. Njegova dimenzija koincidira s dimenzijom slučajne varijable.

Svojstva matematičkog očekivanja:

Disperzija. disperzija nasumična varijabla x broj se zove:

Disperzija je karakteristika rasipanja vrijednosti slučajne varijable x u odnosu na njegovu prosječnu vrijednost M(x). Dimenzija varijance jednaka je dimenziji kvadrata slučajne varijable. Na temelju definicija varijance (8) i matematičkog očekivanja (5) za diskretnu slučajnu varijablu i (6) za kontinuiranu slučajnu varijablu, dobivamo slične izraze za varijancu:

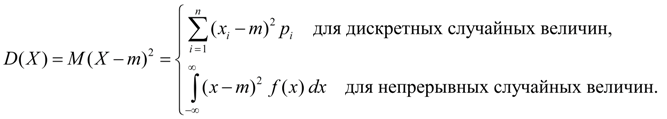(9)

Ovdje m = M(x).

Disperzijska svojstva:

Standardna devijacija:

(11)

Budući da je dimenzija standardne devijacije ista kao kod slučajne varijable, ona se češće od varijance koristi kao mjera disperzije.

distribucijski momenti. Koncepti matematičkog očekivanja i varijance posebni su slučajevi općenitijeg koncepta za numeričke karakteristike slučajnih varijabli - distribucijski momenti. Momenti raspodjele slučajne varijable uvode se kao matematička očekivanja nekih jednostavnih funkcija slučajne varijable. Dakle, trenutak reda k u odnosu na točku x 0 se naziva očekivanje M(x–x 0 )k. Trenuci u odnosu na ishodište x= 0 nazivaju se početni trenuci i označeni su:

(12)

Početni trenutak prvog reda je distribucijski centar razmatrane slučajne varijable:

(13)

Trenuci u odnosu na distribucijski centar x= m nazvao središnjim trenucima i označeni su:

(14)

Iz (7) slijedi da je središnji moment prvog reda uvijek jednak nuli:

Središnji momenti ne ovise o podrijetlu vrijednosti slučajne varijable, jer s pomakom za konstantnu vrijednost IZ njegov centar raspodjele pomaknut je za istu vrijednost IZ, a odstupanje od centra se ne mijenja: x – m = (x – IZ) – (m – IZ).
Sada je očito da disperzija- ovo je središnji moment drugog reda:

Asimetrija. Centralni moment trećeg reda:

(17)

služi za ocjenjivanje asimetrija distribucije. Ako je distribucija simetrična u odnosu na točku x= m, tada će središnji moment trećeg reda biti jednak nuli (kao i svi središnji momenti neparnih redova). Stoga, ako je središnji moment trećeg reda različit od nule, tada distribucija ne može biti simetrična. Veličina asimetrije procjenjuje se korištenjem bezdimenzionalnog koeficijent asimetrije:

(18)

Predznak koeficijenta asimetrije (18) označava desnu ili lijevu asimetriju (slika 2).

Riža. 2. Vrste asimetrije distribucija.

Višak. Centralni moment četvrtog reda:

(19)

služi za ocjenu tzv kurtosis, koji određuje stupanj strmosti (šiljastosti) krivulje distribucije u blizini središta distribucije u odnosu na krivulju normalne distribucije. Budući da je za normalnu distribuciju količina uzeta kao kurtoza:

(20)

Na sl. 3 prikazuje primjere distribucijskih krivulja s različitim vrijednostima kurtoze. Za normalnu raspodjelu E= 0. Krivulje koje su šiljatije od normalne imaju pozitivnu kurtozu, a krivulje s više ravnih vrhova imaju negativnu kurtozu.

Riža. 3. Krivulje raspodjele s različitim stupnjevima strmine (kurtosis).

Trenuci višeg reda u inženjerskim primjenama matematičke statistike obično se ne koriste.

Moda diskretna slučajna varijabla je njegova najvjerojatnija vrijednost. Moda stalan slučajna varijabla je njezina vrijednost pri kojoj je gustoća vjerojatnosti najveća (slika 2). Ako krivulja distribucije ima jedan maksimum, tada se distribucija naziva unimodalni. Ako krivulja distribucije ima više od jednog maksimuma, tada se naziva distribucija polimodalni. Ponekad postoje distribucije čije krivulje nemaju maksimum, već minimum. Takve se raspodjele nazivaju antimodalni. U općem slučaju modus i matematičko očekivanje slučajne varijable se ne podudaraju. U konkretnom slučaju, za modalni, tj. ima modus, simetričnu distribuciju, a pod uvjetom da postoji matematičko očekivanje, ono se poklapa s modusom i središtem simetrije distribucije.

Medijan nasumična varijabla x je njegovo značenje Mi, za koje vrijedi jednakost: tj. jednako je vjerojatno da slučajna varijabla x bit će manje ili više Mi. Geometrijski medijan je apscisa točke u kojoj je površina ispod krivulje distribucije podijeljena na pola (slika 2). U slučaju simetrične modalne distribucije, medijan, mod i srednja vrijednost su isti.