Rang matrice: definicija, metode pronalaženja, primjeri, rješenja. Pronalaženje ranga matrice Što je rang matrice 1123 5814

Također razmotrite važnu praktičnu primjenu teme: proučavanje sustava linearnih jednadžbi za kompatibilnost.

Koji je rang matrice?

Šaljivi epigraf članka sadrži veliku dozu istine. Sama riječ "rang" obično se povezuje s nekom vrstom hijerarhije, najčešće s karijernom ljestvicom. Što čovjek ima više znanja, iskustva, sposobnosti, veza itd. - viši njegov položaj i raspon mogućnosti. U smislu mladih, rang se odnosi na ukupni stupanj "žilavosti".

I naša matematička braća žive po istim principima. Prošetajmo nekoliko proizvoljnih nulte matrice:

Razmislimo ako u matrici samo nule, o kakvom rangu onda možemo govoriti? Svima je poznat neformalni izraz "totalna nula". U društvu matrice sve je potpuno isto:

Nulti rang matricesvaka veličina je nula.

Bilješka : nulta matrica je označena grčkim slovom "theta"

Kako bih bolje razumio rang matrice, u nastavku ću se oslanjati na materijale analitička geometrija. Uzmite u obzir nulu vektor našeg trodimenzionalnog prostora, koji ne postavlja određeni smjer i beskoristan je za gradnju afina osnova. S algebarske točke gledišta, koordinate danog vektora su zapisane matrica"jedan po tri" i logično (u navedenom geometrijskom smislu) pretpostavimo da je rang ove matrice nula.

Sada pogledajmo nekoliko različit od nule vektori stupaca i vektori reda:

Svaka instanca ima barem jedan element koji nije nula, i to je nešto!

Rang bilo kojeg vektora reda (vektora stupca) koji nije nula jednak je jedinici

I općenito govoreći - ako je u matrici proizvoljne veličine ima barem jedan element različit od nule, tada njegov rang ne manje jedinice.

Algebarski vektori reda i stupca su apstraktni do određene mjere, pa se okrenimo opet geometrijskoj asocijaciji. različit od nule vektor postavlja točno definiran pravac u prostoru i pogodan je za građenje osnova, pa će se pretpostaviti da je rang matrice jednak jedan.

Teorijska referenca : u linearnoj algebri, vektor je element vektorskog prostora (definiran kroz 8 aksioma), koji, posebno, može biti uređen red (ili stupac) realnih brojeva s operacijama zbrajanja i množenja realnim brojem definiranim za njih. Za više informacija o vektorima pogledajte članak Linearne transformacije.

linearno ovisna(izraženo jedno kroz drugo). S geometrijskog gledišta, drugi red sadrži koordinate kolinearnog vektora , koji nije unaprijedio stvar u gradnji trodimenzionalna osnova, koji je u tom smislu suvišan. Dakle, rang ove matrice je također jednak jedan.

Prepisujemo koordinate vektora u stupce ( transponirati matricu):

Što se promijenilo u rangu? Ništa. Stupci su proporcionalni, što znači da je rang jednak jedan. Usput, imajte na umu da su sve tri linije također proporcionalne. Mogu se identificirati koordinatama tri kolinearni vektori ravnine, od kojih samo jedan korisno za izradu "ravne" osnove. I to je u potpunom skladu s našim geometrijskim osjećajem ranga.

Važna izjava slijedi iz gornjeg primjera:

Rang matrice po redovima jednak je rangu matrice po stupcima. Već sam to malo spomenuo u lekciji o učinkovitom metode za izračunavanje determinante.

Bilješka : linearna ovisnost redaka dovodi do linearne ovisnosti stupaca (i obrnuto). Ali da bih uštedio vrijeme, a iz navike, gotovo uvijek ću govoriti o linearnoj ovisnosti nizova.

Nastavimo trenirati našeg voljenog ljubimca. Dodajte koordinate drugog kolinearnog vektora matrici u trećem redu :

Je li nam pomogao u izgradnji trodimenzionalne osnove? Naravno da ne. Sva tri vektora hodaju naprijed-nazad duž iste staze, a rang matrice je jedan. Možete uzeti koliko god hoćete kolinearnih vektora, recimo 100, staviti njihove koordinate u matricu 100 x 3, a rang takvog nebodera će i dalje ostati jedan.

Upoznajmo se s matricom čiji redovi linearno neovisni. Par nekolinearnih vektora prikladan je za konstrukciju trodimenzionalne baze. Rang ove matrice je dva.

Koji je rang matrice? Čini se da linije nisu proporcionalne ... tako da, u teoriji, tri. Međutim, rang ove matrice također je jednak dva. Dodao sam prva dva retka i zapisao rezultat na dnu, tj. linearno izraženo treći red kroz prva dva. Geometrijski, redovi matrice odgovaraju koordinatama tri koplanarni vektori, a među ovom trojkom nalazi se i par nekolinearnih drugova.

Kao što vidiš linearna ovisnost u razmatranoj matrici nije očigledan, a danas ćemo samo naučiti kako ga dovesti "na čistu vodu".

Mislim da mnogi ljudi pogađaju koji je rang matrice!

Promotrimo matricu čiji redovi linearno neovisni. Oblik vektora afina osnova, a rang ove matrice je tri.

Kao što znate, svaki četvrti, peti, deseti vektor trodimenzionalnog prostora bit će linearno izražen u terminima baznih vektora. Prema tome, ako se bilo koji broj redaka doda matrici, tada je njen rang i dalje će biti tri.

Slično razmišljanje može se provesti i za matrice većih veličina (jasno, već bez geometrijskog značenja).

Definicija : rang matrice je najveći broj linearno neovisnih redaka. Ili: rang matrice je najveći broj linearno neovisnih stupaca. Da, uvijek se podudaraju.

Iz navedenog proizlazi važna praktična smjernica: rang matrice ne prelazi njezinu minimalnu dimenziju. Na primjer, u matrici četiri reda i pet stupaca. Minimalna dimenzija je četiri, stoga rang ove matrice sigurno neće prelaziti 4.

Notacija: u svjetskoj teoriji i praksi ne postoji općeprihvaćen standard za označavanje ranga matrice, najčešći je onaj: - kako kažu, Englez piše jedno, Nijemac drugo. Stoga, na temelju poznate anegdote o američkom i ruskom paklu, označimo rang matrice domaćom riječi. Na primjer: . A ako je matrica "bezimena", kojih ima puno, onda možete jednostavno napisati .

Kako pronaći rang matrice pomoću minora?

Ako je naša baka imala peti stupac u matrici, onda je trebalo izračunati još jedan minor 4. reda (“plava”, “malina” + 5. stupac).

Zaključak: najveći red minora različitog od nule je tri, pa je .

Možda nisu svi u potpunosti razumjeli ovu frazu: minor 4. reda jednak je nuli, ali među minorima 3. reda bio je jedan različit od nule - dakle, maksimalni red različit od nule manji i jednak tri.

Postavlja se pitanje zašto odmah ne izračunati determinantu? Pa, prvo, u većini zadataka matrica nije kvadratna, a drugo, čak i ako dobijete vrijednost različitu od nule, tada će zadatak biti odbijen s velikom vjerojatnošću, jer obično podrazumijeva standardni "odozdo prema gore" riješenje. A u razmatranom primjeru, nulta determinanta 4. reda čak nam omogućuje da tvrdimo da je rang matrice samo manji od četiri.

Moram priznati da sam analizirani problem sam smislio kako bih što bolje objasnio način graničenja maloljetnika. U stvarnoj praksi sve je jednostavnije:

Primjer 2

Odredite rang matrice metodom rubnih minora

Rješenje i odgovor na kraju lekcije.

Kada algoritam radi najbrže? Vratimo se istoj matrici četiri puta četiri . Očito će rješenje biti najkraće u slučaju "dobro" kutni maloljetnici: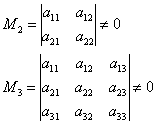

I, ako , onda , inače - .

Razmišljanje nije nimalo hipotetsko - ima mnogo primjera gdje je cijela stvar ograničena samo na kutne minore.

Međutim, u nekim je slučajevima druga metoda učinkovitija i poželjnija:

Kako pronaći rang matrice pomoću Gaussove metode?

Ovaj odjeljak namijenjen je čitateljima koji su već upoznati s Gaussova metoda i malo-pomalo dohvatili ga se.

S tehničkog gledišta, metoda nije nova:

1) koristeći elementarne transformacije, dovodimo matricu u oblik koraka;

2) rang matrice je jednak broju redaka.

Sasvim je jasno da primjenom Gaussove metode ne mijenja se rang matrice, a bit je ovdje krajnje jednostavna: prema algoritmu, tijekom elementarnih transformacija identificiraju se i uklanjaju sve nepotrebne proporcionalne (linearno ovisne) linije, uslijed čega ostaje "suhi ostatak" - maksimalni broj linearno nezavisnih linija.

Transformirajmo staru poznatu matricu s koordinatama tri kolinearna vektora:

(1) Prvi red je dodan drugom retku, pomnožen s -2. Prvi red je dodan u treći red.

(2) Nulti redovi se brišu.

Dakle, postoji jedan redak lijevo, stoga . Nepotrebno je reći da je ovo mnogo brže od izračunavanja devet minora nula 2. reda i tek onda izvlačenja zaključka.

Podsjećam vas da samo po sebi algebarska matrica ništa se ne može promijeniti, a transformacije se rade samo u svrhu saznanja ranga! Usput, zadržimo se opet na pitanju, zašto ne? Matrica izvora 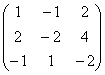nosi informaciju koja se bitno razlikuje od informacije o matrici i redu. U nekim matematičkim modelima (bez pretjerivanja) razlika u jednom broju može biti pitanje života i smrti. ... Sjetio sam se školskih profesora matematike osnovnih i srednjih razreda koji su nemilosrdno smanjivali ocjenu za 1-2 boda za najmanju netočnost ili odstupanje od algoritma. I bilo je užasno razočaranje kada je umjesto naizgled zajamčene “petice” ispala “dobra” ili još lošija. Razumijevanje je došlo mnogo kasnije - kako drugačije povjeriti osobi satelite, nuklearne bojeve glave i elektrane? Ali ne brinite, ne radim u ovim područjima =)

Prijeđimo na sadržajnije zadatke, gdje ćemo se, između ostalog, upoznati s važnim računalnim tehnikama Gaussova metoda:

Primjer 3

Odredite rang matrice koristeći elementarne transformacije

Riješenje: data je matrica četiri puta pet, što znači da njen rang sigurno nije veći od 4.

U prvom stupcu nema 1 ili -1, stoga su potrebni dodatni koraci da bi se dobila barem jedna jedinica. Tijekom cijelog postojanja stranice više puta mi je postavljeno pitanje: "Je li moguće preurediti stupce tijekom elementarnih transformacija?". Evo - preuredite prvi ili drugi stupac i sve je u redu! U većini zadataka gdje Gaussova metoda, stupci se stvarno mogu preuređivati. ALI NEMOJTE. A poanta nije čak ni u mogućoj zabuni s varijablama, poanta je u tome da se u klasičnom tijeku nastave više matematike ova radnja tradicionalno ne razmatra, stoga će se na takav naklon gledati VRLO krivo (ili čak biti prisiljen sve ponoviti) .

Druga točka tiče se brojeva. Tijekom donošenja odluke korisno je voditi se sljedećim osnovnim pravilom: elementarne transformacije trebaju, ako je moguće, reducirati brojeve matrice. Doista, puno je lakše raditi s jedan-dva-tri nego, na primjer, s 23, 45 i 97. A prva radnja nije usmjerena samo na dobivanje jedinice u prvom stupcu, već i na uklanjanje brojeva 7 i 11.

Prvo potpuno rješenje, a zatim komentari:

(1) Prvi red je dodan drugom retku, pomnožen s -2. Prvi red je dodan trećem retku, pomnožen s -3. I gomili: 1. redak, pomnožen s -1, dodan je 4. retku.

(2) Posljednja tri retka su proporcionalna. Izbrisan 3. i 4. redak, drugi redak je premješten na prvo mjesto.

(3) Prvi red je dodan drugom retku, pomnožen s -3.

Matrica reducirana na stepenasti oblik ima dva reda.

Odgovor:

Sada je vaš red da mučite matricu četiri puta četiri:

Primjer 4

Odredite rang matrice Gaussovom metodom

Podsjećam te na to Gaussova metoda ne podrazumijeva jednoznačnu krutost, a vaše rješenje će se najvjerojatnije razlikovati od mog rješenja. Kratki primjer zadatka na kraju lekcije.

Koju metodu koristiti za pronalaženje ranga matrice?

U praksi se često uopće ne govori kojom se metodom treba pronaći rang. U takvoj situaciji treba analizirati uvjet - za neke matrice je racionalnije provesti rješenje kroz minore, dok je za druge mnogo isplativije primijeniti elementarne transformacije:

Primjer 5

Odredite rang matrice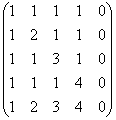

Riješenje: prvi način nekako odmah nestane =)

Malo više, savjetovao sam da se ne diraju stupci matrice, ali kada postoji nulti stupac ili proporcionalni / odgovarajući stupci, onda je još uvijek vrijedno amputirati:

(1) Peti stupac je nula, uklanjamo ga iz matrice. Dakle, rang matrice je najviše četiri. Prvi red se množi s -1. Ovo je još jedna prepoznatljiva značajka Gaussove metode, koja sljedeću radnju čini ugodnom šetnjom:

(2) Svim recima, počevši od drugog, dodan je prvi red.

(3) Prvi red je pomnožen s -1, treći red je podijeljen s 2, četvrti red je podijeljen s 3. Drugi red pomnožen s -1 dodan je petom redu.

(4) Treći redak dodan je petom retku, pomnožen s -2.

(5) Zadnja dva retka su proporcionalna, peti brišemo.

Rezultat je 4 reda.

Odgovor:

Standardna peterokatnica za samostalno istraživanje:

Primjer 6

Odredite rang matrice

Kratko rješenje i odgovor na kraju lekcije.

Treba napomenuti da izraz "rang matrice" nije tako čest u praksi, au većini problema možete bez njega. Ali postoji jedan zadatak u kojem je koncept koji se razmatra glavni lik, au zaključku članka razmotrit ćemo ovu praktičnu primjenu:

Kako istražiti kompatibilnost sustava linearnih jednadžbi?

Često se uz rješavanje sustavi linearnih jednadžbi prema uvjetu, prvo ga je potrebno ispitati na kompatibilnost, odnosno dokazati da neko rješenje uopće postoji. Ključnu ulogu u ovoj provjeri igra Kronecker-Capellijev teorem, koju ću formulirati u traženom obliku:

Ako rang matrice sustava jednako rangu sustav proširene matrice, tada je sustav konzistentan, a ako se zadani broj podudara s brojem nepoznanica, tada je rješenje jedinstveno.

Stoga je za proučavanje kompatibilnosti sustava potrebno provjeriti jednakost , gdje - matrica sustava(zapamtite terminologiju iz lekcije Gaussova metoda), a - sustav proširene matrice(tj. matrica s koeficijentima kod varijabli + stupac slobodnih članova).

Ovaj članak će raspravljati o konceptu kao što je rang matrice i potrebnim dodatnim konceptima. Dat ćemo primjere i dokaze pronalaženja ranga matrice, a također ćemo vam reći što je matrica minor i zašto je toliko važna.

Matrix minor

Da bismo razumjeli što je rang matrice, potrebno je razumjeti takav koncept kao što je manja matrica.

Definicija 1

Minorkmatrica th reda - determinanta kvadratne matrice reda k × k, koja je sastavljena od elemenata matrice A, smještenih u unaprijed odabranim k-redcima i k-stupcima, uz zadržavanje položaja elemenata matrice A.

Pojednostavljeno, ako u matrici A izbrišemo (p-k) redaka i (n-k) stupaca, a od onih elemenata koji ostanu napravimo matricu, zadržavajući raspored elemenata matrice A, tada je determinanta rezultirajuće matrice minor reda k matrice A.

Iz primjera slijedi da su minori prvog reda matrice A sami elementi matrice.

Možemo navesti nekoliko primjera maloljetnika 2. reda. Izaberimo dva retka i dva stupca. Na primjer, 1. i 2. red, 3. i 4. stupac.

S ovim izborom elemenata, minor drugog reda bit će - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

Drugi minor 2. reda matrice A je 0 0 1 1 = 0

Navedimo ilustracije konstrukcije minora drugog reda matrice A:

Minor 3. reda dobiva se brisanjem trećeg stupca matrice A:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

Ilustracija kako se dobiva minor 3. reda matrice A:

Za datu matricu ne postoje minori viši od 3. reda, jer

k ≤ m i n (p , n) = m i n (3 , 4) = 3

Koliko minora k-tog reda ima za matricu A reda p×n?

Broj maloljetnika izračunava se prema sljedećoj formuli:

C p k × C n k , g e C p k = p ! k! (p - k) ! i C nk = n ! k! (n - k) ! - broj kombinacija od p do k, odnosno od n do k.

Nakon što smo odlučili koji su minori matrice A, možemo prijeći na određivanje ranga matrice A.

Rang matrice: metode pronalaženja

Definicija 2

Rang matrice - najviši red matrice, različit od nule.

Oznaka 1

rang (A), Rg(A), Rang(A).

Iz definicije ranga matrice i minora matrice, postaje jasno da je rang nulte matrice jednak nuli, a rang ne-nulte matrice je različit od nule.

Određivanje ranga matrice po definiciji

Definicija 3

Metoda manjeg nabrajanja - metoda koja se temelji na određivanju ranga matrice.

Algoritam radnji popisivanjem maloljetnika :

Potrebno je pronaći rang matrice A reda str× n. Ako postoji barem jedan element koji nije nula, tada je rang matrice barem jednak jedan ( jer je minor 1. reda koji nije jednak nuli).

Zatim slijedi nabrajanje maloljetnika 2. reda. Ako su svi minori 2. reda jednaki nuli, tada je rang jednak jedan. Ako postoji barem jedan minor 2. reda koji nije nula, potrebno je ići na enumeraciju minora 3. reda, a rang matrice će u tom slučaju biti najmanje dva.

Učinimo isto s rangom 3. reda: ako su svi minori matrice jednaki nuli, tada će rang biti jednak dva. Ako postoji barem jedan minor trećeg reda koji nije nula, tada je rang matrice najmanje tri. I tako dalje, po analogiji.

Primjer 2

Nađi rang matrice:

A \u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

Pošto je matrica različita od nule, njen rang je najmanje jednak jedan.

Minor 2. reda - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 nije nula. To implicira da je rang matrice A najmanje dva.

Razvrstavamo minore 3. reda: C 3 3 × C 5 3 \u003d 1 5 ! 3! (5 - 3) ! = 10 komada.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

Minori 3. reda su nula, tako da je rang matrice dva.

Odgovor : Rang (A) = 2.

Određivanje ranga matrice metodom rubnih minora

Definicija 3

Metoda fringing minor - metoda koja vam omogućuje da dobijete rezultat s manje računalnog rada.

Resni minor - minor M o k (k + 1) -ti red matrice A, koji omeđuje minor M reda k matrice A, ako matrica koja odgovara molu M o k "sadrži" matricu koja odgovara molu M.

Pojednostavljeno rečeno, matrica koja odgovara rubnom minoru M dobiva se iz matrice koja odgovara rubnom minoru M o k brisanjem elemenata jednog retka i jednog stupca.

Primjer 3

Nađi rang matrice:

A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

Da bismo pronašli rang, uzimamo minor 2. reda M = 2 - 1 4 1

Zapisujemo sve granične minore:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

Kako bismo potkrijepili metodu graničnih minora, predstavljamo teorem čija formulacija ne zahtijeva bazu dokaza.

Teorem 1

Ako su svi minori koji graniče s minorom k-tog reda matrice A reda p po n jednaki nuli, tada su svi minori reda (k + 1) matrice A jednaki nuli.

Algoritam akcije :

Da biste pronašli rang matrice, nije potrebno proći kroz sve minore, samo pogledajte granice.

Ako su rubni minori jednaki nuli, tada je rang matrice jednak nuli. Ako postoji barem jedan minor koji nije jednak nuli, tada smatramo rubne minore.

Ako su sve nula, tada je Rank(A) dva. Ako postoji barem jedan rubni minor različit od nule, tada nastavljamo s razmatranjem njegovih rubnih minora. I tako dalje, na sličan način.

Primjer 4

Odredite rang matrice metodom rubnih minora

A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

Kako odlučiti?

Kako element a 11 matrice A nije jednak nuli, tada uzimamo minor 1. reda. Počnimo tražiti rubni minor koji nije nula:

2 1 4 2 = 2 x 2 - 1 x 4 = 0 2 0 4 1 = 2 x 1 - 0 x 4 = 2

Našli smo rubni minor 2. reda koji nije jednak nuli 2 0 4 1 .

Nabrojimo rubne minore - (ima ih (4 - 2) × (5 - 2) = 6 komada).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

Odgovor : Rang(A) = 2.

Određivanje ranga matrice Gaussovom metodom (pomoću elementarnih transformacija)

Prisjetite se što su elementarne transformacije.

Elementarne transformacije:

preuređivanjem redaka (stupaca) matrice;
množenjem svih elemenata bilo kojeg retka (stupca) matrice s proizvoljnim brojem k koji nije nula;

dodavanjem elementima bilo kojeg retka (stupca) elemenata koji odgovaraju drugom retku (stupcu) matrice, a koji se množe s proizvoljnim brojem k.

Definicija 5

Određivanje ranga matrice Gaussovom metodom - metoda koja se temelji na teoriji ekvivalencije matrica: ako se matrica B dobije iz matrice A pomoću konačnog broja elementarnih transformacija, tada je Rank(A) = Rank(B).

Valjanost ove tvrdnje proizlazi iz definicije matrice:

u slučaju permutacije redaka ili stupaca matrice, njena determinanta mijenja predznak. Ako je jednak nuli, tada kod permutiranja redaka ili stupaca ostaje jednak nuli;
u slučaju množenja svih elemenata bilo kojeg retka (stupca) matrice s proizvoljnim brojem k, koji nije jednak nuli, determinanta dobivene matrice jednaka je determinanti izvorne matrice, koja se množi prema k;

u slučaju da se elementima određenog retka ili stupca matrice dodaju odgovarajući elementi drugog retka ili stupca, koji se pomnože s brojem k, ne mijenja se njezina determinanta.

Bit metode elementarnih transformacija : matricu, čiji se rang treba pronaći, elementarnim transformacijama svesti na trapezoidnu.

Za što?

Rang matrica ove vrste vrlo je lako pronaći. Jednak je broju redaka koji imaju barem jedan element koji nije nula. A budući da se rang ne mijenja tijekom elementarnih transformacija, to će biti rang matrice.

Ilustrirajmo ovaj proces:

za pravokutne matrice A reda p puta n, čiji je broj redaka veći od broja stupaca:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k

za pravokutne matrice A reda p puta n, čiji je broj redaka manji od broja stupaca:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b p p + 1 ⋯ b p n , R a n k (A) = str

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

za kvadratne matrice A reda n puta n:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k , k< n

Primjer 5

Nađite rang matrice A pomoću elementarnih transformacija:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

Kako odlučiti?

Budući da je element a 11 različit od nule, potrebno je pomnožiti elemente prvog retka matrice A s 1 a 11 = 1 2:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

Elementima 2. retka pribrajamo odgovarajuće elemente 1. retka koji se množe s (-3). Elementima 3. reda pribrajamo elemente 1. reda koji se množe s (-1):

~ A (1) \u003d 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) \u003d \u003d 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

Element a 22 (2) nije nula, pa elemente 2. retka matrice A s A (2) množimo s a 1 a 22 (2) = - 2 3:

A (3) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

Elementima 3. retka dobivene matrice pribrajamo odgovarajuće elemente 2. retka koji se množe s 3 2 ;
na elemente 4. reda - elemente 2. reda, koji se množe s 9 2 ;
na elemente 5. reda - elemente 2. reda koji se množe s 3 2 .

Svi elementi reda su nula. Tako smo uz pomoć elementarnih transformacija matricu sveli na trapezoidni oblik iz čega je vidljivo da je R a n k (A (4)) = 2 . Iz toga slijedi da je rang izvorne matrice također jednak dva.

Komentar

Ako provodite elementarne transformacije, tada približne vrijednosti nisu dopuštene!

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

U svakoj matrici mogu se pridružiti dva ranga: rang retka (rang sustava redova) i rang stupca (rang sustava stupaca).

Teorema

Rang retka matrice jednak je rangu stupca.

Rang matrice

Definicija

Rang matrice$A$ je rang njegovog sustava redaka ili stupaca.

Označava se s $\operatorname(rang) A$

U praksi se za pronalaženje ranga matrice koristi sljedeća izjava: rang matrice jednak je broju redaka koji nisu nula nakon što je matrica reducirana na stepenasti oblik.

Elementarne transformacije nad redovima (stupcima) matrice ne mijenjaju njen rang.

Rang matrice koraka jednak je broju njenih redova koji nisu nula.

Primjer

Vježbajte. Pronađite rang matrice $ A=\left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & ( 7) \ \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3)\end(niz)\desno) $

Riješenje. Koristeći elementarne transformacije nad njezinim redovima, reduciramo matricu $A$ na stepenasti oblik. Da biste to učinili, prvo oduzmite druga dva od trećeg retka:

$$ A \sim \lijevo(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3)\end(array)\desno) $$

Od drugog retka oduzimamo četvrti redak, pomnožen s 4; od treće - dvije četvrtine:

$$ A \sim \lijevo(\begin(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3)\end(array)\desno) $$

Prvih pet dodajemo u drugi red, a tri trećine u treći:

$$ A \sim \lijevo(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(niz)\desno) $$

Zamijenite prvi i drugi red:

$$ A \sim \lijevo(\begin(array)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(niz)\desno) $$

$$ A \sim \lijevo(\begin(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0)\end(array)\right) \Rightarrow \operatorname(rang) A=2 $$

Odgovor.$ \ime operatera (rang) A=2 $

Metoda manjeg ruba

Druga metoda za pronalaženje ranga matrice temelji se na ovom teoremu - metoda manjeg ruba. Bit ove metode je pronaći maloljetnike, počevši od nižih redova i prelazeći na više. Ako je minor $n$-tog reda različit od nule, a svi minori $n+1$-tog reda jednaki su nuli, tada će rang matrice biti jednak $n$.

Primjer

Vježbajte. Pronađite rang matrice $ A=\left(\begin(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0 ) \\ (-1) & (-2) & (6) & (6)\end(array)\right) $ koristeći metodu manjeg ruba.

Riješenje. Minori minimalnog reda su minori prvog reda, koji su jednaki elementima matrice $A$ . Razmotrimo, na primjer, minor $ M_(1)=1 \neq 0 $ . nalazi se u prvom redu i prvom stupcu. Obrubljujući ga drugim retkom i drugim stupcem, dobivamo minor $ M_(2)^(1)=\left| \begin(array)(ll)(1) & (2) \\ (2) & (4)\end(array)\right|=0 $ ; razmotrimo još jedan minor drugog reda, za to obrubljujemo minor $M_1$ uz pomoć drugog reda i trećeg stupca, tada imamo minor $ M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $ , to jest, rang matrice je najmanje dva. Zatim, razmatramo minore trećeg reda koji okružuju minor $ M_(2)^(2) $ . Postoje dva takva minora: kombinacija trećeg retka s drugim stupcem ili s četvrtim stupcem. Izračunavamo te minore.

§3. Rang matrice

Određivanje ranga matrice

Linearni ovisni redovi

Elementarne matrične transformacije

Ekvivalentne matrice

Algoritam za pronalaženje ranga matrice pomoću elementarnih transformacija

§ četiri. Determinante prvog, drugog i trećeg reda

Odrednica prvog reda

Odrednica drugog reda

Odrednica trećeg reda

Sarrusovo pravilo

§5. Izračun determinanti velikih naloga

Algebarsko zbrajanje

Laplaceov teorem

Determinanta trokutaste matrice

Primjena. Pojam determinante P red općenito.

§ 3. Rang matrice

Svaku matricu karakterizira određeni broj koji je važan u rješavanju sustava linearnih jednadžbi. Ovaj broj se zove rang matrice.

Rang matrice jednak je broju njegovih linearno neovisnih redaka (stupaca), kroz koje se linearno izražavaju svi ostali njegovi redovi (stupci).

Redovi (stupci) matrice se nazivaju linearno ovisna ako su im odgovarajući elementi proporcionalni.

Drugim riječima, elementi jednog od linearno zavisnih redaka jednaki su elementima drugog, pomnoženi s istim brojem. Na primjer, redovi 1 i 2 matrice ALI su linearno ovisni ako je , gdje je (λ neki broj).

Primjer. Odredite rang matrice

Riješenje.

Drugi red se dobiva iz prvog ako se njegovi elementi pomnože s -3, treći se dobiva iz prvog ako se njegovi elementi pomnože s 0, a četvrti se red ne može izraziti preko prvog. Ispada da matrica ima dva linearno neovisna retka, jer prvi i četvrti red nisu proporcionalni, stoga je rang matrice 2.

Rang matrice ALI označeno rang A ili r(A).

Iz definicije ranga matrice slijedi:

1. Rang matrice ne prelazi najmanju njezinu dimenziju, tj. za matricu A m × n .

2. Rang matrice je nula samo ako je nula matrica.

U općem slučaju, određivanje ranga matrice prilično je naporno. Da bi se olakšao ovaj zadatak, koriste se transformacije koje čuvaju rang matrice, koje su tzv elementarne transformacije:

1) odbacivanje nultog retka (stupca);

2) množenje svih elemenata retka (stupca) brojem različitim od nule;

3) mijenjanje redoslijeda redaka (kolona);

4) dodavanje elementima jednog retka (stupca) odgovarajućih elemenata drugog retka (stupca), pomnoženih bilo kojim brojem;

5) transpozicija matrice.

Dvije matrice su tzv ekvivalent ako se jedna dobije iz druge konačnim brojem elementarnih transformacija.

Ekvivalencija matrica označena je znakom "~" (ekvivalent).

Uz pomoć elementarnih transformacija, bilo koja matrica se može svesti na trokutasti oblik, tada izračunavanje njezinog ranga nije teško.

Proces izračunavanja ranga matrice pomoću elementarnih transformacija pogledajmo primjer.

Primjer. Odredite rang matrice

A =

Riješenje.

Naš zadatak je dovesti matricu u trokutasti oblik, tj. koristeći elementarne transformacije, osigurajte da su samo nule ispod glavne dijagonale u matrici.

1. Razmotrite prvi redak. Ako element a 11 = 0, tada permutacijom redaka ili stupaca to postižemo a 11 ¹ 0. U našem primjeru, zamijenimo, na primjer, prvi i drugi redak matrice:

A =

Sada element a 11 ¹ 0. Množenjem prvog reda odgovarajućim brojevima i zbrajanjem s ostalim redovima, osigurat ćemo da svi elementi prvog stupca (osim a 11) bile jednake nuli.

2. Razmotrimo sada drugu liniju. Ako element a 22 = 0, tada permutacijom redaka ili stupaca to postižemo a 22 ¹ 0. Ako je element a 22 ¹ 0 (i imamo a 22 = –1 ¹ 0), tada ćemo množenjem drugog retka odgovarajućim brojevima i zbrajanjem s ostalim redovima osigurati da svi elementi drugog stupca (osim a 22) bile jednake nuli.

3. Ako se u procesu transformacije dobiju retci (stupci) koji se u potpunosti sastoje od nula, tada ih odbacujemo. U našem primjeru odbacit ćemo retke 3 i 4:

Posljednja matrica ima stepenasti oblik i sadrži dva reda. Oni su linearno neovisni, stoga je rang matrice 2.

§ četiri. Determinante prvog, drugog i trećeg reda

Među raznolikošću matrica, kvadratne matrice su odvojeno izdvojene. Ova vrsta matrice je dobra jer:

1. Matrice identiteta su kvadratne.

2. Možete množiti i zbrajati bilo koje kvadratne matrice istog reda i dobit ćete matricu istog reda.

3. Kvadratne matrice mogu se podići na potenciju.

Također, samo kvadratne matrice mogu imati determinantu.

Matrična determinanta je poseban broj izračunat prema nekom pravilu. Matrična determinanta ALI označeno:

Ili ravnim zagradama: ,

Ili veliko grčko slovo "delta": Δ( A),

Ili simbol "odrednica": det ( A).

Determinanta matrice prvog reda ALI= (a 11) ili determinanta prvog reda, je broj jednak elementu matrice:

∆1 = =a 11

Determinanta matrice drugog reda ili determinanta drugog reda

Primjer:

Determinanta matrice trećeg reda ili determinanta trećeg reda, je broj koji se izračunava po formuli:

Determinanta trećeg reda može se izračunati pomoću Sarrusovo pravilo .

Sarrusovo pravilo. Prva dva stupca označena su determinantom trećeg reda s desne strane i sa predznakom plus (+) uzimaju zbroj umnožaka triju elemenata koji se nalaze na glavnoj dijagonali determinante i na paraleli "pravih linija". na glavnu dijagonalu, sa znakom minus (-) uzimaju zbroj umnožaka elemenata koji se nalaze na drugoj dijagonali i na njoj paralelnim "pravcima".

Primjer:

Lako je vidjeti da se broj članova u determinanti povećava s njezinim redoslijedom. Općenito, u odrednici P reda, broj članova je 1 2 3 . . . P = P!.

Provjerimo: za Δ 1 broj članova je jednak 1! = 1,

za Δ 2 broj članova je 2! = 1 2 = 2,

za Δ 3 broj članova je 3! = 1 2 3 = 6.

Slijedi da je za determinantu 4. reda broj članova 4! = 1 2 3 4 = 24, što znači da je izračun takve determinante prilično naporan, a o determinantama višeg reda da i ne govorimo. S obzirom na to, računanje determinanti velikih reda nastoje svesti na izračunavanje determinanti drugog ili trećeg reda.

§ 5. Izračun determinanti velikih naloga

Uvedimo nekoliko pojmova.

Neka je dana kvadratna matrica A n-ti red:

Minor M ij element a ij se naziva determinanta ( P– 1. red dobiven iz matrice ALI iscrtavanje ja-th line i j-ti stupac.

Na primjer, element minor a 12 matrica trećeg reda bit će:

Algebarsko zbrajanje ALI ij element a ij je njegov minor, uzet sa predznakom (−1) ja + j:

ALI ij = (−1) ja + jM i J

Drugim riječima, ALI ij = M ij ako ja+j Parni broj,

ALI ij = − M ij ako ja+j neparan broj.

Primjer. Naći algebarske komplemente elemenata drugog retka matrice

Riješenje.

Uz pomoć algebarskih komplemenata mogu se izračunati determinante velikih redova, na temelju Laplaceovog teorema.

Laplaceov teorem. Determinanta kvadratne matrice jednaka je zbroju proizvoda elemenata bilo kojeg od njegovih redaka (stupaca) i njihovih algebarskih komplemenata:

– dekompozicija na i-tom redu;

( je ekspanzija u j-tom stupcu).

Primjer. Izračunajte determinantu matrice dekompozicija na prvom redu.

Riješenje.

Dakle, determinanta bilo kojeg reda može se svesti na izračun nekoliko determinanti manjeg reda. Očito je da je za ekspanziju zgodno odabrati red ili stupac koji sadrži što više nula.

Razmotrimo još jedan primjer.

Primjer. Izračunajte determinantu trokutaste matrice

Riješenje.

Kužim to determinanta trokutaste matrice jednaka je umnošku elemenata njezine glavne dijagonale .

Ovaj važan zaključak olakšava izračunavanje determinante bilo koje trokutaste matrice. To je tim korisnije jer se po potrebi svaka determinanta može svesti na trokutasti oblik. U ovom slučaju koriste se neka svojstva determinanti.

Primjena

Pojam determinante P red općenito.

Općenito, može se dati stroga definicija za determinantu matrice P reda, no za to je potrebno uvesti niz pojmova.

permutacija brojevi 1, 2, ..., n naziva se svaki raspored tih brojeva u određenom redoslijedu. U elementarnoj algebri dokazuje se da je broj svih permutacija iz kojih se može formirati n brojeva je 12...n = n!. Na primjer, tri broja 1, 2, 3 mogu činiti 3! = 6 permutacija: 123, 132, 312, 321, 231, 213.

Kažu da u danoj permutaciji broja ja i j konstituirati inverzija(poremećaj) ako ja> j, ali ja stoji u ovoj permutaciji prije j, odnosno ako je veći broj lijevo od manjeg.

Permutacija se zove čak(ili neparan) ako je ukupan broj inverzija paran (neparan).

Operacija pomoću koje se prelazi s jedne permutacije na drugu, sastavljenu od istih n zove se brojevi zamjena n ti stupanj.

Zamjena koja pretvara jednu permutaciju u drugu piše se u dva retka u zajedničkim zagradama, a brojevi koji zauzimaju ista mjesta u permutacijama koje se razmatraju nazivaju se odgovarajućim i pišu se jedan ispod drugog. Na primjer, simbol

označava permutaciju u kojoj 3 ide u 4, 1 u 2, 2 u 1, 4 u 3. Permutacija se naziva parnom (ili neparnom) ako je ukupni broj inverzija u oba reda zamjene paran (neparan). Svaka zamjena n stupanj se može napisati kao

oni. s prirodnim rasporedom brojeva u gornjem redu.

Neka nam je dana kvadratna matrica reda n

Razmotrite sve moguće proizvode n elementi ove matrice, uzeti jedan i samo jedan iz svakog retka i svakog stupca, tj. djela oblika:

gdje indeksi q 1 , q 2 ,..., q n napraviti neku permutaciju brojeva
1, 2,..., n. Broj takvih proizvoda jednak je broju različitih permutacija iz n likovi, tj. jednaki n!. Radni znak , jednako (–1) q, gdje q je broj inverzija u permutaciji drugih indeksa elemenata.

determinanta n-ti red naziva se algebarski zbroj svih mogućih proizvoda preko n elementi matrice, uzeti jedan i samo jedan iz svakog retka i svakog stupca, tj. djela oblika: . Ujedno i znak djela jednako (–1) q, gdje q je broj inverzija u permutaciji drugih indeksa elemenata.

Linearna algebra

Promotrimo matricu A veličine .

A=
Odaberite k redaka i k stupaca u njemu (
).

Definicija 26:Minor K-ti red matrice A je determinanta kvadratne matrice koja se dobiva iz zadane selekcijom u njoj.

k redaka i k stupaca.

Definicija 27:rang matrica se naziva najveći od nultih redova svojih minora, r(A).

Definicija 28: Poziva se maloljetnik čiji je poredak isti kao i rang osnovni mol.

Izjava:

1. Rang se izražava kao cijeli broj.(
)

2.r=0,
kada je A nula.

Elementarne transformacije matrica.

Elementarne transformacije matrica uključuju sljedeće:

1) množenje svih elemenata bilo kojeg retka (stupca) matrice istim brojem.

2) dodavanje elementima bilo kojeg retka (stupca) matrice odgovarajućih elemenata drugog retka (stupca) pomnoženih s istim brojem;

3) permutacija redaka (stupaca) matrice;

4) odbacivanje nultog retka (stupca);

5) zamjena redaka matrice odgovarajućim stupcima.

Definicija 29: Matrice dobivene jedna iz druge, elementarnim transformacijama, nazivaju se ekvivalentne matrice, označene sa “~“

Glavno svojstvo ekvivalentnih matrica: Rangovi ekvivalentnih matrica su jednaki.

Primjer 18: Izračunajte r(A),

Riješenje: Pomnožite prvi red korak po korak s (-4)(-2)

(-7), a zatim dodajte u drugi, treći i četvrti red.

zamijenite drugi i četvrti red
pomnožite drugi red s (-2) i dodajte četvrtom redu; dodajte drugi i treći red.

dodajte treći i četvrti red.

~
odbaciti nulti red

~
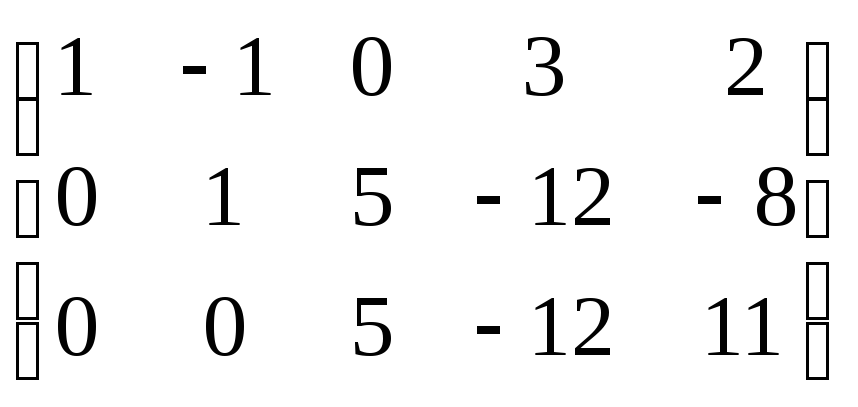r(A)=3
rang izvorne matrice

jednako tri.

Definicija 30: Matricu A nazivamo stepenastom matricom ako su svi elementi glavne dijagonale 0, a elementi ispod glavne dijagonale su nula.

Rečenica:

1) rang matrice koraka jednak je broju njezinih redaka;

2) svaka se matrica može svesti na oblik koraka uz pomoć elementarnih transformacija.

Primjer 19: Pri kojim vrijednostima  matrice
ima rang jednak jedan?

Riješenje: Rang je jednak jedan ako je determinanta drugog reda jednaka nuli, tj.

§6. Sustavi linearnih jednadžbi općeg oblika.

pogled sustav
---(9) naziva se sustav općeg oblika.

Definicija 31: Za dva sustava kažemo da su ekvivalentna (ekvivalentna) ako je svako rješenje prvog sustava rješenje drugog i obrnuto.

U sustavu (1) matrica A=
nazvat ćemo glavnom matricom sustava, i =
sustav proširene matrice

Teorema. Kronecker-Cappelli

Da bi sustav (9) bio konzistentan, potrebno je i dovoljno da rang glavne matrice sustava bude jednak rangu proširene matrice, tj. r(A)=r( )

Teorem 1. Ako je rang matrice zajedničkog sustava jednak broju nepoznanica, tada sustav ima jedinstveno rješenje.

Teorem 2. Ako je rang matrice zajedničkog sustava manji od broja nepoznanica, tada sustav ima beskonačan broj rješenja.

Pravilo za rješavanje proizvoljnog sustava linearnih jednadžbi:

1) pronaći rangove glavne i proširene matrice sustava. Ako a
, onda je sustav nedosljedan.

2) Ako
=r, tada je sustav konzistentan. Pronađite neki osnovni minor reda r. Osnovni ćemo nazvati minor, na temelju kojeg je određen rang matrice.

Nepoznanice čiji koeficijenti ulaze u osnovni minor nazivamo glavnim (bazičnim) i lijevo lijevo, dok preostale nepoznanice nazivamo slobodnima i prenosimo na desnu stranu jednadžbe.

3) Odredite izraze glavnih nepoznanica preko slobodnih. Dobiveno je opće rješenje sustava.

Primjer 20: Istražite sustav i, u slučaju njegove kompatibilnosti, pronađite jedinstveno ili opće rješenje