Η τμηματικά γραμμική συνάρτηση δίνεται από τον τύπο find in. X=1 - σημείο αλλαγής τύπων

7
Μάθημα Άλγεβρας στην τάξη 9Α δάσκαλος Mikitchuk Zh.N. MOU "Γυμνάσιο Νο. 23"19.03.07Θέμα μαθήματος: "Προκαθορισμένες συναρτήσεις" Στόχοι:

κουλτούρα του λόγου

Ως αποτέλεσμα της γενίκευσης του θέματος, οι μαθητές θα πρέπει ξέρω:

δεδομένη λειτουργία

έχω την δυνατότητα να:

να δημιουργήσετε ένα γράφημα μιας τμηματικά δεδομένης συνάρτησης. διαβάστε γράφημα? ορίστε τη συνάρτηση αναλυτικά σύμφωνα με το γράφημα.

Κατά τη διάρκεια των μαθημάτων

Ι. Οργανωτική-ψυχολογική στιγμή. Ας ξεκινήσουμε το μάθημά μας με τα λόγια του D.K. Fadeev "Όποια εργασία κι αν λύσετε, στο τέλος θα έχετε μια χαρούμενη στιγμή - ένα χαρούμενο συναίσθημα επιτυχίας, ενισχύοντας την πίστη στις δικές σας δυνάμεις. Αφήστε αυτά τα λόγια στο μάθημά μας να βρουν πραγματική επιβεβαίωση. II. Έλεγχος εργασιών για το σπίτι. Ας ξεκινήσουμε το μάθημα ως συνήθως με τον έλεγχο d / z. - Επαναλάβετε τον ορισμό μιας τμηματικής συνάρτησης και ένα σχέδιο για τη μελέτη συναρτήσεων.1). Πάνω στο γραφείοαπεικονίστε τις γραφικές παραστάσεις των τμηματικών συναρτήσεων που εφευρέσατε (Εικ. 1,2,3)2). Καρτέλλες.#1. Τακτοποιήστε τη σειρά μελέτης των ιδιοτήτων των συναρτήσεων:

μικρότερη τιμή

Αρ. 2. Σχεδιάστε σχηματικά γραφήματα συναρτήσεων:

Α) y = kx + b, k0; Β) y = kx, k0;

Γ) y = , k0.

3).προφορική εργασία . - 2 λεπτά

Τι είναι η τμηματική συνάρτηση;Μια τμηματική συνάρτηση είναι μια συνάρτηση που ορίζεται διαφορετικούς τύπουςσε διαφορετικά διαστήματα.

Από ποιες συναρτήσεις αποτελούνται οι τμηματικές συναρτήσεις που φαίνονται στα Σχ. 1,2,3; Ποια άλλα ονόματα συναρτήσεων γνωρίζετε; Πώς ονομάζονται οι γραφικές παραστάσεις των αντίστοιχων συναρτήσεων; Είναι το γράφημα οποιασδήποτε συνάρτησης, το σχήμα που φαίνεται στο Σχ. 4; Γιατί;Απάντηση:όχι επειδή εξ ορισμού μιας συνάρτησης, κάθε τιμή της ανεξάρτητης μεταβλητής x σχετίζεται με μία μόνο τιμή της εξαρτημένης μεταβλητής y. 4) Αυτοέλεγχος - 3 minΑπό τα προτεινόμενα γραφήματα και τους αντίστοιχους τύπους που ορίζουν τις συναρτήσεις, επιλέξτε τις σωστές. Από τα ληφθέντα γράμματα των απαντήσεων, φτιάξτε μια γνωστή λέξη. Απάντηση: ΓΡΑΦΗΜΑ Πού στη ζωή, στην επιστήμη, στην καθημερινή ζωή συναντάμε ακόμα τη λέξη ΓΡΑΦΗΜΑ; - Γράφημα της εξάρτησης της μάζας από τον όγκο, - όγκος από την πίεση, - ωράριο λειτουργίας, - πρόγραμμα τρένων, όγκος εργοστασιακή παραγωγήστην περιοχή του Σαράτοφ την περίοδο από το 1980 έως το 2002 .. Σύμφωνα με αυτό το γράφημα, μπορείτε να παρακολουθήσετε την πτώση και την ανάπτυξη της παραγωγής σε μεμονωμένα έτη. - Πείτε μου, το γράφημα της συνάρτησης που παρέχει αυτές τις πληροφορίες. Απάντηση: τμηματική λειτουργία.III. Το μήνυμα του θέματος, ο σκοπός του μαθήματος. Θέμα μαθήματος:"Προκαθορισμένες συναρτήσεις" Στόχος:- στο παράδειγμα μιας τμηματικά δεδομένης συνάρτησης, θυμηθείτε το σχέδιο για τη μελέτη των συναρτήσεων.

επαναλάβετε τα βήματα της κατασκευής μιας τμηματικά δεδομένης συνάρτησης. εφαρμόζουν γενικευμένες γνώσεις στην επίλυση μη τυπικών προβλημάτων.IV. Ενημέρωση γνώσεων που έχουν αποκτηθεί προηγουμένως. Η έννοια της συνάρτησης μας πρωτογνώρισε στην 7η δημοτικού όταν μελετούσαμε γραμμική εξάρτηση. Από την άποψη της μοντελοποίησης πραγματικών διαδικασιών, αυτή η εξάρτηση αντιστοιχεί σε ομοιόμορφες διαδικασίες Παράδειγμα: Κίνηση πεζών με σταθερή ταχύτητασε χρόνο τ. Τύπος: s \u003d vt, γράφημα - ευθύγραμμα τμήματα, που βρίσκονται στο τέταρτο I.
Το κύριο θέμα της 8ης τάξης - τετραγωνική λειτουργία, προσομοίωση ομοιόμορφα επιταχυνόμενων διεργασιών Παράδειγμα: ο τύπος που μελετήσατε στην 9η τάξη για τον προσδιορισμό της αντίστασης ενός θερμαινόμενου λαμπτήρα (R) σε σταθερή ισχύ (P) και μεταβαλλόμενη τάση (U). Τύπος R =

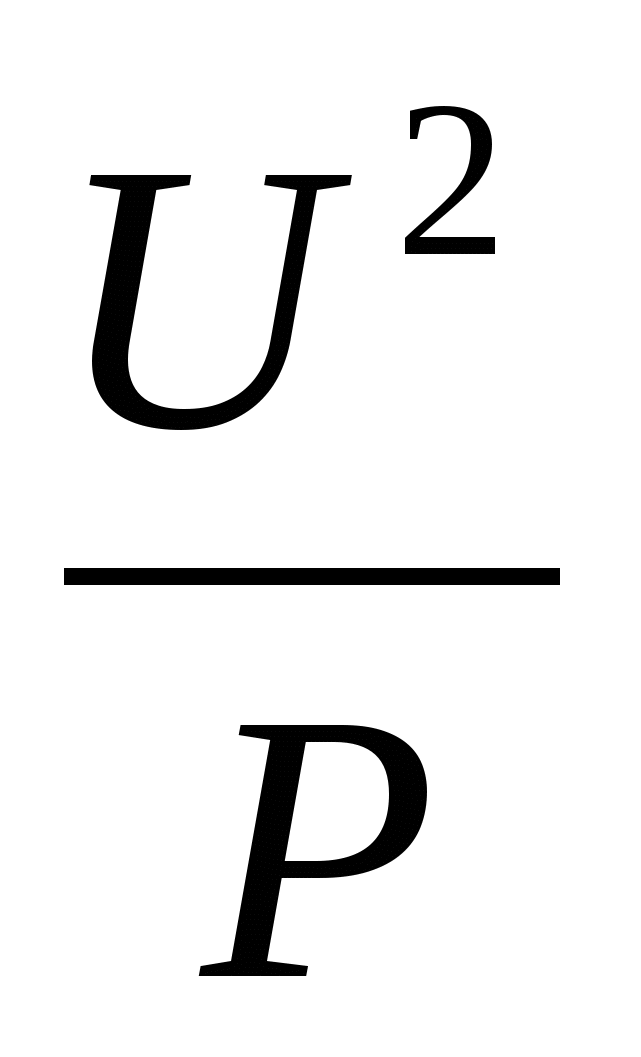, το γράφημα είναι κλάδος παραβολής, που βρίσκεται στο πρώτο τέταρτο.
Για τρία χρόνιαΟι γνώσεις μας για τις συναρτήσεις εμπλουτίστηκαν, ο αριθμός των συναρτήσεων που μελετήθηκαν αυξήθηκε και το σύνολο των εργασιών για την επίλυση των οποίων έπρεπε να καταφύγουμε σε γραφήματα αναπληρώθηκε. Ονομάστε αυτούς τους τύπους εργασιών ... - λύση εξισώσεων?- επίλυση συστημάτων εξισώσεων.- επίλυση ανισοτήτων.- μελέτη των ιδιοτήτων των συναρτήσεων.V. Προετοιμασία των μαθητών για γενικευτικές δραστηριότητες. Ας θυμηθούμε ένα από τα είδη εργασιών, δηλαδή τη μελέτη των ιδιοτήτων των συναρτήσεων ή την ανάγνωση ενός γραφήματος. Ας στραφούμε στο σχολικό βιβλίο. Σελίδα 65 εικ.20α από #250. Ασκηση:διαβάστε το γράφημα της συνάρτησης. Η διαδικασία για την εξέταση μιας συνάρτησης είναι μπροστά μας. 1. τομέας ορισμού - (-∞; +∞)2. άρτιος, περιττός - ούτε ζυγός ούτε περιττός3. μονοτονία - αυξάνεται [-3; +∞), φθίνουσα[-5;-3], σταθερά (-∞; -5];4. περιορισμένο - περιορισμένο από κάτω5. η μεγαλύτερη και η μικρότερη τιμή της συνάρτησης - y naim = 0, y naib - δεν υπάρχει.6. συνέχεια - συνεχής σε ολόκληρο το πεδίο ορισμού.7. εύρος τιμών - , κυρτό και πάνω και κάτω (-∞; -5] και [-2; +∞).VI. Αναπαραγωγή της γνώσης σε νέο επίπεδο. Γνωρίζετε ότι η σχεδίαση και η έρευνα γραφημάτων τμηματικές λειτουργίες, εξετάζονται στο δεύτερο μέρος της εξέτασης της άλγεβρας στην ενότητα συναρτήσεων και αξιολογούνται με 4 και 6 μονάδες. Ας στραφούμε στη συλλογή εργασιών. Σελίδα 119 - Αρ. 4.19-1). Λύση: 1). y \u003d - x, - τετραγωνική συνάρτηση, γράφημα - παραβολή, διακλαδίζεται προς τα κάτω (a \u003d -1, a 0) . x -2 -1 0 1 2 y -4 -1 0 1 4 2) y \u003d 3x - 10, - γραμμική συνάρτηση, το γράφημα είναι μια ευθεία γραμμήΑς φτιάξουμε έναν πίνακα με μερικές τιμέςx 3

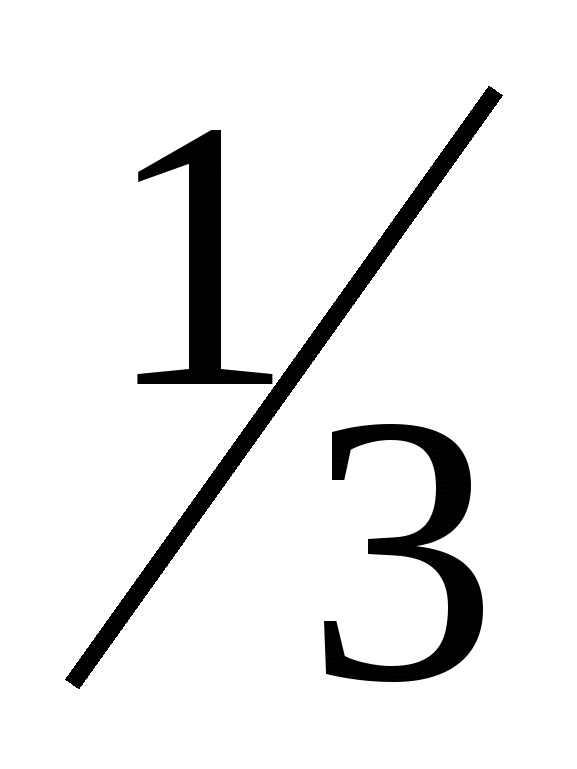3 y 0 -1 3) y \u003d -3x -10, - μια γραμμική συνάρτηση, το γράφημα είναι μια ευθεία γραμμήΑς φτιάξουμε έναν πίνακα με μερικές τιμές x -3 -3 y 0 -1 4) Κατασκευάζουμε γραφήματα συναρτήσεων σε ένα σύστημα συντεταγμένων και επιλέγουμε τμήματα των γραφημάτων σε δεδομένα διαστήματα.
Ας βρούμε από το γράφημα για ποιες τιμές του x οι τιμές της συνάρτησης είναι μη αρνητικές.Απάντηση: f(x)  0 για x = 0 και για

 3 VII. Εργασία σε μη τυπικές εργασίες. Αρ. 4.29-1), σ. 121.Λύση: 1) Απευθείας (αριστερά) y \u003dΤο kx + b διέρχεται από τα σημεία (-4;0) και (-2;2). Άρα -4 k + b = 0, -2 k + b = 2;

k \u003d 1, b \u003d 4, y \u003d x + 4. Απάντηση: x +4 αν x -2 y = αν -2  x 3 £ 3 αν x  3
VIII.Έλεγχος γνώσης. Λοιπόν, ας συνοψίσουμε λίγο. Τι επαναλάβαμε στο μάθημα Σχέδιο έρευνας συνάρτησης, βήματα για τη χάραξη τμηματικού γραφήματος συνάρτησης, καθορισμός μιας συνάρτησης αναλυτικά. Ας ελέγξουμε πώς μάθατε αυτό το υλικό. Δοκιμή για "4" - "5", "3" I επιλογή Αρ. U

2 1 -1 -1 1 X

D(f) = , κυρτό και πάνω και κάτω κατά , κυρτό πάνω και κάτω κατά , μειώνεται κατά ________ Περιορίζεται κατά ____________ τουλάχιστον δεν υπάρχει, στο μέγιστο =_____ Συνεχές σε ολόκληρο τον τομέα του ορισμού E(f) = __________ κάτω και πάνω από ολόκληρο τον τομέα ορισμού

Πίσω μπροστά

Προσοχή! Η προεπισκόπηση της διαφάνειας είναι μόνο για ενημερωτικούς σκοπούς και ενδέχεται να μην αντιπροσωπεύει την πλήρη έκταση της παρουσίασης. Αν ενδιαφέρεσαι αυτή η δουλειάπαρακαλώ κατεβάστε την πλήρη έκδοση.

Σχολικό βιβλίο:Άλγεβρα τάξη 8, επιμέλεια A. G. Mordkovich.

Τύπος μαθήματος:Ανακάλυψη νέας γνώσης.

Στόχοι:

για τον δάσκαλο Οι στόχοι καθορίζονται σε κάθε στάδιο του μαθήματος.

για μαθητή:

Προσωπικοί στόχοι:

Μάθετε να εκφράζετε με σαφήνεια, ακρίβεια, ικανοποίηση τις σκέψεις σας προφορικά και Γραφήκατανοήσει το νόημα της εργασίας.
Μάθετε να εφαρμόζετε τις γνώσεις και τις δεξιότητες που έχετε αποκτήσει στην επίλυση νέων προβλημάτων.
Μάθετε να ελέγχουν τη διαδικασία και το αποτέλεσμα των δραστηριοτήτων τους.

Μετα-στόχοι:

Στη γνωστική δραστηριότητα:

Ανάπτυξη λογική σκέψηκαι ομιλία, η ικανότητα να τεκμηριώνει κανείς λογικά τις κρίσεις του, να πραγματοποιεί απλές συστηματοποιήσεις.
Μάθετε να κάνετε υποθέσεις επίλυση προβλήματοςκατανοούν την ανάγκη για επαλήθευση τους·
Εφαρμόστε τη γνώση σε τυπική κατάστασημάθετε πώς να ολοκληρώνετε εργασίες ανεξάρτητα.
Να πραγματοποιήσει τη μεταφορά γνώσης σε μια αλλαγμένη κατάσταση, να δει την εργασία στο πλαίσιο μιας προβληματικής κατάστασης.

Στις δραστηριότητες ενημέρωσης και επικοινωνίας:

Μάθετε να διεξάγετε διάλογο, αναγνωρίζετε το δικαίωμα σε διαφορετική γνώμη.

Σε αναστοχαστική δραστηριότητα:

Μάθετε να προβλέπετε πιθανές συνέπειεςτις ενέργειές τους·
Μάθετε να εξαλείφετε τις αιτίες των δυσκολιών.

Αντικειμενικοί στόχοι:

Μάθετε τι είναι μια τμηματικά δεδομένη συνάρτηση.
Μάθετε να ορίζετε μια τμηματικά δεδομένη συνάρτηση αναλυτικά σύμφωνα με το γράφημά της.

Κατά τη διάρκεια των μαθημάτων

1. Αυτοδιάθεση να μαθησιακές δραστηριότητες

Σκοπός της σκηνής:

να περιλαμβάνει μαθητές σε μαθησιακές δραστηριότητες·
προσδιορίστε το περιεχόμενο του μαθήματος: συνεχίζουμε να επαναλαμβάνουμε το θέμα των αριθμητικών συναρτήσεων.

Οργάνωση εκπαιδευτική διαδικασίαστο βήμα 1:

Τ: Τι κάναμε στα προηγούμενα μαθήματα;

Δ: Επαναλάβαμε το θέμα των αριθμητικών συναρτήσεων.

Τ: Σήμερα θα συνεχίσουμε να επαναλαμβάνουμε το θέμα των προηγούμενων μαθημάτων, και επίσης σήμερα θα πρέπει να μάθουμε τι νέα πράγματα μπορούμε να μάθουμε για αυτό το θέμα.

2. Επικαιροποίηση γνώσεων και διόρθωση δυσκολιών σε δραστηριότητες

Σκοπός της σκηνής:

εκσυγχρονίζω εκπαιδευτικό περιεχόμενο, απαραίτητο και επαρκές για την αντίληψη νέου υλικού: θυμηθείτε τους τύπους αριθμητικές συναρτήσεις, τις ιδιότητες και τις μεθόδους κατασκευής τους.
εκσυγχρονίζω νοητικές λειτουργίεςαπαραίτητο και επαρκές για την αντίληψη του νέου υλικού: σύγκριση, ανάλυση, γενίκευση.
για να διορθώσετε μια ατομική δυσκολία στη δραστηριότητα, επιδεικνύοντας σε μια προσωπική σημαντικό επίπεδοανεπάρκεια υπάρχουσας γνώσης: η εργασία μιας τμηματικά δεδομένης λειτουργίας αναλυτικά, καθώς και η κατασκευή του γραφήματος της.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 2:

T: Υπάρχουν πέντε αριθμητικές συναρτήσεις στη διαφάνεια. Προσδιορίστε το είδος τους.

1) κλασματικό-ορθολογικό?

2) τετράγωνο?

3) παράλογο?

4) λειτουργία με μονάδα?

5) δύναμη.

Τ: Ονομάστε τους τύπους που τους αντιστοιχούν.

3) ;

4) ;

Τ: Ας συζητήσουμε τι ρόλο παίζει κάθε συντελεστής σε αυτούς τους τύπους;

D: Οι μεταβλητές "l" και "m" είναι υπεύθυνες για τη μετατόπιση των γραφημάτων αυτών των συναρτήσεων προς τα αριστερά - δεξιά και πάνω - κάτω, αντίστοιχα, ο συντελεστής "k" στην πρώτη συνάρτηση καθορίζει τη θέση των κλάδων της υπερβολής: k >0 - οι κλάδοι είναι στο Ι και ΙΙΙ τρίμηνο, κ< 0 - во II и IV четвертях, а коэффициент “а” определяет направление ветвей параболы: а>0 - τα κλαδιά κατευθύνονται προς τα πάνω και< 0 - вниз).

2. διαφάνεια 2

U: Ορίστε αναλυτικά τις συναρτήσεις των οποίων τα γραφήματα φαίνονται στα σχήματα. (θεωρώντας ότι κινούνται y=x 2). Ο δάσκαλος γράφει τις απαντήσεις στον πίνακα.

Δ: 1) );

2);

3. διαφάνεια 3

U: Ορίστε αναλυτικά τις συναρτήσεις των οποίων τα γραφήματα φαίνονται στα σχήματα. (θεωρώντας ότι κινούνται). Ο δάσκαλος γράφει τις απαντήσεις στον πίνακα.

4. διαφάνεια 4

U: Χρησιμοποιώντας τα προηγούμενα αποτελέσματα, ορίστε αναλυτικά τις συναρτήσεις των οποίων τα γραφήματα φαίνονται στα σχήματα.

3. Εντοπισμός των αιτιών των δυσκολιών και καθορισμός του στόχου της δραστηριότητας

Σκοπός της σκηνής:

οργανώνω επικοινωνιακή αλληλεπίδραση, κατά την οποία εντοπίζεται και διορθώνεται η διακριτική ιδιότητα της εργασίας που προκάλεσε δυσκολία στην εκπαιδευτική δραστηριότητα.
συμφωνούν για το σκοπό και το θέμα του μαθήματος.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 3:

Ε: Τι σας προκαλεί πρόβλημα;

Δ: Κομμάτια γραφημάτων παρέχονται στην οθόνη.

Τ: Ποιος είναι ο σκοπός του μαθήματος μας;

Δ: Για να μάθετε πώς να ορίζετε αναλυτικά κομμάτια συναρτήσεων.

Τ: Αναφέρετε το θέμα του μαθήματος. (Τα παιδιά προσπαθούν να διατυπώσουν μόνα τους το θέμα. Ο δάσκαλος το διευκρινίζει. Θέμα: Τεμαχική συνάρτηση.)

4. Χτίζοντας ένα έργο για να βγούμε από μια δυσκολία

Σκοπός της σκηνής:

οργανώστε την επικοινωνιακή αλληλεπίδραση για να δημιουργήσετε ένα νέο τρόπος δράσηςεξαλείφοντας την αιτία της δυσκολίας που εντοπίστηκε·
διορθώσετε νέος τρόποςΕνέργειες.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 4:

Τ: Ας διαβάσουμε ξανά προσεκτικά την εργασία. Ποια αποτελέσματα ζητούνται να χρησιμοποιηθούν ως βοήθημα;

Δ: Προηγούμενο, δηλ. αυτά που είναι γραμμένα στον πίνακα.

Τ: Ίσως αυτοί οι τύποι είναι ήδη η απάντηση σε αυτό το έργο;

Δ: Όχι γιατί. αυτοί οι τύποι ορίζουν το τετραγωνικό και λογική λειτουργία, και τα κομμάτια τους εμφανίζονται στη διαφάνεια.

Τ: Ας συζητήσουμε ποια διαστήματα του άξονα x αντιστοιχούν στα κομμάτια της πρώτης συνάρτησης;

U: Τότε ο αναλυτικός τρόπος καθορισμού της πρώτης συνάρτησης μοιάζει με: αν

Ε: Τι πρέπει να γίνει για να ολοκληρωθεί μια παρόμοια εργασία;

Δ: Γράψτε τον τύπο και προσδιορίστε ποια διαστήματα του άξονα x αντιστοιχούν στα κομμάτια αυτής της συνάρτησης.

5. Πρωτογενής εμπέδωση στον εξωτερικό λόγο

Σκοπός της σκηνής:

να διορθώσετε το μελετώμενο εκπαιδευτικό περιεχόμενο στον εξωτερικό λόγο.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 5:

7. Ένταξη στο σύστημα γνώσης και επανάληψη

Σκοπός της σκηνής:

εξασκηθείτε στις δεξιότητες χρήσης νέου περιεχομένου σε συνδυασμό με προηγουμένως μαθημένο.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 7:

Υ: Ορίστε αναλυτικά τη συνάρτηση, η γραφική παράσταση της οποίας φαίνεται στο σχήμα.

8. Αντανάκλαση δραστηριοτήτων στο μάθημα

Σκοπός της σκηνής:

να διορθώσετε το νέο περιεχόμενο που μάθαμε στο μάθημα.
αξιολογούν τις δικές τους δραστηριότητες στην τάξη.
ευχαριστεί τους συμμαθητές που βοήθησαν να επιτευχθεί το αποτέλεσμα του μαθήματος.
διορθώστε τις ανεπίλυτες δυσκολίες ως κατευθύνσεις για μελλοντικές μαθησιακές δραστηριότητες.
συζητήστε και καταγράψτε τις εργασίες για το σπίτι.

Οργάνωση της εκπαιδευτικής διαδικασίας στο στάδιο 8:

Τ: Τι μάθαμε σήμερα στην τάξη;

Δ: Με μια τμηματικά δεδομένη συνάρτηση.

Τ: Τι δουλειά μάθαμε να κάνουμε σήμερα;

Δ: Ρωτήστε αυτό το είδοςλειτουργεί αναλυτικά.

Τ: Σηκώστε το χέρι σας, ποιος κατάλαβε το θέμα του σημερινού μαθήματος; (Συζητήστε τα προβλήματα με τα υπόλοιπα παιδιά).

Εργασία για το σπίτι

Νο. 21.12(a, c);
Νο. 21.13(a, c);
№22.41;
№22.44.

Οι πραγματικές διεργασίες που συμβαίνουν στη φύση μπορούν να περιγραφούν χρησιμοποιώντας συναρτήσεις. Έτσι, μπορούμε να διακρίνουμε δύο κύριους τύπους ροής διεργασιών που είναι αντίθετες μεταξύ τους - αυτοί είναι βαθμιαίοςή συνεχήςκαι σπασμωδικός(ένα παράδειγμα θα ήταν μια μπάλα που πέφτει και ριμπάουντ). Αν όμως υπάρχουν ασυνεχείς διαδικασίες, τότε υπάρχουν ειδικά μέσα για την περιγραφή τους. Για το σκοπό αυτό, τίθενται σε κυκλοφορία συναρτήσεις που έχουν ασυνέχειες, άλματα, δηλαδή σε διαφορετικά μέρη της αριθμητικής γραμμής, η συνάρτηση συμπεριφέρεται σύμφωνα με διαφορετικούς νόμους και, κατά συνέπεια, δίνεται με διαφορετικούς τύπους. Εισάγονται οι έννοιες των σημείων ασυνέχειας και της αφαιρούμενης ασυνέχειας.

Σίγουρα έχετε ήδη δει συναρτήσεις που ορίζονται από διάφορους τύπους, ανάλογα με τις τιμές του ορίσματος, για παράδειγμα:

y \u003d (x - 3, με x\u003e -3;
(-(x - 3), για x< -3.

Τέτοιες συναρτήσεις ονομάζονται τμηματικάή τμηματικά. Ας καλέσουμε τμήματα της αριθμητικής γραμμής με διαφορετικούς τύπους εργασίας συστατικά στοιχείατομέα. Η ένωση όλων των συστατικών είναι ο τομέας της τμηματικής συνάρτησης. Τα σημεία που διαιρούν το πεδίο ορισμού μιας συνάρτησης σε στοιχεία ονομάζονται οριακά σημεία. Οι τύποι που ορίζουν μια τμηματική συνάρτηση σε κάθε συστατικό πεδίο ορισμού καλούνται εισερχόμενες λειτουργίες. Οι γραφικές παραστάσεις των τμηματικά δεδομένων συναρτήσεων λαμβάνονται ως αποτέλεσμα του συνδυασμού τμημάτων γραφημάτων που είναι κατασκευασμένα σε καθένα από τα διαστήματα διαμερισμάτων.

Γυμνάσια.

Κατασκευάστε γραφήματα τμηματικών συναρτήσεων:

1) (-3, με -4 ≤ x< 0,
f(x) = (0, για x = 0,
(1, στο 0< x ≤ 5.

Η γραφική παράσταση της πρώτης συνάρτησης είναι μια ευθεία γραμμή που διέρχεται από το σημείο y = -3. Ξεκινά από το σημείο με συντεταγμένες (-4; -3), πηγαίνει παράλληλα με τον άξονα της τετμημένης στο σημείο με συντεταγμένες (0; -3). Η γραφική παράσταση της δεύτερης συνάρτησης είναι ένα σημείο με συντεταγμένες (0; 0). Το τρίτο γράφημα είναι παρόμοιο με το πρώτο - είναι μια ευθεία γραμμή που διέρχεται από το σημείο y \u003d 1, αλλά ήδη στην περιοχή από το 0 έως το 5 κατά μήκος του άξονα Ox.

Απάντηση: εικόνα 1.

2) (3 αν x ≤ -4,
f(x) = (|x 2 - 4|x| + 3| εάν -4< x ≤ 4,
(3 - (x - 4) 2 αν x > 4.

Εξετάστε κάθε συνάρτηση ξεχωριστά και σχεδιάστε το γράφημά της.

Άρα, η f(x) = 3 είναι μια ευθεία παράλληλη προς τον άξονα Ox, αλλά χρειάζεται να σχεδιαστεί μόνο στην περιοχή όπου x ≤ -4.

Γράφημα της συνάρτησης f(x) = |x 2 – 4|x| + 3| μπορεί να ληφθεί από την παραβολή y \u003d x 2 - 4x + 3. Έχοντας δημιουργήσει το γράφημά του, το τμήμα του σχήματος που βρίσκεται πάνω από τον άξονα Ox πρέπει να μείνει αμετάβλητο και το τμήμα που βρίσκεται κάτω από τον άξονα της τετμημένης πρέπει να εμφανίζεται συμμετρικά σε σχέση με τον άξονα Ox. Στη συνέχεια εμφανίστε συμμετρικά το τμήμα του γραφήματος όπου
x ≥ 0 για τον άξονα Oy για αρνητικό x. Το γράφημα που προκύπτει ως αποτέλεσμα όλων των μετασχηματισμών παραμένει μόνο στην περιοχή από -4 έως 4 κατά μήκος της τετμημένης.

Η γραφική παράσταση της τρίτης συνάρτησης είναι μια παραβολή, οι κλάδοι της οποίας κατευθύνονται προς τα κάτω και η κορυφή βρίσκεται στο σημείο με τις συντεταγμένες (4; 3). Το σχέδιο απεικονίζεται μόνο στην περιοχή όπου x > 4.

Απάντηση: εικόνα 2.

3) (8 - (x + 6) 2 αν x ≤ -6,
f(x) = (|x 2 – 6|x| + 8| εάν -6 ≤ x< 5,
(3 εάν x ≥ 5.

Η κατασκευή της προτεινόμενης τμηματικά δεδομένης συνάρτησης είναι παρόμοια με την προηγούμενη παράγραφο. Εδώ, τα γραφήματα των δύο πρώτων συναρτήσεων λαμβάνονται από μετασχηματισμούς παραβολής και η γραφική παράσταση της τρίτης είναι μια ευθεία γραμμή παράλληλη προς το Ox.

Απάντηση: εικόνα 3.

4) Να σχεδιάσετε τη συνάρτηση y = x – |x| + (x – 1 – |x|/x) 2 .

Λύση.Το εύρος αυτής της λειτουργίας είναι όλο πραγματικούς αριθμούςεκτός από το μηδέν. Ας ανοίξουμε τη μονάδα. Για να το κάνετε αυτό, εξετάστε δύο περιπτώσεις:

1) Για x > 0, παίρνουμε y = x - x + (x - 1 - 1) 2 = (x - 2) 2 .

2) Για x< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

Έτσι, έχουμε μια τμηματικά δεδομένη συνάρτηση:

y = ((x - 2) 2, για x > 0;
( x 2 + 2x, για x< 0.

Οι γραφικές παραστάσεις και των δύο συναρτήσεων είναι παραβολές, οι κλάδοι των οποίων είναι στραμμένοι προς τα πάνω.

Απάντηση: εικόνα 4.

5) Να σχεδιάσετε τη συνάρτηση y = (x + |x|/x – 1) 2 .

Λύση.

Είναι εύκολο να δούμε ότι το πεδίο ορισμού της συνάρτησης είναι όλοι οι πραγματικοί αριθμοί εκτός από το μηδέν. Μετά την επέκταση της ενότητας, παίρνουμε μια τμηματικά δεδομένη συνάρτηση:

1) Για x > 0, παίρνουμε y = (x + 1 - 1) 2 = x 2 .

2) Για x< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

Ας ξαναγράψουμε.

y \u003d (x 2, για x\u003e 0;
((x – 2) 2 , για x< 0.

Οι γραφικές παραστάσεις αυτών των συναρτήσεων είναι παραβολές.

Απάντηση: εικόνα 5.

6) Υπάρχει συνάρτηση της οποίας το γράφημα είναι επίπεδο συντεταγμένωνΕχει κοινό σημέιομε καμια γραμμη?

Λύση.

Ναι υπάρχει.

Ένα παράδειγμα θα ήταν η συνάρτηση f(x) = x 3 . Πράγματι, η γραφική παράσταση της κυβικής παραβολής τέμνεται με την κατακόρυφη ευθεία x = a στο σημείο (a; a 3). Τώρα ας δοθεί η ευθεία από την εξίσωση y = kx + b. Μετά η εξίσωση
Το x 3 - kx - b \u003d 0 έχει πραγματική ρίζα x 0 (καθώς ένα πολυώνυμο περιττού βαθμού έχει πάντα τουλάχιστον μία πραγματική ρίζα). Επομένως, το γράφημα της συνάρτησης τέμνεται με την ευθεία γραμμή y \u003d kx + b, για παράδειγμα, στο σημείο (x 0; x 0 3).

site, με πλήρη ή μερική αντιγραφή του υλικού, απαιτείται σύνδεσμος στην πηγή.

Αναλυτικός ορισμός συνάρτησης

Δίνεται η συνάρτηση %%y = f(x), x \σε X%%. με σαφή αναλυτικό τρόπο, εάν δοθεί ένας τύπος που υποδεικνύει την ακολουθία των μαθηματικών πράξεων που πρέπει να εκτελεστούν με το όρισμα %%x%% για να ληφθεί η τιμή %%f(x)%% αυτής της συνάρτησης.

Παράδειγμα

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = \sqrt(x), x \geq 0%%.

Έτσι, για παράδειγμα, στη φυσική με ομοιόμορφα επιταχυνόμενη ευθύγραμμη κίνησηη ταχύτητα του σώματος καθορίζεται από τον τύπο %%v = v_0 + a t%%, και τον τύπο για την κίνηση %%s%% του σώματος σε ομοιόμορφη γρήγορη κίνησηστο χρονικό διάστημα από %%0%% έως %%t%% γράφεται ως: %% s = s_0 + v_0 t + \frac(a t^2)(2) %%.

Τμηματικά καθορισμένες συναρτήσεις

Μερικές φορές η υπό εξέταση συνάρτηση μπορεί να οριστεί από διάφορους τύπους που λειτουργούν σε διαφορετικά μέρη του τομέα του ορισμού της, στους οποίους αλλάζει το όρισμα συνάρτησης. Για παράδειγμα: $$ y = \begin(περιπτώσεις) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

Μερικές φορές ονομάζονται συναρτήσεις αυτού του είδους ψηφοφόροςή τμηματικά. Ένα παράδειγμα τέτοιας συνάρτησης είναι %%y = |x|%%

Πεδίο λειτουργίας

Εάν μια συνάρτηση προσδιορίζεται με σαφή αναλυτικό τρόπο χρησιμοποιώντας έναν τύπο, αλλά το εύρος της συνάρτησης με τη μορφή συνόλου %%D%% δεν καθορίζεται, τότε με το %%D%% θα εννοούμε πάντα το σύνολο τιμών του ορίσματος %%x%%, για το οποίο δεδομένης φόρμουλαςέχει το νόημα. Έτσι για τη συνάρτηση %%y = x^2%%, το πεδίο ορισμού είναι το σύνολο %%D = \mathbb(R) = (-\infty, +\infty)%%, αφού το όρισμα %%x% % μπορεί να λάβει οποιεσδήποτε τιμές αριθμός γραμμής. Και για τη συνάρτηση %%y = \frac(1)(\sqrt(1 - x^2))%%, ο τομέας ορισμού θα είναι το σύνολο τιμών %%x%% που ικανοποιεί την ανισότητα %%1 - x^2 > 0%%, m .e. %%D = (-1, 1)%%.

Πλεονεκτήματα του ρητού ορισμού της αναλυτικής συνάρτησης

Σημειώστε ότι ο ρητός αναλυτικός τρόπος ορισμού μιας συνάρτησης είναι αρκετά συμπαγής (ο τύπος, κατά κανόνα, καταλαμβάνει λίγο χώρο), αναπαράγεται εύκολα (ο τύπος είναι εύκολο να γραφτεί) και είναι πιο προσαρμοσμένος στην εκτέλεση μαθηματικών πράξεων και μετασχηματισμών σε λειτουργίες.

Μερικές από αυτές τις πράξεις - αλγεβρικές (πρόσθεση, πολλαπλασιασμός, κ.λπ.) - είναι πολύ γνωστές από σχολικό μάθημαμαθηματικά, άλλα (διαφοροποίηση, ολοκλήρωση) θα μελετηθούν στο μέλλον. Ωστόσο, αυτή η μέθοδος δεν είναι πάντα σαφής, καθώς η φύση της εξάρτησης της συνάρτησης από το όρισμα δεν είναι πάντα σαφής, και μερικές φορές απαιτούνται περίπλοκοι υπολογισμοί για την εύρεση των τιμών της συνάρτησης (εάν είναι απαραίτητοι).

Προδιαγραφή σιωπηρής λειτουργίας

Ορίζεται η συνάρτηση %%y = f(x)%% με σιωπηρό αναλυτικό τρόπο, εάν δοθεί η σχέση $$F(x,y) = 0, ~~~~~~~~~~(1)$$ που συσχετίζει τις τιμές της συνάρτησης %%y%% και το όρισμα %% Χ%%. Εάν δίνονται τιμές ορίσματος, τότε για να βρεθεί η τιμή του %%y%% που αντιστοιχεί σε μια συγκεκριμένη τιμή %%x%%, είναι απαραίτητο να λυθεί η εξίσωση %%(1)%% σε σχέση με το %%y%% στη συγκεκριμένη τιμή του %%x%%.

Πότε για δεδομένη αξίαΗ εξίσωση %%x%% %%(1)%% μπορεί να μην έχει καμία λύση ή περισσότερα από ένα διαλύματα. Στην πρώτη περίπτωση καθορισμένη τιμήΤο %%x%% δεν εμπίπτει στο πεδίο εφαρμογής της σιωπηρής συνάρτησης και στη δεύτερη περίπτωση καθορίζει συνάρτηση πολλαπλών τιμών, το οποίο έχει περισσότερες από μία τιμές για μια δεδομένη τιμή ορίσματος.

Σημειώστε ότι εάν η εξίσωση %%(1)%% μπορεί να λυθεί ρητά ως προς το %%y = f(x)%%, τότε λαμβάνουμε την ίδια συνάρτηση, αλλά ήδη ορισμένη με ρητό αναλυτικό τρόπο. Άρα, η εξίσωση %%x + y^5 - 1 = 0%%

και η ισότητα %%y = \sqrt(1 - x)%% ορίζουν την ίδια συνάρτηση.

Ορισμός παραμετρικής συνάρτησης

Όταν η εξάρτηση του %%y%% από το %%x%% δεν δίνεται απευθείας, αλλά αντίθετα δίνονται οι εξαρτήσεις και των δύο μεταβλητών %%x%% και %%y%% από κάποια τρίτη βοηθητική μεταβλητή %%t%% με τη μορφή

$$ \αρχή(περιπτώσεις) x = \varphi(t),\\ y = \psi(t), \end(περιπτώσεις) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$μιλούν για παραμετρικήη μέθοδος ρύθμισης της συνάρτησης·

τότε η βοηθητική μεταβλητή %%t%% ονομάζεται παράμετρος.

Εάν είναι δυνατόν να εξαιρεθεί η παράμετρος %%t%% από τις εξισώσεις %%(2)%%, τότε καταλήγουν σε μια συνάρτηση που δίνεται από μια ρητή ή σιωπηρή αναλυτική εξάρτηση %%y%% στο %%x%% . Για παράδειγμα, από τις σχέσεις $$ \begin(περιπτώσεις) x = 2 t + 5, \\ y = 4 t + 12, \end(περιπτώσεις), ~~~t \in \mathbb(R), $$ εκτός για την παράμετρο % %t%% παίρνουμε την εξάρτηση %%y = 2 x + 2%%, η οποία θέτει μια ευθεία γραμμή στο επίπεδο %%xOy%%.

Γραφικός τρόπος

Ένα παράδειγμα ενός γραφικού ορισμού μιας συνάρτησης

Τα παραπάνω παραδείγματα δείχνουν ότι ο αναλυτικός τρόπος ορισμού μιας συνάρτησης αντιστοιχεί σε αυτήν γραφική εικόνα , το οποίο μπορεί να θεωρηθεί ως μια βολική και οπτική μορφή περιγραφής μιας συνάρτησης. Μερικές φορές χρησιμοποιείται γραφικό τρόπο ορίζοντας μια συνάρτηση όταν η εξάρτηση του %%y%% στο %%x%% δίνεται από μια γραμμή στο επίπεδο %%xOy%%. Ωστόσο, παρ' όλη τη σαφήνειά του, χάνει σε ακρίβεια, καθώς οι τιμές του ορίσματος και οι αντίστοιχες τιμές της συνάρτησης μπορούν να ληφθούν από το γράφημα μόνο κατά προσέγγιση. Το σφάλμα που προκύπτει εξαρτάται από την κλίμακα και την ακρίβεια της μέτρησης της τετμημένης και της τεταγμένης των επιμέρους σημείων του γραφήματος. Στο μέλλον, θα αναθέσουμε το ρόλο του γραφήματος της συνάρτησης μόνο για να επεξηγήσουμε τη συμπεριφορά της συνάρτησης και επομένως θα περιοριστούμε στην κατασκευή «σκίτσας» γραφημάτων που αντικατοπτρίζουν τα κύρια χαρακτηριστικά των συναρτήσεων.

Τρόπος πίνακα

Σημείωση πίνακαεκχωρήσεις συναρτήσεων, όταν ορισμένες τιμές ορισμάτων και οι αντίστοιχες τιμές συναρτήσεων τοποθετούνται σε έναν πίνακα με συγκεκριμένη σειρά. Τα γνωστά τραπέζια φτιάχνονται έτσι τριγωνομετρικές συναρτήσεις, πίνακες λογαρίθμων κ.λπ. Με τη μορφή πίνακα, η σχέση μεταξύ των ποσοτήτων που μετρώνται σε πειραματικές μελέτες, παρατηρήσεις, δοκιμές.

Το μειονέκτημα αυτής της μεθόδου είναι η αδυναμία άμεσου προσδιορισμού των τιμών της συνάρτησης για τις τιμές του ορίσματος που δεν περιλαμβάνονται στον πίνακα. Εάν υπάρχει βεβαιότητα ότι οι τιμές του ορίσματος που δεν παρουσιάζονται στον πίνακα ανήκουν στον τομέα της εξεταζόμενης συνάρτησης, τότε οι αντίστοιχες τιμές της συνάρτησης μπορούν να υπολογιστούν κατά προσέγγιση χρησιμοποιώντας παρεμβολή και παρέκταση.

Παράδειγμα

Χ	3	5.1	10	12.5
y	9	23	80	110

Αλγοριθμικοί και λεκτικοί τρόποι προσδιορισμού συναρτήσεων

Η λειτουργία μπορεί να ρυθμιστεί αλγοριθμική(ή προγραμματικός) με τρόπο που χρησιμοποιείται ευρέως στους υπολογισμούς υπολογιστών.

Τέλος, μπορεί να σημειωθεί περιγραφικός(ή προφορικός) ένας τρόπος καθορισμού μιας συνάρτησης, όταν ο κανόνας για την αντιστοίχιση των τιμών της συνάρτησης με τις τιμές του ορίσματος εκφράζεται με λέξεις.

Για παράδειγμα, η συνάρτηση %%[x] = m~\forall (x \in )