Pöördmaatriks ja selle omadused. pöördmaatriks

Pöördmaatriksi leidmine- probleem, mida enamasti lahendatakse kahel viisil:

• algebralise liitmise meetod, mille puhul on vaja leida determinandid ja transponeerida maatriksid;
• kõrvaldamise meetod tundmatu gauss, milles on vaja sooritada maatriksite elementaarsed teisendused (liida ridu, korrutada ridu sama arvuga jne).

Eriti uudishimulike jaoks on ka teisi meetodeid, näiteks lineaarsete teisenduste meetod. Selles õppetükis analüüsime kolme mainitud meetodit ja nende meetodite abil pöördmaatriksi leidmise algoritme.

pöördmaatriks AGA, nimetatakse sellist maatriksit

AGA
. (1)

pöördmaatriks , mis tuleb antud ruutmaatriksi jaoks leida AGA, nimetatakse sellist maatriksit

korrutis, mille abil maatriksid AGA paremal on identiteedimaatriks, st
. (1)

Identiteedimaatriks on diagonaalmaatriks, milles kõik diagonaalkirjed on võrdsed ühega.

Teoreem.Iga mitteainsuse (mitteainsuse, mitteainsuse) ruutmaatriksi jaoks võib leida pöördmaatriksi ja pealegi ainult ühe. Spetsiaalse (degenereerunud, ainsuse) ruutmaatriksi jaoks pöördmaatriksit ei eksisteeri.

Ruutmaatriksit nimetatakse mitteeriline(või mitte-mandunud, mitteainsuses), kui selle determinant ei ole võrdne nulliga, ja eriline(või degenereerunud, ainsus), kui selle determinant on null.

pöördmaatriks saab leida ainult ruutmaatriksi jaoks. Loomulikult on ka pöördmaatriks ruut ja antud maatriksiga samas järjekorras. Maatriksit, mille jaoks võib leida pöördmaatriksi, nimetatakse inverteeritavaks maatriksiks.

Sest pöördmaatriks on tabav analoogia arvu pöördarvuga. Iga numbri jaoks a, mis ei ole võrdne nulliga, on olemas arv b et töö a ja b võrdne ühega: ab= 1. Number b nimetatakse arvu pöördarvuks b. Näiteks arvu 7 puhul on pöördväärtus arv 1/7, kuna 7*1/7=1.

Pöördmaatriksi leidmine algebralise liitmise meetodil (liitmaatriks)

Mitteainsuse ruutmaatriksi jaoks AGA pöördväärtus on maatriks

kus on maatriksi determinant AGA, а on maatriksiga seotud maatriks AGA.

Liitunud ruutmaatriksiga A on sama järku maatriks, mille elemendid on algebralised liitmised maatriksi determinandi vastavad elemendid transponeeritud maatriksi A suhtes. Seega, kui

siis

ja

Algoritm pöördmaatriksi leidmiseks algebralise liitmise meetodil

1. Leidke selle maatriksi determinant A. Kui determinant on võrdne nulliga, siis pöördmaatriksi leidmine peatub, kuna maatriks on degenereerunud ja pöördmaatriksi jaoks puudub.

2. Leidke suhtes transponeeritud maatriks A.

3. Arvutage liitmaatriksi elemendid sammus 2 leitud marita algebraliste täienditena.

4. Rakendage valem (2): korrutage arv, pöörddeterminant maatriksid A, 4. sammus leitud liidumaatriksile.

5. Kontrollige sammus 4 saadud tulemust korrutades antud maatriks A pöördmaatriksile. Kui nende maatriksite korrutis on võrdne identiteedimaatriksiga, siis leiti pöördmaatriks õigesti. Vastasel juhul alustage lahendusprotsessi uuesti.

Näide 1 Maatriksi jaoks

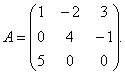
leida pöördmaatriks.

Otsus. Pöördmaatriksi leidmiseks on vaja leida maatriksi determinant AGA. Leiame kolmnurkade reegli järgi:

Seetõttu maatriks AGA on mitteainsus (mitte-mandunud, mitteainsus) ja sellele on olemas pöördväärtus.

Leiame antud maatriksiga seotud maatriksi AGA.

Leiame maatriksi suhtes transponeeritud maatriksi A:

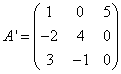
Arvutame liitmaatriksi elemendid maatriksi suhtes transponeeritud maatriksi algebraliste täienditena A:

Seetõttu on maatriks maatriksiga konjugeeritud A, on vormiga

kommenteerida. Elementide arvutamise ja maatriksi transponeerimise järjekord võib olla erinev. Kõigepealt saab arvutada maatriksi algebralised täiendid A, ja seejärel transponeerige algebraliste komplementide maatriks. Tulemuseks peaksid olema liidumaatriksi samad elemendid.

Rakendades valemit (2), leiame maatriksi pöördvõrdeliselt AGA:

Pöördmaatriksi leidmine tundmatute Gaussi eliminatsiooni abil

Esimene samm pöördmaatriksi leidmiseks Gaussi eliminatsiooni abil on maatriksile omistamine A identiteedi maatriks samas järjekorras, eraldades need vertikaalse ribaga. Saame kahekordse maatriksi. Korrutage selle maatriksi mõlemad osad arvuga , siis saame

,

Algoritm pöördmaatriksi leidmiseks tundmatute Gaussi eliminatsiooni abil

1. Maatriksile A määrata samas järjekorras identiteedimaatriks.

2. Teisendage saadud duaalmaatriks nii, et identiteedimaatriks saadakse selle vasakpoolses osas, siis saadakse identiteedimaatriksi asemel automaatselt parempoolses osas pöördmaatriks. Maatriks A vasakpoolses servas teisendatakse identiteedimaatriksiks elementaarsed teisendused maatriksid.

2. Kui maatriksiteisenduse protsessis A identiteedimaatriksis on mis tahes reas või veerus ainult nullid, siis on maatriksi determinant võrdne nulliga ja seetõttu maatriks A on degenereerunud ja sellel pole pöördmaatriksit. Sel juhul pöördmaatriksi edasine leidmine peatub.

Näide 2 Maatriksi jaoks

leida pöördmaatriks.

ja me teisendame selle nii, et identiteedimaatriks saadakse vasakul küljel. Alustame ümberkujundamist.

Korrutage vasaku ja parema maatriksi esimene rida (-3) ja lisage see teisele reale ning seejärel korrutage esimene rida (-4) ja lisage see kolmandale reale, siis saame

.

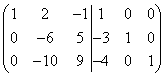Võimaluse korral vältida murdarvud järgnevates teisendustes loome esmalt üksuse duaalmaatriksi vasakpoolses teises reas. Selleks korrutage teine ​​rida 2-ga ja lahutage sellest kolmas rida, siis saame

.

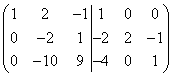Liidame esimese rea teisele ja seejärel korrutame teise rea (-9)-ga ja lisame selle kolmandale reale. Siis saame

.

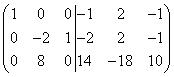Seejärel jagage kolmas rida 8-ga

.

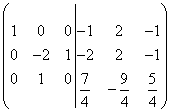Korrutage kolmas rida 2-ga ja lisage see teisele reale. Selgub:

.

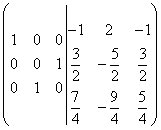Vahetades teise ja kolmanda rea ​​kohad, saame lõpuks:

.

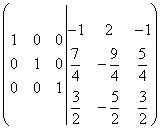Näeme, et identiteedimaatriks saadakse vasakult poolt, seega saadakse pöördmaatriks paremalt poolt. Seega:

.

Arvutuste õigsust saate kontrollida, korrutades algse maatriksi leitud pöördmaatriksiga:

Tulemuseks peaks olema pöördmaatriks.

Näide 3 Maatriksi jaoks

leida pöördmaatriks.

Otsus. Kahekordse maatriksi koostamine

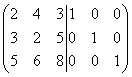
ja me muudame selle.

Korrutame esimese rea 3-ga ja teise 2-ga ja lahutame teisest ning seejärel korrutame esimese rea 5-ga ja kolmanda 2-ga ning lahutame kolmandast reast, siis saame

.

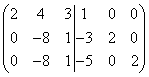Korrutame esimese rea 2-ga ja lisame selle teisele ning seejärel lahutame kolmandast reast teise, siis saame

.

Näeme, et vasakpoolsel kolmandal real osutusid kõik elemendid võrdseks nulliga. Seetõttu on maatriks degenereerunud ja sellel pole pöördmaatriksit. Lõpetame tagurpidi Maria edasise leidmise.

See teema on õpilaste seas üks vihatumaid. Hullem, ilmselt ainult määrajad.

Nipp on selles, et juba pöördelemendi mõiste (ja ma ei räägi praegu ainult maatriksitest) viitab meile korrutamise operatsioonile. Isegi sisse kooli õppekava arvestatakse korrutamist keeruline operatsioon, ja maatriksite korrutamine on üldiselt omaette teema, millele mul on pühendatud terve lõik ja videoõpetus.

Täna me maatriksarvutuste üksikasjadesse ei lasku. Pidage lihtsalt meeles: kuidas maatrikseid tähistatakse, kuidas neid korrutatakse ja mis sellest järeldub.

Ülevaade: maatrikskorrutamine

Kõigepealt lepime kokku noodikirjas. Maatriks $A$ suurusega $\left[ m\times n \right]$ on lihtsalt numbritabel täpselt $m$ rea ja $n$ veeruga:

\=\alussulg(\left[ \begin(maatriks) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(maatriks) \parem])_(n)\]

Et mitte kogemata ridu ja veerge kohati segi ajada (uskuge mind, eksamil võib ühiku segamini ajada kahekohalisega - mis seal mõne rea kohta öelda), vaadake lihtsalt pilti:

Maatriksrakkude indeksite määramine

Mis toimub? Kui asetame standardkoordinaadisüsteemi $OXY$ vasakule ülemine nurk ja suunake teljed nii, et need katavad kogu maatriksi, siis saab selle maatriksi iga lahtri unikaalselt seostada koordinaatidega $\left(x;y \right)$ - see on rea ja veeru number.

Miks on koordinaatsüsteem paigutatud täpselt vasakusse ülemisse nurka? Jah, sest just sealt hakkame me igasuguseid tekste lugema. Seda on väga lihtne meeles pidada.

Miks on $x$ telg suunatud alla, mitte paremale? Jällegi on see lihtne: võtke standardne koordinaatsüsteem (telg $x$ läheb paremale, $y$ telg tõuseb üles) ja pöörake seda nii, et see ümbritseks maatriksit. See on 90 kraadi päripäeva pöörlemine – selle tulemust näeme pildil.

Üldiselt saime aru, kuidas maatriksi elementide indekseid määrata. Nüüd tegeleme korrutamisega.

Definitsioon. Maatriksid $A=\left[ m\times n \right]$ ja $B=\left[ n\times k \right]$, kui esimese veergude arv ühtib teise ridade arvuga, on nimetatakse järjekindlaks.

See on selles järjekorras. Võib olla mitmetähenduslik ja öelda, et maatriksid $A$ ja $B$ moodustavad järjestatud paari $\left(A;B \right)$: kui need on selles järjestuses järjepidevad, siis pole $B üldse vajalik. $ ja $ A $, need. ka paar $\left(B;A \right)$ on järjekindel.

Korrutada saab ainult järjekindlaid maatrikseid.

Definitsioon. Konsistentsete maatriksite $A=\left[ m\times n \right]$ ja $B=\left[ n\times k \right]$ korrutis on uus maatriks $C=\left[ m\times k \right ]$ , mille elemendid $((c)_(ij))$ arvutatakse järgmise valemiga:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Teisisõnu: maatriksi $C=A\cdot B$ elemendi $((c)_(ij))$ saamiseks tuleb võtta esimese maatriksi $i$-rida, $j$ - teise maatriksi veergu ja korrutage seejärel selle rea ja veeru elemendid paarikaupa. Liitke tulemused kokku.

Jah, see on karm määratlus. Sellest tulenevad kohe mitmed faktid:

1. Maatriksikorrutis on üldiselt mittekommutatiivne: $A\cdot B\ne B\cdot A$;
2. Korrutamine on aga assotsiatiivne: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. Ja isegi distributiivne: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. Ja jälle distributiivne: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Ainuüksi korrutustehte mittekommutatiivsuse tõttu tuli korrutamise distributiivsust eraldi kirjeldada vasaku ja parema kordaja-summa jaoks.

Kui sellegipoolest selgub, et $A\cdot B=B\cdot A$, nimetatakse selliseid maatrikseid muutlikeks.

Kõigi maatriksite seas, mis seal millegagi korrutatakse, on erilisi – neid, mis mis tahes maatriksiga $A$ korrutades annavad jällegi $A$:

Definitsioon. Maatriksit $E$ nimetatakse identiteediks, kui $A\cdot E=A$ või $E\cdot A=A$. Ruutmaatriksi $A$ korral võime kirjutada:

Identiteedimaatriks on lahendamisel sagedane külaline maatriksvõrrandid. Ja üldse, sage külaline maatriksimaailmas. :)

Ja selle $E$ tõttu mõtles keegi välja kogu mängu, mis järgmisena kirjutatakse.

Mis on pöördmaatriks

Kuna maatriksi korrutamine on väga aeganõudev toiming (peate korrutama hulga ridu ja veerge), pole ka pöördmaatriksi kontseptsioon kõige triviaalsem. Ja see vajab selgitust.

Võtme definitsioon

Noh, on aeg teada tõde.

Definitsioon. Maatriksit $B$ nimetatakse maatriksi $A$ pöördväärtuseks, kui

Pöördmaatriksit tähistatakse $((A)^(-1))$ (mitte segi ajada astmega!), seega saab definitsiooni ümber kirjutada järgmiselt:

Näib, et kõik on äärmiselt lihtne ja selge. Kuid sellise määratluse analüüsimisel tekib kohe mitu küsimust:

1. Kas pöördmaatriks on alati olemas? Ja kui mitte alati, siis kuidas teha kindlaks: millal see on olemas ja millal mitte?
2. Ja kes ütles, et selline maatriks on täpselt üks? Mis siis, kui mõne algse maatriksi $A$ jaoks on terve hulk pöördväärtusi?
3. Kuidas kõik need "tagurpidi" välja näevad? Ja kuidas te neid tegelikult loete?

Arvutusalgoritmide osas räägime sellest veidi hiljem. Ülejäänud küsimustele vastame aga kohe. Korraldagem need eraldi väidete-lemmade kujul.

Põhiomadused

Alustame sellest, kuidas peaks maatriks $A$ välja nägema, et sellel oleks $((A)^(-1))$. Nüüd veendume, et mõlemad maatriksid peavad olema ruudukujulised ja sama suurusega: $\left[ n\times n \right]$.

Lemma 1. Antud maatriks $A$ ja selle pöördväärtus $((A)^(-1))$. Siis on mõlemad maatriksid ruudukujulised ja nende järjestus $n$ on sama.

Tõestus. Kõik on lihtne. Olgu maatriks $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Kuna korrutis $A\cdot ((A)^(-1))=E$ on definitsiooni järgi olemas, on maatriksid $A$ ja $((A)^(-1))$ järjepidevad selles järjekorras:

\[\begin(joona) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( joondada)\]

See on maatriksi korrutusalgoritmi otsene tagajärg: koefitsiendid $n$ ja $a$ on "transiit" ja peavad olema võrdsed.

Samal ajal on defineeritud ka pöördkorrutis: $((A)^(-1))\cdot A=E$, seega on maatriksid $((A)^(-1))$ ja $A$ samuti kooskõlas järgmises järjekorras:

\[\begin(joona) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( joondada)\]

Seega võime üldistust kaotamata eeldada, et $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Kuid vastavalt $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ definitsioonile on maatriksite mõõtmed täpselt samad:

\[\begin(joona) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(joonda)\]

Seega selgub, et kõik kolm maatriksit - $A$, $((A)^(-1))$ ja $E$ - on ruudu suurus$\left[ n\times n \right]$. Lemma on tõestatud.

No see on juba hea. Näeme, et ainult ruutmaatriksid on pööratavad. Nüüd veendume, et pöördmaatriks on alati sama.

Lemma 2. Antud maatriks $A$ ja selle pöördväärtus $((A)^(-1))$. Siis on see pöördmaatriks ainulaadne.

Tõestus. Alustame vastupidisest: olgu maatriksil $A$ vähemalt kaks pöördjuhtumit — $B$ ja $C$. Seejärel on definitsiooni kohaselt tõesed järgmised võrdsused:

\[\begin(joonda) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(joonda)\]

Lemmast 1 järeldame, et kõik neli maatriksit $A$, $B$, $C$ ja $E$ on samas järjestuses ruudud: $\left[ n\times n \right]$. Seetõttu on toode määratletud:

Kuna maatrikskorrutis on assotsiatiivne (kuid mitte kommutatiivne!), võime kirjutada:

\[\begin(joonda) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\paremnool B=C. \\ \end(joonda)\]

Ainult vastu võetud võimalik variant: kaks pöördmaatriksi eksemplari on võrdsed. Lemma on tõestatud.

Ülaltoodud arutluskäik kordab peaaegu sõna-sõnalt pöördelemendi ainulaadsuse tõestust kõigi jaoks reaalarvud$b\ne 0$. Ainus oluline täiendus on maatriksite mõõtmete arvestamine.

Siiski ei tea me veel midagi selle kohta, kas üldse ruutmaatriks on pöörduv. Siin tuleb meile appi determinant – see on kõigi ruutmaatriksite põhiomadus.

Lemma 3 . Antud maatriks $A$. Kui maatriks $((A)^(-1))$ on selle pöördvõrdeline, siis on algmaatriksi determinant nullist erinev:

\[\left| A \right|\ne 0\]

Tõestus. Teame juba, et $A$ ja $((A)^(-1))$ on ruutmaatriksid suurusega $\left[ n\times n \right]$. Seetõttu on igaühe jaoks võimalik arvutada determinant: $\left| A \right|$ ja $\left| ((A)^(-1)) \parem|$. Kuid toote määraja on võrdne tootega määrajad:

\[\left| A\cdot B \right|=\left| \right|\cdot \left| B \parem|\Paremnool \vasak| A\cdot ((A)^(-1)) \right|=\left| \right|\cdot \left| ((A)^(-1)) \parem|\]

Kuid vastavalt definitsioonile $A\cdot ((A)^(-1))=E$ ja $E$ determinant on alati võrdne 1-ga, nii et

\[\begin(joonda) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\right|; \\ & \left| \right|\cdot \left| ((A)^(-1)) \parem|=1. \\ \end(joonda)\]

Kahe arvu korrutis on võrdne ühega ainult siis, kui kõik need arvud erinevad nullist:

\[\left| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Nii selgub, et $\left| A \right|\ne 0$. Lemma on tõestatud.

Tegelikult on see nõue üsna loogiline. Nüüd analüüsime pöördmaatriksi leidmise algoritmi – ja saab täiesti selgeks, miks põhimõtteliselt ei saa nulldeterminandiga pöördmaatriksit eksisteerida.

Kuid kõigepealt sõnastagem "abi" määratlus:

Definitsioon. Degenereerunud maatriks on ruutmaatriks suurusega $\left[ n\times n \right]$, mille determinant on null.

Seega võime kinnitada, et iga pööratav maatriks on mittedegenereerunud.

Kuidas leida pöördmaatriksit

Nüüd kaalume universaalset algoritmi pöördmaatriksite leidmiseks. Üldiselt on kaks üldtunnustatud algoritmi ja me käsitleme täna ka teist.

See, mida praegu kaalutakse, on väga tõhus maatriksite jaoks, mille suurus on $\left[ 2\x 2 \right]$ ja - osaliselt - suurusega $\left[ 3\x 3 \right]$. Kuid alates suurusest $\left[ 4\x 4 \right]$ on parem seda mitte kasutada. Miks - nüüd saate kõigest aru.

Algebralised liitmised

Sea end valmis. Nüüd hakkab valu olema. Ei, ära muretse: ilus õde seelikus, pitsiga sukad ei tule sulle ja ei tee sulle tagumikku süsti. Kõik on palju proosalisem: teie juurde tulevad algebralised täiendused ja Tema Majesteet "Union Matrix".

Alustame peamisest. Olgu ruutmaatriks suurusega $A=\left[ n\times n \right]$, mille elemendid kannavad nime $((a)_(ij))$. Seejärel saab iga sellise elemendi jaoks määratleda algebralise täiendi:

Definitsioon. Algebraline täiendus $((A)_(ij))$ elemendile $((a)_(ij))$ maatriksi $i$-ndas reas ja $j$-ndas veerus $A=\left [ n \times n \right]$ on vormi konstruktsioon

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Kus $M_(ij)^(*)$ on maatriksi determinant, mis saadakse algsest $A$-st, kustutades sama $i$-nda rea ​​ja $j$-nda veeru.

Jällegi. Maatriksi elemendi algebraline täiendus koordinaatidega $\left(i;j \right)$ on tähistatud kui $((A)_(ij))$ ja arvutatakse vastavalt skeemile:

1. Esiteks kustutame algsest maatriksist $i$-rea ja $j$-nda veeru. Saame uue ruutmaatriksi ja tähistame selle determinandina $M_(ij)^(*)$.
2. Seejärel korrutame selle determinandi väärtusega $((\left(-1 \right))^(i+j))$ - alguses võib see väljend tunduda jahmatav, kuid tegelikult leiame lihtsalt $ ees oleva märgi M_(ij)^(*) $.
3. Arvestame – saame konkreetne number. Need. algebraline liitmine on lihtsalt arv, mitte mingi uus maatriks jne.

Maatriksit $M_(ij)^(*)$ ennast nimetatakse elemendi $((a)_(ij))$ komplementaarseks minooriks. Ja selles mõttes on ülaltoodud algebralise täiendi definitsioon rohkema erijuhtum keeruline määratlus- mida me determinandi tunnis käsitlesime.

Oluline märkus. Tegelikult defineeritakse "täiskasvanute" matemaatikas algebralised liitmised järgmiselt:

1. Võtame ruutmaatriksisse $k$ rida ja $k$ veergu. Nende ristumiskohas saame maatriksi suurusega $\left[ k\times k \right]$ — selle determinanti nimetatakse järgu $k$ minoorseks ja tähistatakse $((M)_(k))$.
2. Seejärel kriipsutame need "valitud" $k$ read ja $k$ veerud maha. Jällegi saame ruutmaatriksi – selle determinanti nimetatakse komplementaarseks minooriks ja tähistatakse $M_(k)^(*)$.
3. Korrutage $M_(k)^(*)$ arvuga $((\left(-1 \right))^(t))$, kus $t$ on (tähelepanu!) kõigi valitud ridade arvude summa ja veerud . See on algebraline liitmine.

Heitke pilk kolmandale sammule: tegelikult on 2 000 $ tingimuste summa! Teine asi on see, et $k=1$ korral saame ainult 2 terminit - need on samad $i+j$ - elemendi $((a)_(ij)) $ "koordinaadid", mille jaoks me oleme otsib algebralist täiendit.

Seega kasutame täna veidi lihtsustatud määratlust. Kuid nagu me hiljem näeme, on see enam kui piisav. Palju olulisem on järgmine:

Definitsioon. Liitmaatriks $S$ ruutmaatriksile $A=\left[ n\times n \right]$ on uus maatriks suurusega $\left[ n\times n \right]$, mis saadakse $A$ asendades $(( a)_(ij))$ algebraliste täiendustega $((A)_(ij))$:

\\Paremnool S=\left[ \begin(maatriks) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(maatriks) \parem]\]

Esimene mõte, mis selle määratluse mõistmise hetkel tekib, on "nii palju peate kokku arvestama!" Lõdvestu: sa pead arvestama, aga mitte nii palju. :)

Noh, see kõik on väga tore, aga milleks see vajalik on? Aga miks.

Peamine teoreem

Lähme natuke tagasi. Pidage meeles, et Lemma 3 väitis, et inverteeritav maatriks $A$ on alati mitteainsus (st selle determinant on nullist erinev: $\left| A \right|\ne 0$).

Seega on ka vastupidi: kui maatriks $A$ ei ole degenereerunud, siis on see alati inverteeritav. Ja seal on isegi otsinguskeem $((A)^(-1))$. Vaata järgi:

Pöördmaatriksi teoreem. Olgu antud ruutmaatriks $A=\left[ n\times n \right]$ ja selle determinant on nullist erinev: $\left| A \right|\ne 0$. Siis eksisteerib pöördmaatriks $((A)^(-1))$ ja see arvutatakse järgmise valemiga:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

Ja nüüd - kõik sama, kuid loetava käekirjaga. Pöördmaatriksi leidmiseks vajate:

1. Arvutage determinant $\left| A \right|$ ja veenduge, et see poleks null.
2. Koostage liitmaatriks $S$, s.o. loendage 100500 algebralist liitmist $((A)_(ij))$ ja asetage need paika $((a)_(ij))$.
3. Transponeerige see maatriks $S$ ja korrutage see mõne arvuga $q=(1)/(\left| A \right|)\;$.

Ja see ongi kõik! Leitakse pöördmaatriks $((A)^(-1))$. Vaatame näiteid:

\[\left[ \begin(maatriks) 3 & 1 \\ 5 & 2 \\\end(maatriks) \right]\]

Otsus. Kontrollime pöörduvust. Arvutame determinandi:

\[\left| A \right|=\left| \begin(maatriks) 3 & 1 \\ 5 & 2 \\\end(maatriks) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinant erineb nullist. Seega on maatriks ümberpööratav. Loome ametiühingu maatriksi:

Arvutame algebralised liitmised:

\[\begin(joona) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\right|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\parem|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\parem|=3. \\ \end(joonda)\]

Pöörake tähelepanu: determinandid |2|, |5|, |1| ja |3| on $\left[ 1\times 1 \right]$ suuruste maatriksite determinandid, mitte moodulid. Need. kui määrajad oleksid negatiivsed arvud, pole vaja "miinust" eemaldada.

Kokku näeb meie ametiühingu maatriks välja selline:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(massiivi)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(massiivi) \right])^(T))=\left[ \begin (massiiv)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(massiivi) \right]\]

See on kõik. Probleem lahendatud.

Vastus. $\left[ \begin(massiivi)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(massiivi) \right]$

Ülesanne. Leidke pöördmaatriks:

\[\left[ \begin(massiivi)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(massiivi) \right] \]

Otsus. Jällegi käsitleme määrajat:

\[\begin(joonda) & \left| \begin(massiivi)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(massiiv) \right|=\begin(maatriks ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(maatriks)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(joonda)\]

Determinant erineb nullist - maatriks on pööratav. Aga nüüd on see kõige tina: peate lugema koguni 9 (üheksa, pagan!) algebralist liitmist. Ja igaüks neist sisaldab määrajat $\left[ 2\times 2 \right]$. Lendas:

\[\begin(maatriks) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(maatriks) 2 & -1 \\ 0 & 1 \\\end(maatriks) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(maatriks) 0 & -1 \\ 1 & 1 \\\end(maatriks) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(maatriks) 0 & 2 \\ 1 & 0 \\\end(maatriks) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(maatriks) 1 & -1 \\ 0 & 2 \\\end(maatriks) \right|=2; \\ \end(maatriks)\]

Lühidalt, liidu maatriks näeb välja selline:

Seetõttu on pöördmaatriks järgmine:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(maatriks) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(maatriks) \right]=\left[ \begin(massiivi)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(massiivi) \right]\]

Noh, see on kõik. Siin on vastus.

Vastus. $\left[ \begin(massiivi)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(massiivi) \right ]$

Nagu näete, teostasime iga näite lõpus kontrolli. Sellega seoses oluline märkus:

Ära ole laisk kontrollima. Korrutage algne maatriks leitud pöördväärtusega – peaksite saama $E$.

Seda kontrolli on palju lihtsam ja kiirem teha, kui otsida viga edasistes arvutustes, kui lahendate näiteks maatriksvõrrandit.

Alternatiivne viis

Nagu ma ütlesin, töötab pöördmaatriksi teoreem hästi suuruste $\left[ 2\x 2 \right]$ ja $\left[ 3\x 3 \right]$ puhul (in viimane juhtum- see pole enam nii "täiuslik"), kuid suurte maatriksite puhul algab kurbus.

Kuid ärge muretsege: on olemas alternatiivne algoritm, mille abil saab rahulikult pöördväärtuse leida isegi maatriksi $\left[10\times 10 \right]$ jaoks. Kuid nagu sageli juhtub, vajame selle algoritmi arvestamiseks veidi teoreetilist tausta.

Elementaarsed teisendused

Maatriksi erinevate teisenduste hulgas on mitu erilist - neid nimetatakse elementaarseteks. Selliseid teisendusi on täpselt kolm:

1. Korrutamine. Võite võtta $i$-nda rea ​​(veeru) ja korrutada selle mis tahes arvuga $k\ne 0$;
2. Lisand. Lisage $i$-ndale reale (veerule) mis tahes muu $j$-s rida (veerg), mis on korrutatud mis tahes arvuga $k\ne 0$ (muidugi on võimalik ka $k=0$, aga mis mõte sellel on Sellest ei muutu aga midagi).
3. Permutatsioon. Võtke $i$-nda ja $j$-nda rida (veerud) ja vahetage need.

Miks neid teisendusi nimetatakse elementaarseteks (suurte maatriksite puhul ei tundu need nii elementaarsed) ja miks neid on ainult kolm – need küsimused jäävad tänasest tunnist välja. Seetõttu me detailidesse ei lasku.

Teine asi on oluline: me peame kõik need perverssused läbi viima seotud maatriksiga. Jah, jah, sa kuulsid õigesti. Nüüd on veel üks määratlus – viimane tänases tunnis.

Lisatud Matrix

Kindlasti lahendasite koolis võrrandisüsteeme liitmise meetodil. Noh, lahutage ühest realt teine, korrutage mõni rida arvuga - see on kõik.

Niisiis: nüüd on kõik endine, kuid juba "täiskasvanu moodi". Valmis?

Definitsioon. Olgu antud maatriks $A=\left[ n\times n \right]$ ja sama suur maatriks $E$ $n$. Seejärel seotud maatriks $\left[ A\left| E\õige. \right]$ on uus $\left[ n\times 2n \right]$ maatriks, mis näeb välja järgmine:

\[\left[ A\left| E\õige. \right]=\left[ \begin(massiivi)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(massiivi) \right]\]

Ühesõnaga võtame maatriksi $A$, paremale omistame sellele vajaliku suurusega identiteedimaatriksi $E$, eraldame need ilu huvides vertikaalse ribaga - siin on lisatud. :)

Mis on saak? Ja siin on see, mis:

Teoreem. Olgu maatriks $A$ inverteeritav. Vaatleme adjointmaatriksit $\left[ A\left| E\õige. \right]$. Kui kasutate elementaarstringi teisendused tuua see kujule $\left[ E\left| B\right. \right]$, st. ridade korrutamisel, lahutamisel ja ümberkorraldamisel saadakse $A$-st parempoolne maatriks $E$, siis vasakpoolne maatriks $B$ on $A$ pöördväärtus:

\[\left[ A\left| E\õige. \paremale]\vasakule[ E\vasak| B\right. \right]\Paremnool B=((A)^(-1))\]

Nii lihtne see ongi! Lühidalt, pöördmaatriksi leidmise algoritm näeb välja järgmine:

1. Kirjutage seotud maatriks $\left[ A\left| E\õige. \right]$;
2. Tehke elementaarsed stringide teisendused, kuni kuvatakse $A$ asemel parempoolne tekst $E$;
3. Loomulikult ilmub midagi ka vasakule - teatud maatriks $B$. See on vastupidine;
4. KASUM! :)

Muidugi, palju lihtsam öelda kui teha. Vaatame siis paari näidet: suuruste $\left[ 3\x 3 \right]$ ja $\left[ 4\x 4 \right]$ jaoks.

Ülesanne. Leidke pöördmaatriks:

\[\left[ \begin(massiivi)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(massiivi) \right]\ ]

Otsus. Koostame lisatud maatriksi:

\[\left[ \begin(massiivi)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 ja 1 \\\end(massiivi) \right]\]

Kuna algse maatriksi viimane veerg on täidetud ühedega, lahutage esimene rida ülejäänud osast:

\[\begin(joona) & \left[ \begin(massiivi)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(massiivi) \right]\begin(maatriks) \allanool \\ -1 \\ -1 \\\end(maatriks)\to \\ & \to \vasak [ \begin(massiiv)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(massiivi) \right] \\ \end(joonda)\]

Rohkem üksusi pole, välja arvatud esimene rida. Kuid me ei puuduta seda, vastasel juhul hakkavad äsja eemaldatud üksused kolmandas veerus "paljunema".

Kuid teise rea saame viimasest kaks korda lahutada - vasakus alanurgas saame ühiku:

\[\begin(joona) & \left[ \begin(massiivi)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(massiivi) \right]\begin(maatriks) \ \\ \downarrow \\ -2 \\\end(maatriks)\to \\ & \left [ \begin(massiiv)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiivi) \right] \\ \end(joonda)\]

Nüüd saame lahutada viimase rea esimesest ja kaks korda teisest - sel viisil "nullime" esimese veeru:

\[\begin(joona) & \left[ \begin(massiivi)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiivi) \right]\begin(maatriks) -1 \\ -2 \\ \uparrow \\\end(maatriks)\to \\ & \ \left[ \begin(massiivi)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiivi) \right] \\ \end(joona)\]

Korrutage teine ​​rida -1-ga ja lahutage see esimesest 6 korda ja lisage viimasele üks kord:

\[\begin(joona) & \left[ \begin(massiiv)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiiv) \right]\begin(maatriks) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiivi) \right]\begin(maatriks) -6 \\ \üles-alla \\ +1 \\\end (maatriks)\to \\ & \to \left[ \begin(massiivi)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(massiivi) \right] \\ \end(joona)\]

Jääb vaid ridade 1 ja 3 vahetamine:

\[\left[ \begin(massiivi)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(massiivi) \right]\]

Valmis! Paremal on vajalik pöördmaatriks.

Vastus. $\left[ \begin(massiivi)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(massiivi) \right ]$

Ülesanne. Leidke pöördmaatriks:

\[\left[ \begin(maatriks) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(maatriks) \right]\]

Otsus. Jällegi koostame lisatud:

\[\left[ \begin(massiivi)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiivi) \right]\]

Laename natuke, muretseme, kui palju me nüüd peame arvestama ... ja hakkame loendama. Alustuseks nullistame esimese veeru, lahutades ridadest 2 ja 3 rea 1:

\[\begin(joona) & \left[ \begin(massiivi)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiivi) \right]\begin(maatriks) \allanool \\ -1 \\ -1 \\ \ \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiivi) \right] \\ \end(joona)\]

Me täheldame ridadel 2-4 liiga palju "miinuseid". Korrutage kõik kolm rida -1-ga ja seejärel põletage kolmas veerg läbi, lahutades ülejäänud rea 3:

\[\begin(joona) & \left[ \begin(massiivi)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(massiivi) \right]\begin(maatriks) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (massiivi) \right]\begin(maatriks) -2 \\ -1 \\ \ülesallanool \\ -2 \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiivi) \right] \\ \end(joona)\]

Nüüd on aeg "praadida" algse maatriksi viimane veerg: lahutada rida 4 ülejäänud osast:

\[\begin(joona) & \left[ \begin(massiivi)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiiv ) \right]\begin(maatriks) +1 \\ -3 \\ -2 \\ \uparrow \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiivi) \right] \\ \end(joona)\]

Lõplik veerg: "põletage läbi" teine ​​veerg, lahutades reast 1 ja 3 rida 2:

\[\begin(joona) & \left[ \begin(massiivi)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( massiiv) \right]\begin(maatriks) 6 \\ \üles-allanool \\ -5 \\ \ \\\end(maatriks)\to \\ & \to \left[ \begin(massiivi)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiivi) \right] \\ \end(joona)\]

Ja jälle identiteedimaatriks vasakul, seega pöördvõrdeline paremal. :)

Vastus. $\left[ \begin(maatriks) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(maatriks) \right]$

Definitsioon 1: Maatriksit nimetatakse degeneratiivseks, kui selle determinant on null.

Definitsioon 2: Maatriksit nimetatakse mitteainsuseks, kui selle determinant ei ole võrdne nulliga.

Maatriksit "A" nimetatakse pöördmaatriks, kui tingimus A*A-1 = A-1 *A = E (identiteedimaatriks) on täidetud.

Ruutmaatriks on inverteeritav ainult siis, kui see pole ainsuses.

Pöördmaatriksi arvutamise skeem:

1) Arvutage maatriksi "A" determinant, kui ∆ A = 0, siis pöördmaatriksit ei eksisteeri.

2) Leidke maatriksi "A" kõik algebralised täiendid.

3) Koostage algebraliste liitmiste maatriks (Aij )

4) Transponeerige algebraliste komplementide maatriks (Aij )T

5) Korrutage transponeeritud maatriks selle maatriksi determinandi pöördarvuga.

6) Käivitage kontroll:

Esmapilgul võib tunduda, et see on raske, kuid tegelikult on kõik väga lihtne. Kõik lahendused põhinevad lihtsal aritmeetilised tehted, lahendamisel on peamine mitte segi minna märkidega "-" ja "+" ning neid mitte kaotada.

Nüüd otsustame koos praktiline ülesanne, arvutades pöördmaatriksi.

Ülesanne: leidke pöördmaatriks "A", mis on näidatud alloleval pildil:

Lahendame kõik täpselt nii, nagu on näidatud pöördmaatriksi arvutamise plaanis.

1. Esimese asjana tuleb leida maatriksi "A" determinant:

Selgitus:

Oleme oma determinanti lihtsustanud, kasutades selle põhifunktsioone. Esiteks lisasime 2. ja 3. reale esimese rea elemendid, korrutasime ühe numbriga.

Teiseks muutsime determinandi 2. ja 3. veergu ning vastavalt selle omadustele muutsime selle ees olevat märki.

Kolmandaks võtsime välja teise rea ühisteguri (-1), muutes sellega uuesti märki ja see muutus positiivseks. Lihtsustasime ka 3. rida samamoodi nagu näite alguses.

Meil on kolmnurkdeterminant, milles diagonaali all olevad elemendid on võrdsed nulliga ja omaduse 7 järgi on see võrdne diagonaali elementide korrutisega. Selle tulemusena saime ∆ A = 26, järelikult on pöördmaatriks olemas.

A11 = 1*(3+1) = 4

A12 \u003d -1 * (9 + 2) \u003d -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Järgmine samm on saadud lisadest maatriksi koostamine:

5. Korrutame selle maatriksi determinandi pöördarvuga, st 1/26-ga:

6. Noh, nüüd peame lihtsalt kontrollima:

Kontrollimise käigus saime identiteedimaatriksi, seega oli otsus tehtud täiesti õigesti.

2 viis pöördmaatriksi arvutamiseks.

1. Maatriksite elementaarne teisendus

2. Pöördmaatriks läbi elementaarmuunduri.

Elementaarne maatriksiteisendus hõlmab:

1. Stringi korrutamine nullist erineva arvuga.

2. Lisamine teise rea mis tahes reale, korrutatuna arvuga.

3. Maatriksi ridade vahetamine.

4. Rakendades elementaarteisenduste ahelat, saame teise maatriksi.

AGA -1 = ?

1. (A|E) ~ (E|A -1 )

2. A -1*A=E

Kaaluge seda praktiline näide reaalarvudega.

Harjutus: Leia pöördmaatriks.

Otsus:

Kontrollime:

Väike selgitus lahenduse kohta:

Esmalt vahetasime maatriksi read 1 ja 2, seejärel korrutasime esimese rea (-1).

Pärast seda korrutati esimene rida (-2) ja lisati maatriksi teisele reale. Seejärel korrutasime 2. rea 1/4-ga.

viimane etapp teisendused oli teise rea korrutamine 2-ga ja liitmine esimesest. Selle tulemusena on meil vasakul identiteedimaatriks, seega on pöördmaatriks parempoolne maatriks.

Pärast kontrollimist veendusime otsuse õigsuses.

Nagu näete, on pöördmaatriksi arvutamine väga lihtne.

Selle loengu lõpetuseks tahaksin pühendada veidi aega ka sellise maatriksi omadustele.

Meetodid pöördmaatriksi leidmiseks, . Vaatleme ruutmaatriksit

Tähistame Δ = det A.

Ruutmaatriksit A ​​nimetatakse mitte-degenereerunud, või mitteeriline kui selle determinant on nullist erinev, ja degenereerunud, või eriline, kuiΔ = 0.

Ruutmaatriks B eksisteerib sama järku ruutmaatriksi A jaoks, kui nende korrutis A B = B A = E, kus E on maatriksitega A ja B sama järku identsusmaatriks.

Teoreem . Selleks, et maatriksil A oleks pöördmaatriks, on vajalik ja piisav, et selle determinant oleks nullist erinev.

Pöördmaatriks maatriksiks A, tähistatud tähega A- 1, seega B = A - 1 ja arvutatakse valemiga

, (1)

kus А i j - maatriksi A elementide a i j algebralised täiendid.

Arvutamine A -1 valemiga (1) maatriksite jaoks kõrge järjekord väga töömahukas, seetõttu on praktikas mugav leida A -1 elementaarteisenduste (EP) meetodil. Mis tahes mitteainsuse maatriksit A ​​saab taandada ainult veergude (või ainult ridade) EP abil identiteedimaatriksiks E. Kui maatriksi A suhtes täiuslikud EP-d rakendatakse samas järjekorras identiteedimaatriksile E, siis on tulemus pöördmaatriks. Maatriksitel A ja E on mugav sooritada EP samaaegselt, kirjutades mõlemad maatriksid kõrvuti läbi joone. Märgime veel kord, et maatriksi kanoonilise vormi otsimisel saab selle leidmiseks kasutada ridade ja veergude teisendusi. Kui teil on vaja leida pöördmaatriks, peaksite teisendusprotsessis kasutama ainult ridu või ainult veerge.

Näide 2.10. Maatriksi jaoks leidke A -1.

Otsus.Esmalt leiame maatriksi A determinandi
seega on pöördmaatriks olemas ja leiame selle valemiga: , kus A i j (i,j=1,2,3) - algmaatriksi elementide a i j algebralised täiendid.

Kus .

Näide 2.11. Elementaarteisenduste meetodil leidke maatriksi jaoks A -1: A=.

Otsus.Parempoolsele algsele maatriksile määrame samas järjekorras identiteedimaatriksi: . Elementaarveeruteisenduste abil taandame vasakpoolse “poole” identiteediks, sooritades samaaegselt just selliseid teisendusi paremal maatriksil.
Selleks vahetage esimene ja teine ​​veerg: ~ . Esimese lisame kolmandasse veergu ja esimese korrutatuna -2-ga teisele: . Esimesest veerust lahutame kahekordistunud teise ja kolmandast - teise korrutatuna 6-ga; . Lisame kolmanda veeru esimesele ja teisele: . Korrutage viimane veerg -1-ga: . Vertikaalsest ribast paremal olev ruutmaatriks on antud maatriksi A pöördmaatriks.
.

Iga mittedegenereerunud maatriks Ja on olemas ja pealegi unikaalne maatriks A -1 selline, et

A*A -1 =A -1 *A = E,

kus E on sama järku identsusmaatriks nagu A. Maatriksit A ​​-1 nimetatakse maatriksi A pöördmaatriksiks.

Kui keegi unustas, täidetakse identiteedimaatriksis, välja arvatud ühtedega täidetud diagonaal, kõik muud positsioonid nullidega, identiteedimaatriksi näide:

Pöördmaatriksi leidmine adjointmaatriksi meetodil

Pöördmaatriks määratakse järgmise valemiga:

kus A ij - elemendid a ij .

Need. Maatriksi pöördväärtuse arvutamiseks peate arvutama selle maatriksi determinandi. Seejärel leidke algebralised liited kõigi selle elementide jaoks ja tehke nendest uus maatriks. Järgmiseks peate selle maatriksi transportima. Ja jagage uue maatriksi iga element algse maatriksi determinandiga.

Vaatame mõnda näidet.

Leidke maatriksi jaoks A -1

Lahendus Leia A -1 adjointmaatriksi meetodil. Meil on det A = 2. Leia maatriksi A elementide algebralised täiendid. In sel juhul maatriksi elementide algebralised täiendid on maatriksi enda vastavad elemendid, mis võetakse valemi kohase märgiga

Meil on A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Moodustame adjointmaatriksi

Transpordime maatriksi A*:

Leiame pöördmaatriksi valemiga:

Saame:

Kasutage adjointmaatriksi meetodit, et leida A -1, kui

Lahendus.Kõigepealt arvutame välja antud maatriksi, et veenduda pöördmaatriksi olemasolus. Meil on

Siin oleme teise rea elementidele lisanud kolmanda rea ​​elemendid, mis on eelnevalt korrutatud (-1), ja seejärel laiendanud determinanti teise rea võrra. Kuna selle maatriksi definitsioon erineb nullist, on selle pöördmaatriks olemas. Adjungintmaatriksi koostamiseks leiame selle maatriksi elementide algebralised täiendid. Meil on

Vastavalt valemile

transpordime maatriksi A*:

Siis valemi järgi

Pöördmaatriksi leidmine elementaarteisenduste meetodil

Lisaks valemist tulenevale pöördmaatriksi leidmise meetodile (seotud maatriksi meetod) on olemas meetod pöördmaatriksi leidmiseks, mida nimetatakse elementaarteisenduste meetodiks.

Elementaarmaatriksiteisendused

Järgmisi teisendusi nimetatakse elementaarmaatriksteisendusteks:

1) ridade (veergude) permutatsioon;

2) rea (veeru) korrutamine nullist erineva arvuga;

3) rea (veeru) elementidele teise rea (veeru) vastavate elementide lisamine, mis on eelnevalt korrutatud teatud arvuga.

Maatriksi A -1 leidmiseks konstrueerime ristkülikukujuline maatriks B = (A|E) järjekordadest (n; 2n), omistades paremal asuvale maatriksile A identiteedimaatriksi E läbi eraldusjoone:

Kaaluge näidet.

Elementaarteisenduste meetodil leidke A -1, kui

Lahendus. Moodustame maatriksi B:

Tähistage maatriksi B ridu läbi α 1 , α 2 , α 3 . Teeme maatriksi B ridadel järgmised teisendused.