Juhusliku suuruse dispersiooni valem. Dispersioon ja standardhälve MS EXCELIS

Sellest omadusest üksi aga uurimiseks ei piisa juhuslik muutuja. Kujutage ette kahte laskurit, kes lasevad märklauda. Üks laseb täpselt ja tabab keskpunkti lähedalt ja teine ... lihtsalt lõbutsedes ja isegi mitte sihtimist. Aga naljakas on see keskmine tulemus on täpselt sama, mis esimesel laskuril! Seda olukorda illustreerivad tinglikult järgmised juhuslikud muutujad:

"Snaiper" oodatud väärtus on siiski võrdne ja huvitav isiksus»: - see on ka null!

Seega on vaja kvantifitseerida, kui kaugele hajutatud täpid (juhusliku muutuja väärtused) sihtmärgi keskpunkti suhtes (ootus). hästi ja hajumine ladina keelest tõlgitud ainult kui dispersioon .

Vaatame, kuidas see numbriline tunnus määratakse ühes õppetunni 1. osa näites:

Seal leidsime sellele mängule pettumust valmistava matemaatilise ootuse ja nüüd peame arvutama selle dispersiooni, mis tähistatud läbi .

Uurime, kui kaugele on võidud/kaotused "hajutatud" keskmise väärtuse suhtes. Ilmselgelt peame selleks arvutama erinevusi vahel juhusliku suuruse väärtused ja tema matemaatiline ootus:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Nüüd tundub, et on vaja tulemused kokku võtta, kuid see viis ei ole hea - sel põhjusel, et vasakule suunatud võnkumised kustutavad üksteist koos paremale suunatud võnkumisega. Nii näiteks "amatöör" laskur (näide ülal) erinevused saavad olema , ja lisamisel annavad nad nulli, nii et me ei saa hinnangut tema tulistamise hajumise kohta.

Sellest tüütusest mööda saamiseks kaaluge moodulid erinevusi, kuid tehnilistel põhjustel on lähenemine juurdunud, kui need on ruudus. Lahendus on mugavam korraldada tabelis:

Ja siin on vaja arvutada kaalutud keskmine ruudu hälvete väärtus. Mis see on? See on nende oma oodatud väärtus, mis on hajumise mõõt:

– määratlus dispersioon. Definitsioonist on kohe selge, et dispersioon ei saa olla negatiivne- harjutamiseks võtke teadmiseks!

Pidagem meeles, kuidas ootust leida. Korrutage ruudus erinevused vastavate tõenäosustega (tabeli jätk):
- piltlikult öeldes on see "tõmbejõud",
ja võta tulemused kokku:

Kas sa ei arva, et võitude taustal osutus tulemus liiga suureks? Täpselt nii – me tegime ruudu ja selleks, et naasta oma mängu dimensiooni juurde, peame võtma ruutjuure. See väärtus helistas standardhälve ja seda tähistatakse kreeka tähega "sigma":

Mõnikord nimetatakse seda tähendust standardhälve .

Mis on selle tähendus? Kui kaldume matemaatilisest ootusest kõrvale keskmiselt vasakule ja paremale standardhälve:

- siis "koonduvad" sellele intervallile juhusliku suuruse kõige tõenäolisemad väärtused. Mida me tegelikult näeme:

Juhtus aga nii, et hajuvuse analüüsimisel töötatakse peaaegu alati dispersiooni mõistega. Vaatame, mida see mängudega seoses tähendab. Kui laskurite puhul räägime tabamuste "täpsusest" märklaua keskpunkti suhtes, siis siin iseloomustab hajuvus kahte asja:

Esiteks on ilmne, et intressimäärade kasvades suureneb ka dispersioon. Näiteks kui me suurendame 10 korda, siis matemaatiline ootus suureneb 10 korda ja dispersioon suureneb 100 korda (niipea, kui see on ruutväärtus). Kuid pange tähele, et mängureeglid pole muutunud! Muutunud on ainult kursid, jämedalt öeldes panustasime 10 rubla, nüüd 100 rubla peale.

Teiseks rohkem huvitav punkt on see, et dispersioon iseloomustab mängu stiili. Parandage mängude määrad vaimselt mingil kindlal tasemel, ja vaadake, mis siin on:

Madala dispersiooniga mäng on ettevaatlik mäng. Mängija kipub valima kõige usaldusväärsemaid skeeme, kus ta ei kaota/võida korraga liiga palju. Näiteks punane/must süsteem ruletis (vt artikli näidet 4 juhuslikud muutujad) .

Suure dispersiooniga mäng. Teda kutsutakse sageli dispersioon mäng. See on seikluslik või agressiivne mängustiil, kus mängija valib "adrenaliini" skeemid. Jätame vähemalt meelde "Martingale", kus mängus olevad summad on suurusjärkude võrra suuremad kui eelmise lõigu "vaikses" mängus.

Olukord pokkeris on orienteeruv: on nn tihe mängijad, kes kipuvad olema ettevaatlikud ja oma mängurahaga "raputama". (bankroll). Pole üllatav, et nende bankroll ei kõigu palju (madal dispersioon). Ja vastupidi, kui mängijal on suur dispersioon, siis on see agressor. Ta võtab sageli riske, teeb suuri panuseid ja võib nii tohutu panga lõhkuda kui ka puruks minna.

Sama juhtub Forexis ja nii edasi – näiteid on palju.

Pealegi pole kõigil juhtudel vahet, kas mäng on senti või tuhandete dollarite eest. Igal tasemel on oma madala ja kõrge dispersiooniga mängijad. Noh, keskmise võidu eest, nagu mäletame, "vastutustundlik" oodatud väärtus.

Tõenäoliselt märkasite, et dispersiooni leidmine on pikk ja vaevarikas protsess. Kuid matemaatika on helde:

Dispersiooni leidmise valem

See valem tuletatud otse dispersiooni definitsioonist ja panime selle kohe ringlusse. Kopeerin plaadi meie mänguga ülalt:

ja leitud ootus .

Arvutame dispersiooni teisel viisil. Kõigepealt leiame matemaatilise ootuse – juhusliku suuruse ruut . Kõrval matemaatilise ootuse määratlus:

AT sel juhul:

Seega vastavalt valemile:

Nagu öeldakse, tunneta erinevust. Ja praktikas on muidugi parem valemit rakendada (kui tingimus ei nõua teisiti).

Valdame lahendamise ja kujundamise tehnikat:

Näide 6

Leidke selle matemaatiline ootus, dispersioon ja standardhälve.

Seda ülesannet leidub kõikjal ja sellel pole reeglina sisulist tähendust.
Võite ette kujutada mitut numbritega lambipirni, mis hullumajas teatud tõenäosustega süttivad :)

Lahendus: Põhilised arvutused on mugav kokku võtta tabelis. Esiteks kirjutame algandmed kahele ülemisele reale. Seejärel arvutame paremas veerus tooted, seejärel ja lõpuks summad:

Tegelikult on peaaegu kõik valmis. Kolmandale reale joonistati valmis matemaatiline ootus: .

Dispersioon arvutatakse järgmise valemiga:

Ja lõpuks standardhälve:
- isiklikult ümardan tavaliselt 2 komakohani.

Kõiki arvutusi saab teha kalkulaatoriga ja veelgi parem - Excelis:

Siin on raske eksida :)

Vastus:

Need, kes soovivad, saavad oma elu veelgi lihtsustada ja minu eeliseid ära kasutada kalkulaator (demo), mis mitte ainult ei lahenda koheselt see ülesanne, vaid ka ehitada temaatiline graafika (tule varsti). Programm suudab laadige alla raamatukogus– kui olete alla laadinud vähemalt ühe õppematerjal või saada teine tee. Aitäh projekti toetamise eest!

Paar ülesannet sõltumatu otsus:

Näide 7

Arvutage definitsiooni järgi eelmise näite juhusliku suuruse dispersioon.

Ja sarnane näide:

Näide 8

Diskreetse juhusliku suuruse annab tema enda jaotusseadus:

Jah, juhusliku suuruse väärtused võivad olla üsna suured (näide alates päris töö) , ja siin kasuta võimalusel Excelit. Nagu, muide, näites 7 - see on kiirem, usaldusväärsem ja meeldivam.

Lahendused ja vastused lehe allosas.

Tunni 2. osa lõpus analüüsime veel üht tüüpiline ülesanne, võiks isegi öelda, väike rebus:

Näide 9

Diskreetsel juhuslikul muutujal võib olla ainult kaks väärtust: ja , ja . Tõenäosus, matemaatiline ootus ja dispersioon on teada.

Lahendus: Alustame teadmata tõenäosusega. Kuna juhuslik suurus võib võtta ainult kaks väärtust, siis vastavate sündmuste tõenäosuste summa:

ja sellest ajast peale .

Jääb üle leida ..., lihtne öelda :) Aga noh, hakkas pihta. Matemaatilise ootuse määratluse järgi:
- asendage teadaolevad väärtused:

- ja sellest võrrandist ei saa midagi enamat välja pigistada, välja arvatud see, et saate selle tavalises suunas ümber kirjutada:

või:

O järgmised sammud Ma arvan, et võite arvata. Loome ja lahendame süsteemi:

Kümnendkohad- see on muidugi täielik häbi; korrutage mõlemad võrrandid 10-ga:

ja jagage 2-ga:

See on palju parem. Esimesest võrrandist väljendame:
(see on lihtsam viis)- asendus 2. võrrandis:

Me ehitame ruuduline ja tehke lihtsustusi:

Korrutame arvuga:

Tulemusena, ruutvõrrand, leidke selle diskrimineerija:
- täiuslik!

ja saame kaks lahendust:

1) kui , siis ;

2) kui , siis.

Esimene väärtuste paar vastab tingimusele. Suure tõenäosusega on kõik õige, kuid sellegipoolest kirjutame jaotusseaduse üles:

ja tehke kontroll, nimelt leidke ootus:

Paljudel juhtudel on vaja tutvustada teist numbriline tunnus kraadi mõõtmiseks hajutatus, väärtuste levik, võetakse juhusliku muutujana ξ , oma matemaatilise ootuse ümber.

Definitsioon. Juhusliku suuruse dispersioon ξ helistas numbrile.

D= M(ξ-M ξ) 2 . (1)

Teisisõnu, dispersioon on matemaatiline ootus juhusliku suuruse väärtuste ruudus kõrvalekalde kohta selle keskmisest väärtusest.

helistas keskmine ruut hälve

kogused ξ .

Kui dispersioon iseloomustab keskmine suurus ruudus hälve ξ alates Mξ, siis võib arvu pidada mõneks keskmine omadus hälve ise, täpsemalt | suurusjärk ξ-Mξ |.

Definitsioon (1) hõlmab dispersiooni kahte järgmist omadust.

1. Dispersioon püsiv väärtus võrdub nulliga. See on üsna kooskõlas hajumise kui "levimõõdu" visuaalse tähendusega.

Tõepoolest, kui

ξ \u003d C, siis Mξ = C ja see tähendab Dξ = M(C-C) 2 = M 0 = 0.

2. Juhusliku suuruse korrutamisel ξ peal konstantne arv Selle dispersiooniga korrutatakse C 2-ga

D(Cξ) = C 2 Dξ . (3)

Tõesti

D(Cξ) = M(C

= M(C .

3. Dispersiooni arvutamiseks on järgmine valem:

. (4)

Selle valemi tõestus tuleneb matemaatilise ootuse omadustest.

Meil on:

4. Kui väärtused ξ 1 ja ξ 2 on sõltumatud, siis on nende summa dispersioon võrdne nende dispersioonide summaga:

Tõestus . Tõestuseks kasutame matemaatilise ootuse omadusi. Lase Mξ 1 = m 1 , Mξ 2 = m 2 siis.

Valem (5) on tõestatud.

Kuna juhusliku suuruse dispersioon on definitsiooni järgi väärtuse matemaatiline ootus ( ξ-m) 2 , kus m = Mξ , siis dispersiooni arvutamiseks võite kasutada 7. jao II peatükis saadud valemeid.

Nii et kui ξ on olemas DSV koos levitamisseadusega

x 1	x 2	...
lk 1	lk 2	...

siis on meil:

. (7)

Kui a ξ pidev juhuslik suurus jaotustihedusega p(x), siis saame:

Dξ= . (8)

Kui dispersiooni arvutamiseks kasutatakse valemit (4), võib saada muid valemeid, nimelt:

, (9)

kui väärtus ξ diskreetne ja

Dξ= , (10)

kui ξ jaotatud tihedusega lk(x).

Näide 1. Laske väärtust ξ on ühtlaselt jaotunud intervallile [ a,b]. Kasutades valemit (10) saame:

Saab näidata, et normaalseaduse kohaselt jaotatud juhusliku suuruse dispersioon tihedusega

p(x)= , (11)

on võrdne σ 2 .

See selgitab tiheduse avaldises (11) sisalduva parameetri σ tähendust tavaline seadus; σ seal on keskmine standardhälve kogused ξ.

Näide 2 . Leidke juhusliku suuruse dispersioon ξ jagatud binoomseaduse järgi.

Lahendus. Kasutades ξ esitust kujul

ξ = ξ 1 + ξ 2 + n(vt näide 2 §7 ptk II) ja dispersioonide lisamise valemi rakendamine sõltumatud kogused, saame

Dξ = Dξ 1 + Dξ 2 + Dξn .

Mis tahes koguste hajutamine ξi (i= 1,2, n) arvutatakse otse:

Dξi = M(ξi) 2 - (Mξ i) 2 = 0 2 q+ 1 2 lk- lk 2 = lk(1-lk) = pq.

Lõpuks saame

Dξ= npq, kus q = 1 -lk.

Rühmitatud andmete jaoks jääkdispersioon - keskmine grupisisesed dispersioonid:

Kus σ 2 j on j-nda rühma rühmasisene dispersioon.

Grupeerimata andmete jaoks jääkdispersioon on ligikaudse täpsuse mõõt, st. regressioonijoone lähendamine algandmetele:
kus y(t) on prognoos vastavalt trendi võrrandile; y t – dünaamika algseeria; n on punktide arv; p on regressioonivõrrandi kordajate arv (selgitavate muutujate arv).
Selles näites nimetatakse seda dispersiooni erapooletu hinnang.

Näide nr 1. Ühe ühingu kolme ettevõtte töötajate jaotust tariifikategooriate kaupa iseloomustavad järgmised andmed:

Töötaja palgakategooria	Tööliste arv ettevõttes
Töötaja palgakategooria	ettevõte 1	ettevõte 2	ettevõte 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Määratlege:
1. hajutamine iga ettevõtte kohta (grupisisene dispersioon);
2. rühmasiseste dispersioonide keskmine;
3. rühmadevaheline hajutamine;
4. kogu dispersioon.

Lahendus.
Enne probleemi lahendamise jätkamist on vaja välja selgitada, milline funktsioon on tõhus ja milline faktoriaalne. Vaadeldavas näites on efektiivne tunnus "Tariifikategooria" ja teguritunnus "Ettevõtte number (nimi).
Siis on meil kolm rühma (ettevõtteid), mille jaoks on vaja arvutada grupi keskmine ja grupisisesed dispersioonid:

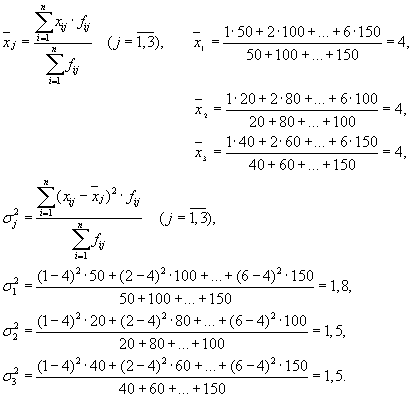
Ettevõte	rühma keskmine,	rühmasisene dispersioon,
1	4	1,8

Grupisisese dispersiooni keskmine ( jääkdispersioon) arvutatakse järgmise valemiga:

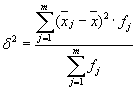
kus saab arvutada:

või:

siis:
Kogu dispersioon on võrdne: s 2 \u003d 1,6 + 0 \u003d 1,6.
Kogu dispersiooni saab arvutada ka ühe kahest järgmisest valemist:

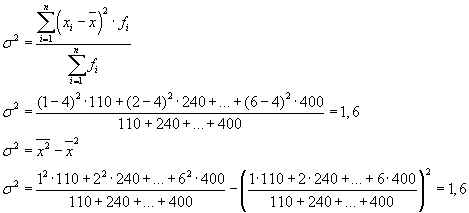
Praktiliste probleemide lahendamisel tuleb sageli tegeleda märgiga, mis võtab vaid kaks alternatiivset väärtust. Sel juhul ei räägi nad mitte tunnuse konkreetse väärtuse kaalust, vaid selle osatähtsusest agregaadis. Kui uuritavat tunnust omavate populatsiooniüksuste osakaal on tähistatud " R"ja mitte omamine - läbi" q”, siis saab dispersiooni arvutada valemiga:
s2 = p × q

Näide nr 2. Vastavalt brigaadi kuue töötaja arengu andmetele määrake rühmadevaheline dispersioon ja hinnake töövahetuse mõju nende tööviljakusele, kui summaarne dispersioon on 12,2.

Töötava brigaadi nr	Tööväljund, tk.
Töötava brigaadi nr	esimeses vahetuses	2. vahetuses
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Lahendus. Esialgsed andmed

X	f1	f2	f 3	f4	f5	f6	Kokku
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Kokku	31	33	37	37	40	38

Siis on meil 6 rühma, mille jaoks on vaja arvutada rühma keskmised ja rühmasisesed dispersioonid.
1. Leidke iga rühma keskmised väärtused.

2. Leidke iga rühma keskmine ruut.

Arvutuse tulemused võtame kokku tabelis:

Grupi number	Grupi keskmine	Grupisisene dispersioon
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Grupisisene dispersioon iseloomustab uuritava (tulemusliku) tunnuse muutust (variatsiooni) rühma sees kõigi tegurite mõjul, välja arvatud rühmitamise aluseks olev tegur:
Arvutame rühmasiseste dispersioonide keskmise valemi abil:

4. Gruppidevaheline dispersioon iseloomustab uuritava (tulemusliku) tunnuse muutumist (variatsiooni) rühmituse aluseks oleva teguri (faktoriaalse tunnuse) mõjul.
Rühmadevaheline hajutamine on määratletud järgmiselt:

kus

Siis

Kogu dispersioon iseloomustab uuritava (tulemusliku) tunnuse muutumist (variatsiooni) eranditult kõigi tegurite (faktoriaalsete tunnuste) mõjul. Ülesande tingimuse järgi on see võrdne 12,2-ga.
Empiiriline korrelatsioon mõõdab, kui suure osa saadud atribuudi kogukõikumistest põhjustab uuritav tegur. See on faktoriaalse dispersiooni ja kogu dispersiooni suhe:

Määrame empiirilise korrelatsiooni:

Tunnustevahelised seosed võivad olla nõrgad või tugevad (lähedased). Nende kriteeriume hinnatakse Chaddocki skaalal:
0,1 0,3 0,5 0,7 0,9 Meie näites on seos tunnuse Y teguri X vahel nõrk
Määramiskoefitsient.

Määratleme määramiskoefitsiendi:

Seega on 0,67% variatsioonist tingitud tunnuste erinevustest ja 99,37% muudest teguritest.
Järeldus: sel juhul ei sõltu töötajate toodang konkreetse vahetuse tööst, s.t. töövahetuse mõju nende tööviljakusele ei ole märkimisväärne ja on tingitud muudest teguritest.

Näide nr 3. Keskmise põhjal palgad ja ruudus hälbed selle väärtusest kahe töötajate rühma puhul, leidke kogu dispersioon, rakendades dispersioonide lisamise reeglit:

Lahendus:
Grupisiseste erinevuste keskmine

Rühmadevaheline hajutamine on määratletud järgmiselt:

Kogu dispersioon on: 480 + 13824 = 14304

Peamised statistika variatsiooni üldistavad näitajad on dispersioon ja standardhälve.

Dispersioon seda aritmeetiline keskmine iga tunnuse väärtuse ruudus hälbed kogukeskmisest. Dispersiooni nimetatakse tavaliselt hälvete keskmiseks ruuduks ja tähistatakse  2 . Olenevalt algandmetest saab dispersiooni arvutada aritmeetilise keskmise, lihtsa või kaalutud keskmise järgi:

 kaalumata (liht)dispersioon;

 kaalutud dispersioon.

Standardhälve on absoluutmõõtmete üldistav tunnus variatsioonid omadus kokkuvõttes. Seda väljendatakse samades ühikutes kui märk (meetrites, tonnides, protsentides, hektarites jne).

Standardhälve on dispersiooni ruutjuur ja seda tähistatakse :

 kaalumata standardhälve;

 kaalutud standardhälve.

Standardhälve on keskmise usaldusväärsuse mõõt. Mida väiksem on standardhälve, seda paremini peegeldab aritmeetiline keskmine kogu esindatud populatsiooni.

Standardhälbe arvutamisele eelneb dispersiooni arvutamine.

Kaalutud dispersiooni arvutamise protseduur on järgmine:

1) määrake aritmeetiline kaalutud keskmine:

2) arvutage valikute kõrvalekalded keskmisest:

3) ruudus iga variandi kõrvalekalle keskmisest:

4) korrutage kõrvalekalded ruudus kaalude (sagedustega):

5) teeb kokkuvõtte laekunud töödest:

6) saadud summa jagatakse kaalude summaga:

Näide 2.1

Arvutage aritmeetiline kaalutud keskmine:

Keskmisest kõrvalekallete väärtused ja nende ruudud on toodud tabelis. Määratleme dispersiooni:

Standardhälve on võrdne:

Kui lähteandmed esitatakse intervallina levitamise seeriad , siis peate esmalt määrama funktsiooni diskreetse väärtuse ja seejärel rakendama kirjeldatud meetodit.

Näide 2.2

Näitame kolhoosi külvipinna jaotuse andmete nisusaagi järgi intervallrea dispersiooni arvutamist.

Aritmeetiline keskmine on:

Arvutame dispersiooni:

6.3. Dispersiooni arvutamine üksikandmete valemi järgi

Arvutustehnika dispersioon keeruline ja suured väärtused valikud ja sagedused võivad olla tülikad. Dispersiooniomadusi kasutades saab arvutusi lihtsustada.

Dispersioonil on järgmised omadused.

1. Muutuva tunnuse kaalude (sageduste) vähenemine või suurendamine teatud arvu kordi ei muuda dispersiooni.

2. Iga tunnuse väärtuse vähendamine või suurendamine sama konstantse väärtuse võrra AGA dispersioon ei muutu.

3. Iga funktsiooni väärtuse vähendamine või suurendamine teatud arv kordi k vähendab või suurendab vastavalt dispersiooni k 2 korda standardhälve  sisse küks kord.

4. Tunnuse dispersioon suvalise väärtuse suhtes on alati suurem kui dispersioon aritmeetilise keskmise suhtes keskmise ja suvalise väärtuse erinevuse ruudu võrra:

Kui a AGA 0, siis saame järgmise võrdsuse:

st tunnuse dispersioon on võrdne tunnuse väärtuste keskmise ruudu ja keskmise ruudu vahega.

Iga omadust saab dispersiooni arvutamisel kasutada eraldi või koos teistega.

Dispersiooni arvutamise protseduur on lihtne:

1) määrata aritmeetiline keskmine :

2) ruudu aritmeetiline keskmine:

3) ruudustage seeria iga variandi kõrvalekalle:

X i 2 .

4) leidke valikute ruutude summa:

5) jagage optsioonide ruutude summa nende arvuga, st määrake keskmine ruut:

6) määrab tunnuse keskmise ruudu ja keskmise ruudu erinevuse:

Näide 3.1 Meil on järgmised andmed töötajate tootlikkuse kohta:

Teeme järgmised arvutused:

Juhusliku muutuja dispersioon on selle muutuja väärtuste leviku mõõt. Väike dispersioon tähendab, et väärtused on rühmitatud üksteise lähedal. Suur dispersioon näitab väärtuste tugevat hajumist. Statistikas kasutatakse juhusliku suuruse dispersiooni mõistet. Näiteks kui võrrelda kahe suuruse väärtuste dispersiooni (näiteks mees- ja naispatsientide vaatlustulemusi), saate testida mõne muutuja olulisust. Dispersiooni kasutatakse ka konstrueerimisel statistilised mudelid, kuna väike hälve võib olla märk sellest, et sobitate väärtusi üle.

Sammud

Näidise dispersiooni arvutamine

Salvestage näidisväärtused. Enamasti on statistikutele kättesaadavad ainult teatud populatsioonide valimid. Näiteks statistikud ei analüüsi reeglina kõigi Venemaa autode agregaadi ülalpidamiskulusid - nad analüüsivad suvaline näidis mitmest tuhandest autost. Selline valim aitab määrata keskmist kulu auto kohta, kuid tõenäoliselt on saadud väärtus tegelikust kaugel.
- Näiteks analüüsime juhuslikus järjekorras võetuna kohvikus müüdud kuklite arvu 6 päeva jooksul. Näidis on järgmine vaade: 17, 15, 23, 7, 9, 13. See on valim, mitte populatsioon, sest meil pole andmeid müüdud kuklite kohta iga kohviku avatud päeva kohta.
- Kui teile antakse üldkogum, mitte väärtuste valim, liikuge järgmise jaotise juurde.
Kirjutage üles valimi dispersiooni arvutamise valem. Dispersioon on mõne suuruse väärtuste leviku mõõt. Mida lähemal on dispersiooni väärtus nullile, seda lähemal on väärtused rühmitatud. Kui töötate väärtuste valimiga, kasutage dispersiooni arvutamiseks järgmist valemit:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2)) on dispersioon. Dispersiooni mõõdetakse ruutühikud mõõdud.
- x i (\displaystyle x_(i))- iga proovi väärtus.
- x i (\displaystyle x_(i)) peate lahutama x̅, ruudu ja seejärel liitma tulemused.
- x̅ – valimi keskmine (valimi keskmine).
- n on valimi väärtuste arv.
Arvutage valimi keskmine. Seda tähistatakse kui x̅. Valimi keskmine arvutatakse nagu tavaline aritmeetiline keskmine: liidetakse kõik valimi väärtused ja jagatakse tulemus valimi väärtuste arvuga.
- Meie näites lisage näidis olevad väärtused: 15 + 17 + 23 + 7 + 9 + 13 = 84
  Nüüd jagage tulemus valimi väärtuste arvuga (meie näites on neid 6): 84 ÷ 6 = 14.
  Valimi keskmine x̅ = 14.
- Valimi keskmine on keskväärtus, mille ümber valimi väärtused jaotuvad. Kui valimi klastris olevad väärtused valimi ümber on keskmised, on dispersioon väike; vastasel juhul on dispersioon suur.
Lahutage valimi igast väärtusest valimi keskmine. Nüüd arvutage erinevus x i (\displaystyle x_(i))- x̅, kus x i (\displaystyle x_(i))- iga proovi väärtus. Iga saadud tulemus näitab, mil määral erineb konkreetne väärtus valimi keskmisest, st kui kaugel see väärtus on valimi keskmisest.
- Meie näites:
  x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
  x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
  x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
  x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
  x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
  x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
- Saadud tulemuste õigsust on lihtne kontrollida, kuna nende summa peab olema võrdne nulliga. See on seotud keskmise väärtuse määratlusega, kuna negatiivsed väärtused(kaugused keskmisest väärtusest väiksemate väärtusteni) on täielikult kompenseeritud positiivsed väärtused(kaugused keskmistest suurte väärtusteni).
Nagu eespool märgitud, erinevuste summa x i (\displaystyle x_(i))- x̅ peab olema võrdne nulliga. See tähendab et keskmine dispersioon on alati võrdne nulliga, mis ei anna mingit ettekujutust teatud suuruse väärtuste levikust. Selle probleemi lahendamiseks tehke kõik erinevused ruuduga x i (\displaystyle x_(i))- x̅. Selle tulemusel saate ainult positiivsed numbrid, mis lisamisel ei anna kunagi 0.
- Meie näites:
  (x 1 (\displaystyle x_(1))-x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
  (x 2 (\displaystyle (x_(2)))-x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
  9 2 = 81
  (-7) 2 = 49
  (-5) 2 = 25
  (-1) 2 = 1
- Olete leidnud erinevuse ruudu - x̅) 2 (\displaystyle ^(2)) iga valimi väärtuse kohta.
Arvutage erinevuste ruudu summa. See tähendab, et leidke valemi osa, mis on kirjutatud järgmiselt: ∑[( x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))]. Siin tähistab märk Σ iga väärtuse ruudu erinevuste summat x i (\displaystyle x_(i)) proovis. Olete juba leidnud erinevused ruudus (x i (\displaystyle (x_(i))-x̅) 2 (\displaystyle ^(2)) iga väärtuse jaoks x i (\displaystyle x_(i)) proovis; nüüd lihtsalt lisage need ruudud.
- Meie näites: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
Jagage tulemus n - 1-ga, kus n on valimi väärtuste arv. Mõni aeg tagasi jagasid statistikud valimi dispersiooni arvutamiseks tulemuse lihtsalt n-ga; sel juhul saad ruudu dispersiooni keskmise, mis sobib ideaalselt antud valimi dispersiooni kirjeldamiseks. Kuid pidage meeles, et iga proov on vaid väike osa. elanikkonnast väärtused. Kui võtate teistsuguse proovi ja teete samad arvutused, saate erineva tulemuse. Nagu selgus, annab n-ga jagamine 1-ga (ja mitte ainult n-ga) rohkem täpne hinnang rahvastiku dispersioon, mis teid huvitab. Jagamine n - 1-ga on muutunud tavapäraseks, seega sisaldub see valimi dispersiooni arvutamise valemis.
- Meie näites sisaldab valim 6 väärtust, st n = 6.
  Valimi dispersioon = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
Dispersiooni ja standardhälbe erinevus. Pange tähele, et valem sisaldab eksponenti, seega mõõdetakse dispersiooni analüüsitud väärtuse ruutühikutes. Mõnikord on sellist väärtust üsna raske kasutada; sellistel juhtudel kasutage standardhälvet, mis on võrdne ruutjuur dispersioonist. Seetõttu on valimi dispersioon tähistatud kui s 2 (\displaystyle s^(2)), a standardhälve proovid - kuidas s (\displaystyle s).
- Meie näites on valimi standardhälve: s = √33,2 = 5,76.
Rahvastiku dispersiooni arvutamine
1. Analüüsige mõnda väärtuste kogumit. Komplekt sisaldab kõiki vaadeldava koguse väärtusi. Näiteks kui uurida elanike vanust Leningradi piirkond, siis hõlmab rahvaarv kõigi selle piirkonna elanike vanust. Agregaadiga töötamise korral on soovitatav luua tabel ja sisestada sellesse agregaadi väärtused. Kaaluge järgmist näidet:
  - Ühes kindlas ruumis on 6 akvaariumi. Igas akvaariumis on järgmine arv kalu:
    x 1 = 5 (\displaystyle x_(1)=5)
    x 2 = 5 (\displaystyle x_(2)=5)
    x 3 = 8 (\displaystyle x_(3)=8)
    x 4 = 12 (\displaystyle x_(4) = 12)
    x 5 = 15 (\displaystyle x_(5) = 15)
    x 6 = 18 (\displaystyle x_(6) = 18)
2. Kirjutage üles populatsiooni dispersiooni arvutamise valem. Kuna populatsioon sisaldab teatud suuruse kõiki väärtusi, võimaldab järgmine valem saada populatsiooni dispersiooni täpse väärtuse. Populatsiooni dispersiooni eristamiseks valimi dispersioonist (mis on vaid hinnang) kasutavad statistikud erinevaid muutujaid:
  - σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n
  - σ 2 (\displaystyle ^(2))- populatsiooni dispersioon (sigma ruudus). Dispersiooni mõõdetakse ruutühikutes.
  - x i (\displaystyle x_(i))- iga koondväärtus.
  - Σ on summa märk. See tähendab iga väärtuse kohta x i (\displaystyle x_(i)) lahutage μ, ruudus ja seejärel lisage tulemused.
  - μ on rahvastiku keskmine.
  - n on väärtuste arv üldpopulatsioonis.
3. Arvutage rahvastiku keskmine.Üldrahvastikuga töötades tähistatakse selle keskmist väärtust μ (mu). Populatsiooni keskmine arvutatakse tavalise aritmeetilise keskmisena: liidetakse kõik üldkogumi väärtused ja jagatakse tulemus üldkogumi väärtuste arvuga.
  - Pidage meeles, et keskmisi ei arvutata alati aritmeetilise keskmisena.
  - Meie näites tähendab populatsioon: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
4. Lahutage üldkogumi igast väärtusest üldkogumi keskmine. Mida lähemal on erinevuse väärtus nullile, seda lähemal on konkreetne väärtus üldkogumi keskmisele. Leidke erinevus populatsiooni iga väärtuse ja selle keskmise vahel ning näete esmalt väärtuste jaotust.
  - Meie näites:
    x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
    x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
    x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
    x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
    x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
    x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
5. Ruudu iga saadud tulemus. Erinevused on nii positiivsed kui ka negatiivsed; kui paned need väärtused numbrireale, siis asuvad need rahvastiku keskmisest paremal ja vasakul. See ei sobi dispersiooni arvutamiseks, kuna positiivne ja negatiivsed arvudüksteist kompenseerida. Seetõttu asetage iga erinevus ruuduga, et saada ainult positiivsed arvud.
  - Meie näites:
    (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) iga populatsiooni väärtuse kohta (i = 1 kuni i = 6):
    (-5,5)2 (\displaystyle ^(2)) = 30,25
    (-5,5)2 (\displaystyle ^(2)), kus x n (\displaystyle x_(n)) – viimane väärtusüldpopulatsioonis.
  - Saadud tulemuste keskmise väärtuse arvutamiseks peate leidma nende summa ja jagama selle n-ga: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / n
  - Nüüd kirjutame ülaltoodud selgituse muutujate abil: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n ja saada valem populatsiooni dispersiooni arvutamiseks.