Pravilo lopitalnog izražavanja. L'Hopitalovo pravilo i otkrivanje neizvjesnosti

Pravilo kaže da ako funkcije f(x) i g(x) imaju sljedeći skup uvjeta:

onda postoji . Štoviše, teorem vrijedi i za druge baze (dokaz će biti dan za navedenu).

Priča

Metodu za otkrivanje ove vrste nesigurnosti objavio je Lopital u svom djelu "Analiza infinitezimala", objavljenom godine. U predgovoru ovom djelu Lopital ističe da se bez imalo zadrške služio otkrićima Leibniza i braće Bernoulli te "nema ništa protiv toga da svoja autorska prava pokažu na što god žele". Johann Bernoulli je preuzeo cjelokupno L'Hospitalovo djelo, a posebno je, nakon L'Hospitalove smrti, objavio djelo pod znamenitim naslovom "Poboljšanje moje metode objavljene u Infinitezimal Analysis za određivanje vrijednosti razlomka, brojnika i nazivnika od kojih ponekad nestane", .

Dokaz

Omjer infinitezimala

Dokažimo teorem za slučaj kada su limesi funkcija jednaki nuli (tzv. nesigurnost oblika ).

Budući da gledamo funkcije f i g samo u desnom punktiranom polususjedstvu točke a, možemo ih kontinuirano redefinirati na ovom mjestu: neka f(a) = g(a) = 0 . Uzmimo malo x iz polususjedstva koje razmatramo i primijenimo Cauchyjev teorem na segment. Ovim teoremom dobivamo:

ali f(a) = g(a) = 0 , zato .

src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> za krajnju granicu i src="/pictures/wiki/files/101/e8b2f2b8861947c8728d4d1be40366d4.png" border="0"> za beskonačnost ,

što je definicija limita omjera funkcija.

Omjer beskonačno velik

Dokažimo teorem za nesigurnosti oblika .

Neka, za početak, granica omjera derivacija bude konačna i jednaka A. Zatim, dok se trudi x do a s desne strane, ovaj odnos se može napisati kao A+ α , gdje je α - (1). Zapišimo ovaj uvjet:

Idemo popraviti t iz segmenta i primijeniti Cauchyjev teorem na sve x iz segmenta:

, što može dovesti do sljedeća vrsta:

Za x, dovoljno blizu a, izraz ima smisla; granica prvog faktora desne strane jednako jedan(jer f(t) i g(t) su konstante i f(x) i g(x) teže beskonačnosti). Stoga je ovaj faktor jednak 1 + β, gdje je β infinitezimalna funkcija kao x do a desno. Zapisujemo definiciju ove činjenice koristeći istu vrijednost kao u definiciji za α:

Utvrdili smo da se omjer funkcija može prikazati u obliku (1 + β)( A+ α) i . Za bilo koji dani, može se pronaći tako da je modul razlike između omjera funkcija i A bio manji, što znači da je granica omjera funkcija stvarno jednaka A .

Ako granica A je beskonačno (recimo da je jednako plus beskonačno), tada

(x))(g"(x))>2M)" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">.

U definiciji β uzet ćemo ; prvi faktor desne strane bit će veći od 1/2 kada x, dovoljno blizu a, a zatim src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">.

Za ostale baze, dokazi su slični danim.

Primjeri

(Samo ako brojnik i nazivnik OBA teže ili 0 ; ili ; ili .)

Zaklada Wikimedia. 2010. godine.

Pogledajte što je "L'Hopitalovo pravilo" u drugim rječnicima:

Povijesno netočan naziv za jedno od osnovnih pravila za otkrivanje nesigurnosti. L. p. pronašao je I. Bernoulli i izvijestio G. L'Hopitala (Vidi L'Hopital), koji je objavio ovo pravilo 1696. Vidi Neodređeni izrazi ... Velika sovjetska enciklopedija

Otkrivanje nesigurnosti oblika smanjenjem granice omjera funkcija na granicu omjera derivacija funkcija koje se razmatraju. Dakle, za slučaj kada realne funkcije f i g definirani su u isprekidanom desnom susjedstvu numeričke točke ... ... Matematička enciklopedija

Bernoullijevo L'Hospitalovo pravilo je metoda za pronalaženje granica funkcija, otkrivajući nesigurnosti oblika u. Teorem koji opravdava metodu kaže da je pod određenim uvjetima granica omjera funkcija jednaka granici omjera njihovih derivacija. ... ... Wikipedia

U matematičkoj analizi, L'Hopitalovo pravilo je metoda za pronalaženje granica funkcija, otkrivajući nesigurnosti oblika 0 / 0 i. Teorem koji opravdava metodu kaže da je pod određenim uvjetima granica omjera funkcija jednaka granici ... ... Wikipedia

Ovisnosti koordinata o vremenu pri kretanju materijalna točka u avionu

Odredite brzinu modula (

A. Modul brzine materijalne točke od vremena izražava se formulom:

B. . Modul ubrzanja materijalne točke od vremena izražava se formulom:

Ove jednadžbe opisuju gibanje materijalne točke s konstantnom akceleracijom

Satelit se okreće oko Zemlje u kružnoj orbiti na visini

Satelit koji se kreće po kružnoj orbiti podložan je sili gravitacije

Ova se formula može pojednostaviti na sljedeći način. Na tjelesnu težinu

Na ovaj način, brzina linije satelit je

i kutnu brzinu

Obje kuglice razmatrane u problemu čine zatvoreni sustav i u slučaju elastični udar i moment količine gibanja sustava i mehanička (kinetička) energija su očuvani. Zapišimo oba zakona očuvanja (uzimajući u obzir nepomičnost druge kuglice prije udara):

Tako je upadna (prva) kuglica uslijed udarca smanjila svoju brzinu s 1,05 m/s na 0,45 m/s, iako se nastavila kretati u istom smjeru, a prethodno nepomična (druga) kuglica poprimila je brzinu jednaku na 1,5 m/s i sada se obje kuglice gibaju po istoj ravnoj liniji iu istom smjeru.

Budući da se masa plina u cilindru mijenja, početno i konačno stanje plina u cilindru ne mogu se povezati ni Boyle-Mariotteovim ni Charlesovim zakonom.Ako se plin u cilindru mijenja izjednačavanjem, tada se početno i krajnje stanje plina u cilindru ne mogu se povezati Boyle-Mariotteovim zakonom.svako stanje napišite Mendeleev-Clapeyronovu jednadžbu

Kako pronaći limit funkcije bez korištenja lopitalovog pravila

Verzija sustava:
7.47 (16.04.2018)

Opće vijesti:
13.04.2018, 10:33

Posljednje pitanje:
26.07.2018, 15:23

Zadnji odgovor:
27.07.2018, 13:48

ODSJEK Matematika

Konzultacije i rješavanje problema iz algebre, geometrije, analize, diskretne matematike.

Najbolji stručnjaci u ovoj sekciji

Zdravo! Imam problema s ovim pitanjem:

Pronađite limit funkcije bez korištenja L'Hopitalovog pravila

lim (2x+3) [ ln (x+2) - ln x ] (ispod lim piše "x teži beskonačnosti")

Bilo je nekoliko primjera ograničenja u zadatku, ali ovaj je bio zbunjujući. Ne znam kako to riješiti. Možda nekako iskoristiti drugu divnu granicu, ali kako (samo ova misao pada na pamet)?

Dopustite mi samo da pitam u istom pitanju postoji li takva izjava problema (ako postoji, objavit ću je kasnije kao plaćeno pitanje): Primjenom Taylorove formule s ostatkom u Lagrangeovom obliku na funkciju, izračunajte vrijednost s točnošću od 0,001; a = 0,29.
Ovdje ne razumijem koja funkcija? Nije postavljeno (?), zadatak zvuči točno onako kako sam ga zapisao. Možda možete sami preuzeti tu funkciju, ali koju?

Status: Konzultacije zatvorene

Pozdrav Aleksandrkib!
To je 2. koji trebate koristiti! Za početak, pojednostavimo:
lim (2x+3) [ ln (x+2) - ln x ] = lim (2x+3) ln ((x+2)/x) = lim (2x+3) ln (1+2/x) = lim ln ((1+2/x)^(2x+3)) = lim ln ((1+2/x)^2x)+lim ln ((1+2/x)^3) [druga granica je nula, jer 2/x teži nuli i ln 1 = 0]
Napravimo promjenu y = x/2, tada je lim ln ((1+2/x)^2x) = 4 lim ln ((1+1/y)^y) = 4 * ln e =4. Odgovor: 4.

Mora postojati neka funkcija.

Šaljite poruke
moderatori mogu
samo članovi portala.
PRIJAVA NA PORTAL »
registracija"

L'Hopitalovo pravilo: teorija i primjeri rješenja

L'Hopitalovo pravilo i otkrivanje neizvjesnosti

Otkrivanje nesigurnosti oblika 0/0 ili ∞/∞ i nekih drugih nesigurnosti koje nastaju pri izračunavanju limita omjera dviju infinitezimalnih ili beskonačno velikih funkcija uvelike je pojednostavljeno pomoću L'Hopitalovog pravila (zapravo dva pravila i komentar na njih ).

suština pravila L'Hospitala je da u slučaju kada izračun granice omjera dviju beskonačno malih ili beskonačno velikih funkcija daje nesigurnosti oblika 0/0 ili ∞/∞, granica omjera dviju funkcija može se zamijeniti granicom omjer njihovih derivata i, na taj način, može se dobiti određeni rezultat.

Prijeđimo na formulaciju L'Hopitalovih pravila.

L'Hopitalovo pravilo za slučaj granice dviju beskonačno malih vrijednosti. Ako funkcije f(x) i g(x a a, i u ovom susjedstvu g‘(x a međusobno jednaki i jednaki nuli

(),

tada je granica omjera tih funkcija jednaka granici omjera njihovih izvodnica

().

L'Hôpitalovo pravilo za slučaj limita dviju beskonačno velikih količina. Ako funkcije f(x) i g(x) diferencijabilne u nekoj okolini točke a, uz moguću iznimku točke a, i u ovom susjedstvu g‘(x)≠0 i ako i ako limiti ovih funkcija kao x teže vrijednosti funkcije u točki a međusobno jednaki i jednaki do beskonačnosti

(),

Drugim riječima, za nesigurnosti oblika 0/0 ili ∞/∞, granica omjera dviju funkcija jednaka je granici omjera njihovih derivacija, ako potonje postoje (konačne ili beskonačne).

Opaske.

1. Pravila L'Hopitala također se primjenjuju kada funkcionira f(x) i g(x) nisu definirani na x = a.

2. Ako se pri računanju granice omjera derivacija funkcija f(x) i g(x) ponovno dolazimo do nesigurnosti oblika 0/0 ili ∞/∞, tada L'Hopitalova pravila treba primjenjivati više puta (najmanje dva puta).

3. L'Hopitalova pravila su također primjenjiva kada argument funkcija (x) teži tome konačni broj a, i do beskonačnosti ( x → ∞).

Nesigurnosti drugih vrsta također se mogu svesti na nesigurnosti tipa 0/0 i ∞/∞.

Otkrivanje nesigurnosti tipa "nula podijeljeno s nulom" i "beskonačno podijeljeno s beskonačnim"

Primjer 1

x=2 dovodi do neodređenosti oblika 0/0. Dakle, izvod svake funkcije i dobivamo

U brojniku je izračunata derivacija polinoma, a u nazivniku derivacija kompleksa logaritamska funkcija. Prije posljednjeg znaka jednakosti izračunata je uobičajena granica, zamjenjujući dvojku umjesto x-a.

Primjer 2 Izračunajte granicu omjera dviju funkcija koristeći L'Hospitalovo pravilo:

Primjer 3 Izračunajte granicu omjera dviju funkcija koristeći L'Hospitalovo pravilo:

Riješenje. Zamjena u dana funkcija vrijednosti x=0 dovodi do neodređenosti oblika 0/0. Stoga izračunavamo derivacije funkcija u brojniku i nazivniku i dobivamo:

Primjer 4 Izračunati

Riješenje. Zamjenom vrijednosti x jednake plus beskonačno u zadanu funkciju dolazi do neodređenosti oblika ∞/∞. Stoga primjenjujemo L'Hopitalovo pravilo:

Komentar. Prijeđimo na primjere u kojima L'Hopitalovo pravilo treba primijeniti dva puta, odnosno doći do granice omjera drugih derivacija, jer je granica omjera prvih derivacija nesigurnost oblika 0/0 ili ∞/∞.

Primjer 5 Izračunajte granicu omjera dviju funkcija koristeći L'Hospitalovo pravilo:

Ovdje se L'Hospitalovo pravilo primjenjuje dvaput, budući da i granica omjera funkcija i granica omjera derivacija daju nesigurnost oblika ∞/∞.

Primjer 6 Izračunati

Ovdje se L'Hospitalovo pravilo primjenjuje dva puta, budući da i granica omjera funkcija i granica omjera derivacija daju nesigurnost oblika 0/0.

Primjer 7 Izračunati

Ovdje se L'Hopitalovo pravilo primjenjuje dva puta, jer i granica omjera funkcija i granica omjera derivacija prvo daju nesigurnost oblika - ∞/∞, a zatim nesigurnost oblika 0/0.

Primjer 8 Izračunati

Ovdje se L'Hospitalovo pravilo primjenjuje dva puta, budući da i granica omjera funkcija i granica omjera derivacija prvo daju nesigurnost oblika ∞/∞, a zatim nesigurnost oblika 0/0.

Sami primijenite L'Hopitalovo pravilo i vidite rješenje

Primjer 9 Izračunati

Trag. Ovdje morate napuhati malo više nego inače na transformaciji izraza ispod znaka granice.

Primjer 10 Izračunati

Trag. Ovdje će se L'Hopitalovo pravilo morati primijeniti tri puta.

Otkrivanje nesigurnosti oblika "nula pomnožena s beskonačnošću"

Primjer 11. Izračunati

(ovdje smo transformirali nesigurnost oblika 0∙∞ u oblik ∞/∞, jer

a zatim primijenio L'Hopitalova pravila).

Primjer 12. Izračunati

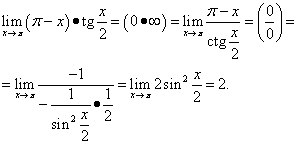
Ovaj primjer koristi trigonometrijski identitet.

Otkrivanje nesigurnosti tipa "nula na nulti potenciju", "beskonačno na nulti potenciju" i "jedan na beskonačnu potenciju"

Nesigurnosti oblika ili se obično svode na oblik 0/0 ili ∞/∞ pomoću logaritma funkcije oblika

Za izračunavanje granice izraza treba koristiti logaritamski identitet, čiji je poseban slučaj također svojstvo logaritma .

Korištenjem logaritamske identičnosti i svojstva kontinuiteta funkcije (da ide preko predznaka granice), granicu treba izračunati na sljedeći način:

Posebno treba pronaći granicu izraza u eksponentu i graditi e do pronađenog stupnja.

Primjer 13

Primjer 14 Izračunajte koristeći L'Hopitalovo pravilo

Primjer 15 Izračunajte koristeći L'Hopitalovo pravilo

Izračunajte granicu izraza u eksponentu

Otkrivanje nesigurnosti oblika "beskonačno minus beskonačno"

Ovo su slučajevi u kojima izračun granice razlike funkcija dovodi do nesigurnosti "beskonačno minus beskonačno": .

Izračun takve granice prema L'Hopitalovom pravilu u opći pogled kako slijedi:

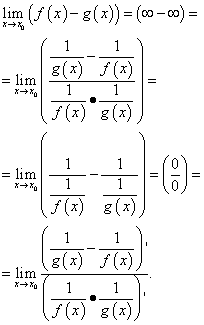
Ove transformacije često rezultiraju složeni izrazi, stoga je preporučljivo koristiti takve transformacije razlike funkcija kao smanjenje na zajednički nazivnik, množenje i dijeljenje istim brojem, korištenje trigonometrijski identiteti itd.

Primjer 16 Izračunajte koristeći L'Hopitalovo pravilo

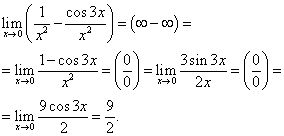
Primjer 17. Izračunajte koristeći L'Hopitalovo pravilo

Izračunajte granice pomoću lopitalovog pravila

Neizvjesnost se također ne opire pretvoriti u ili:

Pravila bolnice L'Hospital

Nastavljamo razvijati temu koju nam je dobacio član Pariške akademije znanosti, markiz Guillaume Francois de Lopital. Članak dobiva izraženu praktičnu boju i u prilično uobičajenom zadatku potrebno je:

Kako se ne bismo smanjivali, granicu indikatora izračunavamo zasebno:

Još jedan Papuanac također odustaje pred formulom. U ovom slučaju:

L'Hopitalova pravila su vrlo moćna metoda koja vam omogućuje brzo i učinkovito uklanjanje ovih nesigurnosti, nije slučajno da se u zbirkama zadataka, u testovima, testovima, često nalazi stabilan pečat: "izračunajte granicu, bez korištenja L'Hopitalovog pravila". Posvećen podebljano zahtjev je moguć sa čista savjest dodijeliti i bilo kojem ograničenju lekcije Ograničenja. Primjeri rješenja, Izvanredna ograničenja. Metode rješavanja ograničenja, Izvanredne ekvivalencije, gdje se javlja nesigurnost "nula do nule" ili "beskonačno do beskonačno". Čak i ako je zadatak formuliran kratko - "izračunaj granice", tada se implicitno podrazumijeva da ćete koristiti sve što želite, ali ne pravila L'Hospitala.

Metamorfoze se nastavljaju, sada je neizvjesnost "nula na nulu" izašla na vidjelo. U principu, možete se riješiti kosinusa tako da naznačite da teži jedinici. Ali mudra je strategija osigurati da nitko ničemu ne dođe do dna. Stoga, odmah primjenjujemo L'Hopitalovo pravilo, kako zahtijeva uvjet problema:

Sličan zadatak za samostalno rješenje:

Kao što vidite, razlikovanje brojnika i nazivnika dovelo nas je do odgovora s pola kruga: pronašli smo dvije jednostavne izvedenice, zamijenili u njima "dva" i pokazalo se da je nesigurnost netragom nestala!

Izračunajte limit funkcije koristeći L'Hopitalovo pravilo

Zauzvrat, drugovi koji piju i egzotičniji drugovi izvlače se na svjetlo. Metoda transformacije je jednostavna i standardna:

Razmatrani primjer je uništen i kroz divne granice , sličan slučaj razmatran je na kraju članka Kompleksne granice.

Odmah ću rezervirati da će pravila biti dana u sažetom "praktičnom" obliku, a ako morate položiti teoriju, preporučujem da se obratite udžbeniku za rigoroznije izračune.

6) Primjenjivo posljednje pravilo informacije do druge divne granice

Objavljivanje nesigurnosti svodi se na prethodno razmatrane nesigurnosti. If, i at, tada primijenite transformaciju

beskonačnost ili nula po nula je primjena L'Hopitalovog pravila: granica omjera dva

U slučaju zadnje tri nesigurnosti moraju se primijeniti transformacije

5) Postoji neodređenost oblika beskonačno u beskonačno.

beskonačno male ili dvije beskonačno velike funkcije jednaka je granici omjera njihovih izvodnica,

3) S obzirom na nesigurnost primijeniti prethodno pravilo

Izračun limita prema L'Hopitalovom pravilu

Učinkovit način za izračunavanje limita funkcija koje imaju singularitete tipa infinity na

Riješenje. 1) Zamjenom utvrđujemo da imamo nesigurnost oblika nula po nula. Riješiti se

Opet smo dobili neizvjesnost forme i ponovno primijenili L'Hospitalovo pravilo

2) Kao iu prethodnom primjeru, imamo neizvjesnost. Prema L'Hopitalovom pravilu, nalazimo

Primjena L'Hopitalovog pravila pokazala je sve mogućnosti u otkrivanju nesigurnosti.

Broj je odabran na takav način da je zadovoljena jednakost (1) i, prema tome, . Dakle, za funkciju na intervalu

U blizini točke x 0 , tj. na (x 0 ,x), uvjeti Cauchyjevog teorema su zadovoljeni za funkcije f(x) i g(x). Dakle, postoji točka sO(x 0 , x) takva da je

L'Hopitalovo pravilo

Međutim, moguća je situacija kada će funkcija imati ekstrem u točki x 0 u slučaju kada derivacija ne postoji.

Neka je funkcija n puta diferencijabilna u susjedstvu točke x 0. Nađimo polinom stupnja ne višeg od n-1, tako da

Neka su funkcije f(x) i g(x) kontinuirane i diferencijabilne u nekoj okolini točke x 0 , osim same točke x 0 . Neka, . Onda ako postoji granica omjera derivacija funkcija, onda postoji granica omjera samih funkcija, a one su međusobno jednake, tj. .

Zaključak: eksponencijalna funkcija(y=a n) uvijek raste brže od zakona potencije (y=x n).

Kao primjer primjene Maclaurinove formule određujemo broj članova u proširenju funkcije u smislu formula izračunati njegovu vrijednost s točnošću od 0,001 za bilo koji x iz intervala [-1,1].

Definicija: Funkcija se zove neopadajući (nepovećavajući) do (a;b) ako je za bilo koji x 1 Objavljeno u Korisni članci

Određivanje limita funkcije u točki prema L'Hopitalovom pravilu

Određivanje limita funkcije, prema L'Hopitalovom pravilu, otkrivajući nesigurnosti oblika 0/0 i ∞/∞.

Kalkulator u nastavku pronalazi granicu funkcije prema L'Hospitalovom pravilu (kroz derivacije brojnika i nazivnika). Pogledajte opis pravila u nastavku.

Limit funkcije u točki - L'Hopitalovo pravilo

Valjane operacije: + - / * ^ Konstante: pi Funkcije: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

L'Hopitalovo pravilo

Ako su ispunjeni sljedeći uvjeti:

granice funkcija f(x) i g(x) su međusobno jednake i jednake nuli ili beskonačnosti:
ili;
funkcije g(x) i f(x) su diferencijabilne u punktiranoj okolini a;
derivacija funkcije g(x) nije jednaka nuli u punktiranoj okolini a
i postoji ograničenje omjera derivacije f(x) i derivacije g(x):

Tada postoji granica omjera funkcija f(x) i g(x):
,

A jednaka je granici omjera derivacije funkcije f(x) i derivacije funkcije g(x):

Formula dopušta korištenje broja pi (pi), eksponenta (e), sljedećih matematičkih operatora:

+ - dodatak
— - oduzimanje
* - množenje
/ - podjela
^ - potenciranje

i sljedeće značajke:

sqrt - kvadratni korijen

korijen str- korijen stupnja str, na primjer root3(x) je kubni korijen

exp - e do navedene snage

lb - logaritam s bazom 2

lg - logaritam s bazom 10

u- prirodni logaritam(na temelju e)

log str- osnovni logaritam str, na primjer log7(x) - logaritam s bazom 7

sinus – sinus

cos - kosinus

tg - tangenta

ctg - kotangens

sec – sekanta

cosec – kosakans

arcsin – arcsinus

arccos - ark kosinus

arctg - arc tangenta

arcctg - arc tangenta

arcsec – arcsekans

arccosec – arkkosekans

versin – versinus

vercos - pokrovna sinusna

haversin – haversinus

exsec – eksekant

excsc - ekskosekant

sh - hiperbolički sinus

ch - hiperbolički kosinus

th - hiperbolička tangenta

cth - hiperbolički kotangens

sech - hiperbolički sekans

csch - hiperbolički kosekans

aps- apsolutna vrijednost(modul)

sgn - signum (znak)

Najam Gazelle ili Sable kombija bez vozača Gazelle-Business, 1 vozač + 2 putnika. Tijelo: 3 m. dužina, 2 m. visina, butka. Volumen kocke 10.5. Motor: UMZ-4216 (benzin), euro-4, 106,8 […]
Podaci za plaćanje poreza i doprinosa u 2017-2018 Podaci za plaćanje poreza u 2017-2018 sastavni su dio svake uplate. Ispravno popunite nalog za plaćanje […]
Usvojen je postupak za razmatranje od strane Vijeća Federacije Državna duma savezni zakon(Članak 103. – 110.) Članak 103. Donošenje saveznog zakona na razmatranje […]
Kriminalni zakon. Opći dio Kaznenopravno pravilo Kaznenopravno pravilo je pravilo ponašanja koje utvrđuje država koje daje sudionicima odnosi s javnošću […]
Veličina kazne za kašnjenje hipoteke je ograničena Dana 24. srpnja na snagu će stupiti zakon koji ograničava visinu kazne za neispunjenje ili nepravilno ispunjenje […]
Kazna za ubojstvo s otežanim okolnostima U skladu s važećim kaznenim zakonom, jednostavno ubojstvo (1. dio članka 105. Kaznenog zakona Ruske Federacije) „kažnjivo je kaznom zatvora […]

Objavljivanje nesigurnosti oblika 0/0 ili ∞/∞ i nekih drugih nesigurnosti koje se javljaju u proračunu ograničiti odnos dviju infinitezimalnih ili beskonačno velikih funkcija znatno je pojednostavljen uz pomoć L'Hospitalovog pravila (zapravo dva pravila i napomene o njima).

Prijeđimo na formulaciju L'Hopitalovih pravila.

L'Hopitalovo pravilo za slučaj granice dviju beskonačno malih vrijednosti. Ako funkcije f(x) i g(x aa, i u ovom susjedstvu g"(x a međusobno jednaki i jednaki nuli

().

L'Hôpitalovo pravilo za slučaj limita dviju beskonačno velikih količina. Ako funkcije f(x) i g(x) diferencijabilne u nekoj okolini točke a, uz moguću iznimku točke a, i u ovom susjedstvu g"(x)≠0 i ako i ako limiti ovih funkcija kao x teže vrijednosti funkcije u točki a međusobno jednaki i jednaki do beskonačnosti

(),

tada je granica omjera tih funkcija jednaka granici omjera njihovih izvodnica

().

Drugim riječima, za nesigurnosti oblika 0/0 ili ∞/∞, granica omjera dviju funkcija jednaka je granici omjera njihovih derivacija, ako potonje postoje (konačne ili beskonačne).

Opaske.

1. Pravila L'Hopitala također se primjenjuju kada funkcionira f(x) i g(x) nisu definirani na x = a.

3. L'Hopitalova pravila također se mogu primijeniti kada argument funkcije (x) teži nekonačnom broju a, i do beskonačnosti ( x → ∞).

Nesigurnosti drugih vrsta također se mogu svesti na nesigurnosti tipa 0/0 i ∞/∞.

Otkrivanje nesigurnosti tipa "nula podijeljeno s nulom" i "beskonačno podijeljeno s beskonačnim"

Primjer 1

x=2 dovodi do neodređenosti oblika 0/0. Dakle, izvod svake funkcije i dobivamo

U brojniku je izračunata derivacija polinoma, au nazivniku - izvod složene logaritamske funkcije. Prije posljednjeg znaka jednakosti, uobičajeno ograničiti, zamjenjujući dvojku umjesto x.

Primjer 2 Izračunajte granicu omjera dviju funkcija koristeći L'Hospitalovo pravilo:

Riješenje. Supstitucija u zadanu funkciju vrijednosti x

Primjer 3 Izračunajte granicu omjera dviju funkcija koristeći L'Hospitalovo pravilo:

Riješenje. Supstitucija u zadanu funkciju vrijednosti x=0 dovodi do neodređenosti oblika 0/0. Stoga izračunavamo derivacije funkcija u brojniku i nazivniku i dobivamo:

Primjer 4 Izračunati

Riješenje. Zamjenom vrijednosti x jednake plus beskonačno u zadanu funkciju dolazi do neodređenosti oblika ∞/∞. Stoga primjenjujemo L'Hopitalovo pravilo:

Sami primijenite L'Hopitalovo pravilo i vidite rješenje

Otkrivanje nesigurnosti oblika "nula pomnožena s beskonačnošću"

Primjer 12. Izračunati

Riješenje. Dobivamo

Ovaj primjer koristi trigonometrijski identitet.

Otkrivanje nesigurnosti tipa "nula na nulti potenciju", "beskonačno na nulti potenciju" i "jedan na beskonačnu potenciju"

Nesigurnosti oblika ili se obično svode na oblik 0/0 ili ∞/∞ pomoću logaritma funkcije oblika

Za izračunavanje limita izraza treba koristiti logaritamski identitet, čiji je poseban slučaj svojstvo logaritma .

Korištenjem logaritamske identičnosti i svojstva kontinuiteta funkcije (da ide preko predznaka granice), granicu treba izračunati na sljedeći način:

Posebno treba pronaći granicu izraza u eksponentu i graditi e do pronađenog stupnja.

Primjer 13

Riješenje. Dobivamo

Primjer 14 Izračunajte koristeći L'Hopitalovo pravilo

Riješenje. Dobivamo

Izračunajte granicu izraza u eksponentu

Primjer 15 Izračunajte koristeći L'Hopitalovo pravilo

Ovaj matematički kalkulator online će vam pomoći ako je potrebno izračunati ograničenje funkcije. Program granična rješenja ne samo da daje odgovor na problem, on vodi detaljno rješenje s objašnjenjima, tj. prikazuje napredak izračuna ograničenja.

Ovaj program može biti koristan za srednjoškolce općeobrazovne škole u pripremi za kontrolni rad i ispite, prilikom provjere znanja prije ispita, roditeljima za kontrolu rješavanja mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo unajmiti učitelja ili kupiti nove udžbenike? Ili samo želite to obaviti što je prije moguće? domaća zadaća matematika ili algebra? U tom slučaju također možete koristiti naše programe s detaljnim rješenjem.

Dakle, možete izvršiti svoje vlastiti trening i/ili njihovo osposobljavanje mlađa braća ili sestara, dok se povećava stupanj obrazovanja u području zadataka koji se rješavaju.

Unesite izraz funkcije
Izračunajte ograničenje

Utvrđeno je da neke skripte potrebne za rješavanje ovog zadatka nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

U pregledniku vam je onemogućen JavaScript.
JavaScript mora biti omogućen da bi se rješenje pojavilo.
Ovdje su upute o tome kako omogućiti JavaScript u svom pregledniku.

Jer Puno je ljudi koji žele riješiti problem, vaš zahtjev je u redu.
Nakon nekoliko sekundi, rješenje će se pojaviti ispod.
Molim pričekajte sekund...

Ako ti uočio grešku u rješenju, tada možete pisati o tome u obrascu za povratne informacije.
Ne zaboravi navesti koji zadatak ti odluči što unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Granica funkcije pri x-> x 0

Neka je funkcija f(x) definirana na nekom skupu X i neka je točka $x_0 \u X $ ili $x_0 \notin X $

Uzmite iz X niz točaka osim x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
konvergirajući prema x*. Vrijednosti funkcije u točkama ovog niza također čine numerički niz
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
te se može postaviti pitanje postojanja njegove granice.

Definicija. Broj A naziva se granica funkcije f (x) u točki x \u003d x 0 (ili u x -> x 0), ako je za bilo koji niz (1) vrijednosti argumenta x koja konvergira k x 0, različitom od x 0, odgovarajući niz (2) funkcije vrijednosti konvergira k broju A.

$$ \lim_(x\to x_0)( f(x)) = A $$

Funkcija f(x) može imati samo jednu granicu u točki x 0. To proizlazi iz činjenice da slijed
(f(x n)) ima samo jednu granicu.

Postoji još jedna definicija limita funkcije.

Definicija Broj A naziva se limitom funkcije f(x) u točki x = x 0 ako za bilo koji broj $\varepsilon > 0 $ postoji broj $\delta > 0 $ takav da za sve \ (x \in X, \; x \neq x_0 \) koja zadovoljava nejednakost $|x-x_0| Korištenjem logičkih simbola, ova se definicija može napisati kao
\((\forall \varepsilon > 0) (\postoji \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Primijetite da nejednakosti \(x \neq x_0 , \; |x-x_0| Prva definicija temelji se na pojmu granice niz brojeva, zbog čega se često naziva definicijom "jezika niza". Druga definicija naziva se definicija "jezika \(\varepsilon - \delta $".
Ove dvije definicije limita funkcije su ekvivalentne i možete koristiti bilo koju od njih, ovisno o tome koja je prikladnija za rješavanje određenog problema.

Imajte na umu da se definicija limita funkcije "u jeziku nizova" također naziva definicijom limita funkcije prema Heineu, a definicija limita funkcije "u jeziku $\varepsilon - \delta $" naziva se i definicija limita funkcije prema Cauchyju.

Granica funkcije pri x->x 0 - i pri x->x 0 +

U nastavku ćemo koristiti pojmove jednostranih limesa funkcije koji su definirani na sljedeći način.

Definicija Broj A naziva se desnom (lijevom) granicom funkcije f (x) u točki x 0 ako za bilo koji niz (1) koji konvergira k x 0, čiji su elementi x n veći (manji) od x 0 , odgovarajući niz (2) konvergira u A.

Simbolički je napisano ovako:
$$ \lim_(x \to x_0+) f(x) = A \; \lijevo(\lim_(x \to x_0-) f(x) = A \desno) $$

Može se dati ekvivalentna definicija jednostranih limita funkcije "u jeziku $\varepsilon - \delta $":

Definicija broj A naziva se desnom (lijevom) granicom funkcije f(x) u točki x 0 ako za bilo koji $\varepsilon > 0 $ postoji $\delta > 0 $ takav da za sve x koji zadovoljavaju nejednakosti \(x_0 Simbolični unosi:

\((\forall \varepsilon > 0) (\postoji \delta > 0) (\forall x, \; x_0

Već smo se počeli baviti limitima i njihovim rješavanjem. Nastavimo u vrućoj potjeri i bavimo se rješenjem ograničenja prema L'Hopitalovu pravilu. Ovaj jednostavno pravilo može vam pomoći da izađete iz podmuklih i teških zamki koje učitelji tako vole koristiti u primjerima na kontrolnom softveru viša matematika i matematičke analize. Rješenje po L'Hopitalovom pravilu je jednostavno i brzo. Glavna stvar je biti u mogućnosti razlikovati.

L'Hopitalovo pravilo: povijest i definicija

Zapravo, ovo nije baš L'Hopitalovo pravilo, nego pravilo L'Hospital-Bernoulli. Formulirao švicarski matematičar Johann Bernoulli, i Francuzi Guillaume Lopital prvi put objavio u svom udžbeniku infinitezimala u slavnom 1696 godina. Možete li zamisliti kako su ljudi morali riješiti ograničenja s otkrivanjem neizvjesnosti prije nego što se to dogodilo? Nismo.

Prije nego što nastavite s analizom L'Hopitalovog pravila, preporučamo pročitati uvodni članak o metodama za njihovo rješavanje. Često se u zadacima nalazi formulacija: pronađite granicu bez korištenja L'Hopitalovog pravila. O tehnikama koje će vam u tome pomoći možete pročitati i u našem članku.

Ako imate posla s granicama razlomka dviju funkcija, budite spremni: uskoro ćete se susresti s neizvjesnošću oblika 0/0 ili beskonačno/beskonačno. Što to znači? U brojniku i nazivniku izrazi teže nuli ili beskonačnosti. Što učiniti s takvim limitom, na prvi je pogled potpuno neshvatljivo. No, primijenite li L'Hopitalovo pravilo i malo razmislite, sve dolazi na svoje mjesto.

Ali formulirajmo L'Hospital-Bernoullijevo pravilo. Da budemo savršeno precizni, izražava se teoremom. L'Hopitalovo pravilo, definicija:

Ako su dvije funkcije diferencijabilne u okolini točke x=a nestaju u ovoj točki, a postoji granica omjera derivacija ovih funkcija, zatim for x težeći tome a postoji granica omjera samih funkcija koja je jednaka granici omjera derivacija.

Zapišimo formulu i sve će odmah postati lakše. L'Hopitalovo pravilo, formula:

Budući da nas zanima praktična strana problema, ovdje nećemo iznositi dokaz ovog teorema. Morat ćete nam vjerovati na riječ ili ga pronaći u bilo kojem udžbeniku matematike i uvjeriti se da je teorem točan.

Usput! Za naše čitatelje sada postoji popust od 10% na

Otkrivanje nesigurnosti prema L'Hopitalovom pravilu

Koje neizvjesnosti L'Hospitalovo pravilo može pomoći u otkrivanju? Ranije smo uglavnom govorili o neizvjesnosti 0/0 . Međutim, to nije jedina neizvjesnost s kojom se može susresti. Evo drugih vrsta neizvjesnosti:

Razmotrimo transformacije koje se mogu koristiti za dovođenje ovih nesigurnosti u oblik 0/0 ili beskonačno/beskonačno. Nakon transformacije bit će moguće primijeniti L'Hospital-Bernoullijevo pravilo i klikati primjere poput oraha.

Nesigurnost vrste beskonačnosti/beskonačnosti svodi na neodređenost forme 0/0 jednostavna transformacija:

Neka postoji proizvod dviju funkcija, od kojih jedna prva teži nuli, a druga - beskonačnosti. Primijenimo transformaciju, a umnožak nule i beskonačnosti pretvara se u neodređenost 0/0 :

Pronaći granice s nesigurnostima tipa beskonačnost minus beskonačnost koristimo sljedeću transformaciju koja dovodi do neizvjesnosti 0/0 :

Da biste koristili L'Hopitalovo pravilo, morate biti u mogućnosti uzimati derivate. Ispod je tablica izvedenica elementarne funkcije, koje možete koristiti pri rješavanju primjera, kao i pravila za izračunavanje derivacija složenih funkcija:

Sada prijeđimo na primjere.

Primjer 1

Pronađite granicu prema L'Hospitalovom pravilu:

Primjer 2

Izračunajte pomoću L'Hopitalovog pravila:

Važna točka! Ako limes druge i sljedećih derivacija funkcija postoji za x težeći tome a , tada se L'Hopitalovo pravilo može primijeniti nekoliko puta.

Nađimo granicu ( n – prirodni broj). Da biste to učinili, primijenite L'Hospitalovo pravilo n jednom:

Želimo vam puno sreće u učenju matematička analiza. A ako trebate pronaći granicu koristeći L'Hopitalovo pravilo, napišite sažetak prema L'Hopitalovom pravilu, izračunajte korijene diferencijalna jednadžba ili čak izračunati tenzor tromosti tijela, obratite se našim autorima. Oni će vam rado pomoći da shvatite zamršenost rješenja.