Formula za disperziju slučajne varijable. Varijanca i standardna devijacija u MS EXCEL-u

Međutim, sama ova karakteristika nije dovoljna za proučavanje slučajna varijabla. Zamislite dva strijelca koji pucaju u metu. Jedan precizno šutira i pogađa blizu centra, a drugi ... samo se zabavlja a ni ne cilja. Ali ono što je smiješno je to prosjek rezultat će biti potpuno isti kao kod prvog strijelca! Ovu situaciju uslovno ilustruju sljedeće slučajne varijable:

"Snajper" očekivana vrijednost je jednako, međutim, i zanimljiva ličnost»: - takođe je nula!

Stoga, postoji potreba da se kvantifikuje koliko daleko rasuti metke (vrijednosti slučajne varijable) u odnosu na centar mete (očekivanje). dobro i rasipanje prevedeno sa latinskog samo kao disperzija .

Pogledajmo kako se ova numerička karakteristika određuje u jednom od primjera iz 1. dijela lekcije:

Tamo smo pronašli razočaravajuće matematičko očekivanje ove igre, a sada moramo izračunati njenu varijansu, koja označeno kroz .

Hajde da saznamo koliko su pobede/gubici "razbacani" u odnosu na prosečnu vrednost. Očigledno, za ovo moramo izračunati razlike između vrijednosti slučajne varijable i ona matematičko očekivanje:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Čini se da je sada potrebno sumirati rezultate, ali ovaj način nije dobar - iz razloga što će se oscilacije lijevo poništiti jedna drugu sa oscilacijama udesno. Tako, na primjer, "amaterski" strijelac (primjer iznad) razlike će biti , a kada se dodaju dat će nulu, tako da nećemo dobiti nikakvu procjenu raspršenosti njegovog pucanja.

Da biste zaobišli ovu smetnju, razmislite moduli razlike, ali iz tehničkih razloga, pristup se ukorijenio kada se kvadriraju. Pogodnije je rasporediti rješenje u tablicu:

I ovdje počinje računati prosjećna težina vrijednost kvadrata odstupanja. Šta je? Njihovo je očekivana vrijednost, što je mjera raspršenja:

– definicija disperzija. Iz definicije je odmah jasno da varijansa ne može biti negativna- obratite pažnju na vežbu!

Prisjetimo se kako pronaći očekivanje. Pomnožite kvadratne razlike sa odgovarajućim vjerovatnoćama (nastavak tabele):
- figurativno rečeno, ovo je "vlačna sila",
i sumirajte rezultate:

Ne mislite li da je na pozadini dobitaka rezultat ispao prevelik? Tako je – bili smo na kvadrat, a da bismo se vratili na dimenziju naše igre, moramo uzeti kvadratni korijen. Ova vrijednost pozvao standardna devijacija i označava se grčkim slovom "sigma":

Ponekad se ovo značenje naziva standardna devijacija .

Šta je njegovo značenje? Ako odstupimo od matematičkog očekivanja lijevo i desno po sredini standardna devijacija:

– tada će najvjerovatnije vrijednosti slučajne varijable biti „koncentrirane“ na ovom intervalu. Šta zapravo vidimo:

Međutim, dogodilo se da se u analizi raspršenja gotovo uvijek operira konceptom disperzije. Hajde da vidimo šta to znači u vezi sa igricama. Ako u slučaju strijelaca govorimo o "preciznosti" pogodaka u odnosu na centar mete, onda ovdje disperzija karakterizira dvije stvari:

Prvo, očigledno je da kako se stope povećavaju, varijansa se takođe povećava. Dakle, na primjer, ako povećamo za 10 puta, onda će se matematičko očekivanje povećati za 10 puta, a varijansa će se povećati za 100 puta (čim je kvadratna vrijednost). Ali imajte na umu da se pravila igre nisu promijenila! Samo su se stope promijenile, grubo govoreći, prije smo se kladili na 10 rubalja, sada 100.

Drugo, više zanimljiva poenta je da varijansa karakteriše stil igre. Mentalno popravi stopu igre na nekom određenom nivou, i pogledajte šta je šta ovdje:

Igra niske varijance je oprezna igra. Igrač ima tendenciju da bira najpouzdanije šeme, u kojima ne gubi/pobeđuje previše u jednom trenutku. Na primjer, crveno/crni sistem u ruletu (vidi primjer 4 članka slučajne varijable) .

Igra velike varijance. Često je zovu disperzija igra. Ovo je avanturistički ili agresivni stil igre gdje igrač bira "adrenalinske" šeme. Da se barem setimo "Martingale", u kojoj su sume u igri za redove veličine veće od „tihe“ igre iz prethodnog paragrafa.

Situacija u pokeru je indikativna: postoje tzv čvrsto igrače koji imaju tendenciju da budu oprezni i "tresaju" svojim sredstvima za igru (bankroll). Nije iznenađujuće da njihov bankroll ne fluktuira mnogo (mala varijansa). Suprotno tome, ako igrač ima veliku varijansu, onda je to agresor. Često rizikuje, pravi velike opklade i može i razbiti ogromnu banku i propasti.

Ista stvar se dešava i na Forexu, i tako dalje - ima mnogo primera.

Štaviše, u svim slučajevima nije bitno da li je igra za peni ili za hiljade dolara. Svaki nivo ima svoje igrače niske i velike varijacije. Pa za prosječnu pobjedu, koliko se sjećamo, "odgovorno" očekivana vrijednost.

Vjerovatno ste primijetili da je pronalaženje varijanse dug i mukotrpan proces. Ali matematika je velikodušna:

Formula za pronalaženje varijanse

Ova formula proizilazi direktno iz definicije varijanse i odmah je puštamo u promet. Kopiraću ploču sa našom igrom odozgo:

i pronađeno očekivanje.

Izračunavamo varijansu na drugi način. Prvo, pronađimo matematičko očekivanje - kvadrat slučajne varijable. By definicija matematičkog očekivanja:

AT ovaj slučaj:

Dakle, prema formuli:

Kako kažu, osjetite razliku. A u praksi je, naravno, bolje primijeniti formulu (osim ako uvjet ne zahtijeva drugačije).

Savladavamo tehniku ​​rešavanja i projektovanja:

Primjer 6

Pronađite njegovo matematičko očekivanje, varijansu i standardnu ​​devijaciju.

Ovaj zadatak se nalazi svuda i, po pravilu, nema smislenog značenja.
Možete zamisliti nekoliko sijalica sa brojevima koje svijetle u ludnici sa određenim vjerovatnoćama :)

Odluka: Pogodno je sumirati glavne proračune u tabeli. Prvo upisujemo početne podatke u gornja dva reda. Zatim izračunavamo proizvode, zatim i na kraju zbrojeve u desnoj koloni:

Zapravo, skoro sve je spremno. U trećem redu nacrtano je gotovo matematičko očekivanje: .

Disperzija se izračunava po formuli:

I na kraju, standardna devijacija:
- lično, obično zaokružujem na 2 decimale.

Svi proračuni se mogu izvršiti na kalkulatoru, a još bolje - u Excelu:

Ovde je teško pogrešiti :)

Odgovori:

Oni koji žele mogu još više pojednostaviti svoj život i iskoristiti moje kalkulator (demo), što ne samo da će odmah riješiti ovaj zadatak, ali i graditi tematske grafike (dođi uskoro). Program može preuzeti u biblioteci– ako ste preuzeli barem jedan edukativni materijal ili dobiti drugi način. Hvala na podršci projektu!

Par zadataka za nezavisna odluka:

Primjer 7

Izračunajte varijansu slučajne varijable iz prethodnog primjera po definiciji.

I sličan primjer:

Primjer 8

Diskretna slučajna varijabla je data vlastitim zakonom distribucije:

Da, vrijednosti slučajne varijable mogu biti prilično velike (primjer iz pravi posao) , a ovdje, ako je moguće, koristite Excel. Kao, usput, u primjeru 7 - brže je, pouzdanije i ugodnije.

Rješenja i odgovori na dnu stranice.

Na kraju 2. dijela lekcije analiziraćemo još jednu tipičan zadatak, moglo bi se čak reći, mali rebus:

Primjer 9

Diskretna slučajna varijabla može uzeti samo dvije vrijednosti: i , i . Vjerovatnoća, matematičko očekivanje i varijansa su poznati.

Odluka: Počnimo s nepoznatom vjerovatnoćom. Kako slučajna varijabla može uzeti samo dvije vrijednosti, onda je zbir vjerovatnoća odgovarajućih događaja:

i od tada .

Ostaje da se pronađe..., lako je reći :) Ali dobro, počelo je. Po definiciji matematičkog očekivanja:
- zamijeniti poznate vrijednosti:

- i ništa se više ne može istisnuti iz ove jednadžbe, osim što je možete prepisati u uobičajenom smjeru:

ili:

O sljedeći koraci Mislim da možete pogoditi. Kreirajmo i riješimo sistem:

Decimale- ovo je, naravno, potpuna sramota; pomnožite obje jednačine sa 10:

i podijeli sa 2:

To je mnogo bolje. Iz 1. jednačine izražavamo:
(ovo je lakši nacin)- zamjena u 2. jednačini:

Mi gradimo na kvadrat i napravi pojednostavljenja:

Množimo sa:

Kao rezultat, kvadratna jednačina, pronađite njegov diskriminant:
- savršeno!

i dobijamo dva rješenja:

1) ako , onda ;

2) ako , zatim .

Prvi par vrijednosti zadovoljava uslov. Sa velikom vjerovatnoćom, sve je tačno, ali, ipak, zapisujemo zakon distribucije:

i izvršite provjeru, odnosno pronađite očekivanje:

U mnogim slučajevima postaje neophodno uvesti još jedan numerička karakteristika za merenje stepena disperzija, širenje vrijednosti, uzeta kao slučajna varijabla ξ , oko njegovog matematičkog očekivanja.

Definicija. Varijanca slučajne varijable ξ nazvao broj.

D= M(ξ-M ξ) 2 . (1)

Drugim riječima, disperzija je matematičko očekivanje kvadrata odstupanja vrijednosti slučajne varijable od njene srednje vrijednosti.

pozvao srednji kvadrat odstupanje

količine ξ .

Ako disperzija karakteriše prosječne veličine kvadratna devijacija ξ od Mξ, onda se broj može smatrati nekim prosečna karakteristika samo odstupanje, tačnije, veličina | ξ-Mξ |.

Definicija (1) implicira sljedeća dva svojstva disperzije.

1. Disperzija konstantna vrijednost jednako nuli. Ovo je sasvim u skladu s vizualnim značenjem disperzije, kao "mjere širenja".

Zaista, ako

ξ \u003d C, onda Mξ = C a to znači Dξ = M(C-C) 2 = M 0 = 0.

2. Prilikom množenja slučajne varijable ξ na konstantan broj Sa svojom varijansom se množi sa C 2

D(Cξ) = C 2 Dξ . (3)

Zaista

D(Cξ) = M(C

= M(C .

3. Postoji sljedeća formula za izračunavanje varijanse:

. (4)

Dokaz ove formule slijedi iz svojstava matematičkog očekivanja.

Imamo:

4. Ako su vrijednosti ξ 1 i ξ 2 su nezavisne, tada je varijanca njihovog zbira jednaka zbroju njihovih varijansi:

Dokaz. Za dokaz koristimo svojstva matematičkog očekivanja. Neka bude Mξ 1 = m 1 , Mξ 2 = m 2 onda.

Formula (5) je dokazana.

Budući da je varijansa slučajne varijable, po definiciji, matematičko očekivanje vrijednosti ( ξ-m) 2 , gdje m = Mξ , zatim za izračunavanje varijanse možete koristiti formule dobijene u Odjeljku 7, Poglavlje II.

Sta ako ξ postoji DSV sa zakonom o distribuciji

x 1	x 2	...
str 1	str 2	...

tada ćemo imati:

. (7)

Ako a ξ kontinuirana slučajna varijabla sa gustinom distribucije p(x), tada dobijamo:

Dξ= . (8)

Ako se za izračunavanje varijanse koristi formula (4), onda se mogu dobiti i druge formule, i to:

, (9)

ako je vrijednost ξ diskretno, i

Dξ= , (10)

ako ξ raspoređeni sa gustinom str(x).

Primjer 1. Neka vrijednost ξ je ravnomjerno raspoređena na segmentu [ a,b]. Koristeći formulu (10) dobijamo:

Može se pokazati da je varijansa slučajne varijable raspoređena prema normalnom zakonu sa gustinom

p(x)= , (11)

je jednako σ 2 .

Ovo pojašnjava značenje parametra σ uključenog u izraz gustine (11) za normalan zakon; σ postoji prosek standardna devijacija količine ξ.

Primjer 2. Pronađite varijansu slučajne varijable ξ distribuiraju prema binomskom zakonu.

Odluka. Koristeći reprezentaciju ξ u obliku

ξ = ξ 1 + ξ 2 + n(vidi primjer 2 §7 pogl. II) i primjenom formule za dodavanje varijansi za nezavisne varijable, dobijamo

Dξ = Dξ 1 + Dξ 2 + Dξn .

Disperzija bilo koje količine ξ i (i= 1,2, n) se izračunava direktno:

Dξi = M(ξi) 2 - (Mξ i) 2 = 0 2 q+ 1 2 str- str 2 = str(1-str) = pq.

Konačno dobijamo

Dξ= npq, gdje q = 1 -p.

Za grupisane podatke rezidualna disperzija - prosek od varijanse unutar grupe:

Gdje je σ 2 j unutargrupna varijansa j -te grupe.

Za negrupisane podatke rezidualna disperzija je mjera tačnosti aproksimacije, tj. aproksimacija linije regresije originalnim podacima:
gdje je y(t) prognoza prema jednadžbi trenda; y t – početni niz dinamike; n je broj bodova; p je broj koeficijenata regresione jednadžbe (broj varijabli koje objašnjavaju).
U ovom primjeru se zove nepristrasna procjena varijanse.

Primjer #1. Raspodjelu radnika tri preduzeća jednog udruženja po tarifnim kategorijama karakterišu sljedeći podaci:

Kategorija plate radnika	Broj radnika u preduzeću
	preduzeće 1	preduzeće 2	preduzeće 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

definirati:
1. disperzija za svako preduzeće (unutargrupna disperzija);
2. prosjek unutargrupnih disperzija;
3. međugrupna disperzija;
4. totalna varijansa.

Odluka.
Prije nego što se pristupi rješavanju problema, potrebno je utvrditi koja je karakteristika efektivna, a koja faktorijalna. U primjeru koji se razmatra, efektivna karakteristika je "Tarifna kategorija", a faktorska karakteristika je "Broj (naziv) preduzeća".
Tada imamo tri grupe (preduzeća) za koje je potrebno izračunati grupni prosjek i unutargrupne varijanse:

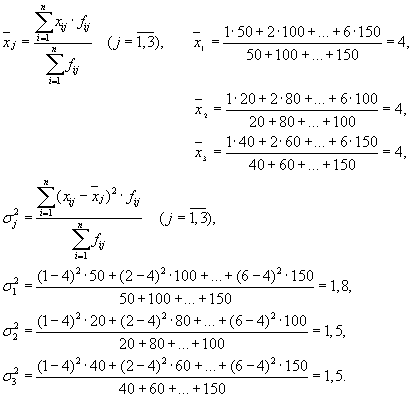
Kompanija	prosek grupe,	varijansa unutar grupe,
1	4	1,8

Prosek varijansi unutar grupe ( rezidualna disperzija) izračunato po formuli:

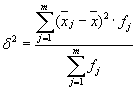
gdje možete izračunati:
ili:

onda:
Ukupna disperzija bit će jednaka: s 2 = 1,6 + 0 = 1,6.
Ukupna varijansa se također može izračunati korištenjem jedne od sljedeće dvije formule:

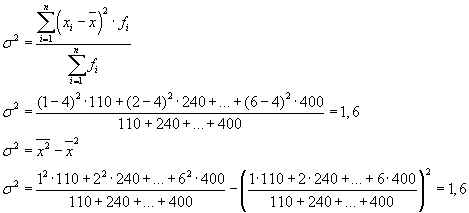
Prilikom rješavanja praktičnih problema često se mora suočiti sa znakom koji ima samo dvije alternativne vrijednosti. U ovom slučaju se ne govori o težini određene vrijednosti neke karakteristike, već o njenom udjelu u agregatu. Ako se udio populacijskih jedinica koje imaju osobinu koja se proučava označava sa " R", a ne posjedovanje - kroz" q“, tada se disperzija može izračunati po formuli:
s 2 = p×q

Primjer #2. Na osnovu podataka o učinku šest radnika brigade utvrditi međugrupnu varijansu i procijeniti uticaj radne smjene na njihovu produktivnost rada ako je ukupna varijansa 12,2.

br. radne brigade	Radni učinak, kom.
	u prvoj smjeni	u 2. smjeni
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Odluka. Početni podaci

X	f1	f2	f 3	f4	f5	f6	Ukupno
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Ukupno	31	33	37	37	40	38

Tada imamo 6 grupa za koje je potrebno izračunati grupnu srednju vrijednost i unutargrupne varijanse.
1. Pronađite prosječne vrijednosti svake grupe.







2. Pronađite srednji kvadrat svake grupe.







Rezultate proračuna sumiramo u tabeli:

Broj grupe	Grupni prosjek	Unutargrupna varijansa
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Unutargrupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine unutar grupe pod utjecajem svih faktora, osim faktora koji leži u osnovi grupisanja:
Izračunavamo prosjek unutargrupnih disperzija koristeći formulu:


4. Međugrupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine pod utjecajem faktora (faktorske osobine) koji leži u osnovi grupisanja.
Međugrupna disperzija se definiše kao:

gdje


Onda

Ukupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine pod utjecajem svih faktora (faktorskih osobina) bez izuzetka. Po uslovu zadatka jednak je 12,2.
Empirijska korelacija mjeri koliko je ukupne fluktuacije rezultirajućeg atributa uzrokovano proučavanim faktorom. Ovo je omjer faktorske varijanse i ukupne varijanse:

Određujemo empirijsku korelaciju:

Odnosi između karakteristika mogu biti slabe ili jake (bliske). Njihovi kriterijumi se vrednuju na Chaddock skali:
0,1 0,3 0,5 0,7 0,9 U našem primjeru, odnos između faktora Y karakteristike X je slab
Koeficijent determinacije.

Definirajmo koeficijent determinacije:

Dakle, 0,67% varijacije je zbog razlika između osobina, a 99,37% zbog drugih faktora.
Zaključak: u ovom slučaju učinak radnika ne zavisi od rada u određenoj smjeni, tj. uticaj radne smjene na njihovu produktivnost rada nije značajan i uzrokovan je drugim faktorima.

Primjer #3. Na osnovu prosjeka plate i kvadrata odstupanja od njegove vrijednosti za dvije grupe radnika, pronađite ukupnu varijansu primjenom pravila za sabiranje varijansi:

Odluka:
Prosjek varijansi unutar grupe

Međugrupna disperzija se definiše kao:


Ukupna varijansa će biti: 480 + 13824 = 14304

Glavni generalizirajući indikatori varijacije u statistici su disperzija i standardna devijacija.

Disperzija to aritmetička sredina kvadratna odstupanja vrijednosti svake karakteristike od ukupne srednje vrijednosti. Varijanca se obično naziva srednjim kvadratom odstupanja i označava se  2 . U zavisnosti od početnih podataka, varijansa se može izračunati iz aritmetičke sredine, jednostavne ili ponderisane:

 neponderisana (jednostavna) disperzija;

 ponderisana varijansa.

Standardna devijacija je generalizirajuća karakteristika apsolutnih dimenzija varijacije osobina u agregatu. Izražava se u istim jedinicama kao i znak (u metrima, tonama, procentima, hektarima, itd.).

Standardna devijacija je kvadratni korijen varijanse i označava se sa :

 neponderisana standardna devijacija;

 ponderisana standardna devijacija.

Standardna devijacija je mjera pouzdanosti srednje vrijednosti. Što je manja standardna devijacija, to bolje aritmetička sredina odražava cjelokupnu zastupljenu populaciju.

Izračunavanju standardne devijacije prethodi izračunavanje varijanse.

Procedura za izračunavanje ponderisane varijanse je kako slijedi:

1) odrediti aritmetički ponderisani prosek:

2) izračunati odstupanja opcija od prosjeka:

3) kvadrat odstupanja svake opcije od srednje vrijednosti:

4) pomnožiti kvadrate odstupanja sa težinama (frekvencijama):

5) sumirati prispele radove:

6) dobijeni iznos se podijeli zbirom pondera:

Primjer 2.1

Izračunajte aritmetički ponderisani prosjek:

Vrijednosti odstupanja od srednje vrijednosti i njihovi kvadrati prikazani su u tabeli. Definirajmo varijansu:

Standardna devijacija će biti jednaka:

Ako su izvorni podaci predstavljeni kao interval distribucijske serije , tada prvo trebate odrediti diskretnu vrijednost značajke, a zatim primijeniti opisanu metodu.

Primjer 2.2

Pokažimo proračun varijanse za intervalnu seriju na podacima o raspodjeli zasijane površine kolektivne farme po prinosu pšenice.

Aritmetička sredina je:

Izračunajmo varijansu:

6.3. Proračun disperzije prema formuli za pojedinačne podatke

Tehnika proračuna disperzija komplikovano, i velike vrijednosti opcije i frekvencije mogu biti glomazne. Proračuni se mogu pojednostaviti korištenjem svojstava disperzije.

Disperzija ima sljedeća svojstva.

1. Smanjenje ili povećanje težine (učestalosti) promjenljive karakteristike za određeni broj puta ne mijenja disperziju.

2. Smanjenje ili povećanje vrijednosti svake karakteristike za istu konstantnu vrijednost ALI disperzija se ne menja.

3. Smanjenje ili povećanje vrijednosti svake karakteristike za određeni broj puta k odnosno smanjuje ili povećava varijansu u k 2 puta standardna devijacija  u k jednom.

4. Varijanca karakteristike u odnosu na proizvoljnu vrijednost je uvijek veća od varijanse u odnosu na aritmetičku sredinu za kvadrat razlike između prosječne i proizvoljne vrijednosti:

Ako a ALI 0, tada dolazimo do sljedeće jednakosti:

tj. varijansa neke karakteristike je jednaka razlici između srednjeg kvadrata vrijednosti karakteristike i kvadrata srednje vrijednosti.

Svako svojstvo se može koristiti samostalno ili u kombinaciji s drugim prilikom izračunavanja varijanse.

Procedura za izračunavanje varijanse je jednostavna:

1) odrediti aritmetička sredina :

2) kvadrat aritmetičke sredine:

3) kvadrat odstupanja svake varijante serije:

X i 2 .

4) pronađite zbir kvadrata opcija:

5) podijeliti zbir kvadrata opcija njihovim brojem, odnosno odrediti prosječan kvadrat:

6) odrediti razliku između srednjeg kvadrata karakteristike i kvadrata srednje vrednosti:

Primjer 3.1 Imamo sljedeće podatke o produktivnosti radnika:

Napravimo sljedeće proračune:

Disperzija slučajne varijable je mjera širenja vrijednosti ove varijable. Mala varijansa znači da su vrijednosti grupisane blizu jedna drugoj. Velika varijansa ukazuje na snažno raspršivanje vrijednosti. U statistici se koristi koncept disperzije slučajne varijable. Na primjer, ako uporedite varijansu vrijednosti dvije veličine (kao što su rezultati opservacija pacijenata muškog i ženskog pola), možete testirati značaj neke varijable. Varijanca se takođe koristi u konstruisanju statistički modeli, budući da mala varijansa može biti znak da preuređujete vrijednosti.

Koraci

Izračun varijance uzorka

1. Zabilježite vrijednosti uzorka. U većini slučajeva statističarima su dostupni samo uzorci određenih populacija. Na primjer, statističari u pravilu ne analiziraju troškove održavanja agregata svih automobila u Rusiji - oni analiziraju slučajni uzorak od nekoliko hiljada automobila. Takav uzorak pomoći će u određivanju prosječne cijene po automobilu, ali najvjerovatnije će rezultirajuća vrijednost biti daleko od stvarne.

   • Na primjer, hajde da analiziramo broj peciva prodanih u kafiću u 6 dana, uzetih nasumično. Uzorak ima sljedeći pogled: 17, 15, 23, 7, 9, 13. Ovo je uzorak, a ne populacija, jer nemamo podatke o prodatim pecivama za svaki dan rada kafića.
   • Ako vam je data populacija, a ne uzorak vrijednosti, pređite na sljedeći odjeljak.

2. Zapišite formulu za izračunavanje varijanse uzorka. Disperzija je mjera širenja vrijednosti neke veličine. Što je vrijednost disperzije bliža nuli, to su vrijednosti bliže grupisane. Kada radite s uzorkom vrijednosti, koristite sljedeću formulu za izračunavanje varijanse:

   • s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2)) je disperzija. Disperzija se meri u kvadratne jedinice mjerenja.
   • x i (\displaystyle x_(i))- svaku vrijednost u uzorku.
   • x i (\displaystyle x_(i)) trebate oduzeti x̅, kvadrirati ga, a zatim dodati rezultate.
   • x̅ – srednja vrijednost uzorka (srednja vrijednost uzorka).
   • n je broj vrijednosti u uzorku.

3. Izračunajte srednju vrijednost uzorka. Označava se kao x̅. Srednja vrijednost uzorka se izračunava kao normalna aritmetička sredina: zbrojite sve vrijednosti u uzorku, a zatim podijelite rezultat s brojem vrijednosti u uzorku.

   • U našem primjeru dodajte vrijednosti u uzorku: 15 + 17 + 23 + 7 + 9 + 13 = 84
     Sada podijelite rezultat s brojem vrijednosti u uzorku (u našem primjeru ima 6): 84 ÷ 6 = 14.
     Srednja vrijednost uzorka x̅ = 14.
   • Srednja vrijednost uzorka je središnja vrijednost oko koje se distribuiraju vrijednosti u uzorku. Ako se vrijednosti u uzorku grupišu oko srednje vrijednosti uzorka, tada je varijansa mala; inače, disperzija je velika.

4. Oduzmite srednju vrijednost uzorka od svake vrijednosti u uzorku. Sada izračunajte razliku x i (\displaystyle x_(i))- x̅, gdje x i (\displaystyle x_(i))- svaku vrijednost u uzorku. Svaki rezultat pokazuje stepen odstupanja određene vrijednosti od srednje vrijednosti uzorka, odnosno koliko je ta vrijednost udaljena od srednje vrijednosti uzorka.

   • U našem primjeru:
     x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
   • Ispravnost dobijenih rezultata je lako provjeriti, jer njihov zbir mora biti jednak nuli. Ovo se odnosi na definiciju prosječne vrijednosti, pošto negativne vrijednosti(udaljenosti od prosječne vrijednosti do manjih vrijednosti) su u potpunosti kompenzirane pozitivne vrijednosti(udaljenosti od prosječnih do velikih vrijednosti).

5. Kao što je gore navedeno, zbir razlika x i (\displaystyle x_(i))- x̅ mora biti jednako nuli. To znači da prosječna varijansa je uvijek jednak nuli, što ne daje nikakvu predstavu o širenju vrijednosti određene veličine. Da biste riješili ovaj problem, kvadrirajte svaku razliku x i (\displaystyle x_(i))- x̅. Ovo će rezultirati samo dobijanjem pozitivni brojevi, koji kada se doda nikada neće dati 0.

   • U našem primjeru:
     (x 1 (\displaystyle x_(1))-x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2))-x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • Našli ste kvadrat razlike - x̅) 2 (\displaystyle ^(2)) za svaku vrijednost u uzorku.

6. Izračunajte zbir kvadrata razlika. Odnosno, pronađite dio formule koji je napisan ovako: ∑[( x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))]. Ovdje znak Σ označava zbir kvadrata razlika za svaku vrijednost x i (\displaystyle x_(i)) u uzorku. Već ste pronašli kvadratne razlike (x i (\displaystyle (x_(i))-x̅) 2 (\displaystyle ^(2)) za svaku vrijednost x i (\displaystyle x_(i)) u uzorku; sada samo dodajte ove kvadrate.

   • U našem primjeru: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. Podijelite rezultat sa n - 1, gdje je n broj vrijednosti u uzorku. Prije nekog vremena, da bi izračunali varijansu uzorka, statističari su jednostavno podijelili rezultat sa n; u ovom slučaju, dobićete srednju vrednost kvadratne varijanse, koja je idealna za opisivanje varijanse datog uzorka. Ali zapamtite da je svaki uzorak samo mali dio. stanovništva vrijednosti. Ako uzmete drugačiji uzorak i izvršite iste proračune, dobit ćete drugačiji rezultat. Kako se ispostavilo, dijeljenje sa n - 1 (a ne samo n) daje više tačna procjena varijabilnost populacije, što je ono što vas zanima. Dijeljenje sa n - 1 postalo je uobičajeno, pa je uključeno u formulu za izračunavanje varijanse uzorka.

   • U našem primjeru uzorak uključuje 6 vrijednosti, odnosno n = 6.
     Varijanca uzorka = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. Razlika između varijanse i standardne devijacije. Imajte na umu da formula sadrži eksponent, pa se varijansa mjeri u kvadratnim jedinicama analizirane vrijednosti. Ponekad je takvom vrijednošću prilično teško upravljati; u takvim slučajevima koristite standardnu ​​devijaciju, koja je jednaka kvadratni korijen od disperzije. Zbog toga se varijansa uzorka označava kao s 2 (\displaystyle s^(2)), a standardna devijacija uzorci - kako s (\displaystyle s).

   • U našem primjeru, standardna devijacija uzorka je: s = √33,2 = 5,76.

   Proračun varijanse stanovništva

   1. Analizirajte neki skup vrijednosti. Skup uključuje sve vrijednosti količine koja se razmatra. Na primjer, ako proučavate starost stanovnika Lenjingradska oblast, tada je u populaciju uključena starost svih stanovnika ovog područja. U slučaju rada sa agregatom, preporučuje se kreiranje tabele i unos vrednosti agregata u nju. Razmotrite sljedeći primjer:

      • U jednoj prostoriji se nalazi 6 akvarijuma. Svaki akvarij sadrži sljedeći broj riba:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. Zapišite formulu za izračunavanje varijanse stanovništva. Budući da populacija uključuje sve vrijednosti određene količine, sljedeća formula vam omogućava da dobijete točnu vrijednost varijanse populacije. Da bi razlikovali varijansu populacije od varijance uzorka (koja je samo procjena), statističari koriste različite varijable:

      • σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n
      • σ 2 (\displaystyle ^(2))- varijansa stanovništva (čita se kao "sigma na kvadrat"). Disperzija se mjeri u kvadratnim jedinicama.
      • x i (\displaystyle x_(i))- svaka vrijednost u agregatu.
      • Σ je predznak zbira. Odnosno, za svaku vrijednost x i (\displaystyle x_(i)) oduzmite μ, kvadratirajte ga, a zatim dodajte rezultate.
      • μ je srednja vrijednost populacije.
      • n je broj vrijednosti u općoj populaciji.

   3. Izračunajte srednju vrijednost stanovništva. Kada se radi sa opštom populacijom, njena prosečna vrednost se označava kao μ (mu). Srednja populacija se izračunava kao uobičajena aritmetička sredina: zbrojite sve vrijednosti u populaciji, a zatim podijelite rezultat s brojem vrijednosti u populaciji.

      • Imajte na umu da se prosjeci ne računaju uvijek kao aritmetička sredina.
      • U našem primjeru, populacija znači: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. Oduzmite srednju vrijednost populacije od svake vrijednosti u populaciji.Što je vrijednost razlike bliža nuli, to je određena vrijednost bliža srednjoj vrijednosti stanovništva. Pronađite razliku između svake vrijednosti u populaciji i njene srednje vrijednosti, i dobićete prvi pogled na distribuciju vrijednosti.

      • U našem primjeru:
        x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
        x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
        x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
        x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
        x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
        x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5

   5. Kvadrirajte svaki rezultat koji dobijete. Vrijednosti razlike bit će i pozitivne i negativne; ako ove vrijednosti stavite na brojevnu pravu, onda će ležati desno i lijevo od srednje vrijednosti populacije. Ovo nije prikladno za izračunavanje varijanse, budući da su pozitivni i negativni brojevi nadoknaditi jedni druge. Stoga kvadrirajte svaku razliku da dobijete isključivo pozitivne brojeve.

      • U našem primjeru:
        (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) za svaku populacijsku vrijednost (od i = 1 do i = 6):
        (-5,5)2 (\displaystyle ^(2)) = 30,25
        (-5,5)2 (\displaystyle ^(2)), gdje x n (\displaystyle x_(n)) – posljednja vrijednost u opštoj populaciji.
      • Da biste izračunali prosječnu vrijednost dobijenih rezultata, potrebno je pronaći njihov zbir i podijeliti ga sa n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / n
      • Sada napišimo gornje objašnjenje koristeći varijable: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n i dobijemo formulu za izračunavanje varijanse populacije.