Основні теореми динаміки. Загальні теореми динаміки
лекція 3. Загальні теореми динаміки
Динаміка системи матеріальних точокє найважливішим розділом теоретичної механіки. Тут в основному розглядаються завдання про рух механічних систем (систем матеріальних точок) кінцевим числомстепенів свободи – максимальною кількістю незалежних параметрів, що визначають положення системи. Головна задачадинаміки системи – вивчення законів руху твердого тіла та механічних систем.
Найбільш простий підхід до дослідження руху системи, що складається з Nматеріальних точок, що зводиться до розгляду рухів кожної окремої точки системи. При цьому повинні бути визначені всі сили, що діють на кожну точку системи, зокрема сили взаємодії між точками.
Визначаючи прискорення кожної точки відповідно до другого закону Ньютона (1.2), отримаємо кожної точки три скалярних диференціальних закону руху другого порядку, тобто. 3 N диференціальний закон руху для всієї системи.
Для знаходження рівнянь руху механічної системиза заданими силами та початковими умовами для кожної точки системи, отримані диференціальні законинеобхідно проінтегрувати. Це завдання важке навіть у разі двох матеріальних точок, які рухаються лише під дією сил взаємодії за законом всесвітнього тяжіння (завдання про два тіла), і виключно важка у разі трьох взаємодіючих точок (задача про три тіла).
Тому потрібно знайти такі способи вирішення завдань, які призводили до розв'язуваних рівнянь і давали уявлення про рух механічної системи. Загальні теореми динаміки, будучи наслідком диференціальних законів руху, дозволяють уникнути складнощів, що виникають при інтегруванні та отримувати необхідні результати.
3. 1. Загальні зауваження
Точки механічної системи нумеруватимемо індексами i, j, kі т.д., які пробігають усі значення 1, 2, 3… N, де N - Число точок системи. Фізичні величини, що належать до k-й точці, позначаються таким самим індексом, що і точка. Наприклад, виражають відповідно радіус-вектор та швидкість k-ї точки.
На кожну точку системи діють сили двоякого походження: по-перше, сили, джерела яких лежать поза системою, звані зовнішнімисилами та позначаються; по-друге, сили з боку інших точок даної системи, звані внутрішнімисилами та позначаються. Внутрішні сили задовольняють третій закон Ньютона. Розглянемо найпростіші властивості внутрішніх сил, що діють всю механічну систему у її стані.
Перше властивість. Геометрична сума всіх внутрішніх сил системи (головний вектор внутрішніх сил) дорівнює нулю.
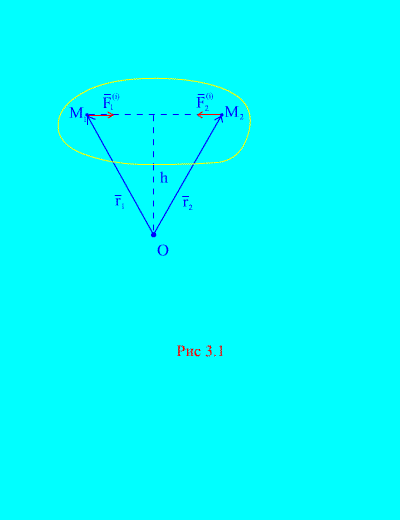
Справді, якщо розглянути будь-які дві довільні точки системи, наприклад, і (Рис. 3.1), то для них ![]() , т.к. сили дії та протидії завжди рівні за модулем, діють вздовж однієї лінії дії у протилежному напрямку, яке з'єднує взаємодіючі точки. Головний вектор внутрішніх сил складається з пар сил взаємодіючих точок, отже
, т.к. сили дії та протидії завжди рівні за модулем, діють вздовж однієї лінії дії у протилежному напрямку, яке з'єднує взаємодіючі точки. Головний вектор внутрішніх сил складається з пар сил взаємодіючих точок, отже
![]() (3.1)
(3.1)
Друга властивість. Геометрична сума моментів всіх внутрішніх сил щодо довільної точки простору дорівнює нулю.
Розглянемо систему моментів сил і щодо точки Про(Рис. 3.1). З (Рис. 3.1). видно що
![]() ,
,
т.к. обидві сили мають однакові плечі та протилежні напрямки векторних моментів. Головний момент внутрішніх сил щодо точки Проскладається з векторної суми таких виразів і дорівнює нулю. Отже,

Нехай задані зовнішні та внутрішні сили, що діють на механічну систему, що складається з Nточок (Рис. 3.2). Якщо до кожної точки системи прикласти рівнодіючу зовнішніх сил і рівнодіючу всіх внутрішніх сил, то для будь-якої k-ї точки системи можна скласти диференціальні рівняння руху Усього таких рівнянь буде N:
а в проекціях на нерухомі осі координат 3 N:
![]() (3.4)
(3.4)
Векторні рівняння (3.3) або еквівалентні їм скалярні рівняння (3.4) є диференціальними законами руху матеріальних точок всієї системи. Якщо всі точки рухаються паралельно до однієї площини або однієї прямої, то число рівнянь (3.4) у першому випадку буде 2 N, у другому N.
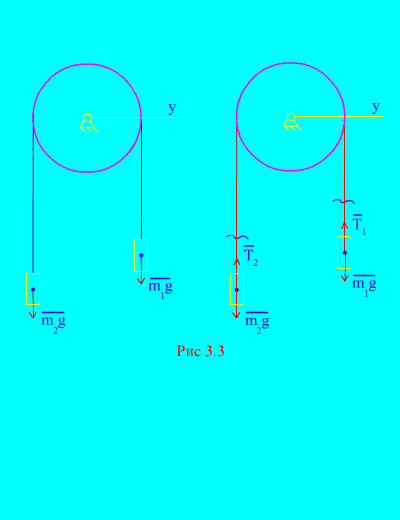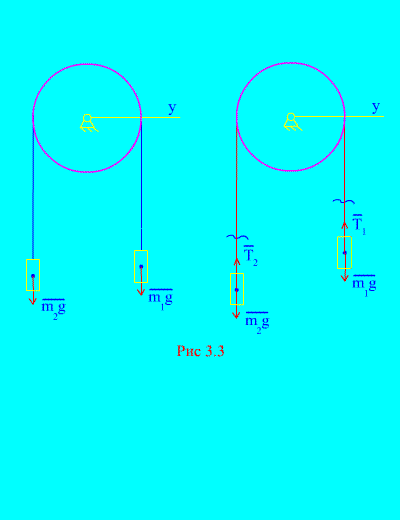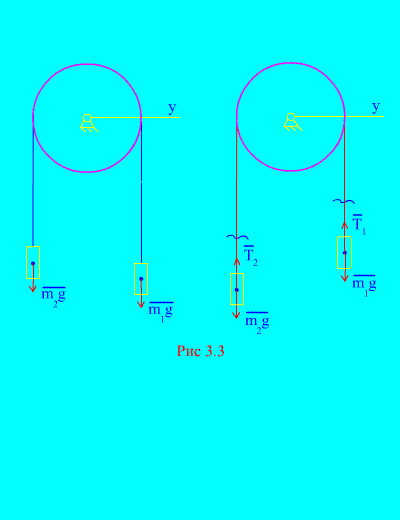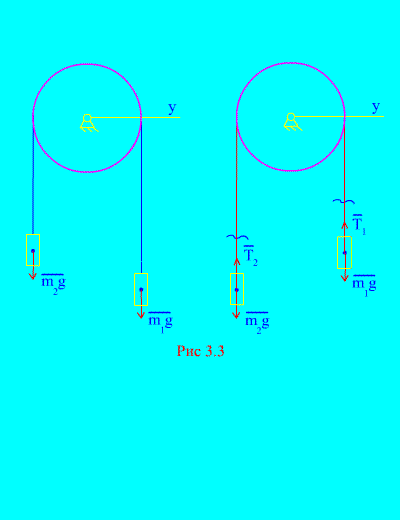
приклад 1.Два вантажі масою і пов'язані між собою нерозтяжним тросом, перекинутим через блок (Рис. 3.3). Нехтуючи силами тертя, а також масою блоку та троса, визначити закон руху вантажів та натягу троса.
Рішення. Система складається з двох матеріальних тіл (пов'язаних нерозтяжним тросом), що рухаються паралельно до однієї осі х.Запишемо диференціальні закони руху у проекціях на вісь хдля кожного тіла.
Нехай правий вантаж опускається з прискоренням, тоді лівий вантаж підніматиметься з прискоренням. Подумки звільняємося від зв'язку (троса) та замінюємо його реакціями та (Рис. 3.3). Вважаючи тіла вільними, складемо диференціальні закони руху у проекції на вісь х(мається на увазі, що натяг нитки є внутрішніми силами, а вага вантажів – зовнішніми):
Оскільки і (тіла пов'язані нерозтяжним тросом), отримуємо
Вирішуючи ці рівняння щодо прискорення та натягу троса Т, отримаємо
 .
.
Зазначимо, що натяг троса при не дорівнює силі тяжкості відповідного вантажу.
3. 2. Теорема про рух центру мас
Відомо, що тверде тіло та механічна система у площині може рухатися досить складно. До першої теореми про рух тіла та механічної системи можна прийти так: кинути к.-л. предмет, що з безлічі скріплених між собою твердих тіл. Зрозуміло, що він полетить параболою. Це виявилося щодо руху точки. Однак тепер об'єкт не є крапкою. Він повертається, погойдується в процесі польоту навколо ефективного центру, який рухається по параболі. Перша теорема про рух складних предметівговорить про те, що якийсь ефективний центр є центр мас предмета, що рухається. Центр мас не обов'язково знаходиться в самому тілі, він може лежати і десь поза ним.
Теорема. Центр мас механічної системи рухається як матеріальна точка масою рівної масівсієї системи, до якої прикладені всі зовнішні сили, що діють систему.
Для доказу теореми перепишемо диференціальні закони руху (3.3) наступному вигляді:
![]() (3.5)
(3.5)
де N - Число точок системи.
Складемо почленно рівняння між собою:
 (а)
(а)
Положення центру мас механічної системи щодо обраної системи координат визначається формулою (2.1):  де М- Маса системи. Тоді ліва частина рівності (а) запишеться
де М- Маса системи. Тоді ліва частина рівності (а) запишеться
Перша сума, що стоїть у правій частині рівності (а), дорівнює головному вектору зовнішніх сил, а остання за якістю внутрішніх сил дорівнює нулю. Тоді рівність (а), з урахуванням (б), перепишеться
![]() , (3.6)
, (3.6)
тобто. добуток маси системи на прискорення центру її маси дорівнює геометричній сумівсіх діючих систему зовнішніх сил.
З рівняння (3.6) слід, що внутрішні сили безпосередньо впливають рух центру мас. Однак у ряді випадків є причиною появи зовнішніх сил, що додаються до системи. Так, внутрішні сили, що приводять у обертання провідні колеса автомобіля, викликають дію на нього зовнішньої сили зчеплення, що додається до обода колеса.
приклад 2.Механізм, розташований у вертикальній площині, встановлений на горизонтальній гладкій площині та прикріплений до неї жорстко закріпленими з поверхнею брусками. Доі L (Рис. 3.4).

Диск 1 радіусом Rнерухомий. Диск 2 масою mта радіусом r скріплений з кривошипом, довжиною R+ rу точці З 2. Кривошип обертається із постійною
кутовий швидкістю. В початковий моменткривошип займав праве горизонтальне становище. Нехтуючи масою кривошипу, визначити найбільше горизонтальне та вертикальне зусилля, що діють на бруски, якщо Загальна масастанини та колеса 1 дорівнює М.Також розглянути поведінку механізму за відсутності брусків.
Рішення. Система складається з двох мас ( N=2 ): нерухомого диска 1 зі станиною та рухомого диска 2. Направимо вісь учерез центр ваги нерухомого диска по вертикалі нагору, вісь х- вздовж горизонтальній площині.
Запишемо теорему про рух центру мас (3.6) у координатній формі
Зовнішніми силами цієї системи є: вага станини та нерухомого диска – Mg, вага рухомого диска – mg, - сумарна горизонтальна реакція болтів; - нормальна сумарна реакція площини. Отже,
Тоді закони руху (б) перепишуться
Обчислимо координати центру мас механічної системи:
 ; (г)
; (г)
як видно з (Рис. 3.4), , , ![]() (кут повороту кривошипу),
(кут повороту кривошипу), ![]() . Підставляючи ці вирази (г) і обчислюючи другі похідні за часом tвід , , отримаємо, що
. Підставляючи ці вирази (г) і обчислюючи другі похідні за часом tвід , , отримаємо, що
 (д)
(д)
Підставляючи (в) та (д) в (б), знаходимо

Горизонтальний тиск, що діє на бруски, має найбільший і найменше значення, коли cos = 1 відповідно, тобто
![]()
![]()
Тиск механізму на горизонтальну площину має найбільше та найменше значення, коли sin відповідно, тобто.
![]()
![]()
Фактично вирішено перше завдання динаміки: за відомими рівняннями руху центру мас системи (д) відновлюються сили, що беруть участь у русі.
В умовах відсутності брусків Kі L (Рис. 3.4), механізм може почати підстрибувати над горизонтальною площиною. Це буде місце, коли , тобто. коли , звідси випливає, що кутова швидкість обертання кривошипа, коли він відбувається підстрибування механізму, повинна задовольняти рівності
 .
.
3. 3. Закон збереження руху центру мас
Якщо головний вектор зовнішніх сил, що діють систему, дорівнює нулю, тобто. , то з(3.6)слід, що прискорення центру мас дорівнює нулю, отже, швидкість центру мас є постійною за модулем і напрямом. Якщо, зокрема, у початковий момент центр мас перебуває у спокої, він спочиває протягом усього часу, поки головний вектор зовнішніх сил дорівнює нулю.
З цієї теореми випливає кілька наслідків.
· Одними внутрішніми силами не можна змінити характер руху центру мас системи.
· Якщо головний вектор зовнішніх сил, що діють на систему, дорівнює нулю, центр мас перебуває в спокої або рухається рівномірно і прямолінійно.
· Якщо проекція головного вектора зовнішніх сил системи на деяку нерухому вісь дорівнює нулю, проекція швидкості центру мас системи на цю вісь не змінюється.
· Пара сил, прикладена до твердого тіла, не може змінити рух центру мас (вона може викликати тільки обертання тіла навколо центру мас).
Розглянемо приклад, що ілюструє закон збереження руху центру мас.

Приклад 3.Два вантажі масами та з'єднані нерозтяжною ниткою, перекинутою через блок (Рис. 3.5), закріплений на клині масою М.Клин спирається на гладку горизонтальну площину. Спочатку система перебувала у спокої. Знайти переміщення клина по площині при опусканні першого вантажу на висоту н.Масою блоку та нитки знехтувати.
Рішення.Зовнішніми силами, що діють на клин разом з вантажами, є сили тяжіння і Mg, а також нормальна реакціягладкої горизонтальної поверхні N. Отже,
Оскільки в початковий момент система перебувала у спокої, маємо .
Обчислимо координату центру мас системи при та в момент t 1 , коли вантаж вагою gопуститься на висоту H.
Для моменту:
 ,
,
де , , х– відповідно координати центру мас вантажів вагою g, g та клина вагою Мg.
Припустимо, що клин на момент часу переміститься в позитивному напрямку осі Oxна величину Lякщо вантаж вагою опуститься на висоту н.Тоді, для моменту
т.к. вантажі разом із клином пересунуться на Lвправо, а вантаж переміститься на відстань по клину вгору. Оскільки , то після обчислень отримаємо
 .
.
3.4. Кількість руху системи
3.4.1. Обчислення кількості руху системи
Кількість руху матеріальної точки називається векторна величина, рівна добуткумаси точки на вектор її швидкості
Одиниця виміру кількості руху -
Кількість руху механічної системи називають векторну суму кількості руху окремих точок системи, тобто.
де N - Число точок системи.
Кількість руху механічної системи можна виразити через масу системи Мта швидкість центру мас. Справді,
тобто. кількість руху системи дорівнює добутку маси всієї системи на швидкість її центру мас.Напрямок збігається з напрямком (Рис. 3.6)

У проекціях на прямокутні осі маємо
де , , - Проекції швидкості центру мас системи.
Тут М- Маса механічної системи; не змінюється під час руху системи.
Цими результатами особливо зручно користуватися при обчисленні кількостей руху твердих тіл.
З формули (3.7) видно, що й механічна система рухається те що її центр мас залишається нерухомим, то кількість руху системи залишається рівним нулю.
3.4.2. Елементарний та повний імпульс сили
Дія сили на матеріальну точку протягом часу dtможна охарактеризувати елементарним імпульсом. Повний імпульс сили за час t, або імпульс сили , визначають за формулою
або у проекціях на координати осі
 (3.8а)
(3.8а)
Одиниця імпульсу сили - .
3.4.3. Теорема про зміну кількості руху системи
Нехай до точок системи додані зовнішні та внутрішні сили. Тоді кожної точки системи можна застосувати диференціальні закони руху (3.3), маю на увазі, що ![]() :
:
 .
.
Підсумовуючи по всіх точках системи, отримаємо
За якістю внутрішніх сил та за визначенням ![]() маємо
маємо
 (3.9)
(3.9)
Помножуючи обидві частини цього рівняння на dt, отримаємо теорему про зміну кількості руху в диференційної форми:
![]() , (3.10)
, (3.10)
тобто. диференціал кількості руху механічної системи дорівнює векторній сумі елементарних імпульсів всіх зовнішніх сил, що діють точки механічної системи.
Обчислюючи інтеграл від обох частин (3.10) за часом від 0 до t, отримаємо теорему в кінцевій чи інтегральній формі
 (3.11)
(3.11)
У проекціях на координатні осі матимемо
Зміна кількості руху механічної системи за часt, Так само векторної сумі всіх імпульсів зовнішніх сил, що діють на точки механічної системи за той же час.
Приклад 4.Вантаж масою m спускається вниз по похилій площинізі стану спокою під дією сили F, пропорційного часу: , де (Рис. 3.7). Яку швидкість набуде тіло через t секунд після початку руху, якщо коефіцієнт тертя ковзання вантажу про похилу площину дорівнює f.
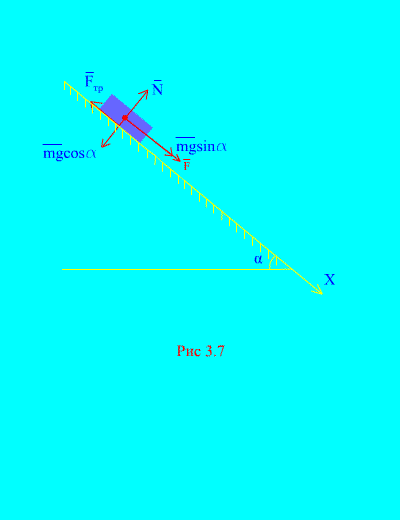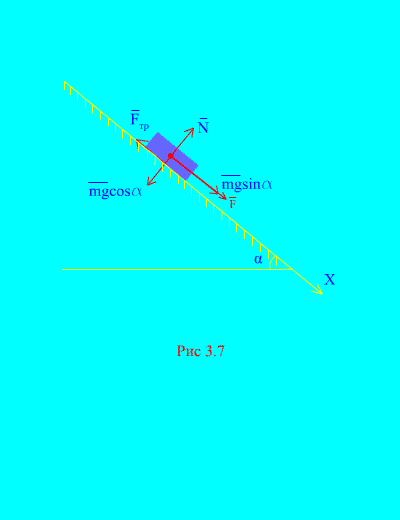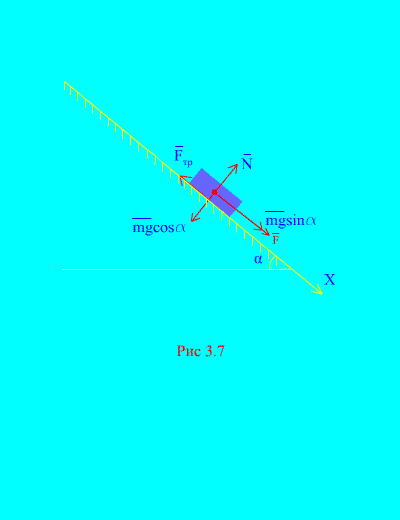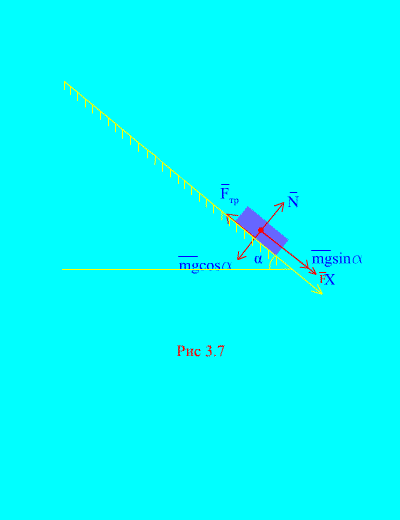
Рішення.Зобразимо сили, що додаються до вантажу: mg - сила тяжкості вантажу, N– нормальна реакція площини, - сила тертя ковзання вантажу на площину, причому . Напрямок усіх сил зображено на (Рис. 3.7).
Направимо вісь хвздовж похилої поверхні вниз. Запишемо теорему про зміну кількості руху (3.11) у проекції на вісь х:
 (а)
(а)
За умовою, т.к. у початковий момент часу вантаж перебував у стані спокою. Сума проекцій імпульсів усіх сил на вісь х дорівнює

Отже,
 ,
,
 .
.
3.4.4. Закони збереження кількості руху
Закони збереження виходять як окремі випадки теореми про зміну кількості руху. Можливі два окремі випадки.
· Якщо векторна сума всіх зовнішніх сил, прикладених до системи, дорівнює нулю, тобто. , то з теореми випливає (3.9) , що ,
тобто. якщо головний вектор зовнішніх сил системи дорівнює нулю, кількість руху системи постійно за величиною і напрямом.
· Якщо проекція головного вектора зовнішніх сил на будь-яку координатну вісьдорівнює нулю, наприклад, Ох, тобто. то проекція кількості руху на цю вісь величина постійна.
Розглянемо приклад застосування закону збереження кількості руху.

Приклад 5.Балістичний маятник є тілом масою , підвішене на довгій нитці (Рис. 3.8).
Куля масою , що рухається зі швидкістю Vі потрапляє в нерухоме тіло, застряє в ньому, і тіло відхиляється. Якою була швидкість кулі, якщо тіло піднялося на висоту h ?
Рішення.Нехай тіло із застрялою кулею набуло швидкості. Тоді, користуючись законом збереження кількості руху при взаємодії двох тіл, можна записати ![]() .
.
Швидкість можна обчислити, скориставшись законом збереження механічної енергії  . Тоді. В результаті знаходимо
. Тоді. В результаті знаходимо
 .
.

Приклад 6. Вода входить у нерухомий канал (Рис. 3.9)змінного перерізу із швидкістю під кутом до горизонту; площа поперечного перерізуканалу при вході; швидкість води у виходу з каналу і становить кут із горизонтом.
Визначити горизонтальну складову реакції, яку вода чинить на стінки каналу. Щільність води  .
.
Рішення.Визначатимемо горизонтальну складову реакції, що надається стінками каналу на воду. Ця сила дорівнює за модулем і протилежна за знаком шуканої сили. Маємо, згідно (3.11а),
 . (а)
. (а)
Обчислюємо масу об'єму рідини, що надходить у канал за час t:
Величина rАV 0 називається секундною масою - маса рідини, що протікає через будь-який переріз труби в одиницю часу.
Така сама кількість води залишає канал за цей же час. Початкова та кінцева швидкості дано за умови.
Обчислимо праву частинурівності (а) яка визначає суму проекцій на горизонтальну вісь зовнішніх сил, що додаються до системи (води). Єдиною горизонтальною силою є горизонтальна складова рівнодіючої реакції стін R x. Ця сила під час руху води є постійною. Тому
 . (В)
. (В)
Підставляючи (б) і (в) до (а), отримуємо
3.5. Кінетичний момент системи
3.5.1. Головний момент кількості руху системи

Нехай - радіус-вектор точки масою системи щодо деякої точки А, яка називається центром (Рис. 3.10).
Моментом кількості руху (кінетичним моментом) точки щодо центру Аназивається вектор , визначається за формулою
![]() . (3.12)
. (3.12)
При цьому вектор спрямований перпендикулярно до площини, що проходить через центр Ата вектор .
Моментом кількості руху (кінетичним моментом) точки щодо осіназивається проекція на цю вісь моменту кількості руху точки щодо будь-якого обраного на цій осі центру.
Головним моментом кількості руху (кінетичним моментом) системи щодо центру Аназивається величина
 (3.13)
(3.13)
Головним моментом кількості руху (кінетичним моментом) системи щодо осіназивається проекція на цю вісь головного моменту кількості руху системи щодо будь-якого обраного на даній осі центру.
3.5.2. Кінетичний момент твердого тіла, що обертається, щодо осі обертання.
Сумісний нерухомий пункт Протіла, що лежить на осі обертання Проz, з початком системи координат Охуz, осі якої будуть обертатися разом із тілом (Рис. 3.11). Нехай - радіус-вектор точки тіла щодо початку координат, його проекції на осі позначимо , , . Векторні проекції кутовий швидкостітіла на самі осі позначимо 0, 0, ().
Досить часто вдається виділити важливі особливостіруху механічної системи, не вдаючись до інтегрування системи диференціальних рівнянь руху. Це досягається застосуванням загальних теорем динаміки.
5.1. Основні поняття та визначення
Зовнішні та внутрішні сили.Будь-яка сила, що діє на точку механічної системи, обов'язково є або активною силою, чи реакцією зв'язку. Усю сукупність сил, що діють на точки системи, можна розділити на два класи інакше: на зовнішні сили та внутрішні сили (індекси е та i - від латинських слів externus - зовнішній та internus - внутрішній). Зовнішніми називаються сили, що діють на точки системи з боку точок і тіл, що не входять до складу системи, що розглядається. Внутрішніми називаються сили взаємодії між точками та тілами аналізованої системи.
Цей поділ залежить від того, які матеріальні точки і тіла включені дослідником у механічну систему, що розглядається. Якщо розширити склад системи, включивши до неї додатково точки і тіла, деякі сили, які для колишньої системи були зовнішніми, для розширеної системи можуть стати внутрішніми.
Властивості внутрішніх сил.Оскільки ці сили є силами взаємодії між частинами системи, вони входять до повної системи внутрішніх сил «двійками», організованими відповідно до аксіоми дії-противодії. У кожної такої «двійки» сил
головний вектор та головний моментщодо довільного центру дорівнюють нулю. Оскільки повна система внутрішніх сил складається лише з «двійок», то
1) головний вектор системи внутрішніх сил дорівнює нулю,
2) головний момент системи внутрішніх сил щодо довільної точки дорівнює нулю.
Масою системи називається арифметична сумамас тк усіх точок і тіл, що утворюють систему:
Центром мас(центром інерції) механічної системи називається геометрична точкаС, радіус-вектор та координати якої визначаються формулами
де - радіуси-вектори та координати точок, що утворюють систему.
Для твердого тіла, що у однорідному полі тяжкості, положення центру мас і центру тяжкості збігаються, в інших випадках це різні геометричні точки.
Разом з інерційною системою відліку часто розглядають одночасно неінерційну систему відліку, що рухається поступально. Її осі координат (осі Кеніга) вибирають так, щоб початок відліку постійно збігався з центром мас механічної системи. Відповідно до визначення центр мас нерухомий в осях Кеніга і знаходиться на початку координат.
Моментом інерції системищодо осі називається скалярна величина рівна сумітворів мас тк усіх точок системи на квадрати їх відстаней до осі:
![]()
Якщо механічною системою є тверде тіло, для знаходження 12 можна скористатися формулою

де - густина, обсяг, займаний тілом.
Розглянемо рух деякої системи матеріальних томен щодо нерухомої системи координат Коли система невільна, її можна розглядати як вільну, якщо відкинути накладені на систему зв'язку і замінити їх дію відповідними реакціями.
Розіб'ємо всі сили, прикладені до системи, на зовнішні та внутрішні; в ті та інші можуть входити реакції відкинутих
зв'язків. Через і позначимо головний вектор і момент зовнішніх сил щодо точки А.
1. Теорема про зміну кількості руху.Якщо - кількість руху системи, то (див.)
тобто справедлива теорема: похідна за часом кількості руху системи дорівнює головному вектору всіх зовнішніх сил.
Замінюючи вектор через його вираз де - маса-системи, - швидкість центру мас, рівняння (4.1) можна надати іншу форму:
Ця рівність означає, що центр мас системи рухається, як матеріальна точкащ, маса якої дорівнює масі системи і до якої прикладена сила, геометрично рівна головному вектору всіх зовнішніх сил системи. Останнє твердження називають теоремою про рух центру мас (центру інерції) системи.
Якщо з (4.1) випливає, що вектор кількості руху постійний за величиною і напрямом. Проектуючи його на осі координат, отримаємо три скалярні перші інтеграли, диференціальні рівняння дзвнзкепня системи:
Ці інтеграли носять назву інтегралів кількості руху. При швидкість центру мас постійна, тобто він рухається рівномірно та прямолінійно.
Якщо проекція головного вектора зовнішніх сил на якусь одну вісь, наприклад, на вісь дорівнює нулю, то маємо один перший інтеграл або якщо рівні нулю» дві проекції головного вектора, то існує два інтеграли кількості руху.
2. Теорема про зміну кінетичного моменту.Нехай А - деяка довільна точка простору (яка рухається або нерухома), яка не обов'язково збігається з якоюсь певною матеріальною точкою системи під час руху. Її швидкість у нерухомій спстемі координат позначимо через Теорему про зміну кінетичного моменту матеріальної системищодо точки А має вигляд
![]()
Якщо точка А нерухома, то й рівність (4.3) набуває більш простого вигляду:
Ця рівність виражає теорему про пзмепіння кінетичного моменту системи щодо нерухомої точки: похідна часу від кінетичного моменту системи, обчисленого щодо деякої нерухомої точки, дорівнює головному моменту всіх зовнішніх сил щодо цієї точки.
Якщо згідно (4.4) вектор кінетичного моменту постійний за величиною і напрямом. Проектуючи його на осі координат, отримаємо скалярних перших інтеграла диференціальних рівнянь двпжеії системи:
Ці інтеграли займають назву інтегралів кінетичного моменту або інтегралів площ.
Якщо точка А збігається з центром мас системи, тоді перше доданок у правій частині рівності (4.3) звертається в нуль і теорема про зміну кінетичного моменту має ту ж форму запису (4.4), що і у разі нерухомої точки А. Зазначимо (див. п. 4 § 3), що в даному випадку абсолютний кінетичний момент системи в лівій частині рівності (4.4) може бути замінений рівний йому кінетичний момент системи в її русі щодо центру мас.
Нехай - деяка постійна вісь або вісь постійного напрямку, що проходить через центр мас системи, а - кінетичний момент системи щодо цієї осі. З (4.4) випливає, що
де - момент зовнішніх сил щодо осі. Якщо весь час руху то маємо перший інтеграл
У роботах С. А. Чаплигіна отримано кілька узагальнень теореми про зміну кінетичного моменту, які застосовані при вирішенні низки завдань про кочення куль. Подальші узагальнення теореми про зміну концептуального моменту та їх застосування в задачах динаміки твердого тіла містяться в роботах. Основні результати цих робіт пов'язані з теоремою про зміну кінетичного моменту щодо рухомої , що постійно проходить через деяку точку А . одиничний вектор, Спрямований вздовж цієї осі. Помноживши скалярно на обидві частини рівності (4.3) і додавши до його обепм частинам доданок отримаємо
При виконанні кінематичної умови
з (4.7) слідує рівняння (4.5). І якщо весь час руху і виконується умова (4.8), існує перший інтеграл (4.6).
Якщо зв'язки системи ідеальні і допускають серед віртуальних переміщень обертання системи як твердого тіла навколо осі і, то головний момент реакцій щодо осі і дорівнює нулю , і тоді величина у правій частині рівняння (4.5) являє собою головний момент всіх зовнішніх активних сил щодо осі і . Рівність нулю цього моменту та здійсненність співвідношення (4.8) будуть у розглянутому випадку достатніми умовамиіснування інтеграла (4.6).
Якщо напрямок осі і незмінно то умова (4.8) запишеться у вигляді
![]()
Ця рівність означає, що проекції швидкості центру мас і швидкості точки А осі та на площину, перпендикулярну до цієї є паралельними. У роботі С. А. Чаплигіна замість (4.9) потрібно виконання менш загальної умовиде X - довільна стала величина.
Зауважимо, що умова (4.8) залежить від вибору точки на . Справді, нехай Р-довільна точка на осі. Тоді
і, отже,
На закінчення відзначимо геометричну інтерпретацію Резалю рівнянь (4.1) та (4.4): вектори абсолютних швидкостейкінців векторів і рівні відповідно до головного вектора і головного моменту всіх зовнішніх сил щодо точки А.
МІНІСТЕРСТВО СІЛЬСЬКОГО ГОСПОДАРСТВА ТА ПРОДОВОЛЕННЯ РЕСПУБЛІКИ БІЛОРУСЬ
Установа освіти «БІЛОРУСЬКИЙ ДЕРЖАВНИЙ АГРАРНИЙ
ТЕХНІЧНИЙ УНІВЕРСИТЕТ"
Кафедра теоретичної механіки та теорії механізмів та машин
ТЕОРЕТИЧНА МЕХАНІКА
методичного комплексу для студентів групи спеціальностей
74 06 Агроінженери я
У 2-х частинах Частина 1
УДК 531.3(07) ББК 22.213я7 Т 33
Укладачі:
кандидат фізико-математичних наук, доцентЮ. С. Біза, кандидат технічних наук, ДоцентН. Л. Ракова, старший викладачІ. О. Тарасевич
Рецензенти:
кафедра теоретичної механіки Установи освіти «Білоруський національний технічний університет» (завідувач
кафедрою теоретичної механіки БНТУ, доктор фізико-математичних наук, професораА. В. Чигарьов);
провідний науковий співробітник лабораторії «Віброзахист механічних систем» ДНУ «Об'єднаний інститут машинобудування
НАН Білорусі», кандидат технічних наук, доцент О. М. Гоман
Теоретична механіка. Розділ «Динаміка»: навчально-
Т33 метод. комплекс. У 2-х ч. Ч. 1/уклад: Ю. С. Біза, Н. Л. Ракова, І. А. Тарасевич. - Мінськ: БДАТУ, 2013. - 120 с.
ISBN 978-985-519-616-8.
В навчально-методичному комплексіпредставлені матеріали щодо вивчення розділу «Динаміка», частина 1, що входить до складу дисципліни «Теоретична механіка». Включає курс лекцій, основні матеріали щодо виконання практичних занять, завдання та зразки виконання завдань для самостійної роботи та контролю навчальної діяльностістудентів очної та заочної формнавчання.
УДК 531.3(07) ББК 22.213я7
ВСТУП................................................. ......................................... | |
1. НАУКОВО-ТЕОРЕТИЧНИЙ ЗМІСТ НАВЧАЛЬНО- | |
МЕТОДИЧНОГО КОМПЛЕКСУ................................................ .. | |
1.1. Глосарій................................................. ................................ | |
1.2. Теми лекцій та їх зміст............................................. .. | |
Глава 1. Введення у динаміку. Основні поняття | |
класичної механіки................................................ .................... | |
Тема 1. Динаміка матеріальної точки........................................................... | |
1.1. Закони динаміки матеріальної точки | |
(закони Галілея – Ньютона) ............................................ .......... | |
1.2. Диференційне рівнянняруху | |
1.3. Дві основні завдання динаміки.......................................... | |
Тема 2. Динаміка відносного руху | |
матеріальної точки................................................ .......................... | |
Питання для повторення............................................... ............. | |
Тема 3. Динаміка механічної системи. | |
3.1. Геометрія мас. Центр мас механічної системи... | |
3.2. Внутрішні сили................................................ .................. | |
Питання для повторення............................................... ............. | |
Тема 4. Моменти інерції твердого тіла. | |
4.1. Моменти інерції твердого тіла | |
щодо осі та полюса.............................................. ..... | |
4.2. Теорема про моменти інерції твердого тіла | |
щодо паралельних осей | |
(теорема Гюйгенса - Штейнера) ............................................ .... | |
4.3. Відцентрові моменти інерції. | |
Питання для повторення............................................... ............ | |
Глава 2. Загальні теореми динаміки матеріальної точки | |
Тема 5. Теорема про рух центру мас системи....................... | |
Питання для повторення............................................... ............. | |
Завдання для самостійного вивчення. | |
Тема 6. Кількість руху матеріальної точки | |
та механічної системи............................................... ................... | |
6.1. Кількість руху матеріальної точки 43 | |
6.2. Імпульс сили................................................ ....................... | |
6.3. Теорема про зміну кількості руху | |
матеріальної точки................................................ .................... | |
6.4. Теорема про зміну головного вектора | |
кількості руху механічної системи.......................... | |
Питання для повторення............................................... ............. | |
Завдання для самостійного вивчення. | |
Тема 7. Момент кількості руху матеріальної точки | |
та механічної системи щодо центру та осі. | |
7.1. Момент кількості руху матеріальної точки | |
щодо центру та осі.............................................. ........... | |
7.2. Теорема про зміну моменту кількості руху | |
матеріальної точки щодо центру та осі...................... | |
7.3. Теорема про зміну кінетичного моменту | |
механічної системи щодо центру та осі. | |
Питання для повторення............................................... ............. | |
Завдання для самостійного вивчення. | |
Тема 8. Робота та потужність сил........................................... ............ | |
Питання для повторення............................................... ............. | |
Завдання для самостійного вивчення. | |
Тема 9. Кінетична енергія матеріальної точки | |
та механічної системи............................................... ................... | |
9.1. Кінетична енергія матеріальної точки | |
та механічної системи. Теорема Кеніга............................... | |
9.2. Кінетична енергія твердого тіла | |
при різному русі............................................... ............. | |
9.3. Теорема про зміну кінетичної енергії | |
матеріальної точки................................................ .................... |
9.4. Теорема про зміну кінетичної енергії | |
механічної системи................................................ ................ | |
Питання для повторення............................................... ............. | |
Завдання для самостійного вивчення. | |
Тема 10. Потенційне силове поле | |
і потенційна енергія............................................... .................. | |
Питання для повторення............................................... ............. | |
Тема 11. Динаміка твердого тіла............................................ ....... | |
Питання для повторення............................................... ............. | |
2. МАТЕРІАЛИ ДЛЯ ПРОВЕДЕННЯ КОНТРОЛЮ | |
ПО МОДУЛЮ................................................ ................................... | |
САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ......................... | |
4. ВИМОГИ ДО ОФОРМЛЕННЯ КОНТРОЛЬНИХ | |
РОБОТ ДЛЯ CТУДЕНТІВ ГЕЛЬНОЇ ТА ЗАОЧНОЇ | |
ФОРМ НАВЧАННЯ................................................ ........................ | |
5. ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДГОТОВКИ | |
ДО ЕКЗАМЕНУ (ЗАЛІКУ) СТУДЕНТІВ | |
ОЧНИЙ І ЗАТКОВИЙ ФОРМ НАВЧАННЯ. | |
6. СПИСОК ЛІТЕРАТУРИ.............................................. ............ |
ВСТУП
Теоретична механіка – наука про загальні закони механічного руху, рівноваги та взаємодії матеріальних тіл.
Це одна з фундаментальних загальнонаукових фізико-математичних дисциплін. Вона є теоретичною основою сучасної техніки.
Вивчення теоретичної механіки, поряд з іншими фізикоматематичними дисциплінами, сприяє розширенню наукового кругозору, формує здібності до конкретного та абстрактного мисленнята сприяє підвищенню загальної технічної культури майбутнього спеціаліста.
Теоретична механіка, будучи науковою базою всіх технічних дисциплін, сприяє розвитку навичок раціональних рішень інженерних завдань, пов'язаних з експлуатацією, ремонтом та конструюванням сільськогосподарських та меліоративних машин та обладнання.
За характером завдань механіку поділяють на статику, кінематику і динаміку. Динаміка – розділ теоретичної механіки, у якому вивчається рух тих матеріальних тіл під впливом прикладених сил.
В навчально-методичномукомплексі (УМК) представлені матеріали щодо вивчення розділу «Динаміка», який включає курс лекцій, основні матеріали для проведення практичних робіт, завдання та зразки виконання для самостійних робітта контролю навчальної діяльності студентів очної та заочної форм навчання.
В в результаті вивчення розділу «Динаміка» студент повинен засвоїти теоретичні основидинаміки та оволодіти основними методами вирішення задач динаміки:
Знати методи розв'язання задач динаміки, загальні теореми динаміки, принципи механіки;
Вміти визначати закони руху тіла залежно від сил, що діють на нього; застосовувати закони та теореми механіки для вирішення завдань; визначати статичні та динамічні реакції зв'язків, що обмежують рух тіл.
Навчальною програмою дисципліни «Теоретична механіка» передбачено загальну кількість аудиторних годин – 136, у т. ч. вивчення розділу «Динаміка» – 36 годин.
1. НАУКОВО-ТЕОРЕТИЧНИЙ ЗМІСТ НАВЧАЛЬНО-МЕТОДИЧНОГО КОМПЛЕКСУ
1.1. Глосарій
Статика - розділ механіки, в якому викладається загальне вчення про сили, вивчається приведення складних системсил до найпростішого вигляду та встановлюються умови рівноваги різних системсил.
Кінематика - це розділ теоретичної механіки, в якому вивчають рух матеріальних об'єктів незалежно від причин, що викликають цей рух, тобто незалежно від сил, що діють ці об'єкти.
Динаміка – розділ теоретичної механіки, у якому вивчається рух тих матеріальних тіл (точок) під впливом прикладених сил.
Матеріальна точка– матеріальне тіло, відмінність у русі точок якого є несуттєвим.
Маса тіла - це скалярна позитивна величина, яка залежить від кількості речовини, що міститься в даному тілі, і визначає його міру інертності при поступальному русі.
Система відліку – система координат, що з тілом, стосовно якого вивчається рух іншого тіла.
Інерційна система- Система, в якій виконуються перший та другий закони динаміки.
Імпульс сили – векторний захід дії сили протягом певного часу.
Кількість руху матеріальної точки - Векторна міра її руху, рівна добутку маси точки на вектор її швидкості.
Кінетична енергія- скалярна мірамеханічного руху.
Елементарна робота сили– це нескінченно мала скалярна величина, що дорівнює скалярному творувектор сили на вектор нескінченного малого переміщення точки додатка сили.
Кінетична енергія- скалярний захід механічного руху.
Кінетична енергія матеріальної точки - скалярна по-
ложительная величина, що дорівнює половині добутку маси точки на квадрат її швидкості.
Кінетична енергія механічної системи - арифметика.
тична сума кінетичних енергій всіх матеріальних точок цієї системи.
Сила – міра механічної взаємодії тіл, що характеризує його інтенсивність та спрямованість.
1.2. Теми лекцій та їх зміст
Розділ 1. Введення у динаміку. Основні поняття
класичної механіки
Тема 1. Динаміка матеріальної точки
Закони динаміки матеріальної точки (закони Галілея – Ньютона). Диференціальні рівняння руху матеріальної точки. Дві основні завдання – динаміки для матеріальної точки. Розв'язання другого завдання динаміки; постійні інтегрування та їх визначення за початковими умовами.
Література:, стор 180-196, , стор 12-26.
Тема 2. Динаміка відносного руху матеріального
Відносний рух матеріальної точки. диференціальні рівняння відносного руху точки; переносна та коріолісова сили інерції. Принцип відносності у класичній механіці. Випадок відносного спокою.
Література: , стор 180-196, , стор 127-155.
Тема 3. Геометрія мас. Центр мас механічної системи
Маса системи. Центр мас системи та її координати.
Література: , стор 86-93, стор 264-265
Тема 4. Моменти інерції твердого тіла
Моменти інерції твердого тіла щодо осі та полюса. Радіус інерції. Теорема про моменти інерції щодо паралельних осей. Осьові моменти інерції деяких тіл.
Відцентрові моменти інерції як характеристика асиметрії тіла.
Література: , стор 265-271, , стор 155-173.
Розділ 2. Загальні теореми динаміки матеріальної точки
та механічної системи
Тема 5. Теорема про рух центру мас системи
Теорема про рух центру мас системи. Наслідки з теореми про рух центру мас системи.
Література: , стор 274-277, , стор 175-192.
Тема 6. Кількість руху матеріальної точки
та механічної системи
Кількість руху матеріальної точки та механічної системи. Елементарний імпульс та імпульс сили за кінцевий проміжок часу. Теорема про зміну кількості руху точки та системи у диференціальній та інтегральній формах. Закон збереження кількості руху.
Література: , стор.280-284, , стор 192-207.
Тема 7. Момент кількості руху матеріальної точки
та механічної системи щодо центру та осі
Момент кількості руху точки щодо центру та осі. Теорема про зміну моменту кількості руху точки. Кінетичний момент механічної системи щодо центру та осі.
Кінетичний момент твердого тіла, що обертається, щодо осі обертання. Теорема про зміну кінетичного моменту системи. Закон збереження кінетичного моменту.
Література: , стор 292-298, , стор 207-258.
Тема 8. Робота та потужність сил
Елементарна робота сили, її аналітичний вираз. Робота сили на кінцевому шляху. Робота сили тяжіння, сили пружності. Рівність нулю суми робіт внутрішніх сил, які у твердому тілі. Робота сил, прикладених до твердого тіла, що обертається довкола нерухомої осі. Потужність. Коефіцієнт корисної дії.
Література: , стор 208-213, , стор 280-290.
Тема 9. Кінетична енергія матеріальної точки
та механічної системи
Кінетична енергія матеріальної точки та механічної системи. Обчислення кінетичної енергії твердого тіла у різних випадках його руху. Теорема Кеніга. Теорема про зміну кінетичної енергії точки у диференціальній та інтегральній формах. Теорема про зміну кінетичної енергії механічної системи у диференціальній та інтегральній формах.
Література: , стор 301-310, , стор 290-344.
Тема 10. Потенційне силове поле та потенційна
Концепція силове поле. Потенційне силове поле та силова функція. Робота сили на кінцевому переміщенні точки у потенційному силовому полі. Потенціальна енергія.
Література: , стор 317-320, , стор 344-347.
Тема 11. Динаміка твердого тіла
Диференціальні рівняння поступального руху твердого тіла. Диференційне рівняння обертального рухутвердого тіла довкола нерухомої осі. Фізичний маятник. Диференціальні рівняння плоского руху жорсткого тіла.
Література: , стор 323-334, , стор 157-173.
Розділ 1. У відання в динаміку. Основні поняття
класичної механіки
Динаміка – розділ теоретичної механіки, у якому вивчається рух тих матеріальних тіл (точок) під впливом прикладених сил.
Матеріальне тіло- Тіло, що має масу.
Матеріальна точка– матеріальне тіло, відмінність у русі точок якого є несуттєвим. Це може бути як тіло, розмірами якого за його руху можна знехтувати, так і тіло кінцевих розмірів, якщо воно рухається поступально.
Матеріальними точками називають також частинки, куди подумки розбивається тверде тіло щодо деяких його динамічних характеристик. Приклади матеріальних точок (рис. 1): а – рух Землі навколо Сонця. Земля – матеріальна точка; б – поступальний рух твердого тіла. Тверде тіло- матері-
альна точка, т. к. V B = V A; a B = a A; в – обертання тіла навколо осі.
Частка тіла – матеріальна точка.
Інертність – властивість матеріальних тіл швидше чи повільніше змінювати швидкість свого руху під дією прикладених сил.
Маса тіла - це скалярна позитивна величина, яка залежить від кількості речовини, що міститься в даному тілі, і визначає його міру інертності при поступальному русі. У класичній механіці маса - величина стала.
Сила – кількісний західмеханічної взаємодії між тілами або між тілом (точкою) та полем (електричним, магнітним тощо).
Сила – векторна величина, що характеризується величиною, точкою додатка та напрямком (лінією дії) (рис. 2: А – точка додатку; АВ – лінія дії сили).
Рис. 2
У динаміці поряд з постійними силами мають місце і змінні сили, які можуть залежати від часу t, швидкості, відстані або від сукупності цих величин, тобто.
F = const;
F = F(t);
F = F(ϑ);
F = F(r);
F = F(t, r, ϑ).
Приклади таких сил наведено на рис. 3: a − | - вага тіла; |
||||||||||
(ϑ) – сила опору повітря; б − | Т = | - Сила тяги |
|||||||||
електровози; в − F = F (r ) – сила відштовхування від центру O або тяжіння до нього.

Система відліку – система координат, що з тілом, стосовно якого вивчається рух іншого тіла.
Інерційна система - система, в якій виконуються перший і другий закони динаміки. Це нерухома система координат або система, що рухається поступово і прямолінійно поступально.
Рух у механіці – це зміна становища тіла у просторі й у часі стосовно іншим тілам.
Простір у класичній механіці тривимірний, що підкоряється евклідовій геометрії.
Час - скалярна величина, що однаково протікає в будь-яких системах рахунку.
Система одиниць – це сукупність одиниць виміру фізичних величин. Для виміру всіх механічних величин достатньо трьох основних одиниць: одиниці довжини, часу, маси чи сили.
Механічна | Розмірність | Позначення | Розмірність | Позначення |
|
величина | |||||
сантиметр | |||||
кілограм- | |||||
Решта одиниць виміру механічних величин – похідні від цих. Застосовуються два типи систем одиниць: міжнародна системаодиниць СІ (або дрібніша – СГС) та технічна система одиниць – МКГСС.
Тема1. Динамікаматеріальної точки
1.1. Закони динаміки матеріальної точки (закони Галілея – Ньютона)
Перший закон (законінерції).
Ізольована від зовнішніх впливівматеріальна точка зберігає свій стан спокою або рухається рівномірно і прямолінійно доти, доки прикладені сили не змусять її змінити цей стан.
Рух, що відбувається точкою за відсутності сил чи під дією врівноваженої системи сил, називається рухом за інерцією.
Наприклад, рух тіла по гладкій (сила тертя дорівнює нулю) го-
різонтальної поверхні (рис. 4: G - вага тіла; N - нормальна реакція площини).
Оскільки G = − N , то G + N = 0.
При ϑ 0 ≠ 0 тіло рухається з тією самою швидкістю; приϑ 0 = 0 тіло спочиває (ϑ 0 – початкова швидкість).
Другий закон (основний закон динаміки).

Твір маси точки на прискорення, яке вона отримує під дією даної сили, дорівнює модулю цієї сили, а її напрямок збігається з напрямом прискорення.
а б
Математично цей закон виражається векторною рівністю
При F = const, | a = const – рух точки рівнозмінний. Ес- |
||||||||||||||
чи a ≠ const, α | - Рух уповільнений (рис. 5, а); | a ≠ const, |
|||||||||||||
a – |
|||||||||||||||
– рух прискорений (рис. 5, б); m – маса точки; |
|||||||||||||||
вектор прискорення; | - Векторні сили; ϑ 0 - Вектор швидкості). | ||||||||||||||
При F = 0,a 0 = 0 = ϑ 0 = const – точка рухається поступово і прямолінійно чи приϑ 0 = 0 – лежить (закон інерції). Другий
закон дозволяє встановити зв'язок між масою m тіла, що знаходиться поблизу земної поверхні, та його вагою G .G = mg , де g –
прискорення вільного падіння.
Третій закон (закон рівності дії та протидії). Дві матеріальні точки діють один на одного з силами, рівними за величиною та спрямованими вздовж прямої, що сполучає
ці точки, у протилежні сторони.
Так як сили F 1 = − F 2 прикладені до різним точкам, то система сил (F 1, F 2) не є врівноваженою, тобто (F 1, F 2) ≈ 0 (рис. 6).
В свою чергу | m a = m a | - Відношення |
|||||||||||||
мас взаємодіючих точок обернено пропорційно їх прискоренням.
Четвертий закон (закон незалежності дії сил). Прискорення, що отримується точкою при дії на неї одночасно.
але кількох сил, одно геометричній сумі тих прискорень, які б точка при дії неї кожної сили окремо.
Пояснення (рис. 7).
т а n
а 1 а кF n
Рівнодійна R сил (F 1, F k, F n).
Оскільки ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = ma n , то
a = a 1 + ...+ a k + ...+ a n = ∑ a k , тобто четвертий закон еквівалентний
k = 1
правилу складання сил.

1.2. Диференціальні рівняння руху матеріальної точки
Нехай на матеріальну точку діє одночасно кілька сил, серед яких є як постійні, так і змінні.
Запишемо другий закон динаміки у вигляді
= ∑ | (t, | |||||||||||||||||||||||||
k = 1 | ||||||||||||||||||||||||||
, ϑ= | r – радіус-вектор, що рухається |
|||||||||||||||||||||||||
точки, то (1.2) містить похідні від r і є диференціальне рівняння руху матеріальної точки у векторній формі або основне рівняння динаміки матеріальної точки.
Проекції векторної рівності (1.2): - на осидекартових координат (рис. 8, а)
max = md | ||||||
= ∑ F kx; | ||||||
k = 1 | ||||||
may = md | ||||||
= ∑ F ky; | (1.3) |
|||||
k = 1 | ||||||
maz = m | = ∑ F kz; | |||||
k = 1 | ||||||
Наприродної осі (рис. 8, б)
maτ | = ∑ F k τ , | ||||
k = 1 | |||||
= ∑ F k n; |
|||||
k = 1 | |||||
mab = m0 = ∑ Fk b
k = 1
Mt oM oa
b on o |
Рівняння (1.3) та (1.4) є диференціальними рівняннями руху матеріальної точки відповідно в декартових осях координат та природних осях, тобто природними диференціальними рівняннями, які зазвичай застосовуються при криволінійному русі точки, якщо траєкторія точки та її радіус кривизни відомі.
1.3. Дві основні завдання динаміки для матеріальної точки та їх вирішення
Перше (пряме) завдання.
Знаючи закон руху і масу точки, визначити силу, що діє наточку.
Для вирішення цього завдання необхідно знати прискорення точки. У задачах цього типу воно може бути задане безпосередньо або заданий закон руху точки, відповідно до якого воно може бути визначено.
1. Так, якщо рух точки задано у декартових координатах
x = f 1 (t ) , y = f 2 (t ) і z = f 3 (t ) , то визначаються проекції прискоро-
ня на осі координатx = | d 2 x | d 2 y | d 2 z | А потім - проект- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ції F x ,F y і F z сили на ці осі: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ,k) = F F z. (1.6) 2. Якщо точка здійснює криволінійний рухі відомий закон руху s = f (t ) , траєкторія точки та її радіус кривизни ρ, то зручно користуватися природними осями, а проекції прискорення на ці осі визначаються за відомими формулами: Стосовно ось a τ = d ϑ = d 2 2 s – дотичне прискорення; dt dt Наголовнунормаль ds 2 a n = ϑ 2 = dt – нормальне прискорення. Проекція прискорення на бінормаль дорівнює нулю. Тоді проекції сили природні осі
Модуль і напрям сили визначаються за формулами:
Друге (зворотне) завдання. Знаючи чинні на точку сили, її масу та початкові умовируху, визначити закон руху точки або будь-які інші її кінематичні характеристики. Початкові умови руху точки в декартових осях – це координати точки x 0 , y 0 , z 0 і проекції початкової швидкості 0 на ці осі ϑ 0 x = x 0 , ϑ 0 y = y 0 іϑ 0 z = z 0 в момент часу, відпо- ний початку руху точки і прийнятий рівним нулю. Розв'язання задач цього типу зводиться до складання диффе- ренціальних рівнянь (або одного рівняння) руху матеріальної точки та їх подальшого вирішення шляхом безпосереднього інтегруванняабо з використанням теорії диференціальних рівнянь. Питання на повторення 1. Що вивчає динаміка? 2. Який рух називається рухом за інерцією? 3. За якої умови матеріальна точка спочиватиме або рухатиметься рівномірно і прямолінійно? 4. У чому суть першого основного завдання динаміки матеріальної точки? Друге завдання? 5. Запишіть природні рівняння руху матеріальної точки. Завдання для самостійного вивчення 1. Точка масою m = 4 кг рухається горизонтальною прямою з прискоренням a = 0,3 t . Визначити модуль сили, що діє на точку у напрямі її руху в момент часу t = 3 c . 2. Деталь масою m = 0,5 кг ковзає вниз по лотку. Під яким кутом до горизонтальної площини повинен розташовуватися лоток, щоб деталь рухалася з прискоренням = 2 м/с 2 ? Кут висловити у градусах. 3. Точка масою m = 14 кг рухається по осіОх з прискоренням a х = 2 t. Визначити модуль сили, що діє на точку у напрямку руху в момент часу t = 5c. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(МЕХАНІЧНІ СИСТЕМИ) - IV варіант
1. Основне рівняння динаміки матеріальної точки, як відомо, виражено рівнянням. Диференціальні рівняння руху довільних точокневільної механічної системи відповідно до двох способів розподілу сил можна записати у двох формах:
(1)
![]() , де k = 1, 2, 3, ..., n - кількість точок матеріальної системи.
, де k = 1, 2, 3, ..., n - кількість точок матеріальної системи.
(2)
![]()
де - маса k-тої точки; - радіус вектор k-тої точки, - задана (активна) сила, що діє на k-ту точку або рівнодіє всіх активних сил, що діють на k-ту точку. - рівнодіюча сил реакцій зв'язків, що діє на k-ту точку; - рівнодіюча внутрішніх сил, що діє на k-ту точку; - рівнодіюча зовнішніх сил, що діє на k-ту точку.
За допомогою рівнянь (1) та (2) можна прагнути вирішувати як перше, так і друге завдання динаміки. Однак вирішення другого завдання динаміки для системи дуже ускладнюється не тільки з математичної точкизору, а й тому, що ми стикаємося з важливими труднощами. Вони у тому, що як системи (1), так системи (2) число рівнянь значно менше числаневідомі.
Так, якщо використовувати (1), то відомими для другого (зворотного) завдання динаміки будуть і , а невідомими будуть і . Векторних рівнянь буде n», а невідомих – «2n».
Якщо ж виходити із системи рівнянь (2), то відомі і частина зовнішніх сил. Чому частина? Справа в тому, що до зовнішніх сил входять і зовнішні реакціїзв'язків, які невідомі. До того ж, невідомими будуть ще й .
Отже, як система (1), і система (2) НЕЗАМКНУТА. Потрібно додавати рівняння, враховуючи рівняння зв'язків і, можливо, ще потрібно накладати деякі обмеження на самі зв'язки. Що робити?
Якщо з (1), можна піти шляхом складання рівнянь Лагранжа першого роду. Але такий шлях не раціональний тому, що чим простіше завдання(менше ступенів свободи), тим важче з погляду математики її вирішувати.
Тоді звернемо увагу на систему (2), де завжди невідомі. Перший крок під час вирішення системи – це треба виключити ці невідомі. Слід мати на увазі, що нас, як правило, не цікавлять внутрішні сили при русі системи, тобто при русі системи не потрібно знати, як рухається кожна точка системи, а достатньо знати як рухається система в цілому.
Таким чином, якщо у різний спосібвиключити із системи (2) невідомі сили, то отримуємо деякі співвідношення, тобто з'являються деякі загальні характеристикидля системи, знання яких дозволяють судити у тому, як рухається система загалом. Ці характеристики вводяться за допомогою так званих загальних теорем динаміки. Таких теорем чотири:
1. Теорема про рух центру мас механічної системи;
2. Теорема про зміні кількості руху механічної системи;
3. Теорема про зміні кінетичного моменту механічної системи;
4. Теорема про зміні кінетичної енергії механічної системи.
 Інформаційний матеріал "куточок юного читача"
Інформаційний матеріал "куточок юного читача" Лікар хто далекі знищити
Лікар хто далекі знищити Де купити сірчану кислоту?
Де купити сірчану кислоту?