Πώς προστίθενται και αφαιρούνται τα διανύσματα. Ιδιότητες πολλαπλασιασμού ενός διανύσματος με έναν αριθμό

Για τη σωστή απεικόνιση των νόμων της φύσης στη φυσική απαιτούνται κατάλληλα μαθηματικά εργαλεία.

Στη γεωμετρία και τη φυσική υπάρχουν ποσότητες που χαρακτηρίζονται και αριθμητική αξίακαι κατεύθυνση.

Συνιστάται να τα αντιπροσωπεύετε ως κατευθυνόμενα τμήματα ή φορείς.

Τέτοιες τιμές έχουν μια αρχή (που αντιπροσωπεύεται από μια τελεία) και ένα τέλος, που υποδεικνύεται με ένα βέλος. Το μήκος του τμήματος ονομάζεται (μήκος).

Ταχύτητα;
επιτάχυνση;
σφυγμός;
δύναμη;
στιγμή;
δύναμη;
κίνηση;
δύναμη πεδίου κ.λπ.

Συντεταγμένες αεροπλάνου

Ας ορίσουμε ένα τμήμα στο επίπεδο που κατευθύνεται από το σημείο A (x1, y1) στο σημείο B (x2, y2). Οι συντεταγμένες του a (a1, a2) είναι οι αριθμοί a1=x2-x1, a2=y2-y1.

Η ενότητα υπολογίζεται χρησιμοποιώντας το Πυθαγόρειο θεώρημα:

Το μηδενικό διάνυσμα έχει την αρχή και το τέλος. Οι συντεταγμένες και το μήκος είναι 0.

Άθροισμα διανυσμάτων

Υπάρχει αρκετούς κανόνες για τον υπολογισμό του ποσού

κανόνας τριγώνου?
κανόνας πολυγώνου.
κανόνας παραλληλογράμμου.

Ο κανόνας πρόσθεσης διανυσμάτων μπορεί να εξηγηθεί χρησιμοποιώντας προβλήματα από τη δυναμική και τη μηχανική. Εξετάστε την προσθήκη διανυσμάτων σύμφωνα με τον κανόνα του τριγώνου χρησιμοποιώντας το παράδειγμα των δυνάμεων που δρουν σε ένα σημειακό σώμα και των διαδοχικών μετατοπίσεων του σώματος στο χώρο.

Ας υποθέσουμε ότι το σώμα μετακινήθηκε πρώτα από το σημείο Α στο σημείο Β και μετά από το σημείο Β στο σημείο Γ. Η τελική μετατόπιση είναι ένα τμήμα που κατευθύνεται από το σημείο έναρξης Α έως το τελικό σημείο Γ.

Το αποτέλεσμα δύο μετατοπίσεων ή το άθροισμά τους s = s1+ s2. Μια τέτοια μέθοδος ονομάζεται κανόνας τριγώνου.

Τα βέλη παρατάσσονται σε μια αλυσίδα το ένα μετά το άλλο, εάν είναι απαραίτητο, πραγματοποιώντας μια παράλληλη μεταφορά. Το συνολικό τμήμα κλείνει την ακολουθία. Η αρχή του συμπίπτει με την αρχή του πρώτου, το τέλος - με το τέλος του τελευταίου. Σε ξένα σχολικά βιβλία αυτή τη μέθοδοπου ονομάζεται "ουρά με κεφάλι".

Οι συντεταγμένες του αποτελέσματος c = a + b είναι ίσες με το άθροισμα των αντίστοιχων συντεταγμένων των όρων c (a1+ b1, a2+ b2).

Το άθροισμα των παράλληλων (συγγραμμικών) διανυσμάτων καθορίζεται επίσης από τον κανόνα του τριγώνου.

Αν δύο αρχικά τμήματα είναι κάθετα μεταξύ τους, τότε το αποτέλεσμα της πρόσθεσής τους είναι η υποτείνουσα του ορθογώνιο τρίγωνο. Το μήκος του αθροίσματος υπολογίζεται χρησιμοποιώντας το Πυθαγόρειο θεώρημα.

Παραδείγματα:

Η ταχύτητα ενός σώματος που ρίχνεται οριζόντια κάθετοςεπιτάχυνση ελεύθερη πτώση.
Με στολή περιστροφική κίνηση ταχύτητα γραμμήςσώμα είναι κάθετο στην κεντρομόλο επιτάχυνση.

Προσθήκη τριών ή περισσότερων διανυσμάτωνπαράγουν σύμφωνα με κανόνας πολυγώνου, "ουρά με κεφάλι"

Ας υποθέσουμε ότι οι δυνάμεις F1 και F2 εφαρμόζονται σε ένα σημειακό σώμα.

Η πείρα αποδεικνύει ότι το συνδυασμένο αποτέλεσμα αυτών των δυνάμεων ισοδυναμεί με τη δράση μιας δύναμης που κατευθύνεται διαγώνια κατά μήκος του παραλληλογράμμου που είναι χτισμένο πάνω τους. Αυτή η προκύπτουσα δύναμη είναι ίση με το άθροισμά τους F \u003d F1 + F 2. Η παραπάνω μέθοδος πρόσθεσης ονομάζεται κανόνας παραλληλογράμμου.

Το μήκος σε αυτή την περίπτωση υπολογίζεται από τον τύπο

Όπου θ είναι η γωνία μεταξύ των πλευρών.

Οι κανόνες του τριγώνου και του παραλληλογράμμου είναι εναλλάξιμοι. Στη φυσική, ο κανόνας του παραλληλογράμμου χρησιμοποιείται συχνότερα, αφού τα κατευθυνόμενα μεγέθη δυνάμεων, ταχυτήτων και επιταχύνσεων εφαρμόζονται συνήθως σε ένα σημείο σώμα. Σε ένα τρισδιάστατο σύστημα συντεταγμένων, ισχύει ο κανόνας του πλαισίου.

Στοιχεία Άλγεβρας

Η προσθήκη είναι μια δυαδική λειτουργία: μπορείτε να προσθέσετε μόνο ένα ζεύγος κάθε φορά.
ανταλλαξιμότητα: το άθροισμα από τη μετάθεση των όρων δεν αλλάζει a + b = b + a. Αυτό είναι σαφές από τον κανόνα του παραλληλογράμμου: η διαγώνιος είναι πάντα η ίδια.
Συνεταιρισμός: το άθροισμα ενός αυθαίρετου αριθμού διανυσμάτων δεν εξαρτάται από τη σειρά πρόσθεσής τους (a + b) + c = a + (b + c).
Το άθροισμα με μηδενικό διάνυσμα δεν αλλάζει κατεύθυνση ή μήκος: a +0= a .
Για κάθε διάνυσμα υπάρχει απεναντι απο. Το άθροισμά τους είναι ίσο με μηδέν a +(-a)=0, και τα μήκη είναι ίδια.

Η αφαίρεση ενός κατευθυνόμενου τμήματος ισοδυναμεί με την προσθήκη του αντίθετου. Οι συντεταγμένες είναι ίσες με τη διαφορά των αντίστοιχων συντεταγμένων. Το μήκος είναι:

Για την αφαίρεση, μπορείτε να χρησιμοποιήσετε έναν τροποποιημένο κανόνα τριγώνου.

Πολλαπλασιασμός με βαθμωτό

Το αποτέλεσμα του πολλαπλασιασμού με ένα βαθμωτό είναι ένα διάνυσμα.

Οι συντεταγμένες του γινομένου λαμβάνονται πολλαπλασιάζοντας με βαθμωτή τις αντίστοιχες συντεταγμένες της πηγής.

Βαθμωτό μέγεθος - αριθμητική αξίαμε πρόσημο συν ή πλην, μεγαλύτερο ή μικρότερο από ένα.

Παραδείγματα σκαλοπάτιαστη φυσική:

βάρος;
χρόνος;
χρέωση;
μήκος;
τετράγωνο;
Ενταση ΗΧΟΥ;
πυκνότητα;
θερμοκρασία;
ενέργεια.

Παραδείγματα:

Η μετατόπιση ενός ομοιόμορφα κινούμενου σώματος είναι ίση με το γινόμενο του χρόνου και της ταχύτητας s = vt.
Η ορμή ενός σώματος είναι η μάζα πολλαπλασιαζόμενη με την ταχύτητα p = mv.
Δεύτερος νόμος του Νεύτωνα. Το προϊόν της μάζας του σώματος και της επιτάχυνσης είναι επισυνάπτεταιπροκύπτουσα δύναμη ma=F.
Η δύναμη που ασκείται σε ένα φορτισμένο σωματίδιο σε ένα ηλεκτρικό πεδίο είναι ανάλογη με το φορτίο F = qE.

Το κλιμακωτό γινόμενο των κατευθυνόμενων τμημάτων a και b είναι ίσο με το γινόμενο των μονάδων και το συνημίτονο της μεταξύ τους γωνίας. Το κλιμακωτό γινόμενο αμοιβαία κάθετων τμημάτων είναι ίσο με μηδέν.

Παράδειγμα:

Η δουλειά είναι κλιμακωτό προϊόνδυνάμεις και μετατοπίσεις A = Fs .

Χ και yπου ονομάζεται διάνυσμα zτέτοια που z+y=x.

Επιλογή 1.Τα σημεία εκκίνησης όλων των διανυσμάτων συμπίπτουν με την προέλευση.

Ας κατασκευάσουμε τη διαφορά των διανυσμάτων και .

Να σχεδιάσετε τη διαφορά των διανυσμάτων z=x-y, πρέπει να προσθέσετε το διάνυσμα Χμε αντίθετο προς yδιάνυσμα y". Αντίθετο διάνυσμα y"χτίζεται απλά:

Διάνυσμα y"είναι απέναντι από το διάνυσμα y, επειδή y+y"= 0, όπου 0 είναι ένα μηδενικό διάνυσμα του κατάλληλου μεγέθους. Στη συνέχεια, πραγματοποιείται η προσθήκη διανυσμάτων Χκαι y":

Από την έκφραση (1) φαίνεται ότι για να κατασκευαστεί η διαφορά των διανυσμάτων, αρκεί να υπολογιστούν οι διαφορές των αντίστοιχων συντεταγμένων των διανυσμάτων Χκαι y.

Ρύζι. ένας

Στο Σχ. 1 σε δισδιάστατο χώρο αντιπροσωπεύει τη διαφορά των διανυσμάτων Χ=(10,3) και y=(2,4).

Υπολογίζω z=x-y=(10-3,3-4)=(7,-1). Ας συγκρίνουμε το αποτέλεσμα που προκύπτει με τη γεωμετρική ερμηνεία. Πράγματι, μετά την κατασκευή του διανύσματος y"και παράλληλη κίνηση του σημείου εκκίνησης του διανύσματος y"μέχρι το τελικό σημείο του διανύσματος Χ, παίρνουμε το διάνυσμα y"", και αφού προσθέσουμε τα διανύσματα Χκαι y"", παίρνουμε το διάνυσμα z.

Επιλογή 2.Τα σημεία εκκίνησης των διανυσμάτων είναι αυθαίρετα.

Ρύζι. 2

Στο Σχ. 2 στον δισδιάστατο χώρο είναι η διαφορά των διανυσμάτων Χ=ΑΒκαι y=CD, όπου ΕΝΑ(1,0), σι(11,3), ντο(1,2), ρε(3.6). Για να υπολογίσετε το διάνυσμα z=x-y, κατασκευασμένο απέναντι από το διάνυσμα yδιάνυσμα y":

Στη συνέχεια, πρέπει να προσθέσετε τα διανύσματα Χκαι y". Διάνυσμα y"κινείται παράλληλα έτσι ώστε το σημείο ΝΤΟ"συνέπεσε με το σημείο σι. Για να γίνει αυτό, υπολογίζονται οι διαφορές στις συντεταγμένες των σημείων σικαι ΑΠΟ.

ov, πρώτα πρέπει να κατανοήσετε μια τέτοια έννοια όπως η αναβολή ενός διανύσματος από ένα δεδομένο σημείο.

Ορισμός 1

Εάν το σημείο $A$ είναι η αρχή κάποιου διανύσματος $\overrightarrow(a)$, τότε το διάνυσμα $\overrightarrow(a)$ λέγεται ότι διαχωρίζεται από το σημείο $A$ (Εικ. 1).

Εικόνα 1. $\overrightarrow(a)$ σχεδιάστηκε από το σημείο $A$

Εισάγουμε το εξής θεώρημα:

Θεώρημα 1

Από οποιοδήποτε σημείο $K$ μπορεί κανείς να σχεδιάσει ένα διάνυσμα $\overrightarrow(a)$ και μόνο ένα.

Απόδειξη.

Υπαρξη:Υπάρχουν δύο περιπτώσεις που πρέπει να εξεταστούν εδώ:

Το διάνυσμα $\overrightarrow(a)$ είναι μηδέν.

Σε αυτήν την περίπτωση, είναι προφανές ότι το επιθυμητό διάνυσμα είναι το διάνυσμα $\overrightarrow(KK)$.

Το διάνυσμα $\overrightarrow(a)$ είναι μη μηδενικό.

Αφήστε το σημείο $A$ να υποδηλώνει την αρχή του διανύσματος $\overrightarrow(a)$ και το σημείο $B$ να υποδηλώνει το τέλος του διανύσματος $\overrightarrow(a)$. Ας τραβήξουμε μια γραμμή $b$ μέχρι το σημείο $K$ παράλληλα με το διάνυσμα$\overrightarrow(a)$. Ας σχεδιάσουμε τα τμήματα $\left|KL\right|=|AB|$ και $\left|KM\right|=|AB|$ σε αυτήν την ευθεία γραμμή. Εξετάστε τα διανύσματα $\overrightarrow(KL)$ και $\overrightarrow(KM)$. Από αυτά τα δύο διανύσματα, το επιθυμητό θα είναι αυτό που θα συν-κατευθυνθεί με το διάνυσμα $\overrightarrow(a)$ (Εικ. 2)

Εικόνα 2. Απεικόνιση του Θεωρήματος 1

Μοναδικότητα:μοναδικότητα προκύπτει αμέσως από την κατασκευή που πραγματοποιήθηκε στην υποενότητα «ύπαρξη».

Το θεώρημα έχει αποδειχθεί.

Αφαίρεση διανυσμάτων. Κανόνας Πρώτος

Ας μας δοθούν τα διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$.

Ορισμός 2

Η διαφορά δύο διανυσμάτων $\overrightarrow(a)$ και $\overrightarrow(b)$ είναι ένα διάνυσμα $\overrightarrow(c)$ το οποίο, όταν προστεθεί στο διάνυσμα $\overrightarrow(b)$, δίνει το διάνυσμα $\ overrightarrow(a)$ , δηλαδή

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Ονομασία:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Θα εξετάσουμε την κατασκευή της διαφοράς δύο διανυσμάτων χρησιμοποιώντας το πρόβλημα.

Παράδειγμα 1

Έστω τα διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$. Κατασκευάστε το διάνυσμα $\overrightarrow(a)-\overrightarrow(b)$.

Λύση.

Ας κατασκευάσουμε ένα αυθαίρετο σημείο $O$ και σχεδιάζουμε τα διανύσματα $\overrightarrow(OA)=\overrightarrow(a)$ και $\overrightarrow(OB)=\overrightarrow(b)$ από αυτό. Συνδέοντας το σημείο $B$ με το σημείο $A$, παίρνουμε το διάνυσμα $\overrightarrow(BA)$ (Εικ. 3).

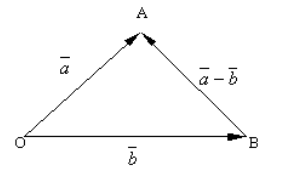
Εικόνα 3. Διαφορά δύο διανυσμάτων

Σύμφωνα με τον κανόνα του τριγώνου για την κατασκευή του αθροίσματος δύο διανυσμάτων, βλέπουμε ότι

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Από τον ορισμό 2, το καταλαβαίνουμε

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Απάντηση:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Από αυτό το πρόβλημα, λαμβάνουμε τον ακόλουθο κανόνα για την εύρεση της διαφοράς δύο διανυσμάτων. Για να βρείτε τη διαφορά $\overrightarrow(a)-\overrightarrow(b)$ χρειάζεστε από αυθαίρετο σημείοΤο $O$ αφήστε στην άκρη τα διανύσματα $\overrightarrow(OA)=\overrightarrow(a)$ και $\overrightarrow(OB)=\overrightarrow(b)$ και ενώστε το τέλος του δεύτερου διανύσματος με το τέλος του πρώτου διανύσματος.

Αφαίρεση διανυσμάτων. Κανόνας Δεύτερος

Θυμηθείτε την ακόλουθη έννοια που χρειαζόμαστε.

Ορισμός 3

Το διάνυσμα $\overrightarrow(a_1)$ ονομάζεται αυθαίρετο για το διάνυσμα $\overrightarrow(a)$ εάν αυτά τα διανύσματα έχουν αντίθετη κατεύθυνση και έχουν το ίδιο μήκος.

Ονομασία:Το διάνυσμα $(-\overrightarrow(a))$ είναι το αντίθετο του διανύσματος $\overrightarrow(a)$.

Για να εισαγάγουμε τον δεύτερο κανόνα για τη διαφορά δύο διανυσμάτων, πρέπει πρώτα να εισαγάγουμε και να αποδείξουμε το ακόλουθο θεώρημα.

Θεώρημα 2

Για οποιαδήποτε δύο διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$ ισχύει η ακόλουθη ισότητα:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Απόδειξη.

Με τον ορισμό 2, έχουμε

Προσθέστε και στα δύο μέρη το διάνυσμα $\left(-\overrightarrow(b)\right)$, παίρνουμε

Εφόσον τα διανύσματα $\overrightarrow(b)$ και $\left(-\overrightarrow(b)\right)$ είναι αντίθετα, τότε $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ overrightarrow (0)$. Εχουμε

Το θεώρημα έχει αποδειχθεί.

Από αυτό το θεώρημα, λαμβάνουμε τον ακόλουθο κανόνα για τη διαφορά δύο διανυσμάτων: Για να βρούμε τη διαφορά $\overrightarrow(a)-\overrightarrow(b)$, πρέπει να αναβάλουμε το διάνυσμα $\overrightarrow(OA)=\overrightarrow( α)$ από ένα αυθαίρετο σημείο $O$, στη συνέχεια, από το ληφθέν σημείο $A$, αναβάλετε το διάνυσμα $\overrightarrow(AB)=-\overrightarrow(b)$ και συνδέστε την αρχή του πρώτου διανύσματος με το τέλος του το δεύτερο διάνυσμα.

Ένα παράδειγμα ενός προβλήματος σχετικά με την έννοια της διαφοράς των διανυσμάτων

Παράδειγμα 2

Έστω το $ADCD$ ένα παραλληλόγραμμο του οποίου οι διαγώνιοι τέμνονται στο $O$. $\overrightarrow(AB)=\overrightarrow(a)$, $\overrightarrow(AD)=\overrightarrow(b)$ (Εικ. 4). Εκφράστε τα ακόλουθα διανύσματα με όρους $\overrightarrow(a)$ και $\overrightarrow(b)$:

α) $\overrightarrow(DC)+\overrightarrow(CB)$

β) $\overrightarrow(BO)-\overrightarrow(OC)$

Εικόνα 4. Παραλληλόγραμμο

Λύση.

α) Προσθέτουμε σύμφωνα με τον κανόνα του τριγώνου, παίρνουμε

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Από τον πρώτο κανόνα για τη διαφορά δύο διανυσμάτων, παίρνουμε

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

β) Εφόσον $\overrightarrow(OC)=\overrightarrow(AO)$, παίρνουμε

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Με το Θεώρημα 2, έχουμε

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Χρησιμοποιώντας τον κανόνα του τριγώνου, τελικά έχουμε

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

ov, πρώτα πρέπει να κατανοήσετε μια τέτοια έννοια όπως η αναβολή ενός διανύσματος από ένα δεδομένο σημείο.

Ορισμός 1

Εικόνα 1. $\overrightarrow(a)$ σχεδιάστηκε από το σημείο $A$

Εισάγουμε το εξής θεώρημα:

Θεώρημα 1

Από οποιοδήποτε σημείο $K$ μπορεί κανείς να σχεδιάσει ένα διάνυσμα $\overrightarrow(a)$ και μόνο ένα.

Απόδειξη.

Υπαρξη:Υπάρχουν δύο περιπτώσεις που πρέπει να εξεταστούν εδώ:

Το διάνυσμα $\overrightarrow(a)$ είναι μηδέν.

Σε αυτήν την περίπτωση, είναι προφανές ότι το επιθυμητό διάνυσμα είναι το διάνυσμα $\overrightarrow(KK)$.

Το διάνυσμα $\overrightarrow(a)$ είναι μη μηδενικό.

Έστω το σημείο $A$ να υποδηλώνει την αρχή του διανύσματος $\overrightarrow(a)$ και το σημείο $B$ το τέλος του διανύσματος $\overrightarrow(a)$. Ας σχεδιάσουμε μια γραμμή $b$ παράλληλη στο διάνυσμα $\overrightarrow(a)$ μέσω του σημείου $K$. Ας σχεδιάσουμε τα τμήματα $\left|KL\right|=|AB|$ και $\left|KM\right|=|AB|$ σε αυτήν την ευθεία γραμμή. Εξετάστε τα διανύσματα $\overrightarrow(KL)$ και $\overrightarrow(KM)$. Από αυτά τα δύο διανύσματα, το επιθυμητό θα είναι αυτό που θα συν-κατευθυνθεί με το διάνυσμα $\overrightarrow(a)$ (Εικ. 2)

Εικόνα 2. Απεικόνιση του Θεωρήματος 1

Το θεώρημα έχει αποδειχθεί.

Αφαίρεση διανυσμάτων. Κανόνας Πρώτος

Ας μας δοθούν τα διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$.

Ορισμός 2

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Ονομασία:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Θα εξετάσουμε την κατασκευή της διαφοράς δύο διανυσμάτων χρησιμοποιώντας το πρόβλημα.

Παράδειγμα 1

Έστω τα διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$. Κατασκευάστε το διάνυσμα $\overrightarrow(a)-\overrightarrow(b)$.

Λύση.

Εικόνα 3. Διαφορά δύο διανυσμάτων

Σύμφωνα με τον κανόνα του τριγώνου για την κατασκευή του αθροίσματος δύο διανυσμάτων, βλέπουμε ότι

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Από τον ορισμό 2, το καταλαβαίνουμε

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

Απάντηση:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Από αυτό το πρόβλημα, λαμβάνουμε τον ακόλουθο κανόνα για την εύρεση της διαφοράς δύο διανυσμάτων. Για να βρούμε τη διαφορά $\overrightarrow(a)-\overrightarrow(b)$, από ένα αυθαίρετο σημείο $O$ πρέπει να παραμερίσουμε τα διανύσματα $\overrightarrow(OA)=\overrightarrow(a)$ και $\overrightarrow( OB)=\overrightarrow(b)$ και συνδέστε το άκρο του δεύτερου διανύσματος με το τέλος του πρώτου διανύσματος.

Αφαίρεση διανυσμάτων. Κανόνας Δεύτερος

Θυμηθείτε την ακόλουθη έννοια που χρειαζόμαστε.

Ορισμός 3

Ονομασία:Το διάνυσμα $(-\overrightarrow(a))$ είναι το αντίθετο του διανύσματος $\overrightarrow(a)$.

Θεώρημα 2

Για οποιαδήποτε δύο διανύσματα $\overrightarrow(a)$ και $\overrightarrow(b)$ ισχύει η ακόλουθη ισότητα:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Απόδειξη.

Με τον ορισμό 2, έχουμε

Προσθέστε και στα δύο μέρη το διάνυσμα $\left(-\overrightarrow(b)\right)$, παίρνουμε

Το θεώρημα έχει αποδειχθεί.

Ένα παράδειγμα ενός προβλήματος σχετικά με την έννοια της διαφοράς των διανυσμάτων

Παράδειγμα 2

α) $\overrightarrow(DC)+\overrightarrow(CB)$

β) $\overrightarrow(BO)-\overrightarrow(OC)$

Εικόνα 4. Παραλληλόγραμμο

Λύση.

α) Προσθέτουμε σύμφωνα με τον κανόνα του τριγώνου, παίρνουμε

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Από τον πρώτο κανόνα για τη διαφορά δύο διανυσμάτων, παίρνουμε

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

β) Εφόσον $\overrightarrow(OC)=\overrightarrow(AO)$, παίρνουμε

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Με το Θεώρημα 2, έχουμε

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Χρησιμοποιώντας τον κανόνα του τριγώνου, τελικά έχουμε

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

Το πώς προστίθενται τα διανύσματα δεν είναι πάντα σαφές στους μαθητές. Τα παιδιά δεν έχουν ιδέα τι κρύβεται πίσω τους. Απλά πρέπει να απομνημονεύσετε τους κανόνες και να μην σκέφτεστε την ουσία. Επομένως, ακριβώς για τις αρχές της πρόσθεσης και της αφαίρεσης διανυσματικών μεγεθών απαιτείται πολλή γνώση.

Η προσθήκη δύο ή περισσότερων διανυσμάτων οδηγεί πάντα σε ένα άλλο. Επιπλέον, θα είναι πάντα το ίδιο, ανεξάρτητα από την υποδοχή της τοποθεσίας του.

Τις περισσότερες φορές σε σχολικό μάθημαη γεωμετρία θεωρεί την προσθήκη δύο διανυσμάτων. Μπορεί να εκτελεστεί σύμφωνα με τον κανόνα ενός τριγώνου ή ενός παραλληλογράμμου. Αυτά τα σχέδια φαίνονται διαφορετικά, αλλά το αποτέλεσμα της δράσης είναι το ίδιο.

Πώς γίνεται η πρόσθεση σύμφωνα με τον κανόνα ενός τριγώνου;

Χρησιμοποιείται όταν τα διανύσματα είναι μη γραμμικά. Δηλαδή δεν κείτονται στην ίδια ευθεία ή παράλληλα.

Σε αυτήν την περίπτωση, το πρώτο διάνυσμα πρέπει να αναβληθεί από κάποιο αυθαίρετο σημείο. Από το άκρο του απαιτείται να γίνει παράλληλη και ίση με τη δεύτερη. Το αποτέλεσμα θα είναι ένα διάνυσμα που ξεκινά από την αρχή του πρώτου και τελειώνει στο τέλος του δεύτερου. Το σχέδιο μοιάζει με τρίγωνο. Εξ ου και το όνομα του κανόνα.

Εάν τα διανύσματα είναι συγγραμμικά, τότε μπορεί να εφαρμοστεί και αυτός ο κανόνας. Μόνο το σχέδιο θα βρίσκεται κατά μήκος μιας γραμμής.

Πώς γίνεται η πρόσθεση παραλληλογράμμου;

Για άλλη μία φορά? ισχύει μόνο για συγγραμμικά διανύσματα. Η κατασκευή πραγματοποιείται σύμφωνα με διαφορετική αρχή. Αν και η αρχή είναι ίδια. Πρέπει να αναβάλουμε το πρώτο διάνυσμα. Και από την αρχή του - το δεύτερο. Με βάση αυτά, συμπληρώστε το παραλληλόγραμμο και σχεδιάστε μια διαγώνιο από την αρχή και των δύο διανυσμάτων. Αυτή θα είναι το αποτέλεσμα. Έτσι προστίθενται τα διανύσματα σύμφωνα με τον κανόνα του παραλληλογράμμου.

Μέχρι στιγμής έχουν γίνει δύο. Τι γίνεται όμως αν υπάρχουν 3 ή 10 από αυτά; Χρησιμοποιήστε το παρακάτω κόλπο.

Πώς και πότε εφαρμόζεται ο κανόνας του πολυγώνου;

Εάν πρέπει να εκτελέσετε την προσθήκη διανυσμάτων, ο αριθμός των οποίων είναι περισσότεροι από δύο, δεν πρέπει να φοβάστε. Αρκεί να τα αφήσετε όλα στην άκρη διαδοχικά και να συνδέσετε την αρχή της αλυσίδας στο τέλος της. Αυτό το διάνυσμα θα είναι το επιθυμητό άθροισμα.

Ποιες ιδιότητες ισχύουν για πράξεις σε διανύσματα;

Σχετικά με το μηδενικό διάνυσμα.Το οποίο ισχυρίζεται ότι όταν προστεθεί σε αυτό, προκύπτει το αρχικό.

Σχετικά με το αντίθετο διάνυσμα.Δηλαδή περίπου ένα που έχει αντίθετη φορά και ίση τιμή σε απόλυτη τιμή. Το άθροισμά τους θα είναι μηδέν.

Σχετικά με την ανταλλαξιμότητα της πρόσθεσης.Ό,τι έγινε γνωστό από τότε δημοτικό σχολείο. Η αλλαγή των θέσεων των όρων δεν αλλάζει το αποτέλεσμα. Με άλλα λόγια, δεν έχει σημασία ποιο διάνυσμα θα αναβληθεί πρώτο. Η απάντηση θα εξακολουθεί να είναι σωστή και μοναδική.

Σχετικά με τη συνειρμικότητα της προσθήκης.Αυτός ο νόμος σας επιτρέπει να προσθέσετε σε ζεύγη οποιαδήποτε διανύσματα από ένα τριπλό και να προσθέσετε ένα τρίτο σε αυτά. Αν το γράψουμε χρησιμοποιώντας σύμβολα, παίρνουμε τα εξής:

πρώτο + (δεύτερο + τρίτο) = δεύτερο + (πρώτο + τρίτο) = τρίτο + (πρώτο + δεύτερο).

Τι είναι γνωστό για τη διαφορά των διανυσμάτων;

Δεν υπάρχει χωριστή λειτουργία αφαίρεσης. Αυτό οφείλεται στο γεγονός ότι είναι, στην πραγματικότητα, προσθήκη. Μόνο στο δεύτερο από αυτά δίνεται η αντίθετη κατεύθυνση. Και τότε όλα γίνονται σαν να εξετάστηκε η προσθήκη διανυσμάτων. Επομένως, πρακτικά δεν μιλούν για τη διαφορετικότητά τους.

Για να απλοποιηθεί η εργασία με την αφαίρεση τους, τροποποιήθηκε ο κανόνας του τριγώνου. Τώρα (κατά την αφαίρεση) το δεύτερο διάνυσμα πρέπει να αναβληθεί από την αρχή του πρώτου. Η απάντηση θα είναι αυτή που συνδέει το τελικό σημείο του minuend με αυτό. Αν και είναι δυνατό να αναβληθεί όπως περιγράφηκε προηγουμένως, απλώς αλλάζοντας την κατεύθυνση του δεύτερου.

Πώς να βρείτε το άθροισμα και τη διαφορά των διανυσμάτων σε συντεταγμένες;

Στο πρόβλημα δίνονται οι συντεταγμένες των διανυσμάτων και απαιτείται να βρεθούν οι τιμές τους για το τελικό. Σε αυτή την περίπτωση, οι κατασκευές δεν χρειάζεται να εκτελεστούν. Δηλαδή, μπορείτε να χρησιμοποιήσετε απλούς τύπους που περιγράφουν τον κανόνα για την προσθήκη διανυσμάτων. Μοιάζουν με αυτό:

a(x, y, z) + b(k, l, m) = c(x+k, y+l, z+m);

a (x, y, z) -in (k, l, m) \u003d c (x-k, y-l, z-m).

Είναι εύκολο να δει κανείς ότι οι συντεταγμένες πρέπει απλώς να προστεθούν ή να αφαιρεθούν, ανάλογα με τη συγκεκριμένη εργασία.

Πρώτο παράδειγμα με λύση

Κατάσταση. Δίνεται ένα ορθογώνιο ABCD. Οι πλευρές του είναι 6 και 8 εκ. Το σημείο τομής των διαγωνίων σημειώνεται με το γράμμα Ο. Απαιτείται ο υπολογισμός της διαφοράς μεταξύ των διανυσμάτων AO και VO.

Λύση. Πρώτα πρέπει να σχεδιάσετε αυτά τα διανύσματα. Κατευθύνονται από τις κορυφές του ορθογωνίου στο σημείο τομής των διαγωνίων.

Αν κοιτάξετε προσεκτικά το σχέδιο, μπορείτε να δείτε ότι τα διανύσματα είναι ήδη ευθυγραμμισμένα έτσι ώστε το δεύτερο από αυτά να έρχεται σε επαφή με το τέλος του πρώτου. Απλώς η κατεύθυνσή του είναι λάθος. Πρέπει να ξεκινήσει από αυτό το σημείο. Αυτό είναι αν προστεθούν τα διανύσματα, και στο πρόβλημα - αφαίρεση. Να σταματήσει. Αυτή η ενέργεια σημαίνει ότι πρέπει να προσθέσετε το αντίθετο διάνυσμα. Άρα, το VO πρέπει να αντικατασταθεί από το OB. Και αποδεικνύεται ότι δύο διανύσματα έχουν ήδη σχηματίσει ένα ζευγάρι πλευρών από τον κανόνα του τριγώνου. Επομένως, το αποτέλεσμα της πρόσθεσής τους, δηλαδή η επιθυμητή διαφορά, είναι το διάνυσμα ΑΒ.

Και συμπίπτει με την πλευρά του ορθογωνίου. Για να καταγράψετε μια αριθμητική απάντηση, θα χρειαστείτε τα ακόλουθα. Σχεδιάστε ένα παραλληλόγραμμο κατά μήκος έτσι ώστε η μεγαλύτερη πλευρά να είναι οριζόντια. Η αρίθμηση των κορυφών ξεκινά από κάτω αριστερά και πηγαίνει αριστερόστροφα. Τότε το μήκος του διανύσματος ΑΒ θα είναι ίσο με 8 cm.

Απάντηση. Η διαφορά μεταξύ AO και VO είναι 8 cm.

Το δεύτερο παράδειγμα και η αναλυτική του λύση

Κατάσταση. Ο ρόμβος ΑΒΓΔ έχει διαγώνιους 12 και 16 εκ. Το σημείο τομής τους σημειώνεται με το γράμμα Ο. Να υπολογίσετε το μήκος του διανύσματος που σχηματίζεται από τη διαφορά των διανυσμάτων ΑΟ και ΒΟ.

Λύση. Ας είναι ο προσδιορισμός των κορυφών του ρόμβου όπως στο προηγούμενο πρόβλημα. Ομοίως με τη λύση του πρώτου παραδείγματος, προκύπτει ότι η επιθυμητή διαφορά είναι ίση με το διάνυσμα ΑΒ. Και το μήκος του είναι άγνωστο. Η λύση του προβλήματος περιορίστηκε στον υπολογισμό μιας από τις πλευρές του ρόμβου.

Για το σκοπό αυτό, πρέπει να λάβετε υπόψη το τρίγωνο ABO. Είναι ορθογώνιο γιατί οι διαγώνιοι του ρόμβου τέμνονται υπό γωνία 90 μοιρών. Και τα πόδια του είναι ίσα με τις μισές διαγώνιες. Δηλαδή 6 και 8 εκ. Η πλευρά που αναζητείται στο πρόβλημα συμπίπτει με την υποτείνουσα σε αυτό το τρίγωνο.

Για να το βρείτε, χρειάζεστε το Πυθαγόρειο θεώρημα. Το τετράγωνο της υποτείνουσας θα είναι ισούται με το άθροισμααριθμοί 6 2 και 8 2 . Μετά τον τετραγωνισμό, λαμβάνονται οι τιμές: 36 και 64. Το άθροισμά τους είναι 100. Από αυτό προκύπτει ότι η υποτείνουσα είναι 10 cm.

Απάντηση. Η διαφορά μεταξύ των διανυσμάτων AO και VO είναι 10 cm.

Τρίτο παράδειγμα με λεπτομερή λύση

Κατάσταση. Να υπολογίσετε τη διαφορά και το άθροισμα δύο διανυσμάτων. Οι συντεταγμένες τους είναι γνωστές: το πρώτο έχει 1 και 2, το δεύτερο έχει 4 και 8.

Λύση. Για να βρείτε το άθροισμα, πρέπει να προσθέσετε την πρώτη και τη δεύτερη συντεταγμένη ανά ζεύγη. Το αποτέλεσμα θα είναι οι αριθμοί 5 και 10. Η απάντηση θα είναι ένα διάνυσμα με συντεταγμένες (5; 10).

Για τη διαφορά, πρέπει να αφαιρέσετε τις συντεταγμένες. Μετά την εκτέλεση αυτής της ενέργειας, θα ληφθούν οι αριθμοί -3 και -6. Θα είναι οι συντεταγμένες του επιθυμητού διανύσματος.

Απάντηση. Το άθροισμα των διανυσμάτων είναι (5; 10), η διαφορά τους είναι (-3; -6).

Τέταρτο παράδειγμα

Κατάσταση. Το μήκος του διανύσματος ΑΒ είναι 6 εκ. Π.Χ. - 8 εκ. Το δεύτερο παραμερίζεται από το άκρο του πρώτου υπό γωνία 90 μοιρών. Υπολογίστε: α) τη διαφορά μεταξύ των μονάδων των διανυσμάτων BA και BC και της ενότητας της διαφοράς μεταξύ BA και BC. β) το άθροισμα των ίδιων ενοτήτων και το μέτρο του αθροίσματος.

Λύση: α) Τα μήκη των διανυσμάτων δίνονται ήδη στο πρόβλημα. Επομένως, δεν είναι δύσκολο να υπολογιστεί η διαφορά τους. 6 - 8 = -2. Η κατάσταση με το συντελεστή διαφοράς είναι κάπως πιο περίπλοκη. Πρώτα πρέπει να μάθετε ποιο διάνυσμα θα είναι το αποτέλεσμα της αφαίρεσης. Για το σκοπό αυτό, θα πρέπει να παραμεριστεί το διάνυσμα ΒΑ, το οποίο κατευθύνεται στο αντίθετη πλευράΑΒ. Στη συνέχεια σχεδιάστε το διάνυσμα BC από το άκρο του, κατευθύνοντάς το προς την αντίθετη κατεύθυνση από την αρχική. Το αποτέλεσμα της αφαίρεσης είναι το διάνυσμα CA. Το μέτρο του μπορεί να υπολογιστεί χρησιμοποιώντας το Πυθαγόρειο θεώρημα. Απλοί υπολογισμοί οδηγούν σε τιμή 10 cm.

β) Το άθροισμα των ενοτήτων των διανυσμάτων είναι 14 εκ. Για να βρεθεί η δεύτερη απάντηση απαιτείται κάποιος μετασχηματισμός. Το διάνυσμα ΒΑ είναι αντίθετο από αυτό που δίνεται - ΑΒ. Και τα δύο διανύσματα κατευθύνονται από το ίδιο σημείο. Σε αυτήν την περίπτωση, μπορείτε να χρησιμοποιήσετε τον κανόνα του παραλληλογράμμου. Το αποτέλεσμα της πρόσθεσης θα είναι μια διαγώνιος, και όχι απλώς ένα παραλληλόγραμμο, αλλά ένα ορθογώνιο. Οι διαγώνιοι του είναι ίσες, πράγμα που σημαίνει ότι ο συντελεστής του αθροίσματος είναι ίδιος με την προηγούμενη παράγραφο.

Απάντηση: α) -2 και 10 cm; β) 14 και 10 cm.