Diện tích của một tam giác là định lý Pitago. Các cách khác nhau để chứng minh định lý Pitago: ví dụ, mô tả và đánh giá
Khi bạn mới bắt đầu học căn bậc hai và cách giải phương trình vô tỉ(các bằng chứa ẩn số dưới dấu gốc), bạn có thể có ý tưởng đầu tiên về chúng công dụng thực tế. Khả năng trích xuất Căn bậc hai của các số cũng cần thiết để giải các bài toán về ứng dụng của định lý Pitago. Định lý này liên hệ độ dài các cạnh của bất kỳ tam giác vuông nào.
Gọi độ dài các cạnh của một tam giác vuông (hai cạnh đồng quy ở một góc vuông) được ký hiệu bằng các chữ cái và, và độ dài cạnh huyền (cạnh dài nhất của tam giác đối diện góc phải) sẽ được ký hiệu bằng chữ cái. Khi đó các độ dài tương ứng được liên hệ với nhau theo quan hệ sau:
Phương trình này cho phép bạn tìm độ dài của một cạnh của tam giác vuông trong trường hợp độ dài của hai cạnh còn lại của nó đã biết. Ngoài ra, nó cho phép bạn xác định xem tam giác được coi có phải là tam giác vuông hay không, với điều kiện là độ dài của tất cả ba bênđã biết trước.
Giải bài toán bằng định lý Pitago
Để củng cố tài liệu, chúng ta sẽ giải các bài toán ứng dụng định lý Pitago sau đây.

Vì vậy, đã cho:
- Chiều dài của một trong các chân là 48, cạnh huyền là 80.
- Chiều dài của chân là 84, cạnh huyền là 91.
Hãy đi đến giải pháp:
a) Thay dữ liệu vào phương trình trên cho kết quả sau:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 hoặc b = -64
Vì độ dài của một cạnh của tam giác không thể được biểu thị số âm, tùy chọn thứ hai sẽ tự động bị loại bỏ.
Câu trả lời cho bức tranh đầu tiên: b = 64.
b) Độ dài của chân của tam giác thứ hai được tìm thấy trong cùng một cách:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 hoặc b = -35
Như trong trường hợp trước, giải pháp phủ định bị loại bỏ.
Trả lời cho bức tranh thứ hai: b = 35

Chúng ta được cho:
- Độ dài các cạnh nhỏ hơn của tam giác lần lượt là 45 và 55, cạnh lớn hơn là 75.
- Độ dài các cạnh nhỏ hơn của tam giác lần lượt là 28 và 45, cạnh lớn hơn là 53.
Chúng tôi giải quyết vấn đề:
a) Cần kiểm tra xem tổng bình phương độ dài các cạnh nhỏ hơn của tam giác đã cho có bằng bình phương độ dài của tam giác lớn hơn hay không:
45 2 + 55 2 = 2025 + 3025 = 5050
Do đó, tam giác thứ nhất không phải là tam giác vuông.
b) Thao tác tương tự được thực hiện:
28 2 + 45 2 = 784 + 2025 = 2809
Do đó, tam giác thứ hai là tam giác vuông.
Đầu tiên chúng ta tìm chiều dài đoạn dài nhất, được tạo thành bởi các điểm có tọa độ (-2, -3) và (5, -2). Đối với điều này, chúng tôi sử dụng công thức đã biếtđể tìm khoảng cách giữa các điểm trong hệ thống hình chữ nhật tọa độ:
Tương tự, chúng ta tìm độ dài của đoạn thẳng nằm giữa các điểm có tọa độ (-2, -3) và (2, 1):
Cuối cùng, chúng tôi xác định độ dài của đoạn giữa các điểm có tọa độ (2, 1) và (5, -2):
Vì có một sự bình đẳng:
thì tam giác tương ứng là tam giác vuông.
Như vậy, chúng ta có thể hình thành câu trả lời cho bài toán: vì tổng bình phương của các cạnh có độ dài nhỏ nhất bằng bình phương của cạnh có chiều dài lớn nhất, các điểm là các đỉnh của một tam giác vuông.
Đế (nằm đúng theo chiều ngang), lẫy (nằm đúng theo chiều dọc) và dây cáp (được kéo theo đường chéo) tương ứng tạo thành một tam giác vuông, định lý Pitago có thể được sử dụng để tìm chiều dài của cáp:
Như vậy, chiều dài của cáp sẽ xấp xỉ 3,6 mét.
Cho: khoảng cách từ điểm R đến điểm P (chân của tam giác) là 24, từ điểm R đến điểm Q (cạnh huyền) - 26.
Vì vậy, chúng tôi giúp Vitya giải quyết vấn đề. Vì các cạnh của tam giác trong hình được cho là tạo thành tam giác vuông, bạn có thể sử dụng định lý Pitago để tìm độ dài của cạnh thứ ba:
Vậy, chiều rộng của ao là 10 mét.
Sergey Valerievich
Định lý Pythagore
Định lý Pythagore- một trong những định lý cơ bản của hình học Euclide, thiết lập mối quan hệ
giữa các cạnh của một tam giác vuông.
Người ta tin rằng nó đã được chứng minh bởi nhà toán học Hy Lạp Pythagoras, người mà sau đó nó được đặt tên.
Công thức hình học của định lý Pitago.
Định lý ban đầu được xây dựng như sau:
Trong một tam giác vuông, diện tích của hình vuông được xây dựng trên cạnh huyền bằng tổng diện tích của các hình vuông,
được xây dựng trên ống thông.
Công thức đại số của định lý Pitago.
Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài các cạnh.
Nghĩa là, biểu thị độ dài cạnh huyền của tam giác qua c và chiều dài của các chân qua một và b:
Cả hai công thức định lý pythagore là tương đương, nhưng công thức thứ hai là cơ bản hơn, nó không
yêu cầu khái niệm về diện tích. Có nghĩa là, tuyên bố thứ hai có thể được xác minh mà không cần biết bất cứ điều gì về khu vực và
bằng cách chỉ đo độ dài các cạnh của một tam giác vuông.
Định lý Pitago ngược.
Nếu bình phương của một cạnh tam giác bằng tổng bình phương của hai cạnh còn lại thì
tam giác là hình chữ nhật.
Hay nói cách khác:
Đối với bất kỳ bộ ba số dương nào một, b và c, như vậy mà
có một tam giác vuông có chân một và b và cạnh huyền c.
Định lý Pitago cho tam giác cân.

Định lý Pitago cho một tam giác đều.

Chứng minh định lý Pitago.
Hiện tại, 367 bằng chứng của định lý này đã được ghi lại trong các tài liệu khoa học. Có lẽ là định lý
Pythagoras là định lý duy nhất có số lượng chứng minh ấn tượng như vậy. Đa dạng như vậy
chỉ có thể được giải thích bởi ý nghĩa cơ bản của định lý đối với hình học.
Tất nhiên, về mặt khái niệm, tất cả chúng có thể được chia thành một số lượng nhỏ các lớp. Nổi tiếng nhất trong số họ:
chứng minh rằng phương pháp khu vực, tiên đề và bằng chứng kỳ lạ(Ví dụ,
qua phương trình vi phân).
1. Chứng minh định lý Pitago về các tam giác đồng dạng.
Chứng minh sau đây của công thức đại số là chứng minh đơn giản nhất trong số các chứng minh được xây dựng
trực tiếp từ tiên đề. Đặc biệt, nó không sử dụng khái niệm diện tích của một hình.
Để cho được ABC có một tam giác vuông C. Hãy vẽ chiều cao từ C và biểu thị
nền tảng của nó thông qua H.
Tam giác ACH tương tự như một hình tam giác AB C về hai góc. Tương tự như vậy, tam giác CBH giống ABC.
Bằng cách giới thiệu ký hiệu:

chúng tôi nhận được:
![]() ,
,
phù hợp với -
Đã gấp một 2 và b 2, chúng tôi nhận được:
hoặc, đã được chứng minh.
2. Chứng minh định lý Pitago bằng phương pháp diện tích.
Các chứng minh sau đây, mặc dù rõ ràng là đơn giản, nhưng không hề đơn giản chút nào. Tất cả bọn họ
sử dụng các tính chất của diện tích, việc chứng minh nó phức tạp hơn việc chứng minh bản thân định lý Pitago.
- Chứng minh thông qua quá trình đẳng tích.
 Sắp xếp bốn hình chữ nhật bằng nhau
Sắp xếp bốn hình chữ nhật bằng nhau
tam giác như trong hình
ở bên phải.
Hình tứ giác có các cạnh c- vuông,
vì tổng của hai góc nhọn là 90 °, và
góc phát triển là 180 °.
Một mặt, diện tích của toàn bộ hình là
diện tích của một hình vuông có cạnh ( a + b), và mặt khác, tổng các khu vực bốn hình tam giác và
![]()
![]()
Q.E.D.
3. Chứng minh định lý Pitago bằng phương pháp thập phân.

Xem xét bản vẽ được hiển thị trong hình, và
xem sự thay đổi bênmột, chúng ta có thể
viết quan hệ sau cho vô hạn
nhỏ gia số bênvới và một(sử dụng sự tương đồng
Hình tam giác):
Sử dụng phương pháp tách biến, chúng tôi nhận thấy:
Một biểu thức tổng quát hơn để thay đổi cạnh huyền trong trường hợp gia số của cả hai chân:
Tích hợp phương trình đã cho và sử dụng các điều kiện ban đầu, chúng tôi nhận được:
Do đó, chúng tôi đi đến câu trả lời mong muốn:
Như dễ dàng nhận thấy, sự phụ thuộc bậc hai trong công thức cuối cùng xuất hiện do tuyến tính
tỷ lệ giữa các cạnh của tam giác và số gia, trong khi tổng liên quan đến độc lập
đóng góp từ sự gia tăng của các chân khác nhau.
Có thể thu được một bằng chứng đơn giản hơn nếu chúng ta giả định rằng một trong các chân không có gia số
(trong trường hợp này Chân b). Sau đó, đối với hằng số tích hợp, chúng tôi nhận được:
(theo Papyrus 6619 của Bảo tàng Berlin). Theo Cantor, harpedonapts, hay "bộ căng dây", tạo ra các góc vuông bằng cách sử dụng các tam giác vuông với các cạnh 3, 4 và 5.
Nó rất dễ dàng để tái tạo phương pháp xây dựng của họ. Hãy lấy một sợi dây dài 12 m và buộc nó dọc theo một dải màu ở khoảng cách 3 m từ đầu này và cách đầu kia 4 m. Một góc vuông sẽ được bao bọc giữa các cạnh dài 3 và 4 mét. Có thể phản đối Harpedonapts rằng phương pháp xây dựng của họ trở nên thừa nếu, ví dụ, hình vuông bằng gỗ được sử dụng bởi tất cả các thợ mộc được sử dụng. Thật vậy, các bản vẽ của người Ai Cập được biết đến trong đó một công cụ như vậy được tìm thấy - ví dụ, các bản vẽ mô tả một xưởng mộc.
Người ta biết thêm phần nào về định lý Pitago giữa những người Babylon. Trong một văn bản có niên đại từ thời Hammurabi, tức là vào năm 2000 trước Công nguyên. e. , một phép tính gần đúng của cạnh huyền của một tam giác vuông được đưa ra. Từ đó, chúng ta có thể kết luận rằng ở Lưỡng Hà, họ có thể thực hiện các phép tính với các tam giác vuông, ít nhất là trong một số trường hợp. Một mặt, dựa trên trình độ hiện tại của toán học Ai Cập và Babylon, mặt khác, dựa trên một nghiên cứu quan trọng về các nguồn Hy Lạp, van der Waerden (một nhà toán học người Hà Lan) đã kết luận rằng có khả năng cao là Định lý cạnh huyền vuông đã được biết đến ở Ấn Độ vào khoảng thế kỷ 18 trước Công nguyên. e.
Khoảng 400 năm trước Công nguyên. e., theo Proclus, Plato đã đưa ra một phương pháp tìm kiếm bộ ba Pitago, kết hợp đại số và hình học. Vào khoảng năm 300 trước Công nguyên. e. Các phần tử của Euclid chứa bằng chứng tiên đề lâu đời nhất của định lý Pitago.
Văn bản
Công thức hình học:
Định lý ban đầu được xây dựng như sau:
Công thức đại số:
Nghĩa là, biểu thị độ dài cạnh huyền của tam giác qua và độ dài của chân qua và:
Cả hai công thức của định lý là tương đương, nhưng công thức thứ hai là cơ bản hơn, nó không yêu cầu khái niệm về diện tích. Có nghĩa là, tuyên bố thứ hai có thể được xác minh mà không cần biết gì về diện tích và chỉ bằng cách đo độ dài các cạnh của một tam giác vuông.
Định lý Pitago ngược:
Chứng minh rằng
Hiện tại, 367 bằng chứng của định lý này đã được ghi lại trong các tài liệu khoa học. Có lẽ, định lý Pitago là định lý duy nhất có số lượng chứng minh ấn tượng như vậy. Sự đa dạng như vậy chỉ có thể được giải thích bởi ý nghĩa cơ bản của định lý đối với hình học.
Tất nhiên, về mặt khái niệm, tất cả chúng có thể được chia thành một số lượng nhỏ các lớp. Nổi tiếng nhất trong số đó: chứng minh bằng phương pháp diện tích, chứng minh tiên đề và ngoại lai (ví dụ, sử dụng phương trình vi phân).
Qua các tam giác đồng dạng
Chứng minh sau đây của công thức đại số là chứng minh đơn giản nhất trong số các chứng minh được xây dựng trực tiếp từ các tiên đề. Đặc biệt, nó không sử dụng khái niệm diện tích hình.

Để cho được ABC có một tam giác vuông C. Hãy vẽ chiều cao từ C và biểu thị cơ sở của nó bằng H. Tam giác ACH tương tự như một hình tam giác ABCở hai góc. Tương tự như vậy, tam giác CBH giống ABC. Giới thiệu ký hiệu
chúng tôi nhận được
Tương đương là gì
Thêm, chúng tôi nhận được
, điều này đã được chứng minhKhu vực chứng minh
Các chứng minh sau đây, mặc dù rõ ràng là đơn giản, nhưng không hề đơn giản chút nào. Tất cả chúng đều sử dụng các tính chất của diện tích, việc chứng minh nó phức tạp hơn việc chứng minh định lý Pitago.
Bằng chứng qua Tương đương
- Sắp xếp bốn tam giác vuông bằng nhau như hình 1.
- Hình tứ giác có các cạnh c là một hình vuông vì tổng của hai góc nhọn là 90 ° và góc thẳng là 180 °.
- Diện tích của toàn hình bằng diện tích hình vuông có cạnh (a + b), mặt khác là tổng diện tích của bốn hình tam giác và diện tích của hình vuông bên trong.
Q.E.D.
Chứng minh của Euclid
Ý tưởng về chứng minh của Euclid như sau: hãy thử chứng minh rằng một nửa diện tích của hình vuông được xây dựng trên cạnh huyền bằng tổng của nửa diện tích của hình vuông được xây dựng trên chân, và sau đó là diện tích của hình vuông lớn và hai hình vuông nhỏ bằng nhau.
Hãy xem xét hình vẽ bên trái. Ta dựng hình vuông trên các cạnh của tam giác vuông trên đó và vẽ tia s từ đỉnh của góc vuông C vuông góc với cạnh huyền AB, nó cắt hình vuông ABIK dựng trên cạnh huyền thành hai hình chữ nhật - BHJI và HAKJ , tương ứng. Nó chỉ ra rằng diện tích của những hình chữ nhật này chính xác bằng diện tích của các hình vuông được xây dựng trên các chân tương ứng.
Hãy thử chứng minh rằng diện tích hình vuông DECA bằng diện tích hình chữ nhật AHJK Để làm được điều này, chúng ta sử dụng một quan sát bổ trợ: Diện tích hình tam giác có cùng chiều cao và đáy như hình đã cho hình chữ nhật bằng một nửa diện tích của hình chữ nhật đã cho. Đây là hệ quả của việc xác định diện tích của một tam giác bằng một nửa tích của đáy và chiều cao. Từ nhận xét này, ta thấy rằng diện tích tam giác ACK bằng diện tích tam giác AHK (không hình vẽ), nghĩa là bằng nửa diện tích hình chữ nhật AHJK.
Bây giờ chúng ta hãy chứng minh rằng diện tích tam giác ACK cũng bằng một nửa diện tích hình vuông DECA. Điều duy nhất cần làm là chứng minh sự bằng nhau của các tam giác ACK và BDA (vì diện tích tam giác BDA bằng một nửa diện tích hình vuông theo tính chất trên). Sự bình đẳng này là hiển nhiên: các tam giác có hai cạnh bằng nhau và góc giữa chúng. Cụ thể - AB = AK, AD = AC - bằng nhau của các góc CAK và BAD dễ dàng chứng minh bằng phương pháp chuyển động: ta quay tam giác CAK 90 ° ngược chiều kim đồng hồ thì rõ ràng các cạnh tương ứng của hai tam giác đó sẽ trùng nhau. (do góc ở đỉnh của hình vuông là 90 °).
Lập luận về sự bằng nhau của diện tích hình vuông BCFG và hình chữ nhật BHJI là hoàn toàn tương tự.
Như vậy, chúng ta đã chứng minh rằng diện tích của hình vuông được xây dựng trên cạnh huyền là tổng diện tích của các hình vuông được xây dựng trên chân. Ý tưởng bằng chứng này minh họa thêm với hình ảnh động ở trên.
Bằng chứng của Leonardo da Vinci
Các yếu tố chính của chứng minh là đối xứng và chuyển động.
Xét hình vẽ, có thể thấy từ đối xứng, đoạn cắt hình vuông thành hai phần giống nhau (vì các hình tam giác và bằng nhau trong cấu tạo).
Sử dụng phép quay 90 độ ngược chiều kim đồng hồ xung quanh điểm, chúng ta thấy sự bằng nhau của các hình tô bóng và.
Bây giờ rõ ràng là diện tích của hình mà chúng ta đã tô bóng bằng tổng của một nửa diện tích của các hình vuông nhỏ (được xây dựng trên chân) và diện tích của hình tam giác ban đầu. Mặt khác, nó bằng một nửa diện tích của hình vuông lớn (được xây dựng trên cạnh huyền) cộng với diện tích của tam giác ban đầu. Như vậy, một nửa tổng diện tích của các hình vuông nhỏ bằng một nửa diện tích của hình vuông lớn, và do đó tổng diện tích của các hình vuông được xây trên chân bằng diện tích của hình vuông được xây dựng trên cạnh huyền.
Chứng minh bằng phương pháp infinitesimal
Chứng minh sau đây bằng phương trình vi phân thường được coi là Nhà toán học người Anh Hardy, sống vào nửa đầu thế kỷ 20.
Xét hình vẽ bên và nhận xét sự thay đổi bên một, chúng ta có thể viết quan hệ sau cho các gia số bên thập phân với và một(sử dụng các tam giác đồng dạng):
Sử dụng phương pháp tách biến, chúng tôi nhận thấy
Một biểu thức tổng quát hơn để thay đổi cạnh huyền trong trường hợp gia số của cả hai chân
Tích hợp phương trình này và sử dụng các điều kiện ban đầu, chúng ta thu được
Do đó, chúng tôi đi đến câu trả lời mong muốn
Dễ dàng nhận thấy rằng sự phụ thuộc bậc hai trong công thức cuối cùng xuất hiện do tỷ lệ tuyến tính giữa các cạnh của tam giác và số gia, trong khi tổng là do sự đóng góp độc lập từ số gia của các chân khác nhau.
Có thể thu được một bằng chứng đơn giản hơn nếu chúng ta giả sử rằng một trong các chân không tăng (trong trường hợp này là chân). Sau đó, đối với hằng số tích hợp, chúng tôi nhận được
Các biến thể và khái quát hóa
Các hình dạng hình học tương tự trên ba mặt
Tổng quát hóa cho tam giác đồng dạng, diện tích hình xanh A + B = diện tích hình xanh lam C
Định lý Pitago sử dụng các tam giác vuông đồng dạng
Một khái quát của định lý Pitago đã được Euclid đưa ra trong công trình của mình Sự khởi đầu, mở rộng diện tích của các hình vuông ở các bên thành các khu vực tương tự hình dạng hình học :
Nếu chúng ta dựng các hình hình học tương tự (xem Hình học Euclide) trên các cạnh của một tam giác vuông, thì tổng của hai hình nhỏ hơn sẽ bằng diện tích của hình lớn hơn.
Ý tưởng chính của sự tổng quát hóa này là diện tích của một hình hình học như vậy tỷ lệ với bình phương của bất kỳ kích thước tuyến tính nào của nó và đặc biệt, với bình phương chiều dài của bất kỳ cạnh nào. Do đó, đối với các số liệu tương tự với các khu vực Một, B và Cđược xây dựng trên các mặt với chiều dài một, b và c, chúng ta có:
Nhưng, theo định lý Pitago, một 2 + b 2 = c 2, sau đó Một + B = C.
Ngược lại, nếu chúng ta có thể chứng minh rằng Một + B = Cđối với ba hình hình học giống nhau mà không sử dụng định lý Pitago, thì chúng ta có thể tự chứng minh định lý đó, chuyển sang hướng ngược lại. Ví dụ: tam giác tâm bắt đầu có thể được sử dụng lại làm tam giác C trên cạnh huyền và hai tam giác vuông đồng dạng ( Một và B) được xây dựng trên hai cạnh còn lại, được hình thành từ kết quả của việc chia trung tâm tam giác cho chiều cao của nó. Khi đó, tổng của hai diện tích nhỏ hơn của hình tam giác hiển nhiên bằng diện tích của hình thứ ba, do đó Một + B = C và, theo các bằng chứng trước đó trong thứ tự ngược lại, chúng ta nhận được định lý Pitago a 2 + b 2 = c 2.
Định lý cosine
Định lý Pitago là trương hợp đặc biệt hơn định lý chung cosin, liên quan đến độ dài của các cạnh trong một tam giác tùy ý:
trong đó θ là góc giữa các cạnh một và b.
Nếu θ là 90 độ thì cos θ = 0 và công thức được đơn giản hóa thành định lý Pitago thông thường.
Tam giác tùy ý
Đối với bất kỳ góc đã chọn nào của một tam giác tùy ý có các cạnh a, b, c ghi một tam giác cân theo cách sao cho các góc bằng nhau tại cơ sở của nó, θ bằng góc đã chọn. Giả sử rằng góc đã chọn θ nằm đối diện với mặt được chỉ ra c. Kết quả là, chúng ta có một tam giác ABD với góc θ, nằm đối diện với cạnh một và các bữa tiệc r. Tam giác thứ hai được tạo thành bởi góc θ, đối diện với cạnh b và các bữa tiệc với Dài S, như nó được hiển thị trên hình ảnh. Thabit Ibn Qurra đã phát biểu rằng các cạnh trong ba hình tam giác này có quan hệ như sau:
Khi góc θ tiến tới góc π / 2, cơ sở Tam giác cân giảm dần, và hai cạnh r và s chồng lên nhau ngày càng ít. Khi θ = π / 2, ADB biến thành một tam giác vuông, r + S = c và chúng ta nhận được định lý Pitago ban đầu.
Hãy xem xét một trong các đối số. Tam giác ABC có cùng các góc với tam giác ABD, nhưng theo thứ tự ngược lại. (Hai tam giác có một góc chung ở đỉnh B, đều có góc θ, đồng thời có góc thứ ba bằng tổng các góc của tam giác) Theo đó, ABC đồng dạng với hình chiếu ABD của tam giác DBA, như hình vẽ trong hình dưới. Hãy để chúng tôi viết mối quan hệ giữa cạnh đối diện và kề với góc θ,
Sự phản chiếu của một tam giác khác cũng vậy,
Nhân các phân số và cộng hai tỷ lệ sau:
Q.E.D.
Tổng quát hóa cho tam giác tùy ý thông qua hình bình hành
Tổng quát hóa cho hình tam giác tùy ý,
khu vực màu xanh lá cây âm mưu = khu vực màu xanh da trời
Chứng minh luận điểm rằng trong hình trên
Hãy tổng quát hóa thêm cho hình tam giác không phải là hình chữ nhật, sử dụng hình bình hành có ba cạnh thay vì hình vuông. (hình vuông là một trường hợp đặc biệt.) Hình trên cho thấy điều đó cho Tam giác nhọn Diện tích hình bình hành cạnh dài bằng tổng diện tích hai cạnh còn lại với điều kiện là hình bình hành có cạnh dài được dựng như hình vẽ (các kích thước được đánh dấu bằng mũi tên là như nhau và xác định các cạnh của hình bình hành dưới). Sự thay thế hình vuông bằng hình bình hành này có sự tương đồng rõ ràng với định lý Pitago ban đầu và được cho là do Pappus của Alexandria lập ra vào năm 4 CN. e.
Hình dưới đây cho thấy tiến trình của việc chứng minh. Hãy nhìn vào phía bên trái của hình tam giác. Hình bình hành bên trái màu xanh có cùng diện tích với phần bên trái của hình bình hành màu xanh vì chúng có cùng đáy b và chiều cao h. Ngoài ra, hộp màu xanh lá cây bên trái có cùng diện tích với hộp màu xanh lá cây bên trái trong hình trên cùng vì chúng có mặt bằng chung(phía trên phía tay trái tam giác) và tổng chiều cao vuông góc với cạnh đó của tam giác. Lập luận tương tự đối với cạnh bên của tam giác, ta chứng minh được rằng hình bình hành dưới có diện tích bằng hai hình bình hành xanh.
Số phức
Định lý Pitago được sử dụng để tìm khoảng cách giữa hai điểm trong hệ tọa độ Descartes, và định lý này đúng với tất cả các tọa độ thực: khoảng cách S giữa hai điểm ( a, b) và ( đĩa CD) bằng
Không có vấn đề gì với công thức nếu số phức được coi là vectơ có thành phần thực x + tôi là = (x, y). . Ví dụ, khoảng cách S giữa 0 + 1 tôi và 1 + 0 tôi tính toán dưới dạng môđun của vectơ (0, 1) − (1, 0) = (−1, 1), hoặc
Tuy nhiên, đối với các phép toán với vectơ có tọa độ phức tạp, cần phải thực hiện một số cải tiến nhất định đối với công thức Pitago. Khoảng cách giữa các điểm với số phức (một, b) và ( c, d); một, b, c, và dđều phức tạp, chúng tôi xây dựng công thức bằng cách sử dụng giá trị tuyệt đối. Khoảng cách S dựa trên sự khác biệt vectơ (một − c, b − d) trong mẫu sau: hãy để sự khác biệt một − c = P+ tôi q, ở đâu P là phần thực sự của sự khác biệt, q là phần ảo và i = √ (−1). Tương tự như vậy, hãy b − d = r+ tôi S. Sau đó:
ở đâu là liên hợp phức tạp của. Ví dụ, khoảng cách giữa các điểm (một, b) = (0, 1) và (c, d) = (tôi, 0) , tính toán sự khác biệt (một − c, b − d) = (−tôi, 1) và kết quả sẽ là 0 nếu các liên từ phức không được sử dụng. Do đó, bằng cách sử dụng công thức cải tiến, chúng tôi nhận được
Mô-đun được định nghĩa như thế này:
Phép đo lập thể
Một khái quát đáng kể của định lý Pitago cho không gian ba chiều là định lý de Gua, được đặt theo tên của J.-P. de Gua: nếu một tứ diện có một góc vuông (như trong một hình lập phương), thì bình phương diện tích của mặt đối diện với góc vuông bằng tổng bình phương diện tích của ba mặt còn lại. Kết luận này có thể được tóm tắt là " N-định lý Pitago chiều ":
Định lý Pythagoras không gian ba chiều nối đường chéo AD với ba cạnh.
Một cách tổng quát khác: Định lý Pitago có thể được áp dụng cho phép lập thể ở dạng sau. Coi như hình khối, như nó được hiển thị trên hình ảnh. Tìm độ dài đường chéo BD bằng định lý Pitago:
trong đó ba cạnh tạo thành một tam giác vuông. Sử dụng đường chéo BD và cạnh thẳng đứng AB để tìm độ dài đường chéo AD, một lần nữa sử dụng định lý Pitago:
hoặc, nếu mọi thứ được viết trong một phương trình:
Kết quả này là một biểu thức 3D để xác định độ lớn của vectơ v(đường chéo AD) được biểu thị theo các thành phần vuông góc của nó ( v k) (ba cạnh vuông góc với nhau):
Phương trình này có thể được xem như một sự tổng quát của định lý Pitago cho một không gian nhiều chiều. Tuy nhiên, kết quả thực sự không hơn gì việc áp dụng lặp đi lặp lại định lý Pitago cho một dãy tam giác vuông trong các mặt phẳng vuông góc liên tiếp.
không gian vector
Trong trường hợp một hệ vectơ trực giao, một đẳng thức xảy ra, còn được gọi là định lý Pitago:
Nếu là hình chiếu của vectơ lên trục tọa độ, thì công thức này trùng với khoảng cách Euclide - và có nghĩa là độ dài của vectơ bằng căn tổng bình phương bình phương của các thành phần của nó.
Tương tự của sự bình đẳng này trong trường hợp hệ thống vô tận vectơ được gọi là đẳng thức Parseval.
Hình học phi Euclid
Định lý Pitago có nguồn gốc từ các tiên đề của hình học Euclid và trên thực tế, không có giá trị đối với hình học phi Euclide, ở dạng nó được viết ở trên. (Nghĩa là, định lý Pitago hóa ra là một dạng tương đương với định đề Euclid về tính song song) Nói cách khác, trong hình học phi Euclid, tỷ số giữa các cạnh của tam giác nhất thiết phải ở dạng khác với định lý Pitago. . Ví dụ, trong hình học hình cầu, cả ba cạnh của một tam giác vuông (giả sử một, b và c) ràng buộc bát phân (một phần tám) của hình cầu đơn vị có độ dài π / 2, điều này mâu thuẫn với định lý Pitago vì một 2 + b 2 ≠ c 2 .
Ở đây hãy xem xét hai trường hợp của hình học phi Euclid - hình học hình cầu và hình hypebol; trong cả hai trường hợp, đối với không gian Euclide cho tam giác vuông, kết quả thay thế định lý Pitago sau định lý cosin.
Tuy nhiên, định lý Pitago vẫn có giá trị đối với hình học hypebol và hình elip nếu thay yêu cầu tam giác là góc vuông bằng điều kiện tổng hai góc của tam giác phải bằng thứ ba. Một+B = C. Khi đó, tỷ lệ giữa các cạnh trông như thế này: tổng diện tích các hình tròn có đường kính một và b bằng diện tích hình tròn có đường kính c.
hình học hình cầu
Đối với bất kỳ tam giác vuông nào trên một hình cầu có bán kính R(ví dụ, nếu góc γ trong tam giác vuông) với các cạnh một, b, c mối quan hệ giữa các bên sẽ như thế này:
Sự bình đẳng này có thể được suy ra là một trường hợp đặc biệtĐịnh lý côsin hình cầu, áp dụng cho tất cả các tam giác cầu:
trong đó cosh là cosin hypebol. Công thức này là một trường hợp đặc biệt của định lý côsin hypebol, áp dụng cho tất cả các tam giác:
trong đó γ là góc có đỉnh đối diện với cạnh c.
ở đâu g ijđược gọi là tensor hệ mét. Nó có thể là một chức năng vị trí. Các không gian cong như vậy bao gồm hình học Riemann như ví dụ chung. Công thức này cũng phù hợp với không gian Euclide khi sử dụng tọa độ đường cong. Ví dụ, cho tọa độ cực:
sản phẩm vector
Định lý Pitago nối hai biểu thức về độ lớn của tích vectơ. Một cách tiếp cận để xác định một sản phẩm chéo yêu cầu nó phải thỏa mãn phương trình:
công thức này sử dụng sản phẩm chấm. Vế phải của phương trình được gọi là định thức Gram đối với một và b, bằng diện tích của hình bình hành do hai vectơ này tạo thành. Dựa trên yêu cầu này, cũng như yêu cầu tích vectơ phải vuông góc với các thành phần của nó một và b theo đó, ngoại trừ các trường hợp nhỏ của không gian 0 và 1 chiều, tích vectơ chỉ được xác định trong ba và bảy chiều. Chúng tôi sử dụng định nghĩa của góc trong N-không gian chiều:
thuộc tính này của tích vectơ cho giá trị của nó ở dạng sau:
Thông qua cơ bản nhận dạng lượng giác Pythagoras, chúng tôi nhận được một hình thức khác để viết giá trị của nó:
Một cách tiếp cận thay thế để xác định sản phẩm chéo sử dụng một biểu thức cho độ lớn của nó. Sau đó, lập luận theo thứ tự ngược lại, chúng tôi nhận được kết nối với sản phẩm vô hướng:
Xem thêm
Ghi chú
- Chủ đề lịch sử: Định lý Pythagoras trong toán học Babylon
- (, tr. 351) tr. 351
- (, Tập I, tr. 144)
- Thảo luận sự kiện lịch sửđược đưa ra trong (, trang 351) trang 351
- Kurt Von Fritz (tháng 4 năm 1945). "Khám phá về khả năng không kích thước của Hippasus ở Metapontum". Biên niên sử Toán học, Sê-ri thứ hai(Biên niên sử của Toán học) 46 (2): 242–264.
- Lewis Carroll, "Câu chuyện với những nút thắt", M., Mir, 1985, tr. 7
- Asger Aaboe Các tập từ lịch sử ban đầu của toán học. - Hiệp hội Toán học Hoa Kỳ, 1997. - Tr 51. - ISBN 0883856131
- Đề xuất Pythagore bởi Elisha Scott Loomis
- Euclid's Các yếu tố: Quyển VI, Mệnh đề VI 31: "Trong tam giác vuông, hình bên chứa góc vuông bằng hình bên chứa góc vuông và tương tự như hình bên chứa góc vuông."
- Lawrence S. Leff công việc được trích dẫn. - Bộ sách Giáo dục của Barron. - P. 326. - ISBN 0764128922
- Howard Whitley Eves§4.8: ... khái quát định lý Pitago // Những khoảnh khắc vĩ đại trong toán học (trước năm 1650). - Hiệp hội Toán học Hoa Kỳ, 1983. - Tr 41. - ISBN 0883853108
- Tâbit ibn Qorra (tên đầy đủ là Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 SCN) là một bác sĩ sống ở Baghdad, người đã viết nhiều về Euclid’s Elements và những người khác các môn toán học.
- Aydin Sayili (tháng 3 năm 1960). "Sự tổng quát của định lý Pitago của Thâbit ibn Qurra". Isis 51 (1): 35–37. DOI: 10.1086 / 348837.
- Judith D. Sally, Paul Sally Bài tập 2.10 (ii) // Tác phẩm được trích dẫn. - P. 62. - ISBN 0821844032
- Để biết chi tiết của việc xây dựng như vậy, hãy xem George Jennings Hình 1.32: Định lý Pitago tổng quát // Hình học hiện đại ứng dụng: với 150 hình. - lần thứ 3. - Springer, 1997. - P. 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcy mục C: Định mức cho một tùy ý N-tuple ... // Giới thiệu về phân tích. - Springer, 1995. - P. 124. - ISBN 0387943692 Xem thêm các trang 47-50.
- Alfred Grey, Elsa Abbena, Simon Salamon Hình học vi phân hiện đại của đường cong và bề mặt với Mathematica. - lần thứ 3. - CRC Press, 2006. - P. 194. - ISBN 1584884487
- Rajendra Bhatia phân tích ma trận. - Springer, 1997. - Tr 21. - ISBN 0387948465
- Stephen W. Hawking công việc được trích dẫn. - 2005. - Tr 4. - ISBN 0762419229
- Eric W. Weisstein CRC bách khoa toàn thư về toán học. - lần 2. - 2003. - Tr 2147. - ISBN 1584883472
- Alexander R. Pruss
Cấp trung
Tam giác vuông. Toàn bộ hướng dẫn minh họa (2019)
TAM GIÁC ĐÚNG. CẤP ĐỘ ĐẦU TIÊN.
Trong các bài toán, một góc vuông là không cần thiết - góc dưới bên trái, vì vậy bạn cần học cách nhận ra một tam giác vuông ở dạng này,

và như vậy

và như vậy 
Điều gì là tốt về một tam giác vuông? Chà ... trước hết, có những điều đặc biệt những cái tên đẹp cho phe của mình.
Chú ý đến bản vẽ!

Hãy nhớ và đừng nhầm lẫn: chân - hai và cạnh huyền - chỉ một(duy nhất, duy nhất và dài nhất)!
Chà, chúng ta đã thảo luận về những cái tên, bây giờ là điều quan trọng nhất: định lý Pitago.
Định lý Pythagore.
Định lý này là chìa khóa để giải nhiều bài toán liên quan đến tam giác vuông. Nó đã được Pythagoras chứng minh trong thời hoàn toàn xa xưa, và kể từ đó nó đã mang lại nhiều lợi ích cho những ai biết đến nó. Và điều tuyệt vời nhất ở cô ấy là cô ấy giản dị.
Cho nên, Định lý Pythagore:
Bạn có nhớ câu chuyện cười: "Quần Pytago tất cả các mặt đều bằng nhau!"?
Hãy vẽ những chiếc quần rất Pytago này và nhìn vào chúng. 
Nó có thực sự giống quần đùi không? Vậy chúng bằng nhau ở những phía nào và ở đâu? Tại sao và câu chuyện cười bắt nguồn từ đâu? Và trò đùa này được kết nối chính xác với định lý Pythagore, chính xác hơn với cách mà chính Pythagoras đã xây dựng định lý của mình. Và anh ấy đã xây dựng nó như thế này:
"Tổng diện tích hình vuông, được xây dựng trên chân, bằng khu vuôngđược xây dựng trên cạnh huyền.
Nghe có vẻ hơi khác một chút, phải không? Và vì vậy, khi Pythagoras vẽ ra tuyên bố của định lý của mình, chỉ một bức tranh như vậy đã xuất hiện.

Trong hình này, tổng diện tích của các hình vuông nhỏ bằng diện tích của hình vuông lớn. Và để bọn trẻ nhớ rõ hơn rằng tổng bình phương của hai chân bằng bình phương cạnh huyền, một người nào đó đã dí dỏm phát minh ra trò đùa này về quần Pythagore.
Tại sao bây giờ chúng ta xây dựng định lý Pitago
Pythagoras có đau khổ và nói về hình vuông không?
Bạn thấy đấy, thời cổ đại không có ... đại số! Không có dấu hiệu và vân vân. Không có chữ khắc. Bạn có thể tưởng tượng những học sinh nghèo thời xưa có thể học thuộc lòng mọi thứ bằng lời nói kinh khủng như thế nào không ??! Và chúng ta có thể vui mừng rằng chúng ta có một công thức đơn giản của định lý Pitago. Hãy lặp lại nó một lần nữa để ghi nhớ tốt hơn:
Bây giờ nó sẽ dễ dàng:
| Bình phương của cạnh huyền bằng tổng bình phương của các chân. |
Vâng, định lý quan trọng nhất về tam giác vuông đã được thảo luận. Nếu bạn đang tự hỏi làm thế nào nó được chứng minh, hãy đọc tiếp. cấp độ tiếp theo lý thuyết, và bây giờ chúng ta hãy chuyển sang ... rừng tối... lượng giác! Đối với các từ khủng khiếp sin, cosine, tiếp tuyến và cotang.
Sin, cosin, tiếp tuyến, cotang trong tam giác vuông.
Trên thực tế, mọi thứ không hề đáng sợ chút nào. Tất nhiên, định nghĩa "thực" của sin, cosine, tiếp tuyến và cotang nên được xem xét trong bài báo. Nhưng bạn thực sự không muốn, phải không? Chúng ta có thể vui mừng: để giải các bài toán về tam giác vuông, bạn chỉ cần điền vào những điều đơn giản sau:
Tại sao tất cả về góc? Góc ở đâu? Để hiểu được điều này, bạn cần biết câu 1 - 4 được viết như thế nào. Nhìn, hiểu và nhớ!
1.
Nó thực sự nghe như thế này:
Còn về góc độ? Có một chân đối diện với góc, tức là, chân đối diện (đối với góc)? Tất nhiên có! Đây là một cathet!
Nhưng những gì về góc độ? Nhìn kĩ. Chân tiếp giáp với góc nào? Tất nhiên, con mèo. Vì vậy, đối với góc, chân tiếp giáp, và
Và bây giờ, hãy chú ý! Hãy nhìn những gì chúng tôi nhận được:
Hãy xem nó tuyệt vời như thế nào:
Bây giờ chúng ta hãy chuyển sang tiếp tuyến và cotang.
Làm thế nào để diễn đạt nó thành lời bây giờ? Chân liên quan gì đến góc? Đối diện, tất nhiên - nó "nằm" đối diện với góc. Và cathet? Liền kề căn góc. Vậy chúng ta đã nhận được gì?
Xem cách đảo ngược tử số và mẫu số?
Và bây giờ một lần nữa các góc và thực hiện trao đổi:
Tóm lược
Hãy viết ngắn gọn những gì chúng ta đã học được.
 |
Định lý Pythagore: |
Định lý tam giác vuông chính là định lý Pitago.
Định lý Pythagore
Nhân tiện, bạn có nhớ rõ chân và cạnh huyền là gì không? Nếu không, hãy nhìn vào bức tranh - làm mới kiến thức của bạn

Có thể bạn đã sử dụng định lý Pitago nhiều lần, nhưng có bao giờ bạn tự hỏi tại sao một định lý như vậy lại đúng. Làm thế nào bạn sẽ chứng minh nó? Hãy làm như người Hy Lạp cổ đại. Hãy vẽ một hình vuông với một cạnh.

Bạn thấy chúng ta đã chia các cạnh của nó thành các đoạn có độ dài và!
Bây giờ chúng ta hãy kết nối các điểm đã đánh dấu

Tuy nhiên, ở đây chúng tôi đã lưu ý một điều khác, nhưng chính bạn hãy nhìn vào bức tranh và suy nghĩ về lý do tại sao.
Diện tích của hình vuông lớn hơn là bao nhiêu? Chính xác,. Còn diện tích nhỏ hơn thì sao? Chắc chắn, . Tổng diện tích bốn góc còn lại. Hãy tưởng tượng rằng chúng ta lấy hai người trong số họ và dựa vào nhau với các cạnh huyền. Chuyện gì đã xảy ra thế? Hai hình chữ nhật. Vì vậy, diện tích "cành giâm" là bằng nhau.
Bây giờ chúng ta hãy tập hợp tất cả lại với nhau.
Hãy biến đổi:
Vì vậy, chúng tôi đến thăm Pythagoras - chúng tôi đã chứng minh định lý của ông ấy theo một cách cổ xưa.
Tam giác vuông và lượng giác
Đối với một tam giác vuông, các quan hệ sau đây là:

Xoang góc nhọn bằng tỷ số của chân đối diện với cạnh huyền
Côsin của một góc nhọn bằng tỷ số của chân kề cạnh cạnh huyền.
Tiếp tuyến của một góc nhọn bằng tỷ số của chân đối diện với chân liền kề.
Cotang của một góc nhọn bằng tỷ số của chân liền kề và chân đối diện.
Và một lần nữa, tất cả điều này dưới dạng một cái đĩa:
Nó rất thoải mái!
Dấu hiệu nhận biết tam giác vuông
I. Trên hai chân

II. Bằng chân và cạnh huyền

III. Theo cạnh huyền và góc nhọn

IV. Dọc theo chân và góc nhọn
một) 
b) 
Chú ý! Ở đây điều rất quan trọng là chân phải "tương ứng". Ví dụ: nếu nó diễn ra như thế này:

VẬY CÁC TAM GIÁC KHÔNG BẰNG NHAU, mặc dù thực tế là chúng có một góc nhọn giống hệt nhau.
Cần phải trong cả hai hình tam giác, chân liền kề hoặc trong cả hai - đối diện.
Bạn có nhận thấy dấu hiệu đẳng thức của tam giác vuông khác với dấu hiệu thông thường của tam giác như thế nào không? Nhìn vào chủ đề “và chú ý đến thực tế là để có sự bằng nhau của các tam giác“ thông thường ”, bạn cần sự bằng nhau của ba yếu tố: hai cạnh và một góc giữa chúng, hai góc và một cạnh giữa chúng hoặc ba cạnh. Nhưng để các tam giác vuông cân bằng nhau thì chỉ cần hai yếu tố tương ứng là đủ. Thật tuyệt vời đúng không?
Xấp xỉ đồng dạng với dấu hiệu đồng dạng của tam giác vuông.
Dấu hiệu nhận biết các tam giác vuông
I. Góc khuất

II. Trên hai chân

III. Bằng chân và cạnh huyền

Đường trung bình trong một tam giác vuông
Tại sao nó như vậy?
Hãy xem xét toàn bộ một hình chữ nhật thay vì một tam giác vuông.
Hãy vẽ một đường chéo và xem xét một điểm - giao điểm của các đường chéo. Bạn biết gì về đường chéo của hình chữ nhật?
Và những gì tiếp theo từ điều này?
Vì vậy, nó đã xảy ra rằng
- - Trung bình:
Hãy nhớ thực tế này! Giúp đỡ rất nhiều!
Điều đáng ngạc nhiên hơn nữa là điều ngược lại cũng đúng.
Có thể thu được lợi ích gì khi trung bình được vẽ cạnh cạnh huyền bằng một nửa cạnh huyền? Hãy nhìn vào bức tranh
Nhìn kĩ. Ta có:, nghĩa là khoảng cách từ điểm đến cả ba đỉnh của tam giác bằng nhau. Nhưng trong một tam giác chỉ có một điểm mà khoảng cách từ đó về cả ba đỉnh của tam giác đều bằng nhau và đây là TRỌNG TÂM CỦA MẠCH NỐI TIẾP. Vậy chuyện gì đã xảy ra?
Vì vậy, hãy bắt đầu với điều này "bên cạnh ...".
Hãy nhìn vào tôi.
Nhưng trong tam giác đồng dạng tất cả các góc đều bằng nhau!
Điều tương tự cũng có thể nói về và
Bây giờ chúng ta hãy cùng nhau vẽ nó:
Công dụng gì có thể được rút ra từ sự giống nhau "gấp ba" này.
Chà, chẳng hạn - hai công thức về chiều cao của một tam giác vuông.
Chúng tôi viết mối quan hệ của các bên tương ứng:

Để tìm chiều cao, chúng tôi giải quyết tỷ lệ và nhận được công thức đầu tiên "Chiều cao trong tam giác vuông":
Vì vậy, hãy áp dụng tương tự:.

Chuyện gì xảy ra bây giờ?
Một lần nữa, chúng tôi giải quyết tỷ lệ và nhận được công thức thứ hai:
Cả hai công thức này phải được ghi nhớ rất tốt và một công thức nào đó sẽ thuận tiện hơn khi áp dụng. Hãy viết lại chúng một lần nữa.
Định lý Pythagore:
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương chân:.

Dấu hiệu nhận biết tam giác vuông:
- trên hai chân:
- dọc theo chân và cạnh huyền: hoặc
- dọc theo chân và góc nhọn lân cận: hoặc
- dọc theo chân và góc nhọn đối diện: hoặc
- bằng cạnh huyền và góc nhọn: hoặc.
Dấu hiệu nhận biết các tam giác vuông:
- một góc nhọn: hoặc
- từ tỷ lệ của hai chân:
- từ tỷ lệ của chân và cạnh huyền: hoặc.
Sin, cosin, tiếp tuyến, cotang trong tam giác vuông
- Sin của một góc nhọn của tam giác vuông là tỷ số của chân đối diện với cạnh huyền:
- Côsin của một góc nhọn của tam giác vuông là tỷ số của chân kề cạnh cạnh huyền:
- Tiếp tuyến của một góc nhọn của tam giác vuông là tỷ số của chân đối diện với chân kề:
- Cotang của góc nhọn của tam giác vuông là tỉ số của chân kề với cạnh đối:.
Chiều cao của một tam giác vuông: hoặc.
Trong một tam giác vuông, trung tuyến được vẽ từ đỉnh của góc vuông bằng một nửa cạnh huyền:.
Diện tích tam giác vuông:
- qua các ống thông:
 Tương tự, tam giác CBH đồng dạng với ABC. Giới thiệu ký hiệu
Tương tự, tam giác CBH đồng dạng với ABC. Giới thiệu ký hiệu  1. Xếp bốn tam giác vuông bằng nhau như hình vẽ bên.
1. Xếp bốn tam giác vuông bằng nhau như hình vẽ bên. 
 Ý tưởng về chứng minh của Euclid như sau: hãy thử chứng minh rằng một nửa diện tích của hình vuông được xây dựng trên cạnh huyền bằng tổng của nửa diện tích của hình vuông được xây dựng trên chân, và sau đó là diện tích của hình vuông lớn và hai hình vuông nhỏ bằng nhau. Hãy xem xét hình vẽ bên trái. Ta dựng hình vuông trên các cạnh của tam giác vuông trên đó và vẽ tia s từ đỉnh của góc vuông C vuông góc với cạnh huyền AB, nó cắt hình vuông ABIK dựng trên cạnh huyền thành hai hình chữ nhật - BHJI và HAKJ , tương ứng. Nó chỉ ra rằng diện tích của những hình chữ nhật này chính xác bằng diện tích của các hình vuông được xây dựng trên các chân tương ứng. Hãy thử chứng minh rằng diện tích hình vuông DECA bằng diện tích hình chữ nhật AHJK Để làm được điều này, chúng ta sử dụng một quan sát bổ trợ: Diện tích hình tam giác có cùng chiều cao và đáy như hình đã cho hình chữ nhật bằng một nửa diện tích của hình chữ nhật đã cho. Đây là hệ quả của việc xác định diện tích của một tam giác bằng một nửa tích của đáy và chiều cao. Từ nhận xét này, ta thấy rằng diện tích tam giác ACK bằng diện tích tam giác AHK (không hình vẽ), nghĩa là bằng một nửa diện tích hình chữ nhật AHJK. Bây giờ chúng ta hãy chứng minh rằng diện tích tam giác ACK cũng bằng một nửa diện tích hình vuông DECA. Điều duy nhất cần làm là chứng minh sự bằng nhau của các tam giác ACK và BDA (vì diện tích tam giác BDA bằng một nửa diện tích hình vuông theo tính chất trên). Sự bình đẳng này là hiển nhiên, các tam giác bằng nhau về hai cạnh và góc giữa chúng. Cụ thể - AB = AK, AD = AC - bằng nhau của các góc CAK và BAD dễ dàng chứng minh bằng phương pháp chuyển động: quay tam giác CAK 90 ° ngược chiều kim đồng hồ thì ta thấy các cạnh tương ứng của hai tam giác đó là sẽ trùng (do góc ở đỉnh của hình vuông là 90 °). Lập luận về sự bằng nhau của diện tích hình vuông BCFG và hình chữ nhật BHJI là hoàn toàn tương tự. Như vậy, chúng ta đã chứng minh rằng diện tích của hình vuông được xây dựng trên cạnh huyền là tổng diện tích của các hình vuông được xây dựng trên chân.
Ý tưởng về chứng minh của Euclid như sau: hãy thử chứng minh rằng một nửa diện tích của hình vuông được xây dựng trên cạnh huyền bằng tổng của nửa diện tích của hình vuông được xây dựng trên chân, và sau đó là diện tích của hình vuông lớn và hai hình vuông nhỏ bằng nhau. Hãy xem xét hình vẽ bên trái. Ta dựng hình vuông trên các cạnh của tam giác vuông trên đó và vẽ tia s từ đỉnh của góc vuông C vuông góc với cạnh huyền AB, nó cắt hình vuông ABIK dựng trên cạnh huyền thành hai hình chữ nhật - BHJI và HAKJ , tương ứng. Nó chỉ ra rằng diện tích của những hình chữ nhật này chính xác bằng diện tích của các hình vuông được xây dựng trên các chân tương ứng. Hãy thử chứng minh rằng diện tích hình vuông DECA bằng diện tích hình chữ nhật AHJK Để làm được điều này, chúng ta sử dụng một quan sát bổ trợ: Diện tích hình tam giác có cùng chiều cao và đáy như hình đã cho hình chữ nhật bằng một nửa diện tích của hình chữ nhật đã cho. Đây là hệ quả của việc xác định diện tích của một tam giác bằng một nửa tích của đáy và chiều cao. Từ nhận xét này, ta thấy rằng diện tích tam giác ACK bằng diện tích tam giác AHK (không hình vẽ), nghĩa là bằng một nửa diện tích hình chữ nhật AHJK. Bây giờ chúng ta hãy chứng minh rằng diện tích tam giác ACK cũng bằng một nửa diện tích hình vuông DECA. Điều duy nhất cần làm là chứng minh sự bằng nhau của các tam giác ACK và BDA (vì diện tích tam giác BDA bằng một nửa diện tích hình vuông theo tính chất trên). Sự bình đẳng này là hiển nhiên, các tam giác bằng nhau về hai cạnh và góc giữa chúng. Cụ thể - AB = AK, AD = AC - bằng nhau của các góc CAK và BAD dễ dàng chứng minh bằng phương pháp chuyển động: quay tam giác CAK 90 ° ngược chiều kim đồng hồ thì ta thấy các cạnh tương ứng của hai tam giác đó là sẽ trùng (do góc ở đỉnh của hình vuông là 90 °). Lập luận về sự bằng nhau của diện tích hình vuông BCFG và hình chữ nhật BHJI là hoàn toàn tương tự. Như vậy, chúng ta đã chứng minh rằng diện tích của hình vuông được xây dựng trên cạnh huyền là tổng diện tích của các hình vuông được xây dựng trên chân.  Xét hình vẽ, ta thấy đoạn thẳng CI cắt hình vuông ABHJ thành hai phần giống nhau (do các tam giác ABC và JHI bằng nhau). Sử dụng phép quay ngược chiều kim đồng hồ 90 độ, chúng ta thấy sự bằng nhau của các hình tô mờ CAJI và GDAB. Bây giờ rõ ràng là chúng ta có diện tích của hình được tô bóng bằng tổng của một nửa diện tích của các hình vuông được xây dựng trên các chân và diện tích của hình tam giác ban đầu. Mặt khác, nó bằng một nửa diện tích của hình vuông được xây dựng trên cạnh huyền, cộng với diện tích của tam giác ban đầu. Bước cuối cùng trong phần chứng minh được để lại cho người đọc.
Xét hình vẽ, ta thấy đoạn thẳng CI cắt hình vuông ABHJ thành hai phần giống nhau (do các tam giác ABC và JHI bằng nhau). Sử dụng phép quay ngược chiều kim đồng hồ 90 độ, chúng ta thấy sự bằng nhau của các hình tô mờ CAJI và GDAB. Bây giờ rõ ràng là chúng ta có diện tích của hình được tô bóng bằng tổng của một nửa diện tích của các hình vuông được xây dựng trên các chân và diện tích của hình tam giác ban đầu. Mặt khác, nó bằng một nửa diện tích của hình vuông được xây dựng trên cạnh huyền, cộng với diện tích của tam giác ban đầu. Bước cuối cùng trong phần chứng minh được để lại cho người đọc.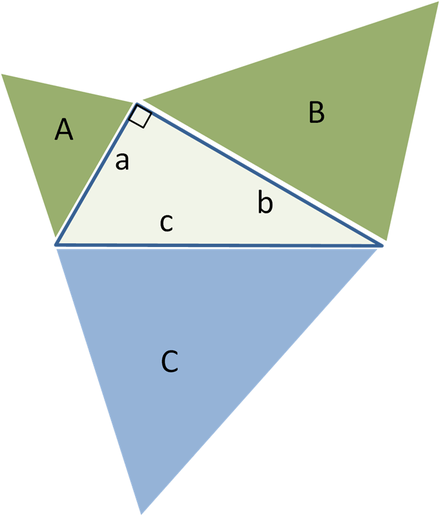




 Tư liệu thông tin "góc bạn đọc trẻ"
Tư liệu thông tin "góc bạn đọc trẻ" Tiến sĩ xa để tiêu diệt
Tiến sĩ xa để tiêu diệt Mua axit sunfuric ở đâu?
Mua axit sunfuric ở đâu?