"funktsiooni omaduste rakendamine võrrandite ja võrratuste lahendamisel". "Võrrandite lahendamine mittestandardsete meetoditega, kasutades funktsioonide omadusi
Teema: Piiratud funktsioonide kasutamise meetodid.
Elu on hea, sest see
sa oskad matemaatikat teha.
(Leonhard Euler)Eesmärgid: uue kastist väljas mõtlemise arendamine, mida saab edukalt rakendada ka teistes valdkondades inimtegevus(küberneetika, arvutitehnoloogia, majandus, radiofüüsika, keemia jne).
Ülesanded: - väljaõpe ülesannete objektiivse ja subjektiivse raskusastme hindamiseks ning nende ülesannete mõistlikuks valikuks eksamil;
Ebatraditsiooniliste ja ebatavaliste arutluskäikude "hotsupanga" loomine.
Tundide ajal:
Org. hetk. Tunni teema formuleerimine õpilaste poolt, täites A- ja B-osa ühtse riigieksami ülesanded ning dekodeerides teema saadud vastuste kahanevas järjekorras. (Nagu oodatud sõnad, krüptige 12 kaarti, mis on nummerdatud vahemikus -2 kuni 10) (Lisa 1 ja 2)
piiranguid
2. Jagage õpilased 2 rühma, andke neile komplekt "Teooria + 10 ülesannet" (lisa 3 ja 4), paluge neil valida need ülesanded, mida saab selles teoreetilises osas täita, põhjendage oma valikut.3. Näidake nende ülesannete edenemist tahvlile õpilaste poolt: Noskova K., Dedevšin I., Veselov I.4. Jaga ülesanded kaardil 2 rühma, et neid lahendada, millele järgneb lehel enesekontroll. valmislahendused. (lisa 5)5. Jagage rühmadesse lehed, mis kirjeldavad uusi mittestandardseid meetodeid võrrandite ja valiku võrratuste lahendamiseks järgmine teema(Koduseks ülesandeks, mida kogudest leida KASUTAGE ülesandeid, mida saab selle meetodiga lahendada) (6. lisa)6. Õpilaste peegeldus (tahvli täitmine) F.I. õpilane1. lisa.
Lahenda need ülesanded ja järjesta vastused kahanevas järjekorras, kogu vastuste järgi meie tunni teema.
Leidke funktsiooni y \u003d 3x 2 -7x + 7 graafiku punkti abstsiss, milles puutujanurga puutuja on -1.
2. lisa
9 2 0 7Funktsioonide uurimine tuletise abil. 10 5 1 -1 Piiratud funktsioonide kasutamise meetod. 4 -2 8 12 Ebavõrdsuse lahendamine graafiliselt.
3 11 6Funktsionaalvõrrandite lahendused.
Uuring
3. lisa
Üks neist tõhusad meetodid võrrandite või võrratuste lahendamine on meetod, mis põhineb piiratud funktsioonide kasutamisel. Kõige kuulsamatele piiratud funktsioonid sisaldama näiteks mõnda trigonomeetrilist; tagurpidi trigonomeetrilised funktsioonid; funktsioonid, mis sisaldavad moodulit, kraadi, juurt c ühtlane aste muud.
Kõige tavalisemad ebavõrdsused on järgmised:
│f(x) │≥
0, -1
≤
sinx ≤
1, -1
≤
cosx ≤
1, -

 -
-

 ,
a f (x) >0, (f(x) ±
g(x))2n ≥
0,
,
a f (x) >0, (f(x) ±
g(x))2n ≥
0,
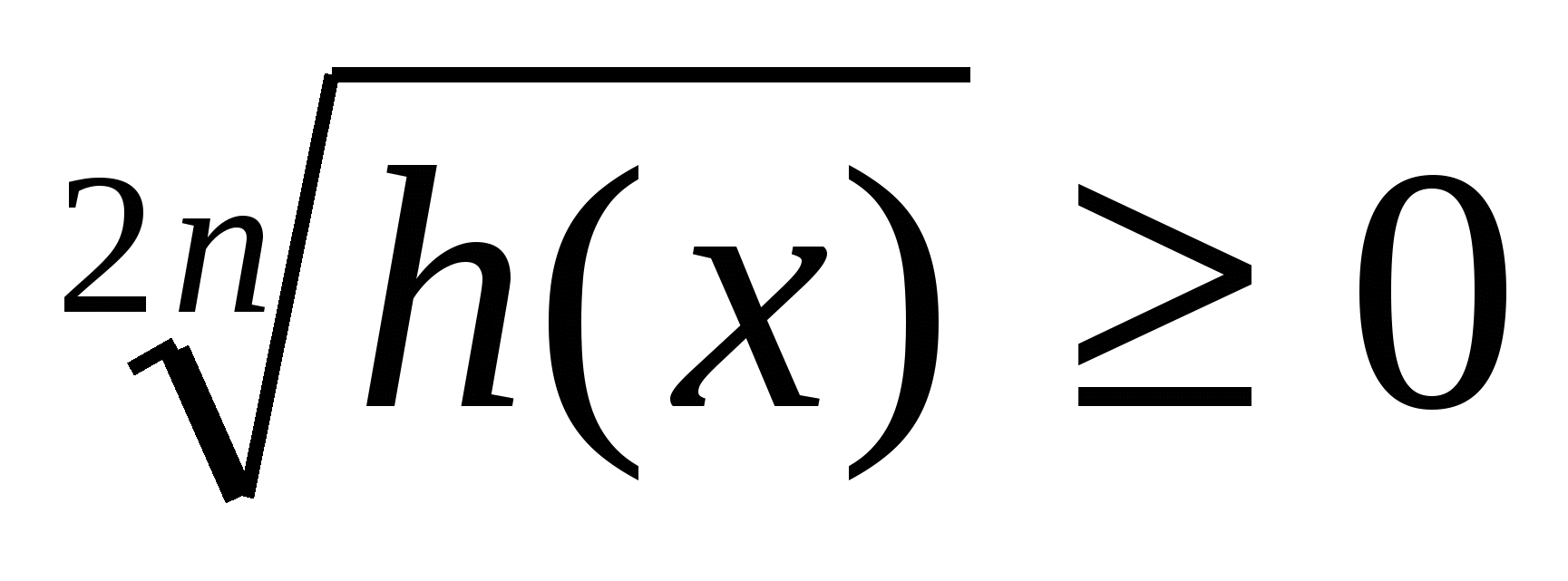 ,
a+
≥
2,
b+
≤
-2
ja paljud teised. Siin n -naturaalarv,
h(x) ≥
0,
a>0,
b
0.
,
a+
≥
2,
b+
≤
-2
ja paljud teised. Siin n -naturaalarv,
h(x) ≥
0,
a>0,
b
0.
Lisaks ülaltoodud lihtsaimatele võrratustele on ka keerulisemaid, eriti trigonomeetrilised ebavõrdsused -,
 ,
,
ja ebavõrdsused vormi moodulitega 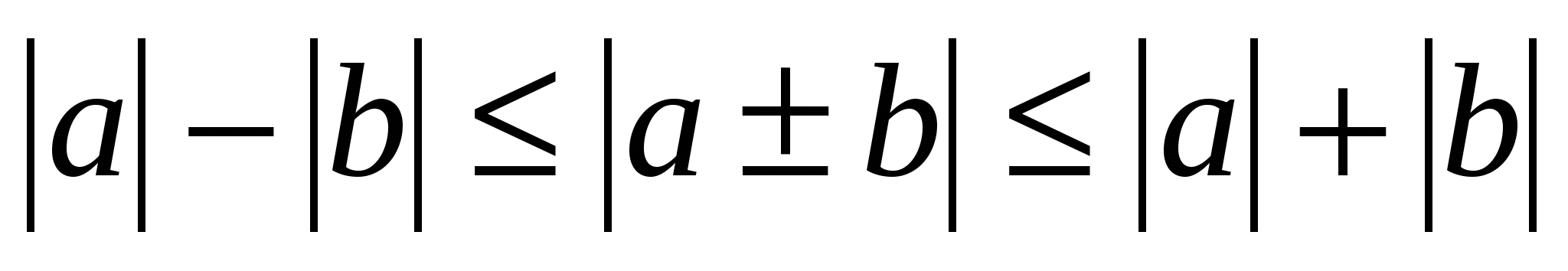 .
.
Näide 1Lahenda võrrand: 
Otsus:
välja valima täisruut võrrandi paremal poolel, st. . Sellest järeldub  . Kuna samal ajal sin π x ≤
1, siis saame võrrandisüsteemi
. Kuna samal ajal sin π x ≤
1, siis saame võrrandisüsteemi 
Lahendades süsteemi teise võrrandi, saame, et x=. Asendades esimesse võrrandisse, veendume, et x leitud väärtus on süsteemi lahendus, mis tähendab, et see on algse võrrandi lahendus.
Vastus: x=.
Näide 2Lahenda võrrand: 

Otsus: kuna Kuid sin2 π x ≤
1. Seega 5+4 sin2 π x ≤
9. Seega saame võrrandisüsteemi: 
Siit saame võrrandisüsteemi  , esimesest võrrandist leiame x \u003d. Asendage see süsteemi teise võrrandiga ja veenduge, et x= on süsteemi lahend ja seega ka algvõrrandi lahendus.
, esimesest võrrandist leiame x \u003d. Asendage see süsteemi teise võrrandiga ja veenduge, et x= on süsteemi lahend ja seega ka algvõrrandi lahendus.
Vastus: x=
4. lisa
Valige pakutud ülesannete loendist need, mida saab lahendada piiratud funktsioonide meetodil.
1. Lahendage võrrand x 2 -4 x=(2-cos  2. Leia kogus täisarvulised lahendused ebavõrdsused x 2 ctg 2
2. Leia kogus täisarvulised lahendused ebavõrdsused x 2 ctg 2 3. Lahenda võrrand
3. Lahenda võrrand 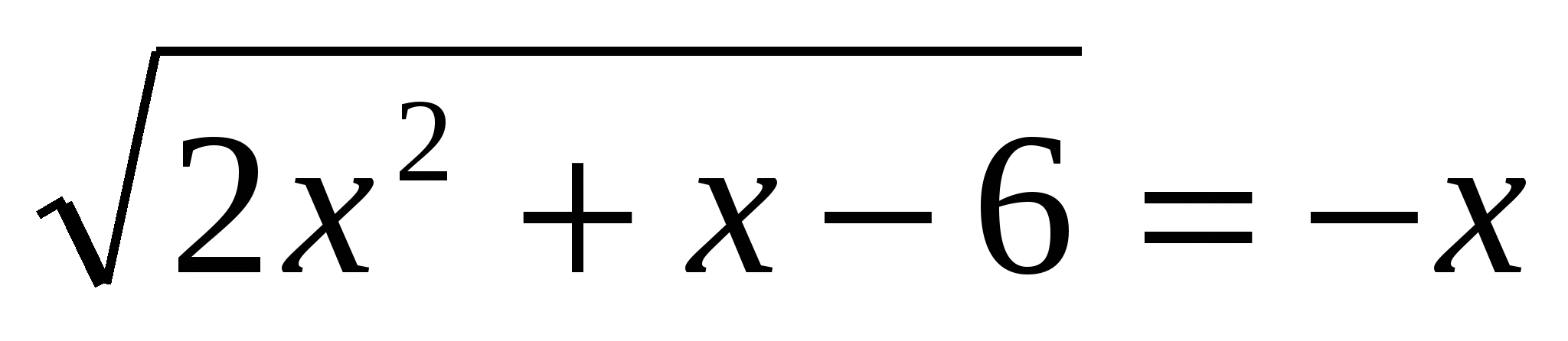 4. Lahendage võrrand 3-(5. Leidke 16-x võrratuse 2 ≥0 tingimust 3 rahuldavate täisarvlahenduste arv tg 2
4. Lahendage võrrand 3-(5. Leidke 16-x võrratuse 2 ≥0 tingimust 3 rahuldavate täisarvlahenduste arv tg 2  6. Lahenda võrrand
6. Lahenda võrrand  7. Lahendage võrrand -25x 2 +40x-23 = ( cos
7. Lahendage võrrand -25x 2 +40x-23 = ( cos  8. Leidke võrrandi x juurte korrutis
8. Leidke võrrandi x juurte korrutis  9. Lahenda võrrand
9. Lahenda võrrand  10. Lahenda võrrand 3- cos 2
10. Lahenda võrrand 3- cos 2 
Enesekontrolli leht.
5. lisa
1. lahendage võrrand
Lahendus: kuna , siis alates ja siis
saame võrrandisüsteemi
lahendame esimese võrrandi, saame x =, asendame selle väärtuse teise võrrandiga
2 . lahendage võrrand 3-
cos 2 Lahendus: kuna , siis alates ja siis
saame võrrandisüsteemi
lahendame teise võrrandi, saame x \u003d, asendame selle väärtuse esimeses võrrandis
seega x= on algse võrrandi lahendus. Vastus: x=
3 . Leidke võrratuse x täisarvuliste lahendite arv 2
+7х-8≤0 tingimust rahuldav ctg 2 ja seejärel leiame x mis tahes lubatud väärtuste korral ruudukujulise trinoomi nullid, Vieta teoreemi järgi lahendame ebavõrdsuse intervallide meetodil
siis. me teame seda
x-i täisarvud on arvud, mille me välistame. Vastus: 8 täisarvulist lahendust 4 . Leidke 16-kordse võrratuse 2 ≥0 tingimust 3 rahuldavate täisarvlahenduste arv tg 2 ja seejärel x mis tahes lubatud väärtuste korral leidke avaldise nullid, x= ja x= Lahendage ebavõrdsus intervallmeetodi abil
siis. me teame seda
x täisarvud on arvud, mille me välistame. Vastus: 7 täisarvulist lahendust
6. lisa
Funktsioonide monotoonsuse kasutamise meetod. Tüüpvõrrandi lahendamisel f (x) \u003d g (x) mõnel juhul on tõhus meetod, mis kasutab funktsioonide y \u003d f (x) ja y \u003d g (x) monotoonsust. Kui funktsioon y \u003d f (x) ) on pidev ja intervalliga suureneb (väheneb). a≤ x ≤ b, ja funktsioon y \u003d g (x) on pidev ja väheneb (suureneb) samal lõigul, siis võrrand f (x) \u003d g (x) lõigul a≤ x ≤ b ei saa olla rohkem kui üks juur, siis tuleb kas püüda leida valiku abil võrrandi kordumatu juur või näidata, et sellist juurt ei eksisteeri. See meetod on eriti efektiivne juhul, kui võrrandi f(x)=g(x) mõlemad osad on funktsiooni ühiseks uurimiseks "ebamugavad". Kommentaar: Kui funktsioon y= f(x) kasvab ja funktsioon y= g(x) kahaneb a≤ x ≤ b ja kus f(a)>g(a), siis võrrandi juured seas a≤ x ≤ b ei.
Näide: lahendage võrrandOtsus: Võrrandi kehtivate väärtuste vahemik on x  . On hästi näha, et selles piirkonnas võrrandi vasak pool suureneb, parem aga kahaneb, s.t. funktsioonif(x)=
. On hästi näha, et selles piirkonnas võrrandi vasak pool suureneb, parem aga kahaneb, s.t. funktsioonif(x)= suureneb ja funktsioong(x)=
suureneb ja funktsioong(x)= - väheneb. Sellega seoses võib algvõrrandil olla ainult üks juur (kui see on olemas). Valikuga leiame selle võrrandi x= juure 2.Vastus: x=2
- väheneb. Sellega seoses võib algvõrrandil olla ainult üks juur (kui see on olemas). Valikuga leiame selle võrrandi x= juure 2.Vastus: x=2
Funktsionaalvõrrandite lahendamise meetod.
Kõige rohkemate hulgas väljakutseid pakkuvad ülesanded USE sisaldab ülesandeid, mille lahendamine on taandatud vormi funktsionaalvõrrandite arvestamisele f(f(….f(x)…))=x või f(g(x))=f(h(x)), kus f(x),g(x),h(x) on mõned funktsioonid ja n≥ 2
Nende funktsionaalvõrrandite lahendamise meetodid põhinevad paljude teoreemide rakendamisel, vaatleme neist ühte.
1. teoreem. Võrrandi juured
f(x)=0 on võrrandi juured f(f(….f(x)…))=x
Näide: Lahendage võrrand x=  ,
kus Ruutjuur võetudnkorda jan≥
1
Otsus: Ülesande tingimusest järeldub, et x>
0. Lasef(x)=
,
kus Ruutjuur võetudnkorda jan≥
1
Otsus: Ülesande tingimusest järeldub, et x>
0. Lasef(x)=
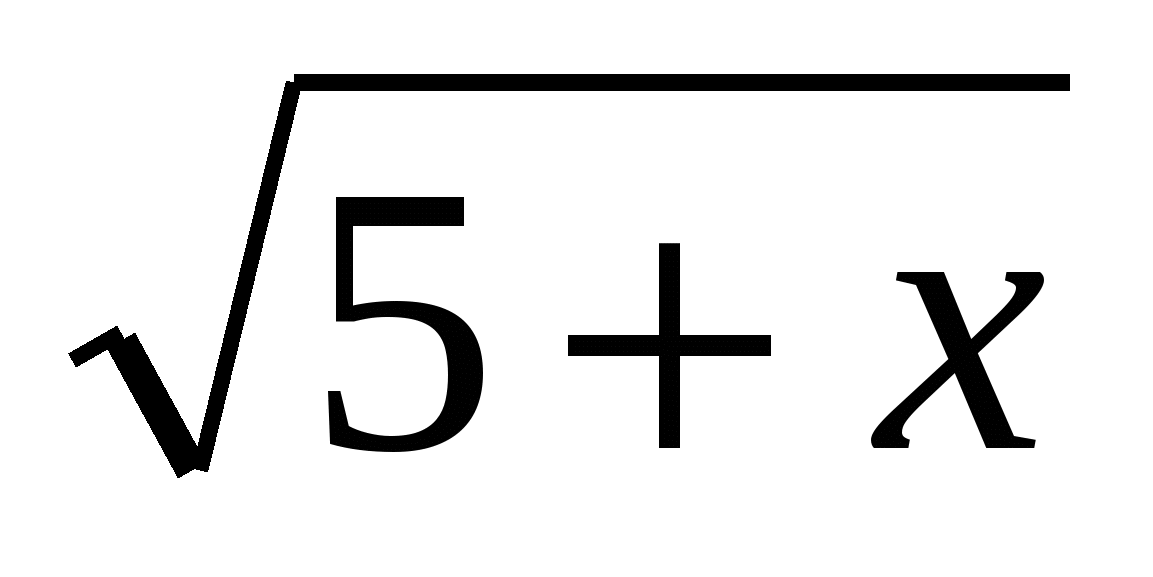 , siis saab meie võrrandit esitada funktsionaalsena
f(
f(….
f(
x)…))=
x.
Kuna x jaoks>
0 funktsioonf(x)=
suureneb jaf(x)
>
0, siis on võrrand x= võrdne võrrandigaf(x)=
x, st.
\u003d x, mille positiivne lahend on x \u003d
, siis saab meie võrrandit esitada funktsionaalsena
f(
f(….
f(
x)…))=
x.
Kuna x jaoks>
0 funktsioonf(x)=
suureneb jaf(x)
>
0, siis on võrrand x= võrdne võrrandigaf(x)=
x, st.
\u003d x, mille positiivne lahend on x \u003d  Vastus: x=
Vastus: x=
Valmistas ja viis läbi matemaatikaõpetaja
MKOU "Keskkool nr 1", Povorino
Kartashova S. A.
2014. aasta
Tunni teema:"Võrrandite lahendamine mittestandardsed meetodid, kasutades funktsioonide omadusi"
Tunni vormiks on loeng, millele järgneb tugevdus. Mõeldud 2 õppetunni jaoks
(Slaid nr 1)
Tunni eesmärgid:
Korrake ja tehke kokkuvõte teadmisi teemal: "Funktsioonide omadused"
Õppige rakendama võrrandite lahendamise funktsionaalset meetodit
Arendada loogiline mõtlemine, vaatlus
Kasvatada aktiivsust, loomingulist algatust.
(slaid number 2)
Varustus: interaktiivne tahvel, esitlusega arvuti.
Tunniplaan:
Aja organiseerimine.
Motivatsioon õppetegevused(teema sõnum, tunni eesmärgid).
Põhiteadmiste aktualiseerimine (põhifunktsioonide omaduste kordamine).
Uue materjali õppimine (funktsionaalne meetod võrrandite lahendamiseks).
Teadmiste kinnistamine (harjutuste lahendamine).
Kokkuvõtteid tehes. Hinnangud.
Tundide ajal.
Õpetaja:
Enamiku eksamitel esinevate võrrandite lahendamiseks piisab kooli matemaatikakursuse valdamisest, kuid samal ajal on vaja osata lahendada mitte ainult standardsete tehnikate abil, mis on mõeldud täielikult teatud tüübid võrrandid, aga ka "mittestandardsed" meetodid, millest täna tunnis räägime. Üks sellistest võrrandite lahendamise meetoditest on funktsionaalne, mis põhineb funktsioonide omaduste kasutamisel. Erinevalt graafiline meetod, funktsioonide omaduste tundmine võimaldab teil leida võrrandi täpsed juured, ilma et oleks vaja funktsioonigraafikuid joonistada. Funktsioonide omaduste kasutamine aitab kaasa võrrandite lahendi ratsionaliseerimisele.
(slaid number 3)
Vastame küsimustele:
Mis on võrrand?
Mis on võrrandi juur?
Mida tähendab võrrandi lahendamine?
Mida nimetatakse funktsiooniks?
Mis on funktsiooni ulatus?
Mis on funktsiooni ulatus?
(slaid number 4)
Kaaluge(slaid number 5)
NÄIDE 1. Lahenda võrrand:
Lahendus: ODZ:
Vastus: Lahendusi pole.
(slaid number 6)
NÄIDE 2. Lahenda võrrand:
Lahendus: ODZ:
ODZ koosneb ühest punktist x=1. Jääb üle kontrollida, kas x=1 on võrrandi juur. Asendades näeme, et x=1 on võrrandi juur.
Vastus: x=1.
Õpetaja:
Mõnikord osutub piisavaks, kui võtta arvesse mitte funktsiooni kogu domeeni, vaid ainult selle alamhulka, millel funktsioon võtab teatud tingimustele vastavad väärtused (näiteks ainult mittenegatiivsed väärtused).
(slaid nr. 7 )
NÄIDE 3.
Otsus. Leiame võrrandi parem- ja vasakpoolses osas funktsioonide definitsioonide domeenide ristumiskoha:
D 1
Piirame komplektiD, arvestades, et võrrandi vasak pool on mittenegatiivne ja seetõttu peaks sama olema parem osa Yu Selleks võtke arvesse kogumi ristumiskohtaDpaljude lahendustega ebavõrdsusele st paljudega . Seetõttu piisab, kui arvestada hulga võrrandiga .
Asenduse abil tagame, et mõlemad elemendid on võrrandi lahenduseks.
Vastus: -3; 2.
(slaid nr. 8 )
NÄIDE 4.
Otsus.
Võttes arvesse asjaolu, et võrrandi juur on x=4.
Vastus: 4.
Õpetaja:
Liigume võrrandite lahendamise juurde, kasutades funktsiooni vahemiku mõistet.
(slaid nr 9–10)
(slaidi number 11)
NÄIDE 1.
Otsus. Nagu , siis pole võrrandil lahendust.
Vastus: lahendusi pole.
NÄIDE 2.
Otsus. ODZ:
Vastus: lahendusi pole.
Õpetaja:
Kui funktsioon f ( x ) intervallil X on ülalt piiratud ja funktsioon g ( x ) on altpoolt piiratud, siis võrrand f ( x ) = g ( x ) on samaväärne süsteemiga
(slaidi number 12)
NÄIDE 3.
Otsus. A-prioor,
Võrdsus saavutatakse, kui
Lahendame süsteemi esimese võrrandi:
arccos(x-1)=π, x-1=-1, x=0.
Kui x=0, muutub teine võrrand õigeks arvuliseks võrrandiks.
Seetõttu on süsteemi ja selle võrrandi lahend x=0.
Vastus: 0.
(slaid nr 13-14)
NÄIDE 4.
Otsus.
Leiame tuletise abil selle funktsiooni maksimumi intervallilt (2;4).
= 0,
g' + -
g 2 3 4 x
Max
g(3)=2.Meil on
Siis antud võrrand on võrdne süsteemiga
Olles lahendanud süsteemi esimese võrrandi, saame x = 3, kontrollides, asendades teise võrrandiga, veendume, et x = 3 on süsteemi ja selle võrrandi lahend.
Vastus: 3.
(slaidi number 15)
Õpetaja:
Seda meetodit leidub sageli matemaatika eksamil. See meetod seisneb selles, et võrrandi üht osa piirab ülalt teatud arv M ja teist osa võrrandist altpoolt sama arv M. Arvu M nimetatakse tavaliseltmajorant ja see meetod onmajorantne meetod . Peamise meetodi puhul, nagu võis arvata, peate hästi aru saama, mis funktsioon on, suutma uurida funktsioonide omadusi.
(slaid number 16)
Harjutused kinnistamiseks, oskuste ja vilumuste arendamiseks.
Klass jaguneb vastavalt valikuvõimalustele 2 rühma.
1 variant.
Tõesta, et võrrandil pole juuri.
Lahenda võrrandid: Vastus: 2.6.
Vastus: 2.
Õpetaja:
Täna käsitlesime funktsioonide omadusi kasutades mittestandardset võrrandite lahendamise meetodit, mis on rakendatav ka võrratuste lahendamisel, kuid sellest räägime mõnes järgnevas õppetükis.
Kokkuvõtete tegemine, hindamine.
(slaidi number 17)
Kodutöö:
"Funktsiooni ulatus" – määratluse ulatus ruutfunktsioon- ükskõik milline tegelik arv. Funktsiooni nimetatakse logaritmiliseks, kui muutuv seisab logaritmi märgi all. logaritmiline funktsioon. Funktsiooni, mille muutuja on eksponendis, nimetatakse eksponentsiaalseks. Ruutfunktsioon.
"Funktsioonide üldomadused" - Üldised omadused funktsioonid. Leidke funktsiooni ulatus. Ühtlane funktsioon. Kas see funktsioon on paaris või paaritu. Määrake graafikult funktsiooni väärtuste kogum. Määrake graafikult X väärtused. Määrake graafikult funktsiooni kahanemise intervallid. Funktsioon f(x) kasvab. Funktsioon y=f(x) on antud.
"Funktsiooni suurendamine ja vähendamine" – siinusfunktsiooni suurendamine ja vähenemine. Vaatleme veel ühte näidet. Väheneva koosinuse intervallid on lõigud, n on täisarv. Olgu näiteks funktsioon f paaris ja kasvab intervallil , kus b>a?0. Funktsioonide suurendamine ja vähendamine. Koosinusfunktsiooni suurendamine ja vähendamine. Alloleval joonisel on kujutatud lõigul [-1;10] defineeritud funktsiooni graafik.
"Järjepidevuse rakendamine" – väljendi tähendus. geomeetriline tunne tuletis. intervalli meetod. Kirjutage funktsiooni graafiku puutuja võrrand. Funktsiooni graafiku puutuja. Graafik on puutuja lähedal. Valem. Arvutame valemi järgi. Kõvera puutuja antud punktis M on sekanti NM piirasend. Hüperbool.
"Funktsiooni ekstreemum" – gaasi rõhu sõltuvus temperatuurist. Tunni teema: “Kasvamise ja vähenemise märgid. Test. Voolutugevuse muutus vooluringi avamisel. Funktsiooni uurimine äärmuseni”. Muuda vahelduvvoolu. Plaan: Voolutugevuse sõltuvus pingest. Gaasi rõhu sõltuvus mahust. Teema: “Funktsioonide suurenemise ja kahanemise märgid.
"Funktsioonid ja nende omadused" - Sõltumatut muutujat nimetatakse - argument. Funktsiooni suurendamine. Funktsiooni määratlus. Isegi ja veidrad omadused. Funktsiooni monotoonsus. Sõltuva muutuja väärtusi nimetatakse funktsiooni väärtusteks. Kõik sõltumatu muutuja väärtused moodustavad funktsiooni -D (f) domeeni. 1. Funktsiooni väärtused on positiivsed.
Kokku teemas 23 ettekannet
Valikuline tegevus"Piiratud funktsiooni atribuudi rakendamine"
Võrratuste ja võrratustega seotud materjal moodustab kooli matemaatikakursusest olulise osa, kuid tunni ajaraam ei võimalda kõiki küsimusi käsitleda.
Lisaks määratakse põhikooli riikliku standardiga kehtestatud matemaatika õpetamise sisu kohustuslik miinimum. õppematerjal kohustuslikuks arvestamiseks, kuid mitte kohustuslikuks assimilatsiooniks (näiteks ebastandardsed meetodid võrrandite ja võrratuste lahendamiseks, võrrandite ja võrratuste lahendamise meetodid parameetriga jne).
Pidades silmas võrrandite ja võrratuste mõistetega seotud materjali tähtsust ja ulatust, on nende uurimine kaasaegne metoodika matemaatika on organiseeritud sisu-metoodiliseks jooneks – võrrandite ja võrratuste reaks. Selle liini kasutuselevõtuks on kolm peamist suunda koolikursus matemaatika.
Võrrandi ja võrratuste rea rakendatud orientatsioon selgus peamiselt uuringus algebraline meetod lahendusi sõnaülesanded. Tekstülesannete lahendamisel kasutatavate matemaatiliste vahendite põhiosa moodustavad võrrandid ja võrratused.
Teoreetiline ja matemaatiline orientatsioon avaldub kahes aspektis: olulisemate võrrandiklasside, võrratuste ja nende süsteemide uurimisel ning sirgega kui tervikuga seotud üldistatud mõistete ja meetodite uurimisel.
Funktsionaaljoonega on tihedalt seotud ka võrrandite ja võrratuste joon. Ühelt poolt võrrandite ja võrratuste real välja töötatud meetodite rakendamine funktsiooni uurimisel. Seevastu funktsionaaljoon mõjutab oluliselt nii võrrandite ja võrratuste rea sisu kui ka selle uurimisstiili. Eelkõige on funktsionaalsed esitused aluseks graafilise visualiseerimise meelitamisel lahendusele ning võrrandite ja võrratuste uurimisele.
Algebra käigus, mida uurime Mordkovitši toimetuse all, valitakse prioriteediks funktsionaal-graafiline joon. Kogu materjal on üles ehitatud jäiga skeemi järgi: funktsioon-teisendus-võrrand.
Eksamil on üsna sageli ülesandeid, mida lahendatakse funktsioonide omadusi kasutades. Seetõttu on soovitatav see materjal valikkursustele kaasa võtta. Kuid siiski eelistan mõnda neist ülesannetest käsitleda tundides, alates 9. klassist.
Funktsioonide omaduste rakendamine võrrandite ja võrratuste lahendamisel
Piiratud vara kasutamine.
Funktsiooni ulatuse kasutamine.
Funktsioonide monotoonsuse kasutamine võrrandite ja võrratuste lahendamisel.
Funktsiooni ulatuse mõiste kasutamine.
- Kasutades paaris või paaritu omadusi ja funktsioonide perioodilisust.
SLAID 2.
Minu kõne oli ainult üks mittestandardsetest võrrandite ja võrratuste lahendamise meetoditest, mis põhinevad võrrandis sisalduvate funktsioonide (ebavõrdsuse) piiritlemise omadusel. Minu pakutud ülesandeid võib arvestada õpilaste eksamiks ettevalmistamiseks ettenähtud tundides (kolm või neli õppetundi) või kasutada ühte või kahte ülesannet tunni kohta, samuti antud materjal saab kasutada valiktunnis (või valikkursusel).
Juba 9. klassis piirdumise omadust uurides juhin tähelepanu selle omaduse olulisusele ja selle kasutamise võimalusele, kui
Funktsiooni väikseima ja suurima väärtuse leidmine;
Funktsiooni väärtuste hulga leidmine.
SLAID3.
Kaalutakse mõne ülesande lahendusi. Esiteks tuleks põhimääratlusi korrata. SLAID 4.
SLAIDIDEL 5–9 vaadeldakse ülesandeid funktsiooni väikseimate või suurimate väärtuste leidmiseks.
SLAID 10.
Funktsioonide piiritusomaduse rakendamine võrrandite ja võrratuste lahendamisel.
1. MAJORANTNE MEETOD (HINDAMISE MEETOD)
Peamise meetodi põhiidee on järgmine:
Olgu meil võrrand ja selline arv on olemas M, mis mis tahes X määratlusalast https://pandia.ru/text/78/376/images/image003_26.gif" width="160" height="23">. Siis on võrrand samaväärne süsteemiga https://pandia. ru/text/78 /376/images/image005_16.gif" width="96" height="35 src=">.
Otsus. Hindame võrrandi mõlemat poolt.
Kõigi väärtuste jaoks X ebavõrdsused https://pandia.ru/text/78/376/images/image007_10.gif" width="188" height="59 src="> on õiged.
Saadud süsteemil pole lahendusi, kuna https://pandia.ru/text/78/376/images/image009_6.gif" width="20" height="20">
Näide 1.2 ..gif" width="157" height="20">.gif" width="75" height="51 src=">.
Süsteemi esimese võrrandi lahenduseks on väärtused https://pandia.ru/text/78/376/images/image014_3.gif" width="201" height="48 src=">.
Seega ![]() süsteemne lahendus.
süsteemne lahendus.
Vastus: ![]() .
.
Näide 1.3. Lahendage ebavõrdsus https://pandia.ru/text/78/376/images/image016_0.gif" width="56" height="19">.gif" width="84" height="21">.gif " width="156 height=61" height="61">.
Vastupidine asendamine: X + 1 = 0 .
Vastus: - 1.
Näide 1.4. Otsige üles kõik parameetrite väärtused a, millest igaühe jaoks on võrrandil lahendid. Leidke need lahendused.
Otsus.
Kirjutame võrrandi ümber kujul . Kõigi väärtuste jaoks X väljendus ![]() seega https://pandia.ru/text/78/376/images/image026_0.gif" width="87" height="19 src="> ja ..gif" width="405" height="91">
seega https://pandia.ru/text/78/376/images/image026_0.gif" width="87" height="19 src="> ja ..gif" width="405" height="91">
Vastus: https://pandia.ru/text/78/376/images/image031_0.gif" width="51" height="41 src=">
2. "KOHTUMINE SERVAL"
Peamise meetodi variatsioon on ülesanded (“ kohtumine äärel), milles võrrandi või võrratuse vasaku ja parema osa väärtuste komplektidel on kordumatu ühine punkt, mis on ühe osa jaoks suurim ja teise jaoks väikseim väärtus.
Kuidas selliste probleemide lahendamist alustada? Esiteks tuua antud võrrandid või ebavõrdsus rohkem selge nägemine: faktooringuga, moodulitest, logaritmidest jne vabanemisega. Seejärel tuleb ülesanne uuesti hoolikalt läbi lugeda, proovida joonistada ülesandes sisalduvatest funktsioonidest graafiline pilt.
 Näide 2.1.
Lahenda võrrand.
Näide 2.1.
Lahenda võrrand.
Otsus. Võrrandi juurt on lihtne ära arvata – see on nii x= 1. Kuid selle ainulaadsust ei ole võimalik monotoonsuse kaalutlustel tõestada, sest võrrandi vasak ega parem pool ei ole monotoonsed funktsioonid. Siin kasutatakse teist ideed..gif" width="191" height="51">. Saadud võrrandi parempoolse külje suurim väärtus on 1 ja see võetakse punktis x= 1..gif" width="185" height="52 src=">). Seetõttu ulatub vasak pool punktini x= 1 oma väikseim väärtus, mis on samuti võrdne 1-ga. Järeldus: võrdsus on täidetud siis ja ainult siis, kui mõlemad osad on samaaegselt võrdsed 1-ga, st kui x = 1.
Näide 2.2. Lahenda võrrand.
1 viis.
Otsus: Pange tähele, et võrrandi vasak pool ei ületa 1, samas kui parem pool ei ole väiksem kui 1. Seetõttu on algsel võrrandil lahendus ainult siis, kui mõlemad pooled on võrdsed ühega. See on võimalik ainult .
Vastus: .
2 moodi. Seda võrrandit saab lahendada graafiliselt. Selleks koostame võrrandi parema ja vasakpoolse osa graafikud samas koordinaatsüsteemis ehk funktsioonigraafiku ja funktsioonigraafiku https://pandia.ru/text/78/376/images/image008_7 .gif" width="37" height=" 19">.
Vastus: .
Näide 2. 3. Lahendage võrrand https://pandia.ru/text/78/376/images/image042_0.gif" width="301" height="35 src=">
siis see võrrand on täidetud ainult siis, kui süsteem  . Süsteemi esimesel võrrandil on üks juur X= 1, kuid see juur ei rahulda teist võrrandit. Seetõttu pole süsteemil lahendusi.
. Süsteemi esimesel võrrandil on üks juur X= 1, kuid see juur ei rahulda teist võrrandit. Seetõttu pole süsteemil lahendusi.
Vastus: Æ
Näide 2.4. Lahendage võrrand https://pandia.ru/text/78/376/images/image045_0.gif" width="105" height="21">, siis võrrandi vasak pool võtab väärtuse vahemikust 2-ni. gif" width=" 137" height="53">..gif" width="217" height="24"> pakub lahendust.
Otsus.
 |
Hinnakem ebavõrdsuse mõlemat poolt. Selleks teisendame võrratuse parema poole, valides täisruudu ..gif" width="71" height="19">.gif" width="121" height="24 src=">.gif " width="51" height ="41">(see tähendab, et toimub "kohtumine äärel").
Vastus:
Näide 2.6. Otsige üles kõik parameetrite väärtused a mille alusel võrrand
Galaeva Jekaterina, Nižni Novgorodi MAOU 149. keskkooli 11. klassi õpilane
Töö on nii rakendusliku kui ka teadusliku iseloomuga. Täielikkuse huvides käsitleti uuringus järgmised küsimused:
– Kuidas kajastuvad funktsiooni omadused võrrandite ja võrratuste lahendamisel?
– Milliseid võrrandeid ja võrratusi lahendatakse definitsioonivaldkonna, väärtuste hulga, muutumatuse omaduste määratlemise kaudu?
– Mis on lahendusalgoritm?
- Arvestati eksamiks valmistumisel KIM materjalides pakutud parameetriga ülesandeid.
Ekaterina uuris oma töös väga erinevaid ülesandeid ja süstematiseeris need vastavalt välimus.
Lae alla:
Eelvaade:
https://accounts.google.com
Slaidide pealdised:
Lahenda ebavõrdsus Lahendus. Funktsioon f (x) = suureneb monotoonselt kogu reaaljoonel ja funktsioon g (x) = väheneb monotoonselt kogu definitsioonipiirkonna ulatuses. Seetõttu on võrratus f (x) > g (x) täidetud, kui x >
Täname tähelepanu eest!
Eelvaade:
Esitluste eelvaate kasutamiseks looge Google'i konto (konto) ja logige sisse: https://accounts.google.com
Slaidide pealdised:
Funktsiooni omaduste rakendamine võrrandite ja võrratuste lahendamisel Töö lõpetas: Galaeva Jekaterina Moskovski rajooni MBOU keskkool nr 149 11 "A" klassi õpilased Juhendaja: Fadejeva I. A. Matemaatikaõpetaja
Põhisuunad: Funktsiooni omaduste uurimine: monotoonsus, piiritus, määratluspiirkond ja invariantsus Õppige tundma põhiväiteid, mida võrrandite, võrratuste ja süsteemide lahendamisel kõige sagedamini kasutatakse Ülesannete lahendamine KIM materjalidest eksamiks valmistumisel
Monotoonsus Funktsioon suureneb, kui suurem väärtus argument vastab funktsiooni suuremale väärtusele. Funktsioon väheneb, kui argumendi suurem väärtus vastab funktsiooni väiksemale väärtusele. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Väide 1. Kui funktsioon y \u003d f (x) on monotoonne, on võrrandil f (x) \u003d c kõige rohkem üks juur. x =2 f(x) = - monotoonselt kahanev, seega teisi lahendeid pole. Vastus: x=2
Väide 2. Kui funktsioon y \u003d f (x) kasvab monotoonselt ja funktsioon y \u003d g (x) väheneb monotoonselt, siis on võrrandil f (x) \u003d g (x) kõige rohkem üks juur. 2 - x \u003d lg (x + 11) + 1 g (x) \u003d 2 - x väheneb monotoonselt ja funktsioon f (x) \u003d log (x + 11) + 1 suureneb domeenis monotoonselt, mis tähendab, et võrrandil f (x ) = g (x) on kõige rohkem üks juur. Valikuga määrame, et x \u003d -1. Ülaltoodud väide kinnitab lahenduse unikaalsust.
a) f (x) ≤ g (x) siis ja ainult siis, kui x ϵ (- ∞ ; x 0 ]; b) f (x) ≥ g (x) siis ja ainult siis, kui x ϵ [x 0; +∞). Selle väite visuaalne tähendus on ilmne. Väide 3. Kui funktsioon y \u003d f (x) kasvab monotoonselt kogu reaalreal, siis funktsioon y \u003d g (x) väheneb monotoonselt kogu reaalreal ja f (x 0) \u003d g (x 0), siis on tõesed järgmised väited:
Lahenda ebavõrdsus Lahendus. Funktsioon f (x) = suureneb monotoonselt kogu reaaljoonel ja funktsioon g (x) = väheneb monotoonselt kogu definitsioonipiirkonna ulatuses. Seetõttu on võrratus f (x) > g (x) täidetud, kui x > 2. Liidame võrratuse domeeni. Seega saame süsteemi Vastus: (2; 5).
Väide 4. Kui funktsioon y \u003d f (x) on monotoonselt kasvav, on võrranditel f (x) \u003d x ja f (f (x)) \u003d x sama juurte hulk, sõltumata nende arvust. investeeringuid. Tagajärg. Kui n on naturaalarv ja funktsioon y \u003d f (x) kasvab monotoonselt, on võrranditel f (x) \u003d x ja n korda sama juurte komplekt.
Lahenda võrrand. Vastus: Otsus. Kui x ≥1, ei ole võrrandi parem pool väiksem kui 1 ja vasak pool väiksem kui 1. Seega, kui võrrandil on juured, siis mis tahes neist on väiksem kui 1. Kui x ≤0 on parempoolne võrrandi pool on mittepositiivne ja vasak pool on positiivne, kuna . Seega kuulub selle võrrandi mis tahes juur vahemikku (0; 1) Korrutades selle võrrandi mõlemad pooled x-ga ning jagades vasaku poole lugeja ja nimetaja x-ga, saame
Kus =. Tähistades läbi t, kus t 0, saame võrrandi = t. Vaatleme funktsiooni f (t)= 1+, mis kasvab selle definitsioonipiirkonnas. Saadud võrrandi saab kirjutada kujul f (f (f (f (t))))= t ja väite 4 järelduvalt on sellel sama lahendite hulk, mis võrrandil f (t)= t, s.t. võrrand 1 + = t, kust. ainuke positiivne juur selle ruutsuuruse võrrandi suhtes on. Niisiis, kus, st. , või. Vastus:
Väide 1. Kui max f (x) = c ja min g (x) = c, siis võrrandil f (x) = g (x) on sama lahendite hulk kui süsteemil Piiratus Vasaku külje maksimaalne väärtus on 1 ja minimaalne väärtus parem pool 1 , mis tähendab, et võrrandi lahend taandatakse võrrandisüsteemiks: , teisest võrrandist leiame võimaliku kandidaadi x=0 ja veendume, et see on esimese võrrandi lahend. Vastus: x=1 .
Lahenda võrrand Lahendus. Kuna sin3x≤1 ja cos4x≤1, ei ületa selle võrrandi vasak pool 7. See võib olla võrdne 7-ga siis ja ainult siis, kust k , n ϵ Z . Jääb üle kindlaks teha, kas on olemas täisarvud k ja n, mis uusim süsteem on lahendused. Vastus: Z
Tundmatu x ja parameetri a probleemide korral mõistetakse definitsioonipiirkonda kõigi järjestatud arvupaaride kogumit (x ; a), millest igaüks on selline, et pärast x ja a vastavate väärtuste asendamist kõikidesse suhetesse probleemi hulka kuuluvad, tehakse need kindlaks. Näide 1. Parameetri a iga väärtuse jaoks lahendage võrratus Lahendus. Leiame selle ebavõrdsuse definitsioonipiirkonna. Millest on selge, et süsteemil pole lahendusi. See tähendab, et võrratuse definitsioonipiirkond ei sisalda ühtegi arvu x ja a paari ning seetõttu pole võrratusel ka lahendeid. Reguleerimisala vastus:
Invariantsus, s.o. võrrandi invariantsus või ebavõrdsus muutuja asendamise suhtes mõnega algebraline avaldis sellest muutujast. Lihtsaim invariantsi näide on paarsus: kui − ühtlane funktsioon, siis on võrrand muutumatu x ja – x muutuse all, kuna = 0. Invariantsus
Leia võrrandi juured. Otsus. Pange tähele, et paar on asendamisel muutumatu. Asendades võrdsusega, saame. Korrutades selle võrdsuse mõlemad pooled 2-ga ja lahutades saadud võrdsusest võrdusliikmete kaupa, leiame 3, kust. Nüüd jääb üle lahendada võrrand, kust võrrandi juurteks on arvud. Vastus:.
Leidke kõik a väärtused, millest igaühe jaoks on võrrandil rohkem kui kolm erinevaid lahendusi. Probleemide lahendamine omaduse parameetriga Monotoonilisus
|x|= positiivne X= |x|= Kahe juure olemasoluks peab lugeja olema positiivne. Seega, kui esimese ja teise võrrandi juured langevad kokku, mis ei vasta tingimuse nõudele: rohkem kui kolme juure olemasolu. Vastus:.
Leidke kõik a väärtused, millest igaühe jaoks on võrrandil kaks juurt. Teisendame võrrandi vormiks JA käsitleme funktsiooni f(x)= defineeritud ja pidevana kogu reaaljoonel. Selle funktsiooni graafik on katkendlik joon, mis koosneb joonelõikudest ja kiirtest, mille iga lüli on osa sirgest kujul y= kt+l . f(x)= Esimese avaldise mooduli mis tahes laienduse korral k ei ületa 8, seega sõltub funktsiooni f(x) suurenemine ja vähenemine teise mooduli laiendusest. Punktis x f(x) väheneb ja x juures suureneb. See tähendab, et x=3 puhul võtab funktsioon kasutusele kõrgeim väärtus. Selleks, et võrrandil oleks kaks juurt, on vajalik f(3) monotoonsuse omadus
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Vastus: a
Leia kõik parameetri a väärtused, millest igaühe puhul on mis tahes reaalväärtuse x korral ebavõrdsus täidetud. Kirjutame võrratuse ümber kujul, võtame kasutusele uue muutuja t = ja vaatleme funktsiooni f (t) = , määratletud ja pidev kogu reaaljoonel. Selle funktsiooni graafik on katkendlik joon, mis koosneb joonelõikudest ja kiirtest, mille iga lüli on osa sirgest, kuhu
Kuna, siis t ϵ [-1; üks]. Funktsiooni y = f (t) monotoonse vähenemise tõttu piisab selle lõigu vasaku serva kontrollimisest. Z. A on tõene Tähendab, et see on võimalik ainult siis, kui arvudel u ja v on sama märk või mõni neist on võrdne nulliga. , = () () 0. Ruuttrinoomide faktoristamisel saame võrratuse (, millest leiame, et a ϵ (-∞; -1] U (2) U [ 4; +∞). Vastus: (-∞ ; -1]U(2)U)
 Infomaterjal "noore lugejanurk"
Infomaterjal "noore lugejanurk" Arst, kes on hävitamisest kaugel
Arst, kes on hävitamisest kaugel Kust osta väävelhapet?
Kust osta väävelhapet?