De oppervlakte van een driehoek is de stelling van Pythagoras. Verschillende manieren om de stelling van Pythagoras te bewijzen: voorbeelden, beschrijving en beoordelingen
Toen je voor het eerst vierkantswortels begon te leren en op te lossen irrationele vergelijkingen(gelijkheden met het onbekende onder het wortelteken), je hebt waarschijnlijk het eerste idee erover praktisch gebruik. Het vermogen om te extraheren Vierkantswortel van getallen is ook nodig voor het oplossen van problemen bij de toepassing van de stelling van Pythagoras. Deze stelling betreft de lengtes van de zijden van een rechthoekige driehoek.
Laat de lengtes van de benen van een rechthoekige driehoek (die twee zijden die in een rechte hoek samenkomen) worden aangegeven met de letters en , en de lengte van de hypotenusa (de langste zijde van de driehoek tegenover juiste hoek) wordt aangegeven met de letter . Dan worden de corresponderende lengtes gerelateerd door de volgende relatie:
Met deze vergelijking kun je de lengte van een zijde van een rechthoekige driehoek vinden in het geval dat de lengte van de andere twee zijden bekend is. Bovendien kunt u hiermee bepalen of de beschouwde driehoek een rechthoekige driehoek is, op voorwaarde dat de lengtes van alle drie kanten vooraf bekend.
Problemen oplossen met behulp van de stelling van Pythagoras
Om het materiaal te consolideren, zullen we de volgende problemen oplossen voor de toepassing van de stelling van Pythagoras.

Dus gegeven:
- De lengte van een van de benen is 48, de hypotenusa is 80.
- De lengte van het been is 84, de hypotenusa is 91.
Laten we naar de oplossing gaan:
a) Vervanging van de gegevens in de bovenstaande vergelijking geeft de volgende resultaten:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 of b = -64
Omdat de lengte van een zijde van een driehoek niet kan worden uitgedrukt negatief nummer, wordt de tweede optie automatisch weggegooid.
Antwoord op de eerste foto: b = 64.
b) De lengte van het been van de tweede driehoek wordt op dezelfde manier gevonden:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 of b = -35
Net als in het vorige geval wordt de negatieve oplossing weggegooid.
Antwoord op de tweede foto: b = 35

Wij zijn gegeven:
- De lengtes van de kleinere zijden van de driehoek zijn respectievelijk 45 en 55, en de grotere zijn 75.
- De lengtes van de kleinere zijden van de driehoek zijn respectievelijk 28 en 45, en de grotere zijn 53.
Wij lossen het probleem op:
a) Het is noodzakelijk om te controleren of de som van de kwadraten van de lengtes van de kleinere zijden van een gegeven driehoek gelijk is aan het kwadraat van de lengte van de grotere:
45 2 + 55 2 = 2025 + 3025 = 5050
Daarom is de eerste driehoek geen rechthoekige driehoek.
b) Dezelfde bewerking wordt uitgevoerd:
28 2 + 45 2 = 784 + 2025 = 2809
Daarom is de tweede driehoek een rechthoekige driehoek.
Eerst vinden we de lengte langste segment, gevormd door punten met coördinaten (-2, -3) en (5, -2). Hiervoor gebruiken we bekende formule om de afstand tussen punten in te vinden rechthoekig systeem coördinaten:
Op dezelfde manier vinden we de lengte van het segment tussen de punten met coördinaten (-2, -3) en (2, 1):
Ten slotte bepalen we de lengte van het segment tussen punten met coördinaten (2, 1) en (5, -2):
Aangezien er een gelijkheid is:
dan is de corresponderende driehoek een rechthoekige driehoek.
We kunnen dus het antwoord op het probleem formuleren: aangezien de som van de kwadraten van de zijden met de kleinste lengte gelijk is aan het kwadraat van de zijde met grootste lengte, zijn de punten de hoekpunten van een rechthoekige driehoek.
De basis (strikt horizontaal geplaatst), de stijl (strikt verticaal geplaatst) en de kabel (diagonaal uitgerekt) vormen respectievelijk een rechthoekige driehoek, de stelling van Pythagoras kan worden gebruikt om de lengte van de kabel te vinden:
De lengte van de kabel zal dus ongeveer 3,6 meter zijn.
Gegeven: de afstand van punt R tot punt P (het been van de driehoek) is 24, van punt R tot punt Q (hypotenusa) - 26.
Dus helpen we Vitya het probleem op te lossen. Aangezien de zijden van de in de figuur getoonde driehoek een rechthoekige driehoek vormen, kun je de stelling van Pythagoras gebruiken om de lengte van de derde zijde te bepalen:
De breedte van de vijver is dus 10 meter.
Sergey Valerievich
de stelling van Pythagoras
de stelling van Pythagoras- een van de fundamentele stellingen van de Euclidische meetkunde, die de relatie tot stand brengt
tussen de zijden van een rechthoekige driehoek.
Er wordt aangenomen dat het werd bewezen door de Griekse wiskundige Pythagoras, naar wie het is vernoemd.
Geometrische formulering van de stelling van Pythagoras.
De stelling was oorspronkelijk als volgt geformuleerd:
In een rechthoekige driehoek is de oppervlakte van het vierkant gebouwd op de hypotenusa gelijk aan de som van de oppervlakten van de vierkanten,
gebouwd op katheters.
Algebraïsche formulering van de stelling van Pythagoras.
In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa gelijk aan de som van de kwadraten van de lengtes van de benen.
Dat wil zeggen, ter aanduiding van de lengte van de hypotenusa van de driehoek door c, en de lengtes van de benen door a en b:
Beide formuleringen stellingen van pythagoras gelijkwaardig zijn, maar de tweede formulering is meer elementair, niet
vereist het begrip gebied. Dat wil zeggen, de tweede verklaring kan worden geverifieerd zonder iets over het gebied te weten en
door alleen de lengtes van de zijden van een rechthoekige driehoek te meten.
De inverse stelling van Pythagoras.
Als het kwadraat van een zijde van een driehoek gelijk is aan de som van de kwadraten van de andere twee zijden, dan
driehoek is rechthoekig.
Of met andere woorden:
Voor elk drietal positieve getallen a, b en c, zoals dat
er is een rechthoekige driehoek met benen a en b en hypotenusa c.
De stelling van Pythagoras voor een gelijkbenige driehoek.

Stelling van Pythagoras voor een gelijkzijdige driehoek.

Bewijzen van de stelling van Pythagoras.
Op dit moment zijn er 367 bewijzen van deze stelling opgenomen in de wetenschappelijke literatuur. Waarschijnlijk de stelling
Pythagoras is de enige stelling met zo'n indrukwekkend aantal bewijzen. zo'n diversiteit
kan alleen worden verklaard door de fundamentele betekenis van de stelling voor de meetkunde.
Natuurlijk kunnen ze conceptueel allemaal worden onderverdeeld in een klein aantal klassen. De meest bekende van hen:
bewijs van gebiedsmethode:, axiomatisch en exotisch bewijs(Bijvoorbeeld,
via differentiaalvergelijkingen).
1. Bewijs van de stelling van Pythagoras in termen van gelijkaardige driehoeken.
Het volgende bewijs van de algebraïsche formulering is het eenvoudigste van de geconstrueerde bewijzen:
rechtstreeks uit de axioma's. Het maakt met name geen gebruik van het concept van het gebied van een figuur.
laten zijn abc er is een rechthoekige driehoek C. Laten we een hoogte tekenen vanaf C en duiden op
zijn basis door H.
Driehoek ACH gelijk aan een driehoek AB C op twee hoeken. Evenzo, de driehoek CBH vergelijkbaar abc.
Door de notatie in te voeren:

we krijgen:
![]() ,
,
welke overeenkomt -
hebben gevouwen a 2 en b 2 krijgen we:
of , die moest worden bewezen.
2. Bewijs van de stelling van Pythagoras door de oppervlaktemethode.
De volgende bewijzen zijn, ondanks hun schijnbare eenvoud, helemaal niet zo eenvoudig. Allemaal
gebruik de eigenschappen van het gebied, waarvan het bewijs ingewikkelder is dan het bewijs van de stelling van Pythagoras zelf.
- Bewijs door equicomplementatie.
 Schik vier gelijke rechthoekige
Schik vier gelijke rechthoekige
driehoek zoals weergegeven in de afbeelding:
rechts.
Vierhoek met zijden c- plein,
aangezien de som van twee scherpe hoeken 90° is, en
de ontwikkelde hoek is 180°.
Het gebied van de hele figuur is enerzijds
oppervlakte van een vierkant met zijde ( a+b), en aan de andere kant, de som van de gebieden vier driehoeken en
![]()
![]()
QED
3. Bewijs van de stelling van Pythagoras door de oneindig kleine methode.

Gezien de tekening in de figuur, en
de kant zien veranderena, we kunnen
schrijf de volgende relatie voor oneindig
klein zijwaartse verhogingenmet en a(overeenkomst gebruiken)
driehoeken):
Met behulp van de methode van scheiding van variabelen vinden we:
Een meer algemene uitdrukking voor het veranderen van de hypotenusa in het geval van verhogingen van beide benen:
Integreren gegeven vergelijking en met behulp van de beginvoorwaarden krijgen we:
Zo komen we tot het gewenste antwoord:
Zoals het gemakkelijk te zien is, verschijnt de kwadratische afhankelijkheid in de uiteindelijke formule als gevolg van de lineaire
evenredigheid tussen de zijden van de driehoek en de incrementen, terwijl de som gerelateerd is aan de onafhankelijke
bijdragen van de increment van verschillende benen.
Een eenvoudiger bewijs kan worden verkregen als we aannemen dat een van de benen geen toename ervaart
(in deze zaak been b). Dan krijgen we voor de integratieconstante:
(volgens Papyrus 6619 van het Berlijnse Museum). Volgens Cantor bouwden harpedonapts, of "snaarspanners", rechte hoeken met behulp van rechthoekige driehoeken met zijden 3, 4 en 5.
Het is heel gemakkelijk om hun constructiemethode te reproduceren. Laten we een touw van 12 m lang nemen en het eraan vastbinden langs een gekleurde strook op een afstand van 3 m van het ene uiteinde en 4 meter van het andere. Tussen zijden van 3 en 4 meter lang wordt een rechte hoek ingesloten. Tegen de Harpedonapts zou kunnen worden ingebracht dat hun bouwmethode overbodig wordt als bijvoorbeeld het houten vierkant wordt gebruikt dat door alle timmerlieden wordt gebruikt. Er zijn inderdaad Egyptische tekeningen bekend waarin zo'n gereedschap wordt gevonden - bijvoorbeeld tekeningen van een timmerwerkplaats.
Er is wat meer bekend over de stelling van Pythagoras onder de Babyloniërs. In één tekst die teruggaat tot de tijd van Hammurabi, dat wil zeggen tot 2000 voor Christus. e. , wordt een benaderende berekening van de hypotenusa van een rechthoekige driehoek gegeven. Hieruit kunnen we concluderen dat ze in Mesopotamië in staat waren om berekeningen uit te voeren met rechthoekige driehoeken, althans in sommige gevallen. Op basis van enerzijds het huidige kennisniveau van de Egyptische en Babylonische wiskunde en anderzijds een kritische studie van Griekse bronnen concludeerde Van der Waerden (een Nederlandse wiskundige) dat de kans groot was dat de hypotenusa vierkante stelling was al bekend in India rond de 18e eeuw voor Christus. e.
Rond 400 voor Christus. e., volgens Proclus, Plato gaf een methode voor het vinden van Pythagoras triples, het combineren van algebra en geometrie. Rond 300 voor Christus. e. De elementen van Euclides bevatten het oudste axiomatische bewijs van de stelling van Pythagoras.
formulering
Geometrische formulering:
De stelling was oorspronkelijk als volgt geformuleerd:
Algebraïsche formulering:
Dat wil zeggen, aanduiding van de lengte van de hypotenusa van de driehoek door, en de lengte van de benen door en:
Beide formuleringen van de stelling zijn equivalent, maar de tweede formulering is meer elementair en vereist niet het concept van oppervlakte. Dat wil zeggen, de tweede verklaring kan worden geverifieerd zonder iets over het gebied te weten en door alleen de lengtes van de zijden van een rechthoekige driehoek te meten.
Inverse stelling van Pythagoras:
Bewijs van
Op dit moment zijn er 367 bewijzen van deze stelling opgenomen in de wetenschappelijke literatuur. Waarschijnlijk is de stelling van Pythagoras de enige stelling met zo'n indrukwekkend aantal bewijzen. Een dergelijke variëteit kan alleen worden verklaard door de fundamentele betekenis van de stelling voor de meetkunde.
Natuurlijk kunnen ze conceptueel allemaal worden onderverdeeld in een klein aantal klassen. De bekendste daarvan: bewijzen met de oppervlaktemethode, axiomatische en exotische bewijzen (bijvoorbeeld met behulp van differentiaalvergelijkingen).
Door gelijkaardige driehoeken
Het volgende bewijs van de algebraïsche formulering is het eenvoudigste bewijs dat rechtstreeks uit de axioma's is opgebouwd. Het maakt met name geen gebruik van het concept van figuurgebied.

laten zijn abc er is een rechthoekige driehoek C. Laten we een hoogte tekenen vanaf C en geef de basis aan met H. Driehoek ACH gelijk aan een driehoek abc op twee hoeken. Evenzo, de driehoek CBH vergelijkbaar abc. Introductie van de notatie
we krijgen
Wat is equivalent?
Toevoegen, we krijgen
, dat moest worden bewezenGebiedsbewijzen
De volgende bewijzen zijn, ondanks hun schijnbare eenvoud, helemaal niet zo eenvoudig. Ze gebruiken allemaal de eigenschappen van het gebied, waarvan het bewijs ingewikkelder is dan het bewijs van de stelling van Pythagoras zelf.
Bewijs via gelijkwaardigheid
- Schik vier gelijke rechthoekige driehoeken zoals weergegeven in figuur 1.
- Vierhoek met zijden c is een vierkant omdat de som van twee scherpe hoeken 90° is en de gestrekte hoek 180° is.
- De oppervlakte van de hele figuur is enerzijds gelijk aan de oppervlakte van een vierkant met een zijde (a + b), en anderzijds de som van de oppervlakten van vier driehoeken en de oppervlakte van het binnenplein.
QED
Het bewijs van Euclides
Het idee van het bewijs van Euclides is als volgt: laten we proberen te bewijzen dat de helft van het gebied van het vierkant gebouwd op de hypotenusa gelijk is aan de som van de halve gebieden van de vierkanten die op de benen zijn gebouwd, en dan de gebieden van de grote en twee kleine vierkanten zijn gelijk.
Beschouw de tekening hiernaast. Daarop bouwden we vierkanten aan de zijkanten van een rechthoekige driehoek en trokken een straal s van het hoekpunt van rechte hoek C loodrecht op de hypotenusa AB, het snijdt het vierkant ABIK, gebouwd op de hypotenusa, in twee rechthoeken - BHJI en HAKJ, respectievelijk. Het blijkt dat de oppervlakten van deze rechthoeken exact gelijk zijn aan de oppervlakten van de vierkanten die op de corresponderende poten zijn gebouwd.
Laten we proberen te bewijzen dat de oppervlakte van het vierkant DECA gelijk is aan de oppervlakte van de rechthoek AHJK. Hiervoor gebruiken we een hulpobservatie: De oppervlakte van een driehoek met dezelfde hoogte en basis als de gegeven rechthoek gelijk is aan de helft van de oppervlakte van de gegeven rechthoek. Dit is een gevolg van het definiëren van het gebied van een driehoek als de helft van het product van de basis en de hoogte. Uit deze waarneming volgt dat de oppervlakte van driehoek ACK gelijk is aan de oppervlakte van driehoek AHK (niet getoond), die op zijn beurt gelijk is aan de helft van de oppervlakte van rechthoek AHJK.
Laten we nu bewijzen dat de oppervlakte van driehoek ACK ook gelijk is aan de helft van de oppervlakte van vierkante DECA. Het enige dat hiervoor moet worden gedaan, is de gelijkheid van driehoeken ACK en BDA bewijzen (aangezien de oppervlakte van driehoek BDA gelijk is aan de helft van de oppervlakte van het vierkant door de bovenstaande eigenschap). Deze gelijkheid is duidelijk: driehoeken zijn gelijk in twee zijden en de hoek ertussen. Namelijk - AB=AK, AD=AC - de gelijkheid van hoeken CAK en BAD is eenvoudig te bewijzen door de bewegingsmethode: laten we de driehoek CAK 90 ° tegen de klok in draaien, dan is het duidelijk dat de overeenkomstige zijden van de twee beschouwde driehoeken zullen samenvallen (vanwege het feit dat de hoek op het hoekpunt van het vierkant 90° is).
Het argument over de gelijkheid van de oppervlakten van het vierkant BCFG en de rechthoek BHJI is volledig analoog.
We hebben dus bewezen dat de oppervlakte van het vierkant gebouwd op de hypotenusa de som is van de gebieden van de vierkanten die op de poten zijn gebouwd. Idee dit bewijs verder geïllustreerd met de animatie hierboven.
Bewijs van Leonardo da Vinci
De belangrijkste elementen van het bewijs zijn symmetrie en beweging.
Beschouw de tekening, zoals te zien is aan de symmetrie, het segment snijdt het vierkant in twee identieke delen (aangezien de driehoeken gelijk zijn in constructie).
Bij een rotatie tegen de klok in van 90 graden rond het punt zien we de gelijkheid van de gearceerde figuren en .
Nu is het duidelijk dat de oppervlakte van de figuur die we gearceerd hebben gelijk is aan de som van de helft van de oppervlakten van de kleine vierkantjes (gebouwd op de poten) en de oppervlakte van de originele driehoek. Aan de andere kant is het gelijk aan de helft van het gebied van het grote vierkant (gebouwd op de hypotenusa) plus het gebied van de oorspronkelijke driehoek. Dus de helft van de oppervlakten van de kleine vierkanten is gelijk aan de helft van de oppervlakte van het grote vierkant, en daarom is de som van de oppervlakten van de vierkanten die op de poten zijn gebouwd gelijk aan de oppervlakte van het gebouwde vierkant op de hypotenusa.
Bewijs met de oneindig kleine methode
Het volgende bewijs door middel van differentiaalvergelijkingen wordt vaak toegeschreven aan de bekende Engelse wiskundige Hardy, die leefde in de eerste helft van de 20e eeuw.
Gezien de tekening in de afbeelding en het observeren van de verandering in zijde: a, kunnen we de volgende relatie schrijven voor oneindig kleine zijincrementen: met en a(met gelijkaardige driehoeken):
Met behulp van de methode van scheiding van variabelen, vinden we:
Een meer algemene uitdrukking voor het veranderen van de hypotenusa in het geval van verhogingen van beide benen
Door deze vergelijking te integreren en de beginvoorwaarden te gebruiken, verkrijgen we:
Zo komen we tot het gewenste antwoord
Het is gemakkelijk in te zien dat de kwadratische afhankelijkheid in de uiteindelijke formule wordt veroorzaakt door de lineaire evenredigheid tussen de zijden van de driehoek en de toenames, terwijl de som het gevolg is van de onafhankelijke bijdragen van de toename van verschillende benen.
Een eenvoudiger bewijs kan worden verkregen als we aannemen dat een van de benen geen toename ervaart (in dit geval het been). Dan krijgen we voor de integratieconstante
Variaties en generalisaties
Gelijkaardige geometrische vormen aan drie zijden
generalisatie voor gelijkaardige driehoeken, oppervlakte van groene cijfers A + B = oppervlakte van blauwe C
Stelling van Pythagoras met gelijkaardige rechthoekige driehoeken
Euclides maakte in zijn werk een generalisatie van de stelling van Pythagoras begin, het uitbreiden van de gebieden van de vierkanten aan de zijkanten naar de gebieden van soortgelijke geometrische vormen :
Als we vergelijkbare geometrische figuren (zie Euclidische meetkunde) construeren aan de zijden van een rechthoekige driehoek, dan is de som van de twee kleinere figuren gelijk aan de oppervlakte van de grotere figuur.
Het belangrijkste idee van deze generalisatie is dat het gebied van een dergelijke geometrische figuur evenredig is met het kwadraat van een van zijn lineaire afmetingen en in het bijzonder met het kwadraat van de lengte van elke zijde. Daarom, voor vergelijkbare figuren met gebieden EEN, B en C gebouwd op zijkanten met lengte a, b en c, we hebben:
Maar volgens de stelling van Pythagoras, a 2 + b 2 = c 2, dan EEN + B = C.
Omgekeerd, als we kunnen bewijzen dat EEN + B = C voor drie vergelijkbare geometrische figuren zonder de stelling van Pythagoras te gebruiken, dan kunnen we de stelling zelf bewijzen, naar tegengestelde richting. De driehoek van het begincentrum kan bijvoorbeeld opnieuw worden gebruikt als een driehoek C op de hypotenusa, en twee gelijkaardige rechthoekige driehoeken ( EEN en B) gebouwd aan de andere twee zijden, die zijn gevormd als gevolg van het delen van de centrale driehoek door zijn hoogte. De som van de twee kleinere oppervlakten van de driehoeken is dan uiteraard gelijk aan de oppervlakte van de derde, dus EEN + B = C en, in navolging van de vorige bewijzen in omgekeerde volgorde, krijgen we de stelling van Pythagoras a 2 + b 2 = c 2 .
Cosinus stelling
De stelling van Pythagoras is speciaal geval meer algemene stelling cosinus, die de lengtes van de zijden in een willekeurige driehoek relateert:
waarbij θ de hoek is tussen de zijkanten a en b.
Als θ 90 graden is, dan is cos θ = 0 en de formule is vereenvoudigd tot de gebruikelijke stelling van Pythagoras.
Willekeurige driehoek
Naar elke gekozen hoek van een willekeurige driehoek met zijden a, b, c schrijf een gelijkbenige driehoek op zo'n manier dat gelijke hoeken aan de basis was θ gelijk aan de gekozen hoek. Laten we aannemen dat de gekozen hoek θ tegenover de aangegeven zijde ligt c. Als resultaat hebben we een driehoek ABD met hoek , die zich tegenover de zijkant bevindt a en feesten r. De tweede driehoek wordt gevormd door de hoek θ, die tegenover de zijde . ligt b en feesten met lang s, zoals op de foto te zien is. Thabit Ibn Qurra verklaarde dat de zijden in deze drie driehoeken als volgt gerelateerd zijn:
Naarmate de hoek θ π/2 nadert, wordt de basis gelijkbenige driehoek neemt af, en de twee zijden r en s overlappen elkaar steeds minder. Als θ = π/2, verandert ADB in een rechthoekige driehoek, r + s = c en we krijgen de initiële stelling van Pythagoras.
Laten we eens kijken naar een van de argumenten. Driehoek ABC heeft dezelfde hoeken als driehoek ABD, maar in omgekeerde volgorde. (De twee driehoeken hebben een gemeenschappelijke hoek bij hoekpunt B, beide hebben hoek , en hebben ook dezelfde derde hoek, door de som van de hoeken van de driehoek) Dienovereenkomstig is ABC vergelijkbaar met de reflectie ABD van driehoek DBA, zoals weergegeven in de onderste figuur. Laten we de relatie schrijven tussen tegenovergestelde kanten en grenzend aan de hoek ,
Zo is de reflectie van een andere driehoek,
Vermenigvuldig de breuken en voeg deze twee verhoudingen toe:
QED
Generalisatie voor willekeurige driehoeken via parallellogrammen
generalisatie voor willekeurige driehoeken,
gebied van groen perceel = gebied blauw
Bewijs van de stelling dat in de bovenstaande figuur
Laten we een verdere generalisatie maken voor niet-rechthoekige driehoeken, met parallellogrammen aan drie zijden in plaats van vierkanten. (vierkanten zijn een speciaal geval.) De bovenste afbeelding laat zien dat voor acute driehoek het gebied van het parallellogram aan de lange zijde is gelijk aan de som van de parallellogrammen aan de andere twee zijden, op voorwaarde dat het parallellogram aan de lange zijde is gebouwd zoals weergegeven in de afbeelding (de afmetingen gemarkeerd met pijlen zijn hetzelfde en bepaal de zijden van het onderste parallellogram). Deze vervanging van vierkanten door parallellogrammen vertoont een duidelijke gelijkenis met de oorspronkelijke stelling van Pythagoras en wordt verondersteld te zijn geformuleerd door Pappus van Alexandrië in 4 CE. e.
De onderste figuur toont de voortgang van het bewijs. Laten we naar de linkerkant van de driehoek kijken. Het linker groene parallellogram heeft dezelfde oppervlakte als de linkerkant van het blauwe parallellogram omdat ze dezelfde basis hebben b en hoogte h. Ook heeft het linker groene vak hetzelfde gebied als het linker groene vak in de bovenste afbeelding omdat ze gemeenschappelijke basis(bovenste linkerkant driehoek) en de totale hoogte loodrecht op die zijde van de driehoek. Als we op dezelfde manier argumenteren voor de rechterkant van de driehoek, bewijzen we dat het onderste parallellogram dezelfde oppervlakte heeft als de twee groene parallellogrammen.
Complexe getallen
De stelling van Pythagoras wordt gebruikt om de afstand tussen twee punten in een Cartesiaans coördinatensysteem te vinden, en deze stelling geldt voor alle echte coördinaten: afstand s tussen twee punten ( een, b) en ( c, d) is gelijk aan
Er zijn geen problemen met de formule als complexe getallen worden behandeld als vectoren met reële componenten x + ik ja = (x, ja). . Bijvoorbeeld de afstand s tussen 0 + 1 i en 1 + 0 i berekenen als modulus van vector (0, 1) − (1, 0) = (−1, 1), of
Voor bewerkingen met vectoren met complexe coördinaten is het echter noodzakelijk om een zekere verbetering aan te brengen in de formule van Pythagoras. Afstand tussen punten met complexe getallen (a, b) en ( c, d); a, b, c, en d zijn allemaal complex, we formuleren met behulp van absolute waarden. Afstand s gebaseerd op vectorverschil (a − c, b − d) in volgende vorm: laat het verschil a − c = p+ik q, waar p is het echte deel van het verschil, q is het imaginaire deel, en i = √(−1). Evenzo, laten we b − d = r+ik s. Dan:
waar is de complexe geconjugeerde van . Bijvoorbeeld de afstand tussen punten (a, b) = (0, 1) en (c, d) = (i, 0) , bereken het verschil (a − c, b − d) = (−i, 1) en het resultaat zou 0 zijn als er geen complexe conjugaten werden gebruikt. Daarom, met behulp van de verbeterde formule, krijgen we
De module is als volgt gedefinieerd:
Stereometrie
Een belangrijke veralgemening van de stelling van Pythagoras voor de driedimensionale ruimte is de stelling van de Gua, genoemd naar J.-P. de Gua: als een tetraëder een rechte hoek heeft (zoals in een kubus), dan is het kwadraat van de oppervlakte van het vlak tegenover de rechte hoek gelijk aan de som van de kwadraten van de oppervlakten van de andere drie vlakken. Deze conclusie kan worden samengevat als " n-dimensionale stelling van Pythagoras":
Stelling van Pythagoras driedimensionale ruimte verbindt de diagonaal AD met drie zijden.
Een andere generalisatie: de stelling van Pythagoras kan in de volgende vorm op stereometrie worden toegepast. Overwegen kubusvormig, zoals op de foto te zien is. Vind de lengte van de diagonaal BD met behulp van de stelling van Pythagoras:
waarbij drie zijden een rechthoekige driehoek vormen. Gebruik de horizontale diagonaal BD en de verticale rand AB om de lengte van de diagonaal AD te vinden, opnieuw met behulp van de stelling van Pythagoras:
of, als alles in één vergelijking is geschreven:
Dit resultaat is een 3D-uitdrukking voor het bepalen van de grootte van de vector v(diagonaal AD) uitgedrukt in termen van zijn loodrechte componenten ( v k) (drie onderling loodrechte zijden):
Deze vergelijking kan worden gezien als een generalisatie van de stelling van Pythagoras voor een multidimensionale ruimte. Het resultaat is echter niets meer dan de herhaalde toepassing van de stelling van Pythagoras op een reeks rechthoekige driehoeken in opeenvolgende loodrechte vlakken.
Vector ruimte
Bij een orthogonaal stelsel van vectoren vindt een gelijkheid plaats, ook wel de stelling van Pythagoras genoemd:
Als is de projectie van de vector op Coördinaatassen, dan valt deze formule samen met de Euclidische afstand - en betekent dat de lengte van de vector gelijk is aan de wortel vierkante som kwadraten van zijn componenten.
Een analoog van deze gelijkheid in het geval eindeloos systeem vectoren heet de gelijkheid van Parseval.
Niet-euclidische meetkunde
De stelling van Pythagoras is afgeleid van de axioma's van de Euclidische meetkunde en is in feite niet geldig voor niet-Euclidische meetkunde, in de vorm waarin deze hierboven is geschreven. (Dat wil zeggen, de stelling van Pythagoras blijkt een soort equivalent te zijn van het parallellisme van Euclides) Met andere woorden, in niet-Euclidische meetkunde zal de verhouding tussen de zijden van de driehoek noodzakelijkerwijs een andere vorm hebben dan de stelling van Pythagoras . Bijvoorbeeld, in sferische meetkunde, alle drie de zijden van een rechthoekige driehoek (zeg a, b en c) die het octant (een achtste) van de eenheidsbol begrenst, hebben een lengte π/2, wat in tegenspraak is met de stelling van Pythagoras omdat a 2 + b 2 ≠ c 2 .
Beschouw hier twee gevallen van niet-euclidische meetkunde - sferische en hyperbolische meetkunde; in beide gevallen, wat betreft de Euclidische ruimte voor rechthoekige driehoeken, volgt het resultaat dat de stelling van Pythagoras vervangt uit de cosinusstelling.
De stelling van Pythagoras blijft echter geldig voor hyperbolische en elliptische meetkunde als de eis dat de driehoek rechthoekig is, wordt vervangen door de voorwaarde dat de som van twee hoeken van de driehoek gelijk moet zijn aan de derde, zeg maar EEN+B = C. Dan ziet de verhouding tussen de zijden er zo uit: de som van de oppervlakten van cirkels met diameters a en b gelijk aan de oppervlakte van een cirkel met een diameter c.
sferische geometrie
Voor elke rechthoekige driehoek op een bol met straal R(bijvoorbeeld als de hoek γ in de driehoek gelijk is) met zijden a, b, c de relatie tussen partijen ziet er als volgt uit:
Deze gelijkheid kan worden afgeleid als een speciaal geval sferische cosinusstelling, die geldt voor alle sferische driehoeken:
waarbij cosh de cosinus hyperbolicus is. Deze formule is een speciaal geval van de cosinusstelling hyperbolicus, die geldt voor alle driehoeken:
waarbij γ de hoek is waarvan het hoekpunt tegenover de zijde ligt c.
waar g ij wordt de metrische tensor genoemd. Het kan een positiefunctie zijn. Dergelijke kromlijnige ruimten omvatten Riemann-meetkunde as algemeen voorbeeld. Deze formulering is ook geschikt voor Euclidische ruimte bij gebruik van kromlijnige coördinaten. Bijvoorbeeld voor Pool coördinaten:
vectorproduct
De stelling van Pythagoras verbindt twee uitdrukkingen voor de grootte van een vectorproduct. Eén benadering voor het definiëren van een uitwendig product vereist dat het voldoet aan de vergelijking:
deze formule gebruikt het puntproduct. De rechterkant van de vergelijking wordt de Gram-determinant genoemd voor a en b, wat gelijk is aan het gebied van het parallellogram gevormd door deze twee vectoren. Op basis van deze eis, evenals de eis dat het vectorproduct loodrecht staat op zijn componenten a en b hieruit volgt dat, met uitzondering van de triviale gevallen van 0- en 1-dimensionale ruimte, het vectorproduct alleen wordt gedefinieerd in drie en zeven dimensies. We gebruiken de definitie van de hoek in n-dimensionale ruimte:
deze eigenschap van het vectorproduct geeft zijn waarde in de volgende vorm:
Door de fundamentele trigonometrische identiteit Pythagoras, we krijgen een andere vorm om de waarde ervan te schrijven:
Een alternatieve benadering voor het definiëren van een uitwendig product gebruikt een uitdrukking voor de omvang ervan. Dan, in omgekeerde volgorde argumenterend, krijgen we een verband met scalair product:
zie ook
Opmerkingen:
- Geschiedenisonderwerp: de stelling van Pythagoras in de Babylonische wiskunde
- ( , blz. 351) blz. 351
- ( , Deel I, p. 144)
- Discussie historische feiten gegeven in (, p. 351) p. 351
- Kurt von Fritz (april 1945). "De ontdekking van incommensurabiliteit door Hippasus van Metapontum". De annalen van de wiskunde, tweede reeks(Annalen van de wiskunde) 46 (2): 242–264.
- Lewis Carroll, "Het verhaal met knopen", M., Mir, 1985, p. 7
- Asger Aaboe Episodes uit de vroege geschiedenis van de wiskunde. - Mathematical Association of America, 1997. - P. 51. - ISBN 0883856131
- Pythagoras propositie door Elisha Scott Loomis
- Euclides elementen: Boek VI, Propositie VI 31: "In rechthoekige driehoeken is de figuur aan de zijde die de rechte hoek insluit gelijk aan de gelijkaardige en op dezelfde manier beschreven figuren aan de zijden die de rechte hoek bevatten."
- Lawrence S. Leff geciteerd werk. - Barron's educatieve serie - P. 326. - ISBN 0764128922
- Howard Whitley Eves§4.8:... veralgemening van de stelling van Pythagoras // Grote momenten in de wiskunde (vóór 1650) . - Mathematical Association of America, 1983. - P. 41. - ISBN 0883853108
- Tâbit ibn Qorra (volledige naam Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 AD) was een arts die in Bagdad woonde en uitgebreid schreef over Euclid's Elements en anderen wiskundige vakken.
- Aydin Sayili (maart 1960). "Thâbit ibn Qurra's generalisatie van de stelling van Pythagoras". Isis 51 (1): 35-37. DOI:10.1086/348837.
- Judith D. Sally, Paul Sally Oefening 2.10(ii) // Aangehaald werk . - P. 62. - ISBN 0821844032
- Voor de details van een dergelijke constructie, zie: George Jennings Figuur 1.32: De gegeneraliseerde stelling van Pythagoras // Moderne meetkunde met toepassingen: met 150 cijfers . - 3e. - Springer, 1997. - P. 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcy item C: Norm voor een willekeurige n-tuple ... // Een inleiding tot analyse . - Springer, 1995. - P. 124. - ISBN 0387943692 Zie ook pagina's 47-50.
- Alfred Gray, Elsa Abbena, Simon Salamon Moderne differentiële meetkunde van krommen en oppervlakken met Mathematica. - 3e. - CRC Press, 2006. - P. 194. - ISBN 1584884487
- Rajendra Bhatia matrixanalyse. - Springer, 1997. - P. 21. - ISBN 0387948465
- Stephen W. Hawking geciteerd werk. - 2005. - P. 4. - ISBN 0762419229
- Eric W. Weisstein CRC beknopte encyclopedie van de wiskunde. - 2e. - 2003. - P. 2147. - ISBN 1584883472
- Alexander R. Pruss
Midden niveau
Rechte driehoek. Volledige geïllustreerde gids (2019)
JUISTE DRIEHOEK. EERSTE LEVEL.
Bij problemen is een rechte hoek helemaal niet nodig - de linkerbenedenhoek, dus je moet leren hoe je een rechthoekige driehoek in deze vorm kunt herkennen,

en in zo'n

en in zo'n 
Wat is er goed aan een rechthoekige driehoek? Nou... ten eerste zijn er speciale mooie namen voor zijn kanten.
Let op de tekening!

Onthoud en verwar niet: benen - twee, en de hypotenusa - slechts één(de enige, unieke en langste)!
Nou, we hebben de namen besproken, nu het belangrijkste: de stelling van Pythagoras.
De stelling van Pythagoras.
Deze stelling is de sleutel tot het oplossen van veel problemen met een rechthoekige driehoek. Het werd bewezen door Pythagoras in onheuglijke tijden, en sindsdien heeft het vele voordelen gebracht voor degenen die het kennen. En het beste aan haar is dat ze eenvoudig is.
Dus, De stelling van Pythagoras:
Herinner je je de grap: "Pythagorasbroeken zijn aan alle kanten gelijk!"?
Laten we deze zeer Pythagoreïsche broek tekenen en ernaar kijken. 
Lijkt het echt op een korte broek? Welnu, aan welke kanten en waar zijn ze gelijk? Waarom en waar komt de grap vandaan? En deze grap hangt precies samen met de stelling van Pythagoras, meer bepaald met de manier waarop Pythagoras zelf zijn stelling formuleerde. En hij formuleerde het als volgt:
"Som oppervlakte van vierkanten, gebouwd op de benen, is gelijk aan vierkante oppervlakte gebouwd op de hypotenusa.
Klinkt het niet een beetje anders, niet? En dus, toen Pythagoras de verklaring van zijn stelling trok, bleek precies zo'n foto.

In deze afbeelding is de som van de oppervlakten van de kleine vierkantjes gelijk aan de oppervlakte van het grote vierkant. En zodat de kinderen beter onthouden dat de som van de vierkanten van de benen gelijk is aan het vierkant van de hypotenusa, heeft iemand geestig deze grap over Pythagoras-broeken uitgevonden.
Waarom formuleren we nu de stelling van Pythagoras?
Heeft Pythagoras geleden en over vierkanten gepraat?
Zie je, in de oudheid was er geen ... algebra! Er waren geen tekenen en ga zo maar door. Er waren geen inscripties. Kun je je voorstellen hoe verschrikkelijk het was voor de arme oude studenten om alles met woorden uit het hoofd te leren??! En we kunnen blij zijn dat we een eenvoudige formulering van de stelling van Pythagoras hebben. Laten we het nog een keer herhalen om het beter te onthouden:
Nu zou het makkelijk moeten zijn:
| Het kwadraat van de hypotenusa is gelijk aan de som van de kwadraten van de benen. |
Welnu, de belangrijkste stelling over een rechthoekige driehoek werd besproken. Als je je afvraagt hoe het is bewezen, lees dan verder. volgende niveaus theorie, en laten we nu verder gaan ... naar donker bos... trigonometrie! Op de verschrikkelijke woorden sinus, cosinus, tangens en cotangent.
Sinus, cosinus, raaklijn, cotangens in een rechthoekige driehoek.
Eigenlijk is alles helemaal niet zo eng. Natuurlijk moet in het artikel naar de "echte" definitie van sinus, cosinus, tangens en cotangens worden gekeken. Maar dat wil je echt niet, hè? We kunnen ons verheugen: om problemen over een rechthoekige driehoek op te lossen, kunt u eenvoudig de volgende eenvoudige dingen invullen:
Waarom draait het allemaal om de hoek? Waar is de hoek? Om dit te begrijpen, moet je weten hoe uitspraken 1 t/m 4 in woorden worden geschreven. Kijk, begrijp en onthoud!
1.
Het klinkt eigenlijk zo:
Hoe zit het met de hoek? Is er een been dat tegenover de hoek ligt, dat wil zeggen het tegenoverliggende been (voor de hoek)? Natuurlijk hebben! Dit is een kathet!
Maar hoe zit het met de hoek? Kijk goed. Welk been grenst aan de hoek? Natuurlijk, de kat. Dus voor de hoek is het been aangrenzend, en
En nu, aandacht! Kijk wat we hebben:
Kijk hoe geweldig het is:
Laten we nu verder gaan met tangens en cotangens.
Hoe het nu onder woorden te brengen? Wat is het been ten opzichte van de hoek? Tegenover natuurlijk - het "ligt" tegenover de hoek. En de kathet? Grenzend aan de hoek. Dus wat hebben we gekregen?
Zie je hoe de teller en noemer worden omgekeerd?
En nu weer de hoeken en maakte de uitwisseling:
Samenvatting
Laten we kort opschrijven wat we hebben geleerd.
 |
De stelling van Pythagoras: |
De stelling van de belangrijkste rechthoekige driehoek is de stelling van Pythagoras.
de stelling van Pythagoras
Trouwens, weet je nog goed wat de benen en hypotenusa zijn? Zo niet, kijk dan naar de afbeelding - ververs je kennis

Het is mogelijk dat je de stelling van Pythagoras al vaak hebt gebruikt, maar heb je je ooit afgevraagd waarom zo'n stelling waar is. Hoe zou je het bewijzen? Laten we doen zoals de oude Grieken. Laten we een vierkant tekenen met een zijde.

Je ziet hoe sluw we de zijkanten in segmenten van lengte verdeelden en!
Laten we nu de gemarkeerde punten verbinden

Hier merkten we echter nog iets anders op, maar je kijkt zelf naar de foto en bedenkt waarom.
Wat is de oppervlakte van het grotere vierkant? Correct, . Hoe zit het met de kleinere oppervlakte? Zeker, . De totale oppervlakte van de vier hoeken blijft. Stel je voor dat we er twee nemen en met hypotenusa tegen elkaar leunen. Wat er is gebeurd? Twee rechthoeken. Het gebied van "stekken" is dus gelijk.
Laten we het nu allemaal op een rijtje zetten.
Laten we transformeren:
Dus bezochten we Pythagoras - we bewezen zijn stelling op een oude manier.
Rechthoekige driehoek en trigonometrie
Voor een rechthoekige driehoek gelden de volgende relaties:

Sinus Scherpe hoek gelijk aan de verhouding van het andere been tot de hypotenusa
De cosinus van een scherpe hoek is gelijk aan de verhouding van het aangrenzende been tot de hypotenusa.
De tangens van een scherpe hoek is gelijk aan de verhouding van het tegenoverliggende been tot het aangrenzende been.
De cotangens van een scherpe hoek is gelijk aan de verhouding van het aangrenzende been tot het tegenoverliggende been.
En nogmaals, dit alles in de vorm van een bord:
Het is zeer comfortabel!
Tekenen van gelijkheid van rechthoekige driehoeken
I. Op twee benen

II. Door been en hypotenusa

III. Door hypotenusa en scherpe hoek

IV. Langs het been en scherpe hoek
a) 
b) 
Aandacht! Hierbij is het erg belangrijk dat de poten "corresponderen". Als het bijvoorbeeld zo gaat:

DAN ZIJN DE DRIEHOEKEN NIET GELIJK, ondanks het feit dat ze één identieke scherpe hoek hebben.
Nodig hebben in beide driehoeken was het been aangrenzend, of in beide - tegenovergestelde.
Is het je opgevallen hoe de tekens van gelijkheid van rechthoekige driehoeken verschillen van de gebruikelijke tekens van gelijkheid van driehoeken? Kijk naar het onderwerp "en let op het feit dat je voor de gelijkheid van "gewone" driehoeken de gelijkheid van hun drie elementen nodig hebt: twee zijden en een hoek ertussen, twee hoeken en een zijde ertussen, of drie zijden. Maar voor de gelijkheid van rechthoekige driehoeken zijn slechts twee corresponderende elementen voldoende. Het is geweldig, toch?
Ongeveer dezelfde situatie met tekenen van gelijkenis van rechthoekige driehoeken.
Tekenen van gelijkenis van rechthoekige driehoeken
I. Acute hoek

II. Op twee benen

III. Door been en hypotenusa

Mediaan in een rechthoekige driehoek
Waarom is het zo?
Beschouw een hele rechthoek in plaats van een rechthoekige driehoek.
Laten we een diagonaal tekenen en een punt beschouwen - het snijpunt van de diagonalen. Wat weet je over de diagonalen van een rechthoek?
En wat volgt hieruit?
Dus het gebeurde dat
- - mediaan:
Onthoud dit feit! Helpt veel!
Wat nog verrassender is, is dat het omgekeerde ook waar is.
Wat heb je eraan dat de mediaan die naar de hypotenusa wordt getrokken gelijk is aan de helft van de hypotenusa? Laten we naar de foto kijken
Kijk goed. We hebben: , dat wil zeggen, de afstanden van het punt tot alle drie de hoekpunten van de driehoek bleken gelijk te zijn. Maar in een driehoek is er maar één punt, waarvan de afstanden ongeveer alle drie de hoekpunten van de driehoek gelijk zijn, en dit is het MIDDEL VAN HET BESCHREVEN CIRCUM. Dus wat gebeurde er?
Dus laten we beginnen met dit "bovendien...".
Laten we eens kijken naar ik.
Maar in gelijkvormige driehoeken zijn alle hoeken gelijk!
Hetzelfde kan gezegd worden over en
Laten we het nu samen tekenen:
Welk nut kan worden getrokken uit deze "drievoudige" gelijkenis.
Nou, bijvoorbeeld - twee formules voor de hoogte van een rechthoekige driehoek.
We schrijven de relaties van de corresponderende partijen:

Om de hoogte te vinden, lossen we de verhouding op en krijgen eerste formule "Hoogte in een rechthoekige driehoek":
Laten we dus de overeenkomst toepassen: .

Wat gaat er nu gebeuren?
Opnieuw lossen we de verhouding op en krijgen de tweede formule:
Beide formules moeten goed worden onthouden en degene die handiger is om toe te passen. Laten we ze nog eens opschrijven.
De stelling van Pythagoras:
In een rechthoekige driehoek is het kwadraat van de hypotenusa gelijk aan de som van de kwadraten van de benen:.

Tekenen van gelijkheid van rechthoekige driehoeken:
- op twee benen:
- langs het been en de hypotenusa: of
- langs het been en de aangrenzende scherpe hoek: of
- langs het been en de tegenovergestelde scherpe hoek: of
- door hypotenusa en scherpe hoek: of.
Tekenen van gelijkenis van rechthoekige driehoeken:
- een scherpe hoek: of
- van de evenredigheid van de twee benen:
- uit de evenredigheid van het been en de hypotenusa: of.
Sinus, cosinus, tangens, cotangens in een rechthoekige driehoek
- De sinus van een scherpe hoek van een rechthoekige driehoek is de verhouding van het tegenoverliggende been tot de hypotenusa:
- De cosinus van een scherpe hoek van een rechthoekige driehoek is de verhouding van het aangrenzende been tot de hypotenusa:
- De tangens van een scherpe hoek van een rechthoekige driehoek is de verhouding van het tegenoverliggende been tot het aangrenzende:
- De cotangens van een scherpe hoek van een rechthoekige driehoek is de verhouding van het aangrenzende been tot het tegenovergestelde:.
Hoogte van een rechthoekige driehoek: of.
In een rechthoekige driehoek is de mediaan getrokken vanaf het hoekpunt van de rechte hoek gelijk aan de helft van de hypotenusa: .
Oppervlakte van een rechthoekige driehoek:
- via de katheters:
 Evenzo is driehoek CBH vergelijkbaar met ABC. Introductie van de notatie
Evenzo is driehoek CBH vergelijkbaar met ABC. Introductie van de notatie  1. Schik vier gelijke rechthoekige driehoeken zoals weergegeven in de afbeelding.
1. Schik vier gelijke rechthoekige driehoeken zoals weergegeven in de afbeelding. 
 Het idee van het bewijs van Euclides is als volgt: laten we proberen te bewijzen dat de helft van het gebied van het vierkant gebouwd op de hypotenusa gelijk is aan de som van de halve gebieden van de vierkanten die op de benen zijn gebouwd, en dan de gebieden van de grote en twee kleine vierkanten zijn gelijk. Beschouw de tekening hiernaast. Daarop bouwden we vierkanten aan de zijkanten van een rechthoekige driehoek en trokken een straal s van het hoekpunt van rechte hoek C loodrecht op de hypotenusa AB, het snijdt het vierkant ABIK, gebouwd op de hypotenusa, in twee rechthoeken - BHJI en HAKJ, respectievelijk. Het blijkt dat de oppervlakten van deze rechthoeken exact gelijk zijn aan de oppervlakten van de vierkanten die op de corresponderende poten zijn gebouwd. Laten we proberen te bewijzen dat de oppervlakte van het vierkant DECA gelijk is aan de oppervlakte van de rechthoek AHJK. Hiervoor gebruiken we een hulpobservatie: De oppervlakte van een driehoek met dezelfde hoogte en basis als de gegeven rechthoek gelijk is aan de helft van de oppervlakte van de gegeven rechthoek. Dit is een gevolg van het definiëren van het gebied van een driehoek als de helft van het product van de basis en de hoogte. Uit deze waarneming volgt dat de oppervlakte van driehoek ACK gelijk is aan de oppervlakte van driehoek AHK (niet getoond), die op zijn beurt gelijk is aan de helft van de oppervlakte van rechthoek AHJK. Laten we nu bewijzen dat de oppervlakte van driehoek ACK ook gelijk is aan de helft van de oppervlakte van vierkante DECA. Het enige dat hiervoor moet worden gedaan, is de gelijkheid van driehoeken ACK en BDA bewijzen (aangezien de oppervlakte van driehoek BDA gelijk is aan de helft van de oppervlakte van het vierkant door de bovenstaande eigenschap). Deze gelijkheid is duidelijk, de driehoeken zijn gelijk in twee zijden en de hoek ertussen. Namelijk - AB=AK,AD=AC - de gelijkheid van de hoeken CAK en BAD is eenvoudig te bewijzen door de bewegingsmethode: laten we de driehoek CAK 90 ° tegen de klok in draaien, dan is het duidelijk dat de overeenkomstige zijden van de twee beschouwde driehoeken zal samenvallen (vanwege het feit dat de hoek op het hoekpunt van het vierkant 90° is). Het argument over de gelijkheid van de oppervlakten van het vierkant BCFG en de rechthoek BHJI is volledig analoog. We hebben dus bewezen dat de oppervlakte van het vierkant gebouwd op de hypotenusa de som is van de gebieden van de vierkanten die op de poten zijn gebouwd.
Het idee van het bewijs van Euclides is als volgt: laten we proberen te bewijzen dat de helft van het gebied van het vierkant gebouwd op de hypotenusa gelijk is aan de som van de halve gebieden van de vierkanten die op de benen zijn gebouwd, en dan de gebieden van de grote en twee kleine vierkanten zijn gelijk. Beschouw de tekening hiernaast. Daarop bouwden we vierkanten aan de zijkanten van een rechthoekige driehoek en trokken een straal s van het hoekpunt van rechte hoek C loodrecht op de hypotenusa AB, het snijdt het vierkant ABIK, gebouwd op de hypotenusa, in twee rechthoeken - BHJI en HAKJ, respectievelijk. Het blijkt dat de oppervlakten van deze rechthoeken exact gelijk zijn aan de oppervlakten van de vierkanten die op de corresponderende poten zijn gebouwd. Laten we proberen te bewijzen dat de oppervlakte van het vierkant DECA gelijk is aan de oppervlakte van de rechthoek AHJK. Hiervoor gebruiken we een hulpobservatie: De oppervlakte van een driehoek met dezelfde hoogte en basis als de gegeven rechthoek gelijk is aan de helft van de oppervlakte van de gegeven rechthoek. Dit is een gevolg van het definiëren van het gebied van een driehoek als de helft van het product van de basis en de hoogte. Uit deze waarneming volgt dat de oppervlakte van driehoek ACK gelijk is aan de oppervlakte van driehoek AHK (niet getoond), die op zijn beurt gelijk is aan de helft van de oppervlakte van rechthoek AHJK. Laten we nu bewijzen dat de oppervlakte van driehoek ACK ook gelijk is aan de helft van de oppervlakte van vierkante DECA. Het enige dat hiervoor moet worden gedaan, is de gelijkheid van driehoeken ACK en BDA bewijzen (aangezien de oppervlakte van driehoek BDA gelijk is aan de helft van de oppervlakte van het vierkant door de bovenstaande eigenschap). Deze gelijkheid is duidelijk, de driehoeken zijn gelijk in twee zijden en de hoek ertussen. Namelijk - AB=AK,AD=AC - de gelijkheid van de hoeken CAK en BAD is eenvoudig te bewijzen door de bewegingsmethode: laten we de driehoek CAK 90 ° tegen de klok in draaien, dan is het duidelijk dat de overeenkomstige zijden van de twee beschouwde driehoeken zal samenvallen (vanwege het feit dat de hoek op het hoekpunt van het vierkant 90° is). Het argument over de gelijkheid van de oppervlakten van het vierkant BCFG en de rechthoek BHJI is volledig analoog. We hebben dus bewezen dat de oppervlakte van het vierkant gebouwd op de hypotenusa de som is van de gebieden van de vierkanten die op de poten zijn gebouwd.  Beschouw de tekening, zoals te zien is aan de symmetrie, het segment CI snijdt het vierkant ABHJ in twee identieke delen (aangezien de driehoeken ABC en JHI gelijk zijn in constructie). Met een rotatie van 90 graden linksom zien we de gelijkheid van de gearceerde figuren CAJI en GDAB. Nu is het duidelijk dat het gebied van de door ons gearceerde figuur gelijk is aan de som van de helft van de gebieden van de vierkanten die op de poten zijn gebouwd en het gebied van de oorspronkelijke driehoek. Aan de andere kant is het gelijk aan de helft van het gebied van het vierkant gebouwd op de hypotenusa, plus het gebied van de oorspronkelijke driehoek. De laatste stap in het bewijs wordt overgelaten aan de lezer.
Beschouw de tekening, zoals te zien is aan de symmetrie, het segment CI snijdt het vierkant ABHJ in twee identieke delen (aangezien de driehoeken ABC en JHI gelijk zijn in constructie). Met een rotatie van 90 graden linksom zien we de gelijkheid van de gearceerde figuren CAJI en GDAB. Nu is het duidelijk dat het gebied van de door ons gearceerde figuur gelijk is aan de som van de helft van de gebieden van de vierkanten die op de poten zijn gebouwd en het gebied van de oorspronkelijke driehoek. Aan de andere kant is het gelijk aan de helft van het gebied van het vierkant gebouwd op de hypotenusa, plus het gebied van de oorspronkelijke driehoek. De laatste stap in het bewijs wordt overgelaten aan de lezer.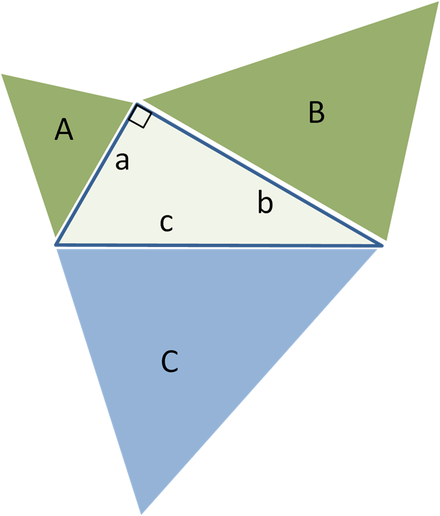




 Het spel "Skyrim": al het geschreeuw Skyrim schreeuw van 4 woorden
Het spel "Skyrim": al het geschreeuw Skyrim schreeuw van 4 woorden The Elder Scrolls V: Skyrim
The Elder Scrolls V: Skyrim The Elder Scrolls V: Skyrim Walkthrough
The Elder Scrolls V: Skyrim Walkthrough