Basisstellingen van de dynamiek. Algemene stellingen van dynamiek

College 3 Algemene stellingen van dynamiek

Dynamiek van het systeem van materiële punten is een belangrijke tak van de theoretische mechanica. Hier beschouwen we vooral de problemen van de beweging van mechanische systemen (systemen van materiële punten) met eindig getal vrijheidsgraden - het maximale aantal onafhankelijke parameters dat de positie van het systeem bepaalt. de belangrijkste taak systeemdynamica - de studie van de bewegingswetten van een star lichaam en mechanische systemen.

De eenvoudigste benadering om de beweging van een systeem te bestuderen, bestaande uit: N materiële punten, wordt teruggebracht tot de overweging van de bewegingen van elk afzonderlijk punt van het systeem. In dit geval moeten alle krachten die op elk punt van het systeem werken, inclusief de krachten van interactie tussen punten, worden bepaald.

Door de versnelling van elk punt te bepalen in overeenstemming met de tweede wet van Newton (1.2), verkrijgen we voor elk punt drie scalaire differentiële bewegingswetten van de tweede orde, d.w.z. 3 N differentiële bewegingswet voor het hele systeem.

Om de bewegingsvergelijkingen te vinden mechanisch systeem: gegeven krachten en beginvoorwaarden voor elk punt van het systeem, verkregen differentiële wetten moet worden geïntegreerd. Dit probleem is zelfs moeilijk in het geval van twee materiële punten die alleen bewegen onder de werking van krachten van interactie volgens de wet van universele aantrekking (het probleem van twee lichamen), en is buitengewoon moeilijk in het geval van drie op elkaar inwerkende punten (de probleem van drie lichamen).

Daarom is het noodzakelijk om dergelijke methoden te vinden voor het oplossen van problemen die zouden leiden tot oplosbare vergelijkingen en om een ​​idee te geven van de beweging van een mechanisch systeem. Algemene stellingen van de dynamiek, die een gevolg zijn van de differentiële bewegingswetten, maken het mogelijk om de complexiteit die ontstaat tijdens integratie te vermijden en de nodige resultaten te verkrijgen.

3.1 Algemene opmerkingen

De punten van het mechanische systeem worden genummerd door indices i, j, k enz. die door alle waarden lopen 1, 2, 3… N, waar N is het aantal systeempunten. Fysieke grootheden gerelateerd aan k e punt worden aangegeven met dezelfde index als het punt. Ze drukken bijvoorbeeld respectievelijk de straalvector en de snelheid uit k-de punt.

Krachten van twee oorsprong werken op elk van de punten van het systeem: ten eerste, krachten waarvan de bronnen buiten het systeem liggen, genaamd extern krachten en aangeduid met ; ten tweede, krachten uit andere punten van dit systeem, genaamd intern krachten en aangeduid met . Interne krachten voldoen aan de derde wet van Newton. Overweeg de eenvoudigste eigenschappen van interne krachten die inwerken op het hele mechanische systeem in een van zijn toestanden.

Eerste eigendom. De geometrische som van alle interne krachten van het systeem (de hoofdvector van interne krachten) is gelijk aan nul.

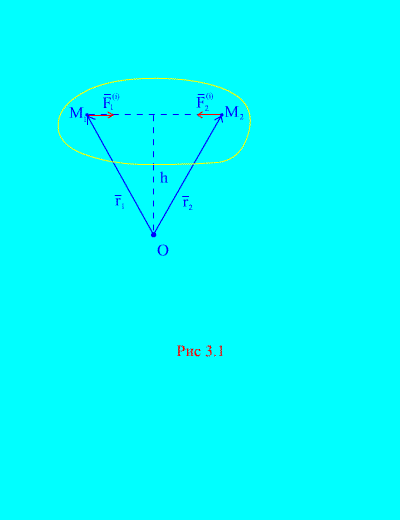
Inderdaad, als we bijvoorbeeld twee willekeurige punten van het systeem beschouwen, en (Afb. 3.1), dan voor hen , omdat de krachten van actie en reactie zijn altijd gelijk in absolute waarde, ze werken langs één actielijn in de tegenovergestelde richting, die de interactiepunten verbindt. De hoofdvector van interne krachten bestaat uit paren krachten van op elkaar inwerkende punten, dus

(3.1)

Tweede eigendom. De geometrische som van de momenten van alle interne krachten ten opzichte van een willekeurig punt in de ruimte is nul.

Overweeg het systeem van krachten en met betrekking tot het punt O(Afb. 3.1). Van (Afb. 3.1). het is duidelijk dat

,

omdat beide krachten hebben dezelfde armen en tegengestelde richtingen van vectormomenten. Het belangrijkste moment van interne krachten over het punt O bestaat uit de vectorsom van dergelijke uitdrukkingen en is gelijk aan nul. Vervolgens,

Laat externe en Interne krachten werkend op een mechanisch systeem bestaande uit: N punten (Afb. 3.2). Als de resultante van externe krachten en de resultante van alle interne krachten worden toegepast op elk punt van het systeem, dan k e punt van het systeem kan men differentiaalvergelijkingen van beweging opstellen. In totaal zullen dergelijke vergelijkingen zijn N:

en in projecties op vaste coördinaatassen 3 N:

(3.4)

Vectorvergelijkingen (3.3) of equivalente scalaire vergelijkingen (3.4) vertegenwoordigen de differentiële bewegingswetten van materiële punten van het hele systeem. Als alle punten evenwijdig aan één vlak of één rechte lijn bewegen, dan is het aantal vergelijkingen (3.4) in het eerste geval gelijk aan 2 N, in de seconde N.

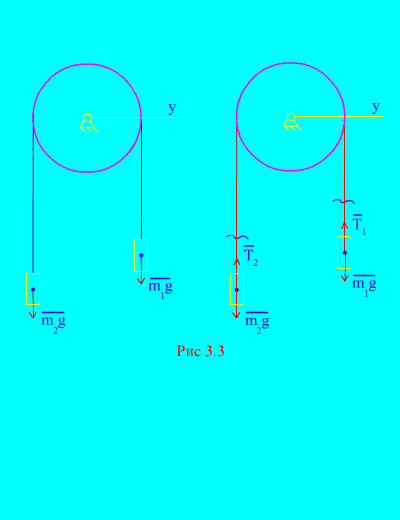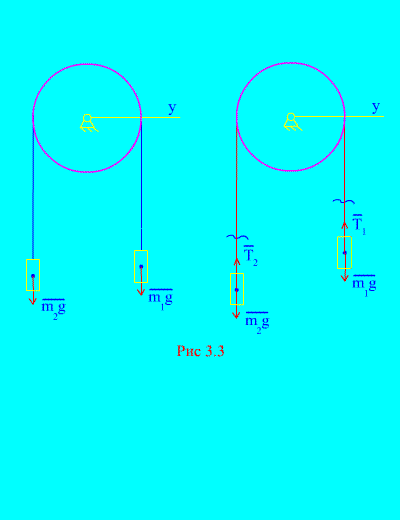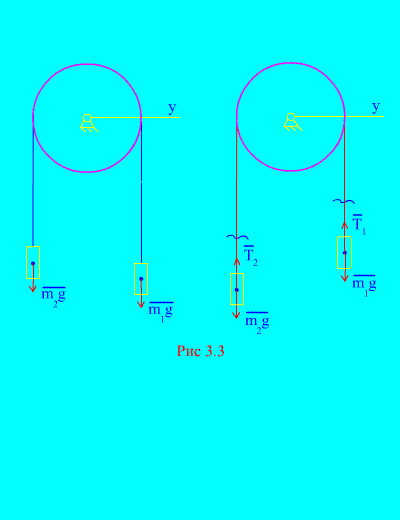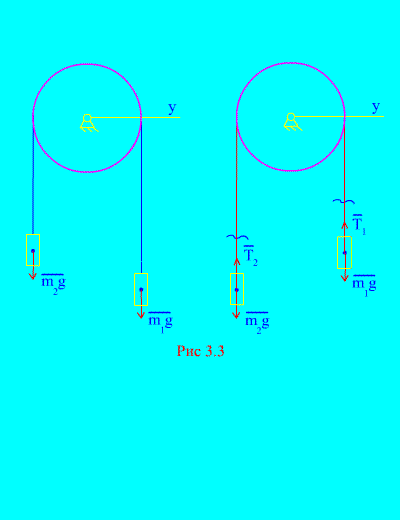
voorbeeld 1 Twee ladingen massa en onderling verbonden door een onrekbare kabel die over een blok wordt gegooid (Afb. 3.3). Het verwaarlozen van de wrijvingskrachten, evenals de massa van het blok en de kabel, bepalen de bewegingswet van goederen en de spanning van de kabel.

Oplossing. Het systeem bestaat uit twee materiële lichamen (verbonden door een niet-verlengbare kabel) die parallel aan één as bewegen X. Laten we de differentiële bewegingswetten opschrijven in projecties op de as X voor iedereen.

Laat het rechter gewicht bij acceleratie dalen, dan zal het linker gewicht bij acceleratie stijgen. We bevrijden ons mentaal van de verbinding (kabel) en vervangen deze door reacties en (Afb. 3.3). Ervan uitgaande dat de lichamen vrij zijn, zullen we de differentiële bewegingswetten samenstellen in de projectie op de as X(wat betekent dat de draadspanningen interne krachten zijn en het gewicht van de belastingen extern):

Aangezien en (de lichamen zijn verbonden door een niet-verlengbare kabel), krijgen we:

Deze vergelijkingen oplossen voor de versnelling en spanning van de kabel T, we krijgen

.

Merk op dat de kabelspanning bij niet gelijk is aan de zwaartekracht van de overeenkomstige belasting.

3. 2. De stelling over de beweging van het massamiddelpunt

Het is bekend dat een stijf lichaam en een mechanisch systeem in een vliegtuig behoorlijk moeilijk kunnen bewegen. De eerste stelling over de beweging van een lichaam en een mechanisch systeem kan op de volgende manier worden bereikt: laat de c.-l vallen. een object dat bestaat uit vele vaste lichamen die aan elkaar zijn bevestigd. Het is duidelijk dat hij in een parabool zal vliegen. Dit werd onthuld bij het bestuderen van de beweging van een punt. Nu is het object echter geen punt. Het draait, zwaait terwijl het rond een effectief centrum vliegt, dat langs een parabool beweegt. Eerste bewegingsstelling moeilijke onderwerpen zegt dat een bepaald effectief middelpunt het zwaartepunt van een bewegend object is. Het zwaartepunt bevindt zich niet noodzakelijk in het lichaam zelf, het kan ergens daarbuiten liggen.

Stelling. Het zwaartepunt van een mechanisch systeem beweegt als een materieel punt met een massa gelijk aan de massa het gehele systeem waarop alle externe krachten die op het systeem inwerken, worden uitgeoefend.

Om de stelling te bewijzen, herschrijven we de differentiële bewegingswetten (3.3) in volgende vorm:

(3.5)

waar N is het aantal systeempunten.

Laten we de vergelijkingen term voor term bij elkaar optellen:

(a)

De positie van het zwaartepunt van het mechanische systeem ten opzichte van het geselecteerde coördinatensysteem wordt bepaald door formule (2.1): waar M is de massa van het systeem. Dan wordt de linkerkant van gelijkheid (a) geschreven

De eerste som, die aan de rechterkant van gelijkheid (a) staat, is gelijk aan de hoofdvector van externe krachten, en de laatste, door de eigenschap van interne krachten, is gelijk aan nul. Dan wordt gelijkheid (a), rekening houdend met (b), herschreven

, (3.6)

die. het product van de massa van het systeem en de versnelling van het massamiddelpunt is gelijk aan geometrische som alle externe krachten die op het systeem inwerken.

Uit vergelijking (3.6) volgt dat interne krachten de beweging van het massamiddelpunt niet direct beïnvloeden. In sommige gevallen zijn ze echter de oorzaak van het optreden van externe krachten die op het systeem worden uitgeoefend. De interne krachten die de aandrijfwielen van de auto roteren, veroorzaken dus de werking daarop van een externe adhesiekracht die op de velg wordt uitgeoefend.

Voorbeeld 2 Het mechanisme, dat zich in een verticaal vlak bevindt, wordt op een horizontaal glad vlak geïnstalleerd en eraan bevestigd met staven die stevig aan het oppervlak zijn bevestigd. Tot en L (Afb. 3.4).

Schijf 1 straal R roerloos. Schijf 2 massa m en straal r vastgemaakt met een slinger, lengte R+ r bij het punt Vanaf 2. De kruk draait constant

hoeksnelheid. BIJ eerste moment de kruk nam de juiste horizontale positie in. Verwaarloos de massa van de krukas, bepaal de maximale horizontale en verticale krachten die op de staven werken, als totale gewicht bed en wiel 1 is gelijk aan M. Houd ook rekening met het gedrag van het mechanisme bij afwezigheid van staven.

Oplossing. Het systeem bestaat uit twee massa's ( N=2 ): een vaste schijf 1 met een frame en een beweegbare schijf 2. Laten we de as richten Bij door het zwaartepunt van de vaste schijf verticaal naar boven, de as X- langs horizontaal vliegtuig.

We schrijven de stelling over de beweging van het massamiddelpunt (3.6) in de coördinatenvorm

De externe krachten van dit systeem zijn: het gewicht van het frame en de vaste schijf - mg, beweegbaar schijfgewicht mg, - de totale horizontale reactie van de bouten, - de normale totale reactie van het vliegtuig. Vervolgens,

Dan worden de bewegingswetten (b) herschreven

Laten we de coördinaten van het massamiddelpunt van het mechanische systeem berekenen:

; (G)

gezien vanaf (Afb. 3.4), , , (draaihoek van de slinger), . Vervanging van deze uitdrukkingen in (r) en het berekenen van de tweede afgeleiden met betrekking tot tijd t van , , krijgen we dat

(e)

Als we (c) en (e) in (b) substitueren, vinden we

De horizontale druk die op de staven werkt, heeft de grootste en kleinste waarde, wanneer omdat = 1 respectievelijk, d.w.z.

De druk van het mechanisme op het horizontale vlak heeft de hoogste en laagste waarden wanneer zonde respectievelijk, d.w.z.

In feite is het eerste probleem van de dynamiek opgelost: volgens de bekende bewegingsvergelijkingen van het zwaartepunt van het systeem (e) worden de krachten die bij de beweging betrokken zijn, hersteld.

Bij afwezigheid van bars K en L (Afb. 3.4), kan het mechanisme beginnen te stuiteren boven het horizontale vlak. Dit zal plaatsvinden wanneer, d.w.z. wanneer volgt daaruit dat de hoeksnelheid van de rotatie van de kruk, waarbij het mechanisme stuitert, aan de gelijkheid moet voldoen

.

3. 3. Wet van behoud van beweging van het massamiddelpunt

Als de hoofdvector van externe krachten die op het systeem inwerken gelijk is aan nul, d.w.z. , dan van(3.6)hieruit volgt dat de versnelling van het massamiddelpunt nul is, daarom is de snelheid van het massamiddelpunt constant in grootte en richting. Als, in het bijzonder, op het beginmoment het massamiddelpunt in rust is, dan is het in rust gedurende de hele tijd totdat de hoofdvector van externe krachten gelijk is aan nul.

Verschillende uitvloeisels volgen uit deze stelling.

· Interne krachten alleen kunnen de aard van de beweging van het massamiddelpunt van het systeem niet veranderen.

· Als de hoofdvector van externe krachten die op het systeem inwerken gelijk is aan nul, dan is het massamiddelpunt in rust of beweegt het uniform en rechtlijnig.

· Als de projectie van de hoofdvector van de externe krachten van het systeem op een vaste as gelijk is aan nul, dan verandert de projectie van de snelheid van het zwaartepunt van het systeem op deze as niet.

· Een paar krachten die op een stijf lichaam worden uitgeoefend, kunnen de beweging van het zwaartepunt niet veranderen (het kan er alleen voor zorgen dat het lichaam rond het zwaartepunt draait).

Laten we een voorbeeld bekijken dat de wet van behoud van beweging van het massamiddelpunt illustreert.

Voorbeeld 3 Twee gewichten met massa's en verbonden door een onrekbare draad die over een blok wordt gegooid (Afb. 3.5), bevestigd op een wig met massa M. De wig rust op een glad horizontaal vlak. Aanvankelijk stond het systeem stil. Vind de verplaatsing van de wig langs het vlak wanneer de eerste lading tot een hoogte wordt neergelaten N. Negeer de massa van het blok en de draad.

Oplossing. De externe krachten die samen met de gewichten op de wig werken, zijn de zwaartekracht, en mg, net zoals normale reactie glad horizontaal oppervlak N. Daarom,

Omdat het systeem op het eerste moment in rust was, hebben we .

Laten we de coördinaat van het massamiddelpunt van het systeem op en op het moment berekenen t 1 wanneer het gewicht van de lading: g afdalen naar een hoogte H.

Voor een moment:

,

waar , , X- respectievelijk de coördinaten van het zwaartepunt van de lasten met een gewicht van g, g en wigweging Mg.

Laten we aannemen dat de wig op het moment van de tijd in de positieve richting van de as beweegt Os door het bedrag L als het gewicht van de lading tot een hoogte valt N. Dan, voor een moment

omdat lasten samen met de wig zullen naar L naar rechts, a zal het gewicht een afstand naar boven op de wig bewegen. Sinds , na berekeningen krijgen we

.

3.4. Hoeveelheid bewegingssysteem

3.4.1. Het momentum van een systeem berekenen

Het momentum van een materieel punt is een vectorgrootheid, gelijk aan het product massa van een punt op zijn snelheidsvector

Maateenheid van de hoeveelheid beweging -

Het momentum van een mechanisch systeem wordt de vectorsom van het momentum van de individuele punten van het systeem genoemd, d.w.z.

waar N is het aantal systeempunten.

Het momentum van een mechanisch systeem kan worden uitgedrukt in termen van de massa van het systeem M en de snelheid van het massamiddelpunt. Werkelijk,

die. het momentum van het systeem is gelijk aan het product van de massa van het hele systeem en de snelheid van het zwaartepunt. De richting is hetzelfde als de richting (Afb. 3.6)

In projecties op rechthoekige assen hebben we:

waarbij , , - projecties van de snelheid van het massamiddelpunt van het systeem.

Hier M is de massa van het mechanische systeem; verandert niet als het systeem beweegt.

Het is vooral handig om deze resultaten te gebruiken bij het berekenen van de momenta van starre lichamen.

Uit formule (3.7) blijkt dat als een mechanisch systeem zo beweegt dat het zwaartepunt stationair blijft, het momentum van het systeem gelijk aan nul blijft.

3.4.2. Elementaire en volledige krachtimpuls

De werking van een kracht op een materieel punt in de tijd dt kan worden gekenmerkt door een elementaire impuls. Totale krachtimpuls in de tijd t, of krachtimpuls , wordt bepaald door de formule

of in projecties op de coördinaten van de as

(3.8a)

De eenheid van krachtimpuls is .

3.4.3. Stelling over de verandering in het momentum van het systeem

Laat externe en interne krachten worden uitgeoefend op de punten van het systeem. Vervolgens kunnen we voor elk punt van het systeem de differentiële bewegingswetten (3.3) toepassen, rekening houdend met het volgende: :

.

Als we alle punten van het systeem optellen, krijgen we:

Door de eigenschap van interne krachten en per definitie wij hebben

(3.9)

Beide zijden van deze vergelijking vermenigvuldigen met dt, verkrijgen we een stelling over de verandering in het momentum in differentiële vorm:

, (3.10)

die. het verschil van het momentum van een mechanisch systeem is gelijk aan de vectorsom van de elementaire impulsen van alle externe krachten die op de punten van het mechanische systeem inwerken.

De integraal van beide delen van (3.10) in de tijd berekenen van 0 tot t, we verkrijgen de stelling in eindige of integrale vorm

(3.11)

In projecties op de coördinaatassen hebben we:

Verandering in momentum van een mechanisch systeem in de loop van de tijdt, is gelijk aan de vectorsom van alle impulsen van externe krachten die tegelijkertijd op de punten van het mechanische systeem inwerken.

Voorbeeld 4 Belasting van massa m naar beneden gaan Hellend vlak vanuit rust onder invloed van een kracht F, evenredig met de tijd: , waar (Afb. 3.7). Wat is de snelheid van het lichaam daarna? t seconden na het begin van de beweging, als de wrijvingscoëfficiënt van de belasting op het hellende vlak gelijk is aan f.

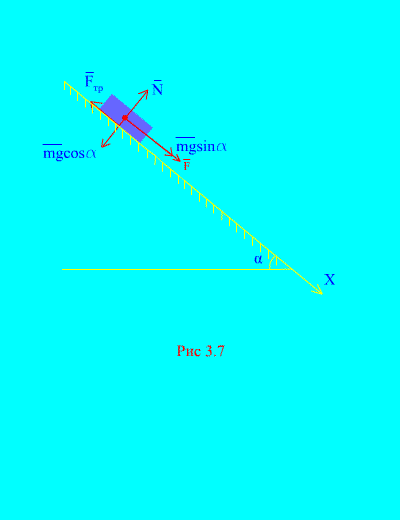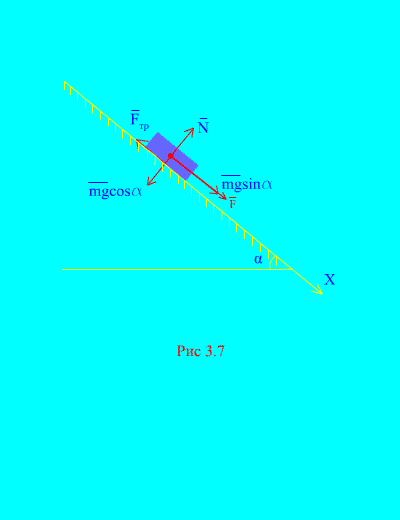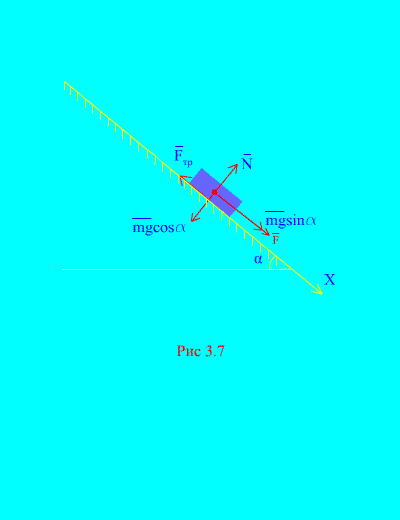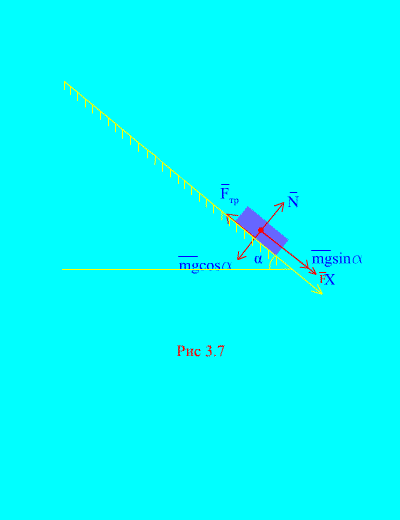
Oplossing. Laten we de krachten weergeven die op de belasting worden uitgeoefend: mg - zwaarte van de lading, N is de normale reactie van het vliegtuig, is de glijdende wrijvingskracht van de belasting op het vliegtuig, en . De richting van alle krachten wordt weergegeven in (Afb. 3.7).

Laten we de as richten X een hellend vlak af. Laten we de stelling schrijven over de verandering in momentum (3.11) in de projectie op de as X:

(a)

Op voorwaarde, want op het eerste moment was de last in rust. De som van de projecties van de impulsen van alle krachten op de x-as is

Vervolgens,

,

.

3.4.4. Wetten van behoud van impuls

Behoudswetten worden verkregen als speciale gevallen van de stelling van impulsverandering. Er zijn twee bijzondere gevallen mogelijk.

· Als de vectorsom van alle externe krachten die op het systeem worden uitgeoefend gelijk is aan nul, d.w.z. , dan volgt uit de stelling (3.9) , wat ,

die. als de hoofdvector van externe krachten van het systeem gelijk is aan nul, dan is het momentum van het systeem constant in grootte en richting.

· Als de projectie van de hoofdvector van externe krachten op een willekeurige coördinaatas is gelijk aan nul, bijvoorbeeld Oh, d.w.z. , dan is de projectie van de hoeveelheid beweging op deze as constant.

Overweeg een voorbeeld van het toepassen van de wet van behoud van impuls.

Voorbeeld 5 Een ballistische slinger is een massa, opgehangen aan een lange draad (Afb. 3.8).

Een kogel van massa die met een snelheid beweegt V en vallen in een bewegingloos lichaam, komt erin vast te zitten, en het lichaam wordt afgebogen. Wat was de snelheid van de kogel als het lichaam tot een hoogte zou stijgen? h ?

Oplossing. Laat het lichaam met de vastzittende kogel snelheid krijgen. Dan, met behulp van de wet van behoud van impuls in de interactie van twee lichamen, kunnen we schrijven: .

Snelheid kan worden berekend met behulp van de behoudswet mechanische energie . Dan . Als resultaat vinden we

.

Voorbeeld 6. Water komt een vast kanaal binnen (Afb. 3.9) variabel gedeelte met een snelheid onder een hoek met de horizon; vierkant dwarsdoorsnede kanaal bij de ingang; de snelheid van het water aan de uitgang van het kanaal en maakt een hoek met de horizon.

Bepaal de horizontale component van de reactie die water uitoefent op de wanden van het kanaal. Dichtheid van water .

Oplossing. We zullen de horizontale component bepalen van de reactie die door de kanaalwanden op water wordt uitgeoefend. Deze kracht is gelijk in absolute waarde en tegengesteld in teken aan de gewenste kracht. We hebben, volgens (3.11a),

. (a)

We berekenen de massa van het vloeistofvolume dat het kanaal binnenkomt gedurende de tijd t:

De waarde van rAV 0 heet tweede massa - de massa vloeistof die per tijdseenheid door een deel van de pijp stroomt.

Dezelfde hoeveelheid water verlaat het kanaal in dezelfde tijd. De begin- en eindsnelheden staan ​​vermeld in de conditie.

Berekenen rechter zijde gelijkheid (a) die de som bepaalt van projecties op de horizontale as van externe krachten die op het systeem (water) worden uitgeoefend. De enige horizontale kracht is de horizontale component van de resulterende reactie van de muren R x. Deze kracht is constant tijdens de gestage beweging van water. Dat is waarom

. (in)

Als we (b) en (c) in (a) substitueren, krijgen we

3.5. Kinetisch moment van het systeem

3.5.1. Belangrijkste moment van momentum van het systeem

Laat de straalvector zijn van een punt met de massa van het systeem ten opzichte van een punt A, het middelpunt genoemd (Afb. 3.10).

Moment van momentum (kinetisch moment) van een punt ten opzichte van het centrum A genaamd vector , bepaald door de formule

. (3.12)

In dit geval is de vector loodrecht gericht op het vlak dat door het centrum gaat MAAR en vector .

Moment van momentum (kinetisch moment) van een punt om een ​​as wordt de projectie op deze as genoemd van het impulsmoment van het punt ten opzichte van een willekeurig gekozen middelpunt op deze as.

Het belangrijkste moment van momentum (kinetisch moment) van het systeem ten opzichte van het centrum A heet de hoeveelheid

(3.13)

Het belangrijkste moment van momentum (kinetisch moment) van het systeem om de as heet de projectie op deze as van het hoofdmoment van het momentum van het systeem ten opzichte van een gekozen op de gegeven midden as.

3.5.2. Momentum van een roterend star lichaam om de rotatie-as

Compatibel vast punt O lichaam liggend op de rotatie-as Oz, met de oorsprong van het coördinatenstelsel Ohuz, waarvan de assen met het lichaam zullen roteren (Afb. 3.11). Laat de straal-vector zijn van het punt van het lichaam ten opzichte van de oorsprong van de coördinaten, de projecties op de assen worden aangegeven met , , . vectorprojecties hoeksnelheid lichamen op dezelfde assen worden aangeduid met 0, 0, ().

Vaak is het mogelijk om onderscheid te maken belangrijke mogelijkheden beweging van een mechanisch systeem zonder toevlucht te nemen tot integratie van het systeem van differentiaalvergelijkingen van beweging. Dit wordt bereikt door algemene stellingen van de dynamiek toe te passen.

5.1. Basisconcepten en definities

Externe en interne krachten. Elke kracht die op een punt in een mechanisch systeem inwerkt, is noodzakelijk ofwel: actieve kracht, of een bindingsreactie. De hele reeks krachten die op de punten van het systeem inwerken, kan op verschillende manieren in twee klassen worden verdeeld: in externe krachten en interne krachten (subscripts e en i - van Latijnse woorden externus - extern en internus - intern). Externe krachten worden krachten genoemd die op punten van het systeem inwerken vanuit punten en lichamen die geen deel uitmaken van het beschouwde systeem. Krachten van interactie tussen punten en lichamen van het beschouwde systeem worden intern genoemd.

Deze verdeling hangt af van welke materiële punten en lichamen door de onderzoeker worden opgenomen in het beschouwde mechanische systeem. Als de samenstelling van het systeem wordt uitgebreid met extra punten en lichamen, kunnen sommige krachten die extern waren voor het vorige systeem intern worden voor het uitgebreide systeem.

Eigenschappen van interne krachten. Aangezien deze krachten interactiekrachten zijn tussen delen van het systeem, zijn ze opgenomen in het volledige systeem van interne krachten in "tweeën", georganiseerd in overeenstemming met het actie-reactieaxioma. Elk van deze "twee" krachten

hoofdvector en belangrijkste punt ten opzichte van een willekeurig middelpunt gelijk zijn aan nul. Aangezien het volledige systeem van interne krachten alleen uit "tweeën" bestaat,

1) de hoofdvector van het systeem van interne krachten is gelijk aan nul,

2) het hoofdmoment van het systeem van interne krachten ten opzichte van een willekeurig punt is gelijk aan nul.

De massa van het systeem is rekenkundige som massa mk van alle punten en lichamen die het systeem vormen:

zwaartepunt(traagheidscentrum) van een mechanisch systeem heet geometrisch punt C, waarvan de straalvector en coördinaten worden bepaald door de formules

waar zijn de straalvectoren en de coördinaten van de punten die het systeem vormen.

Voor een star lichaam in een uniform zwaartekrachtveld vallen de posities van het zwaartepunt en het zwaartepunt samen; in andere gevallen zijn dit verschillende geometrische punten.

Samen met het inertiaalstelsel beschouwt men vaak tegelijkertijd een niet-traagheidsstelsel dat zich naar voren beweegt. De coördinaatassen (Koenig-assen) zijn zo gekozen dat het referentiepunt C altijd samenvalt met het massamiddelpunt van het mechanische systeem. Volgens de definitie ligt het zwaartepunt vast in de Koenig-assen en ligt het aan de oorsprong van de coördinaten.

Het traagheidsmoment van het systeem over de as heet scalair gelijk aan de som de producten van de massa's mk van alle punten van het systeem door de kwadraten van hun afstanden tot de as:

Als het mechanische systeem een ​​star lichaam is, om 12 te vinden, kun je de formule gebruiken:

waar is de dichtheid, het volume dat door het lichaam wordt ingenomen.

Beschouw de beweging van een bepaald systeem van materiële volumes ten opzichte van een vast coördinatensysteem.Als het systeem niet vrij is, kan het als vrij worden beschouwd, als we de beperkingen die aan het systeem zijn opgelegd negeren en hun actie vervangen door de overeenkomstige reacties.

Laten we alle krachten die op het systeem worden uitgeoefend, verdelen in externe en interne; beide kunnen reacties bevatten van weggegooid

verbindingen. Geef aan door en de hoofdvector en het hoofdmoment van externe krachten ten opzichte van punt A.

1. Stelling over de verandering in momentum. Als het momentum van het systeem is, dan (zie )

dat wil zeggen, de stelling is geldig: de tijdsafgeleide van het momentum van het systeem is gelijk aan de hoofdvector van alle externe krachten.

Door de vector te vervangen door zijn uitdrukking waar de massa van het systeem is, is de snelheid van het massamiddelpunt, vergelijking (4.1) kan een andere vorm krijgen:

Deze gelijkheid betekent dat het massamiddelpunt van het systeem beweegt als een materieel punt waarvan de massa gelijk is aan de massa van het systeem en waarop een kracht wordt uitgeoefend die geometrisch gelijk is aan de hoofdvector van alle externe krachten van het systeem. De laatste uitspraak wordt de stelling over de beweging van het massamiddelpunt (traagheidscentrum) van het systeem genoemd.

Als dan uit (4.1) volgt dat de impulsvector constant is in grootte en richting. Door het op de coördinatenas te projecteren, verkrijgen we drie scalaire eerste integralen van de differentiaalvergelijkingen van de dubbele keten van het systeem:

Deze integralen worden impulsintegralen genoemd. Wanneer de snelheid van het massamiddelpunt constant is, d.w.z. het beweegt uniform en rechtlijnig.

Als de projectie van de hoofdvector van externe krachten op een as, bijvoorbeeld op de as, gelijk is aan nul, dan hebben we één eerste integraal, of als twee projecties van de hoofdvector gelijk zijn aan nul, dan zijn er twee integralen van het momentum.

2. Stelling over de verandering van het kinetische moment. Laat A een willekeurig punt in de ruimte zijn (bewegend of stilstaand), dat niet noodzakelijk samenvalt met een bepaald materieel punt van het systeem gedurende de gehele bewegingstijd. De snelheid in een vast coördinatenstelsel wordt aangegeven door Stelling over de verandering in impulsmoment materieel systeem: met betrekking tot punt A heeft de vorm

Als punt A vast is, dan heeft gelijkheid (4.3) een eenvoudiger vorm:

Deze gelijkheid drukt de stelling uit over de verandering in het impulsmoment van het systeem met betrekking tot vast punt: de tijdsafgeleide van het impulsmoment van het systeem, berekend met betrekking tot een vast punt, is gelijk aan het hoofdmoment van alle externe krachten met betrekking tot dit punt.

Als dan, volgens (4.4), de impulsmomentvector constant is in grootte en richting. Door het op de coördinatenas te projecteren, verkrijgen we de scalaire eerste integralen van de differentiaalvergelijkingen van de beweging van het systeem:

Deze integralen worden de integralen van het impulsmoment of de integralen van de gebieden genoemd.

Als punt A samenvalt met het massamiddelpunt van het systeem, dan verdwijnt de eerste term aan de rechterkant van gelijkheid (4.3) en heeft de stelling over de verandering in impulsmoment dezelfde vorm (4.4) als in het geval van een vaste punt A. Merk op (zie 4 § 3) dat in het onderhavige geval het absolute impulsmoment van het systeem aan de linkerkant van gelijkheid (4.4) kan worden vervangen door het gelijke impulsmoment van het systeem in zijn beweging ten opzichte van het centrum van massa.

Laat een constante as zijn of een as met constante richting die door het massamiddelpunt van het systeem gaat, en laat het impulsmoment van het systeem zijn ten opzichte van deze as. Uit (4.4) volgt dat:

waar is het moment van externe krachten om de as. Als we gedurende de hele bewegingstijd de eerste integraal hebben

In de werken van S.A. Chaplygin werden verschillende generalisaties van de stelling over de verandering in impulsmoment verkregen, die vervolgens werden toegepast bij het oplossen van een aantal problemen met het rollen van ballen. Verdere veralgemeningen van de stelling over de verandering van het kpnetologische moment en hun toepassingen in problemen van de dynamiek van een star lichaam zijn opgenomen in de werken. De belangrijkste resultaten van deze werken houden verband met de stelling over de verandering in het kinetische moment ten opzichte van het bewegende moment, dat constant door een bewegend punt A gaat. Laten - eenheid Vector langs deze as gericht. Door scalair te vermenigvuldigen met beide zijden van gelijkheid (4.3) en de term toe te voegen aan beide delen, krijgen we:

Wanneer aan de kinematische voorwaarde is voldaan

vergelijking (4.5) volgt uit (4.7). En als aan voorwaarde (4.8) is voldaan gedurende de hele bewegingstijd, dan bestaat de eerste integraal (4.6).

Als de verbindingen van het systeem ideaal zijn en rotatie van het systeem als een star lichaam rond de as en in het aantal virtuele verplaatsingen mogelijk maken, dan is het hoofdmoment van reacties rond de as gelijk aan nul, en dan is de waarde op de rechterkant van vergelijking (4.5) is het belangrijkste moment van alle externe actieve krachten rond de as en . De gelijkheid tot nul van dit moment en de vervulbaarheid van relatie (4.8) zal in het onderhavige geval zijn voldoende voorwaarden voor het bestaan ​​van de integraal (4.6).

Als de richting van de as onveranderd is, dan kan voorwaarde (4.8) worden geschreven als

Deze gelijkheid betekent dat de projecties van de snelheid van het massamiddelpunt en de snelheid van punt A op de as en op het vlak loodrecht daarop evenwijdig zijn. In het werk van S.A. Chaplygin is in plaats van (4.9) vereist dat minder dan algemene toestand waarbij X een willekeurige constante is.

Merk op dat voorwaarde (4.8) niet afhankelijk is van de keuze van een punt op . Laat P inderdaad een willekeurig punt op de as zijn. Dan

en daarom

Concluderend merken we Resal's geometrische interpretatie van vergelijkingen (4.1) en (4.4) op: de vectoren absolute snelheden de uiteinden van de vectoren en zijn respectievelijk gelijk aan de hoofdvector en het hoofdmoment van alle externe krachten ten opzichte van punt A.

MINISTERIE VAN LANDBOUW EN VOEDSEL VAN DE REPUBLIEK WIT-RUSLAND

Educatieve instelling "WIT-RUSLANDSE STAAT AGRARISCH

TECHNISCHE UNIVERSITEIT"

Afdeling Theoretische Mechanica en Theorie van Mechanismen en Machines

THEORETISCHE MECHANICA

methodologisch complex voor studenten van de groep specialiteiten

74 06 Landbouwtechniek

In 2 delen Deel 1

UDC 531.3(07) LBC 22.213ya7 T 33

Samengesteld door:

Kandidaat Fysische en Wiskundige Wetenschappen, universitair hoofddocent Yu. S. Biza, kandidaat technische wetenschappen, universitair hoofddocent N. L. Rakova, hoofddocent I. A. Tarasevich

Beoordelaars:

Afdeling theoretische mechanica van de onderwijsinstelling "Wit-Russische National" Technische Universiteit" (hoofd

Afdeling Theoretische Mechanica BNTU Doctor in de fysische en wiskundige wetenschappen, professor A. V. Chigarev);

Vooraanstaand onderzoeker van het laboratorium "Vibroprotection of Mechanical Systems" State Scientific Institution "Joint Institute of Mechanical Engineering"

Nationale Academie van Wetenschappen van Wit-Rusland”, kandidaat voor technische wetenschappen, universitair hoofddocent A. M. Goman

theoretische mechanica. Sectie "Dynamiek": educatief

T33 methode. complex. In 2 delen Deel 1 / comp.: Yu. S. Biza, N. L. Rakova, I. A. Tarasevich. - Minsk: BGATU, 2013. - 120 d.

ISBN 978-985-519-616-8.

BIJ educatief en methodisch complex presenteert materiaal over de studie van de sectie "Dynamica", deel 1, dat deel uitmaakt van de discipline "Theoretische mechanica". Inclusief een cursus colleges, basismaterialen voor de implementatie praktische oefeningen, taken en voorbeelden van taken voor zelfstandig werk en controle leeractiviteiten fulltime en correspondentie formulieren aan het leren.

UDC 531.3(07) LBC 22.213ya7

INLEIDING ................................................................. ..................................................
1. WETENSCHAPPELIJKE EN THEORETISCHE INHOUD VAN HET ONDERWIJS
VAN HET METHODOLOGISCHE COMPLEX ................................................ ..
1.1. Woordenlijst................................................. ..............................
1.2. Thema's van lezingen en hun inhoud ................................................. .. ..
Hoofdstuk 1. Inleiding tot dynamiek. Basisconcepten
klassieke mechanica ................................................................. ................. ..................................
Onderwerp 1. Dynamiek van een materieel punt .......................................... ....
1.1. Wetten van materiële puntdynamica
(wetten van Galileo - Newton) ........................................... ... ..........
1.2. Differentiaalvergelijkingen bewegingen
1.3. Twee hoofdtaken van dynamiek ................................................. .............
Onderwerp 2. Dynamiek van relatieve beweging
materieel punt ................................................................. ................. .................................
Herzieningsvragen ................................................................. ................. .............
Onderwerp 3. Dynamiek van een mechanisch systeem ................................................ ....
3.1. Massa geometrie. Massamiddelpunt van een mechanisch systeem......
3.2. Interne krachten ................................................ ................. .................
Herzieningsvragen ................................................................. ................. .............
Thema 4. Traagheidsmomenten van een star lichaam ................................................
4.1. Traagheidsmomenten van een star lichaam
ten opzichte van de as en de pool ................................................. ...................... .....
4.2. Stelling over de traagheidsmomenten van een star lichaam
over parallelle assen
(stelling van Huygens-Steiner) ............................................ ..... ....
4.3. Centrifugale traagheidsmomenten .............................................. .
Herzieningsvragen ................................................................. ................. .............
Hoofdstuk 2

Onderwerp 5. De stelling over de beweging van het massamiddelpunt van het systeem .................................
Herzieningsvragen ................................................................. ................. .............
Taken voor zelfstudie .................................................. .......
Onderwerp 6. De hoeveelheid beweging van een materieel punt
en mechanisch systeem ................................................................. ................ ...................
6.1. Hoeveelheid beweging van een materieel punt 43
6.2. Impuls van kracht .................................................................. .......................
6.3. Stelling over de verandering in momentum
materieel punt ................................................................. ..................................................
6.4. Hoofdvectorveranderingsstelling
momentum van een mechanisch systeem ..................................................
Herzieningsvragen ................................................................. ................. .............
Taken voor zelfstudie .................................................. .......
Onderwerp 7. Moment van momentum van een materieel punt
en mechanisch systeem ten opzichte van het midden en de as ..................................
7.1. Moment van momentum van een materieel punt
ten opzichte van het midden en de as ................................................. ................. ...........
7.2. Stelling over de verandering in impulsmoment
materiaalpunt ten opzichte van het midden en de as ..................
7.3. Stelling over de verandering van het kinetische moment
mechanisch systeem ten opzichte van het midden en de as ..................................
Herzieningsvragen ................................................................. ................. .............
Taken voor zelfstudie .................................................. .......
Thema 8. Arbeid en kracht van krachten ....................................... ... .........
Herzieningsvragen ................................................................. ................. .............
Taken voor zelfstudie .................................................. .......
Onderwerp 9. Kinetische energie van een materieel punt
en mechanisch systeem ................................................................. ................ ...................
9.1. Kinetische energie van een materieel punt
en mechanisch systeem. Stelling van Koenig ..................................
9.2. Kinetische energie van een star lichaam
met verschillende bewegingen ................................................................. ................. .............
9.3. Stelling wijzigen kinetische energie
materieel punt ................................................................. ..................................................

9.4. Stelling van kinetische energieverandering
mechanisch systeem ................................................................. ................. .................
Herzieningsvragen ................................................................. ................. .............
Taken voor zelfstudie .................................................. .......
Onderwerp 10. Potentieel krachtveld
en potentiële energie .................................................. ................. .................
Herzieningsvragen ................................................................. ................. .............
Onderwerp 11. Dynamiek van een star lichaam ................................................ .......... .......
Herzieningsvragen ................................................................. ................. .............
2. MATERIALEN VOOR CONTROLE
PER MODULE .............................................. ...................................................
ONAFHANKELIJK WERK VAN STUDENTEN ..............................
4. EISEN VOOR HET ONTWERP VAN DE CONTROLE
WERKT VOOR VOLTIJD EN CORRESPONDENTIE STUDENTEN
VORMEN VAN OPLEIDING ................................................................. ................. ..................................
5. LIJST MET VOORBEREIDINGSVRAGEN
NAAR HET EXAM (STUDIE) VAN STUDENTEN
VOLTIJDS- EN CORRESPONDENTIEONDERWIJS ................................................ ......
6. LIJST VAN REFERENTIES ................................................ .. .............

INVOERING

Theoretische mechanica - de wetenschap van algemene wetten mechanische beweging, evenwicht en interactie van materiële lichamen.

Dit is een van de fundamentele algemene wetenschappelijke fysische en wiskundige disciplines. Het is de theoretische basis van de moderne technologie.

De studie van theoretische mechanica, samen met andere fysische en wiskundige disciplines, draagt ​​bij aan de verruiming van wetenschappelijke horizonten, vormt het vermogen om concrete en abstract denken en draagt ​​bij aan de verbetering van de algemene technische cultuur van de toekomstige specialist.

Theoretische mechanica, de wetenschappelijke basis van alles technische disciplines, draagt ​​bij aan de ontwikkeling van vaardigheden rationele beslissingen technische taken in verband met de bediening, reparatie en het ontwerp van landbouw- en landwinningsmachines en -apparatuur.

Afhankelijk van de aard van de beschouwde taken wordt de mechanica onderverdeeld in statica, kinematica en dynamica. Dynamiek is een sectie van theoretische mechanica die de beweging van materiële lichamen bestudeert onder invloed van uitgeoefende krachten.

BIJ educatief en methodisch complex (UMK) presenteert materiaal over de studie van de sectie "Dynamiek", waaronder een cursus lezingen, basismaterialen voor dirigeren praktisch werk, taken en uitvoeringsvoorbeelden voor onafhankelijk werk en controle van onderwijsactiviteiten van voltijdse deeltijdstudenten.

BIJ als resultaat van het bestuderen van de sectie "Dynamiek", moet de student leren theoretische basis dynamiek en beheers de basismethoden voor het oplossen van problemen van dynamiek:

Methoden kennen voor het oplossen van problemen van dynamiek, algemene stellingen van dynamiek, principes van mechanica;

De bewegingswetten van een lichaam kunnen bepalen afhankelijk van de krachten die erop inwerken; de wetten en stellingen van de mechanica toepassen om problemen op te lossen; bepalen de statische en dynamische reacties van de bindingen die de beweging van lichamen beperken.

Het curriculum van de discipline "Theoretische mechanica" voorziet in een totaal aantal lesuren - 136, inclusief 36 uur voor het bestuderen van de sectie "Dynamiek".

1. WETENSCHAPPELIJKE EN THEORETISCHE INHOUD VAN HET ONDERWIJS EN METHODOLOGISCH COMPLEX

1.1. Woordenlijst

Statica is een onderdeel van de mechanica dat de algemene doctrine van krachten schetst, de reductie wordt bestudeerd ingewikkelde systemen krachten naar de eenvoudigste vorm en evenwichtscondities worden vastgesteld verschillende systemen krachten.

Kinematica is een onderdeel van de theoretische mechanica waarin de beweging van materiële objecten wordt bestudeerd, ongeacht de oorzaken die deze beweging veroorzaken, d.w.z. ongeacht de krachten die op deze objecten inwerken.

Dynamiek is een onderdeel van de theoretische mechanica dat de beweging van materiële lichamen (punten) onder invloed van uitgeoefende krachten bestudeert.

Materieel punt- een stoffelijk lichaam waarvan het verschil in de beweging van punten onbeduidend is.

De massa van een lichaam is een scalaire positieve waarde die afhangt van de hoeveelheid materie in een bepaald lichaam en bepaalt de mate van traagheid bij voorwaartse beweging.

Referentiesysteem - een coördinatensysteem geassocieerd met het lichaam, in verband waarmee de beweging van een ander lichaam wordt bestudeerd.

traagheidssysteem- een systeem waarin aan de eerste en tweede wet van de dynamiek wordt voldaan.

Het momentum van een kracht is een vectormaat voor de werking van een kracht gedurende een bepaalde tijd.

Hoeveelheid beweging van een materieel punt is de vectormaat van zijn beweging, die gelijk is aan het product van de massa van het punt en de vector van zijn snelheid.

Kinetische energie is een scalaire maat voor mechanische beweging.

Elementair werk van kracht is een oneindig kleine scalaire waarde gelijk aan punt product vector van kracht naar de vector van oneindig kleine verplaatsing van het aangrijpingspunt van de kracht.

Kinetische energie is een scalaire maat voor mechanische beweging.

De kinetische energie van een materieel punt is een scalair

een positieve waarde gelijk aan de helft van het product van de massa van een punt en het kwadraat van zijn snelheid.

De kinetische energie van een mechanisch systeem is een rekenkundige

de kinetische som van de kinetische energieën van alle materiële punten van dit systeem.

Kracht is een maat voor de mechanische interactie van lichamen en kenmerkt de intensiteit en richting ervan.

1.2. Lezingsonderwerpen en hun inhoud

Sectie 1. Inleiding tot dynamiek. Basisconcepten

klassieke mechanica

Onderwerp 1. Dynamiek van een materieel punt

De wetten van de dynamiek van een materieel punt (de wetten van Galileo - Newton). Differentiaalvergelijkingen van beweging van een materieel punt. Twee hoofdtaken van dynamiek voor een materieel punt. Oplossing van het tweede probleem van dynamiek; integratieconstanten en hun bepaling uit beginvoorwaarden.

Referenties:, pp. 180-196, , pp. 12-26.

Onderwerp 2. Dynamiek van de relatieve beweging van het materiaal

Relatieve beweging van een materieel punt. Differentiaalvergelijkingen van relatieve beweging van een punt; draagbare en Coriolis-traagheidskrachten. Het relativiteitsprincipe in de klassieke mechanica. Een geval van relatieve rust.

Referenties: , blz. 180-196, , blz. 127-155.

Thema 3. Geometrie van massa's. Massamiddelpunt van een mechanisch systeem

Massa van het systeem. Het massamiddelpunt van het systeem en zijn coördinaten.

Literatuur:, blz. 86-93, blz. 264-265

Thema 4. Traagheidsmomenten van een star lichaam

Traagheidsmomenten van een star lichaam om de as en de pool. Inertiestraal. Stelling over traagheidsmomenten over evenwijdige assen. Axiale traagheidsmomenten van sommige lichamen.

Centrifugale traagheidsmomenten als kenmerk van lichaamsasymmetrie.

Referenties: , pp. 265-271, , pp. 155-173.

Sectie 2. Algemene stellingen van de dynamiek van een materieel punt

en mechanisch systeem

Onderwerp 5. De stelling over de beweging van het massamiddelpunt van het systeem

De stelling over de beweging van het massamiddelpunt van het systeem. Gevolgen van de stelling op de beweging van het massamiddelpunt van het systeem.

Referenties: , blz. 274-277, , blz. 175-192.

Onderwerp 6. De hoeveelheid beweging van een materieel punt

en mechanisch systeem

Hoeveelheid beweging van een materieel punt en een mechanisch systeem. Elementaire impuls en impuls van kracht voor een eindige tijdsperiode. Stelling over de verandering in het momentum van een punt en een systeem in differentiële en integrale vormen. Wet van behoud van impuls.

Literatuur: , pp. 280-284, , pp. 192-207.

Onderwerp 7. Moment van momentum van een materieel punt

en mechanisch systeem ten opzichte van het midden en de as

Het moment van momentum van een punt om het middelpunt en de as. De stelling over de verandering in het impulsmoment van een punt. Kinetisch moment van een mechanisch systeem om het middelpunt en de as.

Het impulsmoment van een roterend star lichaam om de rotatie-as. Stelling over de verandering in het kinetische moment van het systeem. Wet van behoud van impuls.

Referenties: , blz. 292-298, , blz. 207-258.

Onderwerp 8. Werk en kracht van krachten

Elementair werk van kracht, zijn analytische uitdrukking. Het werk van de kracht op laatste pad. Het werk van de zwaartekracht, elastische kracht. Gelijkheid tot nul van de som van het werk van interne krachten die in een vaste stof werken. Het werk van krachten uitgeoefend op een star lichaam dat rond een vaste as draait. Stroom. efficiëntie.

Referenties: , blz. 208-213, , blz. 280-290.

Onderwerp 9. Kinetische energie van een materieel punt

en mechanisch systeem

Kinetische energie van een materieel punt en een mechanisch systeem. Berekening van de kinetische energie van een star lichaam in verschillende gevallen van zijn beweging. Stelling van Koenig. Stelling over de verandering in de kinetische energie van een punt in differentiële en integrale vormen. Stelling over de verandering in de kinetische energie van een mechanisch systeem in differentiële en integrale vormen.

Referenties: , blz. 301-310, , blz. 290-344.

Onderwerp 10. Potentieel krachtveld en potentiaal

Het concept van een krachtveld. Potentieel krachtveld en krachtfunctie. De arbeid van een kracht op de uiteindelijke verplaatsing van een punt in een potentieel krachtveld. Potentiële energie.

Referenties: , blz. 317-320, , blz. 344-347.

Onderwerp 11. Stijve lichaamsdynamiek

Differentiaalvergelijkingen van translatiebeweging van een star lichaam. Differentiaalvergelijking draaiende beweging star lichaam rond een vaste as. fysieke slinger. Differentiaalvergelijkingen van vlakke beweging van een star lichaam.

Referenties: , blz. 323-334, , blz. 157-173.

Sectie 1. Inleiding tot dynamiek. Basisconcepten

klassieke mechanica

Dynamiek is een onderdeel van de theoretische mechanica dat de beweging van materiële lichamen (punten) onder invloed van uitgeoefende krachten bestudeert.

stoffelijk lichaam- een lichaam dat massa heeft.

Materieel punt- een stoffelijk lichaam waarvan het verschil in de beweging van punten onbeduidend is. Dit kan een lichaam zijn waarvan de afmetingen tijdens zijn beweging kunnen worden verwaarloosd, of een lichaam van eindige afmetingen, als het vooruit beweegt.

Deeltjes worden ook materiële punten genoemd, waarin een vast lichaam mentaal wordt verdeeld bij het bepalen van enkele van zijn dynamische kenmerken. Voorbeelden van materiële punten (Fig. 1): a - de beweging van de aarde rond de zon. De aarde is een materieel punt; b is de translatiebeweging van een star lichaam. Stevig- moeder-

al punt, aangezien V B \u003d V A; een B = een EEN; c - rotatie van het lichaam rond de as.

Een lichaamsdeeltje is een materieel punt.

Traagheid is de eigenschap van materiële lichamen om de snelheid van hun beweging sneller of langzamer te veranderen onder invloed van uitgeoefende krachten.

De massa van een lichaam is een scalaire positieve waarde die afhangt van de hoeveelheid materie in een bepaald lichaam en bepaalt de mate van traagheid tijdens translatiebeweging. In de klassieke mechanica is massa een constante.

Kracht - kwantitatieve maat mechanische interactie tussen lichamen of tussen een lichaam (punt) en een veld (elektrisch, magnetisch, enz.).

Kracht is een vectorgrootheid die wordt gekenmerkt door grootte, aangrijpingspunt en richting (werklijn) (Fig. 2: A - aangrijpingspunt; AB - werklijn van de kracht).

Rijst. 2

In de dynamica zijn er naast constante krachten ook variabele krachten die kunnen afhangen van tijd t, snelheid ϑ, afstand r, of van een combinatie van deze grootheden, d.w.z.

F = constant;

F = F(t);

F = F(ϑ) ;

F = F(r);

F = F(t, r, ) .

	Voorbeelden van dergelijke krachten worden getoond in Fig. 3: een										- lichaamsgewicht;
			(ϑ) – luchtweerstand;b ​​		T =						- trekkracht

elektrische locomotief; c − F = F (r) is de afstotingskracht van het centrum O of de aantrekking ernaartoe.

Referentiesysteem - een coördinatensysteem geassocieerd met het lichaam, in verband waarmee de beweging van een ander lichaam wordt bestudeerd.

Een traagheidssysteem is een systeem waarin aan de eerste en tweede wet van de dynamiek wordt voldaan. Dit is een vast coördinatensysteem of een systeem dat uniform en rechtlijnig beweegt.

Beweging in de mechanica is een verandering in de positie van een lichaam in ruimte en tijd ten opzichte van andere lichamen.

De ruimte in de klassieke mechanica is driedimensionaal, gehoorzaam aan de Euclidische meetkunde.

Tijd is een scalaire grootheid die in alle referentiesystemen op dezelfde manier stroomt.

Een systeem van eenheden is een verzameling meeteenheden fysieke hoeveelheden. Om alle mechanische grootheden te meten, zijn drie basiseenheden voldoende: eenheden van lengte, tijd, massa of kracht.

Mechanisch	Dimensie		Notatie	Dimensie	Notatie
grootte
				centimeter
	kilogram-

Alle andere meeteenheden van mechanische grootheden zijn daarvan afgeleiden. Er worden twee soorten systemen van eenheden gebruikt: internationaal systeem SI-eenheden (of kleiner - CGS) en het technische systeem van eenheden - MKGSS.

Onderwerp1. Materiële puntdynamiek

1.1. De wetten van de dynamiek van een materieel punt (de wetten van Galileo - Newton)

De eerste wet (van traagheid).

afgesloten van externe invloeden een stoffelijk punt handhaaft zijn rusttoestand of beweegt gelijkmatig en rechtlijnig totdat de uitgeoefende krachten het dwingen deze toestand te veranderen.

De beweging die door een punt wordt gemaakt in afwezigheid van krachten of onder de werking van een uitgebalanceerd krachtenstelsel, wordt traagheidsbeweging genoemd.

Bijvoorbeeld, de beweging van een lichaam langs een gladde (wrijvingskracht is nul)

horizontaal oppervlak (Fig. 4: G - lichaamsgewicht; N - normale reactie van het vliegtuig).

Aangezien G = − N , dan is G + N = 0.

Wanneer ϑ 0 ≠ 0 beweegt het lichaam met dezelfde snelheid; bij ϑ 0 = 0 is het lichaam in rust (ϑ 0 is de beginsnelheid).

De tweede wet (basiswet van de dynamiek).

Het product van de massa van een punt en de versnelling die het ontvangt onder de werking van een bepaalde kracht is in absolute waarde gelijk aan deze kracht, en de richting ervan valt samen met de richting van de versnelling.

een b

Wiskundig wordt deze wet uitgedrukt door de vectorgelijkheid

Voor F = const,

a = const - de beweging van het punt is uniform. EU-

of een ≠ const, α

- slow motion (Fig. 5, maar);

een const,

a -

– versnelde beweging (Fig. 5, b) m – puntmassa;

versnellingsvector;

– vectorkracht; ϑ 0 is de snelheidsvector).

Bij F = 0,a 0 = 0 = ϑ 0 = const - het punt beweegt uniform en rechtlijnig, of bij ϑ 0 = 0 - het is in rust (de wet van traagheid). Seconde

de wet stelt je in staat om een ​​verband vast te stellen tussen de massa m van een lichaam in de buurt van aardoppervlak, en zijn gewicht G .G = mg , waarbij g is

versnelling van de zwaartekracht.

De derde wet (de wet van gelijkheid van actie en reactie). Twee materiële punten werken op elkaar in met krachten van gelijke grootte en gericht langs de rechte verbindingslijn

deze punten, in tegengestelde richtingen.

Aangezien de krachten F 1 = − F 2 worden toegepast op verschillende punten, dan is het krachtenstelsel (F 1 , F 2 ) niet in evenwicht, d.w.z. (F 1 , F 2 )≈ 0 (Fig. 6).

Op zijn beurt

m a = m a

- houding

de massa's van de interagerende punten zijn omgekeerd evenredig met hun versnellingen.

De vierde wet (de wet van de onafhankelijkheid van het optreden van krachten). De versnelling ontvangen door een punt onder de actie van een gelijktijdige

maar meerdere krachten, is gelijk aan de geometrische som van die versnellingen die een punt zou ontvangen onder de werking van elke kracht afzonderlijk erop.

Uitleg (afb. 7).

t een n

a 1 a kF n

De resulterende R-krachten (F 1 ,...Fk ,...Fn) .

Aangezien ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = man , dan

a = a 1 + ...+ a k + ...+ a n = ∑ a k , d.w.z. de vierde wet is gelijk aan

k = 1

de regel van de optelling van krachten.

1.2. Differentiaalvergelijkingen van beweging van een materieel punt

Laat op een materieel punt meerdere krachten tegelijk werken, waaronder zowel constanten als variabelen.

We schrijven de tweede wet van de dynamiek in de vorm

= ∑

(t ,

k = 1

, ϑ=

r is de straalvector van de bewegende

punt, dan bevat (1.2) afgeleiden van r en is een differentiaalvergelijking van beweging van een materieel punt in vectorvorm of de basisvergelijking van de dynamica van een materieel punt.

Projecties van vectorgelijkheid (1.2): - op de as van Cartesiaanse coördinaten (Fig. 8, en)

max=md
					= Fkx;
					k = 1
mei=md
					= Fky;	(1.3)
					k = 1
maz=m					= Fkz;
					k = 1

Op de natuurlijke as (Fig. 8, b)

mat				= ∑ Fk τ ,
				k = 1
				= Fkn;
				k = 1

mab = m0 = ∑ Fk b

k = 1

M t oM oa

b aan uit

Vergelijkingen (1.3) en (1.4) zijn differentiaalvergelijkingen van beweging van een materieel punt in respectievelijk de Cartesiaanse coördinaatassen en natuurlijke assen, d.w.z. natuurlijke differentiaalvergelijkingen die gewoonlijk worden gebruikt voor kromlijnige beweging van een punt als de baan van het punt en de kromtestraal is bekend.

1.3. Twee hoofdproblemen van dynamiek voor een materieel punt en hun oplossing

De eerste (directe) taak.

Als u de bewegingswet en de massa van het punt kent, bepaalt u de kracht die op het punt werkt.

Om dit probleem op te lossen, moet u de versnelling van het punt weten. In problemen van dit type kan het direct worden gespecificeerd, of de bewegingswet van een punt wordt gespecificeerd, in overeenstemming waarmee het kan worden bepaald.

1. Dus, als de beweging van een punt wordt gegeven in cartesiaanse coördinaten

x \u003d f 1 (t) , y \u003d f 2 (t) en z \u003d f 3 (t) dan worden de projecties van de versnelling bepaald

op de coördinatenas x =		d2x			d2y			d2z		En dan - project-
F x , F y en F z krachten op deze assen:
				,k ) = F F z . (1.6) 2. Als het punt begaat kromlijnige beweging en de bewegingswet is bekend s = f (t), de baan van het punt en de kromtestraal ρ, dan het is handig om natuurlijke assen te gebruiken, en de versnellingsprojecties op deze assen worden bepaald door de bekende formules: Tangentiële as a τ = d ϑ = d 2 2 s – tangentiële versnelling;dt dt HomeNormaal ds 2 a n = ϑ 2 = dt is de normale versnelling. De projectie van de versnelling op de binormaal is nul. Dan de projecties van de kracht op de natuurlijke assen F=m F=m De modulus en richting van de kracht worden bepaald door de formules: F \u003d F τ 2 + F n 2; want ( ; omdat ( De tweede (omgekeerde) taak. De krachten kennen die op het punt werken, zijn massa en begincondities beweging, bepaal de bewegingswet van een punt of een van de andere kinematische kenmerken ervan. De beginvoorwaarden voor de beweging van een punt in de Cartesiaanse assen zijn de coördinaten van het punt x 0, y 0, z 0 en de projectie van de beginsnelheid ϑ 0 op deze assen ϑ 0 x \u003d x 0, ϑ 0 y \u003d y 0 en ϑ 0 z \u003d z 0 op het moment dat overeenkomt met geeft het begin van de puntbeweging en wordt gelijk aan nul genomen. Het oplossen van dit soort problemen wordt gereduceerd tot het samenstellen van een differentieel differentiaalvergelijkingen (of één vergelijking) van beweging van een materieel punt en hun daaropvolgende oplossing door directe integratie of met behulp van de theorie van differentiaalvergelijkingen. Vragen bekijken 1. Wat bestudeert dynamiek? 2. Wat voor soort beweging wordt inertiële beweging genoemd? 3. Onder welke omstandigheden zal een materieel punt in rust zijn of uniform en rechtlijnig bewegen? 4. Wat is de essentie van het eerste hoofdprobleem van de dynamiek van een materieel punt? Tweede taak? 5. Noteer de natuurlijke differentiaalvergelijkingen van beweging van een materieel punt. Taken voor zelfstudie 1. Een punt met massa m = 4 kg beweegt langs een horizontale rechte lijn met een versnelling a = 0,3 t. Bepaal de module van de kracht die op het punt werkt in de richting van zijn beweging op het tijdstip t = 3 s. 2. Een deel van massa m = 0,5 kg glijdt langs de schaal naar beneden. Onder welke hoek met het horizontale vlak moet de bak zo worden geplaatst dat het onderdeel beweegt met een versnelling a = 2 m / s 2? Hoek express in graden. 3. Een punt met een massa m = 14 kg beweegt langs de Ox-as met een versnelling a x = 2 t . Bepaal de modulus van de kracht die inwerkt op het punt in de bewegingsrichting op tijdstip t = 5 s.

(MECHANISCHE SYSTEMEN) - IV optie

1. De basisvergelijking van de dynamiek van een materieel punt, zoals bekend, wordt uitgedrukt door de vergelijking . Differentiaalvergelijkingen van beweging willekeurige punten van een niet-vrij mechanisch systeem volgens twee manieren om krachten te verdelen, kan in twee vormen worden geschreven:

(1) , waarbij k=1, 2, 3, … , n het aantal punten van het materiële systeem is.

(2)

waar is de massa van het k-de punt; - straalvector van het k-de punt, - gegeven (werkzame) kracht die op het k-de punt werkt of de resultante van alle actieve krachten die op het k-de punt werken. - de resultante van de reactiekrachten van de bindingen, inwerkend op het k-de punt; - resultante van interne krachten die op het k-de punt werken; - de resultante van externe krachten die op het k-de punt werken.

De vergelijkingen (1) en (2) kunnen worden gebruikt om zowel het eerste als het tweede probleem van de dynamiek op te lossen. De oplossing van het tweede probleem van dynamiek voor het systeem wordt echter zeer gecompliceerd, niet alleen met: wiskundig punt visie, maar ook omdat we met fundamentele problemen worden geconfronteerd. Ze liggen in het feit dat zowel voor systeem (1) als voor systeem (2) het aantal vergelijkingen aanzienlijk is minder dan nummer onbekend.

Dus, als we (1) gebruiken, dan is het bekende voor het tweede (inverse) probleem van de dynamiek en , en de onbekenden zijn en . Vectorvergelijkingen zijn " n", en onbekend - "2n".

Als we uitgaan van het stelsel vergelijkingen (2), dan zijn de bekende en een deel van de externe krachten . Waarom een ​​onderdeel? Het feit is dat het aantal externe krachten omvat: externe reacties verbindingen die niet bekend zijn. Daarnaast zullen er ook onbekenden zijn.

Dus zowel systeem (1) als systeem (2) zijn OPEN. We moeten vergelijkingen toevoegen, rekening houdend met de vergelijkingen van relaties, en misschien moeten we nog wat beperkingen opleggen aan de relaties zelf. Wat moeten we doen?

Als we uitgaan van (1), kunnen we het pad volgen van het opstellen van de Lagrange-vergelijkingen van de eerste soort. Maar deze manier is niet rationeel omdat makkelijkere taak(minder vrijheidsgraden), hoe moeilijker het is om het op te lossen vanuit het oogpunt van wiskunde.

Laten we dan aandacht besteden aan het systeem (2), waarbij - altijd onbekend is. De eerste stap bij het oplossen van het systeem is het elimineren van deze onbekenden. Houd er rekening mee dat we in de regel niet geïnteresseerd zijn in interne krachten tijdens de beweging van het systeem, dat wil zeggen, wanneer het systeem beweegt, is het niet nodig om te weten hoe elk punt van het systeem beweegt, maar het is is voldoende om te weten hoe het systeem als geheel beweegt.

Dus, als verschillende manieren uitsluiten van het systeem (2) onbekende krachten, dan krijgen we enkele relaties, d.w.z. sommige Algemene karakteristieken voor het systeem, waarvan de kennis het mogelijk maakt te beoordelen hoe het systeem in het algemeen beweegt. Deze kenmerken worden geïntroduceerd met behulp van de zogenaamde algemene stellingen van de dynamiek. Er zijn vier van dergelijke stellingen:

1. Stelling over beweging van het zwaartepunt van het mechanische systeem;

2. Stelling over verandering in het momentum van een mechanisch systeem;

3. Stelling over verandering in het impulsmoment van een mechanisch systeem;

4. Stelling over verandering in de kinetische energie van een mechanisch systeem.