Kolmnurga pindala on Pythagorase teoreem. Erinevad viisid Pythagorase teoreemi tõestamiseks: näited, kirjeldus ja ülevaated
Millal te esimest korda ruutjuurte õppimist alustasite ja kuidas neid lahendada irratsionaalsed võrrandid(võrrandid, mis sisaldavad juurmärgi all tundmatut), saite neist ilmselt esimese ettekujutuse praktiline kasutamine. Ekstraheerimise võime Ruutjuur arvud on vajalikud ka ülesannete lahendamiseks Pythagorase teoreemi rakendamisel. See teoreem seob mis tahes täisnurkse kolmnurga külgede pikkused.
Olgu täisnurkse kolmnurga jalgade pikkused (need kaks külge, mis koonduvad täisnurga all) on tähistatud tähtedega ja ning hüpotenuusi pikkus (kolmnurga pikim külg vastassuunas) täisnurk) tähistatakse tähega . Seejärel seostatakse vastavad pikkused järgmise seosega:
See võrrand võimaldab teil leida täisnurkse kolmnurga külje pikkuse juhul, kui selle ülejäänud kahe külje pikkus on teada. Lisaks võimaldab see määrata, kas vaadeldav kolmnurk on täisnurkne kolmnurk, eeldusel, et kõigi kolmnurkade pikkused kolm pidu ette teada.
Ülesannete lahendamine Pythagorase teoreemi abil
Materjali kinnistamiseks lahendame Pythagorase teoreemi rakendamiseks järgmised ülesanded.

Nii antud:
- Ühe jala pikkus on 48, hüpotenuus 80.
- Jala pikkus on 84, hüpotenuus on 91.
Läheme lahenduseni:
a) Andmete asendamine ülaltoodud võrrandiga annab järgmised tulemused:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 või b = -64
Kuna kolmnurga külje pikkust ei saa väljendada negatiivne arv, jäetakse teine valik automaatselt kõrvale.
Vastus esimesele pildile: b = 64.
b) Teise kolmnurga jala pikkus leitakse samal viisil:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 või b = -35
Nagu eelmisel juhul, jäetakse negatiivne lahendus kõrvale.
Vastus teisele pildile: b = 35

Meile antakse:
- Kolmnurga väiksemate külgede pikkused on vastavalt 45 ja 55 ning suuremate külgede pikkused 75.
- Kolmnurga väiksemate külgede pikkused on vastavalt 28 ja 45 ning suuremate külgede pikkused 53.
Lahendame probleemi:
a) Tuleb kontrollida, kas antud kolmnurga väiksemate külgede pikkuste ruutude summa on võrdne suurema kolmnurga pikkuse ruuduga:
45 2 + 55 2 = 2025 + 3025 = 5050
Seetõttu ei ole esimene kolmnurk täisnurkne kolmnurk.
b) Sama toiming tehakse:
28 2 + 45 2 = 784 + 2025 = 2809
Seetõttu on teine kolmnurk täisnurkne kolmnurk.
Kõigepealt leiame pikkuse pikim segment, mille moodustavad punktid koordinaatidega (-2, -3) ja (5, -2). Selleks kasutame tuntud valem punktide vahelise kauguse leidmiseks ristkülikukujuline süsteem koordinaadid:
Samamoodi leiame koordinaatidega (-2, -3) ja (2, 1) punktide vahele jääva lõigu pikkuse:
Lõpuks määrame koordinaatidega (2, 1) ja (5, -2) punktide vahelise lõigu pikkuse:
Kuna võrdsus on olemas:
siis on vastav kolmnurk täisnurkne kolmnurk.
Seega saame sõnastada vastuse ülesandele: kuna väikseima pikkusega külgede ruutude summa on võrdne külje ruuduga suurim pikkus, punktid on täisnurkse kolmnurga tipud.
Alus (asub rangelt horisontaalselt), leng (asub rangelt vertikaalselt) ja tross (diagonaalselt venitatud) moodustavad vastavalt täisnurkse kolmnurga, kaabli pikkuse leidmiseks saab kasutada Pythagorase teoreemi:
Seega on kaabli pikkus ligikaudu 3,6 meetrit.
Arvestades: kaugus punktist R punktini P (kolmnurga jalg) on 24, punktist R punktini Q (hüpotenuus) - 26.
Niisiis, aitame Vityal probleemi lahendada. Kuna joonisel kujutatud kolmnurga küljed peaksid moodustama täisnurkse kolmnurga, saate kolmanda külje pikkuse leidmiseks kasutada Pythagorase teoreemi:
Niisiis, tiigi laius on 10 meetrit.
Sergei Valerievitš
Pythagorase teoreem
Pythagorase teoreem- üks eukleidilise geomeetria põhiteoreeme, mis määrab seose
täisnurkse kolmnurga külgede vahele.
Arvatakse, et selle tõestas kreeka matemaatik Pythagoras, kelle järgi see ka nime sai.
Pythagorase teoreemi geomeetriline sõnastus.
Teoreem oli algselt sõnastatud järgmiselt:
Täisnurkses kolmnurgas on hüpotenuusile ehitatud ruudu pindala võrdne ruutude pindalade summaga,
ehitatud kateetritele.
Pythagorase teoreemi algebraline sõnastus.
Täisnurkses kolmnurgas on hüpotenuusi pikkuse ruut võrdne jalgade pikkuste ruutude summaga.
See tähendab läbiva kolmnurga hüpotenuusi pikkust c, ja jalgade pikkused läbi a ja b:
Mõlemad koostised Pythagorase teoreemid on samaväärsed, kuid teine sõnastus on elementaarsem, aga mitte
nõuab pindala mõistet. See tähendab, et teist väidet saab kontrollida ilma piirkonnast midagi teadmata ja
mõõtes ainult täisnurkse kolmnurga külgede pikkusi.
Pythagorase pöördteoreem.
Kui kolmnurga ühe külje ruut on võrdne kahe teise külje ruutude summaga, siis
kolmnurk on ristkülikukujuline.
Või teisisõnu:
Mis tahes positiivsete arvude kolmiku korral a, b ja c, selline, et
on täisnurkne kolmnurk jalgadega a ja b ja hüpotenuus c.
Pythagorase teoreem võrdhaarse kolmnurga jaoks.

Pythagorase teoreem võrdkülgse kolmnurga jaoks.

Pythagorase teoreemi tõestused.
Hetkel on teaduskirjanduses kirja pandud 367 selle teoreemi tõestust. Ilmselt teoreem
Pythagoras on ainus teoreem, millel on nii muljetavaldav hulk tõestusi. Selline mitmekesisus
saab seletada ainult teoreemi fundamentaalse tähtsusega geomeetria jaoks.
Mõistagi võib neid kõiki jagada väheseks arvuks klassideks. Tuntuimad neist:
tõestus pindala meetod, aksiomaatiline ja eksootilised tõendid(Näiteks,
kaudu diferentsiaalvõrrandid).
1. Pythagorase teoreemi tõestus sarnaste kolmnurkade järgi.
Järgmine algebralise formuleeringu tõestus on konstrueeritud tõestustest lihtsaim
otse aksioomidest. Eelkõige ei kasuta see figuuri pindala mõistet.
Las olla ABC on täisnurkne kolmnurk C. Joonistame kõrguse C ja tähistada
selle vundament läbi H.
Kolmnurk ACH sarnane kolmnurgaga AB C kahes nurgas. Samamoodi kolmnurk CBH sarnased ABC.
Märkuse sisseviimisega:

saame:
![]() ,
,
mis sobib -
Olles voltinud a 2 ja b 2, saame:
või , mida tuli tõestada.
2. Pythagorase teoreemi tõestamine pindalameetodil.
Vaatamata näilisele lihtsusele pole järgmised tõestused sugugi nii lihtsad. Kõik nemad
kasutada ala omadusi, mille tõestamine on keerulisem kui Pythagorase teoreemi enda tõestamine.
- Tõestus võrdväärse komplemendi kaudu.
 Korraldage neli võrdset ristkülikukujulist
Korraldage neli võrdset ristkülikukujulist
kolmnurk, nagu pildil näidatud
paremal.
Nelinurk külgedega c- ruut,
kuna kahe teravnurga summa on 90° ja
arendatud nurk on 180°.
Kogu figuuri pindala on ühelt poolt
küljega ruudu pindala ( a+b) ja teisest küljest pindalade summa neli kolmnurka ja
![]()
![]()
Q.E.D.
3. Pythagorase teoreemi tõestamine lõpmatuarvu meetodil.

Arvestades joonisel näidatud joonist ja
jälgides, kuidas pool muutuba, me saame
kirjuta lõpmatu jaoks järgmine seos
väike külgmised juurdekasvudkoos ja a(kasutades sarnasust
kolmnurgad):
Kasutades muutujate eraldamise meetodit, leiame:
Üldisem väljend hüpotenuusi muutmiseks mõlema jala juurdekasvu korral:
Integreerimine antud võrrand ja kasutades algtingimusi, saame:
Seega jõuame soovitud vastuseni:
Nagu on lihtne näha, ilmneb lõplikus valemis ruutsõltuvus lineaarsuse tõttu
proportsionaalsus kolmnurga külgede ja juurdekasvu vahel, samas kui summa on seotud sõltumatuga
panused erinevate jalgade juurdekasvust.
Lihtsama tõestuse saab, kui eeldame, et üks jalg ei koge juurdekasvu
(sisse sel juhul jalg b). Seejärel saame integreerimiskonstandi jaoks:
(Berliini muuseumi Papyrus 6619 järgi). Cantori sõnul ehitasid harpedonaptid ehk "nööripingutid" täisnurki, kasutades täisnurkseid kolmnurki külgedega 3, 4 ja 5.
Nende ehitusmeetodit on väga lihtne reprodutseerida. Võtke 12 m pikkune köis ja siduge see selle külge mööda värvilist riba 3 m kaugusel ühest otsast ja 4 meetri kaugusel teisest otsast. 3–4 meetri pikkuste külgede vahele jääb täisnurk. Harpedonaptidele võib vastu vaielda, et nende ehitusmeetod muutub üleliigseks, kui kasutatakse näiteks kõigi puuseppade kasutatavat puidust ruutu. Tõepoolest, on teada Egiptuse joonised, millelt selline tööriist on leitud - näiteks joonised, mis kujutavad puusepatöökoda.
Babüloonlaste seas on Pythagorase teoreemi kohta mõnevõrra rohkem teada. Ühes tekstis, mis pärineb Hammurapi ajast, see tähendab aastast 2000 eKr. e. , on antud täisnurkse kolmnurga hüpotenuusi ligikaudne arvutus. Sellest võime järeldada, et Mesopotaamias suudeti vähemalt mõnel juhul teha arvutusi täisnurksete kolmnurkadega. Tuginedes ühelt poolt Egiptuse ja Babüloonia matemaatika teadmiste praegusele tasemele ning teiselt poolt Kreeka allikate kriitilisele uurimisele, järeldas Van der Waerden (Hollandi matemaatik), et on suur tõenäosus, et hüpotenuusi ruudu teoreem oli Indias tuntud juba umbes 18. sajandil eKr. e.
Umbes 400 eKr. e. Procluse järgi andis Platon meetodi Pythagorase kolmikute leidmiseks, ühendades algebra ja geomeetria. Umbes 300 eKr. e. Eukleidese elemendid sisaldab Pythagorase teoreemi vanimat aksiomaatilist tõestust.
Sõnastus
Geomeetriline koostis:
Teoreem oli algselt sõnastatud järgmiselt:
Algebraline formuleering:
See tähendab, et tähistab läbiva kolmnurga hüpotenuusi pikkust ja läbivate jalgade pikkust ja:
Teoreemi mõlemad sõnastused on samaväärsed, kuid teine formuleering on elementaarsem, see ei nõua pindala mõistet. See tähendab, et teist väidet saab kontrollida pindala kohta midagi teadmata ja mõõtes ainult täisnurkse kolmnurga külgede pikkusi.
Pythagorase pöördteoreem:
Tõestus
Hetkel on teaduskirjanduses kirja pandud 367 selle teoreemi tõestust. Tõenäoliselt on Pythagorase teoreem ainus teoreem, millel on nii muljetavaldav hulk tõestusi. Sellist mitmekesisust saab seletada ainult teoreemi põhimõttelise tähtsusega geomeetria jaoks.
Mõistagi võib neid kõiki jagada väheseks arvuks klassideks. Tuntuimad neist: tõestused pindalameetodil, aksiomaatilised ja eksootilised tõestused (näiteks diferentsiaalvõrrandite abil).
Läbi sarnaste kolmnurkade
Järgnev algebralise formuleeringu tõestus on otse aksioomidest koostatud tõestustest lihtsaim. Eelkõige ei kasuta see figuuriala mõistet.

Las olla ABC on täisnurkne kolmnurk C. Joonistame kõrguse C ja tähistage selle alust H. Kolmnurk ACH sarnane kolmnurgaga ABC kahes nurgas. Samamoodi kolmnurk CBH sarnased ABC. Noodikirja tutvustamine
saame
Mis on samaväärne
Lisades saame
, mida tuli tõestadaPiirkonna tõendid
Vaatamata näilisele lihtsusele pole järgmised tõestused sugugi nii lihtsad. Kõik need kasutavad ala omadusi, mille tõestamine on keerulisem kui Pythagorase teoreemi enda tõestamine.
Tõestus samaväärsuse kaudu
- Asetage neli võrdset täisnurkset kolmnurka, nagu on näidatud joonisel 1.
- Nelinurk külgedega c on ruut, sest kahe teravnurga summa on 90° ja sirgnurk on 180°.
- Kogu joonise pindala on ühelt poolt võrdne ruudu pindalaga küljega (a + b) ja teiselt poolt nelja kolmnurga pindalade ja pindala summaga. siseväljakult.
Q.E.D.
Eukleidese tõestus
Eukleidese tõestuse idee on järgmine: proovime tõestada, et pool hüpotenuusile ehitatud ruudu pindalast võrdub jalgadele ehitatud ruutude poolte pindalade summaga ja seejärel suur ja kaks väikest ruutu on võrdsed.
Mõelge vasakpoolsele joonisele. Sellele ehitasime täisnurkse kolmnurga külgedele ruudud ja joonistasime täisnurga C tipust s kiirte s, mis on risti hüpotenuusiga AB, see lõikab hüpotenuusile ehitatud ruudu ABIK kaheks ristkülikuks - BHJI ja HAKJ, vastavalt. Selgub, et nende ristkülikute pindalad on täpselt võrdsed vastavatele jalgadele ehitatud ruutude pindaladega.
Proovime tõestada, et ruudu DECA pindala on võrdne ristküliku pindalaga AHJK Selleks kasutame abivaatlust: antud kolmnurga pindala, mille kõrgus ja alus on sama kui antud. ristkülik on võrdne poolega antud ristküliku pindalast. See tuleneb sellest, et kolmnurga pindala on pool aluse ja kõrguse korrutisest. Sellest tähelepanekust järeldub, et kolmnurga ACK pindala on võrdne kolmnurga AHK pindalaga (pole näidatud), mis omakorda on võrdne poolega ristküliku AHJK pindalast.
Tõestame nüüd, et kolmnurga ACK pindala on samuti võrdne poolega DECA ruudu pindalast. Ainus asi, mida selleks teha tuleb, on kolmnurkade ACK ja BDA võrdsuse tõestamine (kuna kolmnurga BDA pindala on ülaltoodud omaduse võrra võrdne poole ruudu pindalaga). See võrdsus on ilmne: kolmnurga kaks külge ja nendevaheline nurk on võrdsed. Nimelt - AB=AK, AD=AC - nurkade CAK ja BAD võrdsust on lihtne tõestada liikumismeetodiga: pöörame kolmnurka CAK 90° vastupäeva, siis on ilmne, et kahe vaadeldava kolmnurga vastavad küljed langevad kokku. (tulenevalt asjaolust, et nurga ruudu tipus on 90°).
Argument ruudu BCFG ja ristküliku BHJI pindalade võrdsuse kohta on täiesti analoogne.
Seega oleme tõestanud, et hüpotenuusile ehitatud ruudu pindala on jalgadele ehitatud ruutude pindalade summa. Idee see tõend illustreeritud täiendavalt ülaltoodud animatsiooniga.
Leonardo da Vinci tõend
Tõestuse põhielemendid on sümmeetria ja liikumine.
Mõelge joonisele, nagu sümmeetriast näha, lõikab segment ruudu kaheks identseks osaks (kuna kolmnurgad ja on ehituselt võrdsed).
Kasutades 90-kraadist vastupäeva pööramist ümber punkti, näeme varjutatud kujundite ja võrdsust.
Nüüd on selge, et meie poolt varjutatud kujundi pindala on võrdne väikeste (jalgadele ehitatud) ruutude pindala ja algse kolmnurga pindala summaga. Teisest küljest on see võrdne poole suure ruudu pindalast (ehitatud hüpotenuusile) pluss esialgse kolmnurga pindala. Seega on pool väikeste ruutude pindalade summast võrdne poolega suure ruudu pindalast ja seetõttu võrdub jalgadele ehitatud ruutude pindalade summa ehitatud ruudu pindalaga. hüpotenuusil.
Tõestus lõpmatu väikese meetodiga
Järgnev tõestus diferentsiaalvõrrandite abil on sageli omistatud üldtuntud Inglise matemaatik Hardy, kes elas 20. sajandi esimesel poolel.
Arvestades joonisel näidatud joonist ja jälgides külje muutust a, saame kirjutada järgmise seose lõpmatute külgmiste juurdekasvude jaoks koos ja a(kasutades sarnaseid kolmnurki):
Kasutades muutujate eraldamise meetodit, leiame
Üldisem väljend hüpotenuusi muutmiseks mõlema jala juurdekasvu korral
Integreerides selle võrrandi ja kasutades algtingimusi, saame
Seega jõuame soovitud vastuseni
On lihtne näha, et lõpliku valemi ruutsõltuvus ilmneb kolmnurga külgede ja sammude vahelise lineaarse proportsionaalsuse tõttu, samas kui summa on tingitud erinevate jalgade juurdekasvu sõltumatutest panustest.
Lihtsama tõestuse saab, kui eeldame, et üks jalg ei koge juurdekasvu (antud juhul jalg). Seejärel saame integratsioonikonstandi jaoks
Variatsioonid ja üldistused
Sarnased geomeetrilised kujundid kolmel küljel
Üldistus jaoks sarnased kolmnurgad, roheliste kujundite pindala A + B = sinise C pindala
Pythagorase teoreem, kasutades sarnaseid täisnurkseid kolmnurki
Pythagorase teoreemi üldistuse tegi Euclid oma töös Algused, laiendades külgedel olevate ruutude alasid sarnaste piirkondadeni geomeetrilised kujundid :
Kui konstrueerida sarnased geomeetrilised kujundid (vt Eukleidiline geomeetria) täisnurkse kolmnurga külgedele, võrdub kahe väiksema kujundi summa suurema kujundi pindalaga.
Selle üldistuse põhiidee seisneb selles, et sellise geomeetrilise kujundi pindala on võrdeline selle lineaarse mõõtme ruuduga ja eriti mis tahes külje pikkuse ruuduga. Seetõttu pindaladega sarnaste näitajate puhul A, B ja C ehitatud külgedele pikkusega a, b ja c, meil on:
Kuid Pythagorase teoreemi kohaselt a 2 + b 2 = c 2, siis A + B = C.
Ja vastupidi, kui suudame seda tõestada A + B = C kolme sarnase geomeetrilise kujundi puhul ilma Pythagorase teoreemi kasutamata saame tõestada teoreemi ennast, liikudes vastupidine suund. Näiteks saab alustavat keskkolmnurka kolmnurgana uuesti kasutada C hüpotenuusil ja kaks sarnast täisnurkset kolmnurka ( A ja B), mis on ehitatud kahele teisele küljele, mis tekivad keskse kolmnurga kõrgusega jagamisel. Kolmnurkade kahe väiksema pindala summa on siis ilmselgelt võrdne kolmanda pindalaga, seega A + B = C ja järgides eelmisi tõestusi vastupidises järjekorras, saame Pythagorase teoreemi a 2 + b 2 = c 2 .
Koosinusteoreem
Pythagorase teoreem on erijuhtum rohkem üldine teoreem koosinused, mis seostab suvalise kolmnurga külgede pikkusi:
kus θ on külgede vaheline nurk a ja b.
Kui θ on 90 kraadi, siis cos θ = 0 ja valem on lihtsustatud tavalise Pythagorase teoreemiga.
Suvaline kolmnurk
Suvalise külgedega kolmnurga mis tahes valitud nurka a, b, c kirjutama võrdhaarse kolmnurga nii, et võrdsed nurgad selle põhjas võrdus θ valitud nurgaga. Oletame, et valitud nurk θ asub näidatud külje vastas c. Selle tulemusena saime kolmnurga ABD nurgaga θ, mis asub külje vastas a ja peod r. Teise kolmnurga moodustab nurk θ, mis on külje vastas b ja peod koos pikk s, nagu pildil näidatud. Thabit Ibn Qurra väitis, et nende kolme kolmnurga küljed on seotud järgmiselt:
Kui nurk θ läheneb π/2-le, siis alus võrdhaarne kolmnurk väheneb ning kaks külge r ja s kattuvad üha vähem. Kui θ = π/2, muutub ADB täisnurkseks kolmnurgaks, r + s = c ja saame esialgse Pythagorase teoreemi.
Vaatame üht argumenti. Kolmnurk ABC on samad nurgad nagu kolmnurgal ABD, kuid vastupidises järjekorras. (Kahel kolmnurgal on tipus B ühine nurk, mõlemal on nurk θ ja neil on ka sama kolmas nurk kolmnurga nurkade summa võrra) Sellest tulenevalt on ABC sarnane kolmnurga DBA peegeldusega ABD, nagu näidatud. alumisel joonisel. Kirjutame vahelise seose vastasküljed ja nurga θ kõrval,
Nii on ka teise kolmnurga peegeldus,
Korrutage murrud ja lisage need kaks suhet:
Q.E.D.
Üldistus suvaliste kolmnurkade jaoks rööpküliku abil
Üldistus jaoks suvalised kolmnurgad,
roheline ala krunt = pindala sinine
Lõputöö tõestus, et ülaltoodud joonisel
Teeme täiendava üldistuse mitteristkülikukujuliste kolmnurkade jaoks, kasutades ruutude asemel rööpkülikuid kolmel küljel. (ruudud on erijuht.) Ülemine joonis näitab, et jaoks terav kolmnurk rööpküliku pindala pikal küljel on võrdne kahe teise külje rööpküliku summaga eeldusel, et pika külje rööpkülik on ehitatud joonisel näidatud viisil (nooltega tähistatud mõõtmed on samad ja määrata alumise rööpküliku küljed). See ruutude asendamine rööpkülikutega sarnaneb selgelt algse Pythagorase teoreemiga ja arvatakse, et selle sõnastas Aleksandria Pappus aastal 4 e.m.a. e.
Alumine joonis näitab tõestuse edenemist. Vaatame kolmnurga vasakut külge. Vasakpoolsel rohelisel rööpkülikul on sama pindala kui sinise rööpküliku vasakul küljel, kuna neil on sama alus b ja kõrgus h. Samuti on vasakpoolsel rohelisel kastil sama ala, mis ülemisel pildil vasakpoolsel rohelisel kastil, sest neil on ühisosa(ülemine vasakul pool kolmnurk) ja kogukõrgus kolmnurga selle küljega risti. Sarnaselt kolmnurga parema külje üle argumenteerides tõestame, et alumisel rööpkülikul on sama pindala kui kahel rohelisel rööpkülikul.
Keerulised numbrid
Pythagorase teoreemi kasutatakse kahe punkti vahelise kauguse leidmiseks Descartes'i koordinaatsüsteemis ja see teoreem kehtib kõigi tõeliste koordinaatide kohta: kaugus. s kahe punkti vahel ( a, b) ja ( c, d) võrdub
Valemiga probleeme ei teki, kui kompleksarve käsitletakse reaalkomponentidega vektoritena x + mina y = (x, y). . Näiteks vahemaa s vahemikus 0 + 1 i ja 1 + 0 i arvutada vektori moodulina (0, 1) − (1, 0) = (−1, 1), või
Keeruliste koordinaatidega vektoritega tehtavate toimingute jaoks on aga Pythagorase valemit vaja teatud määral täiustada. Punktide vaheline kaugus koos kompleksarvud (a, b) ja ( c, d); a, b, c, ja d on kõik keerulised, sõnastame kasutades absoluutväärtused. Kaugus s põhineb vektorite erinevusel (a − c, b − d) sisse järgmine vorm: lase vahet teha a − c = lk+i q, kus lk on erinevuse tegelik osa, q on imaginaarne osa ja i = √(−1). Samamoodi lase b − d = r+i s. Seejärel:
kus on komplekskonjugaat . Näiteks punktide vaheline kaugus (a, b) = (0, 1) ja (c, d) = (i, 0) , arvutage erinevus (a − c, b − d) = (−i, 1) ja tulemus oleks 0, kui komplekskonjugaate ei kasutata. Seega, kasutades täiustatud valemit, saame
Moodul on määratletud järgmiselt:
Stereomeetria
Kolmemõõtmelise ruumi Pythagorase teoreemi oluline üldistus on de Gua teoreem, mis sai nime J.-P. de Gua: kui tetraeedril on täisnurk (nagu kuubil), siis on täisnurga vastas oleva tahu pindala ruut võrdne ülejäänud kolme tahu pindalade ruutude summaga. Selle järelduse võib kokku võtta järgmiselt: n-mõõtmeline Pythagorase teoreem":
Pythagorase teoreem kolmemõõtmeline ruumühendab diagonaali AD kolme küljega.
Veel üks üldistus: Pythagorase teoreemi saab stereomeetriale rakendada järgmisel kujul. Kaaluge risttahukas, nagu pildil näidatud. Leidke diagonaali BD pikkus Pythagorase teoreemi abil:
kus kolm külge moodustavad täisnurkse kolmnurga. Kasutage horisontaalset diagonaali BD ja vertikaalset serva AB, et leida diagonaali AD pikkus, kasutades taas Pythagorase teoreemi:
või kui kõik on kirjutatud ühes võrrandis:
See tulemus on 3D-avaldis vektori suuruse määramiseks v(diagonaal AD), väljendatuna selle risti olevate komponentidena ( v k) (kolm üksteisega risti olevat külge):
Seda võrrandit võib vaadelda kui Pythagorase teoreemi üldistust mitmemõõtmelise ruumi jaoks. Tulemuseks pole aga tegelikult midagi muud kui Pythagorase teoreemi korduv rakendamine täisnurksete kolmnurkade jadale järjestikku risti asetsevatel tasapindadel.
vektorruum
Ortogonaalse vektorite süsteemi korral toimub võrdsus, mida nimetatakse ka Pythagorase teoreemiks:
Kui on vektori projektsioon koordinaatteljed, siis see valem langeb kokku eukleidilise kaugusega - ja tähendab, et vektori pikkus on võrdne juurega ruutsumma selle komponentide ruudud.
Selle võrdsuse analoog kaasuses lõputu süsteem vektoreid nimetatakse Parsevali võrduseks.
Mitteeukleidiline geomeetria
Pythagorase teoreem on tuletatud Eukleidilise geomeetria aksioomidest ja tegelikult ei kehti mitteeukleidilise geomeetria puhul sellisel kujul, nagu see on ülalpool kirjutatud. (See tähendab, et Pythagorase teoreem osutub omamoodi ekvivalendiks Eukleidese paralleelsuse postulaadile) Teisisõnu, mitte-eukleidilises geomeetrias on kolmnurga külgede suhe paratamatult Pythagorase teoreemist erineval kujul. . Näiteks sfäärilises geomeetrias on täisnurkse kolmnurga kõik kolm külge (näiteks a, b ja c), mis seob ühikkera oktanti (kaheksandikku), on pikkusega π/2, mis on vastuolus Pythagorase teoreemiga, sest a 2 + b 2 ≠ c 2 .
Vaatleme siin kahte mitteeukleidilise geomeetria juhtumit – sfäärilist ja hüperboolset geomeetriat; mõlemal juhul, nagu täisnurksete kolmnurkade eukleidilise ruumi puhul, tuleneb Pythagorase teoreemi asendav tulemus koosinusteoreemist.
Siiski jääb Pythagorase teoreem kehtima hüperboolse ja elliptilise geomeetria puhul, kui kolmnurga täisnurksuse nõue asendatakse tingimusega, et kolmnurga kahe nurga summa peab olema võrdne kolmandaga, ütleme A+B = C. Siis näeb külgede suhe välja selline: läbimõõduga ringide pindalade summa a ja b võrdne läbimõõduga ringi pindalaga c.
sfääriline geomeetria
Mis tahes täisnurkse kolmnurga jaoks raadiusega sfääril R(näiteks kui nurk γ kolmnurgas on õige) külgedega a, b, c pooltevahelised suhted näevad välja järgmised:
Seda võrdsust saab tuletada järgmiselt erijuhtum sfäärilise koosinuse teoreem, mis kehtib kõigi sfääriliste kolmnurkade puhul:
kus cosh on hüperboolne koosinus. See valem on hüperboolse koosinusteoreemi erijuhtum, mis kehtib kõigi kolmnurkade puhul:
kus γ on nurk, mille tipp on külje vastas c.
kus g ij nimetatakse meetriliseks tenoriks. See võib olla positsioonifunktsioon. Sellised kõverjoonelised ruumid hõlmavad Riemanni geomeetriat nagu üldine näide. See formulatsioon sobib ka Eukleidilise ruumi jaoks, kui kasutatakse kõverjoonelisi koordinaate. Näiteks selleks polaarkoordinaadid:
vektorprodukt
Pythagorase teoreem ühendab kaks vektorkorrutise suuruse avaldist. Üks lähenemisviis ristkorrutise määratlemiseks nõuab, et see vastaks võrrandile:
see valem kasutab punktkorrutist. Võrrandi paremat poolt nimetatakse Grami determinandiks a ja b, mis on võrdne nende kahe vektori moodustatud rööpküliku pindalaga. Lähtudes sellest nõudest, samuti nõudest, et vektorkorrutis peab olema oma komponentidega risti a ja b sellest järeldub, et vektorkorrutis on defineeritud ainult kolme- ja seitsmemõõtmelisena, välja arvatud 0- ja 1-mõõtmelise ruumi triviaalsed juhud. Kasutame nurga määratlust in n- mõõtmete ruum:
see vektorkorrutise omadus annab selle väärtuse järgmisel kujul:
Põhimõtte kaudu trigonomeetriline identiteet Pythagoras, saame selle väärtuse kirjutamiseks teistsuguse vormi:
Alternatiivne lähenemisviis ristprodukti määratlemiseks kasutab selle suurusjärgu avaldist. Seejärel, vaieldes vastupidises järjekorras, saame seose skalaarkorrutis:
Vaata ka
Märkmed
- Ajaloo teema: Pythagorase teoreem Babüloonia matemaatikas
- ( , lk 351) lk 351
- ( , I köide, lk 144)
- Arutelu ajaloolised faktid antud (, lk 351) lk 351
- Kurt Von Fritz (apr., 1945). "Metapontumi Hippasuse poolt võrreldamatuse avastus". Matemaatika aastaraamatud, teine seeria(Matemaatika aastaraamatud) 46 (2): 242–264.
- Lewis Carroll, "Lugu sõlmedega", M., Mir, 1985, lk. 7
- Asger Aaboe Episoodid matemaatika varasest ajaloost. - Mathematical Association of America, 1997. - Lk 51. - ISBN 0883856131
- Pythagorase propositsioon autor Elisha Scott Loomis
- Eukleidese oma Elemendid: VI raamat, VI 31. väide: "Täisnurksete kolmnurkade korral on täisnurka piiraval küljel olev kujund võrdne sarnaste ja sarnaselt kirjeldatud kujunditega täisnurka sisaldavatel külgedel."
- Lawrence S. Leff viidatud töö. - Barroni õppesari. - Lk 326. - ISBN 0764128922
- Howard Whitley Eves§4.8:...Pythagorase teoreemi üldistus // Suured hetked matemaatikas (enne 1650) . - Ameerika Matemaatikaliit, 1983. - Lk 41. - ISBN 0883853108
- Tâbit ibn Qorra (täisnimi Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826–901 pKr) oli Bagdadis elanud arst, kes kirjutas palju Eukleidese elementidest. ja teised matemaatilised ained.
- Aydin Sayili (märts 1960). "Thâbit ibn Qurra Pythagorase teoreemi üldistus". Isis 51 (1): 35–37. DOI: 10.1086/348837.
- Judith D. Sally, Paul Sally Harjutus 2.10(ii) // Viidatud töö . - Lk 62. - ISBN 0821844032
- Sellise konstruktsiooni üksikasju vt George Jennings Joonis 1.32: Üldistatud Pythagorase teoreem // Kaasaegne geomeetria rakendustega: 150 joonisega . - 3. - Springer, 1997. - Lk 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcyüksus C: Norm suvalise jaoks n-tuple ... // Sissejuhatus analüüsi . - Springer, 1995. - Lk 124. - ISBN 0387943692 Vaata ka lk 47-50.
- Alfred Gray, Elsa Abbena, Simon Salamon Kaasaegne kõverate ja pindade diferentsiaalgeomeetria Mathematicaga. - 3. - CRC Press, 2006. - Lk 194. - ISBN 1584884487
- Rajendra Bhatia maatriksanalüüs. - Springer, 1997. - Lk 21. - ISBN 0387948465
- Stephen W. Hawking viidatud töö. - 2005. - Lk 4. - ISBN 0762419229
- Eric W. Weisstein CRC lühike matemaatika entsüklopeedia. - 2. - 2003. - Lk 2147. - ISBN 1584883472
- Aleksander R. Pruss
Keskmine tase
Täisnurkne kolmnurk. Täielik illustreeritud juhend (2019)
PARIM KOLMNURK. ESIMESE TASE.
Ülesannete korral pole täisnurk üldse vajalik - alumine vasak, nii et peate õppima, kuidas sellel kujul täisnurkset kolmnurka ära tunda,

ja sellises

ja sellises 
Mis on täisnurkses kolmnurgas head? Noh... esiteks on seal erilised ilusad nimed tema külgede jaoks.
Tähelepanu joonisele!

Pidage meeles ja ärge ajage segadusse: jalad - kaks ja hüpotenuus - ainult üks(ainus, ainulaadne ja pikim)!
Noh, arutasime nimesid, nüüd kõige olulisemat: Pythagorase teoreemi.
Pythagorase teoreem.
See teoreem on võti paljude täisnurkse kolmnurgaga seotud probleemide lahendamiseks. Seda tõestas Pythagoras täiesti ammustel aegadel ja sellest ajast alates on see toonud palju kasu neile, kes seda teavad. Ja parim asi tema juures on see, et ta on lihtne.
Niisiis, Pythagorase teoreem:
Kas mäletate nalja: "Pythagorase püksid on igast küljest võrdsed!"?
Joonistame need väga Pythagorase püksid ja vaatame neid. 
Kas see näeb tõesti välja nagu lühikesed püksid? Noh, mis pooltel ja kus nad on võrdsed? Miks ja kust nali tuli? Ja see nali on seotud just Pythagorase teoreemiga, täpsemalt sellega, kuidas Pythagoras ise oma teoreemi sõnastas. Ja ta sõnastas selle järgmiselt:
"Summa ruutude pindala, ehitatud jalgadele, on võrdne ruudu pindala ehitatud hüpotenuusile.
Kas see ei kõla veidi teisiti, kas pole? Ja nii, kui Pythagoras joonistas oma teoreemi avalduse, selgus just selline pilt.

Sellel pildil on väikeste ruutude pindalade summa võrdne suure ruudu pindalaga. Ja et lapsed mäletaksid paremini, et jalgade ruutude summa võrdub hüpotenuusi ruuduga, mõtles keegi vaimukas selle nalja Pythagorase pükste kohta.
Miks me nüüd Pythagorase teoreemi sõnastame
Kas Pythagoras kannatas ja rääkis väljakutest?
Näete, iidsetel aegadel polnud ... algebrat! Mingeid märke polnud ja nii edasi. Silte polnud. Kas kujutate ette, kui kohutav oli vaestel muistsetel õpilastel kõike sõnadega pähe õppida??! Ja me võime olla rõõmsad, et meil on Pythagorase teoreemi lihtne sõnastus. Kordame seda uuesti, et paremini meeles pidada:
Nüüd peaks see olema lihtne:
| Hüpotenuusi ruut võrdub jalgade ruutude summaga. |
Noh, arutati kõige olulisemat teoreemi täisnurkse kolmnurga kohta. Kui te ei tea, kuidas see on tõestatud, lugege edasi. järgmised tasemed teooria ja liigume nüüd edasi ... juurde pime mets... trigonomeetria! Kohutavatele sõnadele siinus, koosinus, puutuja ja kotangent.
Siinus, koosinus, puutuja, kotangens täisnurkses kolmnurgas.
Tegelikult pole kõik üldse nii hirmus. Muidugi tuleks artiklis vaadata siinuse, koosinuse, puutuja ja kotangensi "päris" määratlust. Aga sa tõesti ei taha, eks? Võime rõõmustada: täisnurkse kolmnurga probleemide lahendamiseks võite lihtsalt täita järgmised lihtsad asjad:
Miks on kõik nurga all? Kus on nurk? Selle mõistmiseks peate teadma, kuidas väiteid 1–4 sõnadega kirjutatakse. Vaata, mõista ja jäta meelde!
1.
See kõlab tegelikult nii:
Aga nurk? Kas on jalg, mis on nurga vastas, st vastasjalg (nurga jaoks)? Muidugi on! See on kateet!
Aga kuidas on nurgaga? Vaata lähemalt. Milline jalg külgneb nurgaga? Muidugi, kass. Niisiis, nurga jaoks on jalg külgnev ja
Ja nüüd tähelepanu! Vaata, mis meil on:
Vaadake, kui suurepärane see on:
Liigume nüüd puutuja ja kotangensi juurde.
Kuidas seda nüüd sõnadesse panna? Mis on jalg nurga suhtes? Muidugi vastas – see "lemab" nurga vastas. Ja kateet? Kõrval nurgaga. Mida me siis saime?
Kas näete, kuidas lugeja ja nimetaja on ümber pööratud?
Ja nüüd jälle nurgad ja vahetus tehtud:
Kokkuvõte
Paneme õpitu lühidalt kirja.
 |
Pythagorase teoreem: |
Peamine täisnurkse kolmnurga teoreem on Pythagorase teoreem.
Pythagorase teoreem
Muide, kas mäletate hästi, mis on jalad ja hüpotenuus? Kui ei, siis vaata pilti – värskenda oma teadmisi

On täiesti võimalik, et olete Pythagorase teoreemi juba korduvalt kasutanud, kuid kas olete kunagi mõelnud, miks selline teoreem on tõene. Kuidas sa seda tõestaksid? Teeme nii nagu vanad kreeklased. Joonistame küljega ruudu.

Näete, kui kavalalt me selle küljed pikkusteks jagasime!
Nüüd ühendame märgitud punktid

Siin aga märkisime veel midagi, aga vaata ise pilti ja mõtle, miks.
Kui suur on suurema ruudu pindala? Õigesti,. Aga väiksema alaga? Kindlasti,. Nelja nurga kogupindala jääb alles. Kujutage ette, et me võtsime neist kaks ja nõjatusime hüpotenuusidega üksteise vastu. Mis juhtus? Kaks ristkülikut. Seega on "pistikute" pindala võrdne.
Paneme nüüd kõik kokku.
Muutame:
Niisiis külastasime Pythagorast – tõestasime tema teoreemi iidsel moel.
Täisnurkne kolmnurk ja trigonomeetria
Täisnurkse kolmnurga puhul kehtivad järgmised seosed:

Sinus teravnurk võrdne vastasjala ja hüpotenuusi suhtega
Terava nurga koosinus võrdub külgneva jala ja hüpotenuusi suhtega.
Teravnurga puutuja on võrdne vastasjala ja külgneva jala suhtega.
Teravnurga kotangens on võrdne külgneva jala ja vastasjala suhtega.
Ja veel kord, kõik see taldriku kujul:
See on väga mugav!
Täisnurksete kolmnurkade võrdsuse märgid
I. Kahel jalal

II. Jala ja hüpotenuusiga

III. Hüpotenuusi ja teravnurga järgi

IV. Mööda jalga ja teravnurka
a) 
b) 
Tähelepanu! Siin on väga oluline, et jalad oleksid "vastavad". Näiteks kui see läheb nii:

SIIS EI OLE KOLMNURGAD VÕRDSED, hoolimata asjaolust, et neil on üks identne teravnurk.
Vaja mõlemas kolmnurgas oli jalg külgnev või mõlemas vastas.
Kas olete märganud, kuidas täisnurksete kolmnurkade võrdusmärgid erinevad tavalistest kolmnurkade võrdusmärkidest? Vaadake teemat "ja pöörake tähelepanu asjaolule, et "tavaliste" kolmnurkade võrdsuse jaoks on vaja nende kolme elemendi võrdsust: kaks külge ja nendevaheline nurk, kaks nurka ja nendevaheline külg või kolm külge. Kuid täisnurksete kolmnurkade võrdsuse jaoks piisab ainult kahest vastavast elemendist. See on suurepärane, eks?
Ligikaudu sama olukord täisnurksete kolmnurkade sarnasusmärkidega.
Täisnurksete kolmnurkade sarnasuse märgid
I. Äge nurk

II. Kahel jalal

III. Jala ja hüpotenuusiga

Mediaan täisnurkses kolmnurgas
Miks see nii on?
Mõelge täisnurkse kolmnurga asemel tervele ristkülikule.
Joonistame diagonaali ja vaatleme punkti – diagonaalide lõikepunkti. Mida teate ristküliku diagonaalide kohta?
Ja mis sellest järeldub?
Nii juhtuski
- - mediaan:
Pidage meeles seda fakti! Aitab palju!
Veelgi üllatavam on see, et ka vastupidine on tõsi.
Mida kasu saab sellest, et hüpotenuusile tõmmatud mediaan võrdub poolega hüpotenuusist? Vaatame pilti
Vaata lähemalt. Meil on: , see tähendab, et kaugused punktist kolmnurga kõigi kolme tipuni osutusid võrdseks. Kuid kolmnurgas on ainult üks punkt, mille kaugused on kolmnurga kõik kolm tippu võrdsed, ja see on KIRJELDATUD RINGIME KESK. Mis juhtus?
Nii et alustame sellest "pealegi...".
Vaatame i.
Kuid sarnastes kolmnurkades on kõik nurgad võrdsed!
Sama võib öelda ja
Nüüd joonistame selle koos:
Mis kasu on sellest "kolmekordsest" sarnasusest.
No näiteks - kaks valemit täisnurkse kolmnurga kõrguse jaoks.
Kirjutame vastavate osapoolte suhted:

Kõrguse leidmiseks lahendame proportsiooni ja saame esimene valem "Kõrgus täisnurkses kolmnurgas":
Niisiis, rakendame sarnasust: .

Mis nüüd saab?
Jällegi lahendame proportsiooni ja saame teise valemi:
Neid mõlemaid valemeid tuleb väga hästi meeles pidada ja seda, mida on mugavam rakendada. Paneme need uuesti kirja.
Pythagorase teoreem:
Täisnurkses kolmnurgas on hüpotenuusi ruut võrdne jalgade ruutude summaga:.

Täisnurksete kolmnurkade võrdsuse märgid:
- kahel jalal:
- piki jalga ja hüpotenuusi: või
- piki jalga ja sellega külgnevat teravnurka: või
- piki jalga ja vastassuunas teravnurka: või
- hüpotenuusi ja teravnurga järgi: või.
Täisnurksete kolmnurkade sarnasuse märgid:
- üks terav nurk: või
- kahe jala proportsionaalsusest:
- jala ja hüpotenuusi proportsionaalsusest: või.
Siinus, koosinus, puutuja, kotangens täisnurkses kolmnurgas
- Täisnurkse kolmnurga teravnurga siinus on vastasjala ja hüpotenuusi suhe:
- Täisnurkse kolmnurga teravnurga koosinus on külgneva jala ja hüpotenuusi suhe:
- Täisnurkse kolmnurga teravnurga puutuja on vastasjala ja külgneva jala suhe:
- Täisnurkse kolmnurga teravnurga kootangens on külgneva jala ja vastandi suhe:.
Täisnurkse kolmnurga kõrgus: või.
Täisnurkses kolmnurgas on täisnurga tipust tõmmatud mediaan võrdne poolega hüpotenuusist: .
Täisnurkse kolmnurga pindala:
- läbi kateetrite:
 Samamoodi on kolmnurk CBH sarnane ABC-ga. Noodikirja tutvustamine
Samamoodi on kolmnurk CBH sarnane ABC-ga. Noodikirja tutvustamine  1. Asetage neli võrdset täisnurkset kolmnurka, nagu joonisel näidatud.
1. Asetage neli võrdset täisnurkset kolmnurka, nagu joonisel näidatud. 
 Eukleidese tõestuse idee on järgmine: proovime tõestada, et pool hüpotenuusile ehitatud ruudu pindalast võrdub jalgadele ehitatud ruutude poolte pindalade summaga ja seejärel suur ja kaks väikest ruutu on võrdsed. Mõelge vasakpoolsele joonisele. Sellele ehitasime täisnurkse kolmnurga külgedele ruudud ja joonistasime täisnurga C tipust s kiirte s, mis on risti hüpotenuusiga AB, see lõikab hüpotenuusile ehitatud ruudu ABIK kaheks ristkülikuks - BHJI ja HAKJ, vastavalt. Selgub, et nende ristkülikute pindalad on täpselt võrdsed vastavatele jalgadele ehitatud ruutude pindaladega. Proovime tõestada, et ruudu DECA pindala on võrdne ristküliku pindalaga AHJK Selleks kasutame abivaatlust: antud kolmnurga pindala, mille kõrgus ja alus on sama ristkülik on võrdne poolega antud ristküliku pindalast. See tuleneb sellest, et kolmnurga pindala on pool aluse ja kõrguse korrutisest. Sellest tähelepanekust järeldub, et kolmnurga ACK pindala on võrdne kolmnurga AHK pindalaga (pole näidatud), mis omakorda on võrdne poolega ristküliku AHJK pindalast. Tõestame nüüd, et kolmnurga ACK pindala on samuti võrdne poolega DECA ruudu pindalast. Ainus asi, mida selleks teha tuleb, on kolmnurkade ACK ja BDA võrdsuse tõestamine (kuna kolmnurga BDA pindala on ülaltoodud omaduse võrra võrdne poole ruudu pindalaga). See võrdsus on ilmne, kolmnurgad on kahest küljest ja nendevahelisest nurgast võrdsed. Nimelt - AB=AK,AD=AC - nurkade CAK ja BAD võrdsust on lihtne tõestada liikumismeetodiga: pöörame kolmnurka CAK 90° vastupäeva, siis on ilmne, et kahe vaadeldava kolmnurga vastavad küljed langeb kokku (tänu asjaolule, et nurga ruudu tipus on 90°). Argument ruudu BCFG ja ristküliku BHJI pindalade võrdsuse kohta on täiesti analoogne. Seega oleme tõestanud, et hüpotenuusile ehitatud ruudu pindala on jalgadele ehitatud ruutude pindalade summa.
Eukleidese tõestuse idee on järgmine: proovime tõestada, et pool hüpotenuusile ehitatud ruudu pindalast võrdub jalgadele ehitatud ruutude poolte pindalade summaga ja seejärel suur ja kaks väikest ruutu on võrdsed. Mõelge vasakpoolsele joonisele. Sellele ehitasime täisnurkse kolmnurga külgedele ruudud ja joonistasime täisnurga C tipust s kiirte s, mis on risti hüpotenuusiga AB, see lõikab hüpotenuusile ehitatud ruudu ABIK kaheks ristkülikuks - BHJI ja HAKJ, vastavalt. Selgub, et nende ristkülikute pindalad on täpselt võrdsed vastavatele jalgadele ehitatud ruutude pindaladega. Proovime tõestada, et ruudu DECA pindala on võrdne ristküliku pindalaga AHJK Selleks kasutame abivaatlust: antud kolmnurga pindala, mille kõrgus ja alus on sama ristkülik on võrdne poolega antud ristküliku pindalast. See tuleneb sellest, et kolmnurga pindala on pool aluse ja kõrguse korrutisest. Sellest tähelepanekust järeldub, et kolmnurga ACK pindala on võrdne kolmnurga AHK pindalaga (pole näidatud), mis omakorda on võrdne poolega ristküliku AHJK pindalast. Tõestame nüüd, et kolmnurga ACK pindala on samuti võrdne poolega DECA ruudu pindalast. Ainus asi, mida selleks teha tuleb, on kolmnurkade ACK ja BDA võrdsuse tõestamine (kuna kolmnurga BDA pindala on ülaltoodud omaduse võrra võrdne poole ruudu pindalaga). See võrdsus on ilmne, kolmnurgad on kahest küljest ja nendevahelisest nurgast võrdsed. Nimelt - AB=AK,AD=AC - nurkade CAK ja BAD võrdsust on lihtne tõestada liikumismeetodiga: pöörame kolmnurka CAK 90° vastupäeva, siis on ilmne, et kahe vaadeldava kolmnurga vastavad küljed langeb kokku (tänu asjaolule, et nurga ruudu tipus on 90°). Argument ruudu BCFG ja ristküliku BHJI pindalade võrdsuse kohta on täiesti analoogne. Seega oleme tõestanud, et hüpotenuusile ehitatud ruudu pindala on jalgadele ehitatud ruutude pindalade summa.  Vaatleme joonist, nagu sümmeetriast näha, lõikab segment CI ruudu ABHJ kaheks identseks osaks (kuna kolmnurgad ABC ja JHI on ehituselt võrdsed). Kasutades 90-kraadist vastupäeva pööramist, näeme varjutatud jooniste CAJI ja GDAB võrdsust. Nüüd on selge, et meie poolt varjutatud figuuri pindala on võrdne jalgadele ehitatud ruutude poolte pindalade ja algse kolmnurga pindala summaga. Teisest küljest on see võrdne poolega hüpotenuusile ehitatud ruudu pindalast, millele lisandub algse kolmnurga pindala. Tõestuse viimane etapp jääb lugeja teha.
Vaatleme joonist, nagu sümmeetriast näha, lõikab segment CI ruudu ABHJ kaheks identseks osaks (kuna kolmnurgad ABC ja JHI on ehituselt võrdsed). Kasutades 90-kraadist vastupäeva pööramist, näeme varjutatud jooniste CAJI ja GDAB võrdsust. Nüüd on selge, et meie poolt varjutatud figuuri pindala on võrdne jalgadele ehitatud ruutude poolte pindalade ja algse kolmnurga pindala summaga. Teisest küljest on see võrdne poolega hüpotenuusile ehitatud ruudu pindalast, millele lisandub algse kolmnurga pindala. Tõestuse viimane etapp jääb lugeja teha.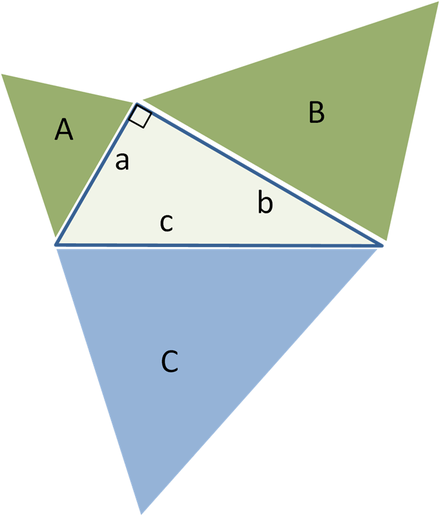




 Kaks pead ja kuus jalga; neli kõnnivad ja kaks lebavad paigal
Kaks pead ja kuus jalga; neli kõnnivad ja kaks lebavad paigal Enesehinnang - mis see on: mõiste, struktuur, tüübid ja tasemed
Enesehinnang - mis see on: mõiste, struktuur, tüübid ja tasemed Cassandra tee ehk Pasta Adventures War on Earth and Underground
Cassandra tee ehk Pasta Adventures War on Earth and Underground