Dünaamika põhiteoreemid. Dünaamika üldteoreemid

3. loeng Dünaamika üldteoreemid

Materiaalsete punktide süsteemi dünaamika on teoreetilise mehaanika oluline haru. Siin käsitleme peamiselt mehaaniliste süsteemide (materiaalsete punktide süsteemide) liikumise probleeme lõplik arv vabadusastmed - maksimaalne arv sõltumatuid parameetreid, mis määravad süsteemi asukoha. peamine ülesanne süsteemidünaamika – jäiga keha ja mehaaniliste süsteemide liikumisseaduste uurimine.

Lihtsaim lähenemine süsteemi liikumise uurimisele, mis koosneb N materiaalsed punktid, taandatakse süsteemi iga üksiku punkti liikumise arvestamisele. Sel juhul tuleb kindlaks määrata kõik süsteemi igale punktile mõjuvad jõud, sealhulgas punktidevahelise vastasmõju jõud.

Määrates iga punkti kiirenduse vastavalt Newtoni teisele seadusele (1.2), saame iga punkti jaoks kolm teist järku skalaarset diferentsiaalliikumise seadust, s.o. 3 N diferentsiaalne liikumisseadus kogu süsteemi jaoks.

Et leida liikumisvõrrandid mehaaniline süsteem antud jõud ja lähtetingimused süsteemi iga punkti jaoks, saadud diferentseeritud seadused tuleb integreerida. See ülesanne on keeruline isegi kahe materiaalse punkti puhul, mis liiguvad ainult vastasmõju jõudude toimel universaalse külgetõmbeseaduse järgi (kahe keha probleem) ja ülimalt keeruline kolme vastastikku mõjuva punkti puhul (kolme keha probleem ).

Seetõttu tuleb probleemide lahendamiseks leida sellised meetodid, mis viiksid lahendatavate võrranditeni ja annaksid aimu mehaanilise süsteemi liikumisest. Dünaamika üldised teoreemid, mis tulenevad diferentsiaalsetest liikumisseadustest, võimaldavad vältida integreerimisel tekkivat keerukust ja saada vajalikke tulemusi.

3.1 Üldised märkused

Mehaanilise süsteemi punktid nummerdatakse indeksitega i, j, k jne, mis läbivad kõiki väärtusi 1, 2, 3… N, kus N on süsteemipunktide arv. Füüsikalised kogused, mis on seotud k punkt on tähistatud sama indeksiga kui punkt. Näiteks väljendavad need vastavalt raadiuse vektorit ja kiirust k- punkt.

Süsteemi mõlemale punktile mõjuvad kahe päritoluga jõud: esiteks jõud, mille allikad asuvad väljaspool süsteemi, nn. välised jõud ja tähistatakse ; teiseks selle süsteemi teistest punktidest pärit jõud, nn sisemine jõud ja tähistatakse . Sisejõud vastavad Newtoni kolmandale seadusele. Mõelge kogu mehaanilisele süsteemile selle mis tahes olekus mõjutavate sisejõudude lihtsaimatele omadustele.

Esimene vara. Süsteemi kõigi sisejõudude geomeetriline summa (sisejõudude põhivektor) on võrdne nulliga.

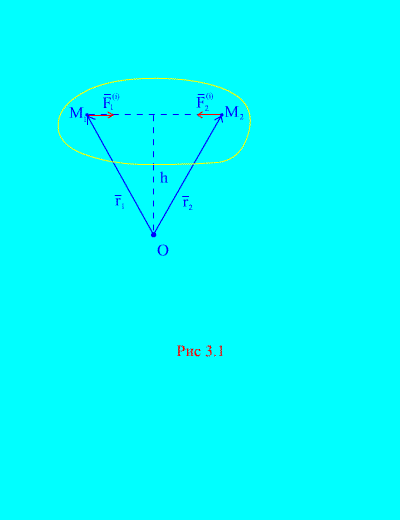
Tõepoolest, kui võtta arvesse süsteemi kahte suvalist punkti, näiteks ja (Joonis 3.1), siis nende jaoks , sest toime- ja reaktsioonijõud on absoluutväärtuselt alati võrdsed, nad toimivad mööda ühte toimejoont vastassuunas, mis ühendab omavahel vastasmõjupunkte. Sisejõudude põhivektor koosneb vastastikku mõjutavate punktide jõudude paaridest, seega

(3.1)

Teine vara. Kõigi sisejõudude momentide geomeetriline summa suvalise ruumipunkti suhtes on null.

Vaatleme jõudude momentide süsteemi ja punkti suhtes O(Joonis 3.1). Alates (Joonis 3.1). see on selge

,

sest mõlemal jõul on samad vektorimomentide harud ja vastupidised suunad. Sisejõudude põhimoment punkti kohta O koosneb selliste avaldiste vektorsummast ja on võrdne nulliga. Seega

Lase välis- ja sisemised jõud toimides mehaanilisele süsteemile, mis koosneb N punktid (Joonis 3.2). Kui süsteemi igale punktile rakendatakse välisjõudude resultant ja kõigi sisejõudude resultant, siis k süsteemi punktis saab koostada liikumise diferentsiaalvõrrandid. Kokku on sellised võrrandid N:

ja projektsioonides fikseeritud koordinaattelgedele 3 N:

(3.4)

Vektorvõrrandid (3.3) või samaväärsed skalaarvõrrandid (3.4) esindavad kogu süsteemi materiaalsete punktide liikumise diferentsiaalseadusi. Kui kõik punktid liiguvad paralleelselt ühe tasapinna või ühe sirgega, siis on võrrandite (3.4) arv esimesel juhul 2 N, teises N.

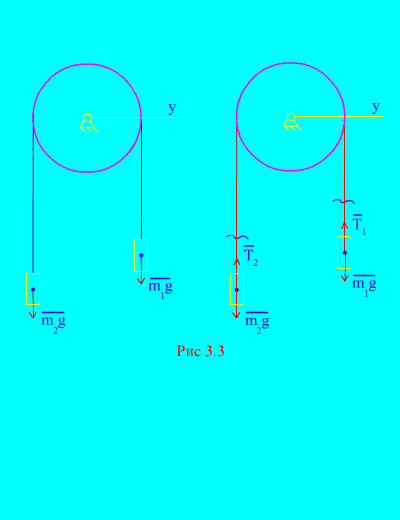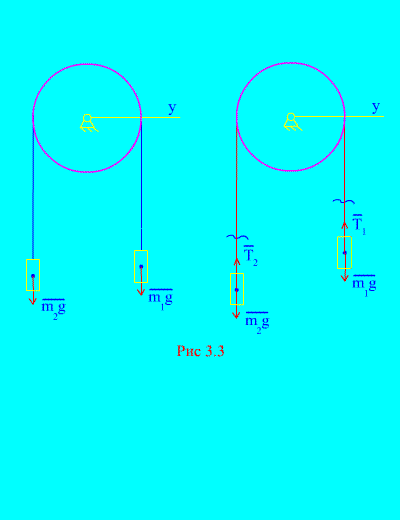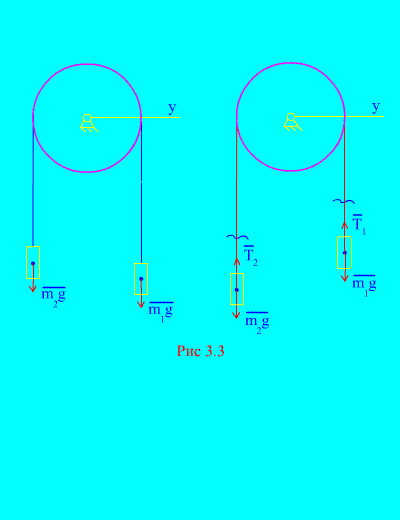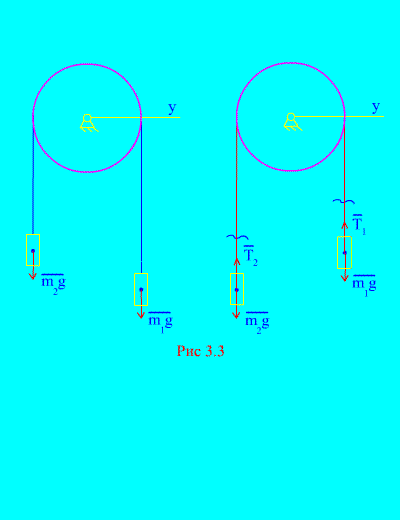
Näide 1 Kaks koormat massi ja on omavahel ühendatud üle ploki visatud pikendamatu kaabliga (Joonis 3.3). Jättes tähelepanuta hõõrdejõude, samuti ploki ja kaabli massi, määrake kauba liikumise seadus ja kaabli pinge.

Otsus. Süsteem koosneb kahest ühe teljega paralleelselt liikuvast materiaalsest kehast (mis on ühendatud pikendamatu kaabliga). X. Kirjutame üles diferentsiaalliikumise seadused projektsioonides teljele X kõigi jaoks.

Paremal raskusel lastakse kiirendusega langeda, siis vasakpoolne raskus tõuseb kiirendusega. Vabastame end vaimselt ühendusest (kaablist) ja asendame selle reaktsioonidega ja (Joonis 3.3). Eeldades, et kehad on vabad, koostame diferentsiaalliikumise seadused projektsioonis teljele X(see tähendab, et keerme pinged on sisemised jõud ja koormuste kaal on välised):

Kuna ja (kehad on ühendatud pikendamatu kaabliga), saame

Nende võrrandite lahendamine köie kiirenduse ja pinge kohta T, saame

.

Pange tähele, et kaabli pinge ei ole võrdne vastava koormuse raskusjõuga.

3. 2. Massikeskme liikumise teoreem

On teada, et jäik keha ja mehaaniline süsteem tasapinnas võivad liikuda üsna raskelt. Esimesele teoreemile keha ja mehaanilise süsteemi liikumise kohta saab jõuda järgmiselt: jätke c.-l. objekt, mis koosneb paljudest omavahel kinnitatud tahketest kehadest. On selge, et ta lendab parabooliga. See selgus punkti liikumist uurides. Kuid nüüd pole objektil punkt. See pöördub, kõigub lennates ümber mõne efektiivse keskuse, mis liigub mööda parabooli. Esimene liikumisteoreem rasked teemadütleb, et teatud efektiivne kese on liikuva objekti massikese. Massikese ei pruugi asuda kehas endas, see võib asuda kusagil väljaspool seda.

Teoreem. Mehaanilise süsteemi massikese liigub materiaalse punktina koos massiga võrdne massiga kogu süsteem, millele rakenduvad kõik süsteemile mõjuvad välised jõud.

Teoreemi tõestamiseks kirjutame diferentsiaalliikumise seadused (3.3) ümber järgmine vorm:

(3.5)

kus N on süsteemipunktide arv.

Liidame võrrandid termini kaupa kokku:

(a)

Mehaanilise süsteemi massikeskme asukoht valitud koordinaatsüsteemi suhtes määratakse valemiga (2.1): kus M on süsteemi mass. Seejärel kirjutatakse võrdsuse (a) vasak pool

Võrdsuse (a) paremal küljel olev esimene summa on võrdne välisjõudude põhivektoriga ja viimane on sisejõudude omaduse järgi võrdne nulliga. Seejärel kirjutatakse võrdsus (a), võttes arvesse (b), ümber

, (3.6)

need. süsteemi massi ja selle massikeskme kiirenduse korrutis on võrdne geomeetriline summa kõik süsteemile mõjuvad välised jõud.

Võrrandist (3.6) järeldub, et sisejõud ei mõjuta otseselt massikeskme liikumist. Kuid mõnel juhul on need süsteemile rakenduvate välisjõudude ilmnemise põhjuseks. Seega põhjustavad auto veorattaid pööravad sisejõud sellele ratta veljele mõjuva välise haardejõu mõju.

Näide 2 Vertikaalsel tasapinnal asuv mehhanism on paigaldatud horisontaalsele siledale tasapinnale ja kinnitatud selle külge jäigalt pinnale kinnitatud vardadega. To ja L (Joonis 3.4).

Plaadi 1 raadius R liikumatuks. Plaadi 2 mass m ja raadius r vändaga kinnitatud, pikkus R+ r punktis Alates 2. Vänt pöörleb konstantselt

nurkkiirus. AT esialgne hetk vänt hõivas õige horisontaalasendi. Jättes tähelepanuta vända massi, määrake varrastele mõjuvad maksimaalsed horisontaalsed ja vertikaalsed jõud, kui kogukaal voodi ja ratas 1 on võrdne M. Mõelge ka mehhanismi käitumisele lattide puudumisel.

Otsus. Süsteem koosneb kahest massist ( N=2 ): raamiga fikseeritud ketas 1 ja liikuv ketas 2. Suuname telje juures läbi fikseeritud ketta raskuskeskme vertikaalselt ülespoole, telg X- kaasa horisontaaltasand.

Kirjutame teoreemi massikeskme (3.6) liikumise kohta koordinaatide kujul

Selle süsteemi välised jõud on: raami ja fikseeritud ketta kaal - mg, liikuv ketta kaal mg, - poltide horisontaalne kogureaktsioon, - tasapinna normaalne kogureaktsioon. Seega

Seejärel kirjutatakse ümber liikumisseadused (b).

Arvutame mehaanilise süsteemi massikeskme koordinaadid:

; (G)

aastast vaadatuna (Joonis 3.4), , , (vända pöördenurk), . Nende avaldiste asendamine (r)-ga ja teise tuletise arvutamine aja suhtes t, , saame selle

(e)

Asendades (c) ja (e) punktiga (b), leiame

Vardadele mõjuval horisontaalsel rõhul on suurim ja väikseim väärtus, millal cos = 1 vastavalt, st.

Mehhanismi rõhul horisontaaltasapinnal on kõrgeim ja madalaim väärtus, kui patt vastavalt, st.

Tegelikult on esimene dünaamika probleem lahendatud: süsteemi massikeskme (e) teadaolevate liikumisvõrrandite järgi taastatakse liikumises osalevad jõud.

Trellide puudumisel K ja L (Joonis 3.4), võib mehhanism hakata põrkama horisontaaltasapinnast kõrgemal. See toimub siis, kui s.t. kui , siis sellest järeldub, et vända pöörlemise nurkkiirus, mille juures mehhanism põrkub, peab vastama võrdsusele

.

3. 3. Massikeskme liikumise jäävuse seadus

Kui süsteemile mõjuvate välisjõudude põhivektor on võrdne nulliga, s.o. , siis alates(3.6)sellest järeldub, et massikeskme kiirendus on null, seega on massikeskme kiirus konstantne suuruse ja suuna poolest. Kui just alghetkel on massikese paigal, siis on see puhkeolekus kogu selle aja, kuni välisjõudude põhivektor on võrdne nulliga.

Sellest teoreemist tulenevad mitmed järeldused.

· Sisejõud üksi ei suuda muuta süsteemi massikeskme liikumise olemust.

· Kui süsteemile mõjuvate välisjõudude põhivektor on võrdne nulliga, siis on massikese paigal või liigub ühtlaselt ja sirgjooneliselt.

· Kui süsteemi välisjõudude peavektori projektsioon mingile fikseeritud teljele on võrdne nulliga, siis süsteemi massikeskme kiiruse projektsioon sellel teljel ei muutu.

· Paar jäigale kehale rakendatud jõudu ei saa muuta selle massikeskme liikumist (see võib põhjustada ainult keha pöörlemise ümber massikeskme).

Vaatleme näidet, mis illustreerib massikeskme liikumise jäävuse seadust.

Näide 3 Kaks raskust massiga ja on ühendatud üle ploki visatud venimatu keermega (Joonis 3.5), kinnitatud massiga kiilule M. Kiil toetub siledale horisontaaltasapinnale. Esialgu oli süsteem puhkeolekus. Leidke kiilu nihe piki tasapinda, kui esimene koorem on langetatud kõrgusele N. Ignoreeri ploki ja keerme massi.

Otsus. Kiilule mõjuvad välisjõud koos raskustega on gravitatsioonijõud , ja mg, sama hästi kui normaalne reaktsioon sile horisontaalne pind N. Seetõttu

Kuna süsteem oli algsel hetkel puhkeolekus, on meil .

Arvutame välja süsteemi massikeskme koordinaadid hetkel ja hetkel t 1 kui koorma kaal g kõrgusele laskuda H.

Hetkeks:

,

kus , , X- vastavalt g, g ja kiilkaalu raskuste raskuste keskpunkti koordinaadid Mg.

Oletame, et kiil liigub ajahetkel telje positiivses suunas Ox summa järgi L kui koorma kaal langeb kõrgusele N. Siis korraks

sest koormad koos kiiluga liiguvad L paremale, a liigub raskus kauguse võrra ülespoole. Kuna , pärast arvutusi saame

.

3.4. Liikumissüsteemi kogus

3.4.1. Süsteemi impulsi arvutamine

Materiaalse punkti impulss on vektorsuurus, võrdne tootega punkti mass selle kiirusvektoril

Liikumise hulga mõõtühik -

Mehaanilise süsteemi impulsi nimetatakse süsteemi üksikute punktide impulsi vektorsummaks, s.o.

kus N on süsteemipunktide arv.

Mehaanilise süsteemi impulsi saab väljendada süsteemi massina M ja massikeskme kiirust. Tõesti,

need. süsteemi impulss on võrdne kogu süsteemi massi ja selle massikeskme kiiruse korrutisega. Suund on sama mis suund (Joonis 3.6)

Projektsioonides ristkülikukujulistele telgedele on meil

kus , , - süsteemi massikeskme kiiruse projektsioonid.

Siin M on mehaanilise süsteemi mass; ei muutu süsteemi liikumise käigus.

Eriti mugav on neid tulemusi kasutada jäikade kehade momentide arvutamisel.

Valemist (3.7) on näha, et kui mehaaniline süsteem liigub nii, et selle massikese jääb paigale, siis jääb süsteemi impulss võrdseks nulliga.

3.4.2. Elementaarne ja täisjõuline impulss

Jõu mõju materiaalsele punktile aja jooksul dt saab iseloomustada elementaarse impulsiga. Kogu jõuimpulss ajas t, või jõuimpulss , määratakse valemiga

või projektsioonides telje koordinaatidele

(3.8a)

Jõuimpulsi ühik on .

3.4.3. Teoreem süsteemi impulsi muutumise kohta

Süsteemi punktidele rakendatakse välis- ja sisejõude. Seejärel saame süsteemi iga punkti jaoks rakendada diferentsiaalseid liikumisseadusi (3.3), pidades silmas, et :

.

Summeerides süsteemi kõik punktid, saame

Sisejõudude omaduse järgi ja määratluse järgi meil on

(3.9)

Selle võrrandi mõlema poole korrutamine arvuga dt, saame teoreemi impulsi muutumise kohta in diferentsiaalne vorm:

, (3.10)

need. mehaanilise süsteemi impulsi diferentsiaal on võrdne kõigi mehaanilise süsteemi punktidele mõjuvate välisjõudude elementaarimpulsside vektorsummaga.

(3.10) mõlema osa integraali arvutamine aja jooksul vahemikus 0 kuni t, saame teoreemi lõplikul või integraalkujul

(3.11)

Projektsioonides koordinaattelgedele saame

Mehaanilise süsteemi impulsi muutus aja jooksult, on võrdne mehaanilise süsteemi punktidele samaaegselt mõjuvate välisjõudude impulsside vektorsummaga.

Näide 4 Massi koormus m laskudes alla kaldtasapind puhkest jõu toimel F, ajaga võrdeline: , kus (Joonis 3.7). Milline on keha kiirus pärast t sekundit pärast liikumise algust, kui koormuse libisemishõõrdetegur kaldtasandil on võrdne f.

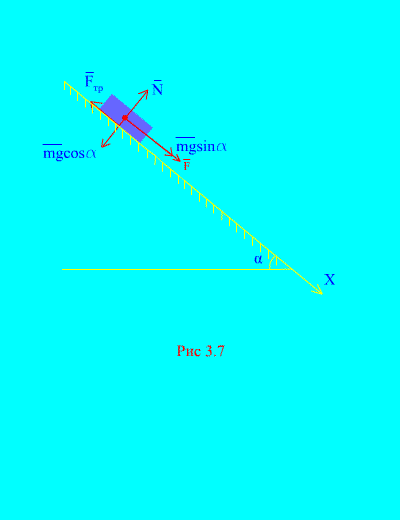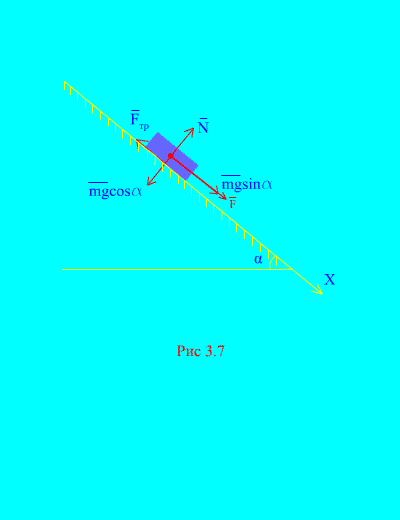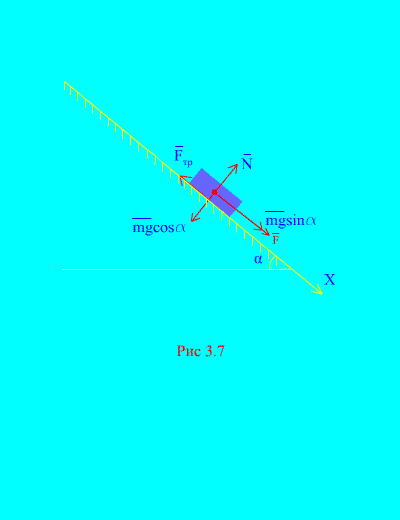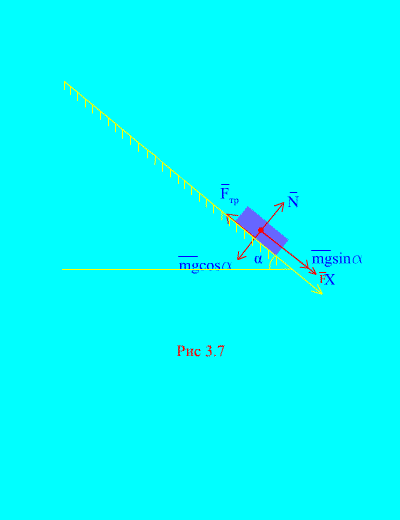
Otsus. Kujutame koormusele rakendatavaid jõude: mg - koormuse raskusjõud, N on tasapinna normaalne reaktsioon, on tasapinnale mõjuva koormuse libisemishõõrdejõud ja . Kõigi jõudude suund on näidatud (Joonis 3.7).

Suuname telje X kaldtasapinnast allapoole. Kirjutame teoreem impulsi muutuse (3.11) kohta projektsioonis teljele X:

(a)

Tingimusel, kuna algsel ajahetkel oli koorem paigal. Kõigi x-teljele mõjuvate jõudude impulsside projektsioonide summa on

Seega

,

.

3.4.4. Impulsi jäävuse seadused

Jäävusseadused saadakse impulsi muutumise teoreemi erijuhtudena. Võimalikud on kaks erijuhtu.

· Kui kõigi süsteemile rakendatavate välisjõudude vektorsumma on võrdne nulliga, s.o. , siis tuleneb see teoreemist (3.9) , mida ,

need. kui süsteemi välisjõudude peavektor on võrdne nulliga, siis on süsteemi impulsi suurus ja suund konstantne.

· Kui välisjõudude peavektori projektsioon mis tahes koordinaatide telg võrdub nulliga, näiteks Oh, st. , siis on liikumise hulga projektsioon sellele teljele konstantne.

Vaatleme näidet impulsi jäävuse seaduse rakendamisest.

Näide 5 Ballistiline pendel on pika nööri küljes riputatud massiline keha (Joonis 3.8).

Kiirusega liikuv massikuul V ja kukkudes liikumatusse kehasse, takerdub sellesse ja keha kaldub kõrvale. Kui suur oli kuuli kiirus, kui keha tõusis kõrgusele h ?

Otsus. Laske kinnikiilunud kuuliga kehal kiirust omandada . Siis, kasutades impulsi jäävuse seadust kahe keha vastastikmõjus, saame kirjutada .

Kiirust saab arvutada jäävusseaduse abil mehaaniline energia . Siis . Selle tulemusena leiame

.

Näide 6. Vesi siseneb fikseeritud kanalisse (Joonis 3.9) muutuv lõik, mille kiirus on horisondi suhtes nurga all; ruut ristlõige kanal sissepääsu juures; vee kiirust kanali väljalaskeava juures ja loob horisondiga nurga.

Määrake reaktsiooni horisontaalne komponent, mida vesi avaldab kanali seintele. Vee tihedus .

Otsus. Määrame kanali seinte poolt veele avaldatava reaktsiooni horisontaalse komponendi. See jõud on absoluutväärtuselt võrdne ja märgilt vastupidine soovitud jõule. Meil on vastavalt (3.11a)

. (a)

Arvutame aja t jooksul kanalisse siseneva vedeliku mahu massi:

RAV 0 väärtust nimetatakse teine ​​mass - vedeliku mass, mis voolab läbi toru mis tahes osa ajaühikus.

Sama palju vett väljub kanalist sama aja jooksul. Alg- ja lõppkiirus on antud tingimuses.

Arvuta parem pool võrdsus (a), mis määrab süsteemile (vesi) mõjutavate välisjõudude projektsioonide summa horisontaalteljele. Ainus horisontaalne jõud on seinte tulemusena tekkiva reaktsiooni horisontaalkomponent Rx. See jõud on vee ühtlase liikumise ajal konstantne. Niisiis

. (in)

Asendades (b) ja (c) punktiga (a), saame

3.5. Süsteemi kineetiline moment

3.5.1. Süsteemi peamine impulsimoment

Olgu süsteemi massiga punkti raadiuse vektor mingi punkti A suhtes, mida nimetatakse keskpunktiks (Joonis 3.10).

Punkti impulsimoment (kineetiline moment). keskuse A suhtes nimetatakse vektoriks , määratakse valemiga

. (3.12)

Sel juhul vektor suunatud risti keskpunkti läbiva tasapinnaga AGA ja vektor .

Punkti impulsimoment (kineetiline moment) telje ümber nimetatakse punkti nurkimpulsi projektsiooniks sellele teljele mis tahes sellel teljel valitud keskpunkti suhtes.

Süsteemi peamine impulsimoment (kineetiline moment) keskpunkti A suhtes nimetatakse koguseks

(3.13)

Süsteemi peamine impulsimoment (kineetiline moment) telje ümber nimetatakse süsteemi impulsi põhimomendi projektsiooniks sellele teljele antud hetkel valitud suhtes. kesktelg.

3.5.2. Pöörleva jäiga keha impulss ümber pöörlemistelje

Ühilduv fikseeritud punkt O keha, mis asub pöörlemisteljel Oz, koordinaatsüsteemi alguspunktiga Ohuz, mille teljed pöörlevad koos kehaga (Joonis 3.11). Laskma olema keha punkti raadiusvektor koordinaatide alguspunkti suhtes, selle projektsioone telgedel tähistatakse , , . Vektorprojektsioonid nurkkiirus Samadel telgedel olevaid kehasid tähistatakse 0, 0, ().

Üsna sageli on võimalik eristada olulised omadused mehaanilise süsteemi liikumine ilma liikumisdiferentsiaalvõrrandite süsteemi integreerimiseta. See saavutatakse üldiste dünaamikateoreemide rakendamisega.

5.1. Põhimõisted ja määratlused

Välised ja sisemised jõud. Iga mehaanilise süsteemi punktile mõjuv jõud on tingimata kumbki aktiivne jõud või sideme reaktsioon. Kogu süsteemi punktidele mõjuvate jõudude kogumi võib erinevalt jagada kahte klassi: välisjõududeks ja sisejõududeks (alamindeksid e ja i – alates Ladinakeelsed sõnad externus - väline ja internus - sisemine). Välisjõududeks nimetatakse jõududeks, mis mõjuvad süsteemi punktidele punktidest ja kehadest, mis ei kuulu vaadeldavasse süsteemi. Vaadeldava süsteemi punktide ja kehade vastasmõju jõude nimetatakse sisemiseks.

See jaotus sõltub sellest, milliseid materiaalseid punkte ja kehasid uurija vaadeldavasse mehaanilisse süsteemi kaasab. Kui süsteemi koostist laiendada lisapunktide ja kehadega, võivad mõned eelmise süsteemi jaoks välised jõud muutuda laiendatud süsteemi jaoks sisemiseks.

Sisejõudude omadused. Kuna need jõud on süsteemi osade vahelise vastasmõju jõud, on nad kaasatud sisejõudude terviklikku süsteemi "kaheteks", mis on organiseeritud vastavalt tegevus-reaktsiooni aksioomile. Iga selline "kaks" jõudu

põhivektor ja Peaasi suvalise keskpunkti suhtes on võrdsed nulliga. Kuna terviklik sisejõudude süsteem koosneb ainult "kahetest", siis

1) sisejõudude süsteemi põhivektor on võrdne nulliga,

2) sisejõudude süsteemi põhimoment suvalise punkti suhtes on võrdne nulliga.

Süsteemi mass on aritmeetiline summa Kõigi süsteemi moodustavate punktide ja kehade mass mk:

raskuskese mehaanilise süsteemi (inertskeskust) nimetatakse geomeetriline punkt C, mille raadiuse vektor ja koordinaadid määratakse valemitega

kus on raadiusvektorid ja süsteemi moodustavate punktide koordinaadid.

Jäiga keha puhul ühtlases gravitatsiooniväljas langevad massikeskme ja raskuskeskme asukohad kokku, muudel juhtudel on need erinevad geomeetrilised punktid.

Koos inertsiaalse tugiraamistikuga käsitletakse sageli samaaegselt ka mitteinertsiaalset tugiraamistikku, mis liigub edasi. Selle koordinaatteljed (Koenigi teljed) on valitud nii, et võrdluspunkt C langeb alati kokku mehaanilise süsteemi massikeskmega. Definitsiooni kohaselt on massikese Koenigi telgedes fikseeritud ja asub koordinaatide alguspunktis.

Süsteemi inertsimoment telje ümber nimetatakse skalaar võrdne summaga süsteemi kõikide punktide masside mk korrutised nende telje vahelise kauguse ruutudega:

Kui mehaaniline süsteem on jäik korpus, võite 12 leidmiseks kasutada valemit

kus on tihedus, keha poolt hõivatud ruumala.

Vaatleme teatud materjalimahtude süsteemi liikumist fikseeritud koordinaatsüsteemi suhtes Kui süsteem ei ole vaba, siis võib seda lugeda vabaks, kui jätta kõrvale süsteemile seatud piirangud ja asendada nende tegevus vastavate reaktsioonidega.

Jagagem kõik süsteemile rakenduvad jõud välisteks ja sisemisteks; mõlemad võivad hõlmata äraviskamise reaktsioone

ühendused. Tähistame peavektorit ja põhivektorit ning välisjõudude põhimomenti punkti A suhtes.

1. Teoreem impulsi muutumise kohta. Kui on süsteemi impulss, siis (vt )

st kehtib teoreem: süsteemi impulsi ajatuletis on võrdne kõigi välisjõudude peavektoriga.

Asendades vektori selle avaldise kaudu, kus on süsteemi mass, on massikeskme kiirus, võib võrrandile (4.1) anda erineva kuju:

See võrdsus tähendab, et süsteemi massikese liigub materiaalse punktina, mille mass on võrdne süsteemi massiga ja millele rakendub jõud, mis on geomeetriliselt võrdne süsteemi kõigi välisjõudude peavektoriga. Viimast väidet nimetatakse teoreemiks süsteemi massikeskme (inertskeskme) liikumise kohta.

Kui siis (4.1) järeldub, et impulsi vektor on suuruselt ja suunalt konstantne. Projekteerides selle koordinaatide teljele, saame süsteemi kaksikahela diferentsiaalvõrrandite kolm esimest skalaarset integraali:

Neid integraale nimetatakse impulsi integraalideks. Kui massikeskme kiirus on konstantne, st see liigub ühtlaselt ja sirgjooneliselt.

Kui välisjõudude peavektori projektsioon mis tahes ühele teljele, näiteks teljel, on võrdne nulliga, siis on meil üks esimene integraal või kui põhivektori kaks projektsiooni on võrdsed nulliga, siis on olemas impulsi kaks integraali.

2. Kineetilise momendi muutumise teoreem. Olgu A mingi suvaline punkt ruumis (liikuv või paigalseisev), mis ei pruugi kogu liikumisaja jooksul ühtida süsteemi ühegi konkreetse materiaalse punktiga. Selle kiirust fikseeritud koordinaatide süsteemis tähistatakse nurkimpulsi muutuse teoreemiga materjali süsteem punkti A suhtes on vorm

Kui punkt A on fikseeritud, on võrdus (4.3) lihtsamal kujul:

See võrdsus väljendab teoreemi süsteemi nurkimpulsi muutumise kohta fikseeritud punkt: süsteemi nurkimpulsi ajatuletis, mis on arvutatud mõne fikseeritud punkti suhtes, on võrdne kõigi välisjõudude põhimomendiga selle punkti suhtes.

Kui siis vastavalt (4.4) nurkmomendi vektor on suuruselt ja suunalt konstantne. Projekteerides selle koordinaatide teljele, saame süsteemi liikumise diferentsiaalvõrrandi esimesed skalaarsed integraalid:

Neid integraale nimetatakse nurkimpulsi integraalideks või alade integraalideks.

Kui punkt A ühtib süsteemi massikeskmega, siis võrdsuse (4.3) parempoolne esimene liige kaob ja teoreem nurkimpulsi muutumise kohta on sama kujuga (4.4) kui süsteemi puhul. fikseeritud punkt A. Pange tähele (vt. 4 § 3), et vaadeldaval juhul saab süsteemi absoluutse nurkimpulssi võrdsuse (4.4) vasakul poolel asendada süsteemi võrdse nurkimpulssiga selle liikumisel punkti suhtes. massikese.

Olgu mingi konstantne telg või konstantse suuna telg, mis läbib süsteemi massikeskpunkti, ja olgu süsteemi nurkimpulss selle telje suhtes. (4.4) järeldub, et

kus on välisjõudude moment telje ümber. Kui kogu liikumisaja jooksul, siis on meil esimene integraal

S. A. Chaplygini töödes saadi nurkmomendi muutumise teoreemi mitu üldistust, mida seejärel rakendati mitmete kuulide veeremise ülesannete lahendamisel. Töödes on toodud kpnetoloogilise momendi muutumise teoreemi edasised üldistused ja nende rakendused jäiga keha dünaamika probleemides. Nende tööde peamised tulemused on seotud teoreemiga nurkimpulsi muutumise kohta liikuva impulsi suhtes, mis läbib pidevalt mõnda liikuvat punkti A. Olgu - ühikvektor suunatud piki seda telge. Korrutades skalaarselt võrdsuse mõlema poolega (4.3) ja liites selle liikme mõlemale osale, saame

Kui kinemaatiline tingimus on täidetud

võrrand (4.5) tuleneb (4.7). Ja kui tingimus (4.8) on täidetud kogu liikumisaja jooksul, siis on esimene integraal (4.6) olemas.

Kui süsteemi ühendused on ideaalsed ja võimaldavad süsteemi kui jäiga keha pöörlemist ümber telje ja virtuaalsete nihete arvus, siis on reaktsioonide põhimoment ümber telje ja võrdne nulliga ning seejärel väärtus võrrandi (4.5) parem pool on kõigi väliste aktiivsete jõudude põhimoment telje ümber ja . Selle hetke võrdsus nulliga ja seose (4.8) rahuldatavus on vaadeldaval juhul piisavad tingimused integraali (4.6) olemasolu jaoks.

Kui telje ja suund on muutumatu, saab tingimuse (4.8) kirjutada kujul

See võrdsus tähendab, et massikeskme kiiruse ja punkti A kiiruse projektsioonid teljel ja sellega risti olevale tasapinnale on paralleelsed. S. A. Chaplygini töös on (4.9) asemel nõutud, et vähem kui üldine seisund kus X on suvaline konstant.

Pange tähele, et tingimus (4.8) ei sõltu punkti valikust . Tõepoolest, olgu P suvaline punkt teljel. Siis

ja seega

Kokkuvõtteks märgime ära Resali võrrandite (4.1) ja (4.4) geomeetrilise tõlgenduse: vektorid absoluutsed kiirused vektorite otsad ja on võrdsed vastavalt põhivektori ja kõigi välisjõudude põhimomendiga punkti A suhtes.

VALGEVENE VABARIIGI PÕLLUMAJANDUS- JA TOIDUMINISTEERIUM

Õppeasutus "VALGEVENE RIIK PÕLLUMAJANDUS

TEHNILINE ÜLIKOOL"

Teoreetilise mehaanika ning mehhanismide ja masinate teooria osakond

TEOREETILINE MEHAANIKA

metoodiline kompleks erialade rühma üliõpilastele

74 06 Põllumajandustehnika

2 osas 1. osa

UDC 531.3(07) LBC 22.213ya7 T 33

Koostanud:

Füüsikaliste ja matemaatikateaduste kandidaat, dotsent Yu. S. Biza, kandidaat tehnikateadused, dotsent N. L. Rakova, vanemõppejõudI. A. Tarasevitš

Arvustajad:

Haridusasutuse teoreetilise mehaanika osakond "Valgevene rahvus Tehnikaülikool» (pea

BNTU teoreetilise mehaanika osakond füüsika- ja matemaatikateaduste doktor, professor A. V. Chigarev);

Riikliku Teadusliku Instituudi "Mehaanikatehnika ühendinstituut" labori "Mehaaniliste süsteemide vibrokaitse" juhtivteadur

Valgevene Riiklik Teaduste Akadeemia”, tehnikateaduste kandidaat, dotsent A. M. Goman

Teoreetiline mehaanika. Jaotis "Dünaamika": hariv

T33 meetod. keeruline. 2 osas 1. osa / koost: Yu. S. Biza, N. L. Rakova, I. A. Tarasevitš. - Minsk: BGATU, 2013. - 120 lk.

ISBN 978-985-519-616-8.

AT hariduslik ja metoodiline kompleks esitab materjale distsipliini "Teoreetiline mehaanika" osa "Dünaamika" 1. osa uurimise kohta. Sisaldab loengute kursust, teostuse algmaterjale praktilised harjutused, ülesanded ja ülesannete näidised iseseisvaks tööks ja kontrolliks õppetegevused täiskohaga ja kirjavahetuse vormidõppimine.

UDC 531.3(07) LBC 22.213a7

SISSEJUHATUS .................................................. ...................................................
1. HARIDUSE TEADUSLIK JA TEOREETILINE SISU
METOODIKA KOMPLEKSIST ................................................................ ..
1.1. Sõnastik................................................................. ................................
1.2. Loengute teemad ja nende sisu ................................................ ...
Peatükk 1. Sissejuhatus dünaamikasse. Põhimõisted
klassikaline mehaanika ................................................... ..................................................
Teema 1. Materiaalse punkti dünaamika................................................ ....
1.1. Materiaalsete punktide dünaamika seadused
(Galileo – Newtoni seadused) ................................................ ..........
1.2. Diferentsiaalvõrrandid liigutused
1.3. Dünaamika kaks peamist ülesannet ................................................... ..............
Teema 2. Suhtelise liikumise dünaamika
materiaalne punkt ................................................... ..........................................
Ülevaatusküsimused ................................................ ..............................
Teema 3. Mehaanilise süsteemi dünaamika ................................................... ....
3.1. Massi geomeetria. Mehaanilise süsteemi massikese......
3.2. Siseväed ................................................... ..................................................
Ülevaatusküsimused ................................................ ..............................
Teema 4. Jäiga keha inertsimomendid .................................................
4.1. Jäiga keha inertsimomendid
telje ja pooluse suhtes ................................................ ......................................
4.2. Teoreem jäiga keha inertsmomentide kohta
paralleeltelgede kohta
(Huygensi-Steineri teoreem) ................................................ ... ...
4.3. Tsentrifugaalsed inertsmomendid .................................................. .
Ülevaatusküsimused ................................................ ..................................
2. peatükk

Teema 5. Teoreem süsteemi massikeskme liikumise kohta ...................................
Ülevaatusküsimused ................................................ ..............................
Iseõppimise ülesanded .................................................. .......
Teema 6. Materiaalse punkti liikumise maht
ja mehaaniline süsteem ................................................... ................................................
6.1. Materiaalse punkti liikumise kogus 43
6.2. Jõuimpulss ................................................... ...................................
6.3. Teoreem impulsi muutumise kohta
materiaalne punkt ................................................... ................................................
6.4. Põhivektori muutmise teoreem
mehaanilise süsteemi impulss ..........................................
Ülevaatusküsimused ................................................ ..............................
Iseõppimise ülesanded .................................................. .......
Teema 7. Materiaalse punkti impulsimoment
ja mehaaniline süsteem keskpunkti ja telje suhtes ...................................
7.1. Materiaalse punkti impulsimoment
keskpunkti ja telje suhtes ................................................ ..............................
7.2. Teoreem nurkimpulsi muutumise kohta
materiaalne punkt keskpunkti ja telje suhtes ......................
7.3. Teoreem kineetilise momendi muutumise kohta
mehaaniline süsteem keskpunkti ja telje suhtes ...................................
Ülevaatusküsimused ................................................ ..............................
Iseõppimise ülesanded .................................................. .......
Teema 8. Jõudude töö ja jõud ................................................ ... .........
Ülevaatusküsimused ................................................ ..............................
Iseõppimise ülesanded .................................................. .......
Teema 9. Materiaalse punkti kineetiline energia
ja mehaaniline süsteem ................................................... ................................................
9.1. Materiaalse punkti kineetiline energia
ja mehaaniline süsteem. Koenigi teoreem........................
9.2. Jäiga keha kineetiline energia
erinevate liigutustega ................................................... ..............................
9.3. Muuda teoreemi kineetiline energia
materiaalne punkt ................................................... ................................................

9.4. Kineetilise energia muutumise teoreem
mehaaniline süsteem ................................................... ................................................
Ülevaatusküsimused ................................................ ..............................
Iseõppimise ülesanded .................................................. .......
Teema 10. Potentsiaalne jõuväli
ja potentsiaalne energia ................................................... ................................................
Ülevaatusküsimused ................................................ ..............................
Teema 11. Jäiga keha dünaamika................................................... ..............
Ülevaatusküsimused ................................................ ..............................
2. KONTROLLIMATERJALID
MOODULI POOLT................................................ ...................................................
ÕPILASTE ISESEISEV TÖÖ ...................................
4. NÕUDED JUHTIMISE KONSTRUKTSIOONILE
TÖÖTAB TÄISKOHA- JA KIRJAÕPILASELE
KOOLITUSE VORMID ................................................ ..........................................
5. ETTEVALMISTUSKÜSIMUSTE LOETELU
ÕPILASTE EKSAMILE (ÕPINGULE).
TÄISTÖÖKOHALINE JA KIRJAVÄLJAÕPE................................................ ......
6. KIRJANDUSTE LOETELU ................................................... ..............

SISSEJUHATUS

Teoreetiline mehaanika – üldseaduste teadus mehaaniline liikumine, materiaalsete kehade tasakaal ja vastastikmõju.

See on üks põhilisi üldteaduslikke füüsikalisi ja matemaatilisi distsipliine. See on kaasaegse tehnoloogia teoreetiline alus.

Teoreetilise mehaanika õpe koos teiste füüsikaliste ja matemaatiliste distsipliinidega aitab kaasa teadusliku silmaringi avardumisele, kujundab oskust konkreetseks ja abstraktne mõtlemine ja aitab kaasa tulevase spetsialisti üldise tehnilise kultuuri parandamisele.

Teoreetiline mehaanika, mis on kõige teaduslik alus tehnilised distsipliinid, aitab kaasa oskuste arendamisele ratsionaalseid otsuseid inseneri ülesanded seotud põllumajandus- ja melioratsioonimasinate ja -seadmete käitamise, remondi ja projekteerimisega.

Vaadeldavate ülesannete olemuse järgi jaguneb mehaanika staatikaks, kinemaatikaks ja dünaamikaks. Dünaamika on teoreetilise mehaanika osa, mis uurib materiaalsete kehade liikumist rakendatud jõudude mõjul.

AT hariv ja metoodiline kompleks (UMK) esitleb materjale rubriigi "Dünaamika" õppe kohta, mis sisaldab loengute kursust, läbiviimise alusmaterjale. praktiline töö, ülesanded ja täitmise näidised jaoks iseseisev töö ja täiskoormusega osakoormusega üliõpilaste õppetegevuse kontroll.

AT "Dünaamika" sektsiooni õppimise tulemusena peab õpilane õppima teoreetiline alus dünaamika ja omandada dünaamika probleemide lahendamise põhimeetodid:

Teadma dünaamikaülesannete lahendamise meetodeid, dünaamika üldteoreeme, mehaanika põhimõtteid;

Oskab määrata keha liikumisseadusi sõltuvalt sellele mõjuvatest jõududest; rakendada ülesannete lahendamisel mehaanika seadusi ja teoreeme; määrata kehade liikumist piiravate sidemete staatilised ja dünaamilised reaktsioonid.

Distsipliini "Teoreetiline mehaanika" õppekava näeb ette auditoorsete tundide koguarvu - 136, sealhulgas 36 tundi rubriigi "Dünaamika" õppimiseks.

1. HARIDUS- JA METOODILISE KOMPLEKSI TEADUSLIKU JA TEOREETILINE SISU

1.1. Sõnastik

Staatika on mehaanika osa, mis kirjeldab üldist jõudude õpetust, uuritakse redutseerimist. keerulised süsteemid jõud kõige lihtsamale kujule ja luuakse tasakaalutingimused erinevaid süsteeme jõud.

Kinemaatika on teoreetilise mehaanika osa, milles uuritakse materiaalsete objektide liikumist, sõltumata seda liikumist põhjustavatest põhjustest, s.t sõltumata nendele objektidele mõjuvatest jõududest.

Dünaamika on teoreetilise mehaanika osa, mis uurib materiaalsete kehade (punktide) liikumist rakendatud jõudude mõjul.

Materiaalne punkt- materiaalne keha, mille punktide liikumise erinevus on ebaoluline.

Keha mass on skalaarne positiivne väärtus, mis sõltub antud kehas sisalduva aine hulgast ja määrab selle inertsi mõõtme edasi liikumine.

Võrdlussüsteem - kehaga seotud koordinaatsüsteem, mille suhtes uuritakse teise keha liikumist.

inertsiaalsüsteem- süsteem, milles dünaamika esimene ja teine ​​seadus on täidetud.

Jõu impulss on vektormõõt, mis näitab jõu mõju teatud aja jooksul.

Materiaalse punkti liikumise hulk on selle liikumise vektormõõt, mis on võrdne punkti massi ja selle kiiruse vektori korrutisega.

Kineetiline energia on mehaanilise liikumise skalaarmõõt.

Elementaarne jõutöö on lõpmata väike skalaarväärtus, mis on võrdne punktitoode jõu vektor jõu rakenduspunkti lõpmatu väikese nihke vektorile.

Kineetiline energia on mehaanilise liikumise skalaarmõõt.

Materiaalse punkti kineetiline energia on skalaar

positiivne väärtus, mis võrdub poolega punkti massi ja selle kiiruse ruudu korrutisest.

Mehaanilise süsteemi kineetiline energia on aritme-

selle süsteemi kõigi materiaalsete punktide kineetiliste energiate kineetiline summa.

Jõud on kehade mehaanilise vastasmõju mõõt, mis iseloomustab selle intensiivsust ja suunda.

1.2. Loengute teemad ja nende sisu

1. jagu. Sissejuhatus dünaamikasse. Põhimõisted

klassikaline mehaanika

Teema 1. Materiaalse punkti dünaamika

Materiaalse punkti dünaamika seadused (Galileo – Newtoni seadused). Materiaalse punkti liikumise diferentsiaalvõrrandid. Kaks peamist dünaamika ülesannet materiaalse punkti jaoks. Dünaamika teise ülesande lahendus; integreerimiskonstandid ja nende määramine algtingimustest.

Viited:, lk 180-196, , lk 12-26.

Teema 2. Materjali suhtelise liikumise dünaamika

Materiaalse punkti suhteline liikumine. Punkti suhtelise liikumise diferentsiaalvõrrandid; kaasaskantavad ja Coriolise inertsjõud. Relatiivsusteooria põhimõte klassikalises mehaanikas. Suhtelise puhkuse juhtum.

Viited: , lk 180-196, , lk 127-155.

Teema 3. Masside geomeetria. Mehaanilise süsteemi massikese

Süsteemi mass. Süsteemi massikese ja selle koordinaadid.

Kirjandus:, lk 86-93, lk 264-265

Teema 4. Jäiga keha inertsimomendid

Jäiga keha inertsmomendid telje ja pooluse ümber. Inertsiraadius. Teoreem paralleeltelgede inertsmomentide kohta. Mõnede kehade aksiaalsed inertsmomendid.

Tsentrifugaalsed inertsimomendid keha asümmeetria tunnusena.

Viited: , lk 265-271, , lk 155-173.

2. jagu. Materiaalse punkti dünaamika üldteoreemid

ja mehaaniline süsteem

Teema 5. Teoreem süsteemi massikeskme liikumise kohta

Teoreem süsteemi massikeskme liikumise kohta. Süsteemi massikeskme liikumise teoreemi tagajärjed.

Viited: , lk 274-277, , lk 175-192.

Teema 6. Materiaalse punkti liikumise maht

ja mehaaniline süsteem

Materiaalse punkti ja mehaanilise süsteemi liikumishulk. Elementaarne impulss ja jõuimpulss piiratud aja jooksul. Teoreem punkti ja süsteemi impulsi muutumise kohta diferentsiaal- ja integraalkujul. Impulsi jäävuse seadus.

Kirjandus: , lk 280-284, , lk 192-207.

Teema 7. Materiaalse punkti impulsimoment

ja mehaaniline süsteem keskpunkti ja telje suhtes

Punkti impulsimoment keskpunkti ja telje ümber. Teoreem punkti nurkimpulsi muutumise kohta. Mehaanilise süsteemi kineetiline moment keskpunkti ja telje ümber.

Pöörleva jäiga keha nurkimment ümber pöörlemistelje. Teoreem süsteemi kineetilise momendi muutumise kohta. Impulsi jäävuse seadus.

Viited: , lk 292-298, , lk 207-258.

Teema 8. Jõude töö ja jõud

Elementaarne jõutöö, selle analüütiline väljendus. Jõu töö edasi lõplik tee. Raskusjõu töö, elastsusjõud. Tahkis mõjuvate sisejõudude töö summa võrdsus nulliga. Kindla telje ümber pöörlevale jäigale kehale rakendatud jõudude töö. Võimsus. Tõhusus.

Viited: , lk 208-213, , lk 280-290.

Teema 9. Materiaalse punkti kineetiline energia

ja mehaaniline süsteem

Materiaalse punkti ja mehaanilise süsteemi kineetiline energia. Jäiga keha kineetilise energia arvutamine selle erinevatel liikumisjuhtudel. Koenigi teoreem. Teoreem punkti kineetilise energia muutumise kohta diferentsiaal- ja integraalkujul. Teoreem mehaanilise süsteemi kineetilise energia muutumisest diferentsiaal- ja integraalkujul.

Viited: , lk 301-310, , lk 290-344.

Teema 10. Potentsiaalne jõuväli ja potentsiaal

Jõuvälja mõiste. Potentsiaalne jõuväli ja jõufunktsioon. Jõu töö punkti lõplikul nihkel potentsiaalses jõuväljas. Potentsiaalne energia.

Viited: , lk 317-320, , lk 344-347.

Teema 11. Jäiga keha dünaamika

Jäiga keha translatsioonilise liikumise diferentsiaalvõrrandid. Diferentsiaalvõrrand pöörlev liikumine jäik keha ümber fikseeritud telje. füüsiline pendel. Jäiga keha tasapinnalise liikumise diferentsiaalvõrrandid.

Viited: , lk 323-334, , lk 157-173.

1. jagu. Sissejuhatus dünaamikasse. Põhimõisted

klassikaline mehaanika

Dünaamika on teoreetilise mehaanika osa, mis uurib materiaalsete kehade (punktide) liikumist rakendatud jõudude mõjul.

materiaalne keha- keha, millel on mass.

Materiaalne punkt- materiaalne keha, mille punktide liikumise erinevus on ebaoluline. See võib olla kas keha, mille mõõtmed võib liikumise ajal tähelepanuta jätta, või lõplike mõõtmetega keha, kui see liigub edasi.

Osakesi nimetatakse ka materiaalseteks punktideks, milleks tahke keha mõne dünaamilise karakteristiku määramisel mõtteliselt jaotatakse. Näited materiaalsetest punktidest (joon. 1): a - Maa liikumine ümber Päikese. Maa on materiaalne punkt; b on jäiga keha translatsiooniline liikumine. Tahke- ema-

al punkt, kuna V B \u003d V A; a B = a A; c - keha pöörlemine ümber telje.

Kehaosake on materiaalne punkt.

Inerts on materiaalsete kehade omadus muuta oma liikumiskiirust rakendatud jõudude toimel kiiremini või aeglasemalt.

Keha mass on skalaarne positiivne väärtus, mis sõltub antud kehas sisalduva aine hulgast ja määrab selle inertsi mõõtme translatsioonilise liikumise ajal. Klassikalises mehaanikas on mass konstant.

Jõud - kvantitatiivne mõõt mehaaniline vastastikmõju kehade või keha (punkti) ja välja (elektriline, magnetiline jne) vahel.

Jõud on vektorsuurus, mida iseloomustavad suurusjärk, rakenduspunkt ja suund (mõjuliin) (joonis 2: A – rakenduspunkt; AB – jõu mõjujoon).

Riis. 2

Dünaamikas on koos konstantsete jõududega ka muutlikud jõud, mis võivad sõltuda ajast t, kiirusest ϑ, vahemaast r või nende suuruste kombinatsioonist, s.t.

F = const;

F = F(t);

F = F(ϑ);

F = F(r);

F = F(t, r, ϑ ) .

	Selliste jõudude näited on näidatud joonistel fig. 3: a										- kehakaal;
			(ϑ) – õhutakistusjõud;b–		T =						- tõmbejõud

elektrivedur; c − F = F (r) on keskpunktist O tõukejõud või selle külgetõmbejõud.

Võrdlussüsteem - kehaga seotud koordinaatsüsteem, mille suhtes uuritakse teise keha liikumist.

Inertsiaalsüsteem on süsteem, milles dünaamika esimene ja teine ​​seadus on täidetud. See on fikseeritud koordinaatsüsteem või süsteem, mis liigub ühtlaselt ja sirgjooneliselt.

Liikumine mehaanikas on keha asukoha muutumine ruumis ja ajas teiste kehade suhtes.

Klassikalise mehaanika ruum on kolmemõõtmeline, järgides eukleidilist geomeetriat.

Aeg on skalaarne suurus, mis voolab kõigis võrdlussüsteemides ühtemoodi.

Mõõtühikute süsteem on mõõtühikute kogum füüsikalised kogused. Kõigi mehaaniliste suuruste mõõtmiseks piisab kolmest põhiühikust: pikkuse, aja, massi või jõu ühikutest.

Mehaaniline	Mõõtmed		Märge	Mõõtmed	Märge
suurusjärk
				sentimeetrit
	kilogramm-

Kõik muud mehaaniliste suuruste mõõtühikud on nende tuletised. Kasutatakse kahte tüüpi ühikusüsteeme: rahvusvaheline süsteem SI ühikud (või väiksemad - CGS) ja ühikute tehniline süsteem - MKGSS.

Teema1. Materjali punkti dünaamika

1.1. Materiaalse punkti dünaamika seadused (Galileo-Newtoni seadused)

Esimene (inertsi) seadus.

isoleeritud välismõjud materiaalne punkt säilitab oma puhkeoleku või liigub ühtlaselt ja sirgjooneliselt, kuni rakendatud jõud sunnivad seda seisundit muutma.

Liikumist, mida punkt teeb jõudude puudumisel või tasakaalustatud jõudude süsteemi toimel, nimetatakse inertsliikumiseks.

Näiteks keha liikumine sujuvalt (hõõrdejõud on null) kulgeb.

horisontaalne pind (joonis 4: G - kehamass; N - tasapinna normaalne reaktsioon).

Kuna G = − N , siis G + N = 0.

Kui ϑ 0 ≠ 0, liigub keha sama kiirusega; kui ϑ 0 = 0 on keha puhkeasendis (ϑ 0 on algkiirus).

Teine seadus (dünaamika põhiseadus).

Punkti massi ja antud jõu mõjul saadava kiirenduse korrutis on absoluutväärtuses selle jõuga võrdne ja selle suund langeb kokku kiirenduse suunaga.

a b

Matemaatiliselt väljendab seda seadust vektori võrdsus

Kui F = konst,

a = const - punkti liikumine on ühtlane. EL-

kas a ≠ konst, α

- aegluubis (joon. 5, kuid);

a ≠ konst,

a -

– kiirendatud liikumine (joonis 5, b) m – punktmass;

kiirendusvektor;

– vektorjõud; ϑ 0 on kiiruse vektor).

Kui F = 0,a 0 = 0 = ϑ 0 = const - punkt liigub ühtlaselt ja sirgjooneliselt või ϑ 0 = 0 juures - on puhkeasendis (inertsi seadus). Teiseks

seadus lubab luua seose lähedal asuva keha massi m vahel maa pind, ja selle kaal G .G = mg , kus g on

gravitatsiooni kiirendus.

Kolmas seadus (tegevuse ja reaktsiooni võrdsuse seadus). Kaks materiaalset punkti mõjuvad üksteisele jõududega, mille suurus on võrdne ja mis on suunatud piki ühendavat sirgjoont

need punktid vastupidistes suundades.

Kuna jõud F 1 = − F 2 rakenduvad erinevad punktid, siis jõudude süsteem (F 1 , F 2 ) ei ole tasakaalus, st (F 1 , F 2 )≈ 0 (joonis 6).

Omakorda

m a = m a

- suhtumine

interakteeruvate punktide massid on pöördvõrdelised nende kiirendustega.

Neljas seadus (jõudude toime sõltumatuse seadus). Punkti võrra samaaegselt saadud kiirendus

vaid mitu jõudu, on võrdne nende kiirenduste geomeetrilise summaga, mille punkt saab iga jõu mõjul sellele eraldi.

Selgitus (joonis 7).

t a n

a 1 a kF n

Tulemuslikud jõud R (F 1 ,...F k ,...F n ) .

Kuna ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = ma n , siis

a = a 1 + ...+ a k + ...+ a n = ∑ a k, st neljas seadus on samaväärne

k = 1

jõudude liitmise reegel.

1.2. Materiaalse punkti liikumise diferentsiaalvõrrandid

Olgu materiaalses punktis korraga mitu jõudu, mille hulgas on nii konstante kui ka muutujaid.

Dünaamika teise seaduse kirjutame vormile

= ∑

(t ,

k = 1

, ϑ=

r on liikumise raadiuse vektor

punktid, siis (1.2) sisaldab r tuletisi ja on materiaalse punkti liikumise diferentsiaalvõrrand vektori kujul või materiaalse punkti dünaamika põhivõrrand.

Vektori võrdsuse (1.2) projektsioonid: - Descartes'i koordinaatide teljel (joon. 8, kuid)

max=md
					= ∑Fkx;
					k = 1
mai=md
					= ∑Fky;	(1.3)
					k = 1
maz=m					= ∑Fkz;
					k = 1

Loodusteljel (joonis 8, b)

matt				= ∑ Fk τ ,
				k = 1
				= ∑ F k n ;
				k = 1

mab = m0 = ∑ Fk b

k = 1

M t oM oa

b o peal

Võrrandid (1.3) ja (1.4) on materjali punkti liikumise diferentsiaalvõrrandid vastavalt Descartes'i koordinaattelgedel ja naturaalsetel telgedel, st looduslikud diferentsiaalvõrrandid, mida tavaliselt kasutatakse punkti kõverjooneliseks liikumiseks, kui punkti trajektoor ja selle kõverusraadius on teada.

1.3. Materiaalse punkti kaks peamist dünaamika probleemi ja nende lahendus

Esimene (otsene) ülesanne.

Teades liikumisseadust ja punkti massi, määrake punktile mõjuv jõud.

Selle probleemi lahendamiseks peate teadma punkti kiirendust. Seda tüüpi ülesannetes saab seda otse täpsustada või täpsustada punkti liikumisseadust, mille järgi seda saab määrata.

1. Seega, kui punkti liikumine on antud Descartes'i koordinaatides

x \u003d f 1 (t), y \u003d f 2 (t) ja z \u003d f 3 (t), siis määratakse kiirenduse projektsioonid

koordinaatide teljel x =		d2x			d2a			d2z		Ja siis - projekt-
F x , F y ja F z jõud nendel telgedel:
				,k ) = F F z . (1,6) 2. Kui punkt kohustab kõverjooneline liikumine ja liikumisseadus on teada s = f (t), punkti trajektoor ja selle kõverusraadius ρ, siis on mugav kasutada looduslikke telgesid ja nende telgede kiirenduse projektsioonid määratakse tuntud valemitega: Tangentsiaalne telg a τ = d ϑ = d 2 2 s – tangentsiaalne kiirendus;dt dt KoduTavaline ds 2 a n = ϑ 2 = dt on normaalkiirendus. Kiirenduse projektsioon binormaalile on null. Siis jõu projektsioonid loomulikele telgedele F=m F=m Jõu moodul ja suund määratakse valemitega: F \u003d F τ 2 + F n 2; cos( ; cos( Teine (pöörd)ülesanne. Teades punktile mõjuvaid jõude, selle massi ja esialgsed tingimused liikumist, määrake punkti liikumisseadus või mõni muu selle kinemaatiline omadus. Punkti liikumise algtingimusteks Descartes'i telgedel on punkti koordinaadid x 0, y 0, z 0 ja algkiiruse ϑ 0 projektsioon neile. teljed ϑ 0 x \u003d x 0, ϑ 0 y \u003d y 0 ja ϑ 0 z \u003d z 0 ajal, mis vastab annab punkti liikumise alguse ja võetakse võrdseks nulliga. Seda tüüpi ülesannete lahendamine taandub diferentsiaali koostamisele materiaalse punkti liikumise diferentsiaalvõrrandid (või üks võrrand) ja nende järgnev lahendus otsene integratsioon või diferentsiaalvõrrandite teooriat kasutades. Ülevaate küsimused 1. Mida dünaamika uurib? 2. Millist liikumist nimetatakse inertsiaalseks liikumiseks? 3. Millistel tingimustel jääb materiaalne punkt paigale või liigub ühtlaselt ja sirgjooneliselt? 4. Mis on materiaalse punkti dünaamika esimese põhiprobleemi olemus? Teine ülesanne? 5. Kirjutage üles materiaalse punkti liikumise loomulikud diferentsiaalvõrrandid. Ülesanded iseõppimiseks 1. Punkt massiga m = 4 kg liigub mööda horisontaalset sirgjoont kiirendusega a = 0,3 t. Määrata punktile selle liikumissuunas mõjuva jõu moodul ajahetkel t = 3 s. 2. Osa massist m = 0,5 kg libiseb aluselt alla. Millise nurga all horisontaaltasandi suhtes peaks kandik asuma nii, et osa liiguks kiirendusega a = 2 m / s 2? Nurga ekspress kraadides. 3. Punkt massiga m = 14 kg liigub mööda Ox-telge kiirendusega a x = 2 t . Määrata punktile liikumissuunas mõjuva jõu moodul ajahetkel t = 5 s.

(MEHAANILISED SÜSTEEMID) - IV variant

1. Materiaalse punkti dünaamika põhivõrrand, nagu teada, on väljendatud võrrandiga . Liikumise diferentsiaalvõrrandid suvalised punktid mittevaba mehaanilise süsteemi kahe jõudude jagamise viisi järgi saab kirjutada kahel kujul:

(1) , kus k=1, 2, 3, … , n on materiaalse süsteemi punktide arv.

(2)

kus on k-nda punkti mass; - k-nda punkti raadiuse vektor, - antud k-ndale punktile mõjuv (aktiiv)jõud või kõigi k-ndale punktile mõjuvate aktiivjõudude resultant. - k-ndale punktile mõjuvate sidemete reaktsioonijõudude resultant; - k-ndale punktile mõjuvate sisejõudude resultant; - k-ndale punktile mõjuvate välisjõudude resultant.

Võrrandeid (1) ja (2) saab kasutada nii esimese kui ka teise dünaamika ülesande lahendamiseks. Kuid süsteemi teise dünaamika probleemi lahendamine muutub väga keeruliseks mitte ainult matemaatiline punkt nägemus, aga ka seetõttu, et seisame silmitsi põhiraskustega. Need seisnevad selles, et nii süsteemi (1) kui ka süsteemi (2) puhul on võrrandite arv märkimisväärne vähem kui arv teadmata.

Seega, kui kasutame (1), siis on dünaamika teise (pöörd)ülesande jaoks tuntud ja , tundmatuteks aga ja . Vektorvõrrandid on " n", ja tundmatu - "2n".

Kui lähtuda võrrandisüsteemist (2), siis teadaolev ja osa välisjõududest . Miks osa? Fakt on see, et välisjõudude arv sisaldab väliseid reaktsioone seoseid, mis on tundmatud. Lisaks tuleb ka tundmatuid.

Seega on nii süsteem (1) kui ka süsteem (2) AVATUD. Peame lisama võrrandeid, võttes arvesse suhete võrrandeid, ja võib-olla peame siiski kehtestama suhetele endile mõned piirangud. Mida teha?

Kui lähtume punktist (1), siis saame järgida esimest tüüpi Lagrange'i võrrandite koostamise teed. Kuid see viis ei ole ratsionaalne, sest lihtsam ülesanne(vähem vabadusastmeid), seda keerulisem on seda matemaatika seisukohalt lahendada.

Seejärel pöörame tähelepanu süsteemile (2), kus - on alati tundmatud. Esimene samm süsteemi lahendamisel on nende tundmatute kõrvaldamine. Tuleb meeles pidada, et reeglina ei huvita meid süsteemi liikumise ajal sisemised jõud ehk süsteemi liikumisel pole vaja teada, kuidas süsteemi iga punkt liigub, vaid piisab, et teada, kuidas süsteem tervikuna liigub.

Seega, kui erinevaid viise süsteemist välja jätma (2) tundmatud jõud, siis saame mõned seosed, st mõned Üldised omadused süsteemi jaoks, mille tundmine võimaldab hinnata, kuidas süsteem üldiselt liigub. Neid tunnuseid tutvustatakse kasutades nn dünaamika üldteoreemid. Selliseid teoreeme on neli:

1. Teoreem umbes mehaanilise süsteemi massikeskme liikumine;

2. Teoreem umbes mehaanilise süsteemi impulsi muutus;

3. Teoreem umbes mehaanilise süsteemi nurkimpulsi muutus;

4. Teoreem umbes mehaanilise süsteemi kineetilise energia muutus.